Prediction of epilepsy based on electroencephalogram (EEG) signals is a rapidly evolving field. Previous studies have traditionally applied 1D processing to the entire EEG signal. However, we have adopted the Gram Matrix method to transform the signals into a 3D representation, enabling modeling of signal relationships across dimensions while preserving the temporal dependencies of the one-dimensional signals. Additionally, we observed an imbalance between local and global signals within the EEG data. Therefore, we introduced multi-level feature extraction, utilizing coattention for capturing global signal characteristics and an inception structure for processing local signals, achieving multigranular feature extraction. Our experiments on the BONN dataset demonstrate that for the most challenging five-class classification task, GRC-Net achieved an accuracy of 93.66%, outperforming existing methods.
EEG signals are indispensable for analyzing brain activity, understanding brain function, and exploring cognitive mechanisms. Therefore, effective processing of EEG signals is crucial in various domains such as speech recognition [5], emotion detection [20], and diagnosing diseases related to brain function [3] [18] [8]. While significant progress has been made in using one-dimensional EEG signal processing for predicting epileptic seizures, there is a growing interest in transforming one-dimensional EEG signal sequences into two-dimensional images to extract deep features from multiple channels for prediction.
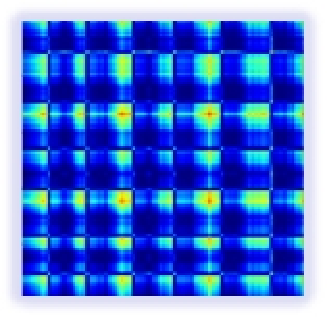
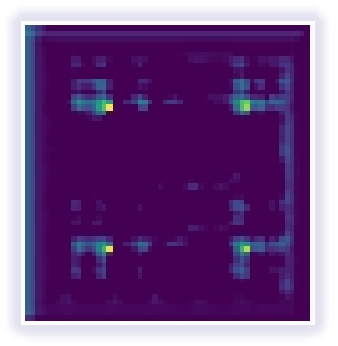
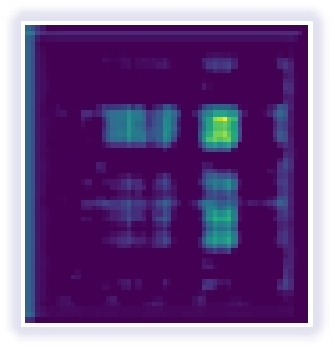
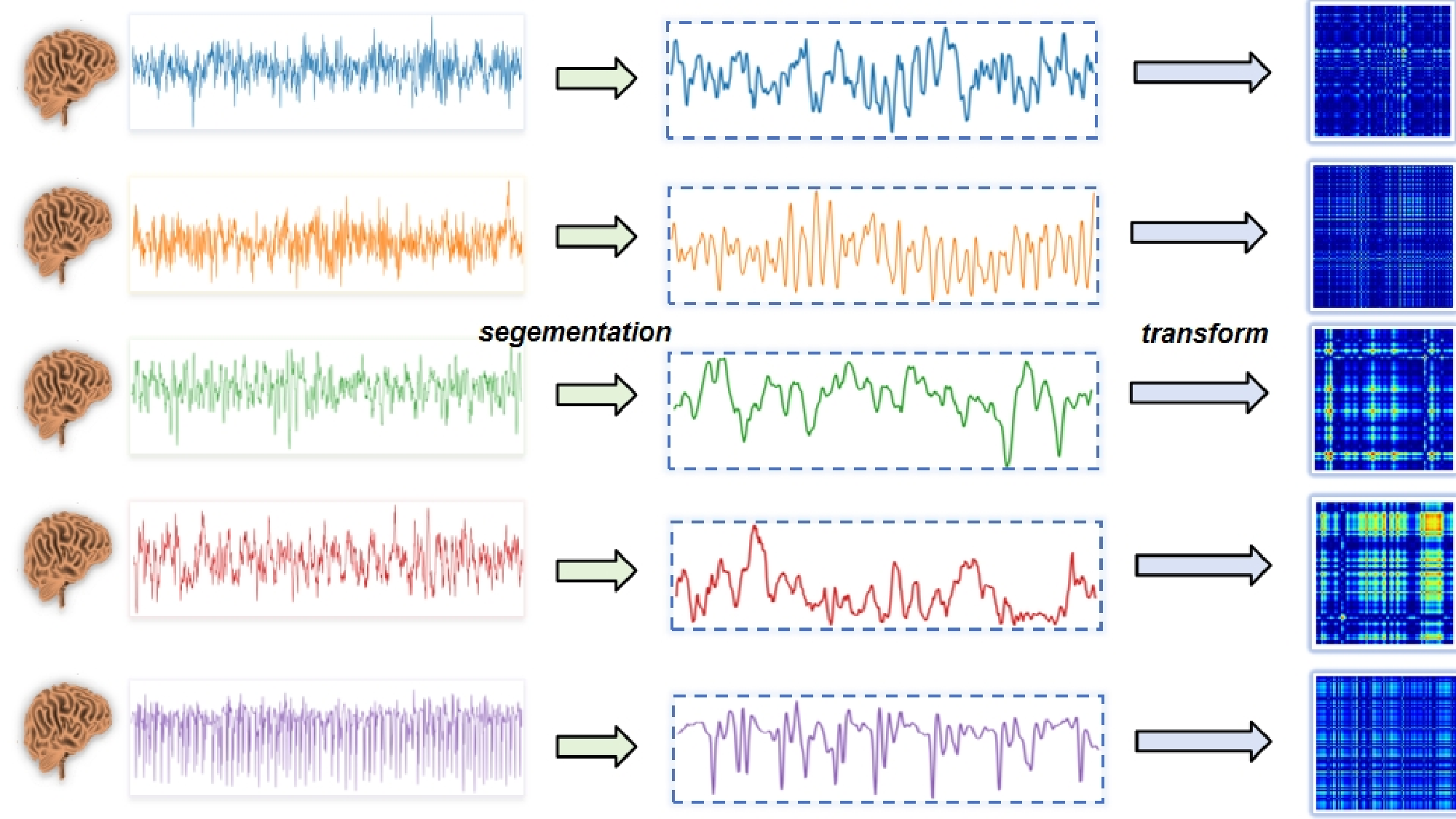
Fig. 1 In the first column of images, the original onedimensional EEG signals from the BoNN dataset are displayed. In the second column, the signals underwent resampling using sliding windows with specified strides. In the third column, the resampled signals were transformed into feature maps using the Gram Matrix method for standardization, while preserving temporal dependencies.
With the emergence of EEG datasets for epileptic analysis, such as BONN, several methods have been proposed for seizure prediction. Although these works identified some issues in using EEG signal processing for seizure prediction, their models addressed them in a rudimentary manner.
Previous studies on EEG signal prediction have mostly relied on one-dimensional time series or simply utilized time series to plot corresponding curves. However, we argue that due to the unidirectional correlation in the horizontal and vertical directions of one-dimensional signals, they may not fully capture the underlying relationships in the data. Moreover, the linear operations on one-dimensional sequences fail to discriminate between the meaningful information in the signal and Gaussian noise. Therefore, the utilization of one-dimensional signals alone for plotting corresponding images may lead to a loss of temporal dependencies in the data, resulting in information loss.
Furthermore,traditional CNN-based models lack the ability to model long-range dependencies and perceptions due to their focus on modeling local information. While some researchers have recognized this issue and attempted to incorporate attention mechanisms in models for long-range global modeling, the original Self-Attention structure in Transformers calculates attention matrices based on interactions between queries and keys, thereby overlooking the relationships between adjacent keys. This limitation still hampers the effectiveness of global modeling.
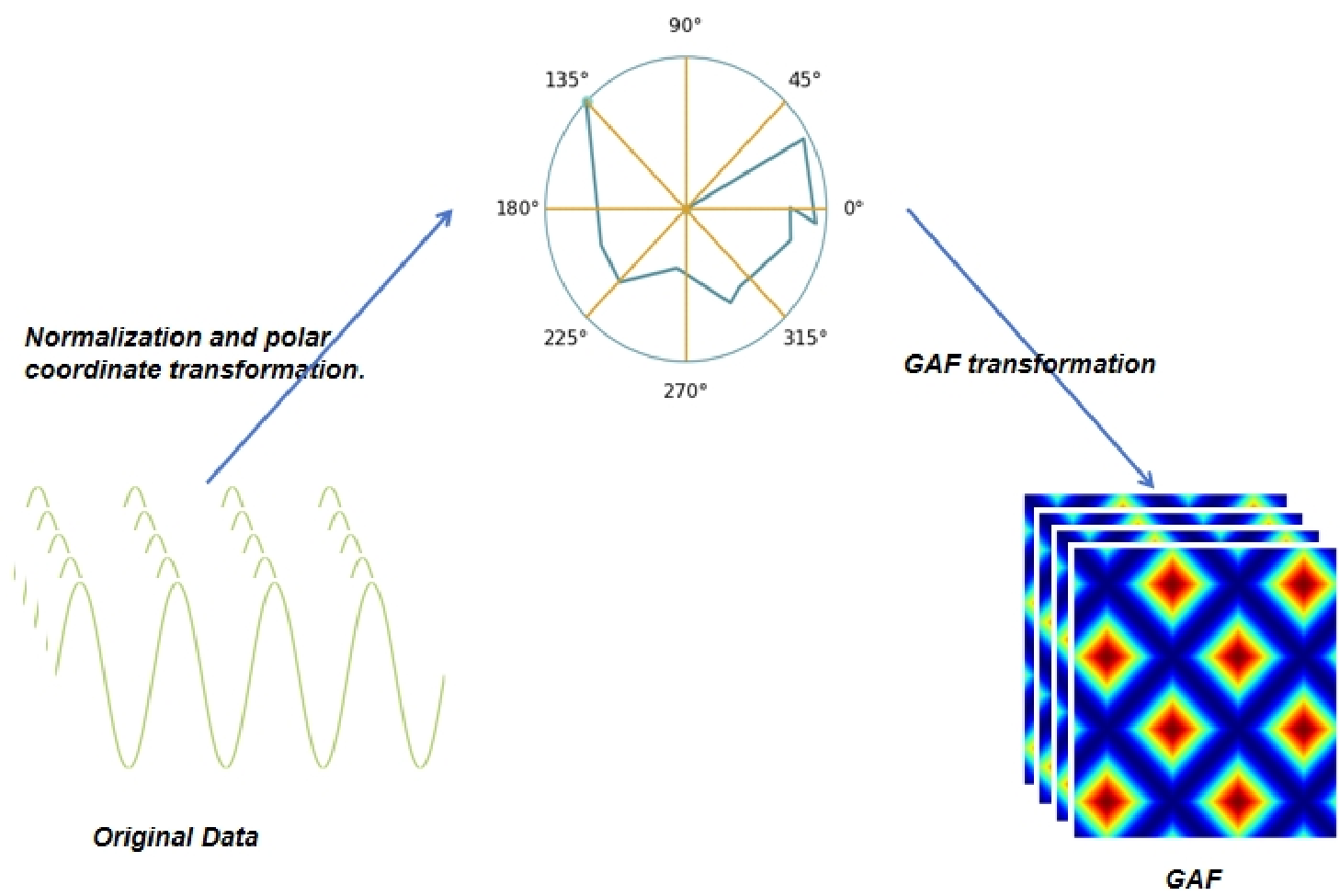
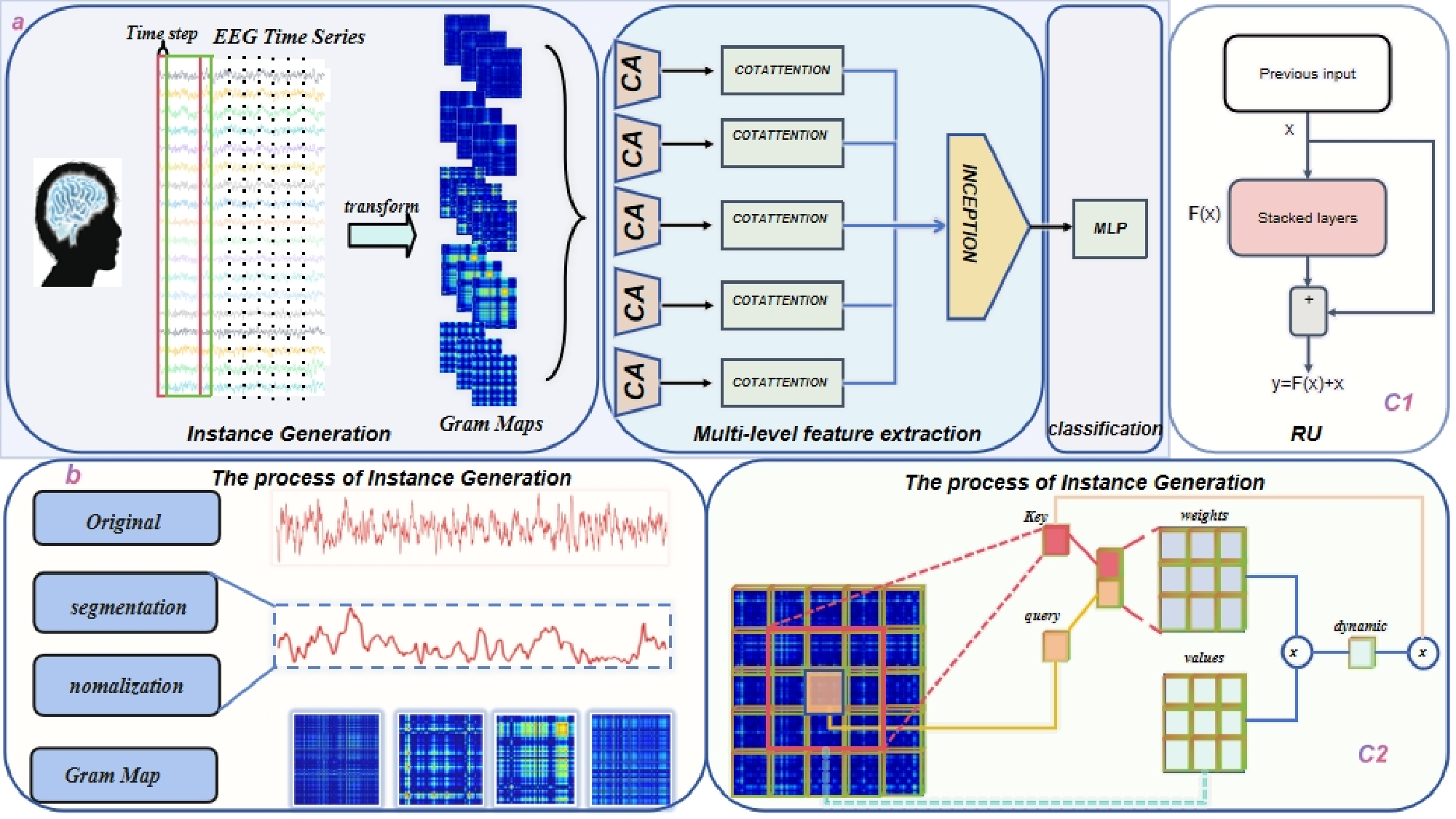
To tackle the primary concern, we propose a technique that converts the original EEG signal based on Gramian Angular Feild(GAF). The GAF method is employed to map one-dimensional EEG signal data onto a polar coordinate system, where as the sequence progresses over time, the corresponding values are distorted between different angular points on the circle. This transformation generates a bidirectional sequence that retains all information without any loss and preserves temporal dependencies. Specifically,as shown in Fig1,we segment the raw data using a sliding window with a specific step size, followed by normalization and signal transformation. Furthermore, to fully leverage the contextual information of the key, we utilize Cotattention. Initially, a 3x3 convolution is applied to the key to model static contextual information. Subsequently, the concatenated output of the query and the modeled key with context information undergoes self-attention using two consecutive 1x1 convolutions to generate dynamic context. The static and dynamic contextual information is ultimately fused to produce the output. Overall,our contributions can be summarized as follows.
- We utilized the Gram Matrix to perform a twodimensional transformation on the one-dimensional signal, thereby avoiding the loss of temporal dependency information during the conversion process. 2. We employ the ResNet with the Cotattention mechanism, we enhanced the internal static contextual information within the attention mechanism, enabling the modeling of both local and global information. Recently, there has been a proliferation in approaches based on Short-Time Fourier Transform for extracting spatial and temporal information from EEG signals. For instance, Zhou et al. [30] proposed a method for automatic seizure detection called Residual-based Inception with Hybrid-Attention Network (RIHANet). This method initially utilizes Empirical Mode Decomposition and Short-Time Fourier Transform (EMD-STFT) for data processing to enhance the quality of time-frequency representation of EEG signals. Lu et al. introduced the CBAM-3D CNN-LSTM model [16], which employs Short-Time Fourier Transform to extract time-frequency planes from time-domain signals for epilepsy classification. Additionally, Kantipudi et al. [12] proposed an improved GBSO-TAENN model, which employs Finite Linear Haar Wavelet Filtering (FLHF) technique for filtering input signals, and utilizes Grasshopper Biologically Swarm Optimization (GBSO) technique to select optimal features by computing the best fitness value, and employs Time-Activated Expandable Neural Network (TAENN) mechanism for classifying EEG signals.
Based on the above survey, most previous studies have been based on extracting features from the onedimensional pulse wave signal and passing these features to a classification model. However, the extracted features did not preserve the temporal dependency of the pulse wave signal, resulting in lower accuracy. Other studies [17] addressed this issue by directly passing the pulse wave signal to an LSTM network. However, LSTM networks have a long training time. While some have converted one-dimensional signals into two-dimensional signals and enhanced performance using networks combined with attention mechanisms, they did not avoid the loss of temporal dependency and the basic attention architecture had limited capabilities for global modeling. In contrast, we mapped the EEG signal to a twodimensional image using the GM, preserving the temporal dependency of the EEG signal. Additionally, leveraging cotattention in the GRC-Net enhanced the ability for global modeling, fundamentally addressing these challenges.
The GRC-Net proposed by us mainly consists of four steps: instance generation, feature extraction, feature aggregation, and classification. In the instance generation step, through the transformation by the GAF, the one-dimensional signal is converted into a two-dimensional image while preserving temporal dependency features.
In the feature extraction stage, the GRC-Net, based on the ResNet architecture, leverages spatial locality and translational equivariance to learn short-range temporal relationships and models long-range temporal relationships through cotattention mechanism. Feature aggregation utilizes the Inception architecture to avoid gradient explosion and classifies the signals through MLP. An overview of the GRC-Net framework used is depicted in Figure 2.
To generate multiple instances from a single record, we adopted a sliding window approach. A window size of 512 and a stride of 128 (with 25% overlap) were selected. Each signal of length 4097 in the training set was divided into 57 sub-signals, with each sub-signal considered as an independent signal instance (SI). Consequently, a total of 5700 instances were created for each class.We partitioned the available signal into nonoverlapping training and testing sets, each accounting for 90% and 10% of the total signal, respectively.
Given a one-dimensional signal instanceSI = {s 1 , . . . , s 57 }, where the time series consists of 57 timestamps t and corresponding actual observed values s, we scale the time series to the interval [-1, 1] using the Min-Max scaler, as shown in Equation ( 1):
Fig. 3 The process of generating GAF involves mapping onedimensional EEG signal data onto polar coordinates, where the sequence evolves over time causing the values to distort between different focal points on the circle, akin to ripples in water. This polar coordinate-based representation offers a novel approach to understanding one-dimensional signals.
Subsequently, by employing angular perspective, GAF is generated by altering spatial dimensions, utilizing angular relationships to uncover hidden characteristics of EEG signals, and the resulting coefficient output makes it easy to distinguish valuable information from Gaussian noise.
Subsequently, we map the scaled sequence values s i to angular values θ and the times are mapped to radius r, allowing the scaled time series to be represented in polar coordinates, as shown in Equation (2,3):
Here, t represents the timestamp, and the interval [0, 1] is divided into N equal parts to regularize the span of the polar coordinates. The encoding mapping in Equation ( 2) has two important properties. Firstly, it is bijective, as cos(Θ) is monotonically decreasing in Θ ∈ [0, π], meaning that for a given time series, there is a unique corresponding value in polar coordinates, and its inverse mapping is also unique. Secondly, unlike Cartesian coordinates, polar coordinates maintain the absolute time relationship.
After mapping the one-dimensional signal to polar coordinates, we can easily utilize the angular perspective to identify temporal correlations within different time intervals by considering the trigonometric functions between each point. The Gramian Angular Field (GAF) is defined as:
where I is a unit row vector [1, 1, . . . , 1], and θ i (i = 1, . . . , n) is the angle between two vectors.After mapping the one-dimensional time series to polar coordinates, each time series of each step length is treated as a one-dimensional metric space. Since GAF is more sparse, the inner product is redefined in Cartesian coordinates as
relative to the traditional inner product, the new inner product includes a penalty term, making it easier to distinguish the required output from Gaussian noise. G is a Gram matrix defined as:
The process of generating GAF is illustrated in the Fig3. GAF incorporates temporal correlations, where the sum of G (i,j | |, i-j=k) over time intervals k is superimposed, and interpreted in terms of relative correlations. When k = 0, the main diagonal of G i,i consists of the raw values of the scaled time series. Utilizing the main diagonal, high-level features learned by deep neural networks can be used to approximate the reconstruction of the time series.
As mentioned earlier, there is an imbalance in the longrange and short-range temporal relationships in EEG signals. Due to the basic architecture of GRC-Net being based on the ResNet architecture, its inherent spatial locality and translational invariance enhance the local modeling capability, thereby improving the ability to learn short-range temporal relationships. To model global information, we introduce the concept of hierarchical feature extraction to address the modeling of long-range temporal relationships.
The first step involves using Coattention to capture the long-range temporal relationships. For a given input X in ∈ R H•W •3 , we first use shallow feature extraction to increase the feature dimension, learn more feature information, and obtain feature maps X ′ (R H•W •3 ). Subsequently, we pass X ′ into the CoT layer, where coattention is employed to further learn contextual key features, enabling global modeling.
Faced with the input feature maps, the CoT layer extracts static and dynamic context features in parallel. The CoT layer learns static context keys by encoding input keys using a 3x3 convolutional layer.
The static context ensures the local features learned by taking advantage of the spatial locality and translational invariance of the convolution. In the dynamic context branch, the relationship between each key and query is used to fuse them and obtain the attention weight matrix between the key and query.
This matrix is then multiplied with the value to achieve a dynamic contextual representation of the input. This process fully integrates the information provided by the keys, queries, and values, enabling dynamic exploration of the global context.
Finally, the dynamic and static contexts are fused to facilitate self-attention learning. This design focuses more on learning rich contexts between adjacent keys than the traditional self-attention mechanism. Simultaneously, this enables the dynamic context to enhance the learning of visual representations under the guidance of the static context, effectively mitigating the limiting effect of the convolutional layer’s receptive field on learning global features.
4 Experiment
The EEG signals dataset originates from Bonn University [2], comprising data from five healthy individuals and five epileptic patients, constituting five subsets denoted as F, S, N, Z, and O. Each subset includes 100 data segments, each lasting for 23.6 seconds with 4097 data points. The signal resolution is 12 bits, with a sampling frequency of 173.61 Hz. The dataset details are summarized in the table 1.
Previous studies have explored various combinations of predictions on the BoNN dataset, such as binary, ternary, and quaternary classification tasks, each with different internal configurations. However, there has been limited targeted prediction specifically for the five-class classification task due to its inherent difficulty. Therefore, we compared the performance of our proposed GRC-Net on the BoNN dataset with other models. Table 1 The comparison highlights the significant advantages of our approach.
Although our research has achieved excellent performance, there are still research gaps that need to be addressed in future studies. Firstly, we focused on the fiveclass classification problem, which, while more complex compared to binary and ternary classification tasks, re-quires further experimental validation. Secondly, our experiments primarily concentrated on the BoNN dataset, without performance validation on other datasets. Lastly, the Gram Matrix (GM) algorithm can be divided into two transformation methods: summation and difference. This study only utilized the summation method and did not explore the effects of signal transformation using the difference method.
In Through our research and methodologies, we can enhance the diagnostic accuracy and treatment effectiveness of epilepsy. Our work provides valuable insights and directions for future epilepsy research and clinical practices, potentially offering improved medical services and care for patients. With ongoing technological advancements and deeper research, we believe that we can continuously refine diagnostic and treatment approaches for epilepsy, ultimately delivering a brighter future for patients.
Finally, we removed the inception architecture, noting that the model’s input remained two-dimensional images without RM processing. We replaced the original
comparison between our proposed model and other models Model Rec(%)↑ Acc(%)↑ Prec(%)↑ F1(%)↑ Dataset inception architecture with the VGG architecture, aiming to maintain the concept of hierarchical feature extraction. It is noteworthy that the RU architecture excels in extracting local features more effectively.
This content is AI-processed based on open access ArXiv data.