MergeRec Model Merging for Data-Isolated Cross-Domain Sequential Recommendation
📝 Original Paper Info
- Title: MergeRec Model Merging for Data-Isolated Cross-Domain Sequential Recommendation- ArXiv ID: 2601.01753
- Date: 2026-01-05
- Authors: Hyunsoo Kim, Jaewan Moon, Seongmin Park, Jongwuk Lee
📝 Abstract
Modern recommender systems trained on domain-specific data often struggle to generalize across multiple domains. Cross-domain sequential recommendation has emerged as a promising research direction to address this challenge; however, existing approaches face fundamental limitations, such as reliance on overlapping users or items across domains, or unrealistic assumptions that ignore privacy constraints. In this work, we propose a new framework, MergeRec, based on model merging under a new and realistic problem setting termed data-isolated cross-domain sequential recommendation, where raw user interaction data cannot be shared across domains. MergeRec consists of three key components: (1) merging initialization, (2) pseudo-user data construction, and (3) collaborative merging optimization. First, we initialize a merged model using training-free merging techniques. Next, we construct pseudo-user data by treating each item as a virtual sequence in each domain, enabling the synthesis of meaningful training samples without relying on real user interactions. Finally, we optimize domain-specific merging weights through a joint objective that combines a recommendation loss, which encourages the merged model to identify relevant items, and a distillation loss, which transfers collaborative filtering signals from the fine-tuned source models. Extensive experiments demonstrate that MergeRec not only preserves the strengths of the original models but also significantly enhances generalizability to unseen domains. Compared to conventional model merging methods, MergeRec consistently achieves superior performance, with average improvements of up to 17.21% in Recall@10, highlighting the potential of model merging as a scalable and effective approach for building universal recommender systems. The source code is available at https://github.com/DIALLab-SKKU/MergeRec.💡 Summary & Analysis
**1. Thorough Empirical Analysis** - The study reveals that entropy-based optimization, effective in computer vision and natural language processing, fundamentally fails to capture multi-intent behavioral patterns inherent in recommendation systems. This is akin to trying to experience diverse flavors by eating only one type of food.2. The First Model Merging Framework for Recommendation Systems
- MergeRec introduces a task vector-based model merging framework that allows effective recommendations without personalized data, similar to friends sharing their unique traits while playing together.
3. Comprehensive Evaluation
- Extensive experiments demonstrate MergeRec’s superior performance compared to existing methods and its ability to generalize effectively to unseen domains, much like a chef adapting to various types of cuisine.
📄 Full Paper Content (ArXiv Source)
<ccs2012> <concept> <concept_id>10002951.10003317.10003347.10003350</concept_id> <concept_desc>Information systems Recommender systems</concept_desc> <concept_significance>500</concept_significance> </concept> </ccs2012>
Introduction

Sequential recommendation (SR) aims to predict the next items a user is likely to prefer based on their interaction history. Recent neural SR models employ various architectures to effectively capture sequential dependencies among items. However, they still face inherent challenges such as the cold-start and data sparsity problems , which limit their generalizability and overall performance.
Cross-domain sequential recommendation (CDSR) has emerged as a promising research direction . CDSR aims to improve recommendation accuracy by either jointly training models across multiple domains or by transferring knowledge from data-rich domains to sparser ones . However, existing CDSR works face three fundamental limitations. (1) User/Item overlap dependency: knowledge transfer typically relies on the presence of overlapping users or items across domains. However, such overlap is extremely limited in practice. We observe that only 16 users and 0 items are shared across eight Amazon domains, reflecting the real-world nature of independently operated domains; (2) Data isolation: in real-world scenarios, access to raw user data is often restricted due to organizational boundaries or privacy regulations . User logs contain sensitive information and cannot be shared across domains due to privacy restrictions, making domain-specific training data inaccessible; (3) Low scalability: joint training across multiple domains incurs substantial computational overhead, making it impractical for large-scale deployment. Consequently, most prior work has been limited to integration of only two or three domains, leaving scalable multi-domain integration largely unresolved.
We suggest that model merging offers an effective alternative for building universal recommender systems. Model merging integrates fine-tuned parameters from multiple domain- or task-specific models into a single unified model. This paradigm provides several advantages that directly address the key limitations of CDSR: (1) It eliminates the need for overlapping users or items across domains; (2) It naturally preserves user privacy, as only model parameters, not sensitive interaction data, are required; (3) It achieves high scalability by avoiding the computational burden of cross-domain joint training.
In this paper, we explore the feasibility of applying model merging to CDSR under a new, realistic problem setting termed data-isolated CDSR. This setting is motivated by practical real-world constraints, where user interaction data can be used only to train domain-specific models and cannot be shared across domains or accessed afterward. Unlike conventional CDSR, which often relies on strong and impractical assumptions (i.e., overlapping users or items), data-isolated CDSR allows domains to be disjoint. Moreover, while privacy-preserving CDSR typically requires access to domain-specific interaction data during model optimization, data-isolated CDSR constructs a universal cross-domain recommender system without accessing any user interaction data, thereby providing a stronger guarantee of user privacy.
Under this setting, however, directly applying existing model merging methods is non-trivial for two key reasons. First, since interaction data are not shared across domains, test-time adaptation schemes, commonly used in the model merging paradigm to optimize merging weights, cannot be applied. Second, even if test data were accessible, leveraging test sequences in sequential recommendation would violate the core assumptions of model merging. While the model merging paradigm explicitly prohibits using training data, these assumptions do not hold in sequential recommender systems. In such systems, test sequences are not independent of the training data but are generated from the same evolving user behavior. Thus, using test-time user interaction sequences during the merging process would inevitably expose training information (Figure 1). Consequently, leveraging test data for model merging is fundamentally incompatible with the data-isolated CDSR setting.
To this end, we propose MergeRec, a novel framework tailored for data-isolated CDSR. MergeRec comprises three key components: (1) merging initialization, (2) pseudo-user data construction, and (3) collaborative merging optimization. First, we synthesize an initial merged model using training-free merging methods based on task vectors, defined as the parameter difference between a fine-tuned model and its corresponding pre-trained model, to capture domain-specific knowledge . Next, we construct pseudo-user data by treating each item in every domain as an individual sequence. Despite its simplicity, MergeRec enables the construction of meaningful samples for merging domains without relying on real user data, effectively simulating cold-start users across domains. Finally, we refine domain-specific merging weights through a recommendation-oriented merging objective.
To design an effective objective function for merging recommender systems, we argue that an ideal merged model should satisfy two fundamental requirements. First, it should be able to decode users’ multiple intents, which are often reflected in domain-specific sequential patterns. Second, the unified model should exhibit strong ranking ability, accurately prioritizing items with the highest click probability within each domain context. We point out that existing adaptive merging methods, i.e., AdaMerging, address only the latter aspect and are therefore insufficient for merging recommender systems (Section 3).
To overcome this limitation, we propose a joint objective that combines: (1) a distillation loss, which leverages the prediction distributions of fine-tuned models as soft labels, and (2) a recommendation loss, which treats the top-1 predicted item from each fine-tuned model for a pseudo-user in its corresponding domain as a hard label. The distillation loss transfers collaborative filtering (CF) signals from the fine-tuned models to the merged model, and the recommendation loss guides the merged model to accurately rank items according to their likelihood of being clicked.
Extensive experiments demonstrate that MergeRec not only preserves the strengths of the individual source models but also generalizes effectively to unseen domains. Compared with existing merging methods and strong baselines, including fine-tuned and joint learning models, MergeRec consistently achieves superior performance. Specifically, MergeRec outperforms joint learning and AdaMerging by average gains of 8.72% and 17.21% on Recall@10, respectively. These results highlight that model merging can be a scalable and efficient paradigm for building universal recommender systems.
Our contribution can be summarized as follows:
-
Thorough empirical analysis: We provide empirical evidence demonstrating that entropy-based optimization, though effective in computer vision and natural language processing, fundamentally fails to capture the multi-intent behavioral patterns inherent in recommender systems.
-
The first model merging framework for recommender systems: We propose MergeRec, a task vector-based model merging framework tailored for recommender systems. MergeRec comprises three key components: (1) training-free merging initialization, (2) privacy-preserving pseudo-user data construction, and (3) a recommendation-oriented merging objective.
-
Comprehensive evaluation: Through extensive experiments across eight Amazon benchmark datasets and four backbone architectures, we demonstrate that MergeRec consistently outperforms existing model merging baselines. Notably, MergeRec exhibits superior generalizability to unseen domains and robust performance under data-scarce conditions.
Preliminaries
Cross-domain Sequential Recommendation
Let $`\mathcal{D}=\{D_1, D_2, ..., D_K\}`$ denote the set of all recommendation domains, where $`D_k`$ denotes the $`k`$-th domain. Each domain $`D_k`$ consists of a set of items $`\mathcal{I}_k`$ and users $`\mathcal{U}_k`$. For an arbitrary user $`u \in \mathcal{U}_k`$, the interaction history is represented as an ordered sequence of items based on timestamps: $`u = \left[ i_{1},\, i_{2},\, \ldots,\, i_{|u|} \right]`$, where $`|u|`$ denotes the number of interactions of user $`u`$. CDSR models aim to predict and rank items in $`\mathcal{I}_k`$ by estimating the probability that user $`u`$ will interact with each item next, conditioned on the user’s past interactions:
\begin{equation}
\mathbf{\theta}^* = \arg\max_\mathbf{\theta} P \bigl(i = i_{|u|+1} \mid u, \mathbf{\theta}\bigr),
\end{equation}where $`\mathbf{\theta}`$ denotes the parameters of the CDSR model.
Text-based Sequential Recommendation
Text-based SR leverages pre-trained language models (PLMs) to encode item-level textual information. By representing both users and items through textual descriptions, this approach enables recommendations for previously unseen (i.e., cold-start) items.
Formally, the textual representation of an item $`t_i`$ is constructed from its attribute descriptions (e.g., title, brand, and category). The textual representation of a user $`t_u`$ is defined as the concatenation of the textual representations of all items the user has interacted with:
\begin{equation}
t_{u} = \left[ t_{i_{1}};\, t_{i_{2}};\, \ldots;\, t_{i_{|u|}} \right],
\end{equation}where $`;`$ denotes the concatenation operator.
Let $`f(\cdot \mid \mathbf{\theta_k})`$ denote a PLM-based encoder with parameters $`\mathbf{\theta}_k \in \mathbb{R}^P`$ fine-tuned on domain $`D_k`$, where $`P`$ is the total number of model parameters. Given the textual inputs $`t_u`$ and $`t_i`$, the encoder produces a user representation vector $`\mathbf{r}_u \in \mathbb{R}^d`$ and an item representation vector $`\mathbf{r}_i \in \mathbb{R}^d`$ by extracting the final hidden state representations:
\begin{equation}
\mathbf{r}_u = f\left( t_u \mid \mathbf{\theta}_k \right), ~~ \mathbf{r}_i = f\left( t_i \mid \mathbf{\theta}_k \right),
\end{equation}where $`d`$ denotes the dimension of the final hidden representations.
The recommendation score $`\hat{y}_{ui}`$ between user $`u`$ and item $`i`$ is computed as the cosine similarity between their representation vectors:
\begin{equation}
\hat{y}_{ui} = \cos(\mathbf{r}_u, \mathbf{r}_i).
\end{equation}The model parameters $`\mathbf{\theta}_k`$ are optimized using a cross-entropy objective:
\begin{equation}
\mathbf{\theta}_k^{*} = \arg\min_{\mathbf{\theta}_k} \, \sum_{u \in \mathcal{U}_k} \left( \log{\hat{y}_{k, ui^+}} + \sum_{i^- \in \mathcal{I}_k} \log{(1 - \hat{y}_{k, ui^-})} \right),
\end{equation}where $`i^+`$ denotes the next item in the user sequence, and $`i^-`$ represents negative items in the domain $`\mathcal{I}_k`$ excluding $`i^+`$. Note that the domain-specific parameters $`\mathbf{\theta}_k`$ are initialized from the pre-trained base model parameters $`\mathbf{\theta}_{base} \in \mathbb{R}^P`$.
Proposed Method: MergeRec
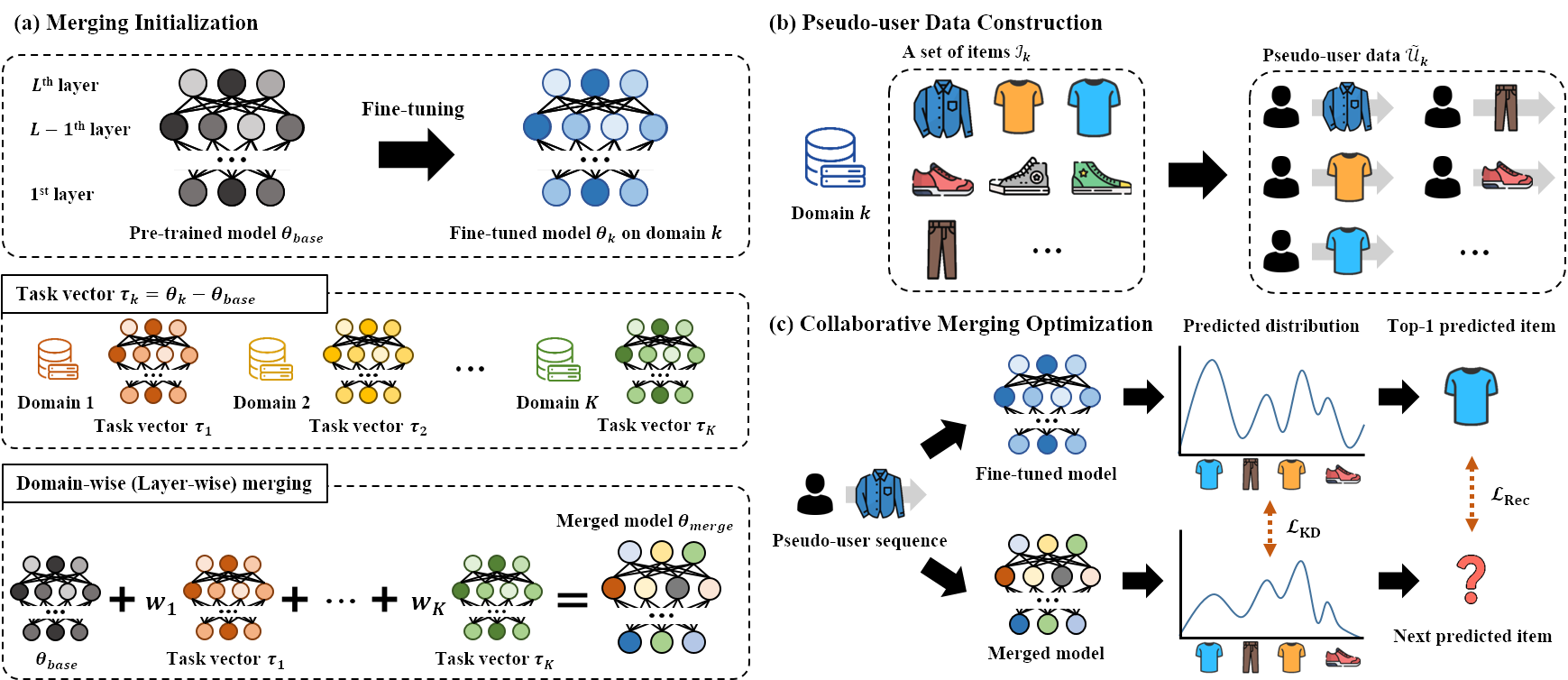
As illustrated in Figure 2, we design the MergeRec framework to address the practical constraint that no interaction data can be shared across domains, termed data-isolated CDSR. MergeRec consists of three key components: (1) Merging Initialization, which consolidates multiple domain-specific fine-tuned models into a single unified model that integrates knowledge across domains; (2) Pseudo-user Data Construction, which synthesizes meaningful merging samples without relying on real user interactions; and (3) Collaborative Merging Optimization, which jointly optimizes a recommendation loss and a knowledge distillation loss to enable recommendation-aware parameter integration. Through this design, MergeRec effectively preserves domain-specific CF signals while ensuring strong generalizability across multiple domains.
Data-isolated CDSR
We formalize a new and realistic setting for cross-domain sequential recommendation, termed data-isolated CDSR. As shown in Table [tab:research_categorization], this setting is characterized by two key requirements: (i) it assumes no overlap across domains, (ii) it prohibits access to user interaction data during cross-domain model construction, in contrast to conventional CDSR. Under data-isolated CDSR, domains may be entirely disjoint in both users and items (e.g., $`\mathcal{U}_k \cap \mathcal{U}_{k'}=\emptyset`$ and $`\mathcal{I}_k \cap \mathcal{I}_{k'}=\emptyset`$ for $`k\neq k'`$), reflecting real-world environments that are independently operated. Moreover, this setting enforces a strict data isolation constraint: raw interaction logs are accessible only within each domain for training domain-specific models and cannot be shared across domains. Consequently, a cross-domain recommender system must be constructed without accessing any domain-specific interaction data. Instead, we assume access only to $`K`$ domain-specific fine-tuned models $`\{\theta_k\}_{k=1}^K`$, while the datasets used to train these models remain completely inaccessible. The goal of data-isolated CDSR is to produce a single universal sequential recommender system that can operate across multiple domains.
Merging Initialization
Problem definition. Let $`f_{\theta_k}(u_k) \rightarrow \hat{y}_k`$ denote an SR model fine-tuned on the private data of domain $`D_k = \{\mathcal{U}_k, \mathcal{I}_k\}`$. For an arbitrary user interaction sequence $`u_k \in \mathcal{U}_k`$, the model outputs a click probability vector $`\hat{\mathbf{y}}_k \in \mathbb{R}^{|\mathcal{I}_k|}`$ over candidate items. Without loss of generality, we assume that the model parameters are composed of $`L`$ layers, i.e., $`\theta = \left\{ \theta^1, \theta^2, ..., \theta^L \right\}`$.
Task vector. A task vector represents the parameter shift required to adapt a pre-trained model to a specific downstream task . In our context, each task corresponds to recommendation within a specific domain. Accordingly, the task vector captures domain-specific knowledge, enabling a pre-trained model to specialize in that domain.
Formally, the task vector $`\boldsymbol{\tau}_k \in \mathbb{R}^P`$ for domain $`k`$ is defined as the difference between the parameters of the fine-tuned model $`\mathbf{\theta}_k`$ and those of the original pre-trained base model $`\mathbf{\theta}_{base}`$:
\begin{equation}
\boldsymbol{\tau}_k = \mathbf{\theta}_k - \mathbf{\theta}_{base}.
\end{equation}where $`P`$ denotes the total number of model parameters.
Domain-wise merging. Domain-wise merging integrates multiple fine-tuned models by combining their task vectors, each weighted by a domain-specific scalar $`w_k`$, and adding them to the base model parameters. The merging weights $`\mathbf{w}=\{w_1, ..., w_K\}`$ can be either uniformly assigned or adaptively learned to reflect domain characteristics . Intuitively, domains containing more distinctive knowledge may receive higher weights, while those sharing similar CF signals may be down-weighted. Formally, domain-wise merging is defined as:
\begin{equation}
\label{eq:domain_wise_merging}
\theta_{merge}=\theta_{base}+\sum_{k=1}^{K}{w_k \cdot \boldsymbol{\tau}_k}.
\end{equation}In this work, we learn the domain-specific weights $`\mathbf{w}`$ in a data-driven manner.
Layer-wise merging. Since different layers in deep neural networks capture different levels of abstraction , applying a single scalar weight per domain may be insufficient to control inter-domain interference. To enable fine-grained integration, we assign independent merging weights to each layer for every domain.
Let $`\theta_k = \{\theta_k^1, \dots, \theta_k^L\}`$ denote the parameters of the fine-tuned model for domain $`k`$. The corresponding layer-wise task vector is defined as $`\boldsymbol{\tau}_k = \{\theta_k^1 - \theta_{\text{base}}^1, ..., \theta_k^L - \theta_{\text{base}}^L\}`$. The layer-wise merging is then defined as:
\begin{equation}
\label{eq:layer_wise_merging}
\theta_{merge}=\left\{ \theta_{base}^l+\sum_{k=1}^{K}{w_k^l \cdot \tau_k^l} \right\}_{l=1}^L.
\end{equation}The layer-specific merging weights $`\mathbf{w}_k = \{w_k^1, \dots, w_k^L\}`$ are similarly learned in a data-driven manner.
Pseudo-user Data Construction
User logs in recommender systems typically contain sensitive personal information and cannot be shared across domains, making it challenging to construct data for learning merging weights. To address this, we propose a novel pseudo-user data construction strategy that represents each item in a domain as a single-item interaction sequence. Our design is grounded in the idea that CF knowledge is encapsulated within domain-specific models and can be transferred without relying on the real user data on which they were trained. By leveraging pseudo-users as surrogate inputs, our approach enables learning merging weights without access to domain-specific fine-tuning data while strictly preserving data isolation.
Formally, we construct the pseudo-user set for domain $`k`$ as:
\begin{equation}
\mathcal{\tilde{U}}_{k} = \left \{ [i] \mid i \in \mathcal{I}_k \right \}.
\end{equation}These synthesized samples emulate plausible cold-start users in each domain and thus provide meaningful signals for model merging. Although each pseudo-user sequence contains no explicit sequential context, it serves as a probe to elicit rich CF knowledge encoded in the corresponding domain-specific model $`f_{\theta_k}`$. We therefore employ each domain-specific model as a teacher, whose conditional distribution $`P_{\theta_k}(\cdot \mid [i])`$ captures the local co-consumption structure around item $`i`$, i.e., next-item likelihoods. By distilling the merged model to align with these teacher distributions, we effectively transfer domain-specific CF signals. We observe that even single-item pseudo-user sequences are sufficient for effective model merging (Section 5), providing a practical and privacy-preserving foundation for collaborative merging optimization. While extending pseudo-user sequences to longer contexts may further enrich the transferred signals, we leave this promising direction for future work.
 style="width:100.0%" />
style="width:100.0%" />
Collaborative Merging Optimization
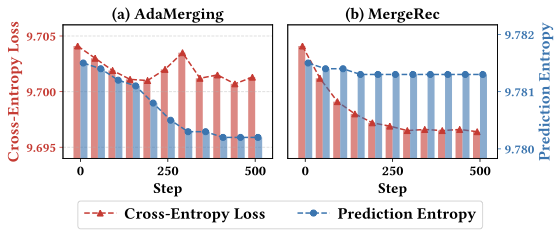
Inadequacy of entropy-based optimization. We examine a representative adaptive merging method, AdaMerging , from the perspective of recommender systems. Figure 3 illustrates the training dynamics of cross-entropy loss and prediction entropy for both AdaMerging and our proposed MergeRec over training iterations on eight datasets, evaluated using test user sequences. The cross-entropy loss reflects alignment with the recommendation objective, whereas prediction entropy measures the confidence of the merged model’s predictions. As shown in Figure 3 (a), AdaMerging successfully reduces prediction entropy during training but fails to achieve a corresponding decrease in cross-entropy loss. This limitation stems from its exclusive focus on entropy minimization, which merely amplifies confidence in the top-1 predicted item. However, users often exhibit multi-intent behavioral patterns rather than a single dominant intent , making entropy-based optimization alone insufficient to capture the rich CF signals learned by domain-specific fine-tuned models.
To overcome this, we introduce a distillation loss that extends beyond entropy-based optimization by explicitly aligning the merged model with teacher distributions derived from domain-specific models. MergeRec (Figure 3 (b)) simultaneously reduces both cross-entropy loss and prediction entropy, demonstrating more consistent and effective optimization toward the recommendation objective.
Joint objective function. We posit that an ideal merged model for cross-domain recommendation should simultaneously satisfy two essential aspects. First, it should effectively capture diverse user intents reflected in behavioral patterns within each domain and retrieve items relevant to those intents. This requires successfully transferring domain-specific CF knowledge from fine-tuned models to the merged model. Second, the merged model should exhibit strong discriminative capability to accurately identify the items that users are most likely to click on within each domain. To jointly address these requirements, we propose the following optimization function:
\begin{equation}
\mathcal{L} = \mathcal{L}_{\text{Rec}} + \lambda \cdot \mathcal{L}_{\text{KD}},
\end{equation}where $`\lambda`$ is a hyperparameter that balances the two losses. In Eqs. [eq:domain_wise_merging] and [eq:layer_wise_merging], we optimize only the merging weights $`w`$, while keeping the base model parameters $`\theta_{base}`$ and the task vector $`\tau`$ fixed. Since only $`K`$ or $`K \times L`$ domain-specific weights are optimized, MergeRec provides a computationally efficient solution.
The knowledge distillation loss $`\mathcal{L}_{\text{KD}}`$ integrates domain-specific CF knowledge encoded in fine-tuned models by aligning the predictions of the merged model with those of the corresponding domain-specific models. For a pseudo-user sequence $`u \in \mathcal{\tilde{U}}_k`$ in domain $`k`$, we minimize the Kullback-Leibler (KL) divergence between the prediction $`\hat{y}_{merge}`$ produced by the merged model $`\theta_{merge}`$ and the prediction $`\hat{y}_{k}`$ produced by the fine-tuned model $`\theta_{k}`$:
\begin{equation}
\begin{split}
\mathcal{L}_{\text{KD}} &= \sum_{k=1}^{K} \sum_{u \in \mathcal{\tilde{U}}_{k}} \text{KL}(\hat{p}_{merge,u} \parallel \hat{p}_{k,u}) \\
&= \sum_{k=1}^{K} \sum_{u \in \mathcal{\tilde{U}}_{k}} \sum_{i \in \mathcal{I}_k} \hat{p}_{merge,ui} \log{\frac{\hat{p}_{merge, ui}}{\hat{p}_{k,ui}}},
\end{split}
\end{equation}where $`\hat{p}_{*}=\text{softmax}(\hat{y}_{*} / T)`$, and $`T`$ denotes the temperature hyperparameter which is empirically set to $`1`$ in our experiments.
The recommendation loss $`\mathcal{L}_{\text{Rec}}`$ encourages the merged model to accurately identify items aligned with user intent by assigning high scores to the next item and low scores to others. Since real user sequences are unavailable, we leverage the top-1 predicted item $`\tilde{i}^+`$, obtained by feeding pseudo-user data into the corresponding fine-tuned model, as a positive pseudo-label:
\begin{equation}
\begin{split}
\mathcal{L}_{\text{Rec}} = \sum_{k=1}^{K} \sum_{u \in \mathcal{\tilde{U}}_{k}} \left( \log{\hat{y}_{merge,u\tilde{i}^+}} + \sum_{i^- \in \mathcal{I}_k} \log{(1 - \hat{y}_{merge,ui^-})} \right).
\end{split}
\end{equation}Experimental Setup
width=0.95
| Backbone | Method | Arts | Beauty | Inst. | Office | Pantry | Sci. | Sports | Toys | |
|---|---|---|---|---|---|---|---|---|---|---|
| RecFormer-base | Zero-shot | 75.46 | 76.04 | 63.66 | 72.15 | 61.61 | 74.23 | 92.85 | 71.11 | 84.94 |
| Joint Learning | 80.17 | 77.37 | 79.53 | 83.26 | 73.37 | 85.34 | 79.96 | 69.62 | 92.94 | |
| Weight Averaging | 89.84 | 91.20 | 83.05 | 90.86 | 77.39 | 93.62 | 99.68 | 86.66 | 93.00 | |
| Task Arithmetic | 88.95 | 91.52 | 81.45 | 88.12 | 83.79 | 92.67 | 98.90 | 81.32 | 82.34 | |
| TIES | 91.08 | 93.29 | 85.60 | 90.57 | 88.22 | 92.75 | 97.68 | 85.56 | 86.25 | |
| AdaMerging (Domain-wise) | 78.91 | 87.26 | 58.66 | 75.81 | 64.78 | 75.02 | 92.56 | 67.97 | 93.11 | |
| AdaMerging (Layer-wise) | 67.36 | 67.17 | 32.92 | 67.36 | 58.54 | 65.64 | 84.54 | 65.24 | 84.93 | |
| MergeRec (Domain-wise) | 92.33* | 96.14* | 83.69 | 90.93 | 84.27 | 95.56* | 100.73* | 84.00 | 93.35* | |
| MergeRec (Layer-wise) | 92.08* | 95.45* | 84.85 | 91.13* | 83.01 | 94.86* | 101.44* | 85.07 | 92.14 | |
| RecFormer-large | Zero-shot | 59.07 | 72.57 | 51.89 | 46.03 | 39.23 | 44.34 | 82.00 | 62.54 | 63.57 |
| Joint Learning | 83.73 | 83.14 | 79.48 | 79.76 | 73.61 | 90.27 | 92.99 | 91.49 | 83.61 | |
| Weight Averaging | 91.23 | 92.27 | 87.10 | 88.94 | 79.13 | 96.46 | 98.32 | 98.88 | 94.36 | |
| Task Arithmetic | 87.99 | 91.32 | 83.32 | 88.26 | 82.78 | 92.08 | 92.99 | 87.80 | 81.14 | |
| TIES | 89.96 | 93.00 | 85.74 | 90.25 | 88.17 | 92.91 | 94.10 | 89.09 | 80.79 | |
| AdaMerging (Domain-wise) | 72.59 | 83.37 | 59.49 | 77.55 | 63.74 | 61.37 | 83.96 | 58.14 | 70.69 | |
| AdaMerging (Layer-wise) | 70.80 | 79.59 | 52.28 | 68.27 | 60.64 | 67.12 | 83.08 | 72.97 | 72.01 | |
| MergeRec (Domain-wise) | 92.99* | 95.19* | 90.08* | 91.75* | 83.39 | 96.20 | 97.41 | 94.74 | 96.64* | |
| MergeRec (Layer-wise) | 92.50* | 94.21* | 89.77* | 90.25 | 82.18 | 96.27 | 97.86 | 96.53 | 96.17* | |
| BLaIR-base | Zero-shot | 41.10 | 45.88 | 35.57 | 31.55 | 27.74 | 47.20 | 54.94 | 34.50 | 42.32 |
| Joint Learning | 83.67 | 82.89 | 97.30 | 83.52 | 73.09 | 91.24 | 74.85 | 92.88 | 94.87 | |
| Weight Averaging | 87.90 | 91.98 | 93.97 | 78.41 | 76.12 | 91.39 | 99.95 | 89.45 | 81.81 | |
| Task Arithmetic | 61.50 | 57.05 | 53.43 | 66.66 | 61.61 | 62.42 | 73.27 | 49.34 | 53.78 | |
| TIES | 82.95 | 84.37 | 78.02 | 78.26 | 87.64 | 77.18 | 88.52 | 87.26 | 77.39 | |
| AdaMerging (Domain-wise) | 60.60 | 67.93 | 52.07 | 53.40 | 44.83 | 50.80 | 72.94 | 72.91 | 73.14 | |
| AdaMerging (Layer-wise) | 68.48 | 73.09 | 61.14 | 68.86 | 55.34 | 57.54 | 83.92 | 74.23 | 70.61 | |
| MergeRec (Domain-wise) | 87.40 | 94.42* | 89.38 | 77.75 | 81.44 | 85.18 | 95.48 | 85.05 | 84.01 | |
| MergeRec (Layer-wise) | 88.01 | 93.53* | 91.83 | 78.98 | 81.15 | 87.82 | 96.55 | 87.45 | 83.06 | |
| BLaIR-large | Zero-shot | 33.44 | 38.42 | 29.99 | 24.55 | 19.23 | 46.48 | 37.83 | 27.84 | 41.70 |
| Joint Learning | 84.59 | 83.33 | 81.01 | 86.78 | 78.56 | 90.60 | 78.48 | 83.85 | 100.63 | |
| Weight Averaging | 88.99 | 92.76 | 89.13 | 83.82 | 76.25 | 93.20 | 103.56 | 86.36 | 81.69 | |
| Task Arithmetic | 78.86 | 82.64 | 79.11 | 65.86 | 74.43 | 83.64 | 93.56 | 73.13 | 67.87 | |
| TIES | 90.90 | 93.78 | 91.09 | 87.76 | 90.01 | 92.58 | 98.36 | 93.67 | 75.35 | |
| AdaMerging (Domain-wise) | 69.27 | 82.21 | 62.36 | 71.76 | 51.16 | 60.90 | 78.41 | 77.27 | 68.45 | |
| AdaMerging (Layer-wise) | 78.22 | 84.78 | 73.80 | 78.57 | 62.43 | 83.01 | 84.04 | 71.51 | 83.00 | |
| MergeRec (Domain-wise) | 91.80* | 97.80* | 93.07* | 91.81* | 80.51 | 89.76 | 102.88 | 90.16 | 82.84 | |
| MergeRec (Layer-wise) | 93.70* | 98.73* | 95.40* | 91.74* | 82.62 | 94.17* | 105.18* | 90.28 | 85.63 |
Datasets. To simulate a cross-domain recommendation environment, we use eight categories from the Amazon dataset1 2: Arts, Beauty, Instruments, Office, Pantry, Scientific, Sports, and Toys. Following existing work , we adopt a 5-core setting, i.e., users and items with fewer than five interactions are removed. Detailed dataset statistics are provided in Appendix 8.
Baselines. We compare MergeRec with the following methods:
-
Zero-shot: Directly applies pre-trained text-based SR models without fine-tuning on a specific domain.
-
Fine-tuning: Fine-tunes pre-trained models using domain-specific interaction data.
-
Joint Learning: Trains a unified model on aggregated multi-domain datasets with shared parameters.
-
Task Arithmetic : Constructs a cross-domain model by linearly adding task vectors to a pre-trained model.
-
TIES : Reduces noise and conflicts between task vectors by selecting parameters with large variance and aligning their signs.
-
AdaMerging : Learns adaptive merging weights in an unsupervised manner by minimizing the prediction entropy of the merged model.
We evaluate all methods on RecFormer-base/large , a representative text-based SR model, and BLaIR-base/large , a language model post-trained on a recommendation corpus, as backbone architectures. For a fair comparison under the data-isolation setting, AdaMerging is adapted to use the same pseudo-user data as MergeRec, treating it as unlabeled inputs for entropy-based optimization. Implementation details are provided in Appendix 9.
Evaluation protocol. Following , we adopt the leave-one-out strategy to split the train, validation, and test datasets. For each user, the most recently interacted item is used for testing, the second most recently interacted item for validation, and the rest for training. Note that the training data is used only for fine-tuning and joint learning. We evaluate recommendation performance using Recall@10 (R@10) and NDCG@10 (N@10). Following , we normalize the performance of each method by that of its corresponding fine-tuned model. The normalized results are reported in Table [tab:overall] and Figures 4, 5, and 7.
Experimental Results
Overall Performance
Table [tab:overall] shows the normalized R@10 of MergeRec and seven baseline methods across eight datasets and four backbone models, where the performance of the fine-tuned model on each dataset is normalized to 100%. The corresponding normalized N@10, unnormalized R@10, N@10 results are provided in Appendix 10.
MergeRec consistently achieves the best average performance across all datasets and backbone models for both the domain-wise and layer-wise variants. Specifically, MergeRec outperforms Joint Learning and AdaMerging with average gains of 8.72% and 17.21%, respectively. This indicates that MergeRec simultaneously enhances the ranking discriminative ability of the merged model and effectively transfers domain-specific CF knowledge from fine-tuned models. Meanwhile, AdaMerging performs substantially worse across all datasets and backbone models, suggesting that merely amplifying prediction confidence is insufficient to capture the diverse CF signals present across multiple domains. Furthermore, MergeRec surpasses training-free model merging methods (i.e., Task Arithmetic and TIES) by average gains of 9.90% and 3.04%, respectively.
Several model merging methods, i.e., MergeRec, Weight Averaging, and TIES, consistently outperform Joint Learning. These results demonstrate that model merging can effectively capture complementary domain knowledge and improve recommendation quality without relying on cross-domain training data. It further highlights the practical advantages of model merging, as it not only reduces computational overhead but also enables synergistic knowledge transfer across domains without end-to-end re-training.
Cross-domain merging is particularly beneficial for data-scarce domains. On the Scientific dataset, MergeRec achieves improvements of 1.44% for RecFormer-base (Domain-wise) and 5.18% for BLaIR-large (Layer-wise) compared to their respective fine-tuned counterparts. These improvements can be attributed to the limited number of users in the Scientific domain, where the merged model benefits more substantially from cross-domain knowledge transferred from other domains.
Overall, these results demonstrate that MergeRec provides a robust and scalable solution for cross-domain model merging in recommender systems, delivering consistent and significant performance gains across diverse domains and backbone architectures.
width=0.95
| Ratio | Method | Inst. | Office | Sci. | |
|---|---|---|---|---|---|
| 1% | Fine-tuning | 0.0989 | 0.0745 | 0.0953 | 0.1268 |
| Task Arithmetic | 0.1069 | 0.0828 | 0.0995 | 0.1385 | |
| TIES | 0.0650 | 0.0158 | 0.0614 | 0.1178 | |
| AdaMerging | 0.0982 | 0.0732 | 0.0898 | 0.1318 | |
| MergeRec | 0.1089 | 0.0859 | 0.1013 | 0.1394 | |
| 5% | Fine-tuning | 0.1057 | 0.0752 | 0.1094 | 0.1325 |
| Task Arithmetic | 0.1101 | 0.0859 | 0.1050 | 0.1392 | |
| TIES | 0.0800 | 0.0812 | 0.1017 | 0.0570 | |
| AdaMerging | 0.1047 | 0.0814 | 0.1023 | 0.1304 | |
| MergeRec | 0.1128 | 0.0888 | 0.1098 | 0.1399 | |
| 10% | Fine-tuning | 0.1118 | 0.0838 | 0.1175 | 0.1341 |
| Task Arithmetic | 0.1107 | 0.0860 | 0.1055 | 0.1405 | |
| TIES | 0.0840 | 0.0809 | 0.1017 | 0.0693 | |
| AdaMerging | 0.0982 | 0.0755 | 0.0935 | 0.1258 | |
| MergeRec | 0.1120 | 0.0887 | 0.1088 | 0.1386 |
Model Merging on Scarce Training Data
Collecting sufficient data is often challenging in the early stages of recommender systems. Under such data-scarce conditions, model merging can offer a promising solution for improving model generalization by leveraging knowledge from data-rich domains. We investigate whether model merging can improve recommendation performance in domains with limited data.
To simulate this scenario, we divide the eight domains into two groups: five source domains (Arts, Beauty, Pantry, Sports, Toys) and three target domains (Instruments, Office, Scientific). We then vary the degree of scarcity in the target domain by randomly sampling $`k\%`$ of users ($`k = 1, 5, 10`$) from the whole user set to construct data-scarce training sets. Each fine-tuned model trained on a data-scarce target domain is subsequently merged with the fine-tuned models trained from the five source domains.
Table 1 compares MergeRec with five merging methods under different levels of data scarcity using the RecFormer-base backbone. MergeRec consistently outperforms the corresponding fine-tuned models, demonstrating its strong ability to transfer knowledge across domains even under extreme data scarcity. Moreover, MergeRec consistently surpasses AdaMerging across all scarcity levels, indicating that our recommendation-oriented optimization captures transferable CF patterns more effectively than the entropy minimization approach. These results confirm that MergeRec can reliably transfer CF signals from data-rich to data-scarce domains.
width=0.85
| Method | Inst. | Office | Sci. | |
|---|---|---|---|---|
| Task Arithmetic | 0.1062 | 0.0817 | 0.0984 | 0.1385 |
| TIES | 0.1062 | 0.0817 | 0.0988 | 0.1380 |
| AdaMerging | 0.0998 | 0.0759 | 0.0901 | 0.1333 |
| MergeRec | 0.1081 | 0.0849 | 0.1002 | 0.1393 |
Unseen-domain performance comparison of task-vector based model merging methods using the RecFormer-base backbone. We train a merged model on the Arts, Beauty, Pantry, Sports, and Toys datasets and test it on the Inst., Office, and Sci. datasets. The metric is Recall@10.
Performance on Unseen Domains
To examine whether model merging remains effective under extreme conditions where no interaction data are available for the target domain, we merge models trained on five source domains (Arts, Beauty, Pantry, Sports, Toys) and evaluate their performance on three unseen target domains (Inst., Office, Sci.). Note that neither interaction data nor domain-specific models from the target domains are used in constructing the merged model.
Table 2 shows the performance of four merging methods on unseen domains. MergeRec consistently outperforms the other methods, achieving improvements of up to 3.92% over Task Arithmetic. These results demonstrate the strong generalizability of MergeRec and highlight its effectiveness in transferring knowledge to entirely unseen domains without relying on any target-domain data.
 style="width:90.0%" />
style="width:90.0%" />
 style="width:100.0%" />
style="width:100.0%" />
 style="width:90.0%" />
style="width:90.0%" />
Further Analysis
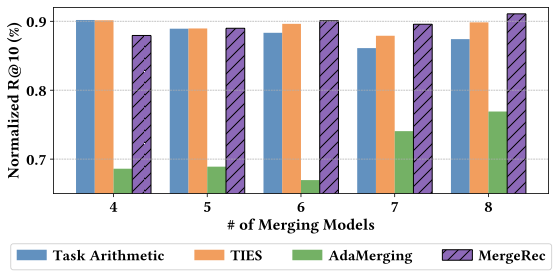
Effect of the number of merged domains. To assess the robustness of MergeRec, we analyze how recommendation performance varies with the number of merged models, as shown in Figure 4. Task Arithmetic and TIES exhibit competitive performance when merging a small number of domains (four or five), but their performance deteriorates as more domains are included, eventually falling behind MergeRec. AdaMerging consistently performs poorly across all settings, indicating that its entropy-based optimization strategy fails to effectively adapt to recommendation tasks. In contrast, MergeRec maintains stable performance regardless of the number of merged domains. Notably, its average performance improves as more domains are integrated, highlighting its strong ability to effectively consolidate and leverage knowledge across an increasing number of diverse domains.
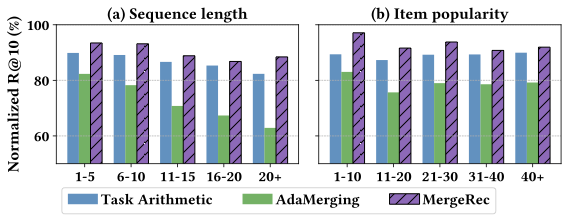
Performance across user and item groups. To further analyze the sources of performance improvements, we partition the test data into multiple groups based on user history length and target item popularity. Figure 5 shows the performance of three merging methods across five sequence-length groups and five item popularity ranges. All methods are evaluated on the eight datasets, and the results are averaged and normalized by the performance of the corresponding fine-tuned model within each group.
As shown in Figure 5 (a), AdaMerging exhibits severe performance degradation as the sequence length increases. This result indicates that AdaMerging struggles to capture CF signals in longer sequences, as it does not learn inter-item relationships during optimization. In contrast, MergeRec consistently achieves the best performance across all sequence lengths by effectively transferring inter-item relationships through the proposed objective function. Figure 5 (b) shows that MergeRec outperforms other methods across all item popularity ranges. Notably, in the least popular item group (1–10), MergeRec achieves substantial performance gains over competing methods, highlighting its ability to leverage cross-domain knowledge to recommend less popular items.
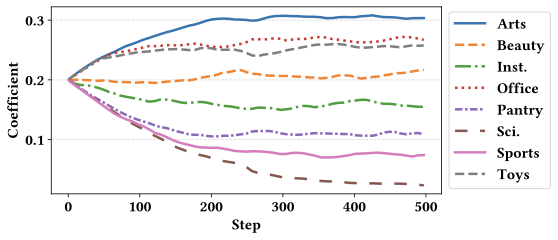
Domain-specific weight dynamics. To understand how the model adapts to different domains during merging, we analyze the training trajectories of the domain-wise merging weights $`\mathbf{w}`$ across eight domains using the RecFormer-base model. Figure 6 illustrates the evolution of each domain’s weight during training. We observe that the weights gradually converge to distinct values for each domain, indicating that the model learns to differentiate the relative importance of individual domains. Notably, domains with larger scales (e.g., Arts and Office) converge to higher weight coefficients. These results suggest that domains exhibiting more complex CF patterns are assigned greater emphasis, enabling the merged model to better preserve domain-specific knowledge. The corresponding results for other backbone models are reported in Appendix 11.
 style="width:95.0%" />
style="width:95.0%" />
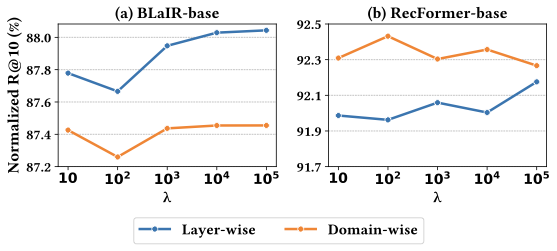
Hyperparameter Sensitivity
Figure 7 depicts the effect of the trade-off hyperparameter $`\lambda`$ on recommendation performance. The results are averaged across all eight datasets and normalized by the performance of the corresponding fine-tuned models. We find that performance generally improves as $`\lambda`$ increases, except for domain-wise merging with the RecFormer-base backbone. This suggests that placing greater emphasis on the knowledge distillation loss is typically more effective. This can be attributed to the model learning the full item-prediction distribution from domain-specific teacher models, which enables the merged model to capture richer and more informative CF signals. In contrast, methods that focus solely on amplifying top-1 prediction confidence provide a more limited supervisory signal.
Related Work
Cross-Domain Sequential Recommendation
CDSR has emerged as an effective approach to alleviate data sparsity and cold-start problems in single-domain recommender systems . Existing CDSR approaches can be categorized into three types: single-target CDSR, dual-target CDSR, and multi-target CDSR. Additionally, privacy-preserving cross-domain recommendation (CDR) has gained increasing attention in privacy-sensitive and federated learning scenarios.
Single-target CDSR. Single-target CDSR is the most extensively studied setting, aiming to improve recommendation performance in a data-scarce target domain by transferring knowledge from data-rich source domains with abundant user-item interactions or auxiliary information. C$`^2`$DSR jointly models intra-sequence and inter-sequence item relationships through graph neural networks and self-attention mechanisms. To enhance self-attention modules, MAN introduces both local and global attention modules to capture domain-specific and cross-domain information. Recently, LLM4CDSR leverages large language models to generate semantic item representations from textual attributes and hierarchical user profiles from interaction sequences, facilitating cross-domain knowledge transfer.
Dual- and multi-target CDSR. Dual- and multi-target CDSR aims to simultaneously improve recommendation performance across multiple domains. DTCDR adopts a multi-task learning framework that bidirectionally transfers user preference representations across domains via shared embeddings. Recent studies have highlighted the negative transfer problem, where knowledge from other domains can fail to provide beneficial contributions. To address this, CGRec and SyNCRec introduce adaptive loss weighting based on estimated transfer gaps between single-domain and cross-domain sequential recommendation tasks. However, these approaches fundamentally rely on overlapping users or items to enable knowledge transfer and do not account for the privacy constraints commonly required in real-world scenarios.
Privacy-preserving CDR. Privacy-preserving CDR aims to improve recommendation performance under settings where access to raw data from individual domains is restricted or entirely unavailable. An early study separates personalized and transferable components to enable privacy-compliant recommendations. P2M2-CDR disentangles domain-common and domain-specific embeddings while applying local differential privacy to perturb shared representations. FedGCDR further adopts federated graph learning with differential privacy-based knowledge extraction and graph expansion to mitigate the negative transfer problem. However, these approaches typically rely on overlapping users across domains and require cross-domain coordination during training, where domain-specific data are used alongside data from other domains (e.g., exchanged model parameters or gradients). Therefore, they do not fully satisfy the data isolation constraint.
In this paper, we pioneer the application of model merging to data-isolated multi-target CDSR, providing a scalable solution for integrated multi-domain recommendations without requiring direct access to domain-specific user interaction data, thereby preserving user privacy.
Model Merging
Model merging aims to improve the generalization of domain-specific fine-tuned models by consolidating knowledge from multiple models trained on diverse domains or tasks into a single model, typically without requiring access to training data. The simplest approaches perform parameter averaging across fine-tuned models that share the same backbone pre-trained model.
Beyond these early methods, task vector-based model merging has been proposed to enable more effective knowledge consolidation. Task vectors are defined as the parameter differences between each fine-tuned model and the pre-trained model. They can be interpreted as directions that encode domain- or task-specific adaptations. Task Arithmetic shows that task vectors can be combined to build multi-task models, or negated to attenuate (or remove) task-specific knowledge. TIES selects parameters with large task-induced changes and resolves sign conflicts to reduce interference. AdaMerging extends linear task-vector composition by learning domain- or layer-wise merging weights through entropy minimization on unlabeled test samples. Although model merging has demonstrated strong effectiveness in computer vision and natural language processing, its potential for recommender systems has remained largely unexplored.
Conclusion
In this work, we addressed the fundamental limitations of existing CDSR under realistic constraints, where user interaction data cannot be shared across domains. To this end, we introduced MergeRec, a novel framework that applies task vector-based model merging to a new problem setting, termed data-isolated CDSR. MergeRec consists of three key components: (1) Merging initialization constructs an initial merged model using training-free task vectors based merging. (2) Pseudo-user data construction synthesizes virtual interaction sequences from domain items, allowing CF signals to be extracted without exposing sensitive user data. (3) Collaborative merging optimization jointly optimizes a recommendation loss and a knowledge distillation loss, facilitating the transfer of domain-specific CF patterns while preserving ranking effectiveness. Extensive experiments confirmed that MergeRec consistently outperforms existing model merging baselines and significantly improves generalization, including on unseen and data-scarce domains, highlighting the potential of model merging as a scalable, privacy-preserving solution for building universal recommender systems.
Ethical Use of Data
This paper utilizes publicly available datasets (Amazon product review datasets) that contain no personally identifiable information and require no Institutional Ethics Review Board approval. All experiments use anonymized interaction sequences released for academic research purposes.
This work was supported by the Institute of Information & communications Technology Planning & Evaluation (IITP) grant and the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. IITP-RS-2019-II190421, IITP-RS-2022-II220680, RS-2025-25442569, NRF-RS-2025-00564083, each contributing 25% to this research).
Dataset Statistics
| Dataset | # Users | # Items | # Inter. | Density |
|---|---|---|---|---|
| Arts | 56,210 | 22,855 | 492,492 | 0.04% |
| Beauty | 22,363 | 12,101 | 198,502 | 0.07% |
| Inst. | 27,530 | 10,611 | 231,312 | 0.08% |
| Office | 101,499 | 27,932 | 798,912 | 0.03% |
| Pantry | 14,180 | 4,968 | 137,769 | 0.20% |
| Sci. | 11,041 | 5,327 | 76,896 | 0.13% |
| Sports | 35,598 | 18,357 | 296,337 | 0.05% |
| Toys | 19,412 | 11,924 | 167,597 | 0.07% |
Dataset statistics including the number of users, items, interactions, and density.
Table 3 summarizes the statistics of each domain, including the number of users, items, interactions, and dataset density. The density is calculated as $`\frac{\#~\text{Interactions}}{\#~\text{Users} \times \#~\text{Items}}`$.
Implementation Details
All methods, including MergeRec and baselines, are implemented in PyTorch. For RecFormer-base , we use the official pre-trained checkpoint3, while for RecFormer-large, we pre-train the model following the protocol described in the original paper. For BLaIR-base4 and BLaIR-large5 , we use the official pre-trained checkpoints available on HuggingFace. Fine-tuning is performed with in-batch negative sampling and a batch size of 64. For merging baselines, we adopt their hyperparameter configurations for the validation-less setting, i.e., no training, validation, or test data are used. Specifically, we set $`w_1 = w_2 = \dots = w_K = 0.4`$ for Task Arithmetic , and $`w=1`$ for TIES . We use the top 20% of the parameters for TIES. For AdaMerging and MergeRec, all coefficients are initialized to $`0.2`$ and optimized for 500 steps using the Adam optimizer with a learning rate of 0.001 and a batch size of 16. For MergeRec, we set $`\lambda = 1{,}000`$ to balance the scale of the two loss functions. All reported performance metrics represent averages computed across five random seeds. For the significance test, we assume that deterministic merging approaches (i.e., Weight Averaging, Task Arithmetic, and TIES) have identical performance values across all five runs.
Overall Performance on Other Metrics
Table [tab:overall_ndcg] shows the normalized N@10 of MergeRec and seven baseline methods across eight datasets on four backbone models, with the performance of the fine-tuned model trained on each dataset set to 100%. In addition, we report the unnormalized R@10 and N@10 results in Table [tab:overall_recall_abs] and Table [tab:overall_ndcg_abs], respectively. We observe similar trends for N@10 (Table [tab:overall_ndcg]) as for R@10 (Table [tab:overall]). (i) MergeRec achieves the best performance on average across all datasets and backbone models. This shows that MergeRec effectively transfers domain-specific knowledge and improves model discrimination, whereas AdaMerging is less effective across the board. (ii) Merging methods like MergeRec, Weight Averaging, and TIES consistently outperform joint learning, demonstrating that parameter merging can efficiently transfer knowledge across domains and reduce computational cost without cross-domain training data. (iii) Cross-domain merging is especially helpful for domains with limited data, such as Scientific, where MergeRec shows notable improvements over fine-tuned models due to more effective knowledge transfer.
Domain-Specific Weight Dynamics on Other Backbones
We further analyze the evolution of domain-specific weights $`\mathbf{w}`$ on the remaining three backbone models: RecFormer-large and BLaIR-base/large. Consistent with our observations for RecFormer-base, we find that domains with larger data scales (e.g., Arts and Office) tend to converge to higher weight coefficients. This trend suggests that these models also prioritize capturing more complex collaborative patterns in large-scale domains, thereby allocating more representational capacity to preserve domain-specific knowledge. In contrast to this general trend, the merging weight for the Pantry dataset in the BLaIR model converges to negative values. This behavior may be attributed to the absence of category information in the Pantry dataset, which differs from other domains and can lead to misalignment during model merging.
(a) Recformer-large 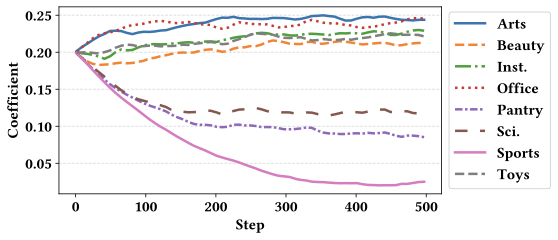 style="width:90.0%" />
style="width:90.0%" />
(b) BLaIR-base 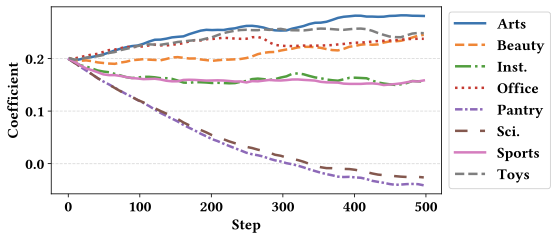 style="width:90.0%" />
style="width:90.0%" />
(c) BLaIR-large 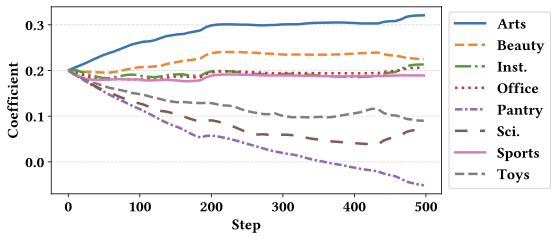 style="width:90.0%" />
style="width:90.0%" />
| Backbone | Method | Arts | Beauty | Inst. | Office | Pantry | Sci. | Sports | Toys | |
|---|---|---|---|---|---|---|---|---|---|---|
| RecFormer-base | Zero-shot | 67.52 | 63.59 | 61.57 | 55.88 | 52.63 | 69.33 | 92.79 | 70.75 | 81.44 |
| Joint Learning | 73.05 | 67.41 | 75.48 | 76.13 | 66.69 | 82.75 | 72.12 | 69.55 | 87.62 | |
| 2-11 | Weight Averaging | 83.15 | 82.88 | 76.42 | 75.67 | 70.29 | 92.37 | 99.68 | 82.70 | 86.20 |
| Task Arithmetic | 84.08 | 86.47 | 75.99 | 76.05 | 76.37 | 91.85 | 99.52 | 78.08 | 75.53 | |
| TIES | 85.60 | 87.16 | 79.61 | 76.52 | 81.25 | 91.95 | 97.59 | 80.72 | 80.11 | |
| AdaMerging (Domain-wise) | 71.17 | 75.47 | 55.19 | 60.35 | 56.45 | 71.09 | 90.67 | 67.83 | 87.15 | |
| AdaMerging (Layer-wise) | 61.61 | 60.94 | 32.01 | 52.35 | 51.36 | 64.14 | 82.60 | 64.32 | 79.22 | |
| 2-11 | MergeRec (Domain-wise) | 86.07* | 87.31 | 76.54 | 79.14* | 76.87 | 94.50* | 100.48* | 80.36 | 84.97 |
| MergeRec (Layer-wise) | 85.37 | 86.18 | 77.32 | 77.77* | 75.39 | 93.82* | 101.00* | 81.55 | 83.87 | |
| RecFormer-large | Zero-shot | 53.55 | 65.05 | 50.33 | 34.05 | 31.26 | 40.96 | 82.63 | 61.27 | 63.58 |
| Joint Learning | 75.76 | 72.09 | 75.48 | 66.50 | 66.67 | 86.94 | 87.67 | 85.34 | 78.60 | |
| 2-11 | Weight Averaging | 85.84 | 86.37 | 81.64 | 76.44 | 74.60 | 94.63 | 98.70 | 91.35 | 88.87 |
| Task Arithmetic | 85.70 | 93.60 | 80.00 | 77.58 | 77.38 | 91.60 | 94.56 | 81.75 | 77.75 | |
| TIES | 87.64 | 94.09 | 81.66 | 80.60 | 82.07 | 92.36 | 96.49 | 83.51 | 76.81 | |
| AdaMerging (Domain-wise) | 67.29 | 77.00 | 56.84 | 61.87 | 56.92 | 55.66 | 82.95 | 56.31 | 69.72 | |
| AdaMerging (Layer-wise) | 64.96 | 71.01 | 51.70 | 53.68 | 54.66 | 62.19 | 81.38 | 69.86 | 69.99 | |
| 2-11 | MergeRec (Domain-wise) | 89.40* | 96.27* | 84.65* | 80.68 | 78.21 | 94.07 | 98.97 | 88.13 | 90.48* |
| MergeRec (Layer-wise) | 88.62* | 93.40 | 85.08* | 78.27 | 77.58 | 94.80 | 99.58 | 89.95 | 90.66* | |
| BLaIR-base | Zero-shot | 33.06 | 32.86 | 33.22 | 23.98 | 20.80 | 40.87 | 45.76 | 34.05 | 40.78 |
| Joint Learning | 78.48 | 79.94 | 97.16 | 79.19 | 67.59 | 88.03 | 68.00 | 92.07 | 92.08 | |
| 2-11 | Weight Averaging | 78.13 | 78.59 | 85.53 | 67.01 | 64.70 | 85.65 | 94.62 | 82.03 | 75.85 |
| Task Arithmetic | 55.37 | 50.11 | 51.82 | 55.54 | 52.30 | 58.80 | 66.56 | 49.09 | 51.86 | |
| TIES | 74.72 | 72.17 | 73.04 | 65.61 | 78.62 | 71.78 | 82.47 | 81.81 | 73.44 | |
| AdaMerging (Domain-wise) | 50.28 | 51.53 | 49.02 | 41.46 | 35.38 | 43.17 | 66.06 | 68.61 | 69.18 | |
| AdaMerging (Layer-wise) | 57.91 | 56.90 | 56.93 | 53.60 | 44.83 | 49.51 | 77.66 | 69.20 | 65.29 | |
| 2-11 | MergeRec (Domain-wise) | 78.30 | 81.33* | 81.78 | 65.59 | 70.51 | 78.22 | 92.14 | 79.46 | 78.36 |
| MergeRec (Layer-wise) | 79.18 | 81.23* | 84.30 | 66.94 | 70.26 | 81.88 | 93.35 | 81.73 | 77.47 | |
| BLaIR-large | Zero-shot | 26.85 | 27.51 | 27.83 | 18.08 | 14.22 | 41.96 | 32.15 | 28.46 | 38.78 |
| Joint Learning | 81.67 | 81.00 | 80.58 | 85.57 | 75.84 | 92.12 | 71.85 | 85.25 | 97.07 | |
| 2-11 | Weight Averaging | 81.50 | 83.19 | 83.57 | 71.84 | 67.74 | 90.68 | 98.42 | 84.70 | 76.31 |
| Task Arithmetic | 73.00 | 73.33 | 77.37 | 57.23 | 66.13 | 81.75 | 89.62 | 75.40 | 65.31 | |
| TIES | 85.74 | 85.71 | 87.92 | 76.38 | 83.56 | 89.96 | 97.93 | 90.85 | 72.04 | |
| AdaMerging (Domain-wise) | 60.21 | 68.38 | 58.18 | 57.61 | 42.43 | 56.16 | 72.01 | 75.84 | 62.50 | |
| AdaMerging (Layer-wise) | 70.67 | 74.10 | 69.21 | 66.94 | 54.57 | 80.67 | 79.05 | 70.79 | 77.29 | |
| 2-11 | MergeRec (Domain-wise) | 84.46 | 86.73* | 85.69 | 78.68 | 72.36 | 87.45 | 100.83* | 86.61 | 77.22 |
| MergeRec (Layer-wise) | 86.65* | 87.64* | 88.94* | 79.21 | 74.91 | 91.43 | 104.19* | 87.27 | 79.87 |
| Backbone | Method | Arts | Beauty | Inst. | Office | Pantry | Sci. | Sports | Toys | |
|---|---|---|---|---|---|---|---|---|---|---|
| RecFormer-base | Zero-shot | 0.0767 | 0.1192 | 0.0445 | 0.0717 | 0.0850 | 0.0664 | 0.1309 | 0.0255 | 0.0706 |
| Fine-tune | 0.1017 | 0.1567 | 0.0699 | 0.0994 | 0.1379 | 0.0895 | 0.1409 | 0.0358 | 0.0831 | |
| Joint Learning | 0.0815 | 0.1212 | 0.0556 | 0.0828 | 0.1012 | 0.0764 | 0.1127 | 0.0249 | 0.0773 | |
| 2-11 | Weight Averaging | 0.0913 | 0.1429 | 0.0580 | 0.0903 | 0.1067 | 0.0838 | 0.1405 | 0.0310 | 0.0773 |
| Task Arithmetic | 0.0904 | 0.1434 | 0.0569 | 0.0876 | 0.1156 | 0.0829 | 0.1394 | 0.0291 | 0.0685 | |
| TIES | 0.0926 | 0.1462 | 0.0598 | 0.0900 | 0.1217 | 0.0830 | 0.1377 | 0.0306 | 0.0717 | |
| AdaMerging (Domain-wise) | 0.0802 | 0.1367 | 0.0410 | 0.0754 | 0.0893 | 0.0671 | 0.1305 | 0.0243 | 0.0774 | |
| AdaMerging (Layer-wise) | 0.0685 | 0.1053 | 0.0230 | 0.0670 | 0.0807 | 0.0588 | 0.1192 | 0.0233 | 0.0706 | |
| 2-11 | MergeRec (Domain-wise) | 0.0939* | 0.1507* | 0.0585 | 0.0904 | 0.1162 | 0.0855* | 0.1420* | 0.0301 | 0.0776* |
| MergeRec (Layer-wise) | 0.0936* | 0.1496* | 0.0593 | 0.0906* | 0.1145 | 0.0849* | 0.1430* | 0.0304 | 0.0766 | |
| RecFormer-large | Zero-shot | 0.0613 | 0.1138 | 0.0374 | 0.0470 | 0.0545 | 0.0415 | 0.1200 | 0.0205 | 0.0557 |
| Fine-tune | 0.1038 | 0.1568 | 0.0721 | 0.1021 | 0.1388 | 0.0935 | 0.1463 | 0.0327 | 0.0877 | |
| Joint Learning | 0.0869 | 0.1304 | 0.0573 | 0.0815 | 0.1022 | 0.0844 | 0.1360 | 0.0299 | 0.0733 | |
| 2-11 | Weight Averaging | 0.0947 | 0.1447 | 0.0628 | 0.0908 | 0.1098 | 0.0902 | 0.1439 | 0.0323 | 0.0827 |
| Task Arithmetic | 0.0913 | 0.1432 | 0.0601 | 0.0901 | 0.1149 | 0.0861 | 0.1360 | 0.0287 | 0.0711 | |
| TIES | 0.0933 | 0.1458 | 0.0618 | 0.0922 | 0.1224 | 0.0869 | 0.1377 | 0.0291 | 0.0708 | |
| AdaMerging (Domain-wise) | 0.0753 | 0.1307 | 0.0429 | 0.0792 | 0.0885 | 0.0574 | 0.1228 | 0.0190 | 0.0620 | |
| AdaMerging (Layer-wise) | 0.0735 | 0.1248 | 0.0377 | 0.0697 | 0.0842 | 0.0628 | 0.1216 | 0.0239 | 0.0631 | |
| 2-11 | MergeRec (Domain-wise) | 0.0965* | 0.1492* | 0.0650* | 0.0937* | 0.1157 | 0.0900 | 0.1425 | 0.0310 | 0.0847* |
| MergeRec (Layer-wise) | 0.0960* | 0.1477* | 0.0647* | 0.0922 | 0.1141 | 0.0900 | 0.1432 | 0.0316 | 0.0843* | |
| BLaIR-base | Zero-shot | 0.0409 | 0.0704 | 0.0224 | 0.0309 | 0.0376 | 0.0431 | 0.0759 | 0.0110 | 0.0355 |
| Fine-tune | 0.0995 | 0.1535 | 0.0631 | 0.0980 | 0.1356 | 0.0913 | 0.1382 | 0.0320 | 0.0840 | |
| Joint Learning | 0.0832 | 0.1272 | 0.0614 | 0.0819 | 0.0991 | 0.0833 | 0.1034 | 0.0297 | 0.0797 | |
| 2-11 | Weight Averaging | 0.0874 | 0.1412 | 0.0593 | 0.0768 | 0.1032 | 0.0834 | 0.1381 | 0.0286 | 0.0687 |
| Task Arithmetic | 0.0612 | 0.0876 | 0.0337 | 0.0653 | 0.0835 | 0.0570 | 0.1013 | 0.0158 | 0.0452 | |
| TIES | 0.0825 | 0.1295 | 0.0492 | 0.0767 | 0.1188 | 0.0705 | 0.1223 | 0.0279 | 0.0650 | |
| AdaMerging (Domain-wise) | 0.0603 | 0.1043 | 0.0329 | 0.0523 | 0.0608 | 0.0464 | 0.1008 | 0.0233 | 0.0614 | |
| AdaMerging (Layer-wise) | 0.0681 | 0.1122 | 0.0386 | 0.0675 | 0.0750 | 0.0525 | 0.1160 | 0.0238 | 0.0593 | |
| 2-11 | MergeRec (Domain-wise) | 0.0869 | 0.1449* | 0.0564 | 0.0762 | 0.1104 | 0.0778 | 0.1320 | 0.0272 | 0.0706 |
| MergeRec (Layer-wise) | 0.0875 | 0.1436* | 0.0579 | 0.0774 | 0.1100 | 0.0802 | 0.1334 | 0.0280 | 0.0698 | |
| BLaIR-large | Zero-shot | 0.0333 | 0.0589 | 0.0205 | 0.0246 | 0.0257 | 0.0429 | 0.0501 | 0.0096 | 0.0339 |
| Fine-tune | 0.0995 | 0.1534 | 0.0683 | 0.1003 | 0.1334 | 0.0923 | 0.1325 | 0.0346 | 0.0813 | |
| Joint Learning | 0.0842 | 0.1278 | 0.0553 | 0.0871 | 0.1048 | 0.0836 | 0.1040 | 0.0290 | 0.0818 | |
| 2-11 | Weight Averaging | 0.0886 | 0.1423 | 0.0609 | 0.0841 | 0.1017 | 0.0860 | 0.1372 | 0.0299 | 0.0664 |
| Task Arithmetic | 0.0785 | 0.1268 | 0.0540 | 0.0661 | 0.0993 | 0.0772 | 0.1240 | 0.0253 | 0.0552 | |
| TIES | 0.0905 | 0.1439 | 0.0622 | 0.0881 | 0.1201 | 0.0854 | 0.1303 | 0.0324 | 0.0613 | |
| AdaMerging (Domain-wise) | 0.0689 | 0.1261 | 0.0426 | 0.0720 | 0.0683 | 0.0562 | 0.1039 | 0.0267 | 0.0556 | |
| AdaMerging (Layer-wise) | 0.0778 | 0.1301 | 0.0504 | 0.0788 | 0.0833 | 0.0766 | 0.1114 | 0.0247 | 0.0675 | |
| 2-11 | MergeRec (Domain-wise) | 0.0913* | 0.1500* | 0.0636* | 0.0921* | 0.1074 | 0.0828 | 0.1363 | 0.0312 | 0.0673 |
| MergeRec (Layer-wise) | 0.0932* | 0.1515* | 0.0651* | 0.0921* | 0.1102 | 0.0869* | 0.1394* | 0.0312 | 0.0696 |
| Backbone | Method | Arts | Beauty | Inst. | Office | Pantry | Sci. | Sports | Toys | |
|---|---|---|---|---|---|---|---|---|---|---|
| RecFormer-base | Zero-shot | 0.0447 | 0.0717 | 0.0212 | 0.0415 | 0.0545 | 0.0381 | 0.0858 | 0.0118 | 0.0331 |
| Fine-tune | 0.0662 | 0.1128 | 0.0344 | 0.0743 | 0.1036 | 0.0550 | 0.0924 | 0.0166 | 0.0407 | |
| Joint Learning | 0.0484 | 0.0760 | 0.0259 | 0.0566 | 0.0691 | 0.0455 | 0.0666 | 0.0116 | 0.0356 | |
| 2-11 | Weight Averaging | 0.0551 | 0.0935 | 0.0263 | 0.0562 | 0.0728 | 0.0508 | 0.0921 | 0.0137 | 0.0351 |
| Task Arithmetic | 0.0557 | 0.0975 | 0.0261 | 0.0565 | 0.0791 | 0.0505 | 0.0920 | 0.0130 | 0.0307 | |
| TIES | 0.0567 | 0.0983 | 0.0274 | 0.0569 | 0.0842 | 0.0506 | 0.0902 | 0.0134 | 0.0326 | |
| AdaMerging (Domain-wise) | 0.0471 | 0.0851 | 0.0190 | 0.0448 | 0.0585 | 0.0391 | 0.0838 | 0.0113 | 0.0354 | |
| AdaMerging (Layer-wise) | 0.0408 | 0.0687 | 0.0110 | 0.0389 | 0.0532 | 0.0353 | 0.0763 | 0.0107 | 0.0322 | |
| 2-11 | MergeRec (Domain-wise) | 0.0570* | 0.0985 | 0.0263 | 0.0588* | 0.0796 | 0.0520* | 0.0929* | 0.0134 | 0.0346 |
| MergeRec (Layer-wise) | 0.0565 | 0.0972 | 0.0266 | 0.0578* | 0.0781 | 0.0516* | 0.0933* | 0.0136 | 0.0341 | |
| RecFormer-large | Zero-shot | 0.0357 | 0.0720 | 0.0174 | 0.0260 | 0.0317 | 0.0235 | 0.0788 | 0.0096 | 0.0266 |
| Fine-tune | 0.0667 | 0.1107 | 0.0346 | 0.0764 | 0.1015 | 0.0574 | 0.0954 | 0.0157 | 0.0419 | |
| Joint Learning | 0.0505 | 0.0798 | 0.0261 | 0.0508 | 0.0677 | 0.0499 | 0.0836 | 0.0134 | 0.0329 | |
| 2-11 | Weight Averaging | 0.0573 | 0.0956 | 0.0283 | 0.0584 | 0.0757 | 0.0543 | 0.0941 | 0.0143 | 0.0372 |
| Task Arithmetic | 0.0572 | 0.1036 | 0.0277 | 0.0593 | 0.0786 | 0.0526 | 0.0902 | 0.0128 | 0.0326 | |
| TIES | 0.0585 | 0.1042 | 0.0283 | 0.0616 | 0.0833 | 0.0530 | 0.0920 | 0.0131 | 0.0322 | |
| AdaMerging (Domain-wise) | 0.0449 | 0.0853 | 0.0197 | 0.0473 | 0.0578 | 0.0319 | 0.0791 | 0.0088 | 0.0292 | |
| AdaMerging (Layer-wise) | 0.0433 | 0.0786 | 0.0179 | 0.0410 | 0.0555 | 0.0357 | 0.0776 | 0.0110 | 0.0293 | |
| 2-11 | MergeRec (Domain-wise) | 0.0596* | 0.1066* | 0.0293* | 0.0617 | 0.0794 | 0.0540 | 0.0944 | 0.0138 | 0.0379* |
| MergeRec (Layer-wise) | 0.0591* | 0.1034 | 0.0295* | 0.0598 | 0.0788 | 0.0544 | 0.0950 | 0.0141 | 0.0380* | |
| BLaIR-base | Zero-shot | 0.0218 | 0.0368 | 0.0103 | 0.0178 | 0.0216 | 0.0238 | 0.0426 | 0.0052 | 0.0165 |
| Fine-tune | 0.0660 | 0.1119 | 0.0309 | 0.0742 | 0.1038 | 0.0582 | 0.0931 | 0.0153 | 0.0404 | |
| Joint Learning | 0.0518 | 0.0895 | 0.0301 | 0.0588 | 0.0702 | 0.0512 | 0.0633 | 0.0141 | 0.0372 | |
| 2-11 | Weight Averaging | 0.0516 | 0.0879 | 0.0265 | 0.0497 | 0.0672 | 0.0498 | 0.0881 | 0.0126 | 0.0306 |
| Task Arithmetic | 0.0365 | 0.0561 | 0.0160 | 0.0412 | 0.0543 | 0.0342 | 0.0620 | 0.0075 | 0.0209 | |
| TIES | 0.0493 | 0.0808 | 0.0226 | 0.0487 | 0.0816 | 0.0418 | 0.0768 | 0.0126 | 0.0296 | |
| AdaMerging (Domain-wise) | 0.0332 | 0.0577 | 0.0152 | 0.0308 | 0.0367 | 0.0251 | 0.0615 | 0.0105 | 0.0279 | |
| AdaMerging (Layer-wise) | 0.0382 | 0.0637 | 0.0176 | 0.0398 | 0.0465 | 0.0288 | 0.0723 | 0.0106 | 0.0263 | |
| 2-11 | MergeRec (Domain-wise) | 0.0517 | 0.0910* | 0.0253 | 0.0487 | 0.0732 | 0.0455 | 0.0858 | 0.0122 | 0.0316 |
| MergeRec (Layer-wise) | 0.0522 | 0.0909* | 0.0261 | 0.0497 | 0.0729 | 0.0477 | 0.0869 | 0.0125 | 0.0313 | |
| BLaIR-large | Zero-shot | 0.0172 | 0.0301 | 0.0091 | 0.0134 | 0.0141 | 0.0237 | 0.0278 | 0.0045 | 0.0150 |
| Fine-tune | 0.0642 | 0.1093 | 0.0328 | 0.0743 | 0.0991 | 0.0565 | 0.0865 | 0.0160 | 0.0388 | |
| Joint Learning | 0.0524 | 0.0886 | 0.0265 | 0.0635 | 0.0752 | 0.0521 | 0.0621 | 0.0136 | 0.0376 | |
| 2-11 | Weight Averaging | 0.0523 | 0.0910 | 0.0274 | 0.0533 | 0.0672 | 0.0513 | 0.0851 | 0.0135 | 0.0296 |
| Task Arithmetic | 0.0468 | 0.0802 | 0.0254 | 0.0425 | 0.0656 | 0.0462 | 0.0775 | 0.0121 | 0.0253 | |
| TIES | 0.0550 | 0.0937 | 0.0289 | 0.0567 | 0.0828 | 0.0508 | 0.0847 | 0.0145 | 0.0279 | |
| AdaMerging (Domain-wise) | 0.0386 | 0.0748 | 0.0191 | 0.0428 | 0.0421 | 0.0317 | 0.0623 | 0.0121 | 0.0242 | |
| AdaMerging (Layer-wise) | 0.0454 | 0.0810 | 0.0227 | 0.0497 | 0.0541 | 0.0456 | 0.0684 | 0.0113 | 0.0300 | |
| 2-11 | MergeRec (Domain-wise) | 0.0542 | 0.0948* | 0.0281 | 0.0584 | 0.0717 | 0.0494 | 0.0872* | 0.0138 | 0.0300 |
| MergeRec (Layer-wise) | 0.0556* | 0.0958* | 0.0292* | 0.0588 | 0.0743 | 0.0517 | 0.0901* | 0.0140 | 0.0310 |
📊 논문 시각자료 (Figures)









