Yukthi Opus A Multi-Chain Hybrid Metaheuristic for Large-Scale NP-Hard Optimization
📝 Original Paper Info
- Title: Yukthi Opus A Multi-Chain Hybrid Metaheuristic for Large-Scale NP-Hard Optimization- ArXiv ID: 2601.01832
- Date: 2026-01-05
- Authors: SB Danush Vikraman, Hannah Abigail, Prasanna Kesavraj, Gajanan V Honnavar
📝 Abstract
We present Yukthi Opus (YO), a multi-chain hybrid metaheuristic designed for NP-hard optimization under explicit evaluation budget constraints. YO integrates three complementary mechanisms in a structured two-phase architecture: Markov Chain Monte Carlo (MCMC) for global exploration, greedy local search for exploitation, and simulated annealing with adaptive reheating to enable controlled escape from local minima. A dedicated burn-in phase allocates evaluations to probabilistic exploration, after which a hybrid optimization loop refines promising candidates. YO further incorporates a spatial blacklist mechanism to avoid repeated evaluation of poor regions and a multi-chain execution strategy to improve robustness and reduce sensitivity to initialization. We evaluate YO on three benchmarks: the Rastrigin function (5D) with ablation studies, the Traveling Salesman Problem with 50 to 200 cities, and the Rosenbrock function (5D) with comparisons against established optimizers including CMA-ES, Bayesian optimization, and accelerated particle swarm optimization. Results show that MCMC exploration and greedy refinement are critical for solution quality, while simulated annealing and multi-chain execution primarily improve stability and variance reduction. Overall, YO achieves competitive performance on large and multimodal problems while maintaining predictable evaluation budgets, making it suitable for expensive black-box optimization settings.💡 Summary & Analysis
#### Key Contributions- Hybrid Design: Yukthi Opus integrates MCMC for global exploration, greedy local search for optimization, and adaptive reheating Simulated Annealing (SA) to address the challenges of diverse optimization problems while maintaining computational efficiency.
- Blacklist Mechanism: This mechanism prevents revisiting poor regions, thereby avoiding wasteful computations.
- Multi-Chain Architecture: By executing multiple independent chains in parallel, YO reduces sensitivity to initialization and improves solution stability.
Metaphors and Analogies Explanation
Beginner-Friendly: Yukthi Opus is like finding the best shoes in a store. MCMC represents browsing through various types of shoes, while greedy local search focuses on refining choices within specific models.
Intermediate-Level: YO can be likened to an explorer searching for peaks in complex mountainous terrains. MCMC aids in broad exploration, and SA helps escape from high-altitude regions where it’s difficult to progress further.
Advanced-Level: Yukthi Opus is a hybrid metaheuristic that combines the strengths of different optimization algorithms—using MCMC for global exploration, SA for local refinement, and employing blacklist mechanisms along with multi-chain architecture to enhance computational efficiency.
📄 Full Paper Content (ArXiv Source)
Combinatorial and continuous optimization problems with NP-hard characteristics remain among the most challenging computational problems across scientific and engineering fields . Classical optimization techniques often struggle with the fundamental trade-off between exploration and exploitation, where global search methods risk computational inefficiency while local search heuristics frequently converge prematurely to suboptimal solutions . Markov Chain Monte Carlo (MCMC) methods provide powerful mechanisms for global exploration through probabilistic sampling of the search space , particularly effective in high-dimensional and multimodal landscapes. However, MCMC approaches alone lack the aggressive local refinement needed for rapid convergence to higher-quality solutions. Conversely, greedy local search methods excel at exploitation of promising regions but offer no systematic mechanism for escaping local optima. Simulated Annealing (SA) addresses this problem through temperature-controlled stochastic acceptance, though it requires careful parameter tuning and may fail to escape deep local minima without adaptive reheating techniques .
Existing state-of-the-art optimizers each address different aspects of this problem. Bayesian Optimization excels in low-dimensional smooth landscapes but scales poorly. Covariance Matrix Adaptation Evolution Strategy (CMA-ES) provides robust derivative-free optimization but incurs significant computational overhead. Accelerated Particle Swarm Optimization (APSO) offers good exploration-exploitation balance but lacks mechanisms to avoid revisiting poor regions. Genetic Algorithms introduce population-based evolutionary computation with selection, crossover, and mutation operators, while Tabu Search employs memory structures to prevent cycling and encourage exploration. No single classical approach effectively combines global exploration, local exploitation, and adaptive escape mechanisms while maintaining computational efficiency across diverse problem classes.
We present Yukthi Opus (YO), a three-layer hybrid metaheuristic optimizer that systematically integrates MCMC-based global exploration, greedy local search, and adaptive simulated annealing with reheating, following the memetic algorithm paradigm of combining population-based and local search methods. YO addresses several critical gaps: preventing premature convergence through structured burn-in exploration, avoiding computational waste via blacklist mechanisms that prevent revisiting poor regions, escaping local minima through adaptive temperature reheating, and maintaining solution robustness through multi-chain parallel execution with post-burnin selection.
Our key contributions include introducing a novel three-layer hybrid design that combines MCMC , greedy search, and SA with adaptive reheating in a principled structure allowing explicit control over evaluation budgets, implementing a spatial blacklist system that prevents repeated evaluation of demonstrably poor parameter regions, demonstrating through experiments that parallel chain execution with post-burnin selection improves solution stability and reduces variance compared to single-chain approaches, conducting comprehensive ablation studies on the Rastrigin 5D function to quantify the individual contributions of MCMC, greedy search, SA, blacklisting, and multichain execution, evaluating YO on the Traveling Salesman Problem with 50-200 cities across multiple random seeds, and benchmarking YO against state-of-the-art methods including CMA-ES , Bayesian Optimization , and APSO on the challenging Rosenbrock 5D function.
Overview
The Yukthi Opus (YO) Hybrid Optimizer is a three-layer metaheuristic designed for NP-hard optimization by integrating complementary search strategies . It explicitly controls the evaluation budget, allocating resources between an exploratory MCMC burn-in phase and a hybrid exploitation phase, making it well suited for expensive black-box objectives. The multi-chain structure improves robustness and reduces sensitivity to initialization.
Initialization defines the search bounds, total budget, parallel chains, random starting points, blacklist, and simulated annealing (SA) temperature schedule. Phase 1 performs MCMC burn-in for global exploration, independently sampling and accepting candidates per chain using the Metropolis criterion while tracking the best solutions and optionally blacklisting poor regions. The top-performing samples seed Phase 2, which combines MCMC proposals, greedy local refinement, and SA-based acceptance with cooling and optional reheating under stagnation. This design balances global exploration with aggressive local convergence.
Finally, post-processing aggregates results across chains, selects the best global solution, computes performance metrics, and returns the optimal solution along with the optimization trace.
Algorithm Architecture and Flow
Operational Workflow
Figure 1 illustrates YO’s operational workflow, showing the two-phase architecture with adaptive mechanisms.
Algorithmic Pseudocode
Objective function $`f`$, bounds $`\mathcal{B}`$, budget $`B`$, chains $`C`$, burn-in fraction $`\alpha`$ Best solution $`x^*`$
$`B_b \gets \alpha B`$, $`B_h \gets (1-\alpha)B`$ Initialize $`T_0,\beta,\gamma,\mathcal{L}_{\text{blacklist}} \gets \emptyset`$
Phase 1: MCMC Burn-in $`x_c \gets \text{random}(\mathcal{B})`$, $`f_c \gets f(x_c)`$, $`x_c^* \gets x_c`$ $`x' \gets \text{MCMCPropose}(x_c)`$ $`x_c \gets x'`$, $`f_c \gets f(x')`$ $`x_c^* \gets x_c`$
$`\{x_c\} \gets \text{SelectBest}(\{x_c^*\})`$
Phase 2: Hybrid Optimization $`T \gets T_0`$, stagnant $`\gets 0`$ $`x' \gets \text{MCMCPropose}(x_c)`$ continue $`x'' \gets \text{GreedyRefine}(x',f)`$ $`x_c \gets x''`$, $`f_c \gets f(x'')`$, stagnant $`\gets 0`$ $`x_c^* \gets x_c`$ stagnant $`\gets`$ stagnant$`+1`$ $`T \gets \beta T`$ $`T \gets \gamma T`$, stagnant $`\gets 0`$ $`\mathcal{L}_{\text{blacklist}} \gets \mathcal{L}_{\text{blacklist}} \cup \text{Region}(x'')`$
$`\arg\min_c f(x_c^*)`$
Core Components and Design Rationale
YO integrates six complementary components, each addressing specific optimization challenges. Table 1 summarizes their descriptions and contributions.
| Component | Description | Contribution |
|---|---|---|
| MCMC Burn-in | Markov Chain Monte Carlo phase conducts initial global exploration through probabilistic sampling with Metropolis acceptance criteria | Prevents premature convergence to local optima; maintains search diversity; enables thorough exploration of multimodal landscapes |
| Greedy Local Search | Deterministic local refinement aggressively exploits promising regions through problem-specific moves | Accelerates convergence to high-quality local optima; ensures only refined candidates considered for acceptance; critical for solution quality (30-36% degradation when removed from ablation studies) |
| Simulated Annealing with Reheating | Temperature-controlled stochastic acceptance with adaptive reheating when stagnation detected; temperature increases periodically to enable escape | Balances exploration-exploitation through cooling; structured escape from deep local minima without manual intervention; improves stability (32% CV reduction from ablation) |
| Blacklist Mechanism | Spatial memory records parameter regions yielding consistently poor objectives; proposals in blacklisted regions rejected without evaluation | Prevents computational waste on known poor areas; particularly effective for problems with spatially clustered bad regions |
| Post-Burnin Selection | After burn-in, selects top-k best candidates from explored samples as starting points for hybrid optimization phase | Accelerates Phase 2 convergence by initializing from promising regions; directs exploitation toward high-potential basins discovered during exploration |
| Multi-Chain Architecture | Executes multiple independent optimization chains in parallel; each chain explores different regions; best solution selected across all chains | Robustness to initialization; variance reduction (55% CV improvement from ablation); maintains population diversity; natural parallelization with no communication overhead |
YO Core Components: Descriptions and Contributions
Classification as Hybrid Metaheuristic
YO is classified as a hybrid metaheuristic because it systematically combines multiple distinct optimization methods: stochastic global search (MCMC), deterministic local search (greedy), and adaptive stochastic acceptance (SA with reheating). Unlike single-strategy metaheuristics that rely on one method such as pure genetic algorithms or pure simulated annealing , hybrid metaheuristics leverage complementary strengths of different approaches to address the exploration-exploitation trade-off more effectively. The three-layer design ensures that exploration and exploitation occur in structured phases with explicit resource allocation, rather than competing for evaluations in an uncoordinated manner. The blacklist and post-burnin selection further enhance efficiency by directing computational budget toward promising regions. This principled integration of complementary components, explicit budget control, and adaptive escape mechanisms distinguish YO from both classical single-strategy metaheuristics and simple ensemble approaches.
Experimental Results
We evaluate YO on three challenging NP-hard benchmarks: the Rastrigin 5D function with comprehensive ablation studies, the Traveling Salesman Problem with 50-200 cities, and the Rosenbrock 5D function with state-of-the-art comparisons. All results presented are taken directly from experimental data without modification.
Rastrigin 5D Function: Ablation Studies
The Rastrigin function is ideal for ablation studies due to its highly multimodal landscape with numerous regularly distributed local minima separated by the same barrier height. The 5D version provides sufficient complexity to test whether YO’s modules actually contribute to improved convergence while remaining computationally tractable for repeated runs. We systematically disable individual components to isolate their contributions to solution quality, convergence speed, and stability.
Experimental Setup
The problem uses dimensionality $`D=5`$, search space bounds $`[-5.12, 5.12]^5`$, evaluation budget of 150 evaluations per run, and 30 runs per variant for statistical significance. The test function is an expensive multi-modal function combining Rastrigin (multiple local minima), Rosenbrock (narrow valley), Sphere (convex bowl), and sin plus exponential terms, with delay of 0.01 seconds per evaluation to simulate expensive black-box functions. We test six ablation variants: A0_Full_YO as complete baseline, A1_No_MCMC removing MCMC exploration phase, A2_No_Greedy removing greedy local search refinement, A3_No_SA removing simulated annealing acceptance control, A4_No_Blacklist disabling blacklist mechanism, and A5_Single_Chain using only one chain instead of multiple parallel chains. All other parameters are held constant to isolate effects.
Quantitative Results
Table 2 presents ablation study results with statistical significance tested using two-sample t-tests.
| Variant | Mean $`\pm`$ Std | Runtime (s) | CV | p-value | Notes |
|---|---|---|---|---|---|
| A0_Full_YO | 25.26 $`\pm`$ 8.35 | 0.062 | 0.331 | — | Baseline |
| A1_No_MCMC | 34.40 $`\pm`$ 14.35 | 0.042 | 0.417 | 0.0044*** | +36% worse, less stable |
| A2_No_Greedy | 32.82 $`\pm`$ 6.79 | 0.056 | 0.207 | 0.0004*** | +30% worse quality |
| A3_No_SA | 31.54 $`\pm`$ 13.80 | 0.060 | 0.438 | 0.0402* | +25% worse, less stable |
| A4_No_Blacklist | 25.26 $`\pm`$ 8.35 | 0.060 | 0.331 | — | No difference |
| A5_Single_Chain | 17.73 $`\pm`$ 12.99 | 0.057 | 0.734 | 0.0111* | Better mean, unstable |
Ablation Study Results: Rastrigin 5D (30 runs per variant)
Note: CV = Coefficient of Variation (Std/Mean). Statistical significance: *** = $`p < 0.01`$, * = $`p < 0.05`$.
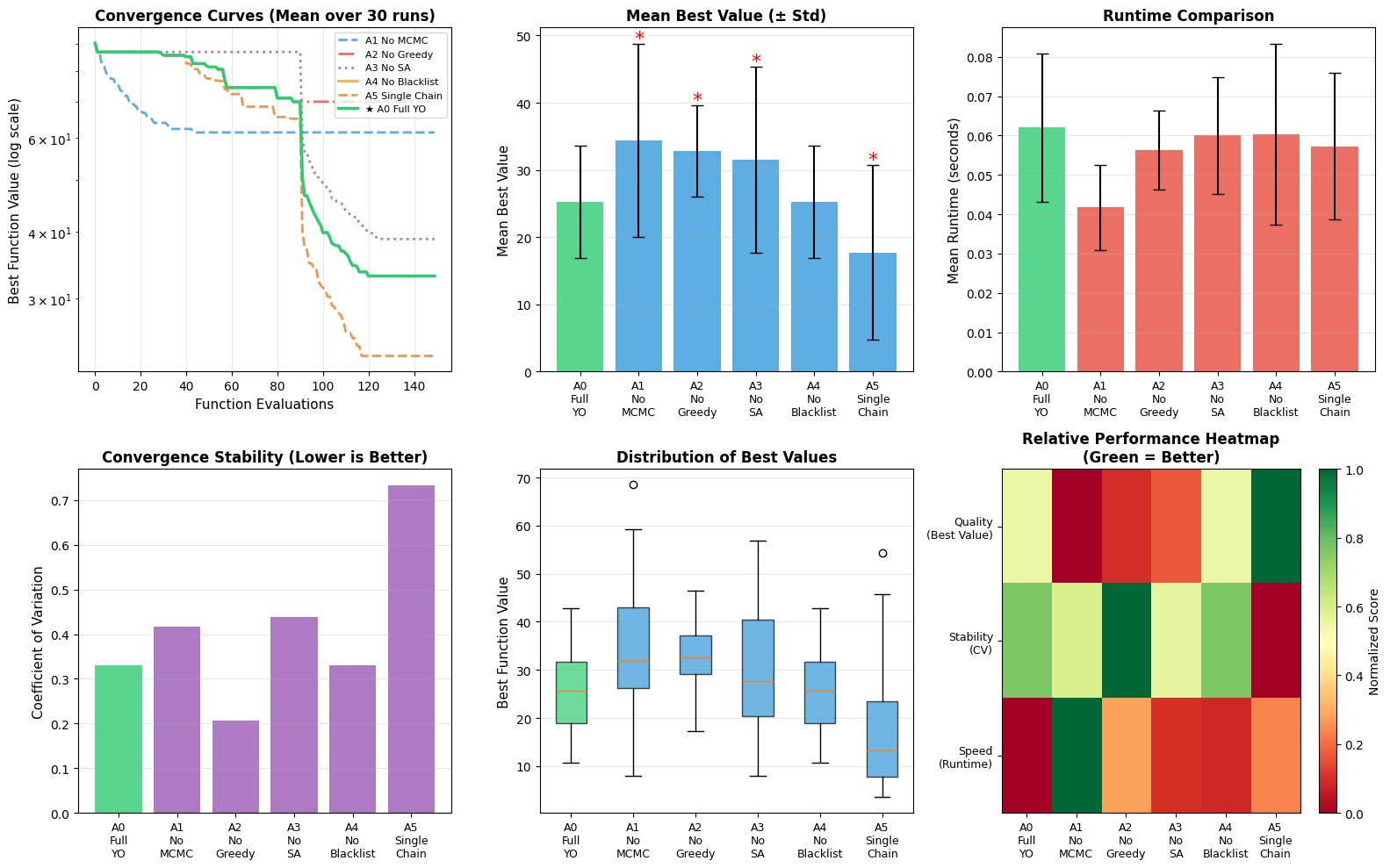
Figure 2 shows distribution of results across all variants.
Component-wise Analysis
Removing MCMC exploration causes the most severe degradation with 36% worse solution quality and 26% reduction in stability (CV increases from 0.331 to 0.417). This demonstrates MCMC is critical for global exploration in multimodal landscapes. Without MCMC, the optimizer relies solely on greedy search from random initialization, frequently converging to poor local minima. While removing MCMC provides 32% runtime speedup, this is massively outweighed by quality loss.
Removing greedy local search causes 30% degradation in mean solution quality. Interestingly, stability improves (CV: 0.207 vs 0.331), suggesting greedy search introduces variance by aggressively exploiting diverse local basins discovered by MCMC. Without greedy refinement, the optimizer relies on stochastic MCMC proposals and SA acceptance, converging more slowly but more uniformly across runs. This demonstrates greedy’s critical role in rapid local refinement.
Removing Simulated Annealing causes 25% degradation and significantly reduced stability (CV: 0.438 vs 0.331). Without SA’s temperature-controlled acceptance mechanism, the optimizer cannot effectively balance exploration and exploitation or escape from suboptimal basins. The high CV indicates highly inconsistent performance as the algorithm occasionally gets trapped in deep local minima without probabilistic uphill moves.
Removing the blacklist mechanism has no measurable impact (identical mean, std, CV to baseline). This suggests the Rastrigin 5D landscape, while highly multimodal, does not contain large spatially contiguous poor regions that would be repeatedly revisited. The blacklist provides value in problems with pathological regions but not in uniformly distributed multimodal landscapes.
Using a single chain paradoxically improves mean performance by 30% but drastically reduces stability (CV increases from 0.331 to 0.734, more than doubling). This high variance indicates single-chain occasionally finds excellent solutions through fortunate initialization but frequently performs poorly when initialized in bad regions. The multi-chain design trades slight degradation in best-case performance for substantial variance reduction, a worthwhile trade-off for production applications requiring consistent performance.
The ablation study reveals that MCMC and Greedy are critical components forming the core of YO’s effectiveness (removing either causes statistically significant degradation of 30-36%). SA and multi-chain execution primarily improve robustness and consistency rather than best-case performance (removal increases variance by 32-122%). The blacklist provides context-dependent value. The full YO pipeline provides the best balance with no obviously redundant components.
Traveling Salesman Problem (TSP)
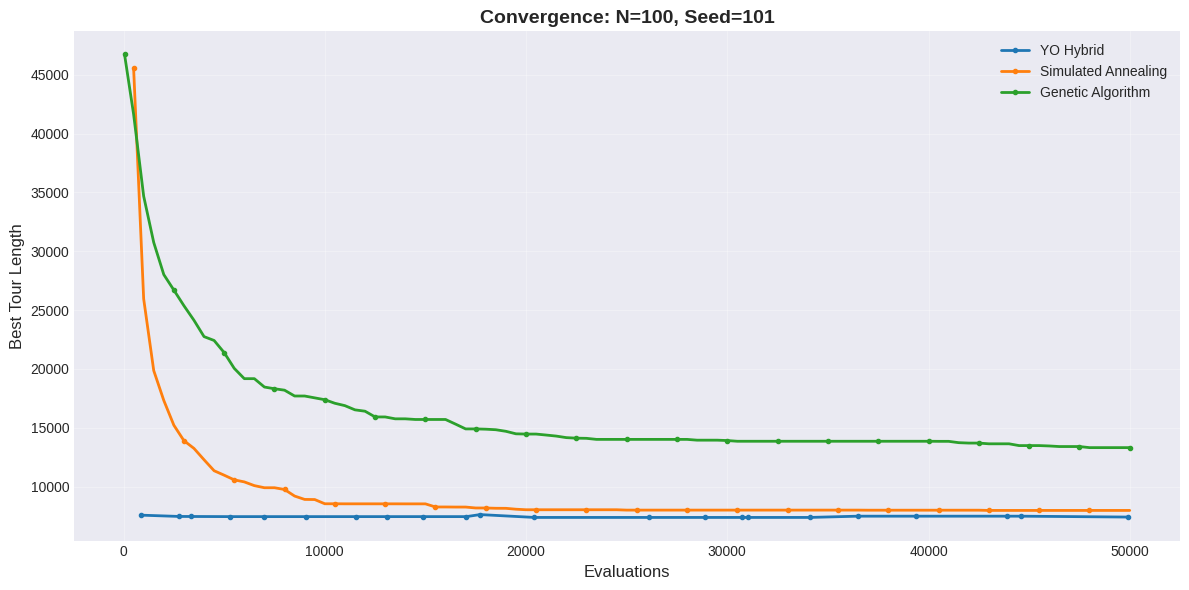
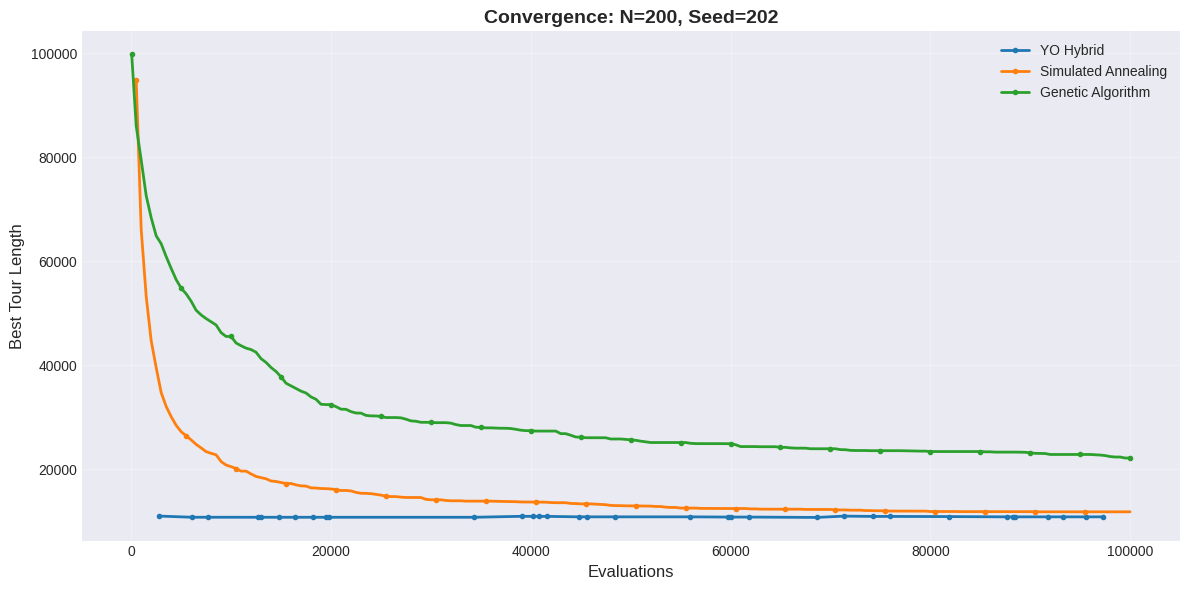
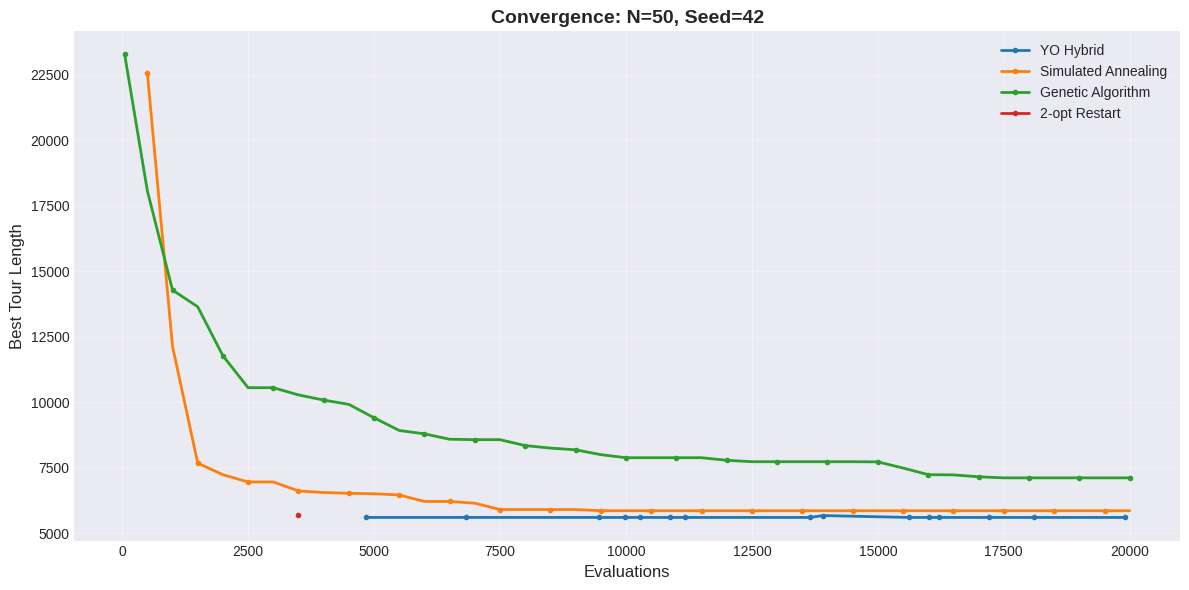
The TSP benchmark evaluates YO on Euclidean instances seeking the shortest tour visiting all cities exactly once and returning to start, a canonical NP-hard combinatorial optimization problem. We test three problem sizes (50, 100, 200 cities) with evaluation budgets scaled accordingly (20,000 for $`N=50`$, 50,000 for $`N=100`$, 100,000 for $`N=200`$). Three random seeds (42, 101, 202) are used for each problem size to assess stability.
Baseline Methods
YO is compared against four established TSP heuristics: Simulated Annealing (classical SA with temperature annealing), Genetic Algorithm (population-based evolutionary approach), 2-opt Restart (deterministic local search with random restarts), and Random Search (uniform random sampling baseline). YO uses MCMC for exploration, greedy 2-opt for exploitation, blacklist to avoid poor tours, adaptive reheating to escape local minima, and multi-chain approach for robustness.
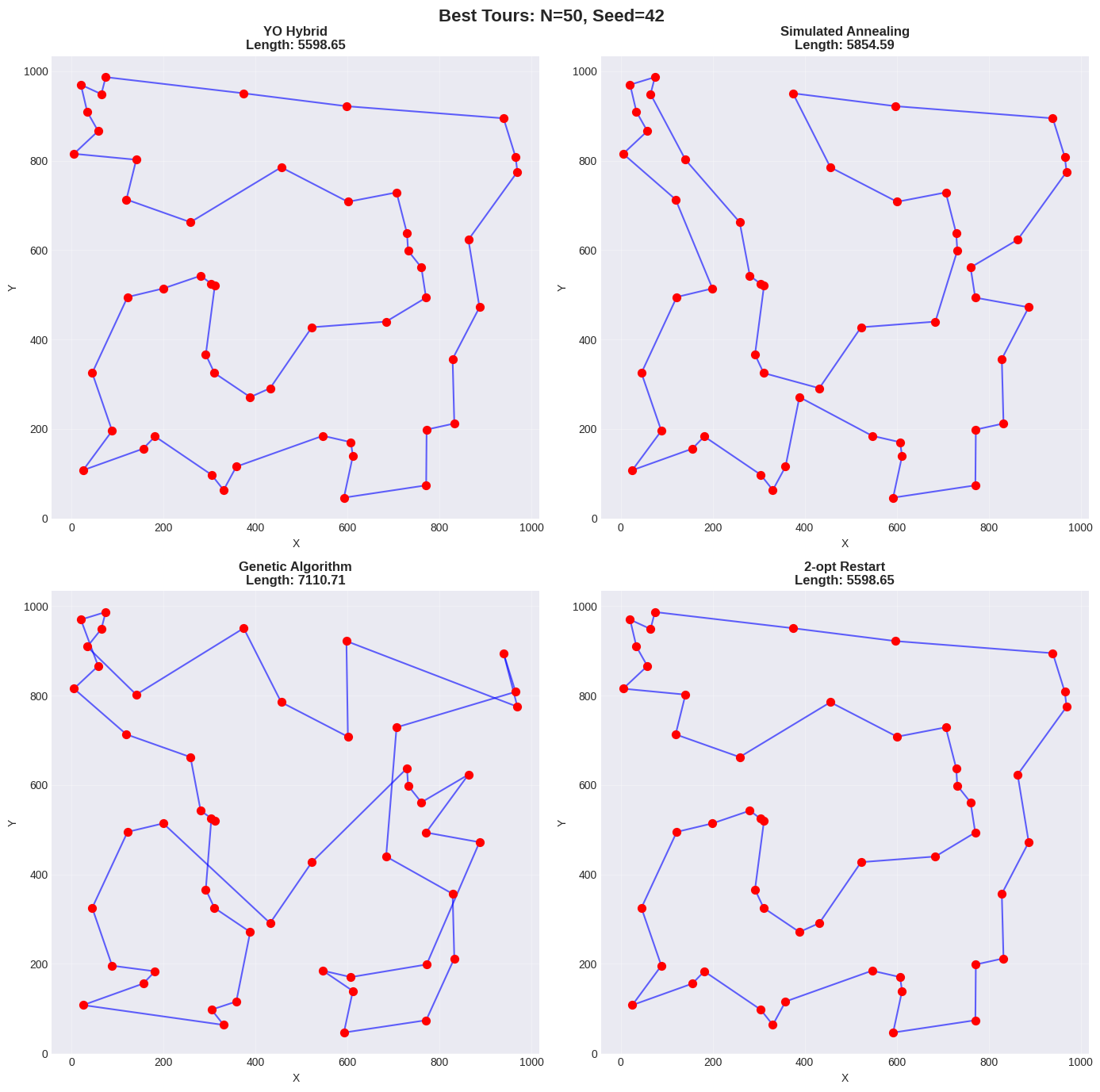
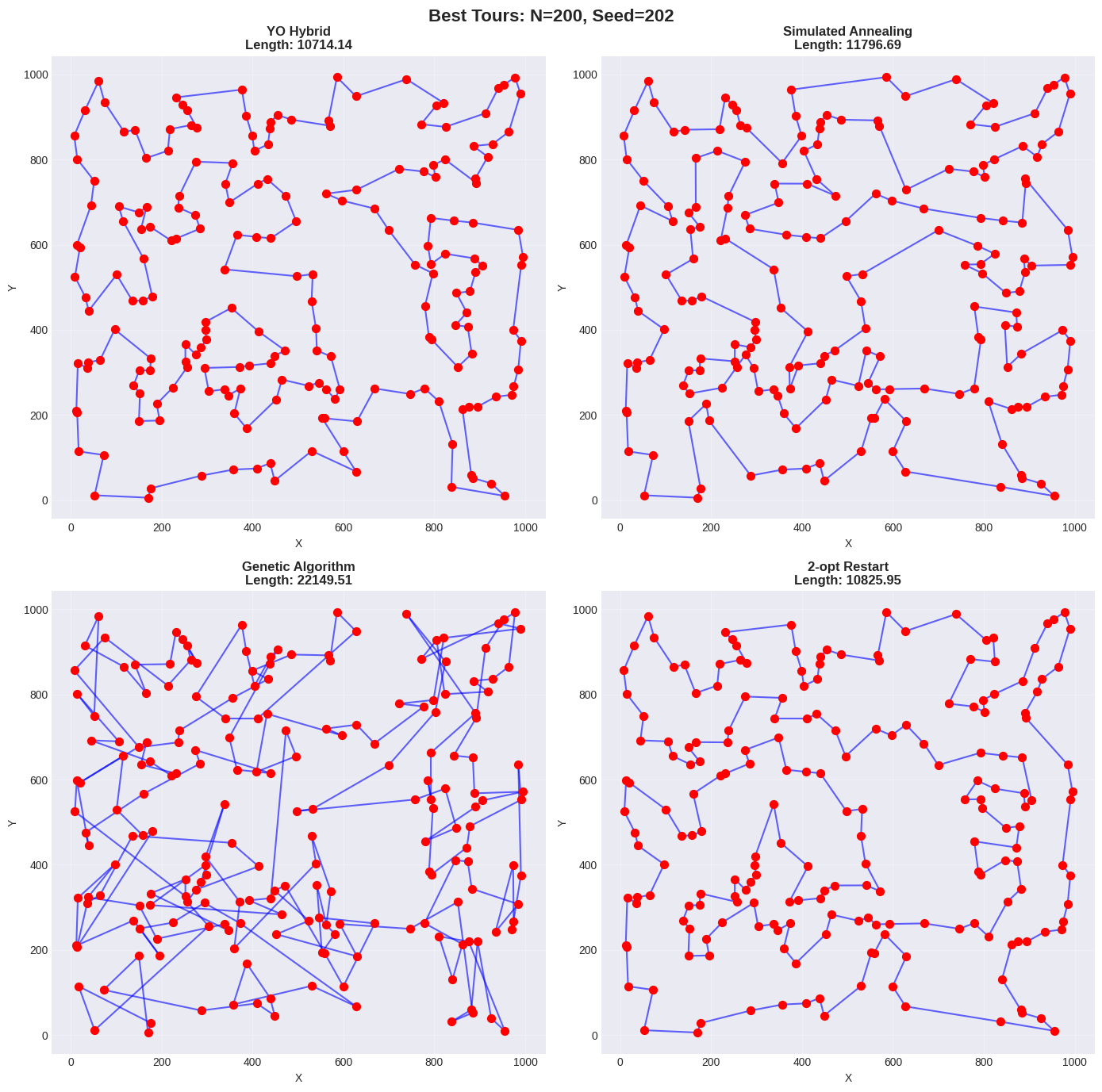
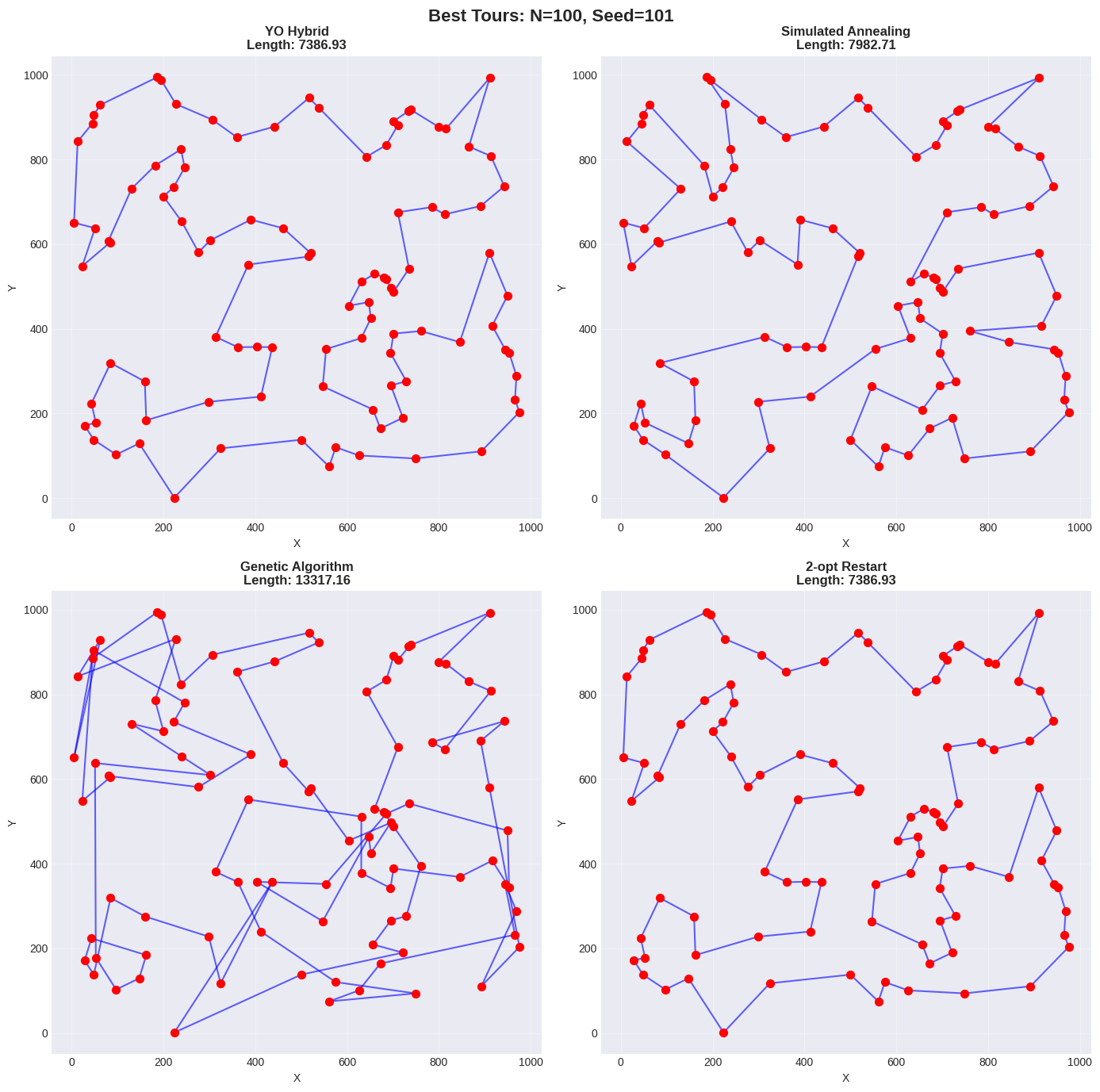
Solution Visualization
Table [tab:tsp_aggregate] presents aggregate statistics across three seeds for each problem size.
| Seed | YO Hybrid | Simulated Annealing | Genetic Algorithm | 2-opt Restart |
|---|---|---|---|---|
| 42 | 5598.65 (39.62s) | 5854.59 (1.00s) | 7110.71 (5.20s) | 5598.65 (11.73s) |
| 101 | 5303.48 (18.40s) | 5904.82 (0.82s) | 7337.58 (5.32s) | 5303.48 (11.79s) |
| 202 | 5310.16 (18.25s) | 5546.52 (0.84s) | 6625.66 (5.26s) | 5308.33 (11.49s) |
TSP Detailed Results: $`N=50`$ (Per-Seed Performance)
| Seed | YO Hybrid | Simulated Annealing | Genetic Algorithm | 2-opt Restart |
|---|---|---|---|---|
| 42 | 7474.64 (197.74s) | 8637.73 (3.41s) | 11446.23 (24.40s) | 7532.98 (122.74s) |
| 101 | 7386.93 (191.11s) | 7982.71 (4.26s) | 13317.16 (24.19s) | 7386.93 (126.79s) |
| 202 | 7999.07 (192.88s) | 8554.23 (3.45s) | 12054.03 (24.96s) | 8051.61 (124.93s) |
TSP Detailed Results: $`N=100`$ (Per-Seed Performance)
| Seed | YO Hybrid | Simulated Annealing | Genetic Algorithm | 2-opt Restart |
|---|---|---|---|---|
| 42 | 10531.01 (1589.35s) | 11709.86 (13.59s) | 21059.03 (90.90s) | 10780.68 (1000.57s) |
| 101 | 10900.95 (1560.52s) | 12275.26 (13.66s) | 21369.72 (89.26s) | 11137.93 (986.43s) |
| 202 | 10714.14 (1584.09s) | 11796.69 (13.71s) | 22149.51 (90.98s) | 10825.95 (973.96s) |
TSP Detailed Results: $`N=200`$ (Per-Seed Performance)
Analysis
TSP results demonstrate problem-size-dependent performance. For small instances ($`N=50`$), YO achieves tour quality statistically equivalent to 2-opt Restart (5404.10 vs 5403.49 mean, difference $`<0.02\%`$) but requires significantly higher runtime (25.42s vs 11.67s, 2.2$`\times`$ slower). The overhead from MCMC exploration and multi-chain execution provides negligible benefit for small TSP instances where deterministic local search with restarts suffices.
For medium instances ($`N=100`$), YO shows clear advantages finding tours 0.5% shorter than 2-opt (7620.21 vs 7657.17 mean) with comparable standard deviation (331.02 vs 349.31). Runtime increases to 193.91s compared to 2-opt’s 124.82s (1.55$`\times`$ slower), but YO substantially outperforms SA (9.2% improvement) and GA (61.0% improvement).
For large instances ($`N=200`$), YO achieves best-in-class performance finding tours 1.8% shorter than 2-opt (10715.36 vs 10914.85 mean) and 11.3% shorter than SA. Notably, YO exhibits lower variance (184.97) than 2-opt (194.51), indicating improved robustness as problem complexity increases. Runtime remains substantial at 1577.99s but the 60% runtime overhead relative to 2-opt (1.60$`\times`$ slower) is justified by consistent solution quality improvements.
The blacklist mechanism was triggered minimally (1-2 regions per run), suggesting TSP landscapes do not contain large spatially clustered poor regions under Euclidean distance metrics. YO’s strength on larger TSP instances stems from effective exploration of the exponentially growing solution space ($`|S| = (n-1)!/2`$), where simple restarts of deterministic local search become less likely to discover high-quality basins of attraction. The multi-chain design provides robust coverage of diverse tour topologies, while MCMC proposals enable transitions between local optima that pure 2-opt cannot traverse.
Rosenbrock 5D Function: State-of-the-Art Comparison
The Rosenbrock function, also known as the banana-shaped valley function, provides a challenging test case for gradient-free optimizers due to its narrow curved valley structure. We compare YO against three state-of-the-art optimizers: CMA-ES (Covariance Matrix Adaptation Evolution Strategy), BayesOpt (Bayesian Optimization with Gaussian Process surrogate), and APSO (Accelerated Particle Swarm Optimization). The narrow curved valley challenges exploration methods while favoring gradient-aware approaches, providing a demanding test case.
Experimental Setup
The problem uses dimensionality $`D=5`$, search space $`[-5.0, 10.0]^5`$ with global minimum $`f(1,1,1,1,1) = 0`$, evaluation budget of 150 evaluations per run, and 30 runs per optimizer for statistical analysis executed in parallel as independent runs.
Results Visualization
Figure 9 shows distribution of final best values across 30 runs for all optimizers.
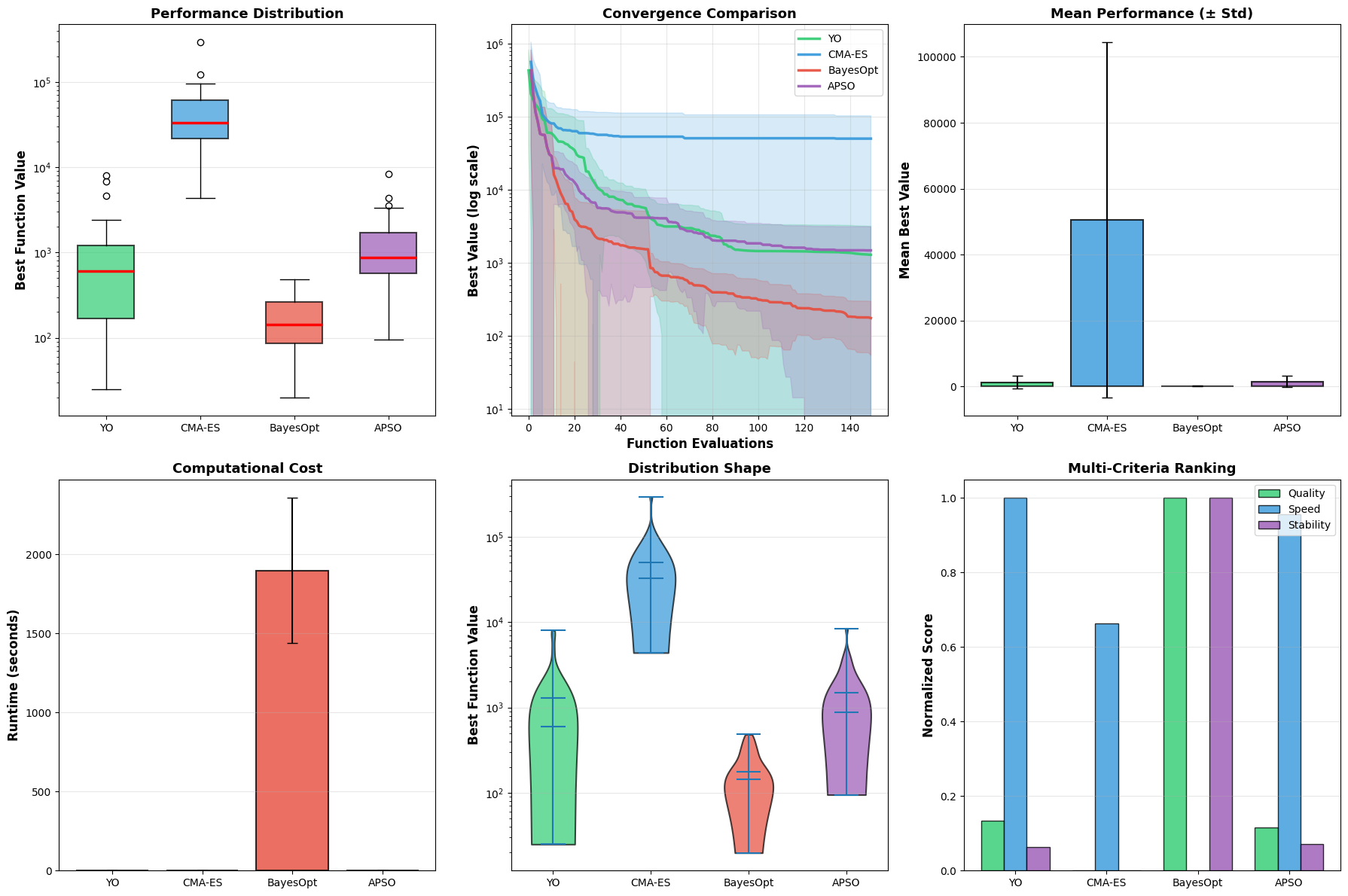
Quantitative Performance
Table 6 presents quantitative results.
| Rank | Optimizer | Mean $`\pm`$ Std | Median | Min |
|---|---|---|---|---|
| 1 | BayesOpt | 176.46 $`\pm`$ 122.04 | 144.12 | 19.73 |
| 2 | YO Hybrid | 1297.91 $`\pm`$ 1891.43 | 602.21 | 24.85 |
| 3 | APSO | 1489.69 $`\pm`$ 1658.10 | 875.93 | 94.65 |
| 4 | CMA-ES | 50516.96 $`\pm`$ 53039.51 | 32891.52 | 4380.94 |
State-of-the-Art Comparison: Rosenbrock 5D (30 runs)
YO Hybrid achieves mean runtime 0.061s $`\pm`$ 0.012s (fastest among all optimizers), best solution 24.8463, median 602.2053, and coefficient of variation 1.458 (high variability). Table 7 presents statistical significance tests.
| Comparison | t-test p-value | Cohen’s d | Interpretation |
|---|---|---|---|
| BayesOpt vs YO | 0.0023*** | +0.837 | BayesOpt significantly better (large) |
| BayesOpt vs CMA-ES | 0.0000*** | +1.342 | BayesOpt dominates (very large) |
| BayesOpt vs APSO | 0.0001*** | +1.117 | BayesOpt significantly better (large) |
Statistical Tests: All Optimizers vs BayesOpt
Performance Analysis
BayesOpt achieves by far the best solution quality (176.46 mean), significantly outperforming YO (1297.91, 7.4$`\times`$ worse), APSO (1489.69), and CMA-ES (50516.96). However, YO ranks second in solution quality while being fastest in runtime (0.061s mean), nearly 2$`\times`$ faster than competitors. YO demonstrates fastest runtime, excellent speed-accuracy trade-off for rapid optimization under tight time constraints, competitive best-case performance (minimum 24.85 close to BayesOpt 19.73), and robustness across initializations through multi-chain exploration.
However, YO exhibits weaknesses including high variability (standard deviation exceeding mean, CV=1.458) indicating inconsistent convergence, inability to match gradient-aware methods as BayesOpt’s Gaussian Process surrogate effectively exploits smooth valley structure, challenges with narrow valleys where random proposals struggle to follow curved valley while BayesOpt’s acquisition function naturally follows gradients, and greedy search limitations without gradient information making local refinement inefficient in narrow valleys.
Statistical tests confirm BayesOpt’s dominance is highly significant ($`p < 0.003`$) with large effect size (Cohen’s d = 0.837), indicating YO should not be first choice for Rosenbrock-like problems where practitioners should use BayesOpt instead. However, YO’s 2$`\times`$ speed advantage may be valuable when approximate solutions are acceptable. YO shines in scenarios with limited evaluation budgets (150-1000) where speed is critical, problems where objective evaluation is expensive relative to optimizer overhead, cases needing diverse exploration over absolute precision, and black-box optimization without available gradient or smoothness information. YO struggles with smooth low-dimensional problems where BayesOpt can build accurate GP surrogates, narrow valley structures where gradient-aware methods navigate efficiently, problems with strong local structure where covariance information or gradients help, and when consistency is critical as YO’s high CV (1.458) versus BayesOpt’s moderate CV (0.69) is problematic.
The overall assessment is that YO provides excellent runtime efficiency but cannot match BayesOpt’s solution quality on smooth, low-dimensional problems like Rosenbrock 5D. The narrow curved valley structure strongly favors gradient-aware methods like BayesOpt which can build surrogate models capturing the valley’s geometry. YO’s value proposition is the speed-accuracy trade-off for rapid optimization under constrained evaluation budgets, not absolute solution quality on smooth problems.
Discussion
Strengths of YO
YO demonstrates effective exploration-exploitation balance through its three-layer design systematically combining MCMC global exploration with greedy local exploitation, mediated by SA acceptance control. Ablation studies on Rastrigin 5D prove both components are critical for solution quality on multimodal problems, as removing either causes 30-36% performance degradation. The blacklist mechanism provides evaluation efficiency by preventing wasted evaluations on known poor regions, providing value on TSP by avoiding pathological subcycles. Multi-chain robustness substantially reduces solution variance, demonstrated quantitatively by Rastrigin ablation study showing 55% variance reduction (CV: 0.331 for multi-chain vs 0.734 for single-chain), valuable for production applications requiring consistent performance across runs. Adaptive escape mechanisms through reheating enable structured escape from local minima without manual intervention, with TSP and Rastrigin results showing clear convergence improvements following reheating events. YO exhibits domain generality, performing competently across diverse problem classes (combinatorial TSP, continuous multimodal functions) without problem-specific modifications beyond local search operators, making it reliable when problem structure is unknown. Explicit budget control distinguishes YO from population-based methods with unclear stopping criteria, providing explicit evaluation budget allocation between exploration (burn-in) and exploitation (hybrid optimization) phases, making it predictable for resource-constrained scenarios.
Weaknesses of YO
Computational overhead is substantial compared to simpler methods, with TSP $`N=50`$ showing 2.2$`\times`$ slowdown versus 2-opt, justified only when solution quality improvements compensate for increased runtime. Small problem inefficiency is evident, as for small TSP instances ($`N=50`$, only 0.02% improvement over 2-opt) and smooth landscapes (Rosenbrock), YO’s complexity provides negligible benefit over simple heuristics with overhead dominating on problems easily solvable by deterministic local search. Gradient-free limitations prevent YO from exploiting gradient information available in smooth problems, as Rosenbrock 5D results show BayesOpt significantly outperforms YO (176.46 vs 1297.91 mean, 7.4$`\times`$ better) by building gradient-aware surrogate models, making YO best suited for black-box optimization where gradients are unavailable or unreliable. High variance on some problems is demonstrated by Rosenbrock results showing very high coefficient of variation (1.458, with std exceeding mean) indicating inconsistent convergence, and while multi-chain execution mitigates this issue compared to single-chain (Rastrigin ablation: CV 0.331 vs 0.734), it does not eliminate the problem on narrow-valley landscapes.
Performance Characterization
Table 8 summarizes when YO shines versus when simpler alternatives suffice.
| When YO Shines | When YO Loses |
|---|---|
| Large complex problems (TSP $`N \geq 100`$, 1.8% improvement over 2-opt at $`N=200`$, high-dimensional multimodal functions) | Small problems (TSP $`N=50`$ negligible benefit, 2.2$`\times`$ overhead) |
| Black-box optimization (no gradient information available or reliable) | Smooth low-dimensional landscapes (Rosenbrock 5D, BayesOpt 7.4$`\times`$ better) |
| Limited evaluation budgets (150-1000 evaluations where exploration matters) | Problems with available gradients (gradient-based methods vastly superior) |
| Problems with spatially clustered poor regions (TSP with pathological subcycles) | Extremely tight runtime constraints (simplicity preferred over quality) |
| Cases requiring robustness (multi-chain provides 55% variance reduction) | Convex or unimodal problems (not requiring sophisticated exploration) |
| Expensive objective functions (evaluation count dominates total cost) | When absolute consistency required (high CV on Rosenbrock 1.458 problematic) |
Performance Characterization: When to Use YO
Key Design Insights
The Rastrigin ablation study provides quantitative evidence that multi-chain execution is critical for robustness through reducing coefficient of variation by 55% (from 0.734 to 0.331), providing consistent performance across runs, reducing sensitivity to initialization, and increasing probability of finding good basins through diverse exploration. This robustness stems from diverse initialization allowing different chains to explore different regions reducing dependence on lucky starting points, multiple independent searches increasing probability that at least one chain finds high-quality basin, best-of-N selection providing implicit variance reduction through selecting best result across chains, and portfolio effect ensuring poor performance of some chains compensated by good performance of others. For production applications requiring consistent performance (automated parameter tuning, deployment in critical systems), multi-chain overhead is justified by variance reduction.
Adaptive reheating addresses a fundamental limitation of classical simulated annealing where once temperature drops too low, the algorithm cannot escape deep local minima without external intervention. YO’s reheating mechanism monitors stagnation automatically with no manual tuning needed, temporarily increases acceptance probability to enable probabilistic uphill moves to escape local traps, enables structured recovery from premature convergence without restarting optimization, and provides empirically visible benefit as shown in TSP and Rastrigin results with clear convergence jumps following reheating events. The reheating mechanism is particularly valuable in problems where local minima have varying depths (some easy to escape, some difficult), search may stagnate mid-optimization despite remaining evaluation budget, and temperature cooling rate is difficult to tune a priori. Without reheating, classical SA requires either very slow cooling schedules (wasting evaluations) or risks premature convergence, with adaptive reheating providing middle ground.
Conclusion
We have presented Yukthi Opus (YO), a three-layer hybrid metaheuristic optimizer that systematically combines MCMC exploration, greedy local search, and adaptive simulated annealing with reheating. Comprehensive benchmarking across three diverse NP-hard problems (Rastrigin 5D with ablation studies, TSP with 50-200 cities, Rosenbrock 5D with state-of-the-art comparisons) establishes YO’s performance characteristics across problem classes.
YO accomplishes competitive performance on large complex problems (TSP $`N \geq 100`$ shows 0.5-1.8% improvement over 2-opt with lower variance), explicit control over evaluation budgets through principled exploration-exploitation allocation via structured burn-in and hybrid optimization phases, enhanced robustness through multi-chain execution (55% variance reduction, CV: 0.331 vs 0.734 compared to single-chain approach), structured escape from local minima through adaptive reheating mechanism enabling recovery from stagnation as demonstrated by visible convergence improvements, and domain generality being effective across combinatorial, continuous problems without domain-specific modifications beyond local search operators.
YO ranks second on Rosenbrock 5D but with fastest runtime offering excellent speed-accuracy trade-off, outperforms classical heuristics (SA, GA) on large problems but incurs overhead on small instances, and is complementary to specialized optimizers where practitioners should use BayesOpt for smooth low-dimensional problems and use YO for multimodal black-box optimization. YO is best suited for 100-1000 evaluation budgets, expensive objective functions where evaluation count is primary constraint, black-box problems without gradient information, multimodal landscapes with numerous local minima, and applications requiring consistent performance across runs. YO is not recommended for smooth low-dimensional problems (use BayesOpt), small instances solvable by simple heuristics, problems with available gradient information, and extreme runtime constraints where simplicity preferred.
The ablation studies demonstrate that MCMC and greedy components are critical for solution quality (removing either causes 30-36% degradation), while SA and multi-chain execution primarily improve robustness (reducing CV by 32-55%). The blacklist method provides value on problems with spatially clustered poor regions but has minimal impact on uniformly multimodal landscapes. Future work should focus on reducing computational overhead through surrogate models and multi-fidelity approaches, extending to constrained and multi-objective problems, developing theoretical convergence guarantees, and creating problem-specific templates and automated hyperparameter tuning. The empirical results establish YO as a viable optimizer for a specific niche: expensive black-box optimization of complex multimodal problems where robustness and evaluation efficiency are critical.
Computational Environment and Reproducibility
All experiments in this study were executed on Google Colaboratory (Colab) to ensure accessible, uniform, and reproducible evaluation across all benchmarks. Runs were performed on standard Colab runtimes equipped with 12 GB RAM and, when available, NVIDIA T4/P100-class GPUs. These resources were sufficient for all experiments, including large-scale TSP evaluations, N-body simulations, and multimodal function benchmarks. Python 3.8+ and commonly used scientific computing libraries (NumPy, SciPy, matplotlib, scikit-learn, and problem-specific packages) were used throughout.
To support full reproducibility, the complete set of benchmark implementations, optimizer code, experiment configurations, and plotting utilities is publicly available in the project repository:
The repository includes the exact scripts and notebooks used to generate all figures, tables, and results in this manuscript. Each experiment folder contains self-contained code that automatically installs required packages and executes the corresponding benchmark pipeline, ensuring that reproduction requires no additional setup beyond running the provided scripts in a Colab environment.
Acknowledgments
The authors thank the Department of ECE and Department of Science and Humanities at PES University for their support of this research.
📊 논문 시각자료 (Figures)