Machine Learning

Robust and Efficient Zeroth-Order LLM Fine-Tuning via Adaptive Bayesian Subspace Optimizer

Reading time: 45 minute
...
#paper #research

πŸ“ Original Paper Info

- Title: Robust and Efficient Zeroth-Order LLM Fine-Tuning via Adaptive Bayesian Subspace Optimizer
- ArXiv ID: 2601.01452
- Date: 2026-01-04
- Authors: Jian Feng, Zhihong Huang

πŸ“ Abstract

Fine-tuning large language models (LLMs) with zeroth-order (ZO) optimization reduces memory by approximating gradients through function evaluations. However, existing methods essentially perform updates in a one-dimensional space, and suffer from collapse or substantial performance degradation under low-precision training. We introduce BSZO, an adaptive \textbf{B}ayesian \textbf{S}ubspace \textbf{Z}eroth-Order \textbf{O}ptimizer, which applies Kalman filtering to combine finite-difference information across multiple perturbation directions within a subspace. By treating each finite-difference measurement as a noisy observation, BSZO builds a posterior distribution over the subspace-projected gradient and updates it through Bayesian inference, with a residual-based adaptive mechanism to adapt to noise variations. Theoretical analysis shows that BSZO improves the convergence rate by a factor of $k/Ξ³$ compared to standard ZO methods. Experiments on RoBERTa, Mistral, and OPT models show that BSZO outperforms the baselines across various tasks, achieving up to 6.67\% absolute average improvement on OPT-13B while remaining robust under fp16/bf16 precision and keeping memory usage close to inference-only baselines (1.00$\times$--1.08$\times$ of MeZO).

πŸ’‘ Summary & Analysis

1. **Utilization of Bayesian Inference and Kalman Filtering** The BSZO algorithm uses Bayesian inference and Kalman filtering to integrate gradient information across multiple perturbation directions. This approach links data from different angles into a unified estimate, leading to more accurate gradient estimation. It's akin to synthesizing opinions from various people by considering the interrelation between their viewpoints rather than evaluating them independently.

  1. Adaptive Residual-Based Mechanism
    The BSZO introduces an adaptive mechanism based on residuals that allows it to adapt to changing curvature conditions during training. This effectively handles noise and improves training stability, leading to faster convergence compared to other methods.

  2. Balancing Convergence Speed and Memory Usage
    Traditional zeroth-order optimizers often require excessive time or memory for learning. BSZO overcomes these limitations by enhancing convergence speed while reducing memory consumption, thus enabling more efficient learning.

πŸ“„ Full Paper Content (ArXiv Source)

# Introduction

Large language models (LLMs) are getting increasingly important in natural language understanding and generation . However, adapting these models to downstream tasks through fine-tuning remains challenging due to their large scale. The standard approach, using first-order optimizers like Adam, requires consuming a large amount of GPU memory. For a 13B-parameter model, this translates to over 100GB of GPU memory, roughly 10$`\times`$ the cost of inference alone . Such requirements put full fine-tuning out of reach for most people, no matter in academia or industry.

Several strategies have been proposed to reduce memory burden. Parameter-efficient fine-tuning (PEFT) methods, including LoRA and Adapters , freeze the base model and only update a small set of additional parameters. But these methods still rely on backpropagation and may underperform full fine-tuning on difficult tasks. An alternative direction is zeroth-order (ZO) optimization, which estimates gradients using only forward passes. MeZO demonstrated that this approach can match the memory footprint of inference, while achieving reasonable accuracy. The catch? ZO methods converge slowly and require significantly more iterations than their first-order counterparts, due to the high variance inherent in finite-difference gradient estimates.

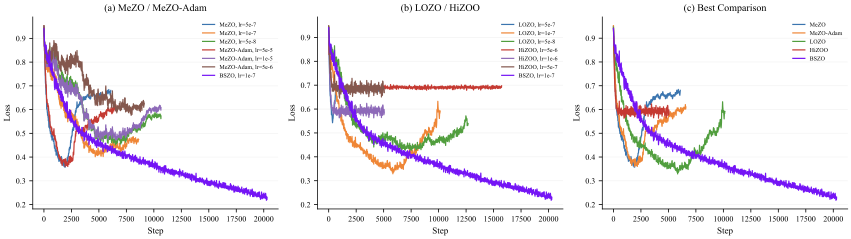
This raises a question: how can we achieve a better trade-off between convergence speed and memory usage? We observe that the existing ZO methods have three main weaknesses. First, most existing ZO optimizers essentially perform updates along a single random direction within each batch. Even with increased forward passes and perturbation directions, they process each perturbation in isolation, simply averaging or using them independentlyβ€”throwing away information about how these measurements relate to each other. Second, the noise level in ZO estimates varies significantly during training, yet most methods do not account for this effect. This rigidity leads to poor adaptation: updates may oscillate wildly around local minima, jump out of the basin, and finally cause training collapse. Moreover, reduced-precision training (fp16/bf16) can cause these methods to collapse or suffer substantial performance degradation, as we show in FigureΒ 1 and TableΒ [tab:llm-results].

/>
Training loss on SST-2 with OPT-13B under bf16 precision. (a)–(b) Existing ZO methods exhibit erratic loss curves across different learning rates, with some runs failing to converge or even diverging. BSZO achieves smooth and steady convergence. (c) Comparison under each method’s best-tuned learning rate.

We propose Bayesian Subspace Zeroth-order Optimization (BSZO) to address these limitations. The main idea is to treat gradient estimation as an inference problem. At each step, we sample $`k`$ random directions to form a low-dimensional subspace and model the projected gradient as a latent variable. Instead of treating each finite-difference query as providing an independent estimate, we use Kalman filtering to aggregate observationsβ€”essentially asking: given what we have measured so far, what is our best guess of the true gradient? This Bayesian formulation accounts for measurement noise and produces more accurate estimates from the same number of forward passes. We further introduce an adaptive mechanism that tracks prediction residuals and adjusts the noise variance on the fly, allowing the algorithm to respond to changing curvature conditions during training.

Our contributions can be summarized as follows:

  1. We propose BSZO, a zeroth-order optimizer that uses Bayesian inference to aggregate gradient information across multiple perturbation directions within a subspace. To our knowledge, this is the first application of Bayesian inference and Kalman filtering to ZO optimization for LLMs.

  2. We design a residual-based adaptive scheme that enables BSZO to adjust the parameter update scale adaptively without manual tuning.

  3. We analyze the convergence of BSZO and show that the rate improves by a factor of $`k/\gamma`$ compared to standard ZO methods.

  4. Experiments on multiple LLMs and benchmarks show that BSZO achieves strong performance across diverse tasks while remaining robust under low-precision training and maintaining memory consumption comparable to MeZO.

Related Work

Zeroth-Order Optimization for LLMs.

Classical derivative-free methods achieve strong sample efficiency via surrogate modeling, but their per-iteration cost grows rapidly with dimension, making them impractical at LLM scale . The SPSA estimator offers a scalable alternative by approximating gradients through random perturbations. Building on this, MeZO introduced memory-efficient ZO fine-tuning for LLMs, matching inference-time memory by regenerating perturbations from random seeds. Follow-up methods target different bottlenecks: Sparse-MeZO restricts updates to influential parameters, HiZOO leverages diagonal Hessian estimates for adaptive preconditioning, LOZO exploits low-rank gradient structure, and TeZO captures temporal correlations across iterations. Despite these advances, most methods adhere to the β€œone batch, one update” paradigm, overlooking the possibility that multiple function evaluations within a batch could support multiple parameter updates. Moreover, some of these methods incur substantial memory overhead; while still lower than full fine-tuning, this conflicts with the original motivation of ZO optimizationβ€”minimizing memory consumption. Since low-precision fine-tuning is essential in memory-constrained scenarios, the robustness of these methods also warrants further evaluation.

Population-Based Gradient Estimation.

An alternative strategy evaluates multiple perturbations per iteration and aggregates them into a single update. Evolution Strategies and Augmented Random Search popularized this paradigm in reinforcement learning. However, these methods typically require a large number of function evaluations per batch to obtain reliable gradient estimates. Given that each forward pass through an LLM is already computationally expensive, such sample-intensive approaches become impractical for language model fine-tuning. This raises a natural question: how can we extract more information from a limited number of function evaluations? Our work addresses this by treating finite-difference measurements as noisy linear observations of the underlying gradient and applying Bayesian inference to fuse information across directions.

Bayesian Inference for Optimization.

Bayesian methods provide a principled way to integrate observations with prior knowledge while quantifying uncertainty. Kalman filtering is the canonical example: it sequentially updates a Gaussian belief over a hidden state as new measurements arrive. Gaussian processes extend this idea to function-space modeling and underpin Bayesian optimization . Our work adapts the Kalman perspective to ZO gradient estimation: we model the projected gradient as a hidden state, interpret each perturbation query as a noisy linear measurement, and update a posterior that pools information across all sampled directions within an iteration. Leveraging the flexibility of the Bayesian framework, we further design an adaptive residual mechanism that effectively fuses both historical and current-batch information. This yields improved gradient estimates without additional memory overhead.

Method

Method SST-2 RTE CB WIC TREC Avg
MeZO 92.22 ($`\pm`$0.42) 66.35 ($`\pm`$3.06) 86.07 ($`\pm`$5.56) 55.20 ($`\pm`$3.73) 85.36 ($`\pm`$2.33) 77.04
MeZO-Adam 92.34 ($`\pm`$0.50) 63.61 ($`\pm`$1.41) 81.07 ($`\pm`$2.71) 52.85 ($`\pm`$4.19) 78.80 ($`\pm`$5.76) 73.73
HiZOO 91.44 ($`\pm`$0.45) 59.21 ($`\pm`$2.46) 76.43 ($`\pm`$1.96) 53.60 ($`\pm`$2.93) 63.44 ($`\pm`$2.61) 68.82
LOZO 91.83 ($`\pm`$0.30) 62.60 ($`\pm`$2.31) 84.29 ($`\pm`$3.87) 54.20 ($`\pm`$1.32) 77.76 ($`\pm`$2.15) 74.14
BSZO 92.66 ($`\pm`$0.21) 67.80 ($`\pm`$1.52) 85.71 ($`\pm`$1.79) 56.05 ($`\pm`$1.47) 84.16 ($`\pm`$0.54) 77.28
BSZO-B 92.27 ($`\pm`$0.41) 68.38 ($`\pm`$1.94) 84.29 ($`\pm`$1.49) 57.21 ($`\pm`$0.98) 84.80 ($`\pm`$1.57) 77.39

parameters $`\theta`$, learning rate $`\eta`$, perturbation scale $`\varepsilon`$, subspace dimension $`k`$, sampling steps $`m`$, prior variance $`\sigma_p^2`$, noise variance $`\sigma_e^2`$, smoothing factor $`\alpha`$, max step $`T`$ Sample $`k`$ random seeds $`\{s_i\}_{i=1}^k`$ Initialize $`\mu \leftarrow \mathbf{0}_k`$, $`\Sigma \leftarrow \sigma_p^2 I_k`$, $`f_0 \leftarrow \mathcal{L}(\theta)`$ Initialize cache $`Y \leftarrow \{\}`$ $`d \leftarrow e_\tau`$ $`\theta \leftarrow \theta + \varepsilon \cdot \textsc{Randn}(n, s_\tau)`$ $`y \leftarrow (\mathcal{L}(\theta) - f_0) / \varepsilon`$ $`\theta \leftarrow \theta - \varepsilon \cdot \textsc{Randn}(n, s_\tau)`$ $`Y[\tau] \leftarrow y`$ $`\triangleright`$ Cache directional derivative $`r \leftarrow (y - d^\top \mu) / \|d\|`$, $`\sigma_e^2 \leftarrow (1-\alpha)\sigma_e^2 + \alpha r^2`$ $`j \leftarrow \arg\max_i \Sigma_{ii}`$ $`\triangleright`$ Find max uncertainty axis $`d \leftarrow e_j`$ $`y \leftarrow Y[j]`$ $`\triangleright`$ Reuse cached value $`K \leftarrow \Sigma d / (d^\top \Sigma d + \sigma_e^2)`$ $`\mu \leftarrow \mu + K (y - d^\top \mu)`$, $`\Sigma \leftarrow \Sigma - K d^\top \Sigma`$ $`\theta \leftarrow \theta - \eta \cdot \mu_i \cdot \textsc{Randn}(n, s_i)`$ $`\theta`$

In this section, we present the Bayesian Subspace Zeroth-order Optimization (BSZO) algorithm, which controls the step size of subspace by the Bayesian method.

Preliminaries

We consider the stochastic optimization problem:

MATH 
\begin{equation}
  \min_{\theta \in \mathbb{R}^n} \mathcal{L}(\theta) := \mathbb{E}_{\xi \sim \mathcal{D}}[\mathcal{L}(\theta; \xi)],
\end{equation}
Click to expand and view more

where $`\theta \in \mathbb{R}^n`$ denotes the model parameters, $`\mathcal{D}`$ is the training dataset, and $`\mathcal{L}(\theta; \xi)`$ is the loss on a minibatch $`\xi`$. We denote the optimal value by $`\mathcal{L}^* := \min_{\theta} \mathcal{L}(\theta)`$.

Assumption 1. The function $`\mathcal{L}`$ is $`L`$-smooth, i.e., there exists $`L>0`$ such that for all $`\theta, \theta'\in \mathbb{R}^n`$,

MATH 
\begin{equation}
    \| \mathcal{L}(\theta) - \mathcal{L}(\theta') \| \leq L \| \theta - \theta' \|.
\end{equation}
Click to expand and view more

Equivalently,

MATH 
\begin{equation}
    \mathcal{L}(\theta)\le\mathcal{L}(\theta') + \nabla \mathcal{L}(\theta')^\top (\theta - \theta') + \frac{L}{2} \| \theta - \theta' \|^2.
\end{equation}
Click to expand and view more

Assumption 2. The stochastic gradient $`\nabla \mathcal{L}(\theta, \xi)`$ has bounded variance, i.e., there exists $`\sigma_g^2\ge 0`$ such that:

MATH 
\begin{equation}
    \mathbb{E}_\xi[\|\nabla \mathcal{L}(\theta; \xi) - \nabla \mathcal{L}(\theta)\|^2] \leq \sigma_g^2, \quad \forall \theta \in \mathbb{R}^n
\end{equation}
Click to expand and view more

Definition 3. Given a set of $`k`$ perturbation vectors $`\{z_1, z_2, \ldots, z_k\}`$, where $`z_i\in\mathbb{R}^n`$ is from Gaussian distribution $`\mathcal{N}(0, I_n)`$, define the subspace basis matrix $`B = [z_1, z_2, \ldots, z_k] \in \mathbb{R}^{n\times k}`$.

Definition 4. The one-side difference of $`\mathcal{L}`$ along the displacement $`d\in\mathbb{R}^k`$ in subspace $`B`$ on minibatch $`\xi`$ is defined as follows:

MATH 
\begin{equation}
    \hat{y}(\theta; \xi, d) = \frac{\mathcal{L}(\theta + \varepsilon Bd; \xi) - \mathcal{L}(\theta; \xi)}{\varepsilon},
\end{equation}
Click to expand and view more

where $`\varepsilon > 0`$ is a small constant.

Bayesian Gradient Estimation

For the $`\mathcal{L}(\theta+\varepsilon Bd)`$, the subspace gradient can be obtained through the chain rule:

MATH 
\begin{equation}
  g_d := \nabla_d \mathcal{L}(\theta+\varepsilon Bd\mid d=0) = \varepsilon B^T g,
\end{equation}
Click to expand and view more

where $`g:=\nabla \mathcal{L}`$ is the real gradient of $`\mathcal{L}`$. In order to keep numerical accuracy controllable, we introduce the concept of normalized subspace gradient as $`\tilde{g} := B^\top g = \frac{g_s}{\varepsilon}\in\mathbb{R}^k`$.

Lemma 5. *For any direction $`d\in\mathbb{R}^k`$ of subspace $`B`$, the expectation of one-side difference $`\hat{y}(d)`$ satisfies:

MATH 
\begin{equation}
    \mathbb{E}[\hat{y}(d)] = d^\top B^\top g + O(\varepsilon L)\approx d^\top \tilde{g}.
\end{equation}
```*

</div>

Based on
Lemma<a href="#lem:expectation-of-onesided-diff" data-reference-type="ref"
data-reference="lem:expectation-of-onesided-diff">5</a>, we can model
the one-side difference $`\hat{y}(d)`$ as a linear observation of the
normalized subspace gradient $`\tilde{g}`$ with Gaussian noise:
``` math
\begin{equation}
  \hat{y}(d) = d^\top \tilde{g} + \nu, \quad \nu \sim \mathcal{N}(0, \sigma_{e}^2 \|d\|^2),
\end{equation}
Click to expand and view more

where $`\nu`$ represents comprehensive noise term. The justification of the variance definition is provided in AppendixΒ 8.2. Then, we adopt a Bayesian approach by placing a Gaussian prior on $`\tilde{g}`$, i.e., $`\tilde{g} \sim \mathcal{N}(0, \sigma_p^2 I_k)`$ which make the posterior computable in closed-form .

Posterior Update In Subspace

According to the standard Bayesian linear regression theory , after $`m`$ perturbations and observations $`(d^{(1)}, \hat{y}^{(1)}), \ldots, (d^{(m)}, \hat{y}^{(m)})`$, the posterior $`\tilde{g} | Y \sim \mathcal{N}(\mu^{(m)}, \Sigma^{(m)})`$ is also a Gaussian distribution, where

MATH 
\begin{equation}
\begin{aligned}
  \Sigma^{(m)} &= \left( \sigma_p^{-2} I_k + D^\top R^{-1} D \right)^{-1}, \\
  \mu^{(m)} &= \Sigma^{(m)} D^\top R^{-1} Y.
\end{aligned}
\end{equation}
Click to expand and view more

Here, $`D = [d^{(1)}, \ldots, d^{(m)}]^\top \in \mathbb{R}^{m \times k}`$ is the design matrix, $`Y = [\hat{y}^{(1)}, \ldots, \hat{y}^{(m)}]^\top \in \mathbb{R}^m`$ is the observation vector, and $`R = \text{diag}(\sigma_e^2 \|d^{(1)}\|^2, \ldots, \sigma_e^2 \|d^{(m)}\|^2)`$ is the noise covariance matrix. When $`m > k`$ or $`\Sigma`$ is already full-rank, we set the new sampling direction to the principal eigenvector of the covariance matrix, i.e., $`d^{(j)} = v_{\max}(\Sigma^{(j-1)})`$.
After getting the posterior mean $`\mu^{(m)}`$, we can use it as the final displacement in subspace $`B`$, which means the parameters updated by:

MATH 
\begin{equation}
  \Delta\theta = - \eta B \mu^{(k)},
\end{equation}
Click to expand and view more

where $`\eta>0`$ is learning rate. In this way, we can use the finite k forward passes to update the parameters k times, with $`\mu^{(k)}`$ controlling the step size in subspace. This means that, for the same batch, the parameters move along a “diagonal” direction rather than a single direction.

Corollary 6. *Under coordinate-axis sampling, i.e., $`m=k`$ and $`d^{(i)}=e_i`$ (the $`i`$-th standard basis vector), then the posterior mean and covariance reduce to:

MATH 
\begin{equation}
\begin{aligned}
  \Sigma^{(k)} &= \gamma I_k, \\
  \mu^{(k)} &= \gamma Y,
\end{aligned}
\end{equation}
```*

</div>

where
$`\gamma := \frac{\sigma_p^2}{\sigma_p^2 + \sigma_e^2} \in (0, 1)`$ is
the shrinkage factor.  
Corollary<a href="#cor:reduced-posterior" data-reference-type="ref"
data-reference="cor:reduced-posterior">6</a> simplifies the form of the
posterior distribution, thereby making the analysis and update easier.
Thus, we adopt coordinate-axis sampling as the default sampling strategy
in BSZO (for the first $`k`$ sampling directions).

<div id="thm:expected-update-direction" class="theorem">

**Theorem 7**. *Let $`\Delta\theta = -\eta B \mu^{(k)}`$. Under
Assumptions <a href="#ass:l-smooth" data-reference-type="ref"
data-reference="ass:l-smooth">1</a> and
Assumption<a href="#ass:bounded-variance" data-reference-type="ref"
data-reference="ass:bounded-variance">2</a>, we have:
``` math
\begin{equation}
    \mathbb{E}[\Delta\theta] = -\eta \gamma k \cdot \nabla \mathcal{L}(\theta) + O(\varepsilon^3)
\end{equation}
```*

</div>

The above theorem shows that the expected update direction aligns with
the negative gradient under coordinate-axis sampling. Furthermore, the
analysis of the expected direction under adaptive sampling is provided
in <a href="#thm:adaptive" data-reference-type="ref+label"
data-reference="thm:adaptive">16</a>
(AppendixΒ <a href="#app:adaptive" data-reference-type="ref"
data-reference="app:adaptive">8.5</a>).

## Algorithm

Clearly, the choice of $`\gamma`$ is crucial. We observe that the norm
of the projected gradient estimated via finite differences remains
stable during the early and middle stages of optimization, but tends to
grow in later stages due to numerical precision limitations, which
restricts the achievable convergence accuracy. To this end, we design a
residual-based mechanism that adaptively adjusts $`\sigma_e`$ after the
$`\tau`$-th sample:
``` math
\begin{equation}
  \begin{aligned}
    r_\tau :=& \frac{\hat{y}^{(\tau)} - d^{(\tau)^\top} \mu^{(\tau-1)}}{\|d^{(\tau)}\|},\\
    (\sigma_{e}^{(\tau)})^2 =& (1-\alpha) (\sigma_{e}^{(\tau-1)})^2 + \alpha r_\tau^2,
  \end{aligned}
\end{equation}
Click to expand and view more

where $`\alpha\in(0,1)`$ is the smoothing factor.

CorollaryΒ 6 shows that under coordinate-axis sampling, the posterior covariance $`\Sigma`$ degenerates into a diagonal matrix with a single distinct eigenvalue, implying that any axis-aligned direction may serve as the adaptive sampling direction when $`j > k`$. The residual-based adaptation breaks this degeneracy by differentiating the diagonal entries of $`\Sigma`$, thereby producing a meaningful adaptive sampling direction. However, the diagonal structure implies that the adaptive sampling direction always coincides with one of the coordinate axes, which can lead to redundant computation. To address this, we cache the $`(d, y)`$ pairs from the first $`k`$ samples within each batch. When $`j > k`$, we directly reuse the cached pair corresponding to the largest diagonal entry of $`\Sigma`$, eliminating the need for an additional forward pass. This extra sample leverages the updated residual to more precisely correct the step size along the direction of greatest uncertainty. In practice, we set $`m = k + 1`$ by default.

The main procedure of BSZO is summarized in AlgorithmΒ [alg:bszo]. Following MeZO , we store perturbation vectors via random seeds rather than explicitly, requiring only $`O(k^2)`$ additional space. A basic version without caching is provided in AlgorithmΒ [alg:bszo-cache] (AppendixΒ 7), which supports arbitrary initial sampling directions and additional adaptive sampling steps. In this version, the adaptive sampling performs extra forward passes to obtain new function values. Typically, the result of this forward pass coincides with the cached value. However, under reduced precision (fp16 or bf16), certain GPU operations use non-deterministic algorithmsΒ , causing function evaluations to differ across calls even with identical inputs and random seeds. Moreover, due to numerical errors, parameters do not fully recover after perturbation and restoration. As a result, the extra forward pass in the basic version yields a value different from the cached one, better reflecting the local landscape at the perturbed point and leading to improved performance (as confirmed in SectionΒ 5.3). To examine this effect, we include the coordinate-axis sampling variant of AlgorithmΒ [alg:bszo-cache] as an experimental baseline (denoted as BSZO-B). 1 compares the memory complexity of different methods, showing that BSZO is also memory-efficient. We analyze the convergence properties of BSZO in the next section.

Method Memory Additional Space
MeZO-SGD $`O(n)`$ $`O(1)`$
MeZO-Adam $`O(n)`$ $`O(n)`$
HiZOO $`O(n)`$ $`O(n)`$
LOZO $`O(n)`$ $`O(1)`$
BSZO (Ours) $`O(n)`$ $`O(k^2)`$

Memory complexity comparison of different methods.

Theoretical Analysis

Model Method SST-2 RTE COPA WIC WSC TREC Avg
3-3 (lr)4-4 (lr)5-7 (lr)8-8 sentiment NLI reasoning topic
OPT-1.3B MeZO 91.74 64.98 76.0 58.78 59.62 80.6 71.95
OPT-1.3B MeZO-Adam 93.35 60.29 75.0 56.58 62.50 79.4 71.19
OPT-1.3B HiZOO 91.51 62.09 77.0 56.58 63.46 66.2 69.48
OPT-1.3B LOZO 92.66 63.18 75.0 56.58 57.69 75.8 70.15
OPT-1.3B BSZO 92.43 66.79 79.0 59.88 64.42 87.0 74.92
OPT-1.3B BSZO-B 93.01 64.98 81.0 59.09 61.54 87.4 74.50
Mistral-7B MeZO 90.94 64.26 88.0 56.58 63.46 88.6 75.31
Mistral-7B HiZOO 93.01 63.90 90.0 55.64 63.46 * 73.20
Mistral-7B LOZO 92.43 61.37 86.0 57.83 63.46 * 72.22
Mistral-7B BSZO 94.50 75.81 87.0 60.03 59.62 90.0 77.83
Mistral-7B BSZO-B 94.04 78.70 87.0 59.72 60.58 91.0 78.51
OPT-13B MeZO 85.89 62.09 80.0 54.55 60.58 59.4 67.09
OPT-13B MeZO-Adam 79.82 61.73 81.0 54.39 57.69 62.2 66.14
OPT-13B HiZOO 72.71 62.46 80.0 52.35 46.15 19.8 55.58
OPT-13B LOZO 86.12 57.04 80.0 55.96 59.62 60.4 66.52
OPT-13B BSZO 93.23 69.31 83.0 56.27 61.54 79.2 73.76
OPT-13B BSZO-B 91.86 71.84 85.0 53.14 64.42 80.8 74.51

Definition 8. Let $`\Sigma = \text{Cov}(\zeta)`$ be the covariance matrix of the gradient noise, the effective noise $`\sigma_e^2`$ can be decomposed as:

MATH 
\begin{equation}
    \sigma_e^2 = \sigma_{\varepsilon}^2 + \text{tr}(\Sigma),
\end{equation}
Click to expand and view more

where $`\text{tr}({\Sigma})\le\sigma_g^2`$ (AssumptionΒ 2). The justification for this definition is provided by LemmaΒ 15 in AppendixΒ 8.2. For analytical tractability, we assume that $`\sigma_e`$ is fixed (taking the worst-case noise across batches gives the same result). The convergence of BSZO is characterized by the following theorem:

Theorem 9. *Under AssumptionsΒ 1 and 2, let $`\tilde{n}=n+k+1`$ be effective dimension. Suppose $`m=k`$ and $`\eta < \frac{2}{L \gamma \tilde{n}}`$. Then, after $`T`$ iterations, the following inequality holds:

MATH 
\begin{equation}
    \frac{1}{T}\sum_{t=0}^{T-1} \mathbb{E}[\|\nabla \mathcal{L}(\theta_t)\|^2] \leq \frac{\mathcal{L}(\theta_0) - \mathcal{L}^*}{\beta(\eta) \eta \gamma k T} + \frac{L \eta \gamma (\tilde{n} \cdot \text{tr}(\Sigma) + n \sigma_\varepsilon^2)}{2\beta(\eta)},
\end{equation}
Click to expand and view more

where $`\beta(\eta) := 1 - \frac{L \eta \gamma \tilde{n}}{2}`$ and $`\sigma_e^2 = \sigma_{\varepsilon}^2 + \text{tr}(\Sigma)`$.*

Corollary 10. *Let $`\eta = \frac{1}{L\gamma\tilde{n}}`$, then $`\beta = 1/2`$, which simplifies TheoremΒ 9 to:

MATH 
\begin{equation}
    \frac{1}{T}\sum_{t=0}^{T-1} \mathbb{E}[\|\nabla \mathcal{L}(\theta_t)\|^2] \leq \frac{2L\gamma\tilde{n}\Delta_0}{kT} + \text{tr}(\Sigma) + \frac{n}{\tilde{n}}\sigma_{\varepsilon}^2,
\end{equation}
Click to expand and view more

where $`\Delta_0 := \mathcal{L}(\theta_0) - \mathcal{L}^*`$.*

According to CorollaryΒ 10, the convergence rate of BSZO is improved by the factor of subspace dimension $`k`$. Although $`\gamma`$ slightly reduces the convergence rate, it is crucial for training stability. We also analyze the convergence under adaptive sampling in 17 (AppendixΒ 8.6).

/>
GPU memory usage comparison across different models. BSZO maintains memory consumption comparable to MeZO, while MeZO-Adam and HiZOO require significantly more memory due to storing optimizer states or Hessian estimates.

Experiments

In this section, we evaluate the performance of BSZO and BSZO-B (SectionΒ 3.4) on various fine-tuning tasks in different language models, comparing them with several baselines: MeZO , MeZO-Adam , HiZOO , and LOZO . Our experiments show that both variants achieve excellent robustness and strong accuracy across most scenarios, requiring only the GPU memory needed for forward propagation, making them more cost-effective than HiZOO and MeZO-Adam.

Experimental Setup

Language Models. The experiments in this paper center on two categories of models: masked Language Models (mLMs) and decoder-only Large Language Models (LLMs). For mLMs, we adopt RoBERTa-large (355M) as the backbone model. For decoder-only LLMs, we select OPT-1.3B and OPT-13B , as well as Mistral-7B .
Datasets. We full fine-tune the above models on tasks from the GLUE , SuperGLUE and TREC benchmarks, including Stanford Sentiment Treebank (SST-2), Boolean Questions (BoolQ) , Recognizing Textual Entailment (RTE) , Choice of Plausible Alternatives (COPA) , Word-in-Context (WIC) , Winograd Schema Challenge (WSC) , CommitmentBank (CB) , and TREC. Following HiZOO , we use the first $`n_1`$ samples (up to 1000) from the training set for training and the next $`n_2`$ samples for validation. The original validation set serves as the test set. See TableΒ 5 in AppendixΒ 9 for specific values of $`n_1`$ and $`n_2`$.
Hyperparameters. For BSZO and BSZO-B, we set the default subspace dimension $`k=2`$ and the number of samples $`m=k + 1`$. This results in 3 forward passes per step for BSZO (with caching) and 4 for BSZO-B (without caching). BSZO matches HiZOO’s forward pass count. As discussed in SectionΒ 3.4, we report results for both BSZO and BSZO-B across all models, with particular focus on comparing them under reduced precision (Mistral-7B in fp16 and OPT-13B in bf16) to examine the caching effect. Other methods use their default hyperparameters. Given the slower convergence of zeroth-order methods, all experiments are trained for up to 20,000 steps , with early stopping applied when validation performance does not improve for 8 evaluations (4,000 steps). For every experiment, we set the perturbation scale to $`\varepsilon=10^{-4}`$ and the batch size to 16. Hyperparameters are tuned via grid search. We select the best configuration based on validation performance and report its test accuracy. Due to memory constraints, we load OPT-13B in bf16 precision and Mistral-7B in fp16 precision, while other models use fp32. All experiments are conducted on a single H200 GPU. More details are provided in AppendixΒ 9.

Performance in Masked Language Models

BSZO achieves stable and competitive performance on mLMs. As shown in TableΒ [tab:roberta], BSZO-B reaches 77.39% average accuracy on RoBERTa-large, surpassing MeZO (77.04%, +0.35%), MeZO-Adam (73.73%, +3.66%), HiZOO (68.82%, +8.57%), and LOZO (74.14%, +3.25%). BSZO achieves 77.28% average accuracy, second only to BSZO-B. BSZO secures top result on SST-2 (92.66%), while BSZO-B excels on RTE (68.38%) and WIC (57.21%). Moreover, BSZO exhibits notably lower variance across tasks (see TableΒ 10 for raw results). Both variants demonstrate strong and consistent performance across all tasks.

Performance in decoder-only models

BSZO performs well on larger LLMs. TableΒ [tab:llm-results] shows that BSZO outperforms baselines on decoder-only models, with gains increasing as model size grows. BSZO-B typically maintains a small lead over BSZO.
OPT-1.3B. BSZO achieves 74.92% average accuracy, the highest among all methods, beating MeZO (71.95%, +2.97%), MeZO-Adam (71.19%, +3.73%), HiZOO (69.48%, +5.44%), and LOZO (70.15%, +4.77%). BSZO-B reaches 74.50% average accuracy. BSZO secures top results on RTE (66.79%), WIC (59.88%), and WSC (64.42%), while BSZO-B excels on COPA (81.0%) and TREC (87.4%). Both variants perform well across most tasks.
Mistral-7B (fp16). BSZO reaches 77.83% on average, ahead of MeZO (75.31%, +2.52%), HiZOO (73.20%, +4.63%), and LOZO (72.22%, +5.61%). It also achieves the best results on SST-2 (94.50%, +1.49% vs HiZOO) and WIC (60.03%, +3.45% vs MeZO). BSZO-B reaches 78.51% on average, excelling on RTE (78.70%) and TREC (91.0%). The small 0.68% gap shows that the two variants perform very similarly.
OPT-13B (bf16). The gains grow larger here. BSZO reaches 73.76% on average, up 6.67% over MeZO (67.09%), 7.62% over MeZO-Adam (66.14%), and 7.24% over LOZO (66.52%). BSZO achieves strong results across tasks, including top performance on WIC (56.27%), with particularly notable gains on SST-2 (93.23%, +7.34% vs MeZO) and TREC (79.2%, +19.8% vs MeZO). BSZO-B reaches 74.51% on average (+7.42% vs MeZO), with stronger balance across tasks. BSZO-B maintains a slight edge with one additional forward pass, though the gap in average accuracy remains very small (0.75%).
Robustness. Reduced precision exposes fragility in several baselines (TableΒ [tab:llm-results]) and FigureΒ 1. HiZOO and LOZO are particularly affected: on Mistral-7B (fp16), both methods suffer from TREC training overflow (*). On OPT-13B (bf16), all baseline methods show varying degrees of performance degradation compared to OPT-1.3B, with HiZOO being especially severeβ€”its average accuracy drops from 69.48% to 55.58%, with TREC collapsing to 19.8% and WSC to 46.15%. We suspect H200’s default TF32 mode introduces errors in Hessian-based estimates. In contrast, BSZO and BSZO-B remain stable throughout all precision settings, with BSZO-B even maintaining performance (from 74.50% to 74.51%).

Memory and Time Efficiency

Memory usage (GB) and per-step time (ms) across different models.
OPT-1.3B Mistral-7B OPT-13B
2-3 (lr)4-5 (lr)6-7 Method Mem Time Mem Time Mem Time
MeZO 9.1 109.7 18.3 283.9 30.0 464.2
MeZO-Adam 19.7 135.1 47.6 373.1 82.1 614.5
HiZOO 15.7 188.0 34.3 540.2 58.9 877.1
LOZO 9.3 102.0 18.3 274.2 30.0 452.0
BSZO 9.8 97.0 18.8 275.7 30.1 440.5

BSZO keeps memory usage low. As shown in FigureΒ 2 and TableΒ 2, BSZO’s memory footprint stays close to MeZO across three model scalesβ€”ranging from 1.00$`\times`$ to 1.08$`\times`$ of MeZO’s usage. In contrast, HiZOO and MeZO-Adam need 1.73$`\times`$–1.96$`\times`$ and 2.16$`\times`$–2.74$`\times`$ more memory because they store additional optimizer states (momentum, Hessian estimates). BSZO avoids this overhead by using only $`O(k^2)`$ extra space for the posterior covariance and adaptive noise estimation.

BSZO runs fast. TableΒ 2 also reports per-step time. BSZO and LOZO are the fastestβ€”both under 100ms per step on OPT-1.3B. HiZOO is roughly 2$`\times`$ slower due to Hessian estimation, and MeZO-Adam incurs extra cost from momentum updates.

Ablation Study

Ablation studies. (a) Effect of subspace dimension k with m = k on OPT-1.3B. (b) Effect of m = kβ€…+β€…1 on OPT-1.3B. (c) Effect of adaptive noise on OPT-1.3B (bf16). (d) Effect of adaptive noise on OPT-13B (bf16). Best results in bold. Full results in fp32 are in TableΒ 11.
(a) Effect of k (b) Effect of m (c) Adaptive Noise
1-3 (lr)4-6 (l)7-9 k SST-2 RTE k SST-2 RTE k w/ w/o
1 92.32 60.29 1 91.74 61.37 1 54.15 55.24
2 92.78 64.26 2 92.43 66.79 2 57.76 56.32
4 92.66 67.51 4 93.58 66.43 4 61.73 56.32
8 93.23 66.07 8 93.23 68.59 8 66.43 57.76
Ablation studies. (a) Effect of subspace dimension k with m = k on OPT-1.3B. (b) Effect of m = kβ€…+β€…1 on OPT-1.3B. (c) Effect of adaptive noise on OPT-1.3B (bf16). (d) Effect of adaptive noise on OPT-13B (bf16). Best results in bold. Full results in fp32 are in TableΒ 11.
(d) Adaptive Noise on OPT-13B (bf16)
1-7 Method SST-2 RTE WSC COPA TREC WIC
w/ adaptive 93.23 69.31 61.54 83.00 79.20 56.27
w/o adaptive 91.97 63.18 58.65 85.00 75.00 54.70

TableΒ 4 shows ablation results on OPT-1.3B for two design choices of BSZO: subspace dimension $`k`$ and sample count $`m`$. In TableΒ 4(a), when $`m=k`$, RTE accuracy climbs from 60.29% ($`k=1`$) to 67.51% ($`k=4`$), while SST-2 peaks at $`k=8`$ (93.23%), suggesting that increasing $`k`$ generally improves performance. In TableΒ 4(b), with extra refinement ($`m=k+1`$), RTE performance improves consistently. Comparing to TableΒ 4(a), $`m=k+1`$ boosts RTE by 1-2% at most $`k`$ levels (e.g., from 64.26% to 66.79% at $`k=2`$, from 66.07% to 68.59% at $`k=8`$). This confirms that the adaptive sampling step refines the posterior estimate (see TableΒ 11 for more details). TableΒ 4(c) investigates adaptive noise under bf16 precision on OPT-1.3B. As $`k`$ grows, the gap between w/ and w/o adaptive noise becomes more pronounced: at $`k=8`$, the adaptive variant leads by 8.67% on RTE, indicating that adaptive noise yields substantial gains in low-precision settings. TableΒ 4(d) validates this on OPT-13B (bf16), where adaptive noise brings improvements on 5 out of 6 tasks, with RTE gaining 6.13%.

Conclusion

In this work, we introduce BSZO, which is the first zeroth-order optimizer that applies Kalman filtering to aggregate gradient information across multiple perturbation directions for LLM fine-tuning. By treating finite-difference measurements as noisy observations of the true gradient, BSZO builds a posterior distribution over the projected gradient and refines it through Bayesian updates. We design a residual-based adaptive mechanism to adjust the perturbation scale adaptively without manual tuning. Our theoretical analysis shows that BSZO improves the convergence rate by a factor of $`k/\gamma`$ over standard ZO methods. Experiments on RoBERTa, Mistral, and OPT show that BSZO achieves strong accuracy across various tasks, remains stable under fp16/bf16 precision where existing methods often collapse, and keeps memory usage close to inference-only baselines.

Software and Data

Our implementation is available at https://github.com/AeonianQuill/BSZO . Datasets used in this work (GLUE, SuperGLUE, TREC) are publicly accessible and should be downloaded separately. Pre-trained models can also be obtained from Hugging Face.

Impact Statement

This paper presents work whose goal is to advance the field of machine learning. There are many potential societal consequences of our work, none of which we feel must be specifically highlighted here.

BSZO Basic Algorithm

We provide a basic version of BSZO without caching optimization, which supports arbitrary sampling directions when $`m > k`$.

parameters $`\theta`$, learning rate $`\eta`$, perturbation scale $`\varepsilon`$, subspace dimension $`k`$, sampling steps $`m`$, prior variance $`\sigma_p^2`$, noise variance $`\sigma_e^2`$, smoothing factor $`\alpha`$, max step $`T`$ Sample $`k`$ random seeds $`\{s_i\}_{i=1}^k`$ Initialize $`\mu \leftarrow \mathbf{0}_k`$, $`\Sigma \leftarrow \sigma_p^2 I_k`$, $`f_0 \leftarrow \mathcal{L}(\theta)`$ $`d \leftarrow d_\tau`$ if $`\tau \leq k`$, else $`d \leftarrow \arg\max_{\|v\|=1} v^\top \Sigma v`$ $`\theta \leftarrow \theta + \varepsilon \cdot d_i \cdot \textsc{Randn}(n, s_i)`$ if $`d_i > 10^{-10}`$ $`y \leftarrow (\mathcal{L}(\theta) - f_0) / \varepsilon`$ $`\theta \leftarrow \theta - \varepsilon \cdot d_i \cdot \textsc{Randn}(n, s_i)`$ if $`d_i > 10^{-10}`$ $`r \leftarrow (y - d^\top \mu) / \|d\|`$, $`\sigma_e^2 \leftarrow (1-\alpha)\sigma_e^2 + \alpha r^2`$ $`K \leftarrow \Sigma d / (d^\top \Sigma d + \sigma_e^2)`$ $`\mu \leftarrow \mu + K (y - d^\top \mu)`$, $`\Sigma \leftarrow \Sigma - K d^\top \Sigma`$ $`\theta \leftarrow \theta - \eta \cdot \mu_i \cdot \textsc{Randn}(n, s_i)`$ $`\theta`$

Theoretical Proofs

Auxiliary Lemmas

Lemma 11 (Expectation of Direction Derivative). *Under AssumptionΒ 1, the one-sided difference satisfies:

MATH 
\begin{equation}
  \mathbb{E}[\hat{y}(d)] = d^\top B^\top g + O(\varepsilon L)
\end{equation}
```*

</div>

<div class="proof">

*Proof.* By
$`\mathbb{E}[\mathcal{L}(\theta;\xi)] = \mathcal{L}(\theta)`$:
``` math
\begin{equation}
  \mathbb{E}[\hat{y}(d)] = \frac{\mathcal{L}(\theta_0 + \varepsilon Bd) - \mathcal{L}(\theta_0)}{\varepsilon}
\end{equation}
Click to expand and view more

By Taylor expansion at $`\theta_0`$:

MATH 
\begin{equation}
  \mathcal{L}(\theta_0 + \varepsilon Bd) = \mathcal{L}(\theta_0) + \varepsilon \langle \nabla \mathcal{L}(\theta_0), Bd \rangle + \frac{\varepsilon^2}{2} (Bd)^\top H (Bd) + O(\varepsilon^3)
\end{equation}
Click to expand and view more

where $`H = \nabla^2 \mathcal{L}(\theta_0)`$ is the Hessian.

Substituting:

MATH 
\begin{equation}
  \mathbb{E}[\hat{y}(d)] = \frac{\varepsilon d^\top B^\top g + \frac{\varepsilon^2}{2} d^\top B^\top H B d + O(\varepsilon^3)}{\varepsilon} = d^\top B^\top g + \frac{\varepsilon}{2} d^\top B^\top H B d + O(\varepsilon^2)
\end{equation}
Click to expand and view more

By AssumptionΒ 1, $`\|H\| \leq L`$, so $`|d^\top B^\top H B d| \leq L\|Bd\|^2`$. Thus the bias is $`O(\varepsilon L)`$.Β β—»

Lemma 12 (Variance of Direction Derivative). Let $`\Sigma = \text{Cov}(\zeta)`$ where $`\zeta = \nabla \mathcal{L}(\theta;\xi) - \nabla \mathcal{L}(\theta)`$. When using the same mini-batch $`\xi`$ for both function evaluations:

  • Conditional variance: $`\text{Var}(\hat{y}(d)|B) = (Bd)^\top \Sigma (Bd) + O(\varepsilon^4)`$

  • Unconditional variance: $`\mathbb{E}_B[\text{Var}(\hat{y}(d)|B)] = \text{tr}(\Sigma) + O(\varepsilon^4)`$

Proof. Key insight: Using the same mini-batch $`\xi`$ for both evaluations causes the noise to be correlated, not independent.

(a) Conditional variance derivation:

For fixed $`\xi`$, Taylor expand the random loss $`\mathcal{L}(\theta;\xi)`$ at $`\theta_0`$:

MATH 
\begin{equation}
  \mathcal{L}(\theta_0 + \varepsilon Bd; \xi) = \mathcal{L}(\theta_0; \xi) + \varepsilon \langle \nabla \mathcal{L}(\theta_0; \xi), Bd \rangle + O(\varepsilon^2)
\end{equation}
Click to expand and view more

Since both evaluations use the same $`\xi`$, the base term $`\mathcal{L}(\theta_0; \xi)`$ cancels:

MATH 
\begin{equation}
  \hat{y}(d) = \frac{\mathcal{L}(\theta_0 + \varepsilon Bd; \xi) - \mathcal{L}(\theta_0; \xi)}{\varepsilon} = \langle \nabla \mathcal{L}(\theta_0; \xi), Bd \rangle + O(\varepsilon)
\end{equation}
Click to expand and view more

Let $`\nabla \mathcal{L}(\theta_0; \xi) = \nabla \mathcal{L}(\theta_0) + \zeta`$ where $`\zeta`$ is zero-mean noise with $`\text{Cov}(\zeta) = \Sigma`$. Given $`B`$:

MATH 
\begin{equation}
  \text{Var}(\hat{y}(d)|B) = \text{Var}(\langle \zeta, Bd \rangle | B) = (Bd)^\top \text{Cov}(\zeta) (Bd) = (Bd)^\top \Sigma (Bd) + O(\varepsilon^2)
\end{equation}
Click to expand and view more

(b) Unconditional variance derivation:

For coordinate-axis sampling $`d = e_i`$, we have $`Bd = z_i \sim \mathcal{N}(0, I_n)`$.

Taking expectation over $`B`$:

MATH 
\begin{equation}
  \mathbb{E}_B[(Bd)^\top \Sigma (Bd)] = \mathbb{E}[z_i^\top \Sigma z_i]
\end{equation}
Click to expand and view more

By the trace trick:

MATH 
\begin{equation}
  \mathbb{E}[z_i^\top \Sigma z_i] = \mathbb{E}[\text{tr}(\Sigma z_i z_i^\top)] = \text{tr}(\Sigma \cdot \mathbb{E}[z_i z_i^\top]) = \text{tr}(\Sigma \cdot I_n) = \text{tr}(\Sigma)
\end{equation}
Click to expand and view more

By AssumptionΒ 2, $`\text{tr}(\Sigma) = \mathbb{E}[\|\zeta\|^2] \leq \sigma_g^2`$.Β β—»

Lemma 13 (High-Dimensional Approximate Orthogonality). Let $`z_1, \ldots, z_k \stackrel{iid}{\sim} \mathcal{N}(0, I_n)`$. When $`n \gg k^2`$:

  • $`\|z_i\|^2 = n \pm O(\sqrt{n})`$

  • For $`i \neq j`$: $`\frac{z_i^\top z_j}{\|z_i\|\|z_j\|} = O(1/\sqrt{n})`$

Proof. (a) Norm concentration:

Since $`\|z_i\|^2 = \sum_{j=1}^n z_{ij}^2 \sim \chi^2(n)`$, we have:

MATH 
\begin{equation}
  \mathbb{E}[\|z_i\|^2] = n, \quad \text{Var}(\|z_i\|^2) = 2n
\end{equation}
Click to expand and view more

By Chebyshev inequality or sub-Gaussian concentration:

MATH 
\begin{equation}
  \mathbb{P}\left(\left|\|z_i\|^2 - n\right| > t\sqrt{n}\right) \leq 2e^{-ct^2}
\end{equation}
Click to expand and view more

Thus $`\|z_i\|^2 = n \pm O(\sqrt{n})`$ with high probability.

(b) Approximate orthogonality:

For independent $`z_i, z_j \sim \mathcal{N}(0, I_n)`$, the inner product $`z_i^\top z_j = \sum_{l=1}^n z_{il} z_{jl}`$ is a sum of $`n`$ independent random variables with:

MATH 
\begin{equation}
  \mathbb{E}[z_i^\top z_j] = 0, \quad \text{Var}(z_i^\top z_j) = \sum_{l=1}^n \text{Var}(z_{il} z_{jl}) = n
\end{equation}
Click to expand and view more

Thus $`z_i^\top z_j = O(\sqrt{n})`$ with high probability. Since $`\|z_i\|\|z_j\| = O(n)`$:

MATH 
\begin{equation}
  \cos\theta_{ij} = \frac{z_i^\top z_j}{\|z_i\|\|z_j\|} = O\left(\frac{\sqrt{n}}{n}\right) = O\left(\frac{1}{\sqrt{n}}\right) \to 0
\end{equation}
Click to expand and view more

This shows that random Gaussian vectors are approximately orthogonal in high dimensions.Β β—»

Lemma 14 (Isserlis’ Theorem Application). *For $`z \sim \mathcal{N}(0, I_n)`$ and symmetric matrices $`A, B`$:

MATH 
\begin{equation}
  \mathbb{E}[(z^\top A z)(z^\top B z)] = \text{tr}(A)\text{tr}(B) + 2\text{tr}(AB)
\end{equation}
Click to expand and view more

In particular, for $`A = I_n`$ and $`B = \Sigma`$:

MATH 
\begin{equation}
  \mathbb{E}[\|z\|^2 \cdot z^\top \Sigma z] = (n+2)\text{tr}(\Sigma)
\end{equation}
```*

</div>

<div class="proof">

*Proof.* By Isserlis’ theorem (Wick’s theorem), for
$`z \sim \mathcal{N}(0, I_n)`$:
``` math
\begin{equation}
  \mathbb{E}[z_i z_j z_k z_l] = \delta_{ij}\delta_{kl} + \delta_{ik}\delta_{jl} + \delta_{il}\delta_{jk}
\end{equation}
Click to expand and view more

Expanding the quadratic forms:

MATH 
\begin{equation}
  (z^\top A z)(z^\top B z) = \sum_{i,j,k,l} A_{ij} B_{kl} z_i z_j z_k z_l
\end{equation}
Click to expand and view more

Taking expectation:

MATH 
\begin{align}
  \mathbb{E}[(z^\top A z)(z^\top B z)] &= \sum_{i,j,k,l} A_{ij} B_{kl} (\delta_{ij}\delta_{kl} + \delta_{ik}\delta_{jl} + \delta_{il}\delta_{jk}) \\
  &= \sum_{i,k} A_{ii} B_{kk} + \sum_{i,j} A_{ij} B_{ij} + \sum_{i,j} A_{ij} B_{ji} \\
  &= \text{tr}(A)\text{tr}(B) + \text{tr}(AB) + \text{tr}(AB^\top)
\end{align}
Click to expand and view more

For symmetric $`A, B`$: $`\text{tr}(AB^\top) = \text{tr}(AB)`$, thus:

MATH 
\begin{equation}
  \mathbb{E}[(z^\top A z)(z^\top B z)] = \text{tr}(A)\text{tr}(B) + 2\text{tr}(AB)
\end{equation}
Click to expand and view more

Setting $`A = I_n`$, $`B = \Sigma`$:

MATH 
\begin{equation}
  \mathbb{E}[\|z\|^2 \cdot z^\top \Sigma z] = n \cdot \text{tr}(\Sigma) + 2\text{tr}(\Sigma) = (n+2)\text{tr}(\Sigma)
\end{equation}
Click to expand and view more

Β β—»

Noise Variance Justification

The observation model $`\hat{y}(d) = d^\top \tilde{g} + \nu`$ with $`\nu \sim \mathcal{N}(0, \sigma_e^2\|d\|^2)`$ is justified as follows.

Lemma 15 (Effective Noise Decomposition). *The effective noise variance decomposes as:

MATH 
\begin{equation}
  \sigma_e^2 = \sigma_\varepsilon^2 + \text{tr}(\Sigma)
\end{equation}
Click to expand and view more

where $`\sigma_\varepsilon^2`$ is the finite-difference approximation error and $`\text{tr}(\Sigma)`$ is the gradient noise variance.*

Proof. Step 1: Decomposition of the observation.

For coordinate-axis sampling with $`d = e_i`$, the direction in parameter space is $`z_i = Bd = Be_i`$ (the $`i`$-th column of $`B`$), where $`z_i \sim \mathcal{N}(0, I_n)`$.

The observation can be decomposed as:

MATH 
\begin{equation}
  y_i = \underbrace{z_i^\top g}_{\text{true signal}} + \underbrace{z_i^\top \zeta}_{\text{gradient noise}} + \underbrace{\epsilon_i}_{\text{finite-diff error}}
\end{equation}
Click to expand and view more

where:

  • $`g = \nabla \mathcal{L}(\theta)`$ is the true gradient

  • $`\zeta = \nabla \mathcal{L}(\theta;\xi) - \nabla \mathcal{L}(\theta)`$ is the stochastic gradient noise with $`\mathbb{E}[\zeta] = 0`$ and $`\text{Cov}(\zeta) = \Sigma`$

  • $`\epsilon_i \sim \mathcal{N}(0, \sigma_\varepsilon^2)`$ is the finite-difference truncation error, independent of $`\zeta`$ and $`z_i`$

Step 2: Identifying the noise term.

The observation noise is defined as $`\nu_i := y_i - z_i^\top g = z_i^\top \zeta + \epsilon_i`$.

Since $`\mathbb{E}[\zeta] = 0`$ and $`\mathbb{E}[\epsilon_i] = 0`$, we have $`\mathbb{E}[\nu_i | z_i] = 0`$.

Step 3: Conditional variance (given $`z_i`$).

Since $`\zeta`$ and $`\epsilon_i`$ are independent:

MATH 
\begin{equation}
  \text{Var}(\nu_i | z_i) = \text{Var}(z_i^\top \zeta | z_i) + \text{Var}(\epsilon_i) = z_i^\top \Sigma z_i + \sigma_\varepsilon^2
\end{equation}
Click to expand and view more

Step 4: Unconditional variance (taking expectation over $`z_i`$).

Using the trace trick from LemmaΒ 12(b):

MATH 
\begin{equation}
  \mathbb{E}_{z_i}[z_i^\top \Sigma z_i] = \mathbb{E}[\text{tr}(\Sigma z_i z_i^\top)] = \text{tr}(\Sigma \cdot \mathbb{E}[z_i z_i^\top]) = \text{tr}(\Sigma \cdot I_n) = \text{tr}(\Sigma)
\end{equation}
Click to expand and view more

Therefore, the effective noise variance is:

MATH 
\begin{equation}
  \sigma_e^2 := \mathbb{E}_{z_i}[\text{Var}(\nu_i|z_i)] = \text{tr}(\Sigma) + \sigma_\varepsilon^2
\end{equation}
Click to expand and view more

By AssumptionΒ 2, $`\text{tr}(\Sigma) = \mathbb{E}[\|\zeta\|^2] \leq \sigma_g^2`$, so $`\sigma_e^2 \leq \sigma_g^2 + \sigma_\varepsilon^2`$.Β β—»

Proof of Main Convergence Theorem

Proof of TheoremΒ 9. Step 1: Single-step descent.

By AssumptionΒ 1 ($`L`$-smoothness):

MATH 
\begin{equation}
  \mathcal{L}(\theta_{t+1}) \leq \mathcal{L}(\theta_t) + \langle g_t, \Delta\theta_t \rangle + \frac{L}{2}\|\Delta\theta_t\|^2
\end{equation}
Click to expand and view more

where $`g_t = \nabla \mathcal{L}(\theta_t)`$ and $`\Delta\theta_t = -\eta B_t \mu_t^{(k)}`$.

Step 2: Inner product term.

By LemmaΒ 12, the observation model is $`y_i = z_i^\top g_t + z_i^\top \zeta + \epsilon_i`$, where $`\zeta`$ is gradient noise with $`\text{Cov}(\zeta) = \Sigma`$, and $`\epsilon_i \sim \mathcal{N}(0, \sigma_\varepsilon^2)`$ is finite-difference error.

Let $`\tilde{g} = g_t + \zeta`$ and $`\epsilon = [\epsilon_1, \ldots, \epsilon_k]^\top`$. Then:

MATH 
\begin{equation}
  Y = B_t^\top \tilde{g} + \epsilon, \quad \mu_t^{(k)} = \gamma Y = \gamma(B_t^\top \tilde{g} + \epsilon)
\end{equation}
Click to expand and view more

The parameter update becomes:

MATH 
\begin{equation}
  B_t \mu_t^{(k)} = \gamma B_t B_t^\top(g_t + \zeta) + \gamma \sum_{i=1}^k z_i \epsilon_i
\end{equation}
Click to expand and view more

Computing the expectation of the inner product. Since $`\mathbb{E}[\zeta] = 0`$, $`\mathbb{E}[\epsilon_i] = 0`$, and $`\zeta`$, $`\epsilon_i`$ are independent of $`B_t`$:

MATH 
\begin{equation}
  \mathbb{E}[\langle g_t, B_t\mu_t^{(k)} \rangle | \theta_t] = \gamma\mathbb{E}[g_t^\top B_t B_t^\top g_t] + \gamma\mathbb{E}[g_t^\top B_t B_t^\top \zeta] + \gamma\sum_{i=1}^k \mathbb{E}[(g_t^\top z_i)\epsilon_i]
\end{equation}
Click to expand and view more

The second term: $`\mathbb{E}[g_t^\top B_t B_t^\top \zeta] = g_t^\top \mathbb{E}[B_t B_t^\top]\mathbb{E}[\zeta] = 0`$.

The third term: $`\mathbb{E}[(g_t^\top z_i)\epsilon_i] = \mathbb{E}[g_t^\top z_i]\mathbb{E}[\epsilon_i] = 0`$ (independence).

The first term: $`\mathbb{E}[g_t^\top B_t B_t^\top g_t] = \mathbb{E}[\|B_t^\top g_t\|^2] = \sum_{i=1}^k \mathbb{E}[(z_i^\top g_t)^2] = k\|g_t\|^2`$.

Therefore:

MATH 
\begin{equation}
  \mathbb{E}[\langle g_t, \Delta\theta_t \rangle | \theta_t] = -\eta\gamma k\|g_t\|^2
\end{equation}
Click to expand and view more

Step 3: Second moment (detailed computation).

From Step 2, $`B_t \mu_t^{(k)} = \gamma B_t B_t^\top \tilde{g} + \gamma \sum_i z_i \epsilon_i`$. Thus:

MATH 
\begin{equation}
  \|B_t \mu_t^{(k)}\|^2 = \gamma^2\|B_t B_t^\top \tilde{g}\|^2 + \gamma^2\left\|\sum_i z_i\epsilon_i\right\|^2 + 2\gamma^2\left\langle B_t B_t^\top \tilde{g}, \sum_i z_i\epsilon_i \right\rangle
\end{equation}
Click to expand and view more

Cross term vanishes: Since $`\epsilon_i`$ is independent of $`B_t`$ and $`\tilde{g}`$, and $`\mathbb{E}[\epsilon_i] = 0`$:

MATH 
\begin{equation}
  \mathbb{E}\left[\left\langle B_t B_t^\top \tilde{g}, \sum_i z_i\epsilon_i \right\rangle\right] = \sum_i \mathbb{E}[\epsilon_i] \cdot \mathbb{E}[\langle B_t B_t^\top \tilde{g}, z_i \rangle] = 0
\end{equation}
Click to expand and view more

First term: We compute $`\mathbb{E}[\|B_t B_t^\top \tilde{g}\|^2]`$ by first conditioning on $`B_t`$, then taking expectation over $`B_t`$.

(A) Given $`B_t`$, taking expectation over $`\zeta`$ (using $`\mathbb{E}[\zeta] = 0`$):

MATH 
\begin{equation}
  \mathbb{E}[\|B_t B_t^\top \tilde{g}\|^2 | B_t] = \|B_t B_t^\top g_t\|^2 + \mathbb{E}[\|B_t B_t^\top \zeta\|^2 | B_t]
\end{equation}
Click to expand and view more

where $`\mathbb{E}[\|B_t B_t^\top \zeta\|^2 | B_t] = \text{tr}((B_t B_t^\top)^2 \Sigma)`$.

(B) Taking expectation over $`B_t`$. For $`\mathbb{E}[\|B_t B_t^\top g\|^2]`$:

MATH 
\begin{equation}
  \|B_t B_t^\top g\|^2 = \sum_{i,j=1}^k (z_i^\top g)(z_j^\top g)(z_i^\top z_j)
\end{equation}
Click to expand and view more

Diagonal terms ($`i = j`$): $`\mathbb{E}[(z_i^\top g)^2 \|z_i\|^2] = (n+2)\|g\|^2`$ (by LemmaΒ 14).

Off-diagonal terms ($`i \neq j`$): By independence of $`z_i`$ and $`z_j`$:

MATH 
\begin{align}
  \mathbb{E}[(z_i^\top g)(z_j^\top g)(z_i^\top z_j)] &= \sum_{a,b,c} g_a g_b \mathbb{E}[(z_i)_a (z_i)_c] \mathbb{E}[(z_j)_b (z_j)_c] \\
  &= \sum_{a,b,c} g_a g_b \delta_{ac} \delta_{bc} = \sum_c g_c^2 = \|g\|^2
\end{align}
Click to expand and view more

Thus:

MATH 
\begin{equation}
  \mathbb{E}[\|B_t B_t^\top g\|^2] = k(n+2)\|g\|^2 + k(k-1)\|g\|^2 = k(n+k+1)\|g\|^2 = k\tilde{n}\|g\|^2
\end{equation}
Click to expand and view more

For $`\mathbb{E}[\text{tr}((B_t B_t^\top)^2 \Sigma)]`$, let $`P = B_t B_t^\top`$:

MATH 
\begin{equation}
  \text{tr}(P^2 \Sigma) = \sum_{i,j} (z_i^\top z_j)(z_i^\top \Sigma z_j)
\end{equation}
Click to expand and view more

Diagonal ($`i=j`$): By LemmaΒ 14, $`\mathbb{E}[\|z\|^2 \cdot z^\top \Sigma z] = (n+2)\text{tr}(\Sigma)`$.

Off-diagonal ($`i \neq j`$): By independence of $`z_i`$ and $`z_j`$:

MATH 
\begin{align}
  \mathbb{E}[(z_i^\top z_j)(z_i^\top \Sigma z_j)] &= \sum_{a,b,c} \Sigma_{bc} \mathbb{E}[(z_i)_a (z_i)_b] \mathbb{E}[(z_j)_a (z_j)_c] \\
  &= \sum_{a,b,c} \Sigma_{bc} \delta_{ab} \delta_{ac} = \sum_a \Sigma_{aa} = \text{tr}(\Sigma)
\end{align}
Click to expand and view more

Thus:

MATH 
\begin{equation}
  \mathbb{E}[\text{tr}(P^2 \Sigma)] = k(n+2)\text{tr}(\Sigma) + k(k-1)\text{tr}(\Sigma) = k\tilde{n} \cdot \text{tr}(\Sigma)
\end{equation}
Click to expand and view more

Second term: For the finite-difference noise:

MATH 
\begin{equation}
  \mathbb{E}\left[\left\|\sum_{i=1}^k z_i \epsilon_i\right\|^2\right] = \sum_{i,j} \mathbb{E}[\epsilon_i \epsilon_j] \mathbb{E}[z_i^\top z_j] = \sum_i \sigma_\varepsilon^2 \cdot n = kn\sigma_\varepsilon^2
\end{equation}
Click to expand and view more

Total second moment:

MATH 
\begin{equation}
  \mathbb{E}[\|B_t\mu_t^{(k)}\|^2] = \gamma^2 k\left(\tilde{n}(\|g_t\|^2 + \text{tr}(\Sigma)) + n\sigma_\varepsilon^2\right)
\end{equation}
Click to expand and view more

Step 4: Combining.

Substituting into the descent inequality:

MATH 
\begin{equation}
  \mathbb{E}[\|\Delta\theta_t\|^2] = \eta^2 \gamma^2 k \tilde{n} \|g_t\|^2 + \eta^2 \gamma^2 k (\tilde{n} \cdot \text{tr}(\Sigma) + n\sigma_\varepsilon^2)
\end{equation}
Click to expand and view more

Thus:

MATH 
\begin{equation}
  \mathbb{E}[\mathcal{L}(\theta_{t+1})] \leq \mathbb{E}[\mathcal{L}(\theta_t)] - \eta\gamma k\|g_t\|^2 + \frac{L\eta^2\gamma^2 k}{2}\left[\tilde{n}\|g_t\|^2 + \tilde{n}\cdot\text{tr}(\Sigma) + n\sigma_\varepsilon^2\right]
\end{equation}
Click to expand and view more

Collecting terms in $`\|g_t\|^2`$:

MATH 
\begin{equation}
  \mathbb{E}[\mathcal{L}(\theta_{t+1})] \leq \mathbb{E}[\mathcal{L}(\theta_t)] - \eta\gamma k\underbrace{\left(1 - \frac{L\eta\gamma\tilde{n}}{2}\right)}_{:=\beta(\eta)}\|g_t\|^2 + \frac{L\eta^2\gamma^2 k(\tilde{n}\cdot\text{tr}(\Sigma) + n\sigma_\varepsilon^2)}{2}
\end{equation}
Click to expand and view more

Step 5: Telescoping sum.

When $`\eta < \frac{2}{L\gamma\tilde{n}}`$, we have $`\beta(\eta) > 0`$. Rearranging:

MATH 
\begin{equation}
  \|g_t\|^2 \leq \frac{1}{\beta(\eta)\eta\gamma k}\left(\mathcal{L}(\theta_t) - \mathcal{L}(\theta_{t+1})\right) + \frac{L\eta\gamma(\tilde{n}\cdot\text{tr}(\Sigma) + n\sigma_\varepsilon^2)}{2\beta(\eta)}
\end{equation}
Click to expand and view more

Summing over $`t = 0, \ldots, T-1`$ and dividing by $`T`$:

MATH 
\begin{equation}
  \frac{1}{T}\sum_{t=0}^{T-1}\mathbb{E}[\|g_t\|^2] \leq \frac{\mathcal{L}(\theta_0) - \mathcal{L}^*}{\beta(\eta)\eta\gamma kT} + \frac{L\eta\gamma(\tilde{n}\cdot\text{tr}(\Sigma) + n\sigma_\varepsilon^2)}{2\beta(\eta)}
\end{equation}
Click to expand and view more

Β β—»

Proof of Expected Update Direction

Proof of TheoremΒ 7. Step 1: Posterior mean unbiasedness.

By CorollaryΒ 6, for coordinate-axis sampling ($`d^{(i)} = e_i`$), the posterior mean is:

MATH 
\begin{equation}
  \mu^{(k)} = \gamma Y = \gamma [y^{(1)}, \ldots, y^{(k)}]^\top
\end{equation}
Click to expand and view more

where $`\gamma = \frac{\sigma_p^2}{\sigma_p^2 + \sigma_e^2}`$.

Each observation satisfies $`y^{(i)} = e_i^\top \tilde{g} + \nu^{(i)} = \tilde{g}_i + \nu^{(i)}`$, where $`\tilde{g} = B^\top g`$ is the true normalized subspace gradient and $`\nu^{(i)}`$ is zero-mean noise.

Taking conditional expectation given $`B`$ and $`g`$ (so $`\tilde{g}^* = B^\top g`$ is fixed):

MATH 
\begin{equation}
  \mathbb{E}[y^{(i)} | B, g] = \tilde{g}^*_i + \mathbb{E}[\nu^{(i)}] = \tilde{g}^*_i
\end{equation}
Click to expand and view more

Thus:

MATH 
\begin{equation}
  \mathbb{E}[\mu^{(k)} | B, g] = \gamma \mathbb{E}[Y | B, g] = \gamma \tilde{g}^* = \gamma B^\top g
\end{equation}
Click to expand and view more

Step 2: Conditional expectation of update.

The parameter update is $`\Delta\theta = -\eta B\mu^{(k)}`$. Taking conditional expectation:

MATH 
\begin{equation}
  \mathbb{E}[\Delta\theta | B] = -\eta B \mathbb{E}[\mu^{(k)} | B] = -\eta \gamma B B^\top g
\end{equation}
Click to expand and view more

Step 3: Expectation over subspace basis.

Taking expectation over $`B = [z_1, \ldots, z_k]`$ where $`z_i \stackrel{iid}{\sim} \mathcal{N}(0, I_n)`$:

MATH 
\begin{equation}
  \mathbb{E}[\Delta\theta] = -\eta\gamma \mathbb{E}[BB^\top] g
\end{equation}
Click to expand and view more

Computing $`\mathbb{E}[BB^\top]`$:

MATH 
\begin{equation}
  BB^\top = \sum_{i=1}^k z_i z_i^\top
\end{equation}
Click to expand and view more
MATH 
\begin{equation}
  \mathbb{E}[BB^\top] = \sum_{i=1}^k \mathbb{E}[z_i z_i^\top] = \sum_{i=1}^k I_n = k I_n
\end{equation}
Click to expand and view more

Therefore:

MATH 
\begin{equation}
  \mathbb{E}[\Delta\theta] = -\eta\gamma k \cdot I_n \cdot g = -\eta\gamma k \cdot \nabla \mathcal{L}(\theta_0)
\end{equation}
Click to expand and view more

Step 4: Higher-order bias.

By LemmaΒ 11, the finite-difference estimator has $`O(\varepsilon L)`$ bias. After multiplication by $`\varepsilon`$ in the update, this becomes $`O(\varepsilon^2 L)`$. Since $`\varepsilon`$ is typically small ($`\sim 10^{-3}`$), we write:

MATH 
\begin{equation}
  \mathbb{E}[\Delta\theta] = -\eta\gamma k \cdot \nabla \mathcal{L}(\theta_0) + O(\varepsilon^3)
\end{equation}
Click to expand and view more

This proves that the expected update direction aligns with the negative gradient, with effective learning rate $`\eta_{eff} = \eta\gamma k`$.Β β—»

Adaptive Sampling Analysis

Theorem 16 (Conditional Unbiasedness of Posterior Mean under Adaptive Sampling). *Let $`\mu^{(m)}`$ denote the posterior mean after $`m`$ adaptive sampling steps. Given the subspace basis $`B`$ and the true gradient $`g`$, for any adaptive sampling strategy $`\pi`$ (where $`d^{(j)}`$ is $`\mathcal{D}_{j-1}`$-measurable), we have:

MATH 
\begin{equation}
  \mathbb{E}[\mu^{(m)} | B, g] = \mathbb{E}\left[ \Sigma^{(m)} D_m^\top R_m^{-1} D_m \mid B \right] \tilde{g}^* = \mathbb{E}[\Gamma_m | B] \cdot \tilde{g}^*
\end{equation}
```*

*In particular, if $`\Sigma^{(m)}`$ is deterministic given $`B`$ (e.g.,
coordinate-axis sampling or any strategy that depends only on
$`\mathcal{D}_{m-1}`$), then:
``` math
\begin{equation}
  \mathbb{E}[\mu^{(m)} | B, g, \mathcal{D}_m] = \Gamma_m \cdot \tilde{g}^*
\end{equation}
```*

*where $`\Gamma_m := I_k - \sigma_p^{-2} \Sigma^{(m)}`$ is the
**shrinkage matrix**.*

</div>

<div class="proof">

*Proof.* **Step 1: Expression for the posterior mean.**

By the standard Bayesian linear regression formula:
``` math
\begin{equation}
  \mu^{(m)} = \Sigma^{(m)} D_m^\top R_m^{-1} Y_m
\end{equation}
Click to expand and view more

where $`Y_m = [y^{(1)}, \ldots, y^{(m)}]^\top`$.

Step 2: Computing the conditional expectation.

Note that $`\Sigma^{(m)}`$ and $`D_m`$ are both $`\mathcal{D}_m`$-measurable. The key is to compute $`\mathbb{E}[Y_m | B, g, \mathcal{D}_m]`$.

For each $`y^{(j)}`$:

MATH 
\begin{equation}
  \mathbb{E}[y^{(j)} | B, g, \mathcal{D}_m] = \mathbb{E}[y^{(j)} | B, g, d^{(j)}] = d^{(j)\top} \tilde{g}^*
\end{equation}
Click to expand and view more

The first equality holds because given $`d^{(j)}`$, $`y^{(j)}`$ is conditionally independent of other $`d^{(i)}`$ ($`i \neq j`$).

Therefore:

MATH 
\begin{equation}
  \mathbb{E}[Y_m | B, g, \mathcal{D}_m] = D_m \tilde{g}^*
\end{equation}
Click to expand and view more

Step 3: Substituting into the posterior mean.

MATH 
\begin{equation}
  \mathbb{E}[\mu^{(m)} | B, g, \mathcal{D}_m] = \Sigma^{(m)} D_m^\top R_m^{-1} \mathbb{E}[Y_m | B, g, \mathcal{D}_m] = \Sigma^{(m)} D_m^\top R_m^{-1} D_m \tilde{g}^*
\end{equation}
Click to expand and view more

Step 4: Simplifying the shrinkage matrix.

By the definition of $`\Sigma^{(m)}`$:

MATH 
\begin{equation}
  (\Sigma^{(m)})^{-1} = \sigma_p^{-2} I_k + D_m^\top R_m^{-1} D_m
\end{equation}
Click to expand and view more

Therefore:

MATH 
\begin{equation}
  D_m^\top R_m^{-1} D_m = (\Sigma^{(m)})^{-1} - \sigma_p^{-2} I_k
\end{equation}
Click to expand and view more

Substituting:

MATH 
\begin{equation}
  \mathbb{E}[\mu^{(m)} | B, g, \mathcal{D}_m] = \Sigma^{(m)} \left[(\Sigma^{(m)})^{-1} - \sigma_p^{-2} I_k\right] \tilde{g}^* = \left(I_k - \sigma_p^{-2} \Sigma^{(m)}\right) \tilde{g}^*
\end{equation}
Click to expand and view more

Defining the shrinkage matrix $`\Gamma_m := I_k - \sigma_p^{-2} \Sigma^{(m)}`$, we obtain:

MATH 
\begin{equation}
  \mathbb{E}[\mu^{(m)} | B, g, \mathcal{D}_m] = \Gamma_m \tilde{g}^*
\end{equation}
Click to expand and view more

Β β—»

Convergence Rate under Adaptive Sampling

Theorem 17 (Convergence Rate under Adaptive Sampling). *Under AssumptionsΒ 1, 2, and isotropic noise, consider the BSZO algorithm with adaptive sampling ($`m`$ samples, where the first $`k`$ samples use coordinate-axis sampling). Let $`\tilde{n}=n+k+1`$ be the effective dimension. Suppose $`\eta < \frac{2}{L \bar{\gamma} \tilde{n}}`$, and define $`\beta(\eta) := 1 - \frac{L \eta \bar{\gamma} \tilde{n}}{2}`$. Then, after $`T`$ iterations, the following inequality holds:

MATH 
\begin{equation}
    \frac{1}{T}\sum_{t=0}^{T-1} \mathbb{E}[\|\nabla \mathcal{L}(\theta_t)\|^2] \leq \frac{\Delta_0}{\beta(\eta) \eta \bar{\gamma} k T} + \frac{L \eta \bar{\gamma} (\tilde{n} \sigma_g^2 + n \sigma_n^2)}{2\beta(\eta)},
\end{equation}
Click to expand and view more

where:*

  • $`\bar{\gamma} := \min_t \bar{\gamma}_t \geq \gamma`$ is the minimum effective shrinkage factor,

  • $`\sigma_g^2`$ is the gradient noise variance, $`\sigma_n^2`$ is the finite-difference approximation noise variance,

  • $`\Delta_0 := \mathcal{L}(\theta_0) - \mathcal{L}^*`$.

Corollary 18. *Let $`\eta = \frac{1}{L\bar{\gamma}\tilde{n}}`$. Then $`\beta = 1/2`$, and the convergence bound simplifies to:

MATH 
\begin{equation}
    \frac{1}{T}\sum_{t=0}^{T-1} \mathbb{E}[\|\nabla \mathcal{L}(\theta_t)\|^2] \leq \frac{2L\bar{\gamma}\tilde{n}\Delta_0}{kT} + \sigma_g^2 + \frac{n}{\tilde{n}}\sigma_n^2.
\end{equation}
```*

</div>

<div class="remark">

*Remark 19*. When $`n \gg k`$, we have $`\tilde{n} \approx n`$, so the
noise floor
$`\sigma_g^2 + \frac{n}{\tilde{n}}\sigma_n^2 \approx \sigma_e^2`$
becomes **decoupled** from the dimension $`n`$.

</div>

<div class="proof">

*Proof.* The proof follows the same structure as
TheoremΒ <a href="#thm:main-convergence-theorem" data-reference-type="ref"
data-reference="thm:main-convergence-theorem">9</a>, with the fixed
$`\gamma`$ replaced by the adaptive effective shrinkage factor
$`\bar{\gamma}_t`$.

**Step 1: Single-step descent.**

By AssumptionΒ <a href="#ass:l-smooth" data-reference-type="ref"
data-reference="ass:l-smooth">1</a> ($`L`$-smoothness):
``` math
\begin{equation}
  \mathcal{L}(\theta_{t+1}) \leq \mathcal{L}(\theta_t) + \langle g_t, \Delta\theta_t \rangle + \frac{L}{2}\|\Delta\theta_t\|^2
\end{equation}
Click to expand and view more

Step 2: Inner product term under adaptive sampling.

By the adaptive sampling theorem (TheoremΒ 16), the expected update direction satisfies:

MATH 
\begin{equation}
  \mathbb{E}[\langle g_t, \Delta\theta_t \rangle | \theta_t] = -\eta \mathbb{E}[\text{tr}(\Gamma_m^{(t)})] \|g_t\|^2 = -\eta \bar{\gamma}_t k \|g_t\|^2
\end{equation}
Click to expand and view more

where $`\bar{\gamma}_t = \frac{1}{k}\text{tr}(\Gamma_m^{(t)}) = 1 - \frac{U_m^{(t)}}{k\sigma_p^2}`$ is the effective shrinkage factor at iteration $`t`$.

Step 3: Second moment (same structure as main theorem).

Following the same derivation as TheoremΒ 9, with $`\gamma`$ replaced by $`\bar{\gamma}_t`$:

MATH 
\begin{equation}
  \mathbb{E}[\|\Delta\theta_t\|^2 | \theta_t] = \eta^2 \bar{\gamma}_t^2 k \tilde{n} \|g_t\|^2 + \eta^2 \bar{\gamma}_t^2 k (\tilde{n} \sigma_g^2 + n \sigma_n^2)
\end{equation}
Click to expand and view more

The key observation is that the second moment structure remains unchanged because:

  • The gradient noise $`\sigma_g^2`$ interacts with $`B_t`$ to produce the $`\tilde{n}`$ factor

  • The finite-difference noise $`\sigma_n^2`$ is independent of $`B_t`$, producing only the $`n`$ factor

Step 4: Combining and bounding.

Substituting into the descent inequality:

MATH 
\begin{equation}
  \mathbb{E}[\mathcal{L}(\theta_{t+1})] \leq \mathbb{E}[\mathcal{L}(\theta_t)] - \eta \bar{\gamma}_t k \left(1 - \frac{L\eta\bar{\gamma}_t\tilde{n}}{2}\right) \mathbb{E}[\|g_t\|^2] + \frac{L\eta^2 \bar{\gamma}_t^2 k (\tilde{n} \sigma_g^2 + n \sigma_n^2)}{2}
\end{equation}
Click to expand and view more

Since $`\bar{\gamma}_t \geq \bar{\gamma} := \min_t \bar{\gamma}_t \geq \gamma`$ (by Lemma in TheoremΒ 16), and assuming $`\eta < \frac{2}{L\bar{\gamma}\tilde{n}}`$, we define $`\beta(\eta) = 1 - \frac{L\eta\bar{\gamma}\tilde{n}}{2} > 0`$.

Rearranging:

MATH 
\begin{equation}
  \mathbb{E}[\|g_t\|^2] \leq \frac{1}{\beta(\eta)\eta \bar{\gamma} k}\left(\mathbb{E}[\mathcal{L}(\theta_t)] - \mathbb{E}[\mathcal{L}(\theta_{t+1})]\right) + \frac{L\eta\bar{\gamma} (\tilde{n} \sigma_g^2 + n \sigma_n^2)}{2\beta(\eta)}
\end{equation}
Click to expand and view more

Step 5: Telescoping sum.

Summing over $`t = 0, \ldots, T-1`$ and dividing by $`T`$:

MATH 
\begin{equation}
  \frac{1}{T}\sum_{t=0}^{T-1} \mathbb{E}[\|\nabla \mathcal{L}(\theta_t)\|^2] \leq \frac{\Delta_0}{\beta(\eta)\eta \bar{\gamma} k T} + \frac{L\eta\bar{\gamma} (\tilde{n} \sigma_g^2 + n \sigma_n^2)}{2\beta(\eta)}
\end{equation}
Click to expand and view more

For the special learning rate $`\eta = \frac{1}{L\bar{\gamma}\tilde{n}}`$, we have $`\beta = 1/2`$, and the bound simplifies to:

MATH 
\begin{equation}
  \frac{1}{T}\sum_{t=0}^{T-1} \mathbb{E}[\|\nabla \mathcal{L}(\theta_t)\|^2] \leq \frac{2L\bar{\gamma}\tilde{n}\Delta_0}{kT} + \sigma_g^2 + \frac{n}{\tilde{n}}\sigma_n^2
\end{equation}
Click to expand and view more

When $`n \gg k`$, we have $`\tilde{n} \approx n`$, so the noise floor $`\sigma_g^2 + \frac{n}{\tilde{n}}\sigma_n^2 \approx \sigma_e^2`$ becomes decoupled from dimension $`n`$.Β β—»

Experiment Details

Split SST-2 BoolQ RTE COPA WIC WSC CB TREC
Training 1000 1000 1000 300 1000 450 200 1000
Validation 500 500 500 100 500 100 50 500

Number of training and validation samples for each dataset.

Hyperparameter configurations for fine-tuning RoBERTa-large.
Algorithm Hyperparameter Values
MeZO Batch size 16
Learning rate {1β€…Γ—β€…10βˆ’4, 1β€…Γ—β€…10βˆ’5, 1β€…Γ—β€…10βˆ’6, 1β€…Γ—β€…10βˆ’7, 1β€…Γ—β€…10βˆ’8}
Ξ΅ 10βˆ’4
MeZO-Adam Batch size 16
Learning rate {1β€…Γ—β€…10βˆ’4, 1β€…Γ—β€…10βˆ’5, 1β€…Γ—β€…10βˆ’6, 1β€…Γ—β€…10βˆ’7, 1β€…Γ—β€…10βˆ’8}
Ξ΅ 10βˆ’4
HiZOO Batch size 16
Learning rate {1β€…Γ—β€…10βˆ’4, 1β€…Γ—β€…10βˆ’5, 1β€…Γ—β€…10βˆ’6, 1β€…Γ—β€…10βˆ’7, 1β€…Γ—β€…10βˆ’8}
Ξ΅ 10βˆ’4
LOZO Batch size 16
Learning rate {1β€…Γ—β€…10βˆ’4, 1β€…Γ—β€…10βˆ’5, 1β€…Γ—β€…10βˆ’6, 1β€…Γ—β€…10βˆ’7, 1β€…Γ—β€…10βˆ’8}
Ξ΅ 10βˆ’4
Rank 2
Interval 50
BSZO Batch size 16
Learning rate {1β€…Γ—β€…10βˆ’4, 1β€…Γ—β€…10βˆ’5, 1β€…Γ—β€…10βˆ’6, 1β€…Γ—β€…10βˆ’7, 1β€…Γ—β€…10βˆ’8}
Ξ΅ 10βˆ’4
k (Subspace dim) 2
m (Samples) 3
BSZO-B Batch size 16
Learning rate {1β€…Γ—β€…10βˆ’4, 1β€…Γ—β€…10βˆ’5, 1β€…Γ—β€…10βˆ’6, 1β€…Γ—β€…10βˆ’7, 1β€…Γ—β€…10βˆ’8}
Ξ΅ 10βˆ’4
k (Subspace dim) 2
m (Samples) 3
All Methods Early stopping patience 4,000
Hyperparameter configurations for fine-tuning OPT-1.3B.
Algorithm Hyperparameter Values
MeZO Batch size 16
Learning rate {1β€…Γ—β€…10βˆ’6, 5β€…Γ—β€…10βˆ’7, 1β€…Γ—β€…10βˆ’7, 5β€…Γ—β€…10βˆ’8, 1β€…Γ—β€…10βˆ’8}
Ξ΅ 10βˆ’4
MeZO-Adam Batch size 16
Learning rate {1β€…Γ—β€…10βˆ’4, 5β€…Γ—β€…10βˆ’5, 1β€…Γ—β€…10βˆ’5, 5β€…Γ—β€…10βˆ’6, 1β€…Γ—β€…10βˆ’6}
Ξ΅ 10βˆ’4
HiZOO Batch size 16
Learning rate {1β€…Γ—β€…10βˆ’5, 5β€…Γ—β€…10βˆ’6, 1β€…Γ—β€…10βˆ’6, 5β€…Γ—β€…10βˆ’7, 1β€…Γ—β€…10βˆ’7}
Ξ΅ 10βˆ’4
LOZO Batch size 16
Learning rate {1β€…Γ—β€…10βˆ’6, 5β€…Γ—β€…10βˆ’7, 1β€…Γ—β€…10βˆ’7, 5β€…Γ—β€…10βˆ’8, 1β€…Γ—β€…10βˆ’8}
Ξ΅ 10βˆ’4
Rank 2
Interval 50
BSZO Batch size 16
Learning rate {1β€…Γ—β€…10βˆ’5, 5β€…Γ—β€…10βˆ’6, 1β€…Γ—β€…10βˆ’6, 5β€…Γ—β€…10βˆ’7, 1β€…Γ—β€…10βˆ’7}
Ξ΅ 10βˆ’4
k (Subspace dim) 2
m (Samples) 3
BSZO-B Batch size 16
Learning rate {1β€…Γ—β€…10βˆ’5, 5β€…Γ—β€…10βˆ’6, 1β€…Γ—β€…10βˆ’6, 5β€…Γ—β€…10βˆ’7, 1β€…Γ—β€…10βˆ’7}
Ξ΅ 10βˆ’4
k (Subspace dim) 2
m (Samples) 3
All Methods Early stopping patience 4,000
Hyperparameter configurations for fine-tuning Mistral-7B.
Algorithm Hyperparameter Values
MeZO Batch size 16
Learning rate {5β€…Γ—β€…10βˆ’7, 1β€…Γ—β€…10βˆ’7, 5β€…Γ—β€…10βˆ’8, 1β€…Γ—β€…10βˆ’8, 5β€…Γ—β€…10βˆ’9}
Ξ΅ 10βˆ’4
HiZOO Batch size 16
Learning rate {1β€…Γ—β€…10βˆ’6, 5β€…Γ—β€…10βˆ’7, 1β€…Γ—β€…10βˆ’6, 5β€…Γ—β€…10βˆ’8, 1β€…Γ—β€…10βˆ’8}
Ξ΅ 10βˆ’4
LOZO Batch size 16
Learning rate {5β€…Γ—β€…10βˆ’7, 1β€…Γ—β€…10βˆ’7, 5β€…Γ—β€…10βˆ’8, 1β€…Γ—β€…10βˆ’8, 5β€…Γ—β€…10βˆ’9}
Ξ΅ 10βˆ’4
Rank 2
Interval 50
BSZO Batch size 16
Learning rate {1β€…Γ—β€…10βˆ’6, 5β€…Γ—β€…10βˆ’7, 1β€…Γ—β€…10βˆ’7, 5β€…Γ—β€…10βˆ’8, 1β€…Γ—β€…10βˆ’8}
Ξ΅ 10βˆ’4
k (Subspace dim) 2
m (Samples) 3
BSZO-B Batch size 16
Learning rate {1β€…Γ—β€…10βˆ’6, 5β€…Γ—β€…10βˆ’7, 1β€…Γ—β€…10βˆ’7, 5β€…Γ—β€…10βˆ’8, 1β€…Γ—β€…10βˆ’8}
Ξ΅ 10βˆ’4
k (Subspace dim) 2
m (Samples) 3
All Methods Early stopping patience 4,000
Hyperparameter configurations for fine-tuning OPT-13B.
Algorithm Hyperparameter Values
MeZO Batch size 16
Learning rate {5β€…Γ—β€…10βˆ’6, 1β€…Γ—β€…10βˆ’6, 5β€…Γ—β€…10βˆ’7, 1β€…Γ—β€…10βˆ’7, 5β€…Γ—β€…10βˆ’8}
Ξ΅ 10βˆ’4
MeZO-Adam Batch size 16
Learning rate {1β€…Γ—β€…10βˆ’4, 5β€…Γ—β€…10βˆ’5, 1β€…Γ—β€…10βˆ’5, 5β€…Γ—β€…10βˆ’6, 1β€…Γ—β€…10βˆ’6}
Ξ΅ 10βˆ’4
HiZOO Batch size 16
Learning rate {1β€…Γ—β€…10βˆ’5, 5β€…Γ—β€…10βˆ’6, 1β€…Γ—β€…10βˆ’6, 5β€…Γ—β€…10βˆ’7, 1β€…Γ—β€…10βˆ’7}
Ξ΅ 10βˆ’4
LOZO Batch size 16
Learning rate {5β€…Γ—β€…10βˆ’6, 1β€…Γ—β€…10βˆ’6, 5β€…Γ—β€…10βˆ’7, 1β€…Γ—β€…10βˆ’7, 5β€…Γ—β€…10βˆ’8}
Ξ΅ 10βˆ’4
Rank 2
Interval 50
BSZO Batch size 16
Learning rate {5β€…Γ—β€…10βˆ’6, 1β€…Γ—β€…10βˆ’6, 5β€…Γ—β€…10βˆ’7, 1β€…Γ—β€…10βˆ’7, 5β€…Γ—β€…10βˆ’8}
Ξ΅ 10βˆ’4
k (Subspace dim) 2
m (Samples) 3
BSZO-B Batch size 16
Learning rate {1β€…Γ—β€…10βˆ’5, 5β€…Γ—β€…10βˆ’6, 1β€…Γ—β€…10βˆ’6, 5β€…Γ—β€…10βˆ’7, 1β€…Γ—β€…10βˆ’7}
Ξ΅ 10βˆ’4
k (Subspace dim) 2
m (Samples) 3
All Methods Early stopping patience 4,000

Raw Experimental Results

We provide the complete raw results of 5 independent runs for each method on RoBERTa-large in TableΒ 10. The mean and standard deviation reported in TableΒ [tab:roberta] are computed from these results.

Raw test accuracy (%) of 5 runs on RoBERTa-large (355M).
Dataset Method Run 1 Run 2 Run 3 Run 4 Run 5
SST-2 MeZO 92.43 92.32 91.74 92.78 91.86
MeZO-Adam 92.32 92.66 91.51 92.43 92.78
HiZOO 91.97 91.86 91.28 91.17 90.94
LOZO 91.63 92.09 91.74 91.51 92.20
BSZO 92.89 92.43 92.78 92.43 92.78
BSZO-B 92.66 91.74 92.32 91.97 92.66
RTE MeZO 69.68 68.95 65.70 65.34 62.09
MeZO-Adam 62.09 64.26 64.62 64.98 62.09
HiZOO 59.21 63.18 57.76 56.68 59.21
LOZO 59.57 63.90 61.01 65.34 63.18
BSZO 68.59 68.23 69.68 66.07 66.43
BSZO-B 67.87 70.04 70.76 66.43 66.79
CB MeZO 87.50 85.71 91.07 76.79 89.29
MeZO-Adam 82.14 83.93 80.36 82.14 76.79
HiZOO 78.57 75.00 75.00 78.57 75.00
LOZO 87.50 82.14 82.14 89.29 80.36
BSZO 83.93 85.71 87.50 87.50 83.93
BSZO-B 85.71 83.93 82.14 85.71 83.93
WIC MeZO 49.69 58.31 52.98 57.52 57.52
MeZO-Adam 54.39 51.10 54.70 46.55 57.52
HiZOO 50.31 54.39 51.10 54.70 57.52
LOZO 54.55 54.55 51.88 55.17 54.86
BSZO 57.68 57.52 55.64 54.70 54.70
BSZO-B 57.99 57.99 55.80 56.58 57.68
TREC MeZO 81.20 86.40 86.40 86.20 86.60
MeZO-Adam 84.80 74.20 71.40 83.00 80.60
HiZOO 65.20 65.20 65.20 62.20 59.40
LOZO 80.40 74.80 77.20 79.20 77.20
BSZO 83.40 84.60 84.40 83.80 84.60
BSZO-B 85.80 84.60 85.20 82.20 86.20
Full ablation studies on OPT-1.3B (fp32). (a) Effect of subspace dimension k with m = k. (b) Effect of observation count m with m = kβ€…+β€…1. (c) Noise-free adaptive sampling. Best per row in bold.
(a) Effect of k (b) Effect of m (c) NF-Adaptive
1-3 (lr)4-6 (l)7-9 k SST-2 RTE k SST-2 RTE k SST-2 RTE
1 92.32 60.29 1 91.74 61.37 1 91.28 63.58
2 92.78 64.26 2 92.43 66.79 2 92.43 65.34
4 92.66 67.51 4 93.58 66.43 4 93.12 66.07
8 93.23 66.07 8 93.23 68.59 8 93.35 69.31

πŸ“Š λ…Όλ¬Έ μ‹œκ°μžλ£Œ (Figures)

Figure 1



Figure 2



A Note of Gratitude

The copyright of this content belongs to the respective researchers. We deeply appreciate their hard work and contribution to the advancement of human civilization.

Related Posts

Start searching

Enter keywords to search articles

↑↓
↡
ESC
⌘K Shortcut