style="width:95.0%;height:6cm" />

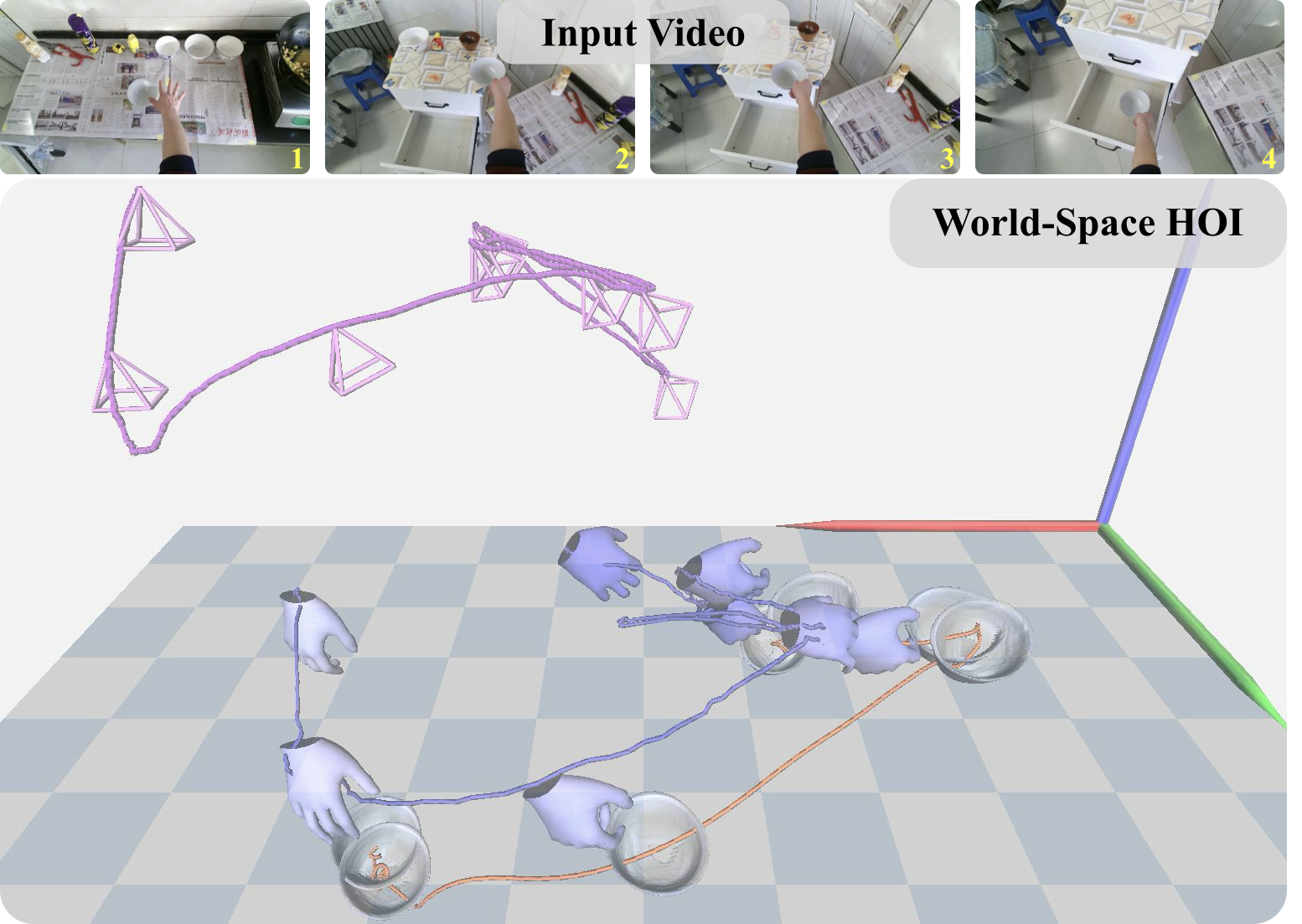
Understanding HOI from egocentric videos is a fundamental problem in computer vision and embodied intelligence. Reconstructing accurate world-space HOI meshes—capturing both spatial geometry and temporal dynamics—is crucial for analyzing human manipulation behavior and enabling downstream applications in embodied AI, robotics, and virtual/augmented reality. Compared to third-person observation, egocentric videos provide richer cues about how humans perceive and act on objects from their own perspective. However, these videos are typically recorded by dynamic cameras in highly unconstrained environments, where frequent occlusions, motion blur, and complex hand–object motion make robust 3D reconstruction extremely challenging. To fully interpret and model human actions, one must recover temporally coherent trajectories of both hands and objects in world coordinates, beyond per-frame geometry in the camera coordinates.

Despite rapid progress in 3D hand and HOI reconstruction, existing methods remain limited when applied to egocentric settings. Most approaches operate at the image or short-sequence level, estimating 3D hand poses  and object poses  frame by frame without enforcing long-term temporal consistency. Moreover, almost all prior HOI and object 6DoF estimation frameworks predict results in camera coordinates , which change dynamically as the wearer moves, making it impossible to obtain consistent global trajectories over time. Some recent works  incorporate differentiable rendering to improve spatial alignment, but these methods are often sensitive to noises and unstable in highly dynamic real-world conditions. Additionally, while egocentric videos inherently encode structural cues between the camera, body, and hands, existing approaches rarely exploit such coupling priors to stabilize motion estimation.

Reconstructing in-the-wild world-space hand–object interactions remains highly challenging. The entanglement of camera and local hand/object motion complicates global trajectory recovery and hinders world-aligned estimation. Real-world scenarios involve unknown objects, demanding template-free reconstruction that generalizes across categories, shapes, and quantities. Robust estimation under occlusion and motion blur is difficult for methods relying on per-frame recognition or differentiable rendering. Furthermore, maintaining spatial–temporal coherence over long egocentric sequences while preventing drift and ensuring plausibility remains an open challenge.

To address these challenges, we propose EgoGrasp, to our knowledge, the first method that reconstructs world-space hand–object interactions (W-HOI) from egocentric monocular videos with dynamic cameras. EgoGrasp adopts a multi-stage “perception–generation–optimization” framework that leverages reliable 3D cues from modern perception systems while introducing a generative motion prior to ensure temporal and global consistency.

EgoGrasp operates in three stages: (1). Preprocessing: We recover accurate camera trajectories and dense geometry from egocentric videos, establishing consistent world coordinates. Initial 3D hand poses and object 6DoFs are extracted and aligned, providing robust spatial grounding and temporal initialization. (2). Motion Diffusion: A two-stage decoupled diffusion model that generates coherent hand–object motion. The first stage produces temporally stable hand trajectories guided by SMPL-X  whole-body poses, mitigating egocentric viewpoint shifts and self-occlusions. The second stage refines hand–object interactions without CAD models, capturing natural dynamics and reducing world drift. (3). Test-time Optimization: A differentiable refinement that optimizes SMPL-X parameters to improve spatial accuracy, temporal smoothness and foot-ground contact consistency. The body is reconstructed only as a structural prior to ensure realistic hand–body coordination, yielding globally consistent trajectories.

We validate EgoGrasp on H2O and HOI4D datasets, achieving state-of-the-art results in world-space hand estimation and HOI reconstruction, with strong global trajectory consistency—demonstrating robustness to dynamic camera motion and in-the-wild conditions.

Our key contributions are summarized as follows:

• Motivated by the requirements of embodied AI, we present a comprehensive analysis of the limitations inherent in current hand pose estimation, hand–object interaction modeling, and object 6DoF tracking approaches. Building upon these insights, we introduce the task of world-space hand–object interaction (W-HOI).

• We further propose a novel framework for W-HOI reconstruction from egocentric monocular videos captured by dynamic cameras. Our approach produces consistent world-space HOI trajectories, while remaining template-free and scalable to arbitrary numbers of objects.

• Extensive experiments demonstrate that EgoGrasp substantially outperforms existing methods on the H2O and HOI4D datasets, thereby establishing new state-of-the-art results for W-HOI reconstruction in real-world settings.

Related Work

Hand Pose Estimation

Hand pose estimation has developed rapidly in recent years, with early methods primarily targeting third-person perspectives under the assumption of minimal occlusion and stable camera viewpoints. Single-hand approaches typically regress MANO  model parameters , while two-hand methods employ implicit modeling or graph convolutions for interaction reconstruction .

Egocentric hand estimation is crucial for teaching robots manipulation tasks from a first-person perspective, facilitating advancements in embodied intelligence and virtual reality. Existing methods  typically reconstruct hand poses in the camera coordinate system, limiting their ability to model hand-object interactions globally. To overcome this, recent studies have explored world-space pose estimation to recover hand poses and trajectories in world coordinates. For example, Dyn-HaMR  integrates SLAM-based camera tracking with hand motion regression to achieve 4D global motion reconstruction. Similarly, HaWoR  decouples hand motion from camera trajectories by leveraging adaptive SLAM and motion completion networks, enabling the modeling of hand-object interactions in the world frame.

Although significant progress has been made, existing egocentric hand estimation methods still overlook essential hand-object interactions (HOI), limiting their applicability in embodied tasks. While recent approaches have improved hand pose reconstruction, they fail to explicitly model the complex dynamics between hands and objects. Furthermore, current methods often underutilize egocentric priors, resulting in reduced robustness and generalization. To address these challenges, our EgoGrasp jointly models hand-object dynamics in world coordinates. Check [tab:method-category-comparison] for differences between previous tasks.

Hand-Object Interaction Estimation

Estimating hand pose and object 6DoF is inherently challenging, especially in hand-object interaction (HOI) scenarios, where the interactions between hand and object further increase the complexity. Existing object 6DoF estimation methods can be broadly categorized as: (1) template-based methods, which rely on predefined CAD models  and auxiliary inputs such as segmentation masks and depth maps; (2) template-free methods, which estimate the 6DoF pose without CAD models and may reconstruct the object mesh, often conditioned on RGB-D inputs and segmentation masks . However, these approaches are often computationally expensive and struggle with robustness under noise, occlusions, and dynamic conditions.

Building on these 6DoF estimation methods, HOI estimation extends them by introducing the additional challenge of estimating hand pose alongside object 6DoF. Template-based methods  only estimate hand pose and object 6DoF, while template-free methods  jointly reason about hand pose, object 6DoF, and object mesh reconstruction. Despite benefiting from joint reasoning, HOI methods face unique challenges such as severe occlusions, dynamic camera motion, and complex hand-object interactions. ContactOpt  and GraspTTA  both directly optimize the contact loss by predicting or generating hand-object contact heatmaps to better construct HOI results. DiffHOI  and G-HOP  also achieve object mesh reconstruction by leveraging differentiable rendering and an implicit SDF field guided by diffusion model priors. Furthermore, their reliance on single-frame estimation often results in poor temporal consistency and unstable motion reconstruction in real-world scenarios.

To address these limitations, we introduce a whole-body diffusion prior model and a unified world-space representation, enabling robust and temporally consistent hand pose estimation, object 6DoF tracking, and mesh reconstruction. Check [tab:method-category-comparison] for differences between previous tasks.

Motion Prior Model In Pose Estimation

All the aforementioned hand-only estimation methods suffer from a critical limitation: the excessive number of degrees of freedom. Due to this high dimensionality, these methods are highly sensitive to various noises, causing hand orientation and positional drift, depth ambiguity, and even left–right hand misclassification. These issues fundamentally hinder stable world-space hand mesh reconstruction.

VPoser  trains a pose prior neural network using large-scale MoCap data to constrain the SMPL-X  parameters, better conforming to the statistical regularities of human motion. RoHM  utilizes diffusion model to implicitly leverage data-driven motion priors. LatentHOI , DiffHOI  and G-HOP  also train diffusion models to provide priors for HOI generation and reconstruction.

Similarly, we construct a decoupled prior model, including a motion diffusion model and a HOI diffusion model, to learn the whole-body pose prior and HOI prior. The whole-body pose explicitly utilizes egocentric prior, constraining hands by arms that conform to the laws of motion.

Method

style="width:98.0%" />

Problem Formulation

Given an egocentric video $`V \in \mathbb{R}^{T \times H \times W \times 3}`$, we aim to accurately reconstruct the world-space motion of dual hands and objects. Different from previous methods that reconstruct left hand and right separately, we reconstruct whole body motion to restrict the range of dual hands: hand poses $`\{\theta_l^t, \theta_r^t \in \mathbb{R}^{15 \times 3}\}_{t=0}^{T}`$, body poses $`\{\theta_b^t \in \mathbb{R}^{21 \times 3}\}_{t=0}^{T}`$, betas $`\{\beta^t \in \mathbb{R}^{10}\}_{t=0}^{T}`$, global orientation $`\{\phi_t^i \in \mathbb{R}^3\}_{t=0}^{T}`$, global root translation $`\{\gamma_t^i \in \mathbb{R}^3\}_{t=0}^{T}`$). For object $`j`$, we reconstruct the mesh $`M_j`$ and global trajectory $`\left\{ d_j^t \in \mathrm{SE}(3) \right\}_{t=0}^{T}`$ in world coordinates.

The proposed framework consists of three main parts: 1) an egocentric video preprocessing pipeline, which extracts initial 3D attributes from the video; 2) a decoupled whole-body diffusion model for HOI, which generates reasonable whole-body poses based on the extracted 3D attributes to constrain hand pose and object 6DoF; and 3) post-optimization, which optimizes the results of the diffusion model based on the extracted 3D attributes. An overview of the proposed framework is visualized in 2.

Egocentric Video Preprocess

The 2D and 3D field has received a great deal of research in recent years, with many outstanding works emerging in various sub-fields. As a highly challenging 3D task, world-space HOI reconstruction necessitates the full utilization of existing advanced methods to construct a systematic egocentric video preprocessing pipeline, providing sufficient and accurate 3D prior knowledge and data attributes for the task. The preprocessing pipeline for world-space HOI (Human-Object Interaction) reconstruction is divided into three major steps: global scene reconstruction, hand reconstruction, and object reconstruction. Each step combines state-of-the-art methods to process egocentric videos, ensuring sufficient and accurate 3D data for downstream tasks.

The 1st step focuses on reconstructing the global scene, including camera parameters and depth maps. We begin by using $`\pi^3`$  to infer the camera intrinsics $`\mathbf{K}`$ (obtained by estimating a normalized focal length and depth shift from local 3D points.), and represent the extrinsics $`\mathbf{E}^t`$ as rotation $`\mathbf{R} \in \mathrm{SO}(3)`$ and translation $`\mathbf{T} \in \mathbb{R}^3`$, and an initial depth map $`D_{\text{raw}}^t`$ for the entire video sequence. Since the depth map produced by $`\pi^3`$ is often noisy and lacks precision, we apply Prompt Depth Anything (PromptDA)  to optimize the depth map, producing a higher-quality depth $`D^t`$.

In the second step, we focus on reconstructing hand poses for each video frame, refining the globally estimated scene from the first step to metric scale, and estimating the ground plane orientation. To achieve this, we utilize a SOTA hand pose estimation method WiLoR , combined with the camera intrinsics $`\mathbf{K}`$ obtained from the 1st step, to estimate the left and right hand poses $`\theta_{lp}^t, \theta_{rp}^t \in \mathbb{R}^{15 \times 3}`$. Next, we rescale the depth map and camera translation from the first step to the metric scale rendered from the MANO depth. Additionally, we employ Language Segment-Anything(LangSAM)  to segment horizontal surfaces such as the ground, tabletops, and other similar features that may appear in the video. By combining this segmentation with the depth map, we apply the RANSAC algorithm to fit the horizontal surfaces and compute the normal vector, which represents the ground orientation. In cases where LangSAM cannot effectively segment the surfaces, we further incorporate the camera intrinsics $`\mathbf{K}`$ with GeoCalib . GeoCalib predicts the ground orientation for each frame, enhancing the robustness of the data pipeline.

In 3rd step, to estimate the inital 6DoF pose $`d_{jp}^t \in \mathrm{SE}(3)`$ for each object $`j`$, we combine GenPose++  and Any6D . GenPose++ predicts relative 6DoF poses for objects based on three key inputs: object masks, depth maps, and camera intrinsics. To get fine-grained, occlusion-free object segmentation, we utilize EgoHOS  to perform initial semantic segmentation on egocentric videos, identifying regions such as the left hand, right hand, left-hand-held object, right-hand-held object, and both-hands-held object. To prove the robustness, we leverage DINOv3  to extract feature embeddings for each segmentation mask. These feature embeddings are clustered using K-Means to assign each mask to a specific object index, resulting in fine-grained and object-specific segmentation masks by further utilizing SAM2 . With optimized object masks in hand, we combine them with the depth map $`D^t`$ to unproject object-specific point clouds $`X_j^t`$. These point clouds serve as the geometric condition to following diffusion models. Since GenPose++ cannot generate object meshes, we reconstruct high-quality object meshes $`M_j`$ for the selected keyframes and estimate their 6DoF poses using Any6D . Keyframes are chosen via a weighted scoring scheme that balances mask area, depth distribution, hand–object distance, and image-boundary truncation, ensuring that only reliable views are used for mesh generation and pose registration. This refinement step ensures that the object poses are highly accurate and consistent, while the generated meshes provide detailed geometric representations of the objects. By combining the relative pose transformations from GenPose++ with the keyframe poses refined by Any6D, we construct a complete and robust 6DoF pose sequence for each object.

Decoupled Whole-Body Diffusion

We propose a decoupled diffusion model designed to jointly constrain and optimize the initial hand pose estimation and object 6DoF predictions. As illustrated in 2, the framework consists of two sub-models: a Whole-body Diffusion Model $`\mathcal{W}`$ and a HOI Diffusion Model $`\mathcal{H}`$. We first employ $`\mathcal{W}`$ to generate a plausible full-body pose. The estimated arm configuration is then adopted as a kinematic prior to constrain hand pose estimations. Finally, we apply $`\mathcal{H}`$ to further refine the predicted object 6DoFs.

Given that HOI involve complex and fine-grained physical dependencies, the two diffusion models should not operate independently or in a purely sequential manner. However, HOI datasets that include full-body poses are extremely limited. Directly training a unified model to simultaneously handle hand pose and object 6DoF would therefore introduce substantial pose bias, impeding the ability of model to learn meaningful full-body motion priors.

To address this challenge, we introduce a decoupled learning strategy. First, we train only the whole-body diffusion model $`\mathcal{W}`$. It takes as input the conditional features $`\mathbf{c}^t`$—which are extracted by a condition encoder $`\phi`$ from the CPF inter-frame transformations $`\Delta\mathbf{T}_{\mathrm{cpf}}^{t-1\rightarrow t}`$, CPF-to-Canonical $`\mathbf{T}_{C\leftarrow \mathrm{cpf}}^t`$ (Please check Supp.Mat. for details.), CPF-to-LeftWrist $`\mathbf{T}_{\mathrm{lw}\leftarrow \mathrm{cpf}}^t`$, and CPF-to-RightWrist transformations $`\mathbf{T}_{\mathrm{rw}\leftarrow \mathrm{cpf}}^t`$. Here, the central pupil frame (CPF)  is defined as the camera extrinsic rotated by $`180^\circ`$ around its $`z`$-axis ($`\mathbf{T}_{\pi z}`$), and the canonical coordinates is derived by projecting the CPF onto the ground plane. The default ground height is set to 1.65m below the highest point of the CPF trajectory. $`\operatorname{FK}_\mathrm{L}(\cdot)`$ and $`\operatorname{FK}_\mathrm{R}(\cdot)`$ refer to the left-hand and right-hand forward kinematics of SMPL-X, respectively. The model also receives the initial hand pose estimation as input and outputs optimized full-body pose parameters. The formulation is given as follows:

\begin{align}
\mathbf{T}_{\mathrm{cpf}}^t &= \mathbf{E}^t \, \mathbf{T}_{\pi z} \in \mathrm{SE}(3),
\vspace{-10pt} \label{eq:cpf_transform} \\
%-------------------------------------
\Delta\mathbf{T}_{\mathrm{cpf}}^{t\rightarrow t+1}
&= \left(\mathbf{T}_{\mathrm{cpf}}^{t}\right)^{-1}\mathbf{T}_{\mathrm{cpf}}^{t+1} \in \mathrm{SE}(3),
\vspace{-10pt} \label{eq:cpf_delta} \\
%-------------------------------------
\mathbf{T}_{\mathrm{lw}}^t &= \operatorname{FK}_\mathrm{L}(\theta_{lp}^t), \,
\mathbf{T}_{\mathrm{rw}}^t = \operatorname{FK}_\mathrm{R}(\theta_{rp}^t),
\vspace{-10pt} \label{eq:lw_rw_transform} \\
%-------------------------------------
\mathbf{T}_{\mathrm{lw}\leftarrow \mathrm{cpf}}^t &=
(\mathbf{T}_{\mathrm{lw}}^t)^{-1}\mathbf{T}_{\mathrm{cpf}}^t,
\mathbf{T}_{\mathrm{rw}\leftarrow \mathrm{cpf}}^t =
(\mathbf{T}_{\mathrm{rw}}^t)^{-1}\mathbf{T}_{\mathrm{cpf}}^t,
\vspace{-10pt} \label{eq:cpf_to_lw_rw} \\
%-------------------------------------
\mathbf{c}^t &= 
\phi\!\Big(
\Delta\mathbf{T}_{\mathrm{cpf}}^{t-1\rightarrow t},
\mathbf{T}_{C\leftarrow \mathrm{cpf}}^t,
\mathbf{T}_{\mathrm{lw}\leftarrow \mathrm{cpf}}^t,
\mathbf{T}_{\mathrm{rw}\leftarrow \mathrm{cpf}}^t
\Big),\vspace{-10pt} \label{eq:context} \\
%-------------------------------------
\mathbf{y}^t &= 
\big[\theta_{lp}^t\; \oplus \;
\theta_{rp}^t\big] \in \mathbb{R}^{90},
\vspace{-5pt} \label{eq:output}
\end{align}

The above are formulas for input variables and $`\oplus`$ denotes concatenation. Let $`\mathbf{z}`$ be the latent variable to be denoised, and $`t_d`$ be the number of denoising steps. The inference formula for the whole-body diffusion model $`\mathcal{W}`$ is as follows.

\begin{equation}
\begin{gathered}
\widehat{\mathbf{z}}_{t_d-1}^{\,1:T}
=\mathcal{W}\!\big(\mathbf{z}_{t_d}^{\,1:T},\;\mathbf{c}^{\,1:T},\;\mathbf{y}^{\,1:T},\;t_d\big),\\
t_d = 0, 1, \dots, 1000, \\
\widehat{\theta}_{\mathrm{full}}^t \;=\; \!\widehat{\mathbf{z}}_{0}^t.
\end{gathered}
\end{equation}

where $`\widehat{\theta}_{\mathrm{full}}^t`$ is the predicted full SMPL-X parameters. The whole-body diffusion model here are trained using the following formula:

\begin{equation}
\begin{gathered}
\mathbf{z}_{t_{d}}^t = \sqrt{\bar{\alpha}_{t_{d}}}\,\mathbf{z}_0^t + \sqrt{1-\bar{\alpha}_{t_{d}}}\,\boldsymbol{\epsilon}, ~~\mathbf{z}_0^t = \theta_{\mathrm{full}}^t, \\
\mathbf{z}_{t_d-1}^{t} 
= \sqrt{\bar{\alpha}_{t_d-1}}\,\mathbf{z}_0^t 
+ \sqrt{1-\bar{\alpha}_{t_d-1}}\,\boldsymbol{\epsilon},
\ \boldsymbol{\epsilon}\sim\mathcal{N}(\mathbf{0},\mathbf{I}),
\end{gathered}
\end{equation}

\begin{equation}
\mathcal{L}_{\mathrm{W}} =
\mathbb{E}_{t,\;\mathbf{z}_0^t,\;\boldsymbol{\epsilon}}
\left[
\left\|
\widehat{\mathbf{z}}_{t_d-1}^{\,1:T}
-
\mathbf{z}_{t_d-1}^{\,1:T}
\right\|_2^2
\right].
\end{equation}

Model-Free and Unbounded HOI

After training the whole-body diffusion model $`\mathcal{W}`$, we freeze its parameters and introduce an additional HOI diffusion model $`\mathcal{H}`$ . This model takes as input the initial object 6DoF predictions, object mesh, object point cloud, the full-body pose parameters and features produced by the whole-body diffusion model $`\mathcal{W}`$, as well as the same conditional features $`\mathbf{c}^t`$. It performs joint denoising alongside the whole-body diffusion model $`\mathcal{W}`$ and outputs refined hand pose parameters and object 6DoF trajectories. During inference, the hand pose predictions generated by the whole-body diffusion model $`\mathcal{W}`$ can be overwritten with those from the HOI diffusion model $`\mathcal{H}`$ to maintain consistency in subsequent denoising iterations. This enables effective training on existing HOI datasets while preserving the full-body motion priors learned from large-scale full-body datasets. The formula is as follows:

\begin{equation}
\begin{gathered}
\widehat{\mathbf{m}}_{j,t_d}^{1:T} = \big[\widehat{\mathbf{o}}_{j,t_d}^{1:T}\; \oplus \;
M_j\; \oplus \;
X_j^{1:T}\; \oplus \;
d_{jp}^{1:T}
\big],\\
\widehat{\mathbf{z}}_{t_d-1}^{1:T},\;
\widehat{\mathbf{o}}_{j,t_d-1}^{1:T}
=\mathcal{H}\!\big(\mathcal{W}\!\big(\mathbf{z}_{t_d}^{1:T},\!\mathbf{c}^{1:T},\!\mathbf{y}^{1:T},\!t_d\big),\!
\widehat{\mathbf{m}}_{j,t_d}^{1:T}\big),\\
t_d\!=\!0,1,\!\dots,\!1000,\ j\!\in\![1,2,\dots,J].
\end{gathered}
\end{equation}

where $`\mathbf{o}_{j}`$ denotes the 6DoF of object $`j`$, $`J`$ denotes the total number of objects. The training formula for the HOI diffusion model $`\mathcal{H}`$ is very similar to that for the whole-body diffusion model $`\mathcal{W}`$, so it will not be repeated here.

By looping through each object within the HOI diffusion $`\mathcal{H}`$, multi-object interactions can be achieved, as shown in [alg:multi_hoi]. Additionally, object meshes have been obtained in 3.2.

Test-time SMPL-X Optimization

At test time, we perform a lightweight, fully differentiable optimization to refine both body and hand poses in axis–angle representation. The objective jointly enforces spatial accuracy, temporal smoothness, and foot–ground consistency. We define several loss functions to ensure realistic and physically plausible motion. (1) Pose anchor Loss $`\mathcal{L}_{anchor}`$ prevents excessive drift by preserving the initialized body configuration. (2) Hand joint loss $`\mathcal{L}_{3D}`$ aligns the predicted 3D hand joints with the target ones. (3) Foot height loss $`\mathcal{L}_{foot-h}`$ anchors toes and ankles near the ground by combining height cues with predicted contact probabilities. (4) Pairwise Anti-Slip Constraint suppresses foot motion during contact and penalizes excessive XY velocity to prevent sliding. (5) Segment-wise Constancy enforces nearly constant XY positions for each continuous contact segment, ensuring spatial consistency. (6) Temporal loss $`\mathcal{L}_{temp}`$ regularizes angular velocity, acceleration, and drift on $`\mathrm{SO}(3)`$, ensuring smooth transitions.

\begin{align}
\mathcal{L}_{\text{total}} &=
\lambda_1 \mathcal{L}_{\text{anchor}}
+ \lambda_2 \mathcal{L}_{\text{3D}}
+ \lambda_3 \mathcal{L}_{\text{foot-h}} \nonumber\\
&\quad + \lambda_4 \mathcal{L}_{\text{foot-p}} + \lambda_5 \mathcal{L}_{\text{foot-s}} + \lambda_6 \mathcal{L}_{\text{temp}},\\
\mathcal{L}_{\text{anchor}} &=
\frac{1}{N} \sum_{t=1}^{T}
\|\theta_t^{\text{body}} -
\hat{\theta}_t^{\text{body}}\|_2,\\
\mathcal{L}_{\text{3D}} &=
\frac{1}{N} \sum_{t=1}^{T}
\|\hat{J}_t^{\text{hand}} -
J_t^{\text{hand}}\|_2,\\
\mathcal{L}_{\text{foot-h}} &=
\frac{1}{N} \sum_{t=1}^{T}
\|\hat{z}_t^{\text{foot}} - z_t^{\text{ref}}\|_2,\\
\mathcal{L}_{\text{foot-p}} =
&\;\frac{1}{T-1} \sum_{t=1}^{T-1}
\sum_{j \in \text{foot}}
w_{t,j}^{\text{contact}}
\|\hat{P}_{t+1,j} - \hat{P}_{t,j}\|_2 \nonumber\\
&\;+ \eta \,
\text{ReLU}\!\left(
\|\dot{\hat{P}}_{t,j}^{xy}\| - v_{\text{thr}}
\right)^{\!2},\\
\mathcal{L}_{\text{foot-s}} &=
\frac{1}{N_{\text{seg}}} \sum_{s}
\sum_{t \in s}
\|\hat{P}_t^{xy} - \bar{\hat{P}}_s^{xy}\|_2,\\
\mathcal{L}_{\text{temp}} &=
\lambda_v \mathcal{L}_{\text{vel}} +
\lambda_a \mathcal{L}_{\text{acc}} +
\lambda_d \mathcal{L}_{\text{drift}},
\end{align}

Where, in $`\mathcal{L}_{temp}`$, we regularize angular velocity, acceleration, and drift in the rotation manifold $`\mathrm{SO}(3)`$ using predicted rotations. We list our balanced hyper parameters in Supp.Mat.

\begin{align}
\mathcal{L}_{\text{vel}} &=
\frac{1}{T-1}\sum_{t=1}^{T-1}
\|\log(\hat{R}_{t+1}\hat{R}_t^\top)\|_2, \\
\mathcal{L}_{\text{acc}} &=
\frac{1}{T-2}\sum_{t=1}^{T-2}
\|\log(\hat{R}_{t+2}\hat{R}_{t+1}^\top)
- \log(\hat{R}_{t+1}\hat{R}_t^\top)\|_2, \\
\mathcal{L}_{\text{drift}} &=
\frac{1}{T-1}\sum_{t=1}^{T-1}
\|\log((\hat{R}_t\hat{R}_0^\top)
(\hat{R}_{t+1}\hat{R}_0^\top)^\top)\|_2.
\end{align}

Experiments

Implementation Details & Metrics

We evaluated hand pose estimation and object 6DoF estimation on the H2O  and HOI4D  datasets. Following Dyn-HaMR  and HaWoR , the metrics employed for hand estimation evaluation included World Mean Per Joint Position Error (W-MPJPE), World-aligned Mean Per Joint Position Position Error (WA-MPJPE), and Mean Per Joint Position Error (MPJPE). And we used Relative Rotation Error (RRE), Relative Translation Error (RTE), in world and local space both, for 6DoF evaluations. World-space metrics are computed over segments of 128 frames, where W-MPJPE involved aligning only the first two frames, whereas WA-MPJPE aligned the entire segment, both using Procrustes Alignment.

We trained the model using PyTorch with 4 NVIDIA A100 GPUs at a learning rate of 2.5e-4, employing AdamW optimizer and cosine annealing. The whole-body diffusion was trained on AMASS , 100STYLE  , and PA-HOI  datasets; HOI diffusion was trained on GRAB , PA-HOI , and HIMO  datasets. Training sequences were sampled at 30 FPS with random lengths ranging from 64 to 256 frames. During test-time optimization, we used learning rates of 2.5e-4, 2.5e-4, and 1.0e-4 to optimize hand pose, body pose, and beta parameters, respectively, and performed a total of 50 optimization steps using AdamW and cosine annealing. PointNet++  was used to process the mesh and point cloud of objects.

Hand-Only Pose Estimation

We demonstrate the superior reconstruction quality of EgoGrasp on the world-space hand pose by comparing it with several other advanced methods, including ACR , IntagHand , HaMeR , Dyn-HaMR , HaWoR , WiLoR .

style="width:95.0%;height:12cm" />

Quantitative Comparisons. [tab:exp_h2o] and [tab:exp_hoi4d] present the quantitative results of EgoGrasp and other competing methods on the H2O and HOI4D datasets. “WiLoR + $`\pi^3`$” denotes the world-coordinate results obtained by transforming the camera-coordinate outputs of WiLoR using the camera extrinsics predicted by $`\pi^3`$, while “WiLoR + GT” denotes the transformation using ground-truth extrinsics. It is evident that traditional camera-coordinate estimation methods, such as ACR, IntagHand, and HaMeR, fail to effectively reconstruct global trajectories.

style="width:95.0%;height:12cm" />

Compared with Dyn-HaMR, WiLoR + $`\pi^3`$, and WiLoR + GT, EgoGrasp achieves the best G-MPJPE and a GA-MPJPE nearly on par with the top-performing method (which uses GT), demonstrating its strong capability for reconstructing hand motion in the world coordinate system. A limitation of EgoGrasp is its relatively higher MPJPE, which results from its design focus on maximizing the accuracy of world-coordinate reconstruction. To address the errors in extrinsic predicted by $`\pi^3`$, EgoGrasp applies frame-wise correction and compensation to the camera-coordinate results, leading to a certain degree of deviation in the camera space. This is justifiable and aligns with the optimization objective.

Qualitative Comparisons. 3 presents a visual comparison of HaWoR, Dyn-HaMR, and EgoGrasp, demonstrating that EgoGrasp achieves superior performance in both fine-grained hand manipulation on the H2O dataset and long-term motion trajectories on the HOI4D dataset. From the last two rows of 3, we observe that HaWoR exhibits severe hand drifting and pose errors, while Dyn-HaMR even misidentifies the left and right hands. Moreover, both methods show clear inaccuracies in reconstructing the world trajectories. In contrast, EgoGrasp achieves substantially more accurate results. It is worth noting that EgoGrasp estimates the hands under a whole-body pose constraint, which helps ensure outcomes that are consistent with natural human motion.

Hand-Object Interaction Estimation

To further evaluate the effectiveness of EgoGrasp in HOI, we conduct a comparative analysis with two state-of-the-art object 6DoF tracking approaches: Any6D  (Origin) and GenPose++ . Additionally, we introduce an enhanced version of Any6D, termed “Any6D (Enhanced)”. This improvement addresses the tendency of the Any6D tracker to drift by incorporating a per-frame pose-variation detector that triggers re-registration whenever a substantial deviation in the estimated transformation is detected.

Quantitative Comparisons. [tab:exp_obj_h2o] and [tab:exp_obj_hoi4d] present the performance of various methods on the H2O and HOI4D datasets for object 6DoF tracking. Here, “Any6D” refers to the original version, while “Any6D (Enh)” refers to our enhanced version. “+ GT” indicates that ground-truth camera extrinsics are used to transform results from the camera coordinate system to the world coordinate system, whereas “+ $`\pi^3`$” denotes the use of camera extrinsics predicted by $`\pi^3`$ for this transformation.

It is evident that, in both local and world coordinates, EgoGrasp achieves substantial improvements over GenPose++ and Any6D across both datasets, with particularly significant gains in rotation estimation. This improvement arises because EgoGrasp comprehensively integrates existing hand pose and full-body constraint priors when reasoning about object 6DoFs, thereby refining unreasonable predictions and ensuring physical consistency in HOI.

Qualitative Comparisons. As shown in 4, only EgoGrasp successfully reconstructs the object trajectory while simultaneously achieving accurate hand pose estimation. This superiority benefits from our HOI diffusion model, which jointly optimizes the initial hand pose and 6DoF estimations. From the last row in 4, we observe that Any6D (Origin), which performs only a single registration, suffers from inadequate tracking, leading to severe drift in the subsequent trajectory. Any6D (Enh), through multiple re-registrations, is able to recover the approximate trajectory, but exhibits pronounced jitter. In contrast, EgoGrasp reconstructs a HOI trajectory in world coordinates that closely matches the GT, achieving consistent, smooth, and physically plausible results.

Ablation Studies

To further demonstrate the validity of EgoGrasp, we implemented two other variants. Specifically, “$`only\,\mathcal{W}`$” refers to using only the whole-body diffusion model while removing the corrective term from the HOI diffusion model; “EgoGrasp (Any6D)” replaces the GenPose++ tracker with the Any6D (Enh) tracker.

[tab:exp_ablation] reports hand-pose evaluations on the H2O and HOI4D datasets. Moreover, by examining the two WiLoR variants (WiLoR + $`\pi^3`$ and WiLoR + GT) in [tab:exp_h2o] and [tab:exp_hoi4d], we observe that all variants—except EgoGrasp—show degraded performance, with G-MPJPE dropping most markedly. These findings show the effectiveness of EgoGrasp for global hand estimation.

[tab:exp_ablation_obj] presents the object 6DoF tracking performance of EgoGrasp (Any6D) and EgoGrasp on the H2O and HOI4D datasets. When compared with the Any6D- and GenPose++-based variants reported in [tab:exp_obj_h2o] and [tab:exp_obj_hoi4d], we find that EgoGrasp yields consistent improvements for both 6DoF tracking methods, particularly in rotation estimation, demonstrating the generalization and robustness of the proposed design.

Conclusion

We introduced EgoGrasp, the first method to reconstruct world-space hand–object interactions (W-HOI) from egocentric monocular videos captured by dynamic cameras in the wild. Our multi-stage framework integrates a robust pre-processing pipeline built on recent spatial intelligence models, a template-free whole-body HOI prior instantiated with decoupled diffusion models, and a multi-objective test-time optimization paradigm enforcing temporal consistency and global trajectory alignment. EgoGrasp yields accurate, physically plausible, and temporally coherent W-HOI trajectories that generalize beyond single-object and template constraints. Experiments on challenging in-the-wild sequences of H2O and HOI4D datasets demonstrate state-of-the-art performance under severe camera motion and hand-object occlusion.

Limitations & future work. The performance of EgoGrasp still depends on the quality of preprocessing results — instability in upstream steps can affect final results. The current pipeline includes several modules, leaving room for simplification. Moreover, mesh generation relies on informative keyframes, and heavy occlusion can make reliable reconstruction difficult. Our future work will focus on developing more streamlined feed-forward model.