Bridging the Semantic Gap for Categorical Data Clustering via Large Language Models
📝 Original Paper Info
- Title: Bridging the Semantic Gap for Categorical Data Clustering via Large Language Models- ArXiv ID: 2601.01162
- Date: 2026-01-03
- Authors: Zihua Yang, Xin Liao, Yiqun Zhang, Yiu-ming Cheung
📝 Abstract
Categorical data are prevalent in domains such as healthcare, marketing, and bioinformatics, where clustering serves as a fundamental tool for pattern discovery. A core challenge in categorical data clustering lies in measuring similarity among attribute values that lack inherent ordering or distance. Without appropriate similarity measures, values are often treated as equidistant, creating a semantic gap that obscures latent structures and degrades clustering quality. Although existing methods infer value relationships from within-dataset co-occurrence patterns, such inference becomes unreliable when samples are limited, leaving the semantic context of the data underexplored. To bridge this gap, we present ARISE (Attention-weighted Representation with Integrated Semantic Embeddings), which draws on external semantic knowledge from Large Language Models (LLMs) to construct semantic-aware representations that complement the metric space of categorical data for accurate clustering. That is, LLM is adopted to describe attribute values for representation enhancement, and the LLM-enhanced embeddings are combined with the original data to explore semantically prominent clusters. Experiments on eight benchmark datasets demonstrate consistent improvements over seven representative counterparts, with gains of 19-27%. Code is available at https://github.com/develop-yang/ARISE💡 Summary & Analysis
1. **Addressing Small Sample Problem:** ARISE uses LLMs to provide external semantic information when statistical signals are insufficient, enabling meaningful clustering even with small samples. This is like using a GPS to find your way in the rain. 2. **Attention-Weighted Encoding:** It emphasizes key tokens from generated descriptions to produce compact and informative semantic embeddings. This can be likened to extracting the most important points from a movie review to create a summary. 3. **Enhancing Traditional Clustering with LLMs:** ARISE shows consistent improvements of 19-27% across various benchmarks, offering new solutions to old problems by leveraging modern tools.📄 Full Paper Content (ArXiv Source)
 />
/>
Introduction
Categorical data are ubiquitous in real-world applications such as medical diagnosis, customer segmentation, and biological research . In these domains, discovering latent patterns through clustering enables critical downstream tasks, including patient stratification, market analysis, and gene function annotation. As an unsupervised approach, clustering can reveal hidden structures directly from raw observations without requiring costly labeled data. However, unlike numerical data that arises from metric spaces where distances are naturally defined, categorical data exist prior to any distance metric, which must be constructed afterwards . This fundamental difference makes similarity measurement the core challenge in categorical clustering. As illustrated in Figure 1(a), without appropriate metric design, all values tend to be treated as equidistant, creating a semantic gap that obscures the latent structure and degrades clustering quality.
To bridge this gap, existing methods attempt to infer value relationships from statistical information within the dataset. Distance-based methods directly measure dissimilarity between objects. Early approaches such as $`k`$-modes treat each attribute mismatch equally, while more sophisticated techniques exploit attribute coupling or multi-metric space fusion to capture value dependencies. Embedding-based approaches take a different route by learning continuous representations that encode value relationships. Despite their differences, these methods share a common assumption that all necessary semantic relationships can be derived from the dataset itself. However, this assumption fails under limited samples. In specialized domains such as rare disease diagnosis or niche market analysis, datasets often contain only tens to hundreds of samples, making it difficult to establish reliable value associations. Under such conditions, statistical signals become weak, and semantically related values become indistinguishable, leading to degraded clustering performance.
To overcome this limitation, external semantic knowledge is needed to supplement insufficient statistical signals. LLMs, pretrained on massive corpora, encode rich semantic knowledge and can provide external evidence beyond the dataset . Recent works such as ClusterLLM and TabLLM have demonstrated the effectiveness of LLMs in text clustering and tabular classification. However, these methods target text data or supervised tasks, and cannot be directly applied to unsupervised categorical clustering. Adapting LLMs to this setting presents several challenges. Querying LLMs incurs non-trivial computational cost, particularly when processing each data instance individually. The stochastic nature of LLM generation may produce inconsistent representations, where identical categorical values receive different embeddings across queries, undermining clustering stability. LLM-generated descriptions often contain verbose or non-discriminative content that dilutes the useful semantic signals and may introduce noise. Moreover, external knowledge must be balanced with data-specific patterns, as over-reliance on LLM outputs may override valid statistical signals learned from the dataset.
This paper, therefore, proposes ARISE (Attention-weighted Representation with Integrated Semantic Embeddings), a framework that integrates LLM-derived semantics into categorical clustering. To ensure efficiency and consistency, ARISE queries LLMs at the attribute-value level, reducing computational cost while guaranteeing that identical values receive identical representations. To extract discriminative features from LLM outputs, an attention-weighted encoding mechanism emphasizes informative tokens without learnable parameters. To balance external knowledge with data-specific patterns, an adaptive fusion module adjusts the contribution of semantic embeddings based on cluster quality. As shown in Figure 1(b), leveraging semantic proximity leads to improved cluster separation compared to non-semantic approaches. Experiments on eight benchmark datasets with four mainstream LLMs confirm that ARISE consistently outperforms seven state-of-the-art counterparts across all the evaluated datasets. The main contributions are summarized as follows:
-
To address the small-sample problem in categorical clustering, a framework is proposed that queries LLMs at the attribute-value level, integrating LLM-derived semantics as external evidence to supplement insufficient statistical signals.
-
An attention-weighted encoding mechanism is proposed to emphasize key tokens in the generated descriptions, producing information compact semantic embeddings that are more discriminative for categorical data clustering.
-
This work provides the first empirical validation that LLMs can sufficiently enhance traditional categorical clustering. Experiments across eight benchmarks demonstrate consistent improvements over seven representative counterparts, with gains of 19–27% on all the evaluated datasets, confirming the value of external semantic knowledge for categorical clustering.
Related Work
Categorical Data Representation and Clustering
The discrete nature of categorical attributes, characterized by the absence of inherent order or distance, necessitates the explicit construction of similarity measures. Statistical inference is the mainstream approach in this domain. While early approaches relied on matching dissimilarities , distance-based methods have evolved toward information-theoretic metrics. Recent works have introduced graph-based perspectives and learnable intra-attribute weighting to adjust feature importance, while others explore multi-metric space fusion for robust clustering. Parallel to metric learning, representation learning aims to map discrete symbols into continuous vector spaces. For heterogeneous or mixed-type data, Het2Hom and QGRL project attributes into homogeneous concept spaces or quaternion graphs, while adaptive partition strategies address clustering through hierarchical merging mechanisms.
Despite these methodological advancements, a fundamental limitation persists. As noted in a recent survey , measuring similarity for categorical data remains challenging due to the lack of well-established distance metrics. When samples are limited, co-occurrence signals become sparse, making value relationships difficult to infer and leading to degraded representations.
Large Language Models for Clustering
Recent advances in LLMs have demonstrated remarkable capabilities in various data understanding tasks . Pre-trained on massive open-domain corpora, LLMs encode extensive world knowledge that can potentially overcome the closed-world constraint. In text clustering, ClusterLLM and recent few-shot approaches utilize LLMs to generate triplet constraints or refine cluster boundaries, demonstrating that external knowledge can significantly enhance structural partitioning. In the context of tabular data, the adaptation of LLMs has focused primarily on supervised prediction and generation. TabLLM and GReaT employ a serialization-based paradigm, converting tabular rows into natural language sentences (e.g., “The color is red…”) to leverage the reasoning capabilities of LLMs. Similarly, pre-training frameworks like TaBERT and TAPAS learn joint representations of textual and tabular data for semantic parsing tasks requiring deep alignment between schema and context.
However, text clustering methods are designed for natural language data, while tabular methods primarily target supervised tasks. Adapting these approaches to unsupervised categorical clustering faces additional challenges. Row-level serialization scales linearly with dataset size ($`\mathcal{O}(N)`$), making iterative clustering prohibitively expensive. Furthermore, standard pooling strategies (e.g., mean pooling or CLS tokens ) may obscure discriminative keywords within generated descriptions. To date, no framework effectively integrates LLM semantics into categorical clustering.
Proposed Method
Given a categorical dataset $`\mathcal{X} = \{x_1, \ldots, x_N\}`$ where each object is described by $`M`$ attributes taking values from $`\mathcal{V} = \bigcup_{j=1}^{M} V_j`$, the clustering problem can be formulated as learning a mapping $`\Phi: \mathcal{X} \rightarrow \mathbb{R}^{D}`$ such that distances in the embedding space reflect semantic similarity. However, categorical values lack inherent distance metrics, creating a gap between raw symbols and meaningful representations. Bridging this gap requires addressing three interdependent challenges, namely extracting semantic knowledge invisible to co-occurrence statistics, encoding variable-length descriptions into discriminative vectors, and preventing distinct values from collapsing in the embedding space. These challenges form a pipeline where each stage depends on its predecessor, as semantic extraction provides input for encoding, and encoding quality determines whether fusion can balance semantics against categorical identity.
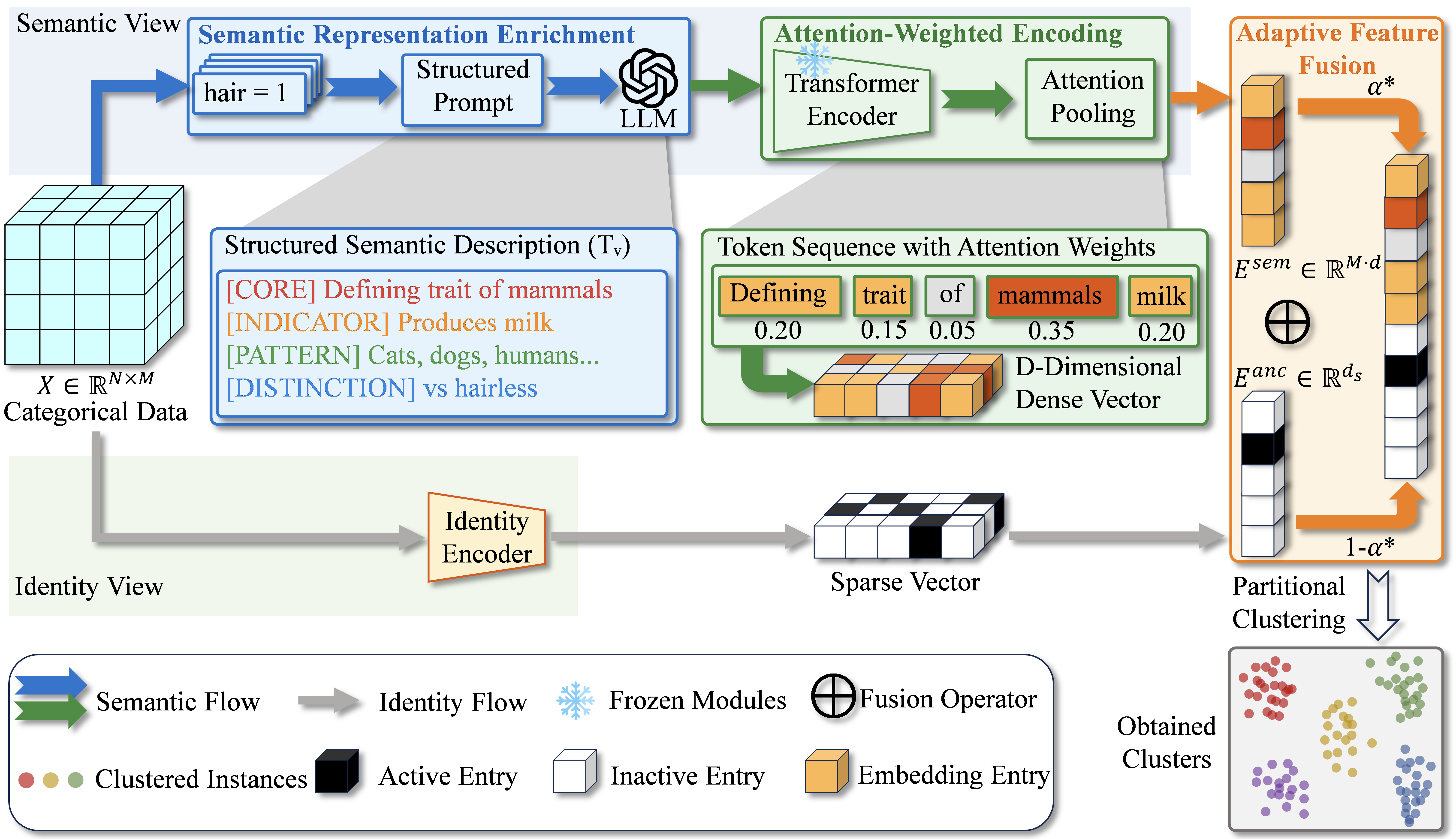
Therefore, ARISE addresses these challenges by leveraging LLMs as external knowledge sources. As illustrated in Figure 2, the framework comprises three components, namely semantic representation enrichment that generates descriptions via value-level LLM queries, attention-weighted encoding that emphasizes informative tokens, and adaptive fusion that anchors semantic representations with identity-preserving features.
| Symbol | Description |
|---|---|
| $`\mathcal{X} = \{x_1, \ldots, x_N\}`$ | Categorical dataset with $`N`$ objects |
| $`x_i = [x_{i,1}, \ldots, x_{i,M}]`$ | Object with $`M`$ attribute values |
| $`\mathcal{A} = \{A_1, \ldots, A_M\}`$ | Set of categorical attributes |
| $`V_j`$; $`\mathcal{V} = \bigcup_{j} V_j`$ | Value domain of $`A_j`$; all unique values |
| $`\mathcal{M}`$; $`\mathcal{E}`$ | LLM; pre-trained Transformer encoder |
| $`T_v`$; $`e_v \in \mathbb{R}^d`$ | Description; embedding for value $`v`$ |
| $`E^{sem} \in \mathbb{R}^{N \times Md}`$ | Semantic representation matrix |
| $`E^{anc} \in \mathbb{R}^{N \times d_s}`$ | Identity-anchoring matrix ($`d_s = |
| $`\alpha \in [0,1]`$; $`Z \in \mathbb{R}^{N \times D}`$ | Fusion weight; fused representation ($`D = d_s + Md`$) |
| $`K`$; $`\mathcal{Y}`$ | Number of clusters; cluster assignment |
Summary of key notations.
 />
/>
Semantic Representation Enrichment
Categorical values often contain latent relationships (e.g., ordinality in “low” vs. “high”) invisible to statistical co-occurrence. LLMs are leveraged to capture these relationships by providing external semantic knowledge.
Distinct from continuous domains where every instance is unique, categorical attributes exhibit high repetition. Accordingly, a value-level querying strategy is adopted, processing the unique vocabulary set $`\mathcal{V}`$ rather than the full dataset. This approach guarantees consistency, as identical values always receive identical descriptions, while significantly reducing computational cost.
To generate these descriptions, a structured prompt $`\mathcal{P}`$ is formulated to organize the description into four aspects, namely definition, indicators, context, and contrast. The description for a value $`v`$ belonging to attribute $`A_j`$ with domain $`V_j`$ is formally obtained as:
\begin{equation}
T_v = \mathcal{M}(\mathcal{P}(v, A_j, V_j)),
\end{equation}yielding the complete set $`\mathcal{T} = \{T_v : v \in \mathcal{V}\}`$ used for downstream encoding.
Computational Amortization. Let $`\mathcal{C}_{query}`$ be the unit cost of LLM querying. By operating on $`\mathcal{V}`$, the total extraction cost is $`\mathcal{O}(|\mathcal{V}| \cdot \mathcal{C}_{query})`$. Instance-level processing requires $`N \times M`$ queries (one per attribute-value pair), whereas value-level processing requires only $`|\mathcal{V}|`$ queries. The reduction ratio is thus $`\rho = 1 - \frac{|\mathcal{V}|}{N \times M}`$. For standard tabular benchmarks where $`N \gg |\mathcal{V}|`$, we have $`\rho \to 1`$ (empirically approaches unity), amortizing the high inference cost of LLMs to a negligible level.
Attention-Weighted Encoding
Given the description set $`\mathcal{T}`$, the next challenge is converting variable-length text into fixed-dimensional vectors for clustering. As discussed in Section 2.2, CLS token embeddings aggregate sequence-level semantics into a single representation, while mean pooling weights all tokens uniformly. Both approaches may obscure discriminative keywords within LLM-generated descriptions. An adaptive pooling strategy is therefore adopted to weight tokens according to their activation levels.
Given description $`T_v`$, a pre-trained Transformer encoder $`\mathcal{E}`$ produces token representations $`[h_1, \ldots, h_L] = \mathcal{E}(T_v) \in \mathbb{R}^{L \times d}`$, where $`L`$ is sequence length and $`d`$ is hidden dimension. Token importance is measured by mean activation:
\begin{equation}
s_t = \frac{1}{d} \sum_{k=1}^{d} h_{t,k},
\end{equation}and the embedding is computed as an attention-weighted sum:
\begin{equation}
a_t = \frac{\exp(s_t)}{\sum_{l=1}^{L} \exp(s_l)}, \quad e_v = \sum_{t=1}^{L} a_t \cdot h_t \in \mathbb{R}^d.
\end{equation}For object $`x_i = [x_{i,1}, \ldots, x_{i,M}]`$, attribute embeddings are concatenated:
\begin{equation}
E_i^{sem} = e_{x_{i,1}} \oplus \cdots \oplus e_{x_{i,M}} \in \mathbb{R}^{Md},
\end{equation}where each original attribute $`A_j`$ occupies dimensions $`[(j-1)d+1, jd]`$, ensuring non-overlapping blocks that prevent cross-attribute interference. Stacking all objects yields the semantic matrix:
\begin{equation}
E^{sem} = [E_1^{sem}; \ldots; E_N^{sem}] \in \mathbb{R}^{N \times Md}.
\end{equation}Dataset $`\mathcal{X}`$, attributes $`\{A_j\}_{j=1}^{M}`$, clusters $`K`$, LLM $`\mathcal{M}`$, encoder $`\mathcal{E}`$ Cluster assignments $`\mathcal{Y}`$
Semantic Representation Enrichment
$`T_v \leftarrow \mathcal{M}(\mathcal{P}(v, A_j, V_j))`$ $`\triangleright`$ Eq. (1)
Attention-Weighted Encoding
Compute $`s_t`$, $`a_t`$, $`e_v`$ from $`\mathcal{E}(T_v)`$ $`\triangleright`$ Eqs. (2)–(3) $`E_i^{sem} \leftarrow e_{x_{i,1}} \oplus \cdots \oplus e_{x_{i,M}}`$; $`E_i^{anc} \leftarrow \mathbf{1}_{x_{i,1}} \oplus \cdots \oplus \mathbf{1}_{x_{i,M}}`$ $`\triangleright`$ Eqs. (4), (6)
Adaptive Feature Fusion
$`\hat{E}^{anc} \leftarrow \textsc{Normalize}(E^{anc})`$; $`\hat{E}^{sem} \leftarrow \textsc{Normalize}(E^{sem})`$; $`\alpha^* \leftarrow 0`$; $`S^* \leftarrow -1`$ $`Z_\alpha \leftarrow (1-\alpha) \hat{E}^{anc} \oplus \alpha \hat{E}^{sem}`$; $`\mathcal{Y}_\alpha \leftarrow k\text{-Means}(Z_\alpha, K)`$ $`\triangleright`$ Eq. (7) $`\alpha^* \leftarrow \alpha`$; $`S^* \leftarrow S(Z_\alpha, \mathcal{Y}_\alpha)`$ $`\triangleright`$ Eq. (8) $`\mathcal{Y} \leftarrow k\text{-Means}(Z_{\alpha^*}, K)`$
Adaptive Feature Fusion
The semantic matrix $`E^{sem}`$ captures conceptual relationships but risks collapsing distinct values when LLMs overgeneralize. To mitigate this, an identity view is introduced as a regularizer to preserve categorical distinctions.
Learnable embeddings and hash-based methods are common choices for identity encoding. Since learnable parameters risk overfitting on small-scale categorical data, one-hot encoding is adopted as a parameter-free alternative:
\begin{equation}
E_i^{anc} = \mathbf{1}_{x_{i,1}} \oplus \cdots \oplus \mathbf{1}_{x_{i,M}} \in \mathbb{R}^{d_s}, \quad d_s = |\mathcal{V}|,
\end{equation}where $`\mathbf{1}_v \in \mathbb{R}^{|\mathcal{V}|}`$ denotes the one-hot vector for value $`v`$. The orthogonal nature of one-hot encoding ensures that categorically distinct values remain linearly separable regardless of semantic similarity.
After column-wise z-score normalization of $`E^{anc}`$ and $`E^{sem}`$, the fused representation is
\begin{equation}
Z_\alpha = (1-\alpha) \cdot \hat{E}^{anc} \oplus \alpha \cdot \hat{E}^{sem} \in \mathbb{R}^{N \times D},
\end{equation}where $`D = d_s + Md`$ and $`\alpha \in [0,1]`$. The fusion weight is selected by maximizing the Silhouette Score over a candidate set $`\mathcal{G}`$:
\begin{equation}
\alpha^* = \arg\max_{\alpha \in \mathcal{G}} S(Z_\alpha, \mathcal{Y}_\alpha), \quad S = \frac{1}{N} \sum_{i=1}^{N} \frac{b_i - a_i}{\max(a_i, b_i)},
\end{equation}where $`a_i`$ and $`b_i`$ denote mean intra-cluster and nearest-cluster distances, respectively. The learned representations are then partitioned into $`K`$ clusters via $`k`$-Means, minimizing:
\begin{equation}
\mathcal{L} = \sum_{k=1}^{K} \sum_{x_i \in C_k} \|\Phi(x_i) - \mu_k\|^2, \quad \text{s.t.} \quad \mu_k = \frac{1}{|C_k|} \sum_{x_i \in C_k} \Phi(x_i),
\end{equation}where $`\Phi(x_i) = (Z_{\alpha^*})_i`$ denotes the $`i`$-th row of $`Z_{\alpha^*}`$. Algorithm [alg:arise] summarizes the complete procedure.
Complexity. The time complexity of ARISE is $`O(|\mathcal{V}| \cdot C_{llm} + NMd + |\mathcal{G}| \cdot NKD)`$, where $`C_{llm}`$ denotes per-query LLM cost.
The complexity is dominated by three stages. In semantic representation enrichment, the LLM is queried once for each unique value in $`\mathcal{V}`$, yielding $`O(|\mathcal{V}| \cdot C_{llm})`$. In attention-weighted encoding, each of the $`N`$ objects requires concatenating $`M`$ pre-computed $`d`$-dimensional embeddings, contributing $`O(NMd)`$. In adaptive feature fusion, the Silhouette Score is evaluated for each candidate $`\alpha \in \mathcal{G}`$, where each evaluation involves $`k`$-Means clustering on $`N`$ objects with $`D`$-dimensional representations into $`K`$ clusters, resulting in $`O(|\mathcal{G}| \cdot NKD)`$. Summing these terms yields the stated bound.
Experiments
This section presents empirical validation of ARISE. Clustering performance is first compared against seven counterparts across four LLM backends. Component contributions are then analyzed through ablation experiments. Scalability is examined with respect to instance count, attribute count, and vocabulary size. Finally, visualization illustrates the structure of learned representations.
| No. | Dataset | Abbr. | $`\boldsymbol{N}`$ | $`\boldsymbol{M}`$ | $`\boldsymbol{K}`$ | $`\boldsymbol{|\mathcal{V}|}`$ | $`\boldsymbol{\bar{v}}`$ | $`\boldsymbol{v_{\max}}`$ | $`\boldsymbol{v_{\min}}`$ | |:–:|:—|:–:|—:|—:|—:|—:|—:|—:|—:| | 1 | Zoo | ZO | 101 | 16 | 7 | 36 | 2.25 | 6 | 2 | | 2 | Lymphography | LY | 148 | 18 | 4 | 59 | 3.28 | 8 | 2 | | 3 | Breast Cancer | BC | 286 | 9 | 2 | 51 | 5.67 | 13 | 2 | | 4 | Soybean | SB | 307 | 35 | 19 | 133 | 3.80 | 7 | 2 | | 5 | Dermatology | DE | 366 | 34 | 6 | 133 | 3.91 | 4 | 2 | | 6 | Solar Flare | SF | 1,066 | 10 | 6 | 31 | 3.10 | 6 | 2 | | 7 | Car Evaluation | CA | 1,728 | 6 | 4 | 21 | 3.50 | 4 | 3 | | 8 | Mushroom | MU | 8,124 | 22 | 2 | 126 | 5.73 | 12 | 2 |
Statistics of the evaluated datasets. $`N`$: instances; $`M`$: attributes; $`K`$: classes; $`|\mathcal{V}|`$: unique values; $`\bar{v}`$, $`v_{\max}`$, $`v_{\min}`$: average, maximum, and minimum attribute cardinality.
Experimental Settings
Eight benchmark categorical datasets from the UCI Machine Learning Repository1 are employed , with statistics in Table 2. The selection spans scales from 101 to 8,124 instances across diverse domains. Five datasets contain fewer than 500 instances, reflecting the reality that categorical data often originates from specialized domains with limited sample availability. This characteristic poses fundamental challenges for statistical co-occurrence methods, providing an ideal testbed for evaluating semantic enrichment.
Seven representative counterparts are compared. Classical symbolic approaches include OHK (One-Hot $`k`$-Means) and KMo ($`k`$-Modes) . Five state-of-the-art methods represent diverse paradigms. COForest learns order-constrained structures via minimum spanning trees. MCDC employs multi-granularity competitive learning with attribute weighting. SigDT recursively partitions data via significance testing. DiSC learns cluster-specific distance matrices from conditional entropy. OCL optimizes value orderings for ordinal distance computation.
Three standard clustering metrics are adopted. Adjusted Rand Index (ARI) measures chance-adjusted pairwise agreement. Normalized Mutual Information (NMI) quantifies shared information between clusters and labels. Clustering Accuracy (ACC) denotes the best-match classification accuracy under optimal permutation.
Implementation details are summarized as follows. All experiments are repeated 10 times with different random initializations. Statistical significance is assessed via the Wilcoxon signed-rank test ($`p < 0.05`$). Evaluated LLMs include GPT-5.1, Claude Opus 4.5, DeepSeek V3.2, and Gemini 3 Pro. The text encoder is all-mpnet-base-v2. The fusion weight $`\alpha`$ is selected via silhouette score.
Clustering Performance Evaluation
Table [tab:main_results] summarizes the quantitative results. ARISE consistently achieves strong performance, securing the best or second-best outcomes in 21 of 24 metric comparisons and establishing a statistically significant lead over the strongest counterpart, SigDT.
Performance gains are particularly pronounced on small-scale datasets (ZO, LY, BC). On BC, statistical methods such as OHK and MCDC exhibit near-zero ARI due to sparse co-occurrence signals, whereas ARISE leverages external semantic knowledge to compensate for insufficient statistical evidence. Results on CA and SF illustrate the boundary conditions of semantic enrichment. On CA, ARISE outperforms all counterparts in ARI, as LLMs effectively capture the ordinal relationships among attribute values. On SF, however, SigDT slightly surpasses ARISE because domain-specific astronomical identifiers lack general semantic associations. This observation suggests that information-theoretic optimization remains competitive in specialized domains with minimal semantic ambiguity.
Analysis of the $`\Delta`$ columns reveals that different LLM backends exhibit varying strengths across datasets. Claude achieves the largest improvement on CA, while the open-weight DeepSeek matches or exceeds proprietary models on LY. Despite these variations, overall performance remains stable across all four backends. Such stability arises from both the rich pretraining corpora underlying modern LLMs, which provide reliable semantic descriptions for common categorical values, and the proposed attention-weighted encoding and adaptive fusion mechanisms, which filter noisy or irrelevant content and reduce sensitivity to backend-specific generation patterns.
Ablation Study
| Dataset | w/o LLM | w/o Attn | ARISE (Ours) |
|---|---|---|---|
| ZO | 0.5961±0.12 | 0.7335±0.05 | 0.7521±0.04 |
| LY | 0.1150±0.02 | 0.2323±0.03 | 0.2352±0.04 |
| SB | 0.3471±0.05 | 0.4401±0.02 | 0.4539±0.02 |
| BC | -0.0029±0.00 | 0.1692±0.00 | 0.1692±0.00 |
| SF | 0.0187±0.01 | 0.0511±0.02 | 0.0417±0.03 |
| CA | 0.0332±0.05 | 0.1777±0.05 | 0.2144±0.03 |
| MU | 0.2451±0.05 | 0.5650±0.12 | 0.5956±0.02 |
| DE | 0.4871±0.21 | 0.7244±0.04 | 0.7519±0.07 |
| Avg. | 0.2174 | 0.3867 | 0.4017 |
Ablation study of ARISE components (ARI metric). Light blue: improvement over baseline; Deep blue: best performance.
To isolate component contributions, three variants are evaluated. The variant w/o LLM removes the semantic view and relies solely on categorical identities. The variant w/o Attn replaces attention-weighted encoding with CLS token pooling, which aggregates sequence information into a single designated position and thus represents a different aggregation paradigm. ARISE denotes the complete framework.
As shown in Table 3, incorporating LLM-derived semantics (w/o Attn) improves performance across all datasets, with average ARI increasing from 0.217 to 0.387. This improvement demonstrates that external semantic knowledge supplements the sparse statistical signals in small-scale categorical data. Attention-weighted encoding (ARISE) provides further gains on most datasets, achieving an average ARI of 0.402. On SF and BC, however, attention-weighted encoding shows comparable or slightly lower performance, likely because specialized scientific or medical terms exhibit limited semantic variation.
 />
/>
 style="width:90.0%" />
style="width:90.0%" />
Scalability Analysis
Figure 3 shows the runtime with respect to instance count $`N`$, attribute count $`M`$, and unique value count $`|\mathcal{V}|`$.
As shown in Figure 3(a), the runtime growth of ARISE with respect to $`N`$ remains linear, matching that of classical symbolic methods such as OHK and KMo. This confirms that semantic enrichment does not elevate the complexity class. Compared with coupling-based methods such as MCDC, OCL, and COForest, ARISE reduces runtime by orders of magnitude. This efficiency gain results from the decoupled architecture, where semantic processing is isolated to an offline preprocessing phase, avoiding the expensive iterative interactions typical of coupling frameworks. Figure 3(b) shows that the runtime with respect to $`M`$ exhibits a similar trend across methods. ARISE scales linearly with the number of attributes, as each attribute embedding is retrieved independently. Figure 3(c) reports the total runtime including offline description generation, which scales linearly with $`|\mathcal{V}|`$. The online clustering time of ARISE remains stable across all vocabulary sizes. Since each value is processed independently during the offline stage, description generation can be parallelized across multiple LLM instances.
Visualization
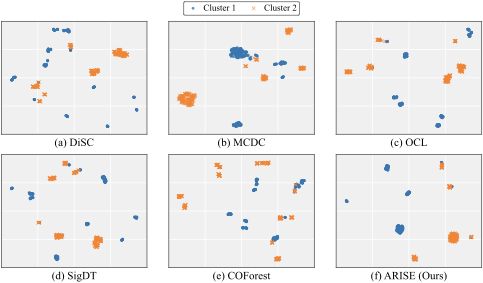
Figure 4 presents UMAP projections on the MU dataset. Counterparts (panels a–e) produce fragmented structures where points from the two classes intermingle across scattered regions. ARISE (panel f) yields two compact and well-separated groups that align closely with the ground-truth class labels. This alignment indicates that semantic enrichment captures class-relevant structure, producing representations with stronger semantic coherence.
Concluding Remarks
This paper has presented ARISE, a framework that integrates external semantic knowledge from LLMs into categorical data clustering. ARISE queries LLMs at the attribute-value level, generating a semantic-enhanced description for each unique value, and emphasizes the key informative tokens through attention-weighting to produce semantic-compact embeddings for each value. ARISE also adaptively integrates the categorical value identity vector into the LLM-enhanced embeddings for regularization, relieving the dominance of LLMs in the representations. Experiments on eight benchmark datasets across seven counterparts validate the efficacy of ARISE, which consistently achieves gains of 19–27% on all the experimental datasets. Moreover, four mainstream LLM options have been considered for the semantic enhancement, with the results indicating the superiority of GPT. The achieved improvements are particularly notable when the data scale is relatively small, confirming the necessity of the external semantic knowledge for the metric space complementation of categorical data. The next avenue of this work could be extending to mixed-type data and prompt tuning of LLMs for domain- and task-specific adaptation.
19
Borisov, V., Seßler, K., Leemann, T., Pawelczyk, M., Kasneci, G.: Language Models are Realistic Tabular Data Generators. In: ICLR (2023)
Cai, S., Zhang, Y., Luo, X., Cheung, Y.M., Jia, H., Liu, P.: Robust Categorical Data Clustering Guided by Multi-Granular Competitive Learning. In: ICDCS, pp. 288–299 (2024)
Chen, J., Ji, Y., Zou, R., Zhang, Y., Cheung, Y.M.: QGRL: Quaternion Graph Representation Learning for Heterogeneous Feature Data Clustering. In: KDD, pp. 297–306 (2024)
Devlin, J., Chang, M.W., Lee, K., Toutanova, K.: BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. In: NAACL, pp. 4171–4186 (2019)
Dinh, T., Wong, H., Fournier-Viger, P., Lisik, D., Ha, M.Q., Dam, H.C., Huynh, V.N.: Categorical Data Clustering: 25 Years Beyond K-modes. Expert Syst. Appl. 272, 126608 (2025)
Dua, D., Graff, C.: UCI Machine Learning Repository. University of California, Irvine, School of Information and Computer Sciences (2019). https://archive.ics.uci.edu
Estévez, P.A., Tesmer, M., Perez, C.A., Zurada, J.M.: Normalized Mutual Information Feature Selection. IEEE Trans. Neural Netw. 20(2), 189–201 (2009)
Feng, S., Zhao, M., Huang, Z., Ji, Y., Zhang, Y., Cheung, Y.M.: Robust Qualitative Data Clustering via Learnable Multi-Metric Space Fusion. In: ICASSP, pp. 1–5 (2025)
Feng, Z., Lin, L., Wang, L., Cheng, H., Wong, K.F.: LLMEdgeRefine: Enhancing Text Clustering with LLM-Based Boundary Point Refinement. In: EMNLP, pp. 18455–18462 (2024)
Gates, A.J., Ahn, Y.Y.: The Impact of Random Models on Clustering Similarity. J. Mach. Learn. Res. 18(87), 1–28 (2017)
He, X., Cai, D., Niyogi, P.: Laplacian Score for Feature Selection. In: NeurIPS, pp. 507–514 (2005)
Hegselmann, S., Buendia, A., Lang, H., Agrawal, M., Ber, X., Sontag, D.: TabLLM: Few-shot Classification of Tabular Data with Large Language Models. In: AISTATS, pp. 5549–5581 (2023)
Herzig, J., Nowak, P.K., Müller, T., Piccinno, F., Eisenschlos, J.: TAPAS: Weakly Supervised Table Parsing via Pre-training. In: ACL, pp. 4320–4333 (2020)
Hu, L., Jiang, M., Liu, X., He, Z.: Significance-Based Decision Tree for Interpretable Categorical Data Clustering. Inf. Sci. 690, 121588 (2025)
Huang, Z.: Extensions to the K-Means Algorithm for Clustering Large Data Sets with Categorical Values. Data Min. Knowl. Discov. 2(3), 283–304 (1998)
Kobayashi, G., Kuribayashi, T., Yokoi, S., Inui, K.: Attention is Not Only a Weight: Analyzing Transformers with Vector Norms. In: EMNLP, pp. 7057–7075 (2020)
McConville, R., Santos-Rodriguez, R., Piechocki, R.J., Craddock, I.: N2D: (Not Too) Deep Clustering via Clustering the Local Manifold of an Autoencoded Embedding. In: ICPR, pp. 5145–5152 (2021)
Modarressi, A., Fayyaz, M., Yaghoobzadeh, Y., Pilehvar, M.T.: GlobEnc: Quantifying Global Token Attribution by Incorporating the Whole Encoder Layer in Transformers. In: NAACL, pp. 258–271 (2022)
Reimers, N., Gurevych, I.: Sentence-BERT: Sentence Embeddings using Siamese BERT-Networks. In: EMNLP, pp. 3982–3992 (2019)
Viswanathan, V., Gashteovski, K., Lawrence, C., Wu, T., Neubig, G.: Large Language Models Enable Few-Shot Clustering. TACL 12, 321–333 (2024)
Yin, P., Neubig, G., Yih, W., Riedel, S.: TaBERT: Pretraining for Joint Understanding of Textual and Tabular Data. In: ACL, pp. 8413–8426 (2020)
Zhang, Y., Cheung, Y.M., Zeng, A.: Het2Hom: Representation of Heterogeneous Attributes into Homogeneous Concept Spaces for Categorical-and-Numerical-Attribute Data Clustering. In: IJCAI, pp. 3758–3765 (2022)
Zhang, Y., Cheung, Y.M.: Learnable Weighting of Intra-Attribute Distances for Categorical Data Clustering with Nominal and Ordinal Attributes. IEEE TPAMI 44(7), 3560–3576 (2022)
Zhang, Y., Cheung, Y.M.: Graph-Based Dissimilarity Measurement for Cluster Analysis of Any-Type-Attributed Data. IEEE TNNLS 34(9), 6530–6544 (2023)
Zhang, Y., Wang, Z., Shang, J.: ClusterLLM: Large Language Models as a Guide for Text Clustering. In: EMNLP, pp. 13903–13920 (2023)
Zhang, Y., Luo, X., Chen, Q., Zou, R., Zhang, Y., Cheung, Y.M.: Towards Unbiased Minimal Cluster Analysis of Categorical-and-Numerical Attribute Data. In: ICPR, pp. 254–269 (2024)
Zhang, Y., Zhao, M., Jia, H., Li, M., Lu, Y., Cheung, Y.M.: Categorical Data Clustering via Value Order Estimated Distance Metric Learning. Proc. ACM Manag. Data 3(6), 1–24 (2025)
Zhang, Y., Zhao, M., Zhang, Y., Cheung, Y.M.: Trending Applications of Large Language Models: A User Perspective Survey. IEEE Trans. Artif. Intell. (2025)
Zhang, Y., Zou, R., Zhang, Y., Zhang, Y., Cheung, Y.M., Li, K.: Adaptive Micro Partition and Hierarchical Merging for Accurate Mixed Data Clustering. Complex Intell. Syst. 11(1), 84 (2025)
Zhao, M., Feng, S., Zhang, Y., Li, M., Lu, Y., Cheung, Y.M.: Learning Order Forest for Qualitative-Attribute Data Clustering. In: ECAI, pp. 1943–1950 (2024)
Zhao, M., Huang, Z., Lu, Y., Li, M., Zhang, Y., Su, W., Cheung, Y.M.: Break the Tie: Learning Cluster-Customized Category Relationships for Categorical Data Clustering. arXiv:2511.09049 (2025)
📊 논문 시각자료 (Figures)



