Practical Geometric and Quantum Kernel Methods for Predicting Skeletal Muscle Outcomes in chronic obstructive pulmonary disease

A major shift in COPD research and management has been the recognition of COPD as a systemic disease with multi-organ involvement. Beyond pulmonary pathology, chronic inflammation, oxidative stress, and hypoxia extend to extrapulmonary tissues and contribute to comorbid conditions including cardiovascular and metabolic disease, osteoporosis, depression, and skeletal muscle dysfunction [8,9,10]. Importantly, these comorbidities are not simply “add-ons” to lung disease. They contribute directly to clinical outcomes, healthcare utilisation, and survival, and they often share pathobiological pathways with airway inflammation [10,11].

Among these systemic manifestations, skeletal muscle dysfunction is one of the most clinically significant because it reduces exercise tolerance, limits daily function, and predicts adverse outcomes independent of respiratory impairment [12,13]. Muscle wasting and weakness are common in COPD, with reported prevalence in the range of 20%-40%, and they are particularly pronounced during advanced disease and exacerbations [14,15]. Lower-limb muscle groups, especially the quadriceps, are often most affected, leading to impaired mobility and reduced performance in functional tests [12,16]. Notably, emerging evidence indicates that muscle dysfunction can occur early in the disease course and may even be present before a formal spirometric diagnosis (pre-COPD). In this early phase, loss of strength can precede measurable loss of muscle mass, meaning that muscle quality and contractile performance may deteriorate while gross muscle size appears preserved [17,18]. Consistent with this sensitivity, experimental work shows that cigarette smoke can directly impair skeletal muscle function in mice through vascular and calcium-handling mechanisms [19]. Together, these observations support a clinically relevant window for earlier identification of individuals at risk of muscle impairment.

Despite the clinical impact, therapeutic options for COPD-associated muscle dysfunction remain limited. Pulmonary rehabilitation improves exercise capacity and quality of life, yet access remains low and benefits are often heterogeneous [20,21,22]. Pharmacological strategies targeting anabolic pathways (e.g., myostatin/activin signalling) can increase muscle mass, but do not consistently translate into functional improvement [23]. This gap reflects the multifactorial nature of muscle dysfunction in COPD. In addition to inactivity and nutritional deficits, chronic inflammation and oxidative stress activate catabolic pathways, impair mitochondrial bioenergetics, and disrupt excitation-contraction coupling [24,15,25]. Oxidative stress, defined as an imbalance between reactive oxygen/nitrogen species and antioxidant defences, is a central driver linking cigarette smoke exposure, inflammatory signalling, and peripheral tissue dysfunction [26,27]. These mechanisms highlight the need for biomarker-guided approaches that can identify individuals at risk, support early intervention, and provide mechanistically grounded targets for therapy [24,28].

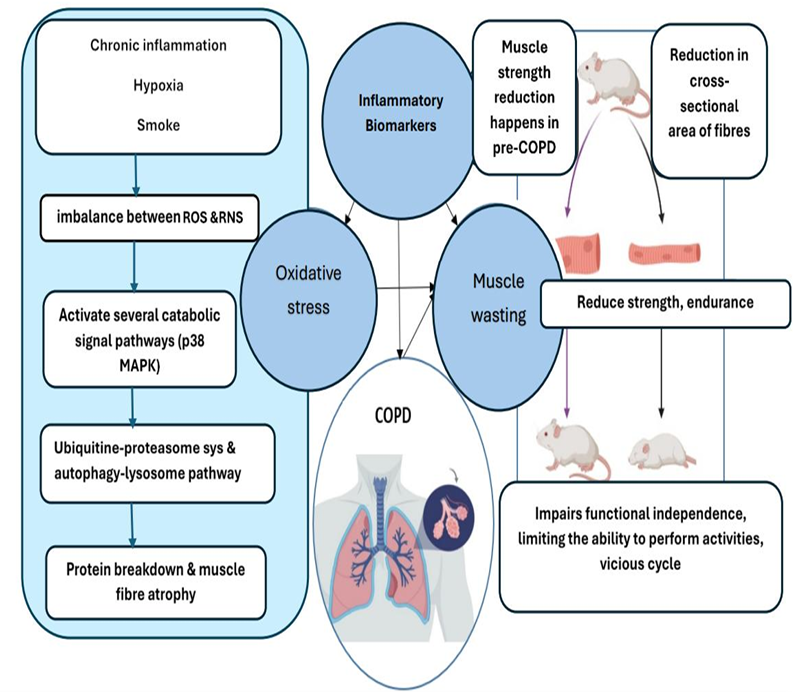
Figure 1: Proposed mechanisms of skeletal muscle wasting in COPD. Oxidative stress and inflammation contribute to muscle wasting, leading to reduced strength/endurance and functional decline. These changes can reinforce systemic inflammation and inactivity, creating a vicious cycle that accelerates disease progression. Created with BioRender.com.

Figure 1 summarises a mechanistic picture of skeletal muscle impairment in COPD and clarifies why inflammatory and airway biomarkers are plausible predictors of downstream muscle outcomes. On the left, chronic inflammation, hypoxia, and cigarette smoke exposure are depicted as upstream drivers of redox imbalance, shifting the system toward excess reactive oxygen and nitrogen species (ROS/RNS). This oxidative/nitrosative stress is shown to activate catabolic signalling pathways (e.g., p38 MAPK), which in turn engage major proteolytic systems including the ubiquitin-proteasome and autophagy-lysosome pathways, leading to net protein breakdown and muscle fibre atrophy.

In parallel, COPD research has moved toward high-dimensional data generation through proteomics and other omics technologies, as well as rich clinical and physiological phenotyping [29,30,31]. While these approaches have yielded candidate biomarker panels and molecular subtypes, they also expose the limitations of traditional univariate analyses when relationships are non-linear, multivariate, and confounded by shared inflammatory pathways [6,30]. Machine learning (ML) provides a natural framework for integrating heterogeneous variables, performing feature selection, and building predictive models that can capture non-linear interactions [32,33]. However, biomarker studies in preclinical settings are often constrained by small sample sizes and strong group effects (e.g., Sham versus cigarette smoke exposure). Without careful evaluation design, these factors can inflate reported performance, destabilise feature rankings, and reduce translational reliability [33,34].

In this work, we develop an interpretable and benchmark-driven modelling framework for predicting COPD-associated muscle outcomes from a compact set of inflammatory, systemic, and muscle-derived measurements collected in a controlled experimental cigarette smoke model [35,36]. We consider three complementary outcomes: tibialis anterior (TA) muscle weight (a proxy of muscle mass), TA specific force (a functional measure), and a muscle quality index defined as specific force divided by muscle weight. Our modelling strategy is intentionally modular and benchmark-driven. We begin with strong and explainable classical baselines, and then investigate two non-Euclidean representations designed to stabilise learning in small-sample regimes: (i) geometry-aware embeddings derived from symmetric positive definite (SPD) descriptors us-ing Stein divergence, and (ii) quantum-kernel-based regression with a clustered kernel feature construction that regularises similarity learning through a low-dimensional Nyström-style approximation.

The main contributions of this paper are as follows:

• We formulate COPD-associated muscle outcome modelling as a small-sample supervised learning problem with two complementary evaluation views: (i) continuous regression of muscle outcomes and (ii) a screening-oriented binary interpretation obtained by thresholding each continuous target at a Sham-referenced value computed on the training set [1,24].

• We establish interpretable classical baselines under explicit feature budgets, including tuned ridge regression, random forests, and shallow decision trees, and we analyse conditiondependent effects using engineered interactions motivated by inflammation and metabolism coupling [33].

• We introduce a geometry-aware representation on the manifold of symmetric positive definite matrices, including outer-product and local-neighbourhood covariance descriptors, Stein-divergence distances to representative prototypes, and an optional unlabeled synthetic SPD augmentation (log-Euclidean perturbations) to stabilise prototype discovery in low-data regimes [37,38,39,40].

• We benchmark practical quantum kernel models for low-dimensional tabular biomarkers, including quantum kernel ridge regression and a clustered quantum kernel feature approach based on a Nyström-style approximation, and we quantify when these quantum lifts improve regression error and/or screening metrics relative to matched classical baselines under the same feature budgets [41,42,43].

• We provide an end-to-end benchmark on an experimental COPD cohort with transparent reporting of splits, hyperparameter grids, and metrics, enabling independent replication and facilitating future comparisons on clinically motivated biomarker panels and outcomes.

The remainder of this paper is organised as follows. Section 2 provides the biological and methodological background that motivates our modelling choices. The subsequent sections describe the dataset and experimental pipeline, report results across modelling families, and discuss implications for biomarker-guided assessment of COPD-associated muscle dysfunction.

2 Background and Related Work

COPD is traditionally defined and staged using spirometry, yet clinical experience and largescale studies consistently show that lung function alone does not fully capture symptom severity, exacerbation risk, or systemic impact [1,7]. Exacerbations represent a major clinical inflection point. They are associated with worsened health status, increased healthcare utilisation, and accelerated decline, and they are commonly accompanied by a systemic inflammatory response [3,4,6]. Biomarkers such as CRP are frequently elevated in acute exacerbation and have also been linked to worse outcomes and increased disease burden [5,6].

A growing body of evidence supports COPD as a systemic inflammatory syndrome in which pulmonary immune activation spills over into the circulation and contributes to comorbid disease [10,9]. Comorbidity prevalence in COPD is high; many individuals have at least one additional chronic condition, and multi-morbidity is common [8,44]. Systemic consequences are partly driven by shared risk factors such as smoking and ageing, but also by chronic inflammatory and metabolic dysregulation that persists beyond the lung [11]. From a translational perspective, this systemic viewpoint motivates two practical needs: (i) biomarkers that reflect extrapulmonary impact and (ii) modelling approaches that integrate multiple measurements to support earlier risk stratification.

Skeletal muscle dysfunction in COPD encompasses both quantitative loss of muscle mass (wasting) and qualitative loss of muscle function (weakness). Clinically, these manifestations contribute to reduced mobility, exercise intolerance, and impaired quality of life [12,16]. Importantly, muscle loss phenotypes have been associated with adverse outcomes in large cohorts, reinforcing muscle health as a key determinant of prognosis [14,13].

A key concept for both biology and modelling is that muscle mass and strength, while related, can dissociate. Strength deficits may occur early, even before overt atrophy, and they may reflect impairments in contractile machinery, neuromuscular activation, mitochondrial function, and calcium handling rather than reductions in bulk alone [17,18,19]. This distinction is clinically relevant because interventions that increase muscle size do not necessarily restore function. For example, pharmacological blockade of activin type II receptors can increase muscle volume in COPD, yet functional improvements may remain modest or absent [23]. For this reason, considering muscle quality-the amount of force generated per unit muscle mass-provides an additional lens on disease impact and on potential mechanisms.

COPD-associated muscle dysfunction is multifactorial, but chronic inflammation and oxidative stress repeatedly emerge as central drivers. Cigarette smoke activates airway epithelial and immune pathways, recruiting innate immune cells such as neutrophils and macrophages and sustaining cytokine production [9,45]. These local inflammatory processes can propagate systemically, with cytokines and acute-phase responses contributing to a pro-catabolic peripheral environment [10,46]. At the muscle level, inflammatory mediators can activate proteolytic systems such as the ubiquitin-proteasome and autophagy-lysosome pathways, leading to net protein breakdown and fibre atrophy [15,47]. Oxidative stress amplifies this process. Reactive oxygen species (ROS) and reactive nitrogen species can damage lipids, proteins, and DNA, impair mitochondrial function, and disrupt excitation-contraction coupling [26,27,48]. Experimental and clinical evidence suggests that ROS-related signalling is a “double-edged sword”: physiological ROS are required for normal adaptation, but excessive and sustained oxidative stress drives dysfunction [25,48]. In preclinical smoke-exposure models, targeting specific sources of oxidative stress (e.g., NADPH oxidase inhibition with apocynin) can prevent loss of muscle mass and function, supporting oxidative stress as a mechanistically relevant and potentially treatable pathway [36].

These biological relationships motivate the biomarker space explored in this work. Markers of airway inflammation (e.g., bronchoalveolar lavage fluid cell counts), systemic inflammation (e.g., CRP), lung cytokine signalling (e.g., TNF-α mRNA), and muscle oxidative stress capture different layers of the inflammatory cascade and provide plausible predictors of muscle outcomes [46,49,50].

Historically, many studies have focused on individual candidate biomarkers such as TNF-α, IL-6, IL-8, and myostatin. While biologically compelling, findings are often heterogeneous across cohorts and disease stages, and no single biomarker has achieved broad validation for COPDassociated muscle dysfunction [15,46,51,28]. This limitation is not unique to muscle outcomes. COPD itself is highly heterogeneous, and biomarker expression is influenced by comorbidities, medications, and acute events [6].

Proteomic and multi-omics profiling has expanded the biomarker search space and has enabled the discovery of molecular subtypes and panels of circulating markers in stable COPD [29,30]. Systemic proteomic signatures have also been linked to exacerbation phenotypes, highlighting the value of integrative molecular profiling [31]. However, high-dimensional omics studies require careful computational design to avoid overfitting, and they raise a practical question for translation: how can we build robust predictors when only a modest number of variables are available in a typical clinical or experimental setting?

Preclinical models provide an important bridge. They allow controlled exposures (e.g., cigarette smoke versus air), controlled timing, and direct tissue sampling, enabling mechanistic exploration of biomarker-outcome links that are difficult to isolate in heterogeneous human cohorts [35,36]. In this setting, multivariate modelling can quantify the joint predictive value of inflammatory and systemic features, identify compact signatures, and provide interpretable hypotheses for downstream mechanistic work.

ML has become a central tool for integrating heterogeneous biomedical variables and identifying predictive signatures. In COPD, supervised models have been used for early diagnosis using quantitative imaging features [32], for subtype classification using multi-omics representations [52], and for exacerbation prediction using explainable models that quantify feature contributions [53]. These studies highlight two practical lessons: (i) multimodal information can improve performance and (ii) interpretability is essential if the goal is biological insight rather than purely predictive accuracy.

For preclinical datasets, the main technical constraints are small sample size and strong group structure. Small n increases the variance of performance estimates and can produce unstable feature selection when hyperparameters are tuned aggressively [33,34]. Group structure (e.g., Sham vs cigarette smoke exposure) can dominate the signal and may lead to models that implicitly “memorise” condition rather than learn biomarker relationships. These challenges make evaluation design a first-order concern. Leakage occurs when test-set information influences preprocessing, feature selection, or hyperparameter tuning, producing overly optimistic performance and misleading conclusions [33]. Therefore, leakage-safe pipelines require that all transforms (imputation, scaling, feature engineering choices, dimensionality reduction) are fit on training data only, with the test split held out for final reporting.

In addition to standard regression metrics, many translational questions are screeningoriented. If a clinically meaningful threshold defines “low” outcomes, continuous predictions can be evaluated for their ability to identify at-risk cases. Importantly, the threshold itself must be derived from the training split only; otherwise, screening metrics become optimistically biased [24]. This paper adopts that principle explicitly.

Beyond standard vectorial representations, a growing body of work encodes observations using symmetric positive definite (SPD) matrices, such as covariance descriptors, and exploits the geometry of the SPD manifold [37]. SPD matrices do not form a Euclidean space under ordinary arithmetic, and naive distances can distort structure. Geometry-aware approaches either embed SPD matrices into tangent spaces or use kernel-based comparisons that respect manifold properties [37].

A practical and widely used similarity measure on SPD matrices is the Jensen-Bregman LogDet divergence, also known as the Stein divergence [38]. For SPD matrices A and B, it is defined as

which is symmetric and non-negative. In small biomedical datasets, an appealing strategy is to construct an SPD descriptor per sample that captures second-order structure among biomarkers (for example, outer products of normalised biomarker vectors, or local covariance estimates from neighbourhoods in feature space). A low-dimensional embedding can then be formed by measuring divergence to a small set of representative prototypes.

To obtain prototypes without relying on Euclidean structure, we use k-medoids clustering (PAM) on a pairwise divergence matrix, selecting medoids as representatives that are themselves observed SPD matrices [40]. Each sample is then represented by its vector of Stein divergences to the medoids, yielding a compact feature representation for standard downstream regressors.

When data are scarce, estimating stable prototypes can be difficult. A practical regularisation is to expand the clustering pool with synthetic SPD matrices generated by interpolation between training descriptors in a log-Euclidean domain [39]. Log-Euclidean interpolation preserves positive definiteness and produces plausible intermediate descriptors while maintaining leakage safety when all synthetic matrices are generated from the training split only. This combination-Stein divergence, k-medoids prototypes, and log-Euclidean augmentationprovides a geometry-aware representation that is lightweight, interpretable, and well matched to low-n settings.

Quantum machine learning provides a principled way to construct feature maps and kernel functions using quantum states [54]. In a quantum kernel approach, a classical input x is encoded into a quantum state |ϕ(x)⟩ through a feature-map circuit. Similarities are computed via state fidelity,

which defines a valid kernel for kernel ridge regression under appropriate regularisation [42,43]. Conceptually, the feature map induces a high-dimensional (often implicit) feature space in which a linear model is fit. This can be attractive for small-sample settings because the non-linearity is expressed through the kernel rather than through many trainable parameters.

In practice, quantum kernels can become overly “peaky” (near-identity), meaning that test samples may have near-zero similarity to training samples after encoding. This behaviour can make the kernel matrix ill-conditioned and can lead to unstable regression. One way to stabilise similarity-based learning is to replace the full n × n kernel representation with a compact set of similarities to representative centres. This idea is closely related to the Nyström approximation for kernel machines [41].

Motivated by this, we consider a clustered quantum-kernel feature construction. A small set of centres is learned from the training split (e.g., via k-means in a low-dimensional parameter space), and each sample is represented as a k-dimensional vector [k(x, c 1 ), . . . , k(x, c k )].

An optional whitening step based on the centre-centre kernel can further stabilise feature geometry and reduce the impact of kernel concentration. This produces a compact, regularised representation that can be used with simple ridge regression.

Variational quantum algorithms provide a complementary approach in which a parameterised quantum circuit is trained directly for a learning objective [55]. For regression, inputs are encoded via a feature map, trainable entangling layers are applied, and measurements are mapped to continuous predictions via a classical readout. Compared with kernel methods, variational models have trainable parameters that can adapt to data, but they may require careful optimisation and circuit design, particularly in low-data regimes [55]. In this work, we benchmark both quantum kernel ridge regression and a variational quantum regressor alongside classical and geometry-aware models under the same leakage-safe preprocessing protocol.

Let n denote the number of experimental subjects (animals), and let {(x i , c i , y i )} n i=1 denote the dataset, where: (i) x i ∈ R d is the vector of measured biomarkers and physiological covariates, (ii) c i ∈ {0, 1} encodes the experimental condition (e.g., Sham vs. chronic smoke exposure), and (iii) y i ∈ R is a continuous target variable.

We considered three regression targets:

1. Muscle mass: Tibialis Anterior (TA) muscle weight, y (w) (mg), 2. Muscle function: Specific force of TA, y (f) (mN),

2. Muscle quality index: y (q) = y (f) /y (w) (mN per mg).

The quality index is computed per subject using the measured force and weight.

For each target, we exclude all outcome columns from the predictor set to avoid target leakage.

All learning problems are posed as supervised regression. In addition, we report screeningstyle classification metrics (receiver-operating characteristic area under the curve, F1-score, precision, recall) by thresholding the continuous target into a binary label (“low” vs. “notlow”); this is described in Section 3.9.

The dataset contains n = 213 subjects with the following observed variables: experimental condition (Sham vs. chronic smoke exposure), bronchoalveolar lavage fluid (BALF) cell counts (total cells, macrophages, neutrophils, lymphocytes), systemic inflammation marker C-reactive protein (CRP), muscle oxidative stress, lung tumor necrosis factor alpha (TNF-α) mRNA, and physiological measures including oxygen consumption (VO 2 ) and locomotor activity. These measurements and the biomedical context are described in detail in the associated thesis. [56] Animal procedures and ethics approvals are described in the original experimental work underlying this dataset; see [56] and references therein.

We used a fixed hold-out test split with test fraction 0.2. The split was stratified by condition to preserve Sham/CS proportions in train and test. Let I tr and I te denote indices of training and test sets.

All data-dependent preprocessing steps (power transforms, scalers, principal component analysis, cluster learning, kernel centering statistics, and any threshold definitions for screening metrics) were fit using training data only and then applied to the test set.

Hyperparameters were selected by 5-fold cross-validation performed on the training set only. For fold k, we denote the fold-specific training/validation indices by I

If condition is included as a predictor, we append c i to the feature vector:

To mitigate skewness and heteroscedasticity in biomedical measurements, we applied the Yeo-Johnson power transform feature-wise [57]. Let T YJ (•; λ) denote the Yeo-Johnson transformation with parameter λ estimated from training data by maximum likelihood. After power transformation, we used either: (i) standard scaling (zero mean, unit variance) or (ii) robust scaling (median/IQR scaling), both fit on training data only.

We denote the full feature preprocessing map by

where Φ includes the power transform and scaler; typically p = d or p = d + 1.

Optionally, we applied the log1p transform to regression targets:

fit-free but used consistently in both training and cross-validation. All metrics reported in tables are computed in original target units by inverting the transform:

To map features to a small number of qubits, we optionally used principal component analysis (PCA) fit on training data, selecting q ≤ p principal components. The reduced representation is:

We then rescaled each component to a bounded angle interval (e.g. [-π/2, π/2]) using a minmax map computed on training data:

These angles are the inputs to quantum circuits.

We benchmark classical baseline predictors and regression models for the three targets under the shared train/test protocol and preprocessing described above. In addition to global-mean and condition-means baselines, we evaluate ridge regression, random forest regression, a shallow decision tree, and a simple condition-axis baseline that regresses on the one-dimensional LDA discriminant score separating Sham vs. CS (“LDA condition axis then Ridge”).

We report two simple reference predictors:

We evaluate three standard regression models.

Ridge regression. Ridge regression [58] fits a linear predictor ŷ = w ⊤ x + b by minimizing min

where α > 0 controls ℓ 2 regularization strength.

Random forest regression. Random forests [59] combine T regression trees trained on bootstrap samples with randomized feature selection at splits. The prediction is the ensemble average of tree predictions.

Shallow decision tree regression. We also train an interpretable CART-style regression tree [60], restricted to small depth and minimum leaf sizes to improve interpretability and reduce variance.

For each model family, hyperparameters are selected by grid search with K = 5 fold crossvalidation on the training set. The selection criterion is root mean squared error (RMSE) measured in the original target units by applying the inverse response transform. We then refit the selected model on the full training set and evaluate once on the held-out test set.

We report RMSE, MAE, and R 2 on the held-out test set, together with percent RMSE for scalenormalised comparison; formal definitions are given in Section 3.9. For the auxiliary screening view, we report ROC-AUC and macro-averaged precision/recall/F 1 as well as balanced accuracy using the thresholding protocol described in Section 3.9 (κ = 0.8 and positive class “low”).

These results show that classical models already perform competitively on muscle weight and specific force, with the experimental condition contributing substantial explanatory power. Next, we test whether a conservative, mechanistically motivated feature expansion can improve predictive performance under the same train/test protocol. The goal is not to increase model capacity arbitrarily, but to introduce low-dimensional composite covariates that reflect well-known inflammatory and physiological couplings (ratios and bilinear products), and to allow feature effects to differ between Sham and CS via interaction terms.

Let x i ∈ R d denote the raw feature vector for subject i after median imputation of missing values (computed from the training set only). We define an engineered feature map ϕ : R d → R d ′ by augmenting x i with the following composite covariates (when the required variables are present in the dataset).

Let N i be neutrophils count, L i lymphocytes count, CRP i blood C-reactive protein, B i total bronchoalveolar lavage fluid (BALF) cell count, S i muscle oxidative stress, V i oxygen consumption VO 2 , and T i lung tumor necrosis factor alpha messenger ribonucleic acid (TNFα mRNA) fold-change from Sham. Using a small constant ε = 10 -9 to prevent division by zero, we add:

All engineered features are deterministic functions of the subject’s covariates and do not use label information.

Let c i ∈ {0, 1} denote the condition indicator, where c i = 0 for Sham and c i = 1 for CS. We include c i as an additional predictor and also introduce interaction features:

This expansion allows the model to represent condition-specific linear effects by learning separate slopes for CS relative to Sham.

All subsequent steps follow the classical baseline protocol exactly: (i) a Yeo-Johnson power transform is fit feature-wise on the training data and applied to both training and test inputs;

(ii) transformed inputs are standardized using training-set mean and standard deviation; (iii) the regression target is trained in log(1 + y) space and inverted back to original units for reporting; (iv) hyperparameters are selected by 5-fold cross-validation on the training set only; and (v) final metrics are computed once on the held-out test set. For screening-style metrics, a threshold τ = 0.8 mean(y | Sham) is used, with the positive class defined as “low”, and we report ROC-AUC, macro-averaged F 1 , weighted F 1 , macro precision, macro recall, and balanced accuracy derived from thresholding the continuous outcome.

3.7 Geometry-informed mapping on the manifold of symmetric positive definite matrices

For small tabular datasets, second-order interactions between covariates can be informative, but explicitly enumerating interaction terms can rapidly increase dimensionality and overfitting risk. To introduce second-order structure while preserving a controlled model capacity, we construct a symmetric positive definite (SPD) matrix descriptor for each sample and exploit the geometry of the SPD manifold. The core idea is to map each sample to a low-dimensional vector of distances to representative SPD prototypes (cluster centres), then concatenate this distance vector with the original covariates and train a regularised linear regressor. Let i ∈ {1, . . . , n} index samples. After train-only preprocessing (Section 3.5), each sample is represented by a feature vector

where p includes the selected continuous covariates and, when enabled, the binary condition indicator encoded as c i ∈ {0, 1} appended as an additional feature. In the COPD experiments reported here, we use a small set of top-ranked covariates (three continuous variables per target, plus condition when included) to ensure that the resulting SPD descriptor remains low-dimensional and numerically stable.

An SPD matrix is a symmetric matrix S ∈ R p×p satisfying v ⊤ Sv > 0 for all nonzero v ∈ R p [61]. We consider two SPD constructions.

(i) Outer-product SPD descriptor (interaction descriptor). Given x i , we optionally normalise to unit Euclidean norm, xi =

with a small δ > 0 to avoid division by zero. The SPD descriptor is then defined as

where ε > 0 is a diagonal jitter and I p is the p × p identity matrix. The rank-one term xi x⊤ i encodes second-order interactions between components of x i , while εI p ensures strict positive definiteness.

(ii) Local-neighbourhood covariance SPD descriptor. To approximate a “local covariance” structure, for each training sample i we form a neighbourhood N i consisting of the k NN nearest neighbours of x i under Euclidean distance in the transformed feature space. Let xi denote the neighbourhood mean and define the empirical covariance

To improve conditioning in small samples, we apply shrinkage toward a scaled identity (Ledoit-Wolf style) [62]

with λ ∈ [0, 1] and ε > 0. For test samples, neighbourhoods are formed with respect to the training set only to preserve a strict train/test separation.

To compare SPD matrices we use the symmetric Stein divergence (also known as the Jensen-Bregman LogDet divergence) [63,64]:

defined for SPD matrices A, B ∈ S p ++ . This divergence is symmetric, nonnegative, and empirically effective for learning tasks on SPD manifolds. In our implementation, positive definiteness is guaranteed by the diagonal jitter εI p in Equations ( 13)-( 15).

To reduce prototype instability when n is small, we optionally augment the training SPD set with unlabeled synthetic SPD matrices. Synthetic SPD matrices are used only to stabilise clustering and are never assigned target labels. In the reported experiments, synthetic SPD samples are generated by geodesic interpolation in the Log-Euclidean geometry [65], which preserves positive definiteness:

where S a and S b are randomly selected training SPD matrices, and log(•) and exp(•) denote the matrix logarithm and exponential. This strategy is consistent with prior work on SPD manifold learning and random projection methods on SPD spaces [66]. Let S train = {S i } i∈train be the training SPD set and S syn be the synthetic SPD set. The clustering pool is S pool = S train ∪ S syn .

Given S pool , we compute the pairwise Stein divergence matrix using Equation ( 16), then select K representative prototypes via K-medoids clustering (Partitioning Around Medoids) [67]. Unlike K-means, K-medoids returns centres that are valid SPD matrices drawn from S pool . Let {C 1 , . . . , C K } denote the selected medoids. Each sample is mapped to a K-dimensional distance vector

Crucially, {C k } K k=1 are computed using training data (and optional synthetic augmentation) only. Test samples are mapped by Equation ( 19) using the fixed training prototypes, ensuring that prototypes are learned from the training split.

Finally, we form the augmented representation

and fit ridge regression ŷi = w ⊤ h i + b,

by minimising min

where α > 0 is selected by cross-validation on the training set. All target transformations (e.g., log(1 + y)) are fit and applied on training data only, and reported test metrics are computed in original physical units after inverse transformation.

We report RMSE, MAE, R 2 , and scale-normalised percent errors (%RMSE and %MAE) on the held-out test set, as defined in Section 3.9.

3.8 Quantum machine learning models

We interpret quantum encoding as a nonlinear feature map into a Hilbert space of q qubits. [68,69] After PCA and min-max scaling, each sample yields θ i ∈ [θ min , θ max ] q . We define a parameterized quantum circuit U (θ) acting on |0⟩ ⊗q , producing a pure state

The circuit uses repeated data re-uploading layers: in each layer, each qubit receives rotations whose angles are proportional to the components of θ, followed by an entangling pattern (e.g. a ring of controlled-NOT gates). A global angle-scale factor s > 0 multiplies input angles to control circuit sensitivity.

We define the fidelity kernel between two samples i, j as

Optionally, we apply a kernel “power” 0 < p ≤ 1:

which can reduce overly sharp kernels by increasing off-diagonal similarities. Let K ∈ R ntr×ntr be the training Gram matrix. Optionally, we center the kernel:

QKR solves the kernel ridge system:

and predicts for a test sample θ * via the centered kernel vector k c, * : ŷ * = k ⊤ c, * α.

Empirically, full QKR can overfit or become numerically unstable on small datasets. We therefore evaluate a clustered/Nyström-style approximation that maps each input to its kernel similarities against a small set of representative centers. First, we run K-means in angle space on training angles {θ i } i∈Itr to obtain centers {µ r } K r=1 . Next, we construct quantum kernel features for each sample:

Nyström whitening (optional). Let K mm ∈ R K×K be the kernel matrix between centers, (K mm ) rs = k(µ r , µ s ). We optionally whiten features by

which corresponds to a Nyström approximation of the implicit feature map. [70] Finally, we fit a classical ridge regressor on the QKF feature vectors.

As an additional hybrid baseline, we also consider a variational quantum regressor: a parameterized quantum circuit with trainable weights W produces a measurement vector m(θ; W), which is mapped to a scalar prediction by a classical linear head:

The parameters (W, w, b) are optimized by gradient descent on mean squared error. This is included as a sanity check rather than a primary model.

Let y i denote the true target in original units and ŷi the prediction (in original units after inverting any target transform). We report:

and coefficient of determination

We also report percent errors for scale-normalised comparison:

where y test is the mean target value in the held-out test set.

To interpret regression models as screening tools, we define a binary label ℓ i ∈ {0, 1} from the continuous target using a threshold τ computed from Sham subjects in the training split. For example, for “low” screening:

We use thresholds such as a fixed fraction of the Sham mean or Sham median computed on the training split. Given regression predictions ŷi , we define a continuous score for ROC-AUC. If the positive class is “low,” we use s i = -ŷ i (larger score indicates stronger evidence of low). If the positive class is “high,” we use s i = ŷi .

We then compute ROC-AUC and classification metrics by thresholding predictions at the same τ : li = I[ŷ i ≤ τ ] (for “low”) or li = I[ŷ i ≥ τ ] (for “high”). We report macro-averaged F 1 , weighted F 1 , macro precision, macro recall, and balanced accuracy.

All models were implemented in Python. Classical models used standard implementations from scikit-learn. Quantum kernels and variational circuits were evaluated using statevector simulation to compute fidelities exactly, and hybrid optimization was implemented using automatic differentiation frameworks for quantum circuits.

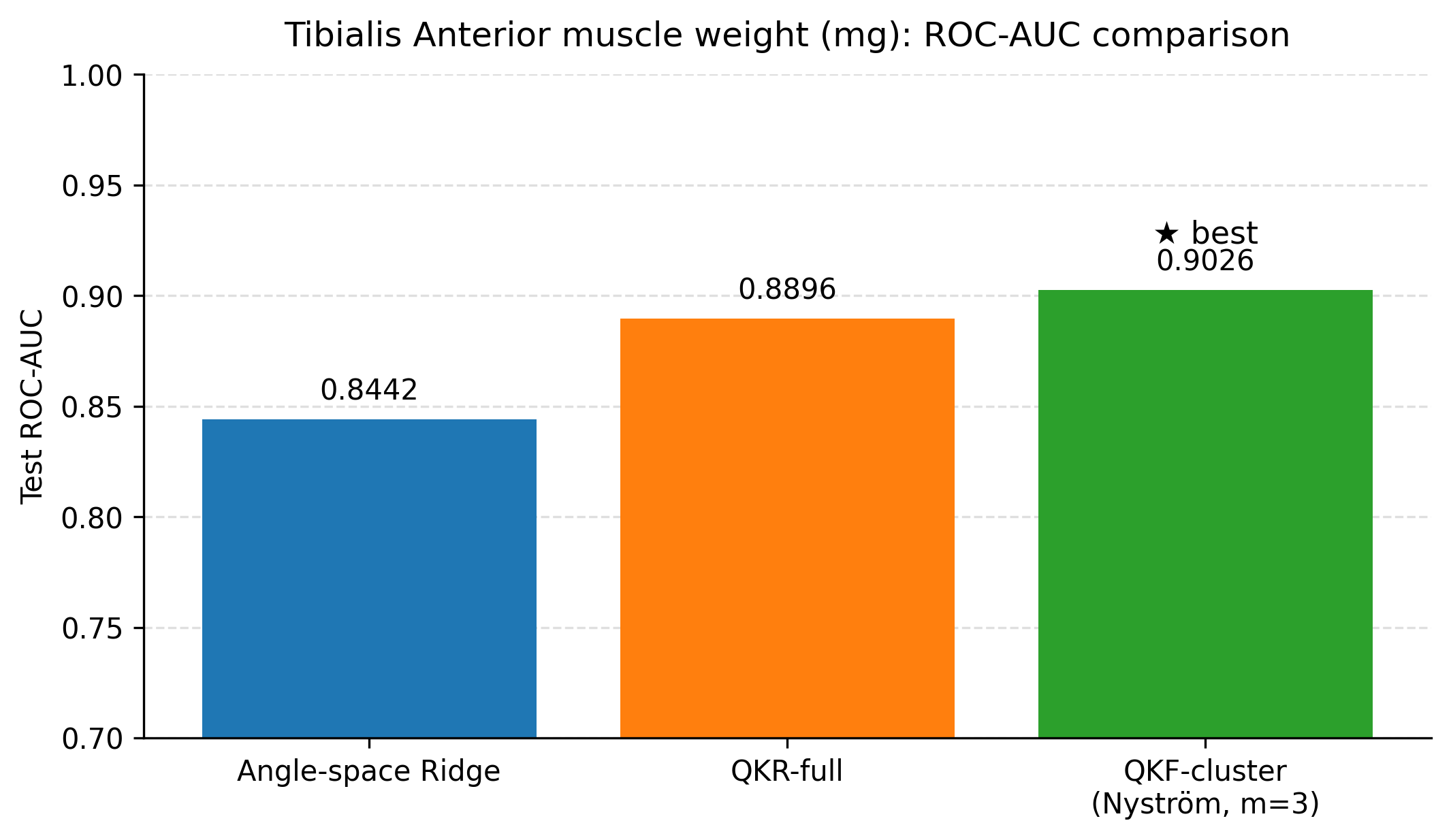
All results are reported on the fixed held-out test split (n test = 43). To keep comparisons transparent across modelling families, we explicitly state the feature budget: classical models use the full biomarker set (optionally with engineered interactions) and may include the condition indicator, SPD models operate on compact biomarker subsets (three selected biomarkers, with the condition indicator appended when specified) and optional SPD distance features, and quantum-kernel models evaluate a matched 4-feature setting (three selected biomarkers plus the condition indicator).

This study evaluated classical machine learning, SPD-geometry-based representations, and quantum-kernel-based learning for predicting three related physiological endpoints in a small tabular dataset: tibialis anterior muscle weight, specific force, and a derived muscle quality index (specific force divided by muscle weight). Across all experiments, we aimed to balance predictive performance with interpretability by reporting both regression metrics (RMSE, MAE, and R 2 ) and screening-oriented metrics obtained by thresholding the continuous targets into clinically interpretable “low” versus “not-low” labels. Summary of key findings. Three consistent observations emerge from the results. First, tuned linear baselines (ridge regression with appropriate feature transformations and feature selection) provide strong performance in this dataset and remain difficult to outperform for several endpoints. Second, incorporating geometry-informed descriptors derived from symmetric positive definite (SPD) constructions can yield measurable improvements for muscle weight when used as additional features alongside a biomarker-only ridge baseline. Third, quantum-kernel learning provides its clearest benefit for muscle weight, where the best quantum-kernel regressor reduced test RMSE relative to both the tuned classical baselines and the SPD-augmented ridge regression. In the compact feature setting used here, the best quantum configurations also reduced test RMSE for specific force and the muscle quality index relative to the strongest classical baselines.

Cross-method comparison. Interpretation of the muscle weight result. The muscle weight endpoint exhibited the most consistent gains from non-linear representations that preserve local structure. The SPD distance-vector construction provides a compact summary of how each sample relates to a small number of prototype regions in a geometry-aware space. When concatenated with a biomarker-only ridge baseline, this distance vector improved muscle weight RMSE (test RMSE = 4.55 mg versus 4.79 mg). The quantum-kernel regressor further improved muscle weight RMSE, suggesting that the feature map induced by the quantum circuit provides an additional non-linear separation that is useful for this endpoint. This improvement was observed on a held-out test set under the same evaluation protocol used for the classical and SPD models, reducing the likelihood that the gain is solely a consequence of increased model capacity.

A practical implication is that muscle weight, in this dataset, appears to benefit from representations that capture interaction structure beyond linear effects. This aligns with the physiological expectation that inflammatory markers and cell counts can influence muscle mass through interacting pathways rather than purely additive mechanisms.

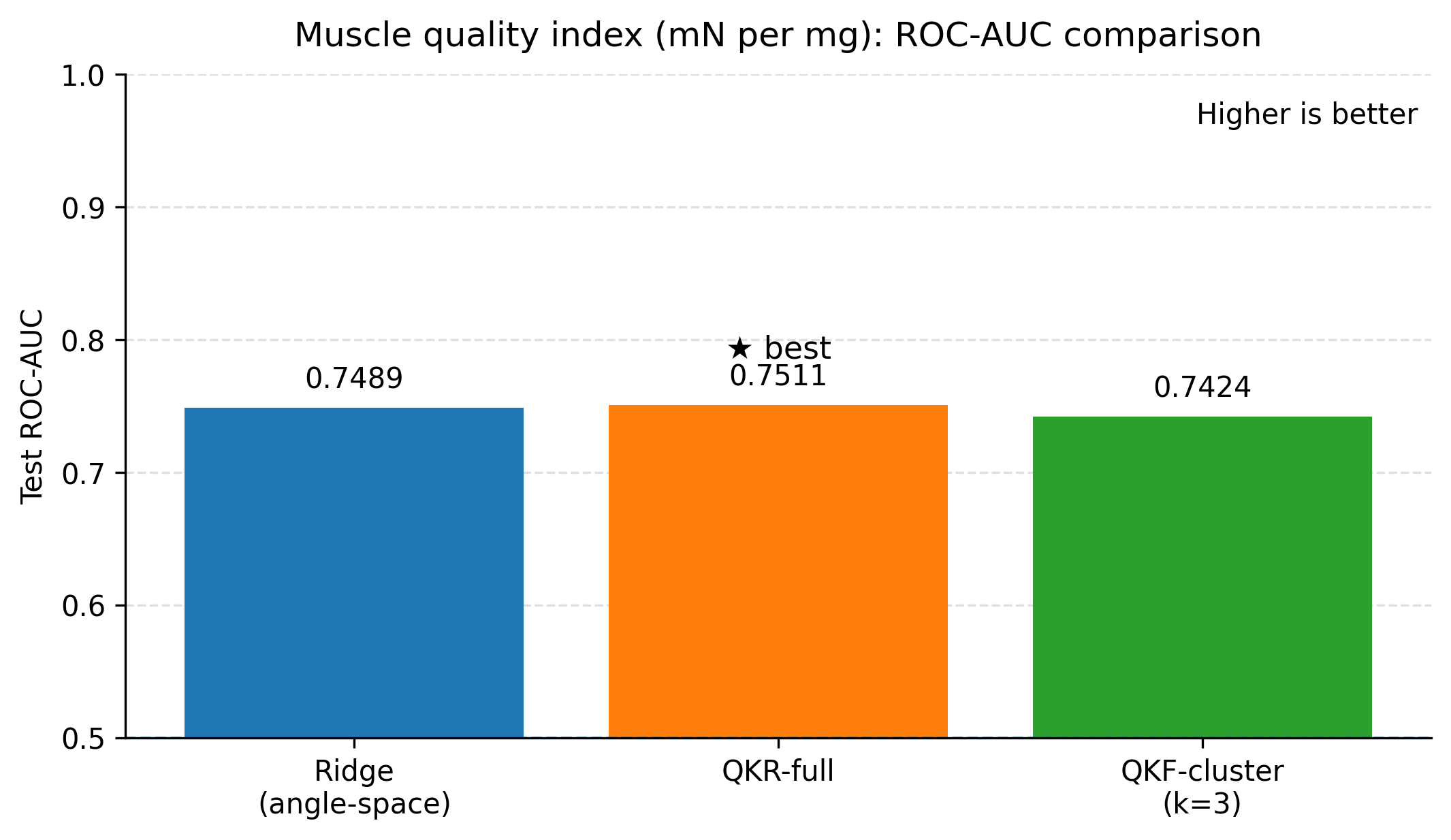
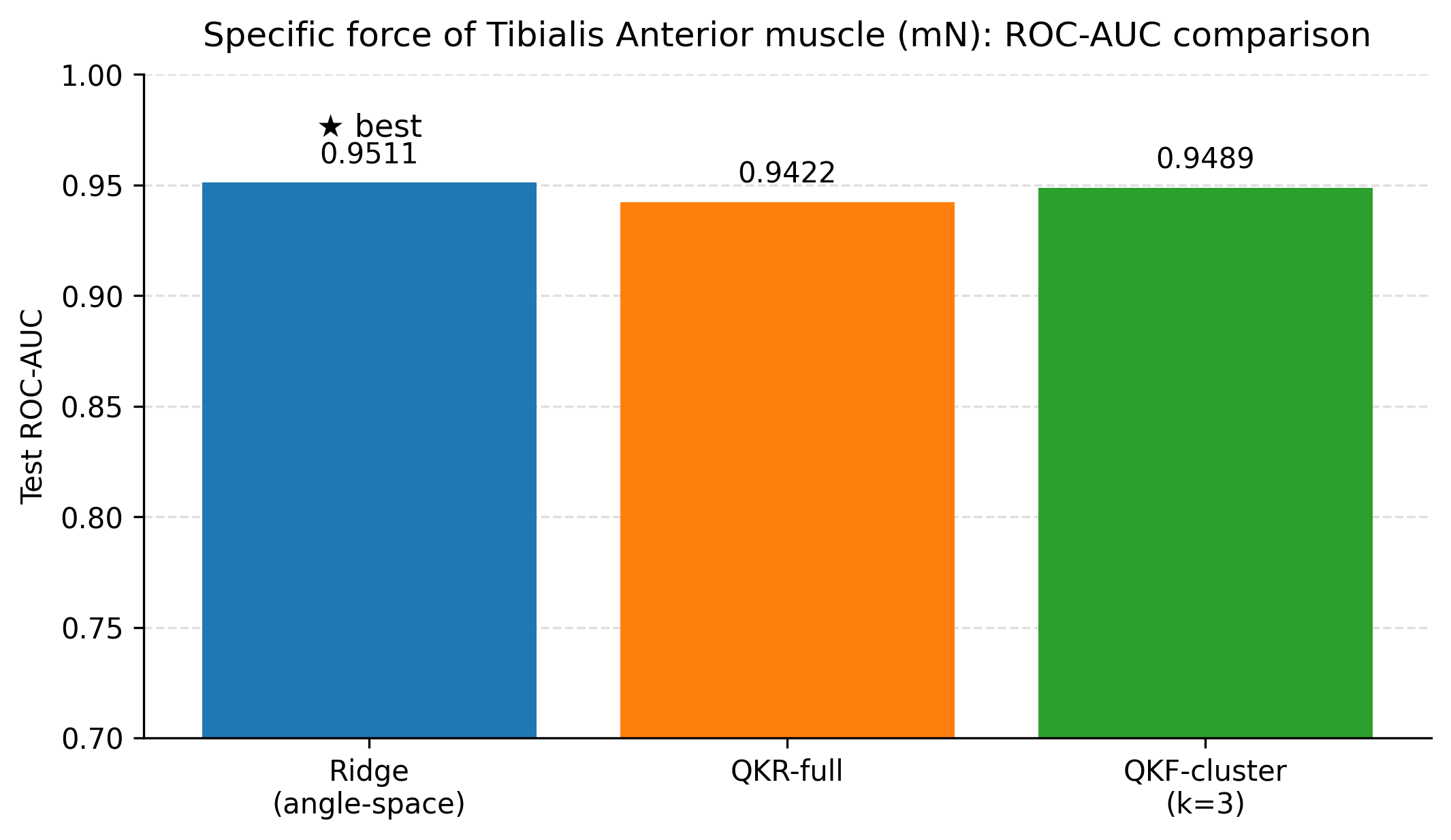
Force and quality results under the tested settings. For specific force and the derived quality index, the best quantum configurations achieved lower RMSE than the strongest classical and SPD baselines on the fixed test split. The differences between full quantum kernel ridge regression and clustered Nyström features were small on these endpoints, and an anglespace ridge baseline within the same compact feature budget performed similarly. This pattern suggests that, for force and quality, the primary gains stem from the compact feature selection and the resulting nonlinear similarity modelling, rather than from requiring deeper circuits.

A cautious interpretation is still warranted: the present dataset supports a quantum-kernel advantage under the evaluated feature budgets and search ranges, but broader claims require repeated-split evaluation and external validation. This distinction is important for practical deployment in biomedical settings, where endpoint-dependent modelling strategies may be preferable to a single universal model.

Role of screening-oriented metrics. In addition to regression metrics, we reported ROC-AUC and classification scores by thresholding each continuous endpoint into a binary label (for example, “low” defined as a fraction of the Sham-group reference statistic). These screening metrics are included to provide a complementary perspective: they evaluate whether models preserve clinically meaningful ranking and separation, even when absolute errors differ. However, because the primary task is continuous prediction, these classification scores should be interpreted as secondary descriptors of model behaviour rather than as the optimisation target. In particular, thresholds reflect a design choice that can be tuned depending on downstream screening objectives and prevalence constraints.

Limitations. Several limitations should be acknowledged. The dataset size is small, which increases uncertainty in point estimates of generalisation performance. Although we used crossvalidation for hyperparameter selection, additional robustness checks such as repeated splits across multiple random seeds and external validation cohorts would further strengthen the conclusions. The quantum results are obtained using simulated quantum circuits rather than hardware execution; therefore, these results reflect the representational properties of the quantum feature map rather than the impact of hardware noise. Finally, the present work focuses on a limited set of quantum circuit families and kernel constructions; alternative encodings, problemspecific ansatz designs, and hybrid fusion strategies may yield additional improvements.

Implications and future directions. The results suggest a practical strategy for small biomedical tabular datasets: begin with strong classical baselines, add geometry-informed descriptors when there is evidence of local-structure effects, and then evaluate quantum kernels as a targeted enhancement rather than a replacement. For future work, we recommend: (i) repeated-seed evaluation to quantify variance in RMSE and R 2 , (ii) ablation studies that isolate the contribution of SPD distance vectors when appended to quantum feature representations,

We studied prediction of muscle outcomes an experimental chronic obstructive pulmonary disease cohort from a compact set of inflammatory and bronchoalveolar lavage biomarkers. The classical baselines show that low-dimensional models already capture substantial signal when the condition indicator is available, and shallow decision trees provide an interpretable view of the dominant predictors and their condition-dependent interactions.

Building on these baselines, we evaluated two nonlinear feature lifts that are compatible with small tabular datasets. First, a geometry-informed embedding based on symmetric positive definite (SPD) descriptors and Stein divergence provides a modest but consistent improvement for tibialis anterior muscle weight when only three biomarkers are used (test RMSE 4.55 mg versus 4.79 mg for a biomarker-only ridge baseline), with the improvement realised by representing each animal through distances to a small set of representative SPD prototypes. Second, quantum kernel ridge regression yields the lowest test RMSE among the ridge-regularised models considered when the condition indicator is included (4.41 mg with R 2 0.605), outperforming a ridge baseline trained on the same angle-embedded features (4.70 mg with R 2 0.553). The clustered Nyström quantum kernel feature model attains the best screening ROC-AUC (0.903) with regression performance close to the full quantum kernel, suggesting that clustering can reduce computational cost while preserving the utility of the quantum kernel lift. In the compact feature setting used here, quantum models also reduced test RMSE for specific force (1898 mN) and for the muscle quality index (45.86 mN per mg) relative to the strongest classical baselines on the same split.

Overall, these findings indicate that geometry-aware descriptors and quantum kernels can act as complementary nonlinear feature maps in low-data, low-feature biomedical prediction problems, while preserving interpretability through explicit feature budgets and transparent model selection. The immediate priorities for strengthening these claims are repeated-split evaluation with confidence intervals, external validation on independent cohorts, and systematic sensitivity analyses over feature budgets, prototype counts, and kernel hyperparameters.

Table 4 reports additional SPD variants for muscle weight, including local-covariance descriptors and a reference outer-product configuration. The “best” outer-product SPD row corresponds to the configuration used for the cross-method comparison in Fig. 2.

and