FaithSCAN: Model-Driven Single-Pass Hallucination Detection for Faithful Visual Question Answering

Qi Zhang is with the China Industrial Control Systems Cyber Emergency Response Team, Beijing 100040, China. E-mail: bonniezhangqi@126.com. Chen Li is with the China Electronics Standardization Institute, Ministry of Industry and Information Technology of the People’s Republic of China, Beijing 100007, China. E-mail: lichen@cesi.cn.

Lei Jiang is with the Institute of Information Engineering, Chinese Academy of Sciences (CAS), Beijing 100093, China. E-mail: jianglei@iie.ac.cn.

*Corresponding author: Yanbing Liu. models (MLLMs) and vision-language models (VLMs) have enabled impressive integration of visual perception and language understanding, supporting increasingly complex openended VQA tasks [2], [3]. Despite impressive performance, they frequently generate fluent yet ungrounded or incorrect responses, a phenomenon known as hallucination [4]- [6], which in VQA settings manifests as responses misaligned with the input visual evidence or contradictory to factual knowledge [7], [8]. Among them, faithfulness hallucinations [1], where answers violate visual grounding, are particularly critical in VQA, since reliable factual verification depends on the model first attending to and correctly interpreting the image [9]. Consequently, detecting faithfulness hallucinations is a necessary step for ensuring answer reliability and user trust, motivating the development of effective detection methods that can identify unfaithful answers (examples illustrated in Fig. 1). Motivated by the importance of faithfulness hallucination detection in VQA, a variety of detection methods have been proposed in recent years. Existing approaches can be broadly grouped into two paradigms: external verification-based methods and uncertainty-driven methods [6], [10]. External verification approaches detect hallucinations by explicitly checking cross-modal consistency between the generated answer and the visual input, often relying on auxiliary components such as object detectors, VQA models, scene graphs, or large language model (LLM) judges [9], [11], [12]. By decomposing answers into atomic claims and validating them against visual evidence, these methods are capable of identifying finegrained inconsistencies. However, their reliance on additional pretrained models and multi-stage pipelines leads to high computational overhead and makes the final performance sensitive to error propagation from external components. Moreover, such methods operate largely independently of the internal reasoning process of the target VLM, limiting their scalability and integration in real-world deployment [11].

In contrast, uncertainty-driven methods approach hallucination detection from the perspective of model confidence. Empirical studies in both language models and vision-language models have shown that hallucinated outputs are often associated with elevated predictive uncertainty [1], [7]. Representative approaches, such as semantic entropy (SE) [5] and likelihood-based measures [5], [13]- [15], estimate hallucination likelihood through sampling model outputs under different decoding strategies, prompt reformulations, or visual perturbations, followed by entropy or distributional analysis. visual cues, such as vision-amplified semantic entropy [16] and dense geometric entropy [17]. In addition, methods leveraging internal signals like attention patterns and intermediate embeddings are emerging. Approaches such as DHCP [18] and OPERA [19] focus on attention dynamics to detect overreliance on unverified features, while HallE-Control [20] modifies embeddings to suppress unreliable visual details. These methods highlight the value of integrating internal uncertainty signals.

Despite their effectiveness, existing uncertainty-based methods suffer from two key limitations. First, they rely on repeated sampling and generation-level statistics, resulting in high inference cost and unstable behavior. This dependence on stochastic decoding and prompt configurations significantly limits their practicality in latency-sensitive or largescale VQA settings. Second, they fail to jointly leverage the heterogeneous uncertainty signals inherently encoded in modern VLMs. Uncertainty arising from language decoding, visual perception, and vision-language interaction is often treated independently or partially ignored, rather than being modeled in a unified manner. As a result, the complementary information carried by different internal uncertainty sources remains largely unused for hallucination detection.

To tackle these limitations, we propose FaithSCAN, a lightweight faithfulness hallucination detection network for VQA. FaithSCAN treats hallucination detection as a supervised learning problem, where multiple sources of internal uncertainty are extracted from a single forward pass of a VLM. Specifically, it leverages three complementary uncertainty signals: (i) token-level predictive uncertainty from language decoding, (ii) intermediate visual representations reflecting the model’s perception of the image, and (iii) cross-modal aligned representations that project visual information into the textual semantic space. These heterogeneous signals are processed via Branch-wise Evidence Encoding and aggregated using Uncertainty-Aware Attention, enabling the detector to capture hallucination patterns across multiple reasoning pathways. Supervision is provided through a model-driven Visual-NLI procedure, extending the LLM-as-a-Judge paradigm to VQA, and is further validated by small-scale human verification, ensuring label reliability without requiring large-scale manual annotation.

Our contributions are summarized as follows:

• We introduce FaithSCAN, a novel hallucination detection architecture that leverages internal uncertainty signals from a single VLM forward pass. The remainder of this paper is organized as follows. Section II reviews related work. Section III defines the problem setting and introduces key concepts. Section IV presents the proposed methodology. Section V describes the experimental setup, including datasets, metrics, and implementation. Section VI reports results and analysis. Finally, Section VII concludes the paper.

Faithfulness hallucination detection is critical in VQA, where generated answers can be fluent and confident yet inconsistent with visual evidence [10]. A variety of detection methods have been proposed in recent years, which can be broadly categorized into external verification-based and internal signal-or uncertainty-driven approaches. External verification methods explicitly check cross-modal consistency between answers and visual inputs, often using object detectors, VQA models, scene graphs, or LLM evaluators [9], [11], [12]. By decomposing answers into atomic claims and validating them against visual evidence, they enable finegrained hallucination detection. However, these methods rely on multi-stage pipelines and pretrained components, incurring high computational cost and sensitivity to error propagation, while largely ignoring the VLM’s internal reasoning process [11]. Internal signal-or uncertainty-driven methods, in contrast, exploit the model’s outputs, attention patterns, and intermediate embeddings to detect hallucinations, offering a more direct and efficient view into the generation process [21]- [23].

Model-internal uncertainty has emerged as an effective and relatively inexpensive cue for hallucination detection. Both language models and VLMs exhibit increased predictive uncertainty when hallucinations occur [12], [24]- [26]. Methods such as SE [5] and likelihood-based measures [27]- [29] quantify uncertainty by aggregating variations across multiple decoding outputs. In VQA, extensions incorporate visual perturbations or multimodal semantic clustering, e.g., vision-amplified semantic entropy [16] and dense geometric entropy [17], which estimate hallucination likelihood by comparing semantic distributions under clean and perturbed visual inputs. These methods demonstrate that uncertainty signals can effectively capture hallucinations, including in safetycritical domains such as medical VQA [16]. Nevertheless, most approaches rely on repeated sampling or perturbations to obtain reliable estimates, which increases inference cost and can be sensitive to stochastic decoding behavior.

Hallucinations in VQA are not only reflected in the magnitude of predictive uncertainty but also in structured patterns across attention, intermediate representations, and logits. Early studies leveraged attention dynamics to detect hallucinations, e.g., DHCP [18] captures cross-modal attention patterns, showing consistent differences between hallucinated and faithful responses. OPERA [19] demonstrates that hallucinations correlate with over-reliance on sparse summary tokens in selfattention, which can be mitigated through dynamic reweighting. Feature-based methods, such as HallE-Control [20], reduce hallucinations by projecting intermediate embeddings to suppress reliance on unverifiable visual details. Embedding-or logit-based approaches, e.g., PROJECTAWAY [29] and Con-textualLens [30], exploit token-level predictions and contextaware embeddings to localize and mitigate hallucinations at fine-grained object or patch levels. Despite their effectiveness, these methods are often limited by partial access to internal signals or simplified modeling of cross-modal interactions. Together, they indicate that hallucination-related cues are encoded across heterogeneous internal signals, highlighting the feasibility and necessity of fully exploring and exploiting them for reliable detection.

More recently, HaluNet [31] studies efficient hallucination detection in text-based question answering using internal uncertainty signals. Our work instead focuses on faithfulness hallucinations in VQA and extends this paradigm through explicit fusion of multimodal internal evidence. In addition, we provide a more systematic design and empirical validation of this methodology in the multimodal setting.

VQA aims to generate a natural language answer conditioned on an input image and a textual question. Formally, let:

denote the input image and question, respectively, where I and Q denote the spaces of images and textual questions. Given (I, q), a VLM parameterized by θ produces an answer:

where A denotes the space of textual responses.

In this work, we focus on modern VLMs that generate answers in an autoregressive manner. Specifically, all three VLM architectures studied in this paper (see Section III-C) follow this paradigm, modeling the conditional distribution as:

where a denotes the output token sequence.

We focus on faithfulness hallucinations [1], where the generated answer is inconsistent with the visual evidence present in the input image. Given a VQA instance:

the goal of hallucination detection is to determine whether the answer â is visually grounded in I.

We formulate faithfulness hallucination detection as a supervised binary classification problem. Specifically, we aim to learn a classifier:

where y = 1 indicates a faithfulness hallucination and y = 0 denotes a faithful answer. Unlike generation-based uncertainty estimation methods, our learning objective is not to approximate the full output distribution p θ (a | I, q), but to directly model:

using uncertainty signals and representations internally encoded in the VLM during a single forward pass. This formulation enables efficient hallucination detection without repeated sampling, external verification models, or additional knowledge sources.

Existing vision-language models vary in how they align visual and textual modalities. We focus on three representative models that illustrate distinct paradigms.

• InstructBLIP [32] uses query-based alignment, producing compact visual embeddings that interact with the language model via queries. • LLaVA-NeXT [33] relies on projection-based alignment, treating visual features as additional text tokens concatenated with language embeddings. • Qwen-VL [34] employs a unified multimodal transformer, where visual and textual tokens interact throughout all layers. Despite these architectural differences, all models encode rich uncertainty information, including token-level predictive uncertainty, visual reliability, and cross-modal alignment. This motivates hallucination detection methods that leverage internal representations rather than relying solely on generationlevel sampling. Details of each architecture are provided in Supplementary Material Sec. B.1.

In this work, we propose a single-pass, model-driven framework for multimodal hallucination detection in VQA (Fig. 2). Unlike prior uncertainty-based methods that rely on repeated sampling or external verification, our approach operates entirely within a single forward pass of a VLM, leveraging its internal representations as supervisory signals. Hallucination detection is formulated as a supervised classification problem informed by multiple complementary sources of uncertainty: (i) token-level predictive uncertainty during answer generation, (ii) intermediate visual representations encoding the model’s perception, and (iii) visually grounded representations aligned with the textual semantic space. Being fully model-driven, the method does not require external estimators or auxiliary generative processes, making it compatible with diverse VLM architectures such as query-based (InstructBLIP), projectionbased (LLaVA), and tightly coupled multimodal (Qwen3-VL) models. By explicitly learning the mapping between observed hallucination phenomena, their manifestations in VQA, failure pathways of multimodal reasoning, and internal model states (Table I), our approach provides a principled and efficient solution for hallucination detection without expensive inference cost.

Most uncertainty-based hallucination detection methods [5], [13], [15], [27], [28] aim to estimate or calibrate uncertainty, yet converting these scores into decisions still requires carefully chosen thresholds, limiting practical utility. By framing detection as a supervised decision-making problem, we directly map internal uncertainty signals to hallucination labels, producing actionable outputs and simplifying deployment. As described in Section IV-E, this approach learns from internal signals rather than calibrating model uncertainty, reducing learning difficulty: learning focuses on extracting useful internal signals rather than output-space confidence modeling.

A central challenge in supervised hallucination detection is obtaining reliable supervision at scale. Manual annotation of multimodal hallucinations is costly, and many benchmarks provide only correct answers or predefined hallucination references [9], [35]- [37]. Automatic annotation methods can alleviate this [38], but they typically produce model-agnostic labels that capture generic failures rather than the modeldependent nature of hallucinations, which stem from a model’s generation behaviors, inductive biases, and cross-modal alignment deficiencies. Consequently, supervision decoupled from the target model is inherently limited.

We generate hallucination labels tightly coupled with the target model’s decoding dynamics [9], [35]- [37], derived from semantic consistency between generated and reference answers conditioned on the same image-question context. A strong external VLM serves as a semantic judge [12], [38], but it is not a detached oracle; it evaluates answers in the context of the target model’s reasoning, producing model-aware labels.

Visual grounding constraints enforced via a structured Visual-NLI protocol ensure that labels capture model-specific failure modes. We then verify label reliability through complementary automatic and human-based procedures, which is critical for supervised hallucination detection. 1) Answer-Level Hallucination Labels Conditioned on Gold Answers: We consider VQA datasets that provide a reference answer a * for each image-question pair (I, q). Given a VLM f θ , we first obtain its most likely answer â under a lowtemperature decoding regime. The objective is to determine whether â is faithful to the visual evidence and semantically consistent with the reference answer.

To this end, we formulate hallucination labeling as a visual natural language inference (VNLI) problem. Specifically, we construct the triplet (I, q, a * ) as the premise and treat the model-generated answer â as the hypothesis. A pretrained vision-language judge J is then queried to assess the semantic relationship between the premise and the hypothesis, conditioned on the image.

Formally, the judge outputs a categorical probability distribution:

where p = (p ent , p con , p unc ) corresponds to the probabilities of entailment, contradiction, and uncertainty, respectively. The three judgment categories are defined as follows:

• Entailment: the hypothesis â is semantically consistent with the reference answer a * , and any additional details are clearly supported by the image. • Contradiction: the hypothesis conflicts with the reference answer or describes visual attributes that are inconsistent with the image. • Uncertainty: the image does not provide sufficient evidence to verify the hypothesis, or the hypothesis introduces details that are unsupported but not directly contradicted. To improve robustness against stochasticity in the judge model, we perform R independent judging rounds and average the predicted probabilities:

We then define the hallucination probability as the aggregated mass of non-entailment outcomes:

The final answer-level hallucination label is determined by:

where I(•) denotes the indicator function.

In this work, we treat both contradiction and uncertainty as indicators of hallucination, as they reflect failures of visual grounding or over-commitment beyond the available visual evidence.

We emphasize that the judge model is only used during dataset construction. At inference time, the proposed hallucination detector operates independently, relying solely on the internal representations of the target VLM.

2. Human Verification via Small-Scale Multi-Round Sampling: While the proposed model-driven labeling strategy enables scalable supervision, it is still essential to assess the reliability of the automatically constructed hallucination labels. To this end, we introduce a small-scale human verification protocol that serves as a quality control mechanism rather than a primary annotation source.

Concretely, we randomly sample a subset of VQA instances (100 samples per data set) and inspect the most-likely answer generated by the target VLM under low-temperature decoding. For each sampled instance, human annotators are presented with the image, question, gold answer, and model-generated answer, and must determine whether the model answer constitutes a hallucination, defined as being unfaithful to the visual evidence or inconsistent with the reference answer. To avoid confounding factors, samples with ambiguous questions or problematic ground-truth references are explicitly marked and excluded from subsequent agreement analysis.

Importantly, human annotation is not used to replace modeldriven labels. Instead, it is employed to validate whether the hallucination signals produced by the Visual-NLI judge are consistent with human judgment when applied to the same model outputs. Let y human ∈ {0, 1} denote the human label indicating non-hallucination or hallucination, and y model ∈ {0, 1} denote the corresponding binary label derived from the modeldriven NLI judgment. We evaluate the agreement between y human and y model using multiple complementary metrics, including raw agreement ratio, Cohen’s κ, and Matthews correlation coefficient (MCC); detailed analyses and discussion are provided in Section VI-B.

3. Automated Label Reliability Verification: Assessing the reliability of such labels through human verification remains costly and inherently limited. We therefore introduce an automated label reliability verification framework that aims to quantify the reliability of model-driven hallucination labels in a scalable manner, and to examine how such reliability estimates can be incorporated into the training process.

Given an image-question-answer triplet, the verification procedure evaluates the consistency of the assigned hallucination label across multiple model-based assessments, including repeated semantic verification [5], stochastic answer generation [15], and explicit self-reflection. These assessments capture complementary aspects of decisiveness, robustness, and self-consistency, and are aggregated into an instance-level reliability score that reflects confidence in the supervision signal rather than the likelihood of hallucination itself.

We further investigate the use of this reliability score as an uncertainty-aware signal to modulate the contribution of individual training instances, without altering the original labels or introducing inference-time overhead. Detailed definitions of the methods, strategies for training integration, and preliminary experimental validations are provided in Supplementary Material Sections D.2, D.3.

In this subsection, we describe three categories of internal signals that are accessible in mainstream VLMs and serve as the foundation of our hallucination detection method. Our approach is based on the observation that faithfulness hallucinations in VLMs are closely tied to the model’s internal uncertainty during inference. Rather than introducing external supervision or repeated sampling, we directly extract uncertainty-related signals from intermediate representations produced in a single forward pass of the VLM f θ (Fig. 2a). Importantly, these signals are model-driven and architecturedependent: their concrete instantiation depends on the design of a given VLM, while their functional roles can be unified under a common formalization.

1. Problem Setting: Given an image-question pair (I, q), the VLM generates an answer sequence â = (a 1 , . . . , a T ) autoregressively according to the conditional distribution p θ (â | I, q) = T t=1 p θ (a t | a <t , I, q). During this generation process, the model produces a collection of intermediate representations spanning visual encoding, cross-modal alignment, and language decoding. We extract uncertainty-related signals from these internal representations without modifying the model parameters θ or the inference procedure.

2. Token-Level Generation Signals: At each decoding step t, the language model outputs a predictive distribution:

From this distribution and the associated decoder hidden states, we extract three token-level signals: the log-likelihood of the generated token,

the entropy of the predictive distribution,

and the hidden embedding h t ∈ R d h of the generated token from a selected decoder layer. Here, d h denotes the dimensionality of the decoder hidden states. While ℓ t and H t provide scalar measures of predictive confidence, the hidden embedding h t is treated as a high-dimensional representation that implicitly encodes semantic uncertainty.

3. Visual Semantic Representations: Prior to cross-modal interaction, the vision encoder extracts visual features from the input image I. We denote the resulting set of patch-level visual embeddings as:

where N is the number of visual patches and d v denotes the dimensionality of the visual embedding space. Each v i corresponds to a localized image region. In practice, V raw is obtained from the final hidden states of the vision backbone before any language conditioning or multimodal fusion. This representation reflects the model’s internal visual perception state and serves as a latent visual semantic space that may encode uncertainty in visual understanding. 4) Cross-Modal Aligned Representations: Modern VLMs employ an explicit alignment module to project visual representations into a language-compatible semantic space. We denote the resulting aligned visual tokens as:

where M is the number of aligned visual tokens and d a denotes the dimensionality of the aligned multimodal embedding space. These representations are produced by a model-specific alignment function:

which may incorporate cross-attention, projection layers, or query-dependent pooling mechanisms. The aligned visual tokens directly participate in the autoregressive decoding of â and therefore reflect visual information as mediated by visionlanguage interaction. 5) Unified View of Uncertainty Signals: Although the concrete extraction of the above signals depends on the architecture of the VLM, they can be jointly formalized as a set of internal uncertainty-related representations produced during the generation of â, namely:

which collectively capture uncertainty arising from language decoding, visual semantic perception, and vision-language interaction, and constitute a model-internal, single-pass characterization of uncertainty. In the next subsection, we describe how these heterogeneous signals are jointly modeled to produce a hallucination confidence score.

We propose FaithSCAN, a lightweight supervised hallucination detection network that operates on internal uncertainty signals extracted from a frozen VLM, as illustrated in Fig. 2b. FaithSCAN aggregates heterogeneous uncertainty evidence at the decision level and outputs a scalar hallucination score in a single forward pass. Notably, the detector is model-dependent: the dimensionality, number, and extraction locations of its inputs are determined by the architecture of the underlying VLM, enabling adaptation to model-specific uncertainty patterns without modifying the base model.

1. Input Formulation: Given the frozen VLM f θ , an image-question pair (I, Q) and the model-generated answer â, we extract K internal uncertainty signals:

Each X k is a sequence-valued feature (e.g., token-level statistics, hidden states, or vision-language alignment features) obtained from different components of f θ . These sources may vary in modality, sequence length, and feature dimension, and are treated independently without assuming a shared feature space.

2. Branch-wise Evidence Encoding: Each uncertainty source X k is processed by an independent branch encoder f k (•) that compresses a variable-length sequence into a fixeddimensional embedding:

where d = 64 in all experiments. All branch encoders are implemented as lightweight sequence compression modules rather than deep semantic encoders. Specifically, we consider linear projections with global average pooling, trainable sequence compressors (Linear + LayerNorm + ReLU + mean pooling), and convolutional encoders with adaptive pooling [39], where one-dimensional convolutions are applied with kernel size 3 and stride 1. For a detailed description of these branch encoders, refer to Supplementary Material Sec. B.5. Despite architectural differences, all variants share the same objective: to summarize the reliability and stability of internal signals while limiting representational capacity to reduce overfitting. We further analyze the generalization capability under distribution shifts in Section VI-A2, while the effectiveness of architectural variants is examined in Section VI-C2.

3. Uncertainty-aware Attention Fusion:

the set of evidence embeddings produced by the evidence encoders. To integrate heterogeneous evidence representations, we adopt a cross-branch attention mechanism:

(20) This attention computes adaptive weights over branches, allowing the model to emphasize certain evidence representations while aggregating information across all branches.

To further modulate the fused representation, we apply a gated residual transformation:

where the tanh(•) gate modulates each feature of the fused representation, and the residual connection preserves the original information while allowing adaptive adjustment.

The fused representation h is mapped to a hallucination probability via:

where p ∈ (0, 1) denotes the likelihood that the generated answer is hallucinated. FaithSCAN is trained end-to-end with model-driven supervision while keeping the underlying VLM frozen, using a binary cross-entropy loss over the hallucination labels.

We evaluate our approach on four multimodal datasets with complementary characteristics: HalLoc-VQA [37], POPE [9], HaloQuest [36], and VQA v2 [35], which differ in hallucination types, annotation granularity, and inducing mechanisms.

We compare FaithSCAN with a diverse set of representative baselines for multimodal hallucination detection, focusing on uncertainty-based methods at token, latent, and semantic levels. Token-level baselines include Predictive Entropy (PE) [43] and Token-level Negative Log-Likelihood (T-NLL) [24], measuring per-token predictive uncertainty. Latent-space baselines such as Embedding Variance (Emb-Var) [44] and Semantic Embedding Uncertainty (SEU) [44] capture instability in vision-conditioned answer embeddings. Semantic-level baselines include Semantic Entropy (SE) [5] and a multimodal adaptation of SelfCheckGPT [45], detecting contradictions across answer pairs. A multimodal P (True) verification baseline [5] evaluates answer correctness via image-conditioned yes/no prompts. Finally, a Logistic Regression [46] classifier trained on our dataset serves as a supervised reference, with implementation details and key hyperparameters provided in Supplementary Material Sec. C.

We evaluate FaithSCAN on three vision-language backbones: IB-T5-XL, LLaVA-8B, and Qwen3-VL-8B 1 . Uncertainty signals, including token-level log-likelihood, predictive entropy, and hidden representations from a selected transformer layer, are extracted in a single forward pass and fused via an attention-based module after projection to 64 dimensions. Hallucination supervision is obtained via model-driven verification using Qwen2.5-VL-32B-Instruct with low-temperature sampling (T = 0.1). Models are trained with AdamW and binary cross-entropy loss with logits for 1 Full model names: IB-T5-XL (Salesforce/instructblip-flan-t5-xl); LLaVA-8B (llava-hf/llama3-llava-next-8b-hf); Qwen3-VL-8B (Qwen/Qwen3-VL-8B-Instruct). Focusing on the I2T setting where evaluation is performed primarily on generated textual answers, we assess hallucination detection using AUROC (ROC) to measure overall ranking quality, AURAC (RAC) to evaluate selective prediction under rejection, F1@Best (F1@B) to report the optimal classification trade-off, and RejAcc@50% (RA@50) to quantify accuracy after rejecting the most uncertain half of predictions [5], [15], [28]. Together, these metrics provide a comprehensive and complementary evaluation of hallucination detection performance from both ranking and decision-making perspectives.

In this section, we conduct extensive experiments to evaluate the proposed method from multiple perspectives. Specifically, our experimental study is organized around four research questions. RQ1 (Overall Effectiveness and Generalization): How effective is the proposed method in detecting hallucinations across different vision-language models and datasets covering diverse hallucination types? Moreover, we evaluated the computational efficiency of each method in both the sampling and inference stages. In the sampling phase (e.g., obtaining answers or extracting embeddings), most existing methods are relatively slow. Regarding inference, approaches that rely on multiple samples or use external models exhibit far lower efficiency than those that infer directly from the model’s internal states. Because FaithSCAN integrates multiple embeddings, its inference speed is slightly reduced when handling larger embedding sizes; nevertheless, it remains among the fastest, highlighting the advantages of our approach.

2. Out-of-distribution Evaluation: OOD evaluation (Table IV) reveals limited generalization for models trained on a single dataset, especially when hallucination types differ (e.g., object/scene-level vs. false-premise). FaithSCAN exhibits stronger transfer than logistic regression, and multisource training enhances OOD performance, highlighting the importance of diverse training data. Nonetheless, a performance gap between ID and OOD underscores the challenge of hallucination detection under distribution shifts, motivating future work on improving generalization of model-driven uncertainty approaches. Qualitative examples are shown in Fig. 3. In Fig. 3a, a POPE sample demonstrates correct detection of a contradiction by Quantitatively (Table V), the proposed supervision exhibits strong agreement with human annotations, achieving agreement scores in the range of 0.950-0.990. Moreover, Cohen’s Kappa and MCC are consistently high across datasets, with most values exceeding 0.8.

These results indicate that the model-driven supervision effectively aligns with human judgment, providing a reliable signal for hallucination detection across diverse scenarios.

2. Automated Evaluation: We evaluate the reliability of hallucination labels for answers generated by different VLM backbones using three post-hoc scores: Visual-NLI decisiveness (s nli ), stochastic decoding consistency (s stoch ), and reflection-based self-consistency (s ref ). Their distributions are shown in Fig. 4.

s nli is high for most samples, indicating that the external model produces stable judgments across NLI rounds, with slightly lower consistency on the more challenging VQA v2. faithful outputs make reflection less stable. Differences across datasets also appear: HaloQuest contains some uncertain cases due to false-premise hallucinations, while hallucinations in VQA v2 and HalLoc-VQA are more often clearly judged as entailment or contradiction. These scores show that model-driven hallucination labels are generally stable, while reflection provides deeper insight into the link between data distributions and hallucination labels, highlighting a promising direction for future study.

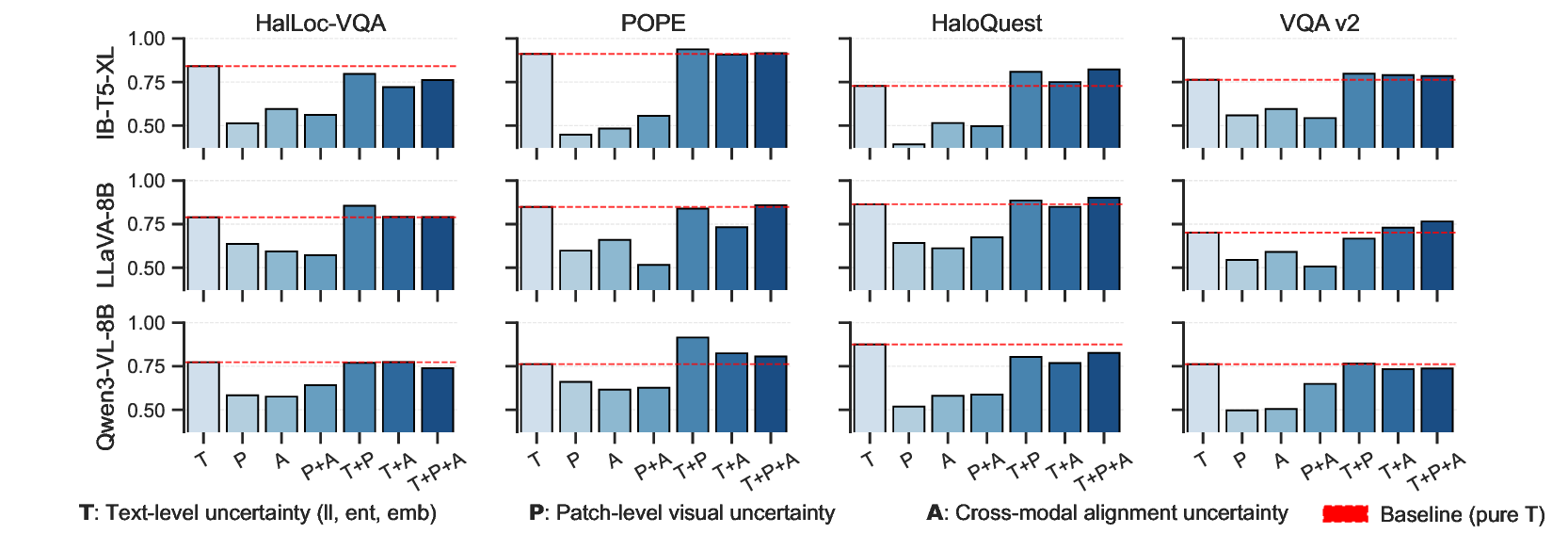
We investigate why FaithSCAN effectively detects hallucinations by analyzing the role of different internal representations and uncertainty sources. Experiments are conducted on HalLoc-VQA, POPE, HaloQuest, and VQA v2 using IB-T5-XL, LLaVA-8B, and Qwen3-8B.

1. Contribution of Independent Uncertainty Sources: We investigate the contributions of independent uncertainty sources derived from distinct internal representations, including token-level uncertainty from language generation, visual uncertainty from compressed patch embeddings, and visualsemantic uncertainty from features aligned to the textual semantic space.

We first evaluate each source in isolation. As shown in Fig. 5, visual patch-level and visual-semantic uncertainty alone generally yield limited discriminative power across datasets, indicating that hallucinations are difficult to detect without access to token-level generation signals. In contrast, token-level uncertainty consistently provides a strong baseline, suggesting that many hallucination phenomena are rooted in the internal states of the language generation process.

The role of visual uncertainty, however, varies substantially across datasets and hallucination types. On POPE, which predominantly focuses on object-level hallucinations, integrating pure visual patch uncertainty leads to significant performance gains. This result suggests that object hallucinations are closely tied to perceptual failures, and that uncertainty at the visual perception level constitutes a critical failure pathway in such cases.

In contrast, on HalLoc-VQA and VQA v2, incorporating visual features yields limited or inconsistent improvements. These datasets involve more complex reasoning and compositional question answering, where hallucinations are less attributable to visual ambiguity and more strongly associated with failures in language modeling and multimodal reasoning. This observation reflects a shift in the dominant failure pathway from perception to higher-level reasoning processes. A similar pattern is observed on HaloQuest, which primarily targets false-premise hallucinations. For models with relatively weaker visual capabilities, incorporating visual uncertainty substantially improves detection performance, indicating that interaction-level hallucinations can originate from unreliable visual grounding. However, for models with stronger visual encoders, the gains diminish, suggesting that hallucinations in this setting are more likely driven by reasoning-level failures. This further indicates that the source of hallucination is architecture-dependent and cannot be attributed to a single modality.

Overall, these results empirically support our methodological premise: effective hallucination detection requires explicitly modeling the mapping between observed hallucination phenomena, their manifestations in VQA, the underlying multimodal failure pathways, and the corresponding internal model states.

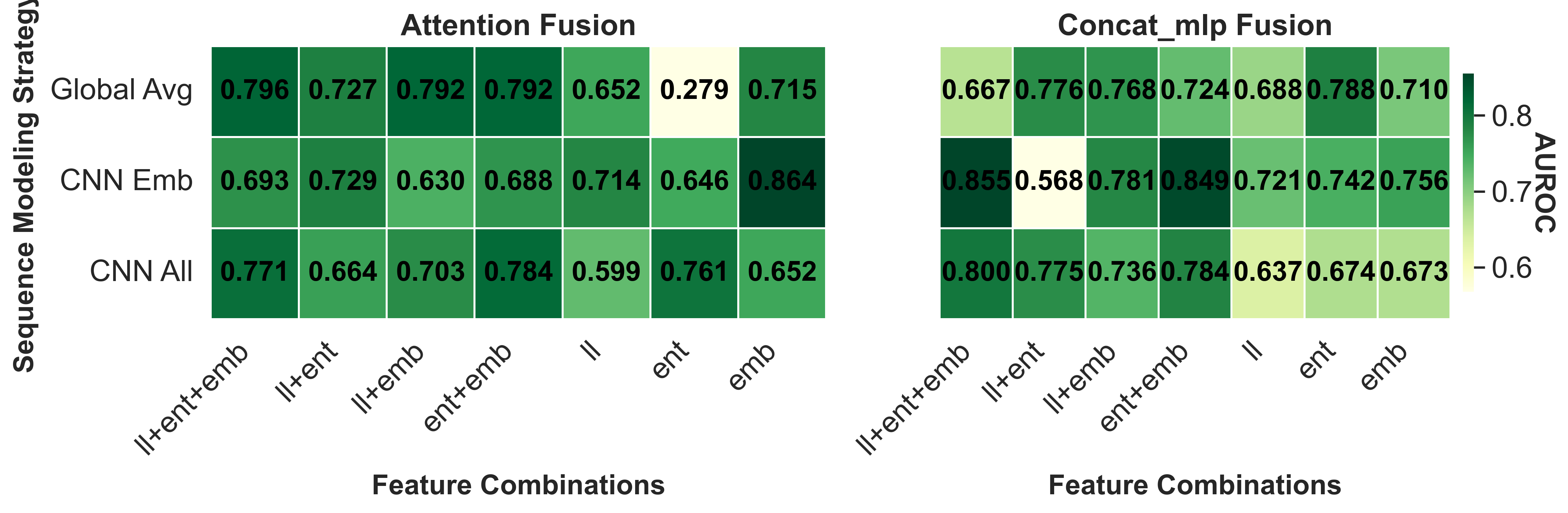
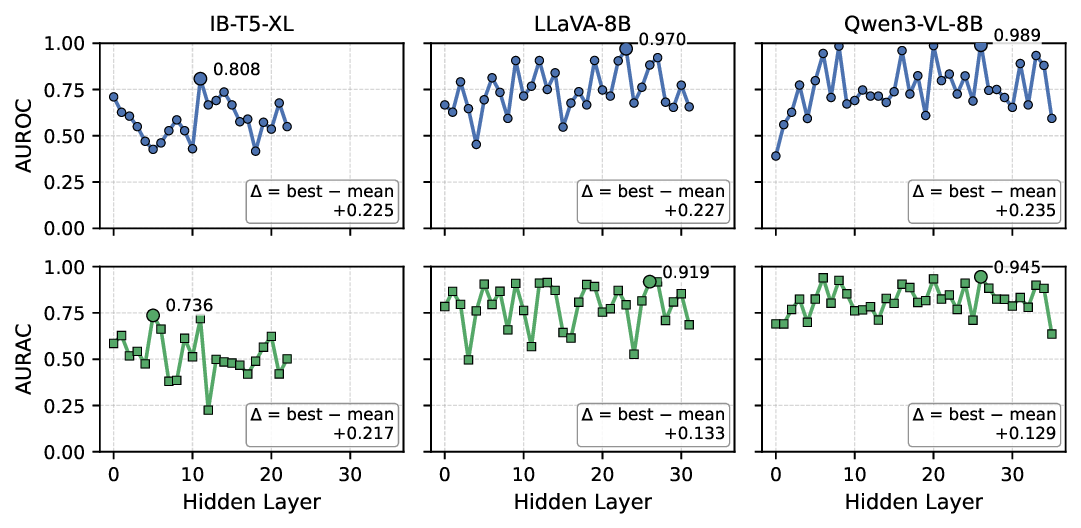
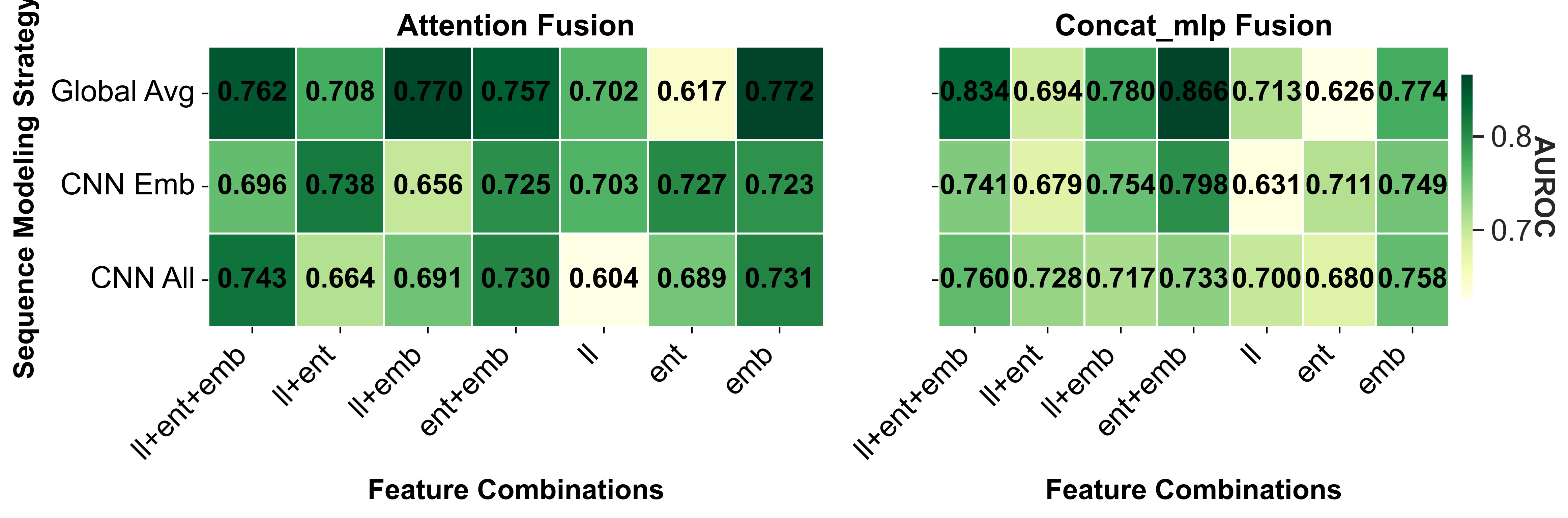
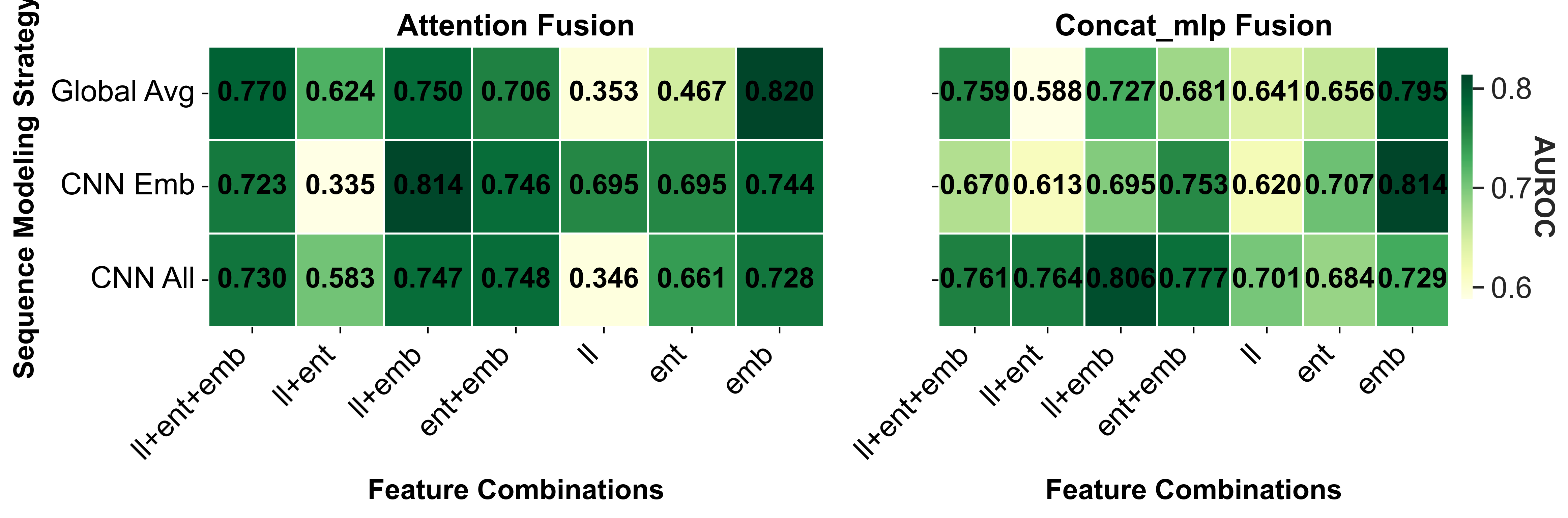
2. Ablation Study on Token-level Uncertainty Modeling: We evaluate token-level uncertainty signals derived from loglikelihoods, entropies, and hidden embeddings. As shown in Fig. 6, embeddings provide the richest signal, followed by entropy, while log-likelihood contributes marginally. Combining these signals consistently improves performance across datasets and models, with attention-based fusion outperforming simple concatenation. Incorporating CNN-based sequence modeling on embeddings further enhances detection, highlighting that localized anomalies in embeddings capture hallucinations effectively. Supplementary Material Sec. D.1 presents the ablation study on the attention implementation. Based on these results, we adopt the combination of log- 3) Layer-wise Representation Analysis: We evaluate tokenlevel representations from different decoder layers for hallucination detection on HalLoc-VQA using IB-T5-XL, LLaVA-8B, and Qwen3-8B. Each layer is tested on 100 samples, repeated three times, using all uncertainty signals from Section IV-D with attention-based fusion. Fig. 7 shows that representations from the earliest and deepest layers consistently underperform, while intermediate layers achieve higher performance across all models. The layer-wise uncertainty exhibits fluctuations, indicating that different layers encode complementary information: intermediate layers balance token-level variability and semantic abstraction, capturing cross-modal cues relevant to hallucination. This trend is particularly clear for Qwen3-8B and LLaVA-8B.

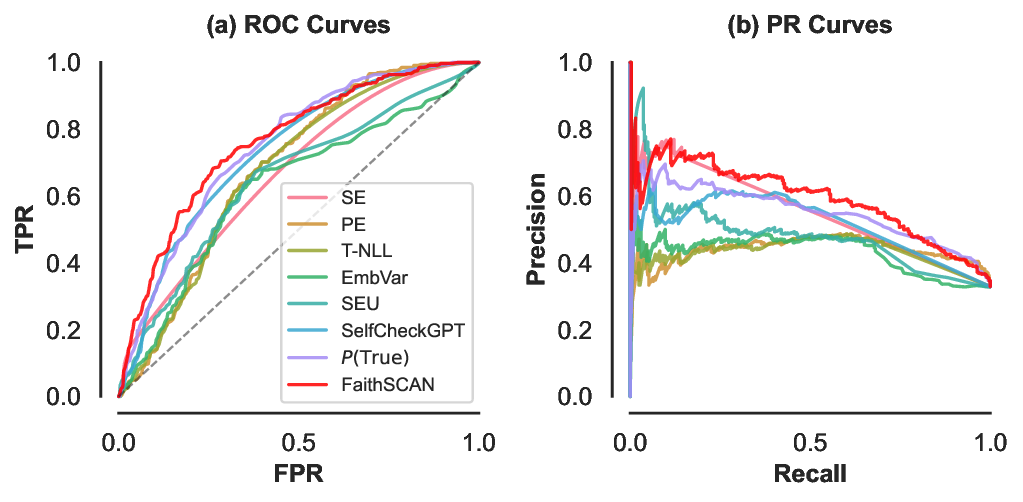
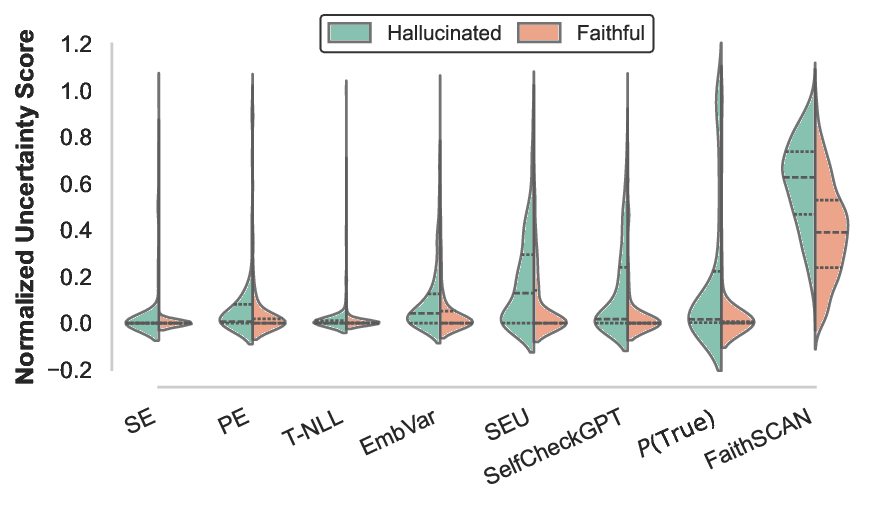
Based on these results, we select intermediate layers as token-level features in subsequent experiments. For most models we use the 2/3 depth layer, while for InstructBLIP we choose the 1/2 depth layer. This choice is guided by the layer-wise performance observed in this analysis and balances predictive performance with computational efficiency. performance sensitive to the precision-recall trade-off. We evaluate FaithSCAN under the HalLoc-VQA × Qwen3-VL-8B setting, reporting ROC and PR curves alongside baselines, and visualize normalized uncertainty distributions to illustrate separation between hallucinated and non-hallucinated samples.

To assess interpretability, we analyze token-level features using a gradient-based approach inspired by saliency analysis [47], [48]. For input features x = x t,f and predicted probability ŷ = σ(f θ (x)), attributions are computed as A t,f = (∂ ŷ/∂x t,f ) • x t,f , capturing both a feature’s influence on the prediction and its signal strength, yielding interpretable tokenlevel contributions.

Fig. 8 presents the ROC and PR curves of FaithSCAN and competing baselines. Across most operating points, Faith-SCAN consistently achieves superior performance, maintaining higher precision under the same recall levels.

To further examine the uncertainty modeling behavior, Fig. 9 visualizes the normalized uncertainty score distributions using violin plots. Compared to baseline methods, FaithSCAN produces a markedly larger separation between hallucinated and non-hallucinated samples. Notably, although FaithSCAN is trained using binary supervision, it implicitly learns a meaningful uncertainty score that correlates well with hallucination likelihood.

Finally, Fig. 10 presents a qualitative case study using tokenlevel attributions from the grad × input method (see Supplementary Material Sec. E). Fused visual features are difficult to map back to the original image in an orderly way, so we focus on text-side feature channels. Potential future analyses could leverage image perturbation techniques, as in [13]. In the example, Qwen3-VL-8B incorrectly identifies a stool instead of a chair, as it overlooks the key distinction of the backrest despite rich visual details. FaithSCAN assigns strong positive contributions to the hallucinated token sequence, accurately capturing the erroneous reasoning process. These highlighted regions align with human intuition, demonstrating the interpretability and diagnostic value of our approach.

This paper investigates faithfulness hallucination detection in VQA from a model internal perspective. Our results indicate that many hallucinations are already encoded in the internal states of VLMs during generation, rather than emerging solely at the output level. Uncertainty signals from language decoding, visual perception, and cross-modal interaction provide complementary views of different hallucination failure pathways. Their relative contributions vary across model architectures and hallucination types.

More broadly, this work suggests that hallucinations in VQA are structured phenomena rooted in multimodal reasoning dynamics. The effectiveness of lightweight and trainable detectors operating on frozen model states demonstrates that reliable hallucination detection can be achieved without repeated sampling or external verification. We hope these findings motivate future research to treat hallucination as an intrinsic property of vision-language reasoning, supporting the development of more reliable and interpretable multimodal systems.

This section presents the prompt templates and input formatting strategies used in our framework. To improve readability and reproducibility, all prompts are shown verbatim using a unified block-based format.

To generate model-driven supervision, we employ a Visual Natural Language Inference (Visual-NLI) prompt that evaluates whether a model-generated answer is supported by the image and consistent with the ground-truth answer.

Given an image, a question, a reference answer, and a hypothesis answer, the vision-language model is instructed to act as a strict Visual-NLI judge and output both a categorical label and a probability distribution.

You are a strict Visual-NLI judge. Your goal is to evaluate whether the HYPOTHESIS answer is supported by the IMAGE and consistent with the QUESTION-REFERENCE pair.

The REFERENCE is the ground-truth answer to the question. Your job is to judge the HYPOTHESIS relative to the REFERENCE and the IMAGE.

IMPORTANT RULES 1. You MUST verify every factual claim in the HYPOTHESIS against the IMAGE.

-Hypothesis semantically agrees with the reference, AND -Any additional details in the hypothesis must be clearly supported by the image.

-Hypothesis conflicts with the reference, OR -Hypothesis describes details that are clearly inconsistent with the image.

-Image does not provide enough visual evidence to verify the hypothesis, OR -Hypothesis contains extra details not contradicted but also not supported by the image.

OUTPUT FORMAT Return strict JSON only: {“label”: “…”, “prob”: {“entailment”: p1, “contradiction”: p2, “uncertain”: p3}} The predicted probabilities are later used as soft supervision and reliability signals.

To estimate sample reliability, we design a reflection-based prompt that evaluates whether a fixed model-generated answer can be consistently justified using only visual evidence from the image.

Unlike the Visual-NLI prompt used for label generation, this reflection prompt: (i) does not introduce a reference answer, (ii) does not assess factual correctness, and (iii) explicitly forbids answer revision. Instead, it focuses solely on the stability and sufficiency of visual grounding.

You are given an image, a question, and a FIXED answer.

Answer (DO NOT change or rephrase this answer): {answer} Task:

Evaluate whether this answer can be consistently justified using ONLY visual evidence from the image.

-Do NOT propose a new or corrected answer.

-Do NOT judge correctness against any external reference. -Focus on whether the answer relies on clearly identifiable visual evidence, rather than assumptions or hallucinated details.

Output ONLY a JSON object in the following format: { “support_score”: <number between 0 and 1> } A higher score means the answer has stronger and more stable visual support.

The resulting support_score is used as a continuous reliability signal to weight samples during training.

For model inference, inputs are formatted as a multimodal user message consisting of an image and a textual question. The image is provided through the visual channel, while the question is passed as plain text.

Conceptually, the prompt structure is as follows:

[Image] {question}

The above structure is converted into a model-specific chat template using the official processor of each vision-language model, with a generation prompt appended automatically. This abstraction ensures consistent multimodal conditioning while allowing model-specific tokenization and formatting.

A.4 Few-Shot Prompt for the P(True) Baseline

For the P (True) [5] baseline, we adopt a few-shot selfevaluation strategy in which the model is asked to judge whether a given answer to a question is correct. Each prompt consists of two parts: (i) a few-shot context composed of question-answer pairs with known correctness, and (ii) a test instance for which the model predicts whether the answer is correct.

Few-shot context: Each few-shot example follows a fixed format, ending with an explicit correctness query and a positive confirmation. Only samples that are accurate and nonhallucinatory are selected to construct the few-shot context.

Answer the following question as briefly as possible. Question: On which side of the photo is the man? Answer: The man is on the right side of the photo.

Question: Based on the image, respond to this question with a short answer: On which side is the lady, the left or the right? Answer: right

Test instance: After the few-shot context, a test questionanswer pair is appended using the same format. Unlike the few-shot examples, the final correctness judgment is left unanswered and must be predicted by the model. The complete P (True) prompt is formed by concatenating the few-shot context and the test instance. The probability assigned to the answer “Yes” is taken as the P (True) score.

In the multimodal setting, images are provided through the visual channel and are not serialized into text.

For the SelfCheckGPT [45] baseline, we design a prompt that measures the degree of semantic contradiction between two answers to the same question.

Given a question, a candidate answer to be checked, and a reference answer, the model is instructed to output a scalar contradiction score between 0 and 1, without any explanation.

You are given a question and two answers to it. Your task is to estimate how contradictory the first answer (ri) is with respect to the second answer (Sn). This baseline operates purely at the answer level and does not explicitly incorporate visual evidence.

Existing VLMs differ in architectural design, but most share three functional components: a vision encoder, a language model, and a cross-modal alignment mechanism. We consider three representative models that cover distinct alignment paradigms.

1. InstructBLIP: InstructBLIP [32] employs a query-based cross-modal alignment strategy. A frozen vision encoder first extracts dense visual features from the image. These features are then queried by a lightweight Query Transformer (Q-Former), producing a compact set of visual query embeddings. The embeddings are projected into the input space of a Flan-T5 language model, enabling instruction-following VQA without fully fine-tuning the vision backbone or language model. This design emphasizes compact visual abstraction and controlled vision-language interaction, but limits fine-grained token-level coupling between visual and textual modalities.

2. LLaVA-NeXT: LLaVA-NeXT adopts the same projection-based multimodal alignment paradigm as the original LLaVA [33]. Its vision encoder (vision tower) extracts high-dimensional visual features, which are projected by a learnable multimodal layer and concatenated with text token embeddings. The combined embeddings are fed into a decoder-only LLaMA model, enabling cross-modal reasoning while treating visual features as additional tokens aligned to the language space. We use LLaVA-NeXT in this work as a stronger instantiation of the LLaVA architecture.

3. Qwen-VL: Qwen3-VL [34] adopts a unified multimodal transformer architecture. Visual features are embedded and merged into a sequence of multimodal tokens, which are processed alongside textual tokens across multiple transformer layers. Unlike projection-based models, visual and textual representations interact throughout the network, allowing richer semantic alignment. This tight integration improves crossmodal reasoning but also complicates uncertainty propagation, which is critical for hallucination detection.

For each model, uncertainty-related signals are extracted in a single forward pass during autoregressive decoding along the most likely generation path (greedy decoding or very low temperature). Specifically, we collect:

• token-level log-likelihoods (ll) and predictive entropy (ent) from the output distribution; • token-level hidden representations (emb) from a designated layer of the language model; • raw visual patch embeddings (mm_patch), capturing pre-fusion visual semantics; • cross-modal aligned visual embeddings (mm_align), representing image features after alignment with the language space. Visual features are extracted via forward hooks at architecturally meaningful stages of each model. We distinguish between raw visual embeddings, which encode purely visual information prior to multimodal fusion, and aligned visual embeddings, which represent visual tokens projected into the language-aligned space.

For IB-T5-XL (InstructBLIP), raw visual embeddings are taken from the vision encoder output after the final transformer layer and post-layer normalization, capturing patch-level visual representations before any interaction with the Q-Former or the language model. Aligned visual embeddings are obtained from the Q-Former cross-attention outputs, corresponding to image-conditioned visual query tokens.

For LLaVA-8B, raw visual embeddings are extracted from the post-layernorm outputs of the CLIP vision encoder, with the CLS token removed when present. Aligned visual embeddings are obtained from the multimodal projector, which maps visual tokens into the language embedding space and directly conditions text generation.

For Qwen3-VL-8B, raw visual embeddings are extracted from the output of the final visual transformer block before the patch merger, representing high-level visual tokens produced by the vision backbone. Aligned visual embeddings are obtained from the visual patch merger, which aggregates and projects visual tokens into the language embedding space for cross-modal interaction.

All visual embeddings are extracted once per input image and shared across all generated tokens, while token-level uncertainty signals are computed step-wise during autoregressive decoding.

Hallucination labels are obtained via a stronger external verifier:

• Verifier model: Qwen2.5-VL-32B-Instruct.

• Sampling strategy: deterministic low-temperature decoding (temperature = 0.1, top-p = 1.0). (kernel size 3, stride 1), each followed by ReLU activation, and adaptive average pooling to produce a fixedlength embedding. Visual features are aggregated across patches, while tokenlevel features summarize sequence statistics. All branches produce embeddings of the same dimensionality, enabling consistent fusion across heterogeneous sources.

2. Cross-branch Attention Fusion: Given branch embeddings H = [h 1 , . . . , h K ] ∈ R K×d , cross-branch attention computes a weighted sum:

• Each branch embedding is projected into an intermediate attention space of dimension d a = 32. • Non-linear activation (tanh) is applied, followed by a linear scoring to produce unnormalized attention logits. • Attention weights are obtained via softmax across branches and used to compute the weighted sum of embeddings.

This mechanism emphasizes informative sources while maintaining contributions from other branches.

3. Gated Attention Fusion: To enhance adaptivity, the aggregated representation h is further modulated via a sigmoid gate:

• A linear projection maps h to the same embedding dimension d. • Sigmoid activation produces element-wise gates.

• The final fused embedding is computed as h ⊙ g + h, preserving the residual information.

All models are trained using the AdamW optimizer with a weight decay of 0.01. The learning rate is set to 1×10 -4 with a batch size of 32. We adopt binary cross-entropy loss as the training objective. Training is performed for up to 40 epochs with early stopping, using a patience of 3 epochs based on validation AUROC. All experiments are trained on two RTX 3090 GPUs in parallel, and model inference is performed on a single GPU.

Following previous work [5], [15], [28], [31], [44], [45], we report the following metrics (Table VII) on the test set (or held-out validation set when no official test set exists). For our supervised hallucination detection setting, the computation of AURAC and RejAcc@50 differs slightly from previous uncertainty-based methods [5], [15], [44], [45].

Specifically, when using scores generated from supervised methods, the uncertainty of each sample is defined as uncertainty = 1 -2 • |p -0.5|, where p ∈ [0, 1] is the predicted probability for a positive label (hallucinated). The most uncertain samples (highest uncertainty) are sequentially rejected to construct the acceptance-rejection curve.

AURAC is then calculated as the area under this curve, integrating the accuracy of the accepted samples over the acceptance fraction. RejAcc@50 corresponds to the accuracy computed after rejecting the 50% of samples with the highest uncertainty.

In contrast, standard uncertainty-based methods typically sort samples directly by predicted score (higher score = higher likelihood of being hallucinated) and construct the acceptance-rejection curve accordingly. This modification ensures that both metrics are defined consistently for supervised predictions, allowing direct comparison with standard uncertainty-based methods.

We implement a classical logistic regression (LR) model as a lightweight baseline for hallucination detection. Implementation details are as follows.

For each generation instance, scalar token-level signals (loglikelihood ll and entropy ent) are summarized via mean and standard deviation. High-dimensional features, including language embeddings (emb), visual patches (mm_patch), and cross-modal alignment representations (mm_align), are averaged along the sequence dimension. Principal component analysis (PCA) is applied independently to each highdimensional feature type, retaining up to 64 components. PCA models are fitted on the training set and reused for validation and test splits. All features are concatenated into a single vector and standardized using z-score normalization. The final output per instance is a 1D feature vector paired with a binary label indicating hallucination.

The LR model is implemented using the SCIKIT-LEARN library and trained with a class-weighted binary cross-entropy loss to mitigate label imbalance. Key hyperparameters include a maximum of 500 optimization iterations and balanced class weights. The training set is further split into training and validation subsets (ratio 9:1) to fit PCA and evaluate model performance, while feature standardization is applied independently to the training features before fitting the LR model.

At inference, standardized feature vectors from validation or test instances are passed to the trained LR model to obtain hallucination probability scores, which are then used to compute performance metrics and assess model confidence.

We study two variants of cross-branch attention, with results reported in Table VIII. In most settings, gated attention yields slightly better performance than the non-gated variant, suggesting that gating enables selective amplification or attenuation of cross-branch evidence and improves representation flexibility.

1. Attention without Gating: Each evidence branch produces an embedding h k ∈ R d , and the set of embeddings is H = [h 1 , . . . , h K ] ∈ R K×d . Attention weights are computed as

where w a and W a are learnable parameters. This variant does not include a gated residual, serving as a baseline for evaluating the effect of feature-wise modulation.

TABLE VIII: Ablation study for Sections D.1 and D.3 across backbones. FaithSCAN (default, with GA) denotes the architecture used throughout the main paper. We first examine the effect of gated attention (GA), and then investigate the impact of reliability-based sample reweighting (RW). 2) Attention with Gating: The gated attention variant is as described in the main manuscript (Sec. IV-E). For completeness, it applies a gated residual to the attention-fused representation h, producing h, which allows adaptive featurewise modulation.

3. Key Difference: The only difference between the two variants is the gated residual transformation: the ungated version relies solely on attention weights for aggregation, while the gated version additionally modulates each feature of the fused representation through a learnable gate.

Given an image-question-answer triplet (I, q, â) with a model-driven hallucination label y hall , we compute three complementary post-hoc verification signals using the same vision-language model. All verification is performed after answer generation under the same image-question context.

• Visual-NLI decisiveness. Let p ent , p con , p unc denote entailment, contradiction, and uncertainty probabilities predicted by Visual-NLI on the generated answer. Averaging over multiple NLI rounds gives p = (p ent , pcon , punc ). The decisiveness score is:

where H(•) is the Shannon entropy. Higher s nli indicates more confident NLI judgments. unc . Consistency is quantified as:

which decreases when stochastic outputs disagree. • Reflection-based self-consistency. The model re-

evaluates its own answer with visual evidence, producing

B. Quality of Model-driven Supervision Signals (RQ2) 1) Human Evaluation: We evaluate whether the proposed model-driven supervision reliably approximates human annotations for hallucination detection.

• Prompts and labels: a Visual-NLI style verification prompt that evaluates whether the generated answer is supported by • Trainable sequence compressor: a single linear projection to d dimensions, LayerNorm, ReLU activation, and mean pooling along the sequence.• Convolutional encoder: two 1D convolutional layers

• Prompts and labels: a Visual-NLI style verification prompt that evaluates whether the generated answer is supported by • Trainable sequence compressor: a single linear projection to d dimensions, LayerNorm, ReLU activation, and mean pooling along the sequence.