Introduction

beings constitute one of the most intelligent biological species on Earth. The human body functioning as a highly optimized distributed ecosystem composed of approximately 37.2 trillion specialized cells. These cells cooperate through organ systems such as the nervous, cardiovascular, respiratory, muscular and skeletal systems, each performing localized computations while contributing to global physiological stability. For example, the nervous system exemplifies distributed processing: the heart contains roughly 40000 neurons that regulate cardiac rhythm, the gut (the second brain) consists of nearly 500 million neurons responsible for autonomous digestive control, each retina contains over 100 million to process visual signals, and the spinal cord hosts millions of neurons that execute low-latency reflexive responses . This hierarchical yet decentralized biological architecture parallels modern computing paradigm called Distributed Computing Continuum Systems (DCCS) , integrates edge devices, intermediate fog nodes and cloud infrastructures into a unified computational fabric capable of allocating tasks based on latency, energy constraints and computational load. DCCS face significant operational challenges due to their heterogeneous and continuously evolving infrastructures. Nodes vary in computational capacity, storage, connectivity, and reliability, which demands orchestration mechanisms capable of adapting to fluctuating workloads, node mobility, and dynamic network conditions. Similar forms of fluctuation are intrinsic to the human body as well.

Considering these similarities, integrating biological models into DCCS offers a promising approach to addressing several of its core challenges, as discussed in . In this paper, we explore and simulate one such direction by mapping biological self-regulation processes to DCCS to enable self-healing behavior and strengthen system resilience. The human body provides a natural model for distributed self-regulation , as it can detect disruptions, isolate damaged regions, and restore function while maintaining overall stability. Processes such as wound healing, immune response, and distributed neuronal decision making coordinate sensing, feedback, and adaptation across heterogeneous components, demonstrating a scalable and decentralized form of resilience. Adopting these principles into DCCS architectures allows systems to contain failures rapidly, reconfigure affected nodes, and maintain service continuity under dynamic and uncertain conditions.

Biological Basis

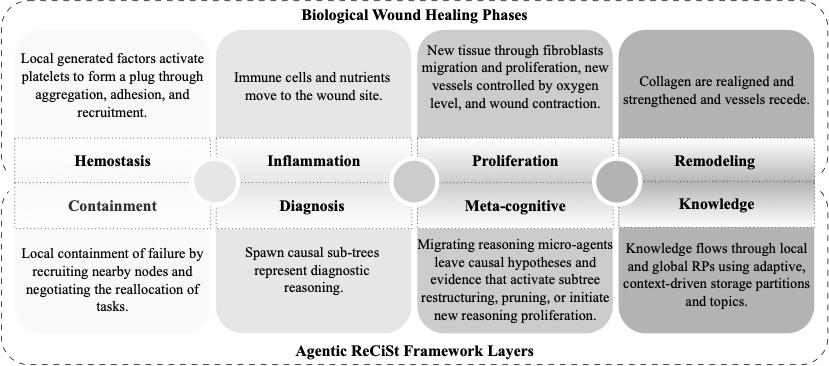
Biological wound healing is a multi-phase process that shows an intrinsic capacity to detect tissue damage, initiate targeted responses, and restore functional integrity without external intervention. To provide necessary biological context for computing-field readers, we outline four phases of wound healing  including Hemostasis, Inflammation, Proliferation, and Remodeling phases.

Hemostasis

is the initial phase of wound healing and constitutes the body’s immediate response to vascular injury. After tissue damage, local blood vessels undergo vasoconstriction to limit blood flow and reduce blood loss. Platelets are then activated by thrombin and exposed fibrillar collagen, a process supported by the collagen-associated amino acids proline and hydroxyproline. Activated platelets adhere to the collagen matrix and aggregate to form an initial platelet plug while releasing mediators such as fibrinogen, which promotes further aggregation. Additional mediators enhance adhesion to collagen and recruit more platelets to the injury site. Concurrently, endothelial cells produce prostacyclin to prevent excessive platelet accumulation. The platelet–fibrinogen complex is subsequently converted to fibrin, forming a stabilizing polymeric network. This fibrin mesh creates a hemostatic clot that seals the wound, prevents additional blood loss.

Inflammation

During the inflammatory phase, the body initiates a defense response to prevent infection and clear cellular debris. Vasodilation occurs, increasing blood flow to the wound site and facilitating the delivery of immune cells, oxygen, and essential nutrients. White blood cells migrate to the injured area to eliminate bacteria, pathogens, and damaged cells. Concurrently, various growth factors are released to stimulate tissue repair processes and recruit additional cells involved in healing.

Proliferation

phase focuses on healing and reconstruction of the damaged tissue. This phase is characterized by the replacement of the provisional fibrin matrix with a new extracellular matrix composed of collagen fibers, proteoglycans, and fibronectin, thereby reestablishing tissue integrity and functionality. A key event in this stage is angiogenesis, the formation of new capillaries to replace damaged vasculature and ensure adequate oxygen and nutrient supply to regenerating tissue. Fibroblasts, major effector cells of this phase, migrate into the wound site under the influence of factors released by platelets and macrophages. Their migration follows the alignment of fibrillar structures within the extracellular matrix and is facilitated by localized secretion of proteolytic enzymes. Once positioned in the wound, fibroblasts proliferate and synthesize matrix components such as fibronectin, hyaluronan, collagen, and proteoglycans, supporting new matrix construction and cellular ingrowth. Angiogenesis proceeds through oxygen-dependent regulation: hypoxia increases Hypoxia-Inducible Factor (HIF), which induces Vascular Endothelial Growth Factor (VEGF) for neovascularization, whereas reoxygenation degrades HIF and reduces VEGF. As vascularization improves, fibroblast proliferation decreases, epithelialization restores the epidermal barrier, and myofibroblasts contract the wound to reduce its size.

Remodeling/maturation

During the this phase of tissue repair, the newly formed tissue undergoes progressive strengthening, reorganization, and functional refinement. Collagen fibers are realigned and remodeled to enhance the tensile strength and elasticity of the regenerated tissue, contributing to the restoration of structural integrity. Concurrently, the vascular network that had proliferated during earlier stages of healing undergoes regression. As a result, the wound gradually loses its characteristic red or pink coloration, signifying the completion of tissue maturation.

Motivation

Motivated by these observations, we introduce ReCiSt, a bio-inspired agentic self-healing architecture for resilient DCCS. Fig. 1 illustrates the mapping of biological wound-healing phases to the self-healing layers in the ReCiSt framework. Hemostasis corresponds to the system’s immediate fault response, where isolation and mitigation are initiated; in ReCiSt, this function is performed by the Containment Layer, which negotiates rerouting of affected services to stable neighboring nodes to prevent cascading disruptions. The Inflammation Phase, reflecting the biological immune response, aligns with the Diagnosis Layer, where operational data are collected and analyzed to determine the fault’s nature and scope. In the Proliferation Phase, associated with new tissue and vessel formation, the Meta-Cognitive Layer enables micro-agent proliferation, dynamic reasoning, and the creation of new communication pathways through updated routing tables. Finally, the Remodeling Phase, where biological tissue strengthens, corresponds to the Knowledge Layer, which propagates knowledge across the distributed continuum system through coordinated local and global Rendezvous Points (RP).

style="width:99.0%" />

ReCiSt framework is designed to detect disruptions, diagnose their underlying causes, regulate its internal reasoning processes, and optimize its distributed knowledge structures to achieve consistent system performance under uncertain conditions. These capabilities are enabled by Language Models (LMs)-powered agents that execute localized containment, perform causal discovery, regulate internal reasoning through meta-cognitive mechanisms, and manage adaptive knowledge-sharing structures that reorganize in response to contextual drift. Achieving this level of adaptability requires agentic capabilities in each phase to enable systems to regulate their own reasoning processes and adjust internal decision-making structures as operational demands evolve .

Contributions

• We propose ReCiSt framework aims to provide an adaptive and agentic self-healing system that initiates defensive responses through reflexive local containment, and discovers causal dependencies inspired from human body’s self healing mechanism, i.e., wound healing.

• ReCiSt enables adaptive self-regulation of the agent’s internal reasoning via migratory micro-agents.

• ReCiSt supports knowledge sharing through local and global RPs using adaptive, context-driven storage.

• Our framework is designed to operate effectively across heterogeneous datasets that vary in scale, structure, failure characteristics, and operational context.

We implement a prototype of the ReCiSt framework and evaluate it on multiple public DCCS datasets using different LMs, showing effective self-healing with reduced recovery time, controlled agent resource overhead, and improved decision quality.

Related works

Resilience is becoming a key research focus in distributed infrastructures, especially within the communications community. Recent 6G roadmaps explicitly prioritize resilience as a core standardization target for future network architectures . Altaweel et al. propose an identity-based routing protocol for mission-critical fog and edge deployments in adaptive routing under dynamic network conditions. Similarly, Nakayama et al. develop a resilient architecture for multipath communication in mobile networks. In , a log-based fault tolerance for dynamic workloads has been explored through serverless runtime designs.

Notable contributions foreground resilience through data- and workload-oriented strategies that exploit machine learning (ML) for prediction and coordination. Sen et al. develop a resilient edge–cloud architecture that combines server failure prediction with optimized virtual machine (VM) migration and multi-hop routing to ensure seamless service continuity. Díaz et al. employ federated ML failure prediction together with optimization heuristics to select deployment configurations that improve fault tolerance in edge workloads, while Kashyap et al. focus on proactive resource allocation in dynamic fog environments by forecasting per-task resource demands and guiding task partitioning to mitigate node failures. Through these solutions are fault-tolerance, but extensive training data and learning cycles, limiting their responsiveness to immediate or unpredictable system changes.

Some other recent works underscores the difficulty of distinguishing faults from slowdowns under uncertain conditions. For example, proposes gossip-based communication with migrating agents as an effective decentralized detection mechanism. Subsequent frameworks introduce knowledge-driven and dynamically generated self-healing agents capable of prediction, diagnosis, and autonomous service redeployment . Additional advances automate the generation and evolutionary optimization of multi-agent workflows and develop structured context-management architecture that equip Large Language Model (LLM)-driven agents with memory as version-controlled file system for coherent distributed reasoning . Emerging self-learning paradigms further couple task generation, policy optimization, and reward evaluation into closed-loop processes that iteratively refine agent capabilities . LLM-driven multi-agent systems with specialized roles extend these capabilities by jointly analyzing traffic patterns, monitoring performance, and detecting suspicious activities to determine optimized mitigation strategies for adaptive network management .

In communication networks, agentic mechanisms employ intent-aware reasoning to support real-time resource allocation under fluctuating conditions . At the same time, diagnosis pipelines that integrate hierarchical reasoning, multi-pipeline, and fine-tuned smaller LLMs improve root-cause analysis and failure localization in cloud networks , while LLM-based, proactive fault-tolerance frameworks in edge networks orchestrate containment, diagnosis, and recovery tools to mitigate failures before services degrade . These research attempt to achieve fully autonomous and embedding self-improved agent mechanisms, yet not achieved desired solutions within resource limit environments.

Given our emphasis on bio-inspired strategies, we observed that existing research in this area remains relatively sparse. Fro example, demonstrates how biological mechanisms can help continuous network reorganization to maintain scalability and robustness in heterogeneous sensing environments. Similar inspiration in autonomic network-management by mapping molecular biology onto system- and device-level control processes , and enable hardware to evolve and repair itself in response to structural faults . Multi-agent, bio-inspired framework further shows how self-managing entities negotiate to restore performance during complex scheduling disruptions . Recent communication-network architectures integrate evolutionary, immune, and neural models to accelerate fault detection and repair , and biologically inspired machine-learning frameworks apply swarm and immune metaphors to achieve rapid, distributed recovery from failures . Active inference has been proposed as a resilience strategy for DCCS , rooted in bio-inspired models that emulate the human brain’s continuous reasoning and adaptation.

Most existing literature focus on efficient fault detection and autonomous recovery supported by AI- or ML-based decision mechanisms. However, these approaches are often constrained by their dependence on pretrained models, externally supplied decision policies, and large datasets, which limits their ability to handle previously unseen or evolving faults. Furthermore, their computational and data-intensive nature reduces practicality in distributed environments with heterogeneous resource capacities. Overcoming these limitations requires self-healing mechanisms that can reason about disruptions, adapt internal decision processes, and dynamically reorganize knowledge structures to sustain performance under uncertain conditions.

System Model and Problem formulation

A DCCS can be formally represented as a graph $`G = (\mathcal{N}, E)`$, where $`\mathcal{N} = \{N_1, N_2, \ldots, N_n \}`$ is the set of heterogeneous nodes (spanning IoT devices, edge, fog, and cloud resources) and $`E`$ is the set of communication links between them. Each node $`N_i`$ is described by its attributes $`(\mathcal{C}_i, \mathcal{M}_i, \mathcal{S}_i, \mathcal{V}_i)`$, where $`\mathcal{C}_i`$ denotes computational capacity (such as CPU/GPU cycles), $`\mathcal{M}_i`$ is the device storage status, the device condition such as down, available (space available to run more tasks), busy (resource occupied by tasks), and recovering represents $`\mathcal{S}_i\in \{00,11,01,10\}`$, and $`\mathcal{V}_i\in \{00,11,01,10\}`$ indicates corresponding to {low, medium, high, critical} vulnerability. Tasks $`\mathcal{T} = \{\tau_1, \tau_2, \ldots, \tau_m \}`$ arrive dynamically and need to be mapped to $`N_i`$ for execution. Assume that a node $`N_i`$ can compute one or more $`\mathcal{T}`$ depends on its $`(\mathcal{C}_i, \mathcal{M}_i, \mathcal{S}_i, \mathcal{V}_i)`$. The task allocation at time $`t`$ can be specified by an allocation function $`A(t): \mathcal{T} \rightarrow \mathcal{N},\ A(t, \tau_j) = N_i`$, such that $`A(t, \tau_j) = N_i`$ assigns task $`\tau_j`$ to node $`N_i`$ if $`\mathcal{S}_i = \{10\}`$ along with $`c_j\leq C_i`$ and $`m_j \leq M_i`$. Each communication link between node $`N_i`$ and $`N_j`$ is $`e_{ij} \in E`$ has a bandwidth $`b_{ij} \geq \delta`$, where $`\delta`$ is bandwidth threshold. The end-to-end latency of task $`\tau_j`$ under allocation function $`\mathcal{A}`$ is defined as $`l_j (A) \leftarrow l_j^{net} (A) + l_j^{com}(A)`$, where $`l_j^{net} (A)`$ is network latency and $`l_j^{com}(A)`$ is computational latency. The overall latency of the system is $`\mathcal{L}(A) = \frac{1}{m}\sum_{j=1}^{m} l_j(A)`$.

Failures in the DCCS are captured through failure scenarios $`\omega`$, where $`F_\omega(t)\subseteq\mathcal{N}`$ denotes the set of nodes that become unavailable at time $`t`$. When a node $`N_i \in F_\omega(t)`$, its operational state transitions to $`\mathcal{S}_i(t)=\text{down}`$, which disrupts all tasks currently assigned to it (i.e., those satisfying $`A(t,\tau_j)=N_i`$). Once the self-healing process is initiated, the node enters a recovering state, $`\mathcal{S}_i(t^+)=\text{recovering}`$, and the system executes a healing procedure that detects the failure, isolates the affected tasks, and reallocates them to surviving nodes whose operational states and resources allow execution. This produces an updated allocation defined as $`A_\omega(t^+) = \text{Heal}\!\left(A(t),F_\omega(t)\right)`$. For each task $`\tau_j`$ under scenario $`\omega`$, we define the completion indicator $`I_j(A,\omega)=\{0~or~1\}`$, where 1 if $`\tau_j`$ successfully completes under $`A_\omega(t^+)`$, 0 otherwise, and compute the resilience of the allocation strategy as

\begin{equation}
    \label{eq:resilience}
    \mathcal{R}(A)=
    \mathbb{E}_\omega \left[
        \frac{1}{m}\sum_{j=1}^{m} I_j(A,\omega)
    \right],
\end{equation}

which quantifies the expected fraction of tasks that the system can successfully complete despite node failures, state transitions (down $`\rightarrow`$ recovering), and the associated self-healing operations. Resource utilization is defined by jointly considering CPU and memory usage as

\begin{equation}
    \mathcal{U}(A) =
    \alpha
    \frac{\sum_{i\in\mathcal{N}} \text{cpu\_load}(N_i)}{\sum_{i\in\mathcal{N}} \mathcal{C}_i}
    +
    (1-\alpha)
    \frac{\sum_{i\in\mathcal{N}} \text{mem\_load}(N_i)}{\sum_{i\in\mathcal{N}} \mathcal{M}_i},
    \label{eq:utilization}
\end{equation}

where $`0 < \alpha \leq 1`$ controls the relative importance of compute and memory utilization. The DCCS controller aims to determine an allocation strategy that jointly optimizes latency, resource utilization, and resilience. The resulting multi-objective optimization problem is formulated as

\begin{align}
    &\min_{A}\ \mathcal{L}(A), 
    \qquad
    \max_{A}\ \mathcal{U}(A), 
    \qquad
    \max_{A}\ \mathcal{R}(A),
    \label{eq:objective}
\end{align}\vspace{-0.6cm}
\begin{flalign*}
\text{subject to:} &&
\end{flalign*}\vspace{-0.8cm}
\begin{align}
    &\sum_{\tau_j \in \mathcal{T}: A(t,\tau_j)=N_i} c_j 
      \le \mathcal{C}_i,
    \qquad \forall N_i \in \mathcal{N},
    \label{eq:objective:a} \\
    &\sum_{\tau_j \in \mathcal{T}: A(t,\tau_j)=N_i} m_j 
      \le \mathcal{M}_i,
    \qquad \forall N_i \in \mathcal{N},
    \label{eq:objective:b} \\
    &\mathcal{S}_{A(t,\tau_j)} = \text{available},
    \qquad \forall \tau_j \in \mathcal{T},
    \label{eq:objective:c} \\
    &\mathcal{V}_{A(t,\tau_j)} \in \{\text{low}, \text{medium}\}
    \quad \text{for critical tasks } \tau_j,
    \label{eq:objective:d} \\
    &b_{ij} \ge \delta 
        \qquad \forall e_{ij} \in E,
    \label{eq:objective:e} \\
    &A(t,\tau_j) \in \mathcal{N},
    \qquad \forall \tau_j \in \mathcal{T}.
    \label{eq:objective:f}
\end{align}

The ReCiSt Framework

As described in the motivation, the ReCiSt framework operates through a self-healing pipeline comprising the Containment, Diagnosis, Meta-cognitive, and Knowledge layers, shown in Fig. 2.

Containment Layer

This Layer functions as the initial defense and immediate response to make sure uninterrupted services in the ReCiSt framework (top-left of Fig. 2 and Algorithm.[Layer1]). The system must accurately determine when system deviates from its healthy operational behavior. Due to the heterogeneity of devices, their diverse logging formats , and inconsistent sensing capabilities across the continuum, ReCiSt uses LM-driven monitoring agents $`\alpha=\{\alpha_1,\alpha_2,\ldots\}`$ to perform continuous system state monitoring. Each agent $`\alpha_\imath`$ maintains updated information regarding the operational state $`\mathcal{S}_i`$, vulnerability level $`\mathcal{V}_i`$, and active task set $`\mathcal{T}_i`$ of all nodes within its $`k`$-neighborhood $`\mathcal{N}_\imath^{(k)}`$. Fault identification begins when $`\alpha_\imath`$ periodically broadcasts a lightweight control signal to every node $`N_i \in \mathcal{N}_\imath^{(k)}`$. Each node must acknowledge this probe within a predefined interval $`\Delta t`$ by reporting its instantaneous state $`\mathcal{S}_i(t)`$ and a minimal heartbeat vector summarizing its current operational load. If a node fails to respond within $`\Delta t`$, meaning no acknowledgment is received from $`N_i`$ during the probe window, agent $`\alpha_\imath`$ classifies this as an abnormal deviation from expected behavior and triggers. It is important to note that at this stage the system does not yet know the exact cause or type of failure. The detected deviation merely indicates that the node has departed from its nominal operating conditions. All such nodes are preliminarily marked as faulty by the Containment Layer, it is included in a failure set denoted by $`F(t)=\{\,N_i \mid \text{Containment Layer flagged } N_i \text{ at time } t\,\}.`$

When a node $`N_i`$ is detected when its state becomes $`\mathcal{S}_i(t)=00`$ for any value of $`\mathcal{V}_i`$, which triggers the node’s internal Neural Reflex System to broadcast a localized containment request to its $`k_N`$ nearest candidate nodes, represented as the set $`k_N=\{N_j \mid N_j \text{ receives a reflex request from agent} \}`$. Each node $`N_j \in k_N`$ responds by reporting its $`\mathcal{C}_j`$ and $`\mathcal{M}_j`$, along with $`\mathcal{S}_j(t)=\{11\}`$. The Containment Layer request these responses to identify neighbors suitable for redistributing the task set $`\mathcal{T}_i`$ that was previously running on $`N_i`$. A suitability condition is satisfied when all responding neighbors report $`\mathcal{S}_j(t)=11`$ for every $`N_j`$, after which node $`N_i`$ transitions to an available coordination state $`\mathcal{S}_i(t^+)=10`$. If the computational capacity and memory of any single neighbor, denoted $`\mathcal{C}_j`$ and $`\mathcal{M}_j`$, are insufficient for executing the full task set $`\mathcal{T}_i`$, meaning $`\mathcal{C}_j < \mathcal{C}_i`$ of $`\mathcal{T}_i`$ or $`\tau_x\forall x\leq |\mathcal{T}_i|`$ and $`\mathcal{M}_j < \mathcal{M}_i`$ of $`\mathcal{T}_i`$ or $`\tau_y\forall y\leq |\mathcal{T}_i|`$, then the Containment Layer identifies a subset of $`p`$ nodes from the $`k_N`$ candidates to cooperatively distribute and execute the workload of $`\mathcal{T}_i`$ or $`\tau_x`$. Through this process, they cooperate to establish a dynamic plug structure that enables the formation of temporary routing rules. The main agent analyzes task dependencies and redistributes the $`N_i`$ computational workload across the $`N_j`$ to reduce the risk of cascading failures. The identified failed nodes are transmitted to subsequent layers for further analysis and cure.

Diagnosis Layer

Once the Containment Layer signals an abnormal deviation, the system transitions into the Diagnosis Layer (bottom-left of Fig. 2), which corresponds to the inflammation stage in biological wound healing. In human physiology, inflammation functions as the initial analytical response, wherein leukocytes migrate to the wound site, identify the nature of the damage, and classify its severity before any tissue repair begins. Analogously, in the ReCiSt framework, the Diagnosis Layer determines the underlying cause, scope, and structural characteristics of the deviated nodes identified in the Containment Layer. At this stage, the system performs structured causal examination to produce a precise, machine-interpretable representation of the failure.

For each $`N_i\in F(t)`$, the Diagnosis Layer retrieves the corresponding system, network, custom logs, etc., generated during the interval $`[t-\Delta_d,t]`$, where $`\Delta_d`$ is the diagnosis window size. Let $`\mathcal{L}_i`$ denote the aggregated log structure for node $`N_i`$: $`\{\mathcal{L}_i=\mathcal{L}_i^{sys}\cup \mathcal{L}_i^{net}\cup \mathcal{L}_i^{cust} \cup ... \}`$ with each component capturing distinct operational dimensions.

The Diagnosis Layer transforms raw log entries into a structured set of observable entities. Each entity corresponds to an event, performance metric, internal state transition, or resource indicator associated with the failure. These entities are instantiated as nodes within a diagnosis variable set $`\mathcal{X}_i=\{x_{i1},x_{i2},\ldots,x_{im}\},`$ which forms the foundation of a graph-based representation of the fault. Each $`x_{ij}\in\mathcal{X}_i`$ is a symbolic or numeric descriptor derived from $`\mathcal{L}_i`$, such as CPU anomalies, memory spikes, link degradation indicators, task stalls, or error codes. Next, this layer infer causal dependencies among elements of $`\mathcal{X}_i`$. These dependencies define how one internal change leads to another, forming a causal structure that characterizes the faults or abnormal operations. For every ordered pair $`(x_{ia},x_{ib}) \forall a, b \in m`$, the system evaluates whether a causal relationship exists. A causal relation is encoded as:

\begin{equation}
    x_{ia}\rightarrow x_{ib}\quad \text{iff}\quad \Phi(x_{ia},x_{ib})=1,
\end{equation}

where $`\Phi(\cdot)`$ is an LM-driven relation-identification function that integrates temporal precedence, log semantics, and learned causal priors. All these causal relations identified for $`N_i`$ form a directed edge set:

\begin{equation}
    \mathcal{E}_i=\{\, (x_{ia},x_{ib}) \mid \Phi(x_{ia},x_{ib})=1 \,\}.
\end{equation}

The pair $`(\mathcal{X}_i,\mathcal{E}_i)`$ therefore constructs a directed graph $`G_i^{diag}`$:

\begin{equation}
\label{eq:causalGraph}
    G_i^{diag} = (\mathcal{X}_i,\mathcal{E}_i),
\end{equation}

which represents the fine-grained causal structure underlying the observed malfunction.

To enhance robustness, the Diagnosis Layer employs an ensemble of parallel reasoning sub-trees. Each sub-tree corresponds to a specialized causal reasoning pathway trained to capture a specific dependency type, such as resource overload, network instability, task-level contention, thermal anomalies, or firmware events. Let the ensemble be represented by $`\Psi_i=\{\psi_i^{(1)},\psi_i^{(2)},\ldots,\psi_i^{(q)}\}`$, where $`\psi_i^{(k)}`$ is the $`k`$-th sub-tree applied to node $`N_i`$. Each $`\psi_i^{(k)}`$ extracts a localized causal subgraph $`T_i^{(k)}`$ from $`G_i^{diag}`$:

\begin{equation}
    T_i^{(k)}=(\mathcal{X}_i^{(k)},\mathcal{E}_i^{(k)}), \quad \text{with}\ \mathcal{X}_i^{(k)}\subseteq\mathcal{X}_i,\ \mathcal{E}_i^{(k)}\subseteq\mathcal{E}_i.
\end{equation}

The union of all such sub-trees forms the consolidated diagnosis structure,

\begin{equation}
    \bar{G}_i^{diag}=\bigcup_{k=1}^{q}T_i^{(k)},
\end{equation}

which encodes multilevel, multi-causal interpretations of the failure. This consolidated graph is stored in the node’s diagnosis memory and later transmitted to the Meta-cognitive Layer for reasoning-path restructuring and micro-agent generation. By now, each fault node $`N_i`$ or link is represented not merely as an isolated malfunction but as a structured causal system that explains why the perceived deviation occurred.

Meta-Cognitive Layer

Following the diagnostic phase, the system enters the Meta-Cognitive Layer (middle of Fig. 2), which corresponds to the proliferation stage in biological wound healing. In human tissue, proliferation involves fibroblast activity, extracellular matrix deposition, and angiogenesis that collectively restore structural support and reestablish functional connectivity around the wound site. In the ReCiSt framework, the Meta-Cognitive Layer plays an analogous role at the cognitive level: it reorganizes and extends the causal structures derived from the Diagnostic Layer, manages the generation and regulation of reasoning micro-agents, and refines explanatory pathways so that the system can progress from a raw fault description to a set of coherent and operationally useful hypotheses. The procedural flow of this layer is depicted in Algorithm [Layer3].

This Layer refine Eq.([eq:causalGraph]) into a set of viable explanatory and corrective pathways. To accomplish this, the main-agent associated with $`N_i`$ spawns a population of reasoning micro-agents as shown in Eq. [eq:microAgent],

\begin{equation}
\label{eq:microAgent}
    \mathcal{A}_i^{micro}=\{a_i^{(1)},a_i^{(2)},\ldots,a_i^{(r)}\},
\end{equation}

where $`r`$ is determined adaptively based on the complexity of the causal graph. Each micro-agent $`a_i^{(k)}`$ traverses a path using Depth-first search (DFS) within $`\bar{G}_i^{diag}`$, seeking to construct a causal explanation of the fault. A path is defined as an ordered sequence of diagnostic variables:

\begin{equation}
    p^{(k)} = (x_{i\ell_1},x_{i\ell_2},\ldots,x_{i\ell_\eta}), \quad \text{with } (x_{i\ell_j},x_{i\ell_{j+1}})\in\mathcal{E}_i,
\end{equation}

where $`\eta`$ is the depth explored by the micro-agent. For each path $`p^{(k)}`$, the micro-agent produces a structured hypothesis

\begin{equation}
    H_i^{(k)} = \Lambda(p^{(k)},\mathcal{L}_i),
\end{equation}

where $`\Lambda(\cdot)`$ is an LM-driven operator that integrates the path structure with supporting evidence extracted from the logs $`\mathcal{L}_i`$. Each hypothesis $`H_i^{(k)}`$ is assigned a meta-cognitive evaluation score computed through Eq. [eq:Score]

\begin{equation}
\label{eq:Score}
    \Gamma(H_i^{(k)}) = w_1 C_{coh}(H_i^{(k)}) + w_2 C_{safe}(H_i^{(k)}) + w_3 C_{util}(H_i^{(k)}),
\end{equation}

where $`C_{coh}`$ measures causal coherence, $`C_{safe}`$ quantifies safety of the inferred solution, $`C_{util}`$ reflects operational feasibility, and $`(w_1,w_2,w_3)`$ are normalization weights.

The core adaptive mechanism of the Meta-Cognitive Layer is the regulation of micro-agent proliferation, guided by the feedback produced by $`\Gamma(H_i^{(k)})`$. Analogous to fibroblasts proliferating more rapidly when matrix integrity is low, the system increases the population of micro-agents when current hypotheses exhibit low confidence or poor safety. Formally, proliferation is triggered when $`\Gamma(H_i^{(k)}) < \theta_{pro}`$, where $`\theta_{pro}`$ is the proliferation threshold. When triggered, the set $`\mathcal{A}_i^{micro}`$ is expanded, and new exploratory paths are generated by inserting auxiliary nodes or diverting traversal directions in $`\bar{G}_i^{diag}`$. This parallels biological angiogenesis, where new vessels extend into damaged regions to restore connectivity; here, new inferential edges are added to enhance the diversity and depth of cognitive exploration.

Conversely, when hypotheses exhibit high confidence and safety, the system inhibits further proliferation by enforcing the condition $`\Gamma(H_i^{(k)}) \geq \theta_{inh}`$, which suppresses additional micro-agent generation. This feedback-driven balance between activation and inhibition stabilizes the reasoning ecosystem and prevents unnecessary expansion of computational effort. As micro-agents accumulate evidence and refine hypotheses, the causal graph $`\bar{G}_i^{diag}`$ undergoes structural reorganization. Let $`\Delta\mathcal{X}_i^{(k)}`$ and $`\Delta\mathcal{E}_i^{(k)}`$ denote modifications induced by hypothesis $`H_i^{(k)}`$. The updated cognitive structure becomes Eq. [eq:NewCogStructure],

\begin{equation}
\label{eq:NewCogStructure}
    \bar{G}_i^{meta} = \left(\mathcal{X}_i \cup \bigcup_{k}\Delta\mathcal{X}_i^{(k)},\, \mathcal{E}_i \cup \bigcup_{k}\Delta\mathcal{E}_i^{(k)}\right).
\end{equation}

Eq. [eq:NewCogStructure] is directly analogous to the biological formation of new provisional tissue that strengthens the wound region. Once $`\bar{G}_i^{meta}`$ reaches a stable configuration, the Meta-Cognitive Layer identifies an optimal hypothesis:

\begin{equation}
    H_i^{*} = \arg\max_{k} \Gamma(H_i^{(k)}),
\end{equation}

which serves as the definitive causal explanation and preliminary corrective strategy for node $`N_i`$. This output is then propagated to the Knowledge Layer, which corresponds to the remodeling stage in wound healing and is responsible for global system realignment, routing updates, and reintegration of the recovered node.

Knowledge Layer

After the Meta-Cognitive Layer selects an optimal hypothesis $`H_i^{*}`$ for a failed node $`N_i`$, the system enters the Knowledge Layer (right of Fig. 2), which mirrors the remodeling phase in biological wound healing. In physiology, remodeling strengthens the extracellular matrix, reorganizes tissue fibers, and integrates the repaired region back into the larger functional structure. Analogously, the Knowledge Layer consolidates, restructures, and disseminates the refined causal and corrective knowledge produced during recovery, thereby supporting stable long-term adaptation within the DCCS. The operational workflow of this layer is detailed in Algorithm [Layer4].

The Knowledge Layer is organized around a collection of local and global RPs, which function as adaptive coordination and storage nodes for distributed agents. Each RP maintains a structured knowledge base composed of topic-oriented segments. A topic corresponds to a failure class, and its associated representations include the causal explanations, hypotheses, and corrective strategies derived from the Meta-Cognitive Layer. For a given RP, let the set of stored topics be denoted $`\mathcal{Z}^{RP} = \{Z_1, Z_2, \ldots, Z_u\}`$, where each topic $`Z_j`$ contains multiple partitions, each representing a unique or semantically distinct reasoning outcome: $`Z_j = \{P_j^{(1)}, P_j^{(2)}, \ldots, P_j^{(m_j)}\}`$.

When a new knowledge package $`\mathcal{K}_i^{meta}`$ arrives from the Meta-Cognitive Layer, its topic descriptor is first extracted and encoded into an embedding representation $`\mathbf{e}_{topic} = \phi_{topic}(z_i)`$, where $`z_i`$ is the textual or symbolic topic label associated with $`\mathcal{K}_i^{meta}`$ and $`\phi_{topic}(\cdot)`$ is the embedding model for topic encoding. Each stored topic $`Z_j`$ also has a representative embedding $`\mathbf{e}_{Z_j}`$. The semantic proximity between the new topic and an existing topic is computed using

\begin{equation}
    M_T(z_i, Z_j) = \text{STS}\bigl(\mathbf{e}_{topic}, \mathbf{e}_{Z_j}\bigr),
\end{equation}

where $`STS`$ denotes a semantic textual similarity operator. If the maximum similarity across all stored topics satisfies Eq. [eq:similarityIndex]

\begin{equation}
\label{eq:similarityIndex}
    \max_{j} M_T(z_i, Z_j) < \theta_{topic},
\end{equation}

with $`\theta_{topic}`$ as the topic-matching threshold, a new topic $`Z_{u+1}`$ is created and appended to $`\mathcal{Z}^{RP} \leftarrow \mathcal{Z}^{RP} \cup \{Z_{u+1}= \{P_{u+1}^{(1)}\}\}`$. Otherwise, the new knowledge instance is associated with the closest matching topic $`Z_{j^*}`$, where $`j^{*} = \arg\max_{j} M_T(z_i, Z_j)`$.

Within the selected topic $`Z_{j^*}`$, the system next evaluates whether the reason or explanation associated with $`H_i^{*}`$ matches an existing partition. Its embedding is obtained as $`\mathbf{e}_{reason} = \phi_{reason}(H_i^{*})`$, and its similarity to each stored reason embedding $`\mathbf{e}_{P_{j^*}^{(k)}}`$ is computed as $`M_R = \text{STS}\bigl(\mathbf{e}_{reason}, \mathbf{e}_{P_{j^*}^{(k)}}\bigr)`$. If the maximum similarity satisfies $`\max_{k} M_R < \theta_{reason}`$, the Knowledge Layer creates a new partition $`P_{j^*}^{(m_{j^*}+1)}`$ within the topic $`Z_{j^*}`$. Otherwise, the knowledge instance reinforces the existing partition with which it best aligns, so no structural growth occurs.

As topics and partitions evolve, this layer performs adaptive reorganization to ensure coherence and reduce redundancy. When two partitions within a topic exhibit high mutual similarity, i.e.,

\begin{equation}
    \text{STS}\left(\mathbf{e}_{P_{j^*}^{(k_1)}}, \mathbf{e}_{P_{j^*}^{(k_2)}}\right) \ge \theta_{merge},
\end{equation}

they are merged into a unified representation. Conversely, if a partition exhibits significant internal semantic drift, quantified by a deviation metric $`\text{DIV}(\cdot)`$ exceeding a divergence threshold, the partition is split into multiple sub-partitions using Eq. [eq:subPartition].

\begin{equation}
\label{eq:subPartition}
    \text{DIV}\bigl(P_{j^*}^{(k)}\bigr) > \theta_{split}.
\end{equation}

To maintain global system consistency, each local RP periodically synchronizes its topics and partitions with global RPs through

\begin{equation}
    \mathcal{Z}^{RP}_{global} \leftarrow \text{MERGE}\bigl(\mathcal{Z}^{RP}_{global}, \mathcal{Z}^{RP}_{local}\bigr),
\end{equation}

where conflicts are resolved using similarity-based merging rules and versioning metadata. Through these topic- and partition-level reorganizations, this layer incrementally strengthens the ReCiSt framework. This process mirrors the remodeling phase of wound healing, during which tissue is reorganized, strengthened, and integrated into surrounding structures. The resulting knowledge topology enables scalable coordination among distributed agents, supports robust context-aware decision making, and maintains long-term resilience within the DCCS.

ReCiSt’s Computational efficiency

Although the ReCiSt framework incorporates LM- and agent-driven operations whose runtimes depend on model size, inference hardware, and system load, the algorithmic structure can still be analyzed through asymptotic complexity. Each LM invocation or prompt-driven reasoning step is treated as an oracle operation with amortized constant cost $`O(1)`$, since its latency does not scale with the size of the DCCS. Under this assumption, the Containment Layer (Algorithm [Layer1]) performs two dominant operations: neighbor-status probing over the adjacency set $`\mathcal{N}_i`$ of size $`d_i`$, which requires $`O(d_i)`$ time, and computation of the $`k`$-nearest neighbors $`\mathcal{N}_i^{(k)}`$, which requires $`O(d_i \log k)`$ due to distance evaluation and heap-based top-$`k`$ selection. Thus, the Containment Layer incurs $`O(d_i \log k)`$ time per monitored node. The Diagnostic Layer (Algorithm [Layer2]) parses the log file $`\mathcal{L}_i`$ of size $`L_i`$ for each failed node $`N_i`$ and constructs a diagnostic graph with $`m_i`$ extracted variables, leading to a pairwise causal evaluation cost of $`O(m_i^2)`$; its total complexity is therefore $`O(L_i + m_i^2)`$. The Meta-Cognitive Layer (Algorithm [Layer3]) generates $`r_i`$ reasoning micro-agents and explores $`p_i`$ diagnostic paths extracted from the subtrees $`\Psi_i`$. Since LM reasoning steps are treated as oracle operations, the complexity reduces to $`O(p_i + r_i)`$. The Knowledge Layer (Algorithm [Layer4]) compares each topic embedding against $`u`$ stored topics in $`\mathcal{Z}^{RP}`$ and then evaluates the reason embedding against the $`m_j`$ partitions of the selected topic $`Z_j`$, resulting in $`O(u + m_j)`$ time for each knowledge update. The overall self-healing cost for a failed node $`N_i`$ is $`O(d_i \log k + L_i + m_i^2 + p_i + r_i + u + m_j)`$, reflecting the structural complexity of the ReCiSt pipeline independent of LM inference overhead.

Performance Evaluations

This section presents the experimental evaluation of the proposed ReCiSt framework. It first describes the experimental setup and performance metrics, followed by discussion of numerical results for each dataset.

Setup

The ReCiSt framework is implemented in Google Colab using an Intel(R) Xeon(R) CPU to represent the cloud computing environment. The LMs evaluated for ReCiSt are deployed in the cloud and accessed via the OpenAI API. The experimental setup includes geographically $`k`$ distributed agents among $`n`$ computing computing nodes. We assume that each agent $`i`$ ping its K-NN and subsequently initiates log acquisition from nodes that fail to respond within a specified time frame, using baseboard management controllers. Details about the computing machine, network and communications configurations are discussed along with datasets.

Models

All agents employed in the experimental evaluation were implemented using LangChain 1.0.8 . The memory module was developed as a custom repository type constructed with Pydantic . For embedding generation, we utilized the text-embedding-3-small model, a small embedding model developed by OpenAI . To estimate semantic similarity, we adopted all-MiniLM-L6-v2, a sentence-transformer model  specifically designed for semantic textual similarity tasks, enabling the computation of meaningful similarity scores between textual inputs. For our evaluation, we employ a reasoning model suited to the computational resources of the distributed computing continuum. This setting demands models capable of advanced, multi-step reasoning and capable to operate efficiently on heterogeneous and constrained computing environments. To meet these requirements, we rely on various OpenAI models , including o4-mini-2025-04-16, the latest small model in the o-series, which offers strong reasoning capabilities with low latency. The gpt-5-mini-2025-08-07 model provides fast performance and high reasoning abilities. The gpt-5-nano-2025-08-07 serves as the most fast option. The gpt-5.1-2025-11-13 model for agentic tasks.

Performance Metrics

The self-healing process of ReCiSt framework mainly depend on its agents (within four layers) and their accurate and timely decision making process. So, our evaluation metrics reflect around the effectiveness of agent operations . In particular, the time required for self-healing, depth of analysis to avoid uncertainties, amount of micro-agents invoked during self-healing and the computational overhead for failure diagnosis, negotiation, solution discovery, and solution storage. Our evaluations further analyzed quality of agent decisions under failure conditions. This includes the rates of successful, supporting, and harmful responses, as well as the structural complexity induced by agent reasoning. These metrics are defined as follows.
Time Taken for Self-Healing: This metric measures the elapsed time from failure detection to successful recovery completing all four stages of ReCiSt pipeline.
CPU Consumption of the Agent: This metric quantifies the CPU usage by an agent while performing fault diagnosis, negotiation with other agents, and self-healing process.
Sub-tree Depth Complexity: This metric show how deep the agent is started analyzing the fault.
Micro-Agent Invocations: This metric shows the number of micro-agent calls, representing the coordination and communication overhead required for each recovery process.
Quality of Decision-making: This metrics shows the decision-making of each mic-agent in the form of acceptance, rejection, harmful or best categories defined as Accepted Rate: The ratio of supporting responses that provide constructive and actionable guidance to the total number of responses. *Harmful Rate:*The ratio of responses that may degrade key performance indicators, such as CPU utilization, latency, or memory consumption, and negatively affect system behavior to the total number of responses. Rejected Rate: The ratio of responses lacking sufficient evidence or justification to the total number of responses. Best Rate: The ratio of responses that demonstrate strong evidentiary support, clear causal reasoning, and compliance with operational safety principles to the total number of responses. Reasoning Depth Rate(RDR): The ratio of system-level micro-agent invocations to the total number of instantiated micro-agents.

Results and Analysis

In this section, we evaluate performance and analyze numerical results on various datasets i.e., Cloud Stateless Dataset   from IEEE DataPort and Loghub . The Loghub collection includes different categories of logs from systems such as ZooKeeper, Hadoop, OpenSSH and Blue Gene/L supercomputer. The subsequent sections are organized by providing dataset-wise performance evaluations and discussions. At the end, we summarize the quality of decision-making metric for all five categories of datasets.

Cloud Stateless Dataset

The Cloud Stateless System dataset consists of measurements collected at 5-second intervals from three cloud-based Linux virtual machines configured with 1vCPU, 1GB of memory, and a 10GB disk, all operating under a dynamically varying workload. Each record contains a timestamp alongside resource utilization and performance metrics collected through Prometheus, including cpu_usage and memory_usage (percentage utilization), bandwidth_inbound and bandwidth_outbound (throughput in GB/s or MB/s), tps (requests per second), response_time (latency in seconds or milliseconds), and status (system status, 0 for healthy and 1 for unhealthy). Collectively, these variables offer a comprehensive temporal representation of device load, network activity, service throughput, and operational responsiveness. The failures are characterized by elevated response times and irregular bandwidth consumption, arising from network-related bottlenecks that manifest through congestion and latency spikes. These unhealthy intervals reflect performance constraints driven by fluctuations in data flow and fluctuating workload conditions, with increased CPU load appearing in some instances.

Fig. [fig:healingtimee] shows the time taken for self-healing across multiple failure instances along the dataset timeline for four models. It is noteworthy that all models successfully able to achieve self-healing, but different times. Our analysis noted that o4-mini model achieves the lowest self-recovery times, typically remaining below 300 sec ($`\approx`$5 min). Similarly, gpt-5.1 demonstrates low recovery times, often under 400 sec ($`\approx`$6–7 min), with several instances showing rapid recovery of as little as 43 sec. In contrast, gpt-5-nano’ recovery times were ranged from $`\approx`$250 sec ($`\approx`$4 min) to over 1,200 sec ($`\approx`$20 min). The gpt-5-mini model shows higher recovery times, frequently exceeding 700–800 sec ($`\approx`$12–13 min), indicating slower self-healing. Fig. [fig:CPUusage5] depicted the CPU utilization of different models across multiple failure instances at failure time mentioned in dataset. We noted that CPU utilization remains generally stable across all models while running ReCiSt agents. Numerically, gpt-5-mini remains around $`\approx`$13%, o4-mini operates in a similar $`\approx`$13% range, gpt-5.1 averages around $`\approx`$15%, and gpt-5-nano close to $`\approx`$14%, indicating controlled computational overhead..

Fig. [fig:microagentcalls1] and Fig. [fig:microagentcalls2] shows in the number of paths in DFS and the number of micro-agents used for self-healing. Form Fig. [fig:microagentcalls1], we observe gpt-5.1 was the most structural complexity, which consistently generated larger sub-trees ranging from 6 to 25 paths. Nevertheless, both gpt-5.1 and o4-mini resolved failures without traversing the entire search space. This pattern highlights a strong capacity for selective path elimination and early solution detection despite an initially expansive reasoning structure. In comparison, gpt-5-nano explored sub-trees spanning $`\approx`$4 to 16 paths, with 4 to 25 micro-agent calls. Fig. [fig:microagentcalls2], it is clear that the gpt-5-mini showed moderate structural complexity, generating 6 to 12 paths with 7 to 15 micro-agent calls, while o4-mini balances reasoning depth and computational overhead with 5 to 12 paths and 5 to 12 calls.

Zookeper Dataset

ZooKeeper is a centralized service that supports configuration management, naming, distributed synchronization, and group services. The log data were collected from a laboratory deployment consisting of 32 machines. Within this environment, the observed failures appeared as interrupted or broken connections. Fig. [fig:zootime] depicted the self-healing time across two failure instances along the ZooKeeper dataset timeline for four models. It shows that gpt-5.1 achieves the lowest self-recovery times, typically ranging between 30 and 80 seconds. Also, o4-mini demonstrates slightly higher then gpt-5.1 recovery times i.e., 80-280 seconds. In contrast, gpt-5-mini shows higher recovery times, exceeding 1200 seconds, reflecting deeper but slower recovery behavior. Fig. [fig:zoocpu] illustrates the CPU utilization of different models across two failure instances at the failure times reported in the ZooKeeper dataset. We observe the CPU utilization remains stable across all models. For example, gpt-5-mini results $`\approx`$13%, o4-mini operate nearly 14% range, gpt-5.1 averages $`\approx`$13%, and gpt-5-nano close to 11%, indicating controlled computational overhead. From Fig. [fig:zoosub], gpt-5.1 and gpt-5-nano exhibit similar structural complexity, with sub-trees ranging from 8 to 9 paths, whereas o4-mini shows a more compact structure. From Fig. [fig:zoocall], we further see that gpt-5-mini incurs higher structural complexity, generating 8 to 17 paths with $`\approx`$10-23 micro-agent calls, while o4-mini maintains lower reasoning depth and computational overhead with 4 to 7 paths and about 1 call. gpt-5-nano also demonstrates low overhead, requiring 2-4 micro-agent calls, highlighting efficient reasoning under Zookeper dataset.

Hadoop Dataset

Hadoop is a big data processing framework. In Loghub, the Hadoop log data were from a five-node cluster operating under fault-injection scenarios, including machine outages, network disconnections, and disk full events, and their results shown in Fig. 5.

From, Fig. [fig:Hadoophealingtimee] we notice the self-healing time observed across five failure instances over the Hadoop dataset timeline for the four evaluated models. The plots show that gpt-5.1 reach comparatively low recovery times, frequently remaining below 100 seconds. Also, o4-mini demonstrates fast recovery behavior, with healing times largely confined to a narrow range of approximately 60–130 seconds. In contrast, gpt-5-nano self-healing times ranging between 200 and 500 seconds, which is slightly higher than gpt-5.1 and o4-mini. Finally the gpt-5-mini result slowest among all spanning from 200 seconds to values exceeding up to 1,000 seconds. CPU utilization of Hadoop datasets and their failures are depicted in Fig. [fig:haddopCPUusage5]. The CPU usage in Hadoop dataset remains well controlled across all models. Numerically, gpt-5-nano and gpt-5-mini both exhibit average utilization of CPU is $`\approx`$14%, while gpt-5.1 and o4-mini operate at marginally higher i.e., around 15%. From Fig. [fig:hadooptreedepth], we observe notable differences in failure complexity across the evaluated models. For example, gpt-5-mini shows the highest structural complexity, with sub-trees comprising $`\approx`$14–20 paths. In contrast, o4-mini maintains simpler structures, typically limited to about 5–10 paths. From Fig. [fig:hadoopmicroagentcalls2], we noticed clear variation in micro-agent invocation patterns. For instance, o4-mini relies on only 1–2 micro-agent calls across the five observed failure instances. gpt-5-nano requires between 1 and 6 micro-agent calls. By comparison, gpt-5.1 invokes a larger number of micro-agent calls, reaching up to 35 in one case, suggesting an intensive reasoning process. Even though there were many ups and downs, all four models were successful in reaching a self-healing state on Hadoop dataset within ReCiSt framework.

OpenSSH Dataset

OpenSSH is a widely used tool for secure remote access based on the SSH protocol. The corresponding OpenSSH dataset contains log records related to authentication-related events and general system activities. In this dataset, possible failures are associated with broken or unsuccessful authentication attempts, including SSH authentication failures arising from brute-force attacks or mistaken login attempts. These failures and time taken to self-healing are depicted in Fig. [fig:SSHhealingtimee]. From this, we noticed that gpt-5.1 is the fastest self-recovery agent, typically ranging between 27 and 42 seconds. Other side, o4-mini also demonstrates faster recovery gpt-5-nano and gpt-5-mini in the range of $`\approx`$87–107 seconds. But, gpt-5-nano and gpt-5-mini show lower recovery times, exceeding 300-800 seconds. In terms of CPU utilization as shown in Fig. [fig:SSHCPUusage5] gpt-5.1 incurs the highest CPU utilization at approximately 15%, followed by o4-mini at around 14%. Alternately, both gpt-5-nano and gpt-5-mini maintain lower utilization levels, close to 13%. In terms of analysis depth and number of micro-agent calls as depicted in Fig. [fig:SSHtreedepth] and Fig. [fig:SSHmicroagentcalls2], respectively, gpt-5-mini shows the most complex structures, with sub-trees spanning $`\approx`$13–16 paths and requiring about 5–17 micro-agent calls. In contrast, o4-mini, gpt-5-nano, and gpt-5.1 demonstrate simpler recovery structures, typically involving $`\approx`$2–15 paths and only 1–2 micro-agent calls.

Blue Gene/L (BGL) Dataset

The Blue Gene/L (BGL) dataset is an open log collection from a supercomputing system comprising 131,072 processors and 32768 GB of memory. It contains alert messages reflecting diverse system failures, including fatal I/O errors, hardware and operating system faults, kernel-level failures, communication outages, machine-check interrupts, kernel panics, and CPU or cache-related hardware faults. Fig. [fig:bglhealingtimee] depicts the self-healing time across nine failure instances along the BGL dataset timeline for the evaluated models. It shows gpt-5.1 and o4-mini are the fastest self-recovery agents, taking below 250 seconds for gpt-5.1 and under 150 seconds for o4-mini. In contrast, gpt-5-nano and gpt-5-mini demonstrate slower recovery, with healing times exceeding 500 seconds and 1,200 seconds, respectively. The CPU usage of BGL data is plotted using Fig. [fig:bglCPUusage5] showing nine failure instances at the reported failure times in the BGL dataset. This confirms that gpt-5.1 and o4-mini incur slightly higher CPU utilization, $`\approx`$11%, whereas gpt-5-nano and gpt-5-mini operate at lower utilization levels, close to 9%. From Fig. [fig:bglmicroagentcalls1] and Fig. [fig:bglmicroagentcalls], gpt-5-mini and gpt-5.1 exhibit more complex diagnosis structures, with sub-trees spanning approximately 3–15 paths and requiring between 1 and 22 micro-agent calls. In contrast, o4-mini and gpt-5-nano demonstrate simpler diagnosis structures, typically involving approximately 2–7 DFS paths and 1–8 micro-agent calls.

Quality of Agent Decisions

We also evaluate the micro-agents’ decision during the reasoning process to quantify their decision-making quality. In this process, we noted for each failure case, the rate of constructive guidance responses, the rate of responses with the potential to degrade key performance indicators and negatively affect system behavior, the rate of responses exhibiting inadequate evidentiary support, and the rate of responses demonstrating strong evidence. These evaluation further clarify causal reasoning, and adherence to operational safety principles. Further, we correlate these measurements in relation to the reasoning-depth ratio, defined as the proportion of system-level micro-agent invocations based on sub-trees depth. A summary of these results shown in Table. [tab:rate].

From Table. [tab:rate], the Cloud Stateless dataset achieve supportive response in gpt-5-mini, reflected in its high acceptance rate $`\approx`$95% with a full reasoning depth rate of 100%. This superior performance in deep and consistent reasoning achieved although an higher harmful response rate of 31.8% is noted. In contrast, gpt-5 nano shows high rejection rate $`\approx`$24% and a heavy reliance on extended micro-agent-level reasoning chains $`\approx`$98%, which does not translate into improved response quality $`\approx`$7%. We confirm that the results indicate in this dataset are having deeper reasoning traces alone are insufficient for ensuring high-quality or safe outputs. Moreover, o4-mini demonstrates low rate of harmful outputs across several failures $`\approx`$5%, alongside a high reasoning depth rate 9% and high rate of the best solutions $`\approx`$53%, shows better-calibrated internal reasoning. Similarly, for the ZooKeeper and OpenSSH datasets, there is no rejected and harmful responses resulted by all four models. Also, gpt-5-nano, gpt-5.1, and o4-mini achieving a best response rate of 100%. However, this performance is obtained with relatively low reasoning depth (e.g., 27.9% for gpt-5-nano and 15% for o4-mini). This clearly show that effective recovery can be achieved without deep reasoning when fault patterns are simple. In more complex environments such as BGL and Hadoop, variability becomes more significant. For example, in BGL, gpt-5-mini balances a high accepted response rate $`\approx`$78.1% with substantial reasoning depth $`\approx`$63.9% and a harmful rate of 11%. These outcomes confirm the effectiveness of feedback-driven, meta-cognitive control in balancing response quality, safety, and computational effort across diverse domains.

Conclusion

This paper proposed ReCiSt, a bio-inspired agentic self-healing framework that mapped biological wound-healing phases into autonomous containment, diagnosis, meta-cognitive reasoning, and knowledge remodeling layers to enhance resilience in DCCS. The proposed approach was implemented and tested using LM-powered agents and evaluated with multiple LMs, including gpt-5.1, gpt-5-mini, gpt-5-nano, and o4-mini, across public and heterogeneous datasets, specifically the Cloud Stateless system dataset and LogHub datasets including ZooKeeper, Hadoop, OpenSSH, and BGL. These datasets captured diverse failure types ranging from network disruptions and authentication faults to large-scale supercomputing errors. Overall, models such as gpt-5.1 and o4-mini exhibited the fastest recovery, achieving self-healing within tens of seconds, while maintaining CPU utilization below 10%. Even though there were many ups and downs, all the models were confirming its suitability for resilient and heterogeneous computing environments. Primary limitation of our work is in a controlled experimental environment using offline log datasets and cloud-based execution. Real-time factors such as live network congestion, hardware heterogeneity, mobility, security constraints, and long-running operational drift were not explicitly exercised in the current setup. In the future, our framework will be deployed and validated in real-world continuum environments and assess its robustness under live workloads and evolving failure conditions.