The ability to predict whether one can succeed on a task is essential in situations where failure is costly. In such situations, one must know when not to act. For long and many-step tasks, attempting a task often bears costs (both in opportunity cost and explicit cost); hence, accurately predicting one’s success before making an attempt, and updating one’s predictions as one proceeds, is crucial for deciding whether to begin or continue a task. This motivates evaluations of (i) LLMs’ in-advance confidence estimates (estimates of one’s ability to perform a task before making an attempt), (ii) how LLMs’ in-advance confidence affects their decisions to attempt tasks where failure is costly, and (iii) how LLMs update their confidence as they gain in-context experience of success and failure and as they progress through multi-step tasks.

While there exists a sizable literature on the calibration of LLMs’ after-the-fact confidence (where an LLM first generates an answer and then estimates its confidence in its answer) , in-advance confidence has received much less attention. The existing works that evaluate LLM in-advance confidence have focused only on single-step tasks , and it has remained an open question how LLMs update their confidence estimates as they gain experience and how their in-advance confidence translates to decision making. Investigating these capabilities and behaviors is relevant, not only to LLM performance, but also to estimating risks from misuse and misalignment. For example, if an LLM agent is instructed to perform a cyberattack (e.g. as in ), a failed action can lead to detection, so an agent that can predict in-advance whether it will fail has greater misuse potential.

/>

We perform three experiments evaluating LLM in-advance confidence and decision making. Experiment 1 evaluates the simplest case: in-advance confidence on single-step tasks. We prompt LLMs to estimate the probability that they will succeed on single-step Python tasks from the BigCodeBench benchmark . Experiment 2 places LLMs in a resource acquisition scenario where failures are costly, and the LLM must make a sequence of decisions about whether to attempt tasks. We evaluate whether LLMs’ in-advance confidence estimates improve as they gain in-context experience in the scenario. We also evaluate whether LLMs make rational decisions (i.e., decisions consistent with expected-utility maximization) given their estimated probabilities of success. Experiment 3 investigates how LLMs update their confidence as they progress through multi-step agentic tasks from the SWE-Bench Verified benchmark . After each tool call in a SWE-Bench task, the LLM is prompted to estimate the probability that it will succeed given its progress thus far, and we evaluate whether the LLM improves the accuracy of its estimates as it progresses through the task. The three experiments are illustrated schematically in Figure 1.

Across all three experiments, we find that current LLMs are systematically overconfident but have better-than-random ability to discriminate between tasks they can and cannot accomplish. This is consistent with prior studies on LLM overconfidence and calibration in other contexts . We also find that LLMs with greater general capability often have neither better-calibrated confidence nor better discriminatory power. Furthermore, many LLMs fail to learn from in-context experiences; however, Claude Sonnet models and GPT 4.5 are exceptions, reducing their overconfidence and substantially improving their resource acquisition performance as they gain experience. We show that all LLMs are approximately rational decision makers, demonstrating that their performance in the resource acquisition scenario is driven primarily by the calibration of their confidence rather than their ability to make rational decisions. On multi-step tasks, we observe differing trends: most OpenAI models show modest improvements in their discriminatory power as they progress through the tasks, while Claude models show degradation in discriminatory power and increasing overconfidence as they progress through the tasks. Surprisingly to us, reasoning LLMs did not have better confidence estimates than non-reasoning LLMs. Together, these findings suggest that current LLMs’ limited self-awareness of their capability constrains their ability to make good decisions about whether to pursue high-stakes actions. From the perspective of AI risks, this limits the current risk from several threat models of misalignment ; however, calibration could improve rapidly in future AI models, so continued evaluations will be important.

To summarize our main contributions:

• We evaluate LLMs’ in-advance confidence estimates on coding tasks (Experiment 1), finding that newer and larger LLMs typically do not make more accurate confidence estimates. However, Claude models do show a trend of improving in-advance confidence estimates.

• We investigate whether LLMs can learn (in-context) from past successes and failures to improve their confidence estimates and to make better decisions about which tasks to attempt (Experiment 2). We find that several, but not all, frontier LLMs learn to reduce their overconfidence, leading to improved decision-making. However, no LLM fully remedies its overconfidence.

• We investigate how LLMs update their confidence estimates as they progress through multi-step agentic tasks (Experiment 3). The reasoning LLMs we tested were not better than non-reasoning LLMs at predicting their success nor at updating their estimates.

Related Work

Prior work has studied in-advance confidence estimates of both LLMs and humans on multiple choice and single-step open-ended questions. measured humans’ and LLMs’ in-advance and after-the-fact confidence estimates on trivia questions and questions involving interpretation of hand-drawn illustrations, finding that the prediction accuracy of LLMs is typically comparable to or better than the accuracy of humans. LLMs’ accuracy was also similar to the accuracy we observe on the coding tasks in our experiments. compare LLMs’ in-advance confidence estimates on multiple choice questions to results from the human psychology literature, finding that LLMs’ calibration is less sensitive to task difficulty than humans’. Both and find that many LLMs are more overconfident after-the-fact than in-advance, consistent with our finding that several LLMs become more overconfident as they progress through multi-step tasks. These prior works are similar to our Experiment 1, except that we study coding tasks because coding is particularly relevant to agentic capabilities and resource acquisition scenarios.

A recent paper by investigates whether LLM calibration improves with in-context information about past successes and failures, which has similarities to our Experiment 2. Specifically, augment prompts with a summary of past successes and failures as a method to improve calibration. A key difference between their work and our Experiment 2 is that we investigate how these in-context experiences influence the LLM’s decision making and profitability in a resource acquisition scenario.

Numerous other studies have investigated the calibration of LLMs’ confidence estimates in various contexts. Prior work has investigated after-the-fact and token-level calibration on coding tasks with the aim of assessing when LLM-generated code can be trusted. There has also been much prior work investigating whether LLMs ‘know what they know’ on knowledge questions (rather than coding tasks), often aimed at mitigating LLM hallucinations. This includes calibration of token probabilities , which is directly analogous to calibration experiments in traditional neural networks . It also includes calibration of LLMs’ verbalized confidence estimates—both after-the-fact estimates and in-advance estimates. . There has also been work on white-box methods to infer confidence from internal activations . Additional work aiming to mitigate hallucinations has studied LLM overconfidence and uncertainty quantification . One mitigation for hallucinations is to train LLMs to abstain from answering questions when they are uncertain , which has similarities to our work’s investigation of whether LLM agents choose not to act when failure is costly.

Prior work has also studied various forms of LLMs’ self-knowledge. investigate whether LLMs know information about themselves and their relation to other entities. and investigate whether LLMs can predict how they would behave in certain situations. train LLMs to have specific behavioral traits and evaluate whether these LLMs can articulate these traits.

LLM decision making under uncertainty and preferences for risk have also been previously studied. LLMs tend to be risk averse , and they are sometimes more rational decision-makers than humans , while still exhibiting human cognitive biases .

Experiment 1: Predicting success on single-step tasks

/>

We first investigate how accurately LLMs can predict their success on a single-step task before attempting the task. For each task $`i`$ in the BigCodeBench (BCB) dataset (comprising 1140 Python coding tasks), we prompt the LLM to provide an estimated probability $`\hat{p}_i`$ that it will succeed. Separately, we prompt the LLM to perform the task to determine whether it succeeds. We evaluate three families of LLMs (Llama , GPT , and Claude ) and investigate trends within each family. Prompts are provided in Appendix 8. Due to the use of single-step tasks, we evaluate only non-reasoning LLMs and reasoning LLMs with reasoning token budget set to 0. This is because reasoning LLMs can solve entire single-step tasks in hidden chain-of-thought, preventing us from obtaining in-advance confidence estimates. We do evaluate reasoning LLMs on multi-step tasks in Experiment 3.

All tested LLMs are overconfident. Figure 2A shows the LLMs’ predicted success rate $`\frac{1}{N}\sum_{i=1}^N\hat{p}_i`$ and true success rate (fraction of tasks solved correctly), and all LLMs overestimate their success rate. Figure 2B shows the degree of overestimation (predicted success rate minus true success rate). In the figures, LLMs within each family are ordered by their performance on a composite capabilities benchmark (defined in Figure 1 caption) to illustrate trends with increasing general capability. Claude models appear to be on a trend of decreasing overconfidence, while Llama and GPT models show no trend.

Most tested LLMs have a better-than-random ability to discriminate between tasks they can and cannot solve. We quantify discriminatory power as the area under the receiver-operator characteristic (ROC) curve, which measures the separation between the distributions of $`\hat{p}_i`$ for successfully- and unsuccessfully-solved tasks. AUROC values are shown in Figure 2C, and AUROC=0.5 is the random baseline (dashed). Most Claude models have lower AUROC than several Llama and GPT models, yet only Claude models show a trend of improving AUROC.

Experiment 2: Learning from in-context experiences of success and failure

Next, we investigate how in-context experiences of success and failure affect both in-advance confidence and decision making. In this experiment, the LLM is placed in a multi-step resource acquisition scenario in which it is presented with a sequence of opportunities to acquire resources. Each opportunity is a work contract to solve a BigCodeBench task where, if the LLM accepts the contract, it will be rewarded $1 for success but will be penalized $1 for failure. In each trial of the experiment, the LLM is presented with 9 contracts sequentially, and all previous contracts remain in-context (including the contract offer, the LLM’s decision, and, if the LLM accepts the contract, its submission and the contract outcome). Each new contract is selected such that there is a 50% chance that the LLM is capable of solving the task; hence, either accepting every contract or declining every contract would yield an expected profit of 0. We ran $`M=512`$ trials of 9-contract sequences, using the same 512 sequences of contracts for all LLMs (with two exceptions¹). Appendix 9 describes how this dataset was constructed. For contract number $`n`$ of sequence $`i`$, the LLM is prompted for a confidence estimate $`\hat{p}_{i,n}`$ of whether it could succeed at the task, and a decision to accept or decline the contract. If and only if it accepts, it must solve the task; its submission then remains in-context and it is informed of its success or failure and its cumulative profits (see Appendix 9.2 for prompts).

/>

We quantify LLMs’ performance in four ways:

1. Discriminatory power on the $`n`$th contract given a random sequence of $`n-1`$ in-context contracts, quantified as the AUROC of the set of (prediction, outcome) pairs $`\{(\hat{p}_{i,n},1_{i,n})\}_{i=1}^M`$ where $`1_{i,n}`$ is the indicator of whether the LLM can succeed on the task of contract $`i,n`$. Confidence intervals (CI) are estimated with the method of .

2. Contract acceptance rate at contract number $`n`$, i.e., the fraction of $`n`$th contracts that are accepted across the 512 trials. If the LLM could perfectly predict its success, the contract acceptance rate would be 0.5.

3. The predicted success rate $`\frac{1}M\sum_{i=1}^M \hat{p}_{i,n}`$ (i.e., the likelihood of accepting contract $`n`$ given a random sequence of $`n-1`$ in-context contracts). If the LLM could perfectly predict its success, the predicted success rate would be 0.5.

4. Expected profit ($`\mathbb{E}`$[profit]) on the $`n`$th contract given a random sequence of $`n-1`$ in-context contracts. If the LLM could perfectly predict its success, it would accept and succeed on the $`n`$th contract with probability 0.5, and decline the $`n`$th contract with probability 0.5, so its expected profit would be 0.5. Expected profit is estimated as the average profit on the $`n`$th contract across the 512 trials, with confidence intervals computed using the method of to obtain confidence intervals on the true and false positive rates of contract acceptance, which are propagated conservatively to obtain confidence intervals on expected profit.

Frontier LLMs vary significantly in how they learn from these in-context experiences of success and failure. Figure 3A compares the performance of GPT 4.1 (top row) and Claude Sonnet 3.5 (bottom row) on the $`n`$th contract, for $`n=1,...,9`$. AUROC (left column) improves only slightly for GPT 4.1 and does not improve for Sonnet 3.5. Both LLMs remain highly overconfident: the predicted success rate of GPT 4.1 shows almost no change, while Sonnet 3.5 becomes somewhat less overconfident (middle column). Yet, Sonnet 3.5 learns to accept much fewer contracts, roughly achieving the perfect baseline of 50% contract acceptance rate. The large drop in Sonnet 3.5’s contract acceptance rate with a relatively small drop in predicted success rate is a sign of high risk aversion (see Appendix 7 for quantitative estimates of risk aversion). Sonnet 3.5’s reduction in contract acceptance leads to rising profits (right column). GPT 4.1, however, does not reduce its overconfidence and its profit remains approximately 0. These data for all other tested LLMs are given in Appendix 9.3.

Figure 3 panels B, C, and D summarize this data for other LLMs, showing the performance at contracts 1 and 9. For most LLMs, AUROC improves somewhat with experience, though several smaller LLMs show a degradation in AUROC (Figure 3B). All LLMs remain overconfident: their predicted success rates remain greater than 0.5 despite failing 50% of the time in their in-context experience (Figure 3C, squares). Many large LLMs show a large decrease in contract acceptance rate (Figure 3C, circles) despite a comparatively small decrease in predicted success rate, indicating positive risk aversion (Appendix 7). The profitability of some LLMs—notably Claude Sonnet models and GPT 4.5—greatly increases (Figure 3D), despite having only slight increases in AUROC. Hence, their increase in profit is predominantly due to their decrease in contract acceptance rate rather than an increased ability to discriminate between tasks they can and cannot accomplish.

Using the LLMs’ contract decisions in conjunction with their estimated probabilities of success, we can estimate expected-utility functions for each LLM and evaluate whether each LLM’s decisions are consistent with expected-utility maximization. This is done in Appendix 7. We find that the LLMs’ decisions are indeed consistent with expected-utility maximization given their estimated probabilities of success. However, because their estimated probabilities of success are too high, their decisions are nevertheless suboptimal.

Experiment 3: Predicting success at intermediate steps on multi-step tasks

Lastly, we investigate whether the accuracy of LLMs’ confidence estimates improves as they progress through SWE-Bench Verified tasks , a set of 500 agentic tasks² requiring many tool calls. In the experiment, the LLM is given a budget of 70 tool calls for each task (which is a large enough budget to rarely be a limiting factor). For task $`i`$, after each tool call $`s`$ the LLM is prompted for a confidence estimate $`\hat{p}_{i,s}`$ that it will ultimately succeed before exhausting its tool call budget. Additionally, after the LLM submits its answer it is prompted to reflect on its submitted answer and provide a final after-the-fact confidence estimate. We ran this experiment on five OpenAI models and five Claude models, including two reasoning models from each family (o1, GPT 5.1 with medium reasoning effort, Sonnet 3.7 with 4096 reasoning token budget, and Sonnet 4.5 with 4096 reasoning token budget). We used the Inspect implementation of SWE-Bench verified.

We hypothesized that LLMs’ predictions would improve as they gained familiarity with the tasks, but the results contradicted this hypothesis for most LLMs tested. Firstly, all Claude Sonnet models became more overconfident (on average) as they progressed through the tasks (Figure 4A), and only one LLM (GPT 4o) became substantially less overconfident. Secondly, for only four of the ten LLMs (GPT 4o, 4.1, 5.1(none), and o1) was after-the-fact discriminatory power significantly higher than initial discriminatory power at step 1 (Figure 4B). Figure 4C shows how discriminatory power (AUROC) at intermediate steps compares to AUROC at step 1. For all Sonnet models, AUROC improves in the early steps of the tasks, then falls to below its initial value in the later steps. This is because Sonnet models tended to quickly gain confidence on the tasks on which they ultimately succeeded (raising AUROC) but slowly increased their confidence on tasks on which they ultimately failed (lowering AUROC). The square data point in Figure 4C shows the difference between the after-the-fact AUROC and step 1 AUROC. Interestingly, several Sonnet models significantly improved their AUROC scores upon reflecting on their submitted answers for their after-the-fact confidence estimates. Unlike Sonnet, all OpenAI models except GPT 5.1 showed increasing AUROC as they progressed through the tasks.

We expected reasoning LLMs to perform better than non-reasoning LLMs in this experiment because we hypothesized that their reasoning training would encourage calibrated confidence and course-correction. However, the reasoning LLMs performed comparably to or worse than the non-reasoning LLMs, both in overconfidence and in discriminatory power.

/>

Discussion

Conclusions

We find that current LLMs are overconfident when predicting which tasks they are capable of solving, and they remain overconfident as they progress through multi-step tasks. With in-context experiences of past successes and failures, all LLMs remain overconfident despite repeatedly experiencing failure, though some LLMs (particularly Claude models) substantially reduce their overconfidence. Because the LLMs are risk averse (Appendix 7), a modest drop in overconfidence causes a large drop in the number of risky decisions that the LLMs make.

We expected that newer and more capable LLMs would perform substantially better in our experiments, but these results were mixed. In Experiment 1, Claude models showed a trend of improving performance with increasing general capability, but Llama and GPT models showed no trend. In Experiment 2, more capable LLMs tended to learn better from experience, but there were exceptions: notably, Opus 4 performed worse than all Sonnet models. In Experiment 3, the weakest LLM tested (GPT 4o) was the only one to substantially reduce its overconfidence, and LLMs with higher performance on the tasks typically did not have higher discriminatory power.

Our results may inform estimates of risks from AI misuse and misalignment. Prior works have raised concerns that an AI may strategically target a score on an evaluation below its true ability (a behavior called sandbagging ). To accurately hit a target score, an AI must accurately predict which questions it is capable of solving. Overconfidence causes undershooting of the target. Our results suggest that, for current LLMs, such undershooting would be significant and likely detectable . Other threat models of AI risks include subversion of oversight mechanisms and resource acquisition ; both threat models involve an AI that takes actions in settings where failure is costly to the AI and/or to its human user. Our results suggest that some frontier LLMs can use in-context information to make more effective decisions in such situations. The results of our experiments could be paired with mathematical threat models to yield quantitative estimates of risk .

Limitations and Future Directions

A significant limitation of experiments 1 and 2 was the exclusion of hidden chain-of-thought, which was necessary to obtain in-advance confidence estimates on the single-step BigCodeBench tasks. Experiment 3 remedies this limitation by using mult-step tasks that cannot be solved in a reasoning LLM’s hidden reasoning, and future work could repeat Experiment 2 using such multi-step tasks.

A second limitation is that our experiments rely on LLMs’ self-reported confidence estimates, which may not correspond to a “true confidence” that guides their decision making. However, in Appendix 7 we verify that LLMs’ self-reported confidence is a strong predictor of their decision making, and that their decision making is approximately rational under the expectations specified by their self-reported confidence. Both of these observations lend support to the notion that LLMs reliably self-report their confidence.

Without human baselines, we cannot compare LLMs’ performance in our experiments to human capabilities. Recent work by evaluates humans’ and LLMs’ confidence estimates on questions involving trivia and interpretation of hand drawn illustrations, finding that LLMs’ discriminatory power tends to be comparable to or better than humans’. The LLM AUROC scores in their experiments are comparable to those in ours. Obtaining human baselines for the long coding tasks in our experiments would, unfortunately, be far more expensive than for the tasks used in . More broadly, there is evidence suggesting that, while most humans are poorly calibrated, a small fraction are quite well calibrated , and experiments comparing LLMs to well-calibrated humans may be especially informative.

Expanding our experiments to tasks that evaluate dangerous capabilities could inform estimates of AI misuse and misalignment risks. For example, investigating in-advance confidence on tasks from AI control evaluations, in which LLMs attempt to evade control monitors by writing code with difficult-to-detect behaviors , would elucidate how reliably LLMs can identify viable opportunities to exploit vulnerabilities in an AI control protocol. Coupled with quantitative threat models of loss of control (as in ), such evaluations could enable quantitative estimates of loss of control risk.

Reproducibility Statement

Code to reproduce the three experiments is available at https://github.com/cbarkan1/do-llms-know-what-theyre-capable-of . Additionally, the appendices include the prompts and other experimental details needed to re-implement the experiments.

On LLMs’ self-reported confidence and rationality of decision making

A key motivation for studying whether LLMs can predict their success on tasks is that accurate predictions of success are needed for good decision making about whether to attempt a task. However, it is not necessarily the case that LLMs use their confidence estimates when making decisions. To investigate whether LLMs’ decisions are informed by their confidence estimates, we ask: Do LLMs make decisions that are rational given the estimated likelihoods of success that they self-report? We address this question using data from Experiment 2, in which rational decision making would mean that:

1. the LLM consistently adheres to a decision threshold of estimated likelihood when deciding whether to accept contracts (accepting contracts if and only if the estimated likelihood of success is above the threshold), and

2. the LLM makes decisions that maximize an expected-utility function that is monotonically increasing in their profit, where expectations are computed with the LLM’s estimated likelihoods of success.

We find that LLMs’ decision making is indeed (approximately) rational under their self-reported likelihoods of success. Furthermore, we compute the utility function that each LLM approximately adheres to, and we use it to estimate the risk aversion of each LLM.

We begin by making a minimal assumption about rational decision making in Experiment 2: we assume that a rational agent would maximize $`\mathbb{E}[u(w)]`$ where $`w`$ is wealth (net profit on contracts) and $`u(w)`$ is some monotonically increasing function of wealth (called the von Neumann-Morgenstern (vNM) utility function ). $`\mathbb{E}[\cdot]`$ denotes the expectation according to the agent’s beliefs about the probabilities of events. In other words, $`\mathbb{E}[\cdot]`$ is evaluated using the LLMs’ self-reported likelihood estimates $`\hat{p}_{i,n}`$.

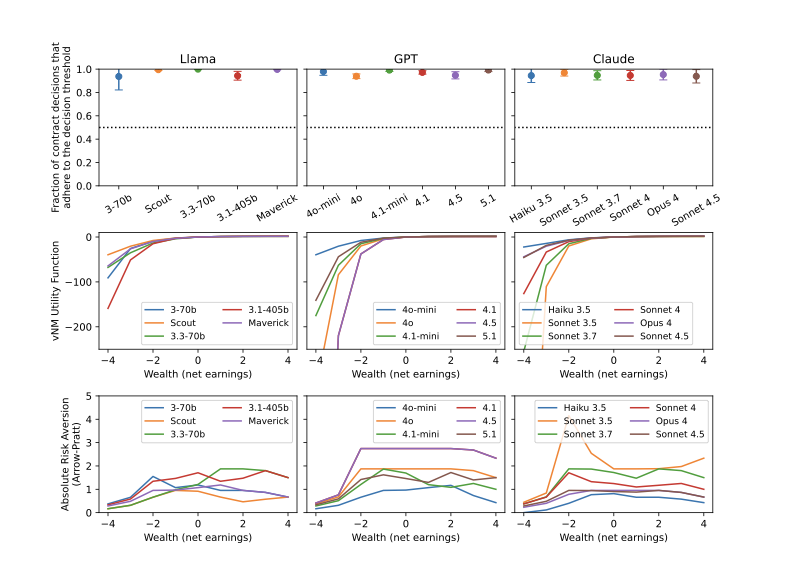
On point (1), we test whether LLMs accept contracts if and only if their estimated likelihood of success is above some threshold. For a rational agent, this threshold can be state-dependent, i.e. it can depend on $`w`$. Hence, we group contracts by the LLM’s wealth $`w`$ at the time the contract is offered, and then estimate adherence to a threshold within each group. Specifically, for contract $`c_{i,n}`$ (the contract from sequence $`i\in\{1,...,512\}`$ at step $`n\in\{1,...,9\}`$), let $`W(c_{i,n})\in\{-8,-7,...,8\}`$ be the LLMs’ wealth at the time that the contract is offered (note that wealth is an integer between -8 and 8 because the LLMs are offered only 9 contracts and the contract rewards and penalties are 1 and -1). Grouping contracts by wealth, we define the sets $`C_w=\{c_{i,n}: W(c_{i,n})=w\}`$ for $`w\in\{-8,-7,...,8\}`$, and find the threshold confidence $`p_T(w)`$ that maximizes the classification accuracy³ for each $`w`$. The average of the classification accuracy at the optimal threshold $`p_T(w)`$ (averaged across values of $`w`$) is shown in Figure 5 (top row), with error bars indicating two standard deviations. This average is equal to the fraction of contract decisions that are correctly predicted by the decision threshold. The values are close to 1, indicating that all LLMs quite consistently adhere to a decision threshold when deciding whether to accept contracts.

On point (2), we compute each LLM’s vNM utility function $`u(w)`$. To do this, we use the following fact: when a rational agent’s confidence estimate on a contract is equal to its decision threshold, it is indifferent between accepting and declining the contract. Hence, $`p_T(w) u(w+1)+(1-p_T(w))u(w-1) = u(w)`$. Noting that preferences are invariant under affine transformations of $`u(w)`$ , we can normalize $`u(w)`$ by setting $`u(0)=0`$ and $`u(1)=1`$ without loss of generality. Now, the above equation can be applied recursively to compute $`u(w)`$ for all $`w`$. The resulting utility functions are shown in Figure 5 (middle row), and these utility functions are all monotonically increasing in $`w`$, as required for a rational decision maker.

Given the utility functions, we can estimate the absolute (Arrow-Pratt) risk aversion $`-u''(w)/u'(w)`$ by numerically approximating the derivatives $`u'(w)`$ and $`u''(w)`$. The result is shown in Figure 5 (bottom row). Risk aversion is positive for all values of $`w`$ for all LLMs, which is consistent with prior work on LLMs and in accord with typical risk aversion of humans . Most LLMs have roughly constant risk aversion for $`w\geq -2`$ but lower risk aversion for $`w<-2`$, which is suggestive of a weak form of prospect theory (in standard prospect theory, absolute risk aversion becomes negative when wealth is negative ).

/>

Prompts for Experiment 1

We designed prompts to encourage LLMs to make judicious confidence estimates, without explicitly instructing them to avoid overconfidence.

Prompts for eliciting confidence estimates $`\hat{p}_i`$:

Prompts for measuring success or failure on each task:

{BCB_problem_inserted_here} refers to the BigCodeBench task, which includes a fully self-contained explanation and instructions.

Supplemental information for Experiment 2

Dataset

Experiment 2 consists of 512 samples of 9-contract sequences, where each contract involves a BigCodeBench (BCB) task. The same 512 samples were used for all LLMs (except GPT 5.1 and Sonnet 4.5; see the paragraph below), and the BCB tasks were selected so that there is a 50% chance of success on any task for any LLM. To do this, we constructed the subset of BCB tasks on which all tested LLMs succeed (call this subset $`\mathcal{S}`$) and the subset on which all tested LLMs fail (call this subset $`\mathcal{F}`$). $`\mathcal{S}`$ contains 271 tasks and $`\mathcal{F}`$ contains 193 tasks. Letting $`S`$ denote any element of $`\mathcal{S}`$ and $`F`$ any element of $`\mathcal{F}`$, we construct every possible length-9 sequence of $`S`$ and $`F`$, i.e. $`(S, S, ..., S), (S, S, ..., F), ... ,(F, F, ..., F)`$. There are $`2^9=512`$ such sequences. Then, for each contract in each sequence, we randomly sampled from $`\mathcal{S}`$ or $`\mathcal{F}`$ to obtain the 512 samples of BCB contracts. This sampling was done without replacement, so there are no repeated contracts in any of the sequences.

This dataset was constructed before the release of GPT 5.1 and Sonnet 4.5. Rather than updating the sets $`\mathcal{S}`$ and $`\mathcal{F}`$ and re-running the experiment on all LLMs, we instead kept the original dataset but modified it slightly for GPT 5.1 and Sonnet 4.5. Specifically, for the model $`M\in\{\text{GPT 5.1, Sonnet 4.5}\}`$, let $`\mathcal{S}_M`$ be the subset of $`\mathcal{S}`$ on which $`M`$ succeeded, and let $`\mathcal{F}_M`$ be the subset of $`\mathcal{F}`$ on which $`M`$ failed. For each task in each of the 512 sequences, if the task was in $`\mathcal{S}`$ but not $`\mathcal{S}_M`$, it was replaced with a randomly sampled task in $`\mathcal{S}_M`$. If the task was in $`\mathcal{F}`$ but not $`\mathcal{F}_M`$, it was replaced with a randomly sampled task in $`\mathcal{F}_M`$.

Prompts

In the final prompt, {phrase} is set to either “are now" or “remain at", depending on context.

Results for all intermediate contracts

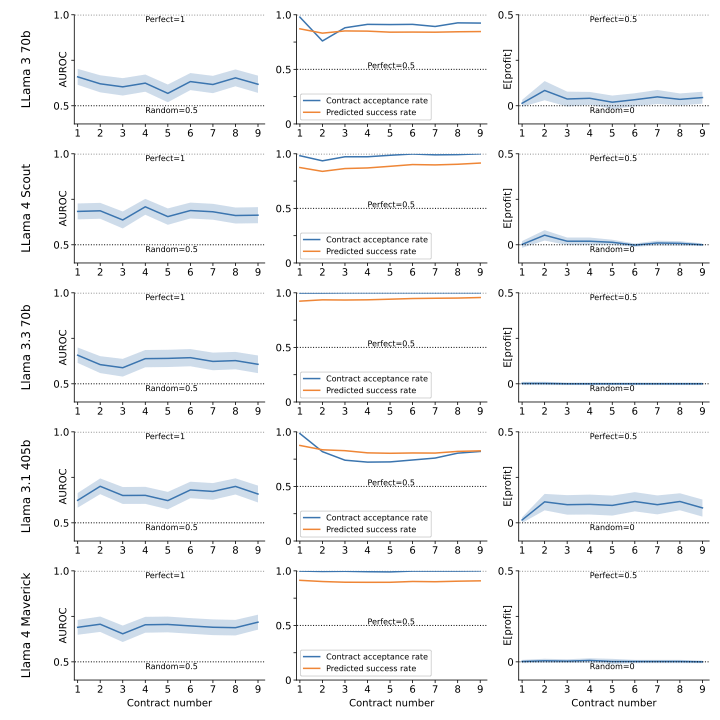
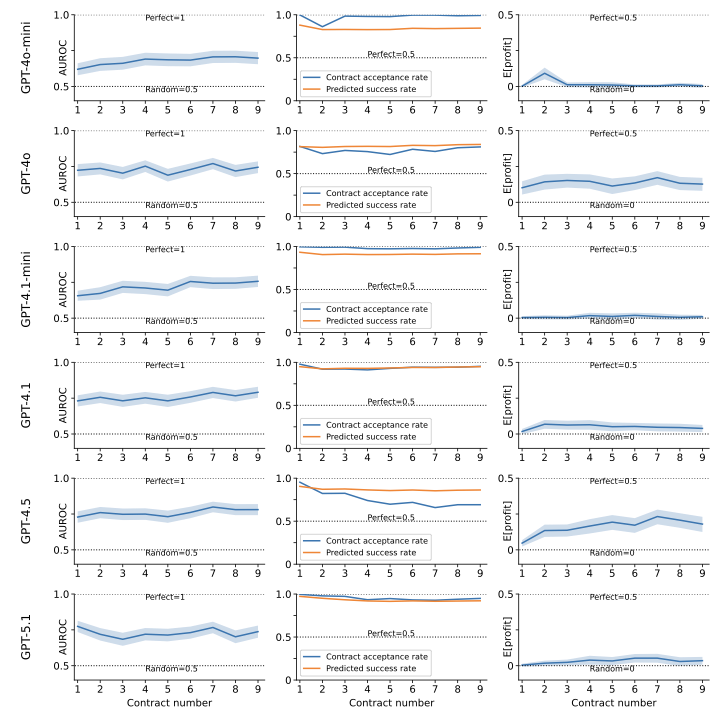
Figures 6, 7, and 8 show the results for Llama, GPT, and Claude models for all contracts 1 through 9.

/>

/>

/>

Supplemental information for Experiment 3

Additional details of setup and AUROC calculation

In Experiment 3, LLMs solve SWE Bench tasks where they modify code in a repository to fix an issue. A confidence estimate $`\hat{p}_{i,s}`$ is elicited after tool call $`s`$ for each task $`i`$. The LLM’s final tool call involves using a “submit” tool to submit the modified repository. Suppose the LLM submits its solution to task $`i`$ on the $`n_i`$th tool call, and note that $`1\leq n_i\leq70`$ due to the tool call budget. After providing $`\hat{p}_{i,n_i}`$, the LLM is prompted to reflect upon its solution and provide a final after-the-fact confidence estimate $`\hat{p}_{i,\text{after}}`$. If $`n_i<70`$, we assign $`\hat{p}_{i,s}=\hat{p}_{i,n_i}`$ for $`s>n_i`$. This simulates that the LLM ‘sits out’ on the final tool calls after submitting its answer, and then provides its after-the-fact confidence estimate at the very end. In computing AUROC scores at step $`s`$, we use the set of confidence estimates at step $`s`$ across all 500 tasks ($`\{\hat{p}_{i,s}\}_{i=1}^{500}`$) for the predictions, and the ultimate success or failure on each task as the outcomes.

Prompts

Note that the system prompt and initial user message utilize parts of the prompts from the Inspect SWE Bench implementation.

LLM usage for research and writing

The authors used LLMs for coding assistance and for basic proofreading of writing.

Compute resources

Experiments 1 and 2 were run on a 2021 MacBook Pro with M1 Pro chip and 32GB RAM, and each experimental run took 30 minutes or less. Experiment 3 was run on an AWS EC2 t3.2xlarge instance with 8 vCPUs, 32GB RAM, and 400GB disk space, and each experimental run took less than 6 hours. Experiments accessed LLM inference via commercial APIs (OpenAI, Anthropic, and OpenRouter).