Multi-modal cross-domain mixed fusion model with dual disentanglement for fault diagnosis under unseen working conditions
📝 Original Paper Info
- Title: Multi-modal cross-domain mixed fusion model with dual disentanglement for fault diagnosis under unseen working conditions- ArXiv ID: 2512.24679
- Date: 2025-12-31
- Authors: Pengcheng Xia, Yixiang Huang, Chengjin Qin, Chengliang Liu
📝 Abstract
Intelligent fault diagnosis has become an indispensable technique for ensuring machinery reliability. However, existing methods suffer significant performance decline in real-world scenarios where models are tested under unseen working conditions, while domain adaptation approaches are limited to their reliance on target domain samples. Moreover, most existing studies rely on single-modal sensing signals, overlooking the complementary nature of multi-modal information for improving model generalization. To address these limitations, this paper proposes a multi-modal cross-domain mixed fusion model with dual disentanglement for fault diagnosis. A dual disentanglement framework is developed to decouple modality-invariant and modality-specific features, as well as domain-invariant and domain-specific representations, enabling both comprehensive multi-modal representation learning and robust domain generalization. A cross-domain mixed fusion strategy is designed to randomly mix modality information across domains for modality and domain diversity augmentation. Furthermore, a triple-modal fusion mechanism is introduced to adaptively integrate multi-modal heterogeneous information. Extensive experiments are conducted on induction motor fault diagnosis under both unseen constant and time-varying working conditions. The results demonstrate that the proposed method consistently outperforms advanced methods and comprehensive ablation studies further verify the effectiveness of each proposed component and multi-modal fusion. The code is available at: https://github.com/xiapc1996/MMDG.💡 Summary & Analysis
1. **Dual Disentanglement Framework:** The paper proposes a new approach to simultaneously disentangle invariance and specificity at both the modality level and domain level. This allows the model to operate stably across various working conditions. 2. **Multi-domain Mixed Fusion Mechanism:** The paper introduces a mechanism for randomly mixing each modality across different source domains, reducing domain bias and enhancing generalization ability. 3. **Triple-modal Fusion Module:** A new method is proposed for adaptively combining data from multiple heterogeneous modalities to maximize the use of information provided by each sensor.Simple Explanation:
- Easy Understanding: The paper suggests a way to mix various sensor data effectively and extract only important information, helping create models that work stably across different machine conditions.
- Intermediate Level: This research proposes methods for combining sensor data and separating critical features under varying working conditions. It ensures stable operation of the model even in unseen situations.
- Advanced Level: The paper introduces a novel approach to fuse multi-domain sensor data and disentangle common and specific characteristics, allowing models to operate effectively across different conditions, including those that have not been encountered before.
📄 Full Paper Content (ArXiv Source)
[style=chinese]
[style=chinese]
[style=chinese]
Fault diagnosis , Multi-modal fusion , Domain generalization , Feature disentanglement , Unseen working conditions
_set:nn stm / mktitle nologo
Introduction
As modern machinery moves toward higher levels of automation and complexity, the demand for equipment reliability has become increasingly stringent. Unexpected failures may result in substantial economic losses, unplanned downtime, and even catastrophic accidents . To mitigate these risks, industries are deploying large-scale sensor networks to continuously monitor diverse signals such as vibration, current, and acoustic . By leveraging these monitoring data, fault diagnosis can be performed to detect anomalies at an early stage and enable timely maintenance interventions .
Recently, intelligent data-driven fault diagnosis methods based on deep learning have attracted substantial attention due to their strong ability to automatically learn discriminative representations from raw sensor measurements. Compared with traditional physics-based approaches and conventional machine-learning methods that rely heavily on hand-crafted feature engineering, deep learning methods eliminate the need for complex prior expert knowledge and manual feature extraction, thereby demonstrating highly promising diagnostic performance . For example, vibration signals of rotating machinery can be directly fed into deep learning models, allowing them to automatically learn relevant features for fault diagnosis. Borghesani et al. leveraged 1D convolutional neural network (CNN) to accomplish bearing fault diagnosis and attempted to explain the vibration feature extraction process. Liu et al. designed a residual network with multiscale kernels for motor fault diagnosis using vibration signals. However, raw one-dimensional signals often exhibit complex temporal characteristics and non-stationary behaviors, which may limit the ability of conventional 1D models to fully capture informative patterns. To better represent the underlying time-frequency structures of vibration signals, many studies transform 1D vibration signals into 2D time-frequency representations with short-time fourier transform (STFT) or wavelet transform , and then employ 2D networks to extract more expressive features from these transformed images. Nevertheless, vibration signals may exhibit limited sensitivity to certain electrical faults in electromechanical machines such as motors . Consequently, motor current signals have also been widely adopted for fault diagnosis . For example, Jimenez-Guarneros et al. designed a lightweight 1D CNN to diagnose mechanical and electrical faults of induction motor with current signals. Furthermore, acoustic signals also contain fault-related information and have therefore been explored for machinery fault diagnosis. Zhang et al. employed acoustic signals together with a graph convolutional network (GCN) to diagnose bearing faults, while Xiao et al. utilized a denoising autoencoder to achieve motor fault diagnosis based on acoustic measurements. These studies collectively demonstrate the effectiveness of deep learning-based diagnostic methods using acoustic signals.
Despite the remarkable progress of intelligent fault diagnosis methods, their generalization ability remains a major obstacle to practical applications as machines typically operate under variable working conditions. Domain shifts induced by changes in operating speed and load can significantly degrade the performance of models trained on data from source conditions. To address this issue, domain adaptation (DA) techniques have been extensively investigated to improve the robustness of diagnostic models under distribution shifts. By aligning feature distributions from source domains to target domains, these methods aim to mitigate the adverse effects of condition variability and enable more reliable cross-condition fault diagnosis . Consequently, DA based on discrepancy minimization and domain adversarial learning and subdomain adaptation (SDA) methods have demonstrated effectiveness in machinery fault diagnosis across various working conditions.
Nevertheless, a major limitation hindering the practical applications of DA methods is their reliance on target domain data for distribution alignment. In real industrial scenarios, this requirement is often difficult to satisfy as machines frequently operate under newly emerging or previously unseen working conditions for which no samples have been collected in advance. To overcome this constraint, domain generalization (DG) has emerged as an attractive alternative, aiming to learn models that can generalize to unseen target conditions without accessing any target-domain samples during training . Instead of explicitly aligning source and target distributions, DG seeks to extract domain-invariant and discriminative features from multiple source domains, thereby enhancing the model’s robustness to distribution shifts and demonstrating promising performance in unseen-condition fault diagnosis . Most DG-based fault diagnosis methods aims to achieve domain alignment through domain adversarial learning or by minimizing domain divergence , such that the domain-invariant features extracted from source domains are more likely to generalize to unseen domains. In addition, several studies have explored data augmentation or meta-learning strategy to enhance model’s generalization ability. However, most existing methods primarily emphasize learning domain-invariant representations, while overlooking the specific features closely correlated with distinct working conditions.
Moreover, existing DG-based fault diagnosis studies rely on a single sensing modality, typically vibration signals. However, using only one type of signal often limits the diagnostic generalization, as different signals capture complementary fault-related characteristics as we mentioned above, particularly for electromechanical machines. Therefore, in the context of DG-based fault diagnosis, multi-modal fusion offers additional potential to enhance robustness against unseen operating conditions, since combining multiple modalities can reduce the reliance on any single domain-specific feature distribution and promote more stable cross-domain generalization. Although numerous studies have explored multi-sensor fusion approaches for fault diagnosis , including data-level fusion , feature-level fusion , and decision-level fusion , significant challenges remain under variable working conditions. First, most existing methods are limited to processing 1D signals from multiple sensors with the same modality sampled at the same frequency. Therefore, they cannot accommodate scenarios in which time-frequency representations are extracted under variable operating conditions, or when different modalities naturally have different sampling frequencies. Second, most methods directly fused data or features from multiple sensors without considering their intrinsic correlations and modality-specific characteristics for specific faults. Moreover, to our best knowledge, there is currently no literature addressing fault diagnosis under unseen working conditions using multi-modal data. Consequently, designing a multi-modal fusion framework that can enhance model generalization across unseen conditions remains a challenging and open problem.
To tackle the aforementioned challenges and limitations, this paper proposes a multi-modal cross-domain mixed fusion model with dual disentanglement for fault diagnosis. First, multi-modal data are encoded by respective encoders to obtain dedicated modality embeddings. Second, a cross-domain mixed fusion mechanism is proposed to randomly mix each modality across various source domains, thereby mitigating domain bias and enriching cross-domain feature diversity. Subsequently, a dual disentanglement framework is designed to separately disentangle modality-invariant and modality-specific representation, and domain-invariant and domain-specific representation disentanglement, enabling more robust domain generalization. Furthermore, a triple-modal fusion module based on multiple cross-attention is developed to achieve deep and adaptive fusion of heterogeneous modalities. To evaluate the proposed method, we conducted experiments on induction motors and collected vibration, current, and acoustic signals under both constant and varying working conditions. Extensive fault diagnosis experiments on unseen working conditions were performed, and both comparative and ablation studies consistently validate the effectiveness and superiority of the proposed method. The main contributions of this work are summarized as follows:
-
A dual disentanglement framework jointly disentangling invariance and specificity at both the modality level and the domain level is proposed for enhanced multi-modal DG for fault diagnosis.
-
A multi-modal cross-domain mixed fusion mechanism is designed for modality augmentation to mitigate domain bias and enhance generalization.
-
A triple-modal fusion module is introduced to achieve adaptive and complementary fusion of multiple heterogeneous modalities.
The reminder of the paper is organized as follows. Section 2 introduces some related work regarding multi-modal fusion and DG. The proposed method is described in detail in Section 3. The experiments and results are presented in Section 4, and Section 5 concludes the paper.
Related work
Domain generalization
Different from DA, DG removes the constraint of accessing to target domain data during training. This setting is more consistent with real-world fault diagnosis scenarios, where data from new working conditions are typically unavailable in advance. As a result, DG has attracted extensive research attention . The mainstream idea in DG is to learn invariant representations across multiple source domains. Therefore, domain adversarial learning has become the most widely adopted approaches, which introduces a domain discriminator to adversarially train the feature extractor to learn domain-invariant features that are able to confuse the discriminator. For example, Chen et al. leveraged adversarial learning to exploit domain-invariant features for bearing fault diagnosis under unseen working conditions. Shi et al. designed a weighting strategy for domain adversarial learning based on domain transferability, achieving remarkable performance on multiple bearing datasets. Some works explicitly aligned feature distributions from multiple source domains. For example, Pu et al. introduced $`\alpha`$-PE divergence for distribution alignment for gearbox fault diagnosis under variable working conditions.
However, these methods primarily emphasize the extraction of domain-invariant features while neglecting the importance of domain-specific characteristics that are closely associated with individual working conditions. This leads to the loss of condition-related information, which can limit both robustness and classification performance when the model encounters working conditions differing substantially from those during training. Consequently, Zhao et al. proposed to combined invariance and specificity for fault diagnosis generalization and proposed a DG network with separate subnetworks for domain-invariant and domain-specific feature extraction, and the similarity to source domains are estimated to select specificity for each target sample. Other studies have attempted to address this issue from the perspective of causal learning by simultaneously modeling causal and non-causal features. Li et al. proposed a causal consistency network (CCN) to learn causal features with machines and conditions jointly. Similarly, Jia et al. proposed to disentangle fault-related causal factors and domain-related non-causal factors by a causal aggregation loss. He et al. extracted the non-causal factors with a domain classifier and decoupled them with causal features by a mutual information loss for induction motor fault diagnosis. Although these approaches improve generalization, they mostly involved additional classifiers or decoders for causal and non-causal factor learning, or incorporated complex modules for specificity extraction and selection. Moreover, all existing methods were designed for single-modal data.
Multi-modal fusion
In the context of fault diagnosis, fusing signals from multiple sensors has received substantial attention. The fusion strategies can generally be categorized into three types: data-level fusion, feature-level fusion, and decision level fusion . Data-level fusion directly combines raw data from multiple sensors without any information loss , while it is often limited to single-modal or homogeneous data. Feature-level fusion integrates intermediate representations for the combination of complementary features from multiple signals. Some studies fused multi-source representations through direct feature concatenation , while others rely on average pooling operations . More recently, cross-attention mechanisms have been introduced to enhance multi-feature interaction , though existing work focuses on fusing only two feature sources, limiting its scalability. Decision-level fusion aggregates the outputs of multiple classifiers or decision modules through decision theory such as Dempster-Shafer (D-S) evidence theory and soft-voting rule , while these methods relies heavily on the accuracy of individual models.
Some studies have considered information fusion from multiple heterogeneous modalities for fault diagnosis. For example, Sun et al. fused acoustic signals and infrared thermal (IRT) images with a correlation fusion module for gearbox and bearing-rotor system fault diagnosis. Ying et al. also proposed a feature fusion module based on Dirichlet distribution and D-S evidence theory to fuse acoustic signals and IRT images for fault diagnosis. However, these methods mainly focus on information fusion while overlooking the specificity within each modality, and they were designed for constant working conditions without condition bias. Recently, Zhang et al. investigated a DA method with multi-modal fusion by combining MMD loss and modality consistency loss. Their approach enables fault diagnosis across working conditions, while it follows a DA paradigm rather than DG, and thus requires access to target-domain data.
Methodology
Overview of the method
In this paper, we aim to address the multi-modal domain generalization problem for fault diagnosis under unseen working conditions. We assume there exist $`M`$ source domains $`\{\mathscr{D}_m^s\}_{m=1}^M`$, each corresponding to a specific working condition. In the $`m`$-th source domain, there are $`N_m^s`$ samples which all have fault labels, forming a sub-dataset $`D_m^s=\left\{(\mathbf{x}_i^{s_m}, y_i^{s_m})\right\}_{i=1}^{N_m^s}`$. Multichannel vibration, current, and acoustic signals collected from multiple source domains are used in this work. Therefore, each sample $`\mathbf{x}_i^{s_m}`$ consists of three heterogeneous modalities, which can be expressed as $`\mathbf{x}_i^{s_m}=\left(\mathbf{x}_i^{s_m,v}, \mathbf{x}_i^{s_m,c}, \mathbf{x}_i^{s_m,a}\right)`$, where $`\mathbf{x}_i^{s_m,v}\in\mathcal{X}^{(v)}`$, $`\mathbf{x}_i^{s_m,c}\in\mathcal{X}^{(c)}`$, $`\mathbf{x}_i^{s_m,a}\in\mathcal{X}^{(a)}`$. Here, $`\mathcal{X}^{(v)}\subset \mathbb{R}^{L_v\times C_v}`$ denotes the space of $`C_v`$ channel vibration signals with a length of $`L_v`$. $`\mathcal{X}^{(c)}\subset \mathbb{R}^{L_c\times C_c}`$ represents the space of $`C_c`$ channel current signals with a length of $`L_c`$. And $`\mathcal{X}^{(a)}\subset \mathbb{R}^{L_a\times C_a}`$ represents the space of $`C_a`$ channel acoustic signals with a length of $`L_a`$. Accordingly, the overall multi-modal heterogeneous input space is formulated as the Cartesian product, i.e., $`\mathbf{x}_i^{s_m}\in \mathcal{X}=\mathcal{X}^{(v)}\times\mathcal{X}^{(c)}\times\mathcal{X}^{(a)}`$. All the source domains share a common fault label space $`\mathcal{Y}=\{1,2,\ldots,K\}`$, i.e., $`y_i^{s_m}\in\mathcal{Y}`$ for each source sample, where $`K`$ is the number of health condition class. The complete multi-domain training data are obtained as $`D^s=\bigcup_{m=1}^MD_m^s`$. As the source domain data comes from multiple working conditions, the marginal probability distributions are non-identical among different domains, i.e., $`P_i^s(X)\neq P_j^s(X)`$, $`i\neq j`$, where $`\mathscr{D}_m^s=\{\mathcal{X}_m^s,P_m^s(X)\}`$. The objective of this work is to learn a model $`f:\mathcal{X}\rightarrow \mathcal{Y}`$ that generalizes to the previously unseen target domain $`\mathscr{D}^t=\{\mathcal{X}^t,P^t(X)\}`$ without accessing any data from this domain. Notably, $`P^t(X)\neq P_m^s(X)`$, $`\forall m=1,2,\ldots,M`$, while the label space remains consistent across domains, i.e., $`\mathcal{Y}^t=\mathcal{Y}`$.
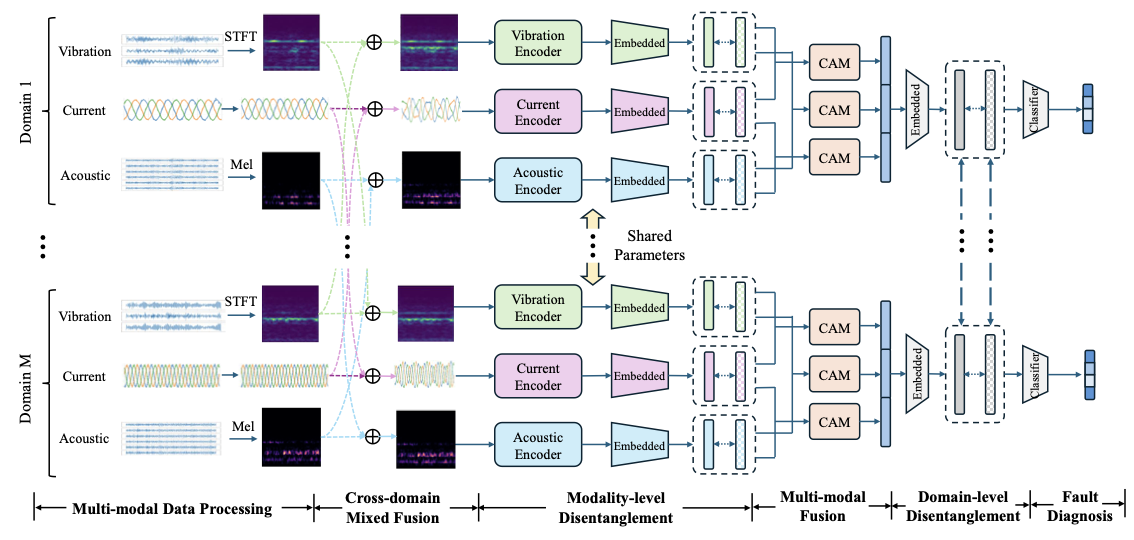
To realize this target, a multi-modal cross-domain mixed fusion model with dual disentanglement is proposed for fault diagnosis under unseen working conditions. The framework is illustrated as Fig. 1. Preprocessing is conducted including transforming vibration signals into time-frequency representations and transforming acoustic signals into Mel-spectrograms. Cross-domain mixed fusion is firstly applied to randomly mix each modality across source domains to achieve modality augmentation. Afterward, modality-invariant representations shared by the three modalities and modality-specific representations unique to each modality are extracted and disentangled. These disentangled features from three modalities are then fused through a triple-modal fusion module to form comprehensive representations for each source domain. Subsequently, domain-invariant and domain-specific features are further learned and disentangled across all source domains to capture both shared and condition-dependent characteristics. Finally, a fault classifier is attached to accomplish fault diagnosis.
 />
/>
Cross-domain mixed fusion
As discussed above, 1D vibration signals often exhibit pronounced non-stationary characteristics under varying working conditions. Time-frequency representations are therefore more effective for capturing fault-related patterns that evolve over time and across frequency bands. We leverage STFT to convert each vibration channel into a 2D time-frequency image, and the images from multiple channels are stacked to form a multichannel image $`\hat{\mathbf{x}}_i^{s_m,v}\in\mathbb{R}^{H_v\times W_v\times C_v}`$. For acoustic signals, Mel-spectrograms are utilized to project the linear frequency spectrum into a perceptually inspired nonlinear scale, which can reduce redundancy in high-frequency regions, emphasize lower-frequency components where fault information is typically concentrated, and enhance the signal-to-noise ratio. Similarly, the Mel-spectrograms from multiple channels are stacked, forming a multichannel image $`\hat{\mathbf{x}}_i^{s_m,a}\in\mathcal{R}^{H_a\times W_a\times C_a}`$. The current signals are directly input to the network as $`\hat{\mathbf{x}}_i^{s_m,c}=\mathbf{x}_i^{s_m,c}`$.
The proposed cross-domain mixed fusion mechanism aims to improve robustness to domain shifts by introducing random cross-domain perturbations at the modality level. For each sample, each modality is randomly mixed with the corresponding modality with same fault category drawn from other source domains. This operation increases intra-class modality diversity and encourages the model to learn more modality-robust and domain-agnostic representations. Specifically, for each sample $`\hat{\mathbf{x}}_i^{s_m}=\left(\hat{\mathbf{x}}_i^{s_m,v}, \hat{\mathbf{x}}_i^{s_m,c}, \hat{\mathbf{x}}_i^{s_m,a}\right)`$ with fault label $`k`$ from the $`m`$-th domain, data of each modality $`\hat{\mathbf{x}}_i^{s_m,l}, l=\{v,c,a\}`$ are performed cross-domain fusion separately. For $`\hat{\mathbf{x}}_i^{s_m,l}`$, there is 50% probability to randomly choose a source domain $`\mathscr{D}_n^s, n\neq m`$ from the rest $`M-1`$ source domains, and subsequently randomly select a sample with the same label $`k`$, i.e., $`\hat{\mathbf{x}}_j^{s_n}=\left(\hat{\mathbf{x}}_j^{s_n,v}, \hat{\mathbf{x}}_j^{s_n,c}, \hat{\mathbf{x}}_j^{s_n,a}\right)`$. The mixed fusion operation is performed through linear fusion of the corresponding modality of these two samples, expressed as follows:
\begin{equation}
\tilde{\mathbf{x}}_i^{s_m,l} = \begin{cases}
\alpha\hat{\mathbf{x}}_i^{s_m,l} + (1-\alpha)\hat{\mathbf{x}}_j^{s_n,l}, & \beta_1<0.5\\
\hat{\mathbf{x}}_i^{s_m,l}, & \beta_1\geq0.5
\end{cases}, \beta_1\sim U(0,1).
\end{equation}The fusion coefficient $`\alpha`$ is sampled from Beta distribution similar to Mixup , whereas extra operation is introduced to realize external interpolation close to the original data. Firstly, a value $`\alpha^\prime`$ is obtained from Beta distribution as
\begin{equation}
\alpha^\prime\sim Beta(0.2, 0.2).
\end{equation}Subsequently, external interpolation is realized with 50% probability by generating a coefficient larger than but close to 1, formulated as
\begin{equation}
\alpha = \begin{cases}
2-\text{max}(\alpha^\prime, 1-\alpha^\prime), & \beta_2<0.5\\
\alpha^\prime, & \beta_2\geq0.5
\end{cases}, \beta_2\sim U(0,1).
\end{equation}For all modality in a sample, the procedure is performed separately, thereby enhancing the intra-class and inter-domain modality diversity for more robust input space. The fused output $`\tilde{\mathbf{x}}_i^{s_m}=\left(\tilde{\mathbf{x}}_i^{s_m,v}, \tilde{\mathbf{x}}_i^{s_m,c}, \tilde{\mathbf{x}}_i^{s_m,a}\right)`$ is then input to the model.
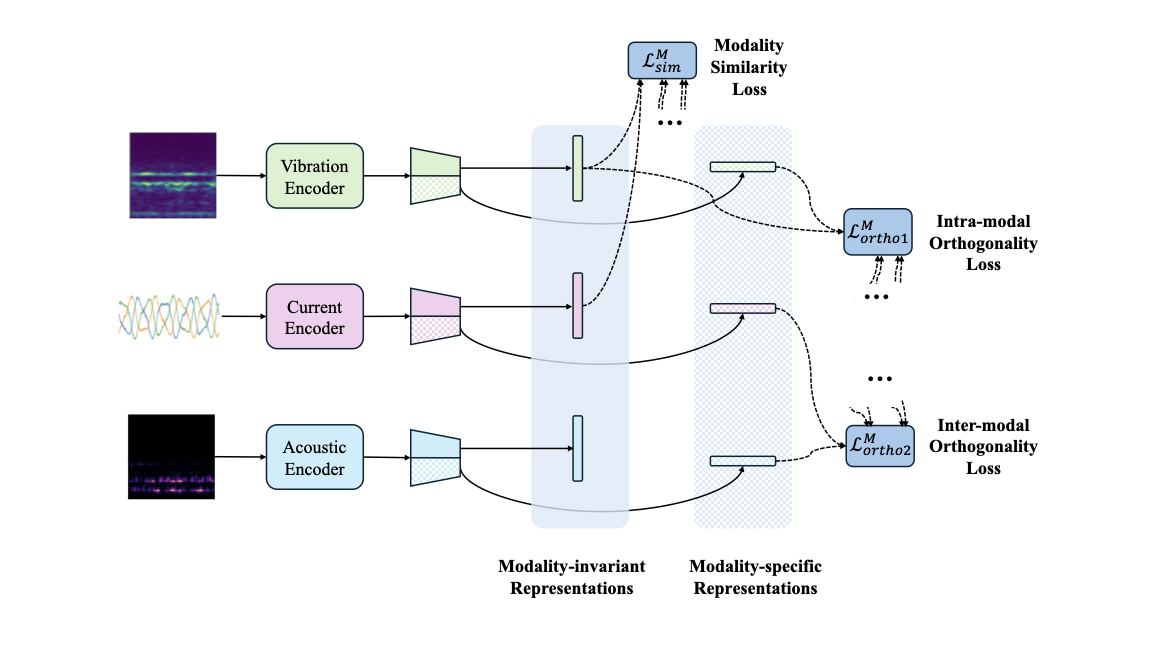
Modality-level disentanglement
Fig. 2 illustrates the modality-level disentanglement process. Three encoders are designed to extract representations from each sensing modality independently, implemented using residual networks (ResNets). Specifically, 2D ResNets are adopted for vibration and acoustic modalities to process their corresponding time-frequency and Mel-spectrogram images, while a 1D ResNet is employed for the current modality to handle multichannel temporal signals. Given a cross-domain mix fused modality input $`\tilde{\mathbf{x}}_i^{s_m,l}`$, the feature extraction can be expressed as
\begin{equation}
\mathbf{f}_i^{s_m,l}=E^{(l)}\left(\tilde{\mathbf{x}}_i^{s_m,l}\right),l\in\{v,c,a\},
\end{equation}where $`E^{(l)}(\cdot)`$ denotes the encoder for the $`l`$ modality.
 style="width:80.0%" />
style="width:80.0%" />
Although these representations are extracted independently, they inherently contain both information shared across modalities and modality-specific characteristics. As multi-modal signals are collected from the same machine under identical health states and working condition, they should exhibit invariant characteristics related to the underlying fault and working condition, thereby sharing common motives for fault diagnosis. Consequently, extracting these modality-invariant representations helps reveal correlated fault-related features consistently manifested in multiple modalities. On the other hand, each modality also contains specific features, as sensors with various modality capture diverse aspects of machine operation. Features from different modalities may also exhibit various sensitivities to particular fault types. Therefore, aligning the modality-invariant parts while separating the modality-specific components is thus beneficial for multi-modal collaborative fault diagnosis. Inspired by , a modality-level disentanglement strategy is introduced to explicitly decouple these two types of information.
For each modality, the extracted feature $`\mathbf{f}_i^{s_m,l}`$ is further transformed by two separate embedding networks, which are respectively designed to learn modality-invariant representations and modality-specific representations. Specifically, this process is formulated as
\begin{equation}
\mathbf{z}_i^{s_m,l,inv}=G_{inv}^{(l)}\left(\mathbf{f}_i^{s_m,l}\right),\mathbf{z}_i^{s_m,l,spe}=G_{spe}^{(l)}\left(\mathbf{f}_i^{s_m,l}\right),
\end{equation}where $`G_{inv}^{(l)}(\cdot)`$ and $`G_{spe}^{(l)}(\cdot)`$ denote the modality-invariant and modality-specific embedding networks for the $`l`$ modality, respectively. The modality-invariant representations $`\mathbf{z}_i^{s_m,l,inv}`$ are expected to encode fault-related semantics that are consistent across multiple modalities, whereas the modality-specific representations $`\mathbf{z}_i^{s_m,l,spe}`$ preserve distinctive characteristics arising from heterogeneous sensing mechanisms. To explicitly disentangle the modality-invariant and modality-specific components, three sets of loss functions are introduced as follows.
(1) Modality similarity loss. The modality-invariant representations extracted from different modalities are expected to share similar distributions in the embedding space. Consequently, a modality-level MMD loss is introduced to explicitly align the distributions of invariant representations across modalities. Specifically, the MMD loss is computed pairwise among vibration, current, and acoustic modalities within the same source domain, and the overall invariant alignment loss is defined as
\begin{equation}
\begin{aligned}
\mathcal{L}_{sim}^M &= \sum_{l_1\neq l_2}\text{MMD}\left(\mathbf{z}^{s_m,l_1,inv}, \mathbf{z}^{s_m,l_2,inv}\right)\\
&=\sum_{l_1\neq l_2}\left[\frac{1}{(N_m^s)^2}\sum_{i=1}^{N_m^s}\sum_{j=1}^{N_m^s}k\left(\mathbf{z}_i^{s_m,l_1,inv}, \mathbf{z}_j^{s_m,l_1,inv}\right) + \frac{1}{(N_m^s)^2}\sum_{i=1}^{N_m^s}\sum_{j=1}^{N_m^s}k\left(\mathbf{z}_i^{s_m,l_2,inv}, \mathbf{z}_j^{s_m,l_2,inv}\right)\right.\\
&\phantom{=\;\;}\left.- \frac{2}{(N_m^s)^2}\sum_{i=1}^{N_m^s}\sum_{j=1}^{N_m^s}k\left(\mathbf{z}_i^{s_m,l_1,inv}, \mathbf{z}_j^{s_m,l_2,inv}\right)\right],
\end{aligned}
\end{equation}where $`k(\cdot, \cdot)`$ denotes kernel function. By minimizing this loss, the invariant subspaces of different modalities are encouraged to follow similar distributions.
(2) Intra-modality orthogonality loss. While invariant representations should capture shared semantics, modality-specific representations are expected to encode complementary information that is independent of the invariant components. To prevent information redundancy and leakage between these two subspaces, an orthogonality constraint is imposed within each modality. Specifically, a covariance-based orthogonality loss is adopted to minimize the statistical dependency between modality-invariant and modality-specific representations. For each modality $`l`$, this loss is formulated as
\begin{equation}
\mathcal{L}_{ortho1}^M = \sum_{l\in\{v,c,a\}}\left\|\text{Cov}\left(\mathbf{z}^{s_m,l,inv}, \mathbf{z}^{s_m,l,spe}\right)\right\|_2,
\end{equation}where $`\text{Cov}(\cdot)`$ denotes the sample covariance matrix computed after mean normalization. Minimizing this constraint encourages the modality-specific representations to capture information that is uncorrelated with the shared invariant features.
(3) Inter-modality orthogonality loss. In addition to the separation within each modality, modality-specific representations from different modalities should also remain distinctive because the shared components should be included in the modality-invariant representations of each modality. Excessive correlation among modality-specific representations across modalities may weaken their complementarity. As a result, an inter-modality orthogonality constraint is further introduced by minimizing the covariance between modality-specific representations from different modalities. The loss is defined as
\begin{equation}
\mathcal{L}_{ortho2}^M = \sum_{l_1\neq l_2}\left\|\text{Cov}\left(\mathbf{z}^{s_m,l_1,spe}, \mathbf{z}^{s_m,l_2,spe}\right)\right\|_2,
\end{equation}Minimizing this loss further promotes the specificity of these representations and enhances the complementary nature of heterogeneous sensing information.
The proposed modality-level disentanglement framework is realized by jointly optimizing the three parts of losses, represented as
\begin{equation}
\mathcal{L}_m = \mathcal{L}_{sim}^M + \mathcal{L}_{ortho1}^M + \mathcal{L}_{ortho2}^M.
\end{equation}It will enable effective decoupling of shared and specific information across multiple modalities. The disentangled representations could provide a foundation for multi-modal fusion and subsequent domain-level disentanglement.
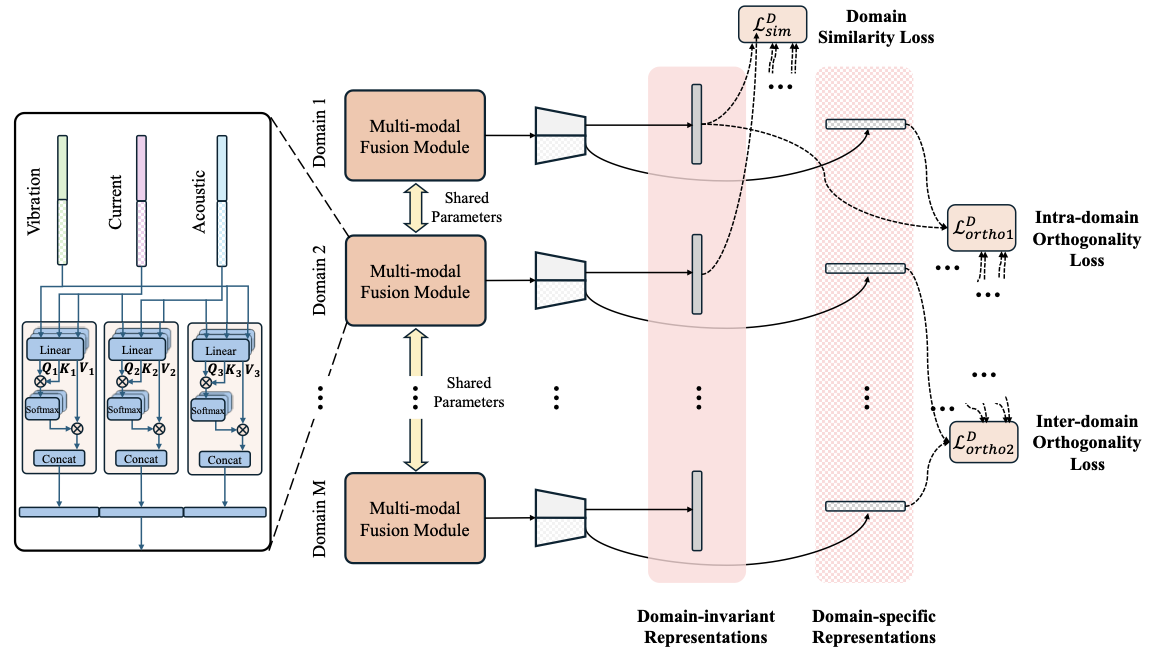
Triple-modal fusion module
 style="width:90.0%" />
style="width:90.0%" />
After modality-level feature disentanglement, the modality-invariant and modality-specific representations from all three modalities are integrated through a multi-modal fusion module based on a multi-head cross-attention mechanism (CAM), as illustrated as Fig. 3. Instead of directly performing joint fusion over all three modalities, we follow a pairwise fusion paradigm , where each pair of heterogeneous modalities is fused independently. This design allows the model to explicitly capture fine-grained inter-modal interactions while avoiding excessive complexity and information interference that may arise from direct triple-modal fusion.
Firstly, for each modality pair $`l_p`$ and $`l_q`$, the modality-invariant and modality-specific representations are first concatenated to form the modality-aware embedding
\begin{equation}
\mathbf{z}^{s_m,l}=\left[\mathbf{z}^{s_m,l,inv}, \mathbf{z}^{s_m,l,spe}\right], l\in\{l_p,l_q\}.
\end{equation}The query, key, and value matrices in CAM are linearly projected into $`H`$ attention heads as
\begin{equation}
\mathbf{Q}_h^{s_m,l_p}=\mathbf{z}^{s_m,l_p}\mathbf{W}_{Q,h}^{(l_p)},
\mathbf{K}_h^{s_m,l_q}=\mathbf{z}^{s_m,l_q}\mathbf{W}_{K,h}^{(l_q)},
\mathbf{V}_h^{s_m,l_q}=\mathbf{z}^{s_m,l_q}\mathbf{W}_{V,h}^{(l_q)},
\end{equation}where $`\mathbf{W}_{Q,h}^{(\cdot)}`$, $`\mathbf{W}_{K,h}^{(\cdot)}`$, and $`\mathbf{W}_{V,h}^{(\cdot)}`$ are learnable projection matrices for the $`h`$-th head. The fused output is subsequently computed as
\begin{equation}
\hat{\mathbf{z}}_h^{s_m,(l_p,l_q)}=\text{softmax}\left(\dfrac{\mathbf{Q}_h^{s_m,l_p}\left(\mathbf{K}_h^{s_m,l_q}\right)^T}{\sqrt{d_k}}\right)\mathbf{V}_h^{s_m,l_q},
\end{equation}where $`d_k`$ denotes the dimensionality of the key vectors. This operation allows modality $`l_p`$ to selectively attend to informative components of modality $`l_q`$, thereby capturing cross-modal dependencies and complementary fault-related patterns. Three modality pairs, i.e., vibration and current, current and acoustic, and acoustic and vibration are fused through this process, respectively, and the three fused embeddings are subsequently concatenated as the comprehensive representations of the input from a single domain, formulated as
\begin{equation}
\hat{\mathbf{z}}^{s_m} = \left[\text{Concat}\left(\hat{\mathbf{z}}_1^{s_m,(v,c)},\ldots,\hat{\mathbf{z}}_H^{s_m,(v,c)}\right), \text{Concat}\left(\hat{\mathbf{z}}_1^{s_m,(c,a)},\ldots,\hat{\mathbf{z}}_H^{s_m,(c,a)}\right), \text{Concat}\left(\hat{\mathbf{z}}_1^{s_m,(a,v)},\ldots,\hat{\mathbf{z}}_H^{s_m,(a,v)}\right)\right].
\end{equation}Domain-level disentanglement
Since samples from different source domains originate from distinct working conditions but share the same fault label space, the obtained representations fusing multi-modal information contain both domain-invariant information that is shared across different working conditions and domain-specific characteristics that are correlated with particular operating conditions. Therefore, we propose to extract fault-discriminative features that are insensitive to domain variations while preserving domain-specific information that reflects working condition characteristics from the multi-modal fused representations. To this end, a domain-level disentanglement framework is further introduced to explicitly decouple domain-invariant and domain-specific representations across multiple source domains as illustrated as Fig. 3. Similar to the modality-level design, the fused representation of each sample is projected into two complementary subspaces through two separate embedding networks, yielding a domain-invariant representation and a domain-specific representation, respectively, formulated as
\begin{equation}
\mathbf{h}_i^{s_m,inv}=F_{inv}\left(\hat{\mathbf{z}}_i^{s_m}\right),
\mathbf{h}_i^{s_m,spe}=F_{spe}\left(\hat{\mathbf{z}}_i^{s_m}\right),
\end{equation}where $`F_{inv}`$ and $`F_{spe}`$ denote the domain-invariant and domain-specific embedding networks, respectively. Three sets of domain-level disentanglement loss functions are then designed as follows.
(1) Domain similarity loss. The domain-invariant representations from different source domains are expected to follow similar distributions, as they encode fault-related semantics that should generalize across unseen working conditions. To enforce this property, a domain-level MMD loss is introduced to align the invariant feature distributions among all source domains. Formally, the domain similarity loss is defined as
\begin{equation}
\begin{aligned}
\mathcal{L}_{sim}^D &= \sum_{m\neq n}\text{MMD}\left(\mathbf{h}_i^{s_m,inv}, \mathbf{h}_i^{s_n,inv}\right)\\
&=\sum_{m\neq n}\left[\frac{1}{(N_m^s)^2}\sum_{i=1}^{N_m^s}\sum_{j=1}^{N_m^s}k\left(\mathbf{h}_i^{s_m,inv}, \mathbf{h}_j^{s_m,inv}\right) + \frac{1}{(N_n^s)^2}\sum_{i=1}^{N_n^s}\sum_{j=1}^{N_n^s}k\left(\mathbf{h}_i^{s_n,inv}, \mathbf{h}_j^{s_n,inv}\right)\right.\\
&\phantom{=\;\;}\left.- \frac{2}{N_m^sN_n^s}\sum_{i=1}^{N_m^s}\sum_{j=1}^{N_n^s}k\left(\mathbf{h}_i^{s_m,inv}, \mathbf{z}_j^{s_n,inv}\right)\right].
\end{aligned}
\end{equation}By minimizing this loss, the model is encouraged to learn domain-agnostic representations that are robust to working condition variations.
(2) Intra-domain orthogonality loss. While invariant representations capture shared fault semantics, domain-specific representations are intended to model working-condition-related characteristics. To prevent redundancy between these two subspaces, an orthogonality constraint is imposed within each domain by minimizing the statistical dependence between domain-invariant and domain-specific representations. Specifically, a covariance-based orthogonality loss is formulated as
\begin{equation}
\mathcal{L}_{ortho1}^D = \sum_{m=1}^{M}\left\|\text{Cov}\left(\mathbf{h}_i^{s_m,inv}, \mathbf{h}_i^{s_m,spe}\right)\right\|_2.
\end{equation}This loss facilitates a clear separation between the domain-invariant subspace and the domain-specific subspace to prevent information leakage.
(3) Inter-domain orthogonality loss. In addition, domain-specific representations from different source domains should remain distinctive, as each domain corresponds to a unique working condition. There should be limited correlation among domain-specific features across domains. As a result, an inter-domain orthogonality constraint is introduced to minimize the covariance between domain-specific representations from different source domains, defined as
\begin{equation}
\mathcal{L}_{ortho2}^D = \sum_{m\neq n}\left\|\text{Cov}\left(\mathbf{h}_i^{s_m,spe}, \mathbf{h}_i^{s_n,spe}\right)\right\|_2.
\end{equation}The proposed domain-level disentanglement is achieved by jointly optimizing the domain similarity loss, the intra-domain orthogonality loss, and the inter-domain orthogonality loss, formulated as follows.
\begin{equation}
\mathcal{L}_d = \mathcal{L}_{sim}^D + \mathcal{L}_{ortho1}^D + \mathcal{L}_{orth2}^D.
\end{equation}This optimization enables separation of shared and specific features across source working conditions, thereby enhancing generalization towards unseen working conditions. Combined with the modality-level disentanglement and multi-modal fusion modules, the ultimate representations are utilized for fault diagnosis.
Overall objective function
The learned domain-invariant and domain-specific representations are concatenated as input of a fault classifier to obtain the predicted fault probability $`\hat{y}_i^{s_m}`$. To ensure discriminative capability for fault diagnosis, a cross-entropy loss is employed on the source domain samples. The classification loss is formulated as
\begin{equation}
\mathcal{L}_{cls}=\frac{1}{M}\sum_{m=1}^{M}\frac{1}{N_m^s}\text{CE}\left(\hat{y}_i^{s_m}, y_i^{s_m}\right),
\end{equation}where $`\text{CE}`$ denotes the cross-entropy loss.
The proposed framework is trained in an end-to-end manner by jointly optimizing the fault classification objective and the dual-level disentanglement loss. The overall loss function is defined as a weighted combination of these three parts, represented as
\begin{equation}
\mathcal{L} = \mathcal{L}_{cls} + \lambda_m\mathcal{L}_m + \lambda_d\mathcal{L}_d,
\end{equation}where $`\lambda_m`$ and $`\lambda_d`$ are non-negative trade-off parameters for the modality-level disentanglement and the domain-level disentanglement, respectively. After training on multiple source domains, the well-trained model is directly used on the target domain under unseen working conditions without any sample involved in the training process.
Experimental verification
Dataset construction
To validate the proposed multi-modal DG method for fault diagnosis under unseen conditions, an induction motor fault dataset was constructed using a Drivetrain Dynamics Simulator (DDS) platform, as shown in Fig. 4. The test motor drives a gearbox transmission system that is coupled to an electromagnetic load, while the rotating speed of the motor is precisely regulated by a motor controller. Multi-modal sensing signals are synchronously acquired during operation. Specifically, a triaxial vibration sensor is mounted on the motor housing to capture motor vibration signals along three orthogonal directions. Three-phase stator current signals are collected using three current sensors. In addition, a microphone array consisting of six microphones is deployed in proximity to the test motor to record acoustic signals. The vibration and current signals are sampled at a frequency of 5,120 Hz, and the microphones have a sampling rate of 44,100 Hz.
 style="width:75.0%" />
style="width:75.0%" />
| Class label | Fault type | Abbreviation |
|---|---|---|
| 1 | Normal | N |
| 2 | Broken rotor bar | BRB |
| 3 | Stator winding fault | SWF |
| 4 | Parallel misaligned rotor | PMR |
| 5 | Bearing fault | BF |
| 6 | Rotor bow | RB |
| 7 | Angular misaligned rotor | AMR |
| 8 | Rotor unbalance | RU |
Categories of motor health states.
Eight test motors with different health states were employed in the experiments, including one healthy motor (N) and seven faulty motors, as summarized in Table 1. The broken rotor bar (BRB) motor contains three fractured bars in the rotor cage. The stator winding fault (SWF) motor exhibits inter-turn short-circuit faults in the stator windings. The parallel misaligned rotor (PMR) fault corresponds to a radial displacement of the rotor relative to the motor centerline while maintaining parallel alignment with the shaft axis. In contrast, the angular misaligned rotor (AMR) fault is characterized by a radial displacement occurring at only one end of the rotor. For the bearing fault (BF) motor, two bearings of the motor have an inner race defect and an outer race defect, respectively. The rotor bow (RB) fault indicates that the rotor shaft is permanently bent, while the rotor unbalance (RU) fault is introduced by attaching unbalanced masses to the rotor to generate asymmetric centrifugal forces.
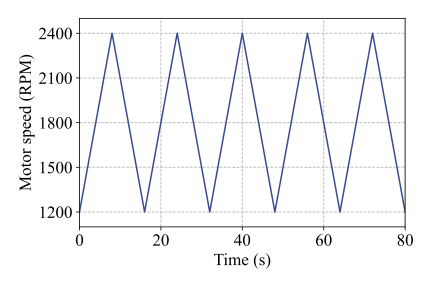
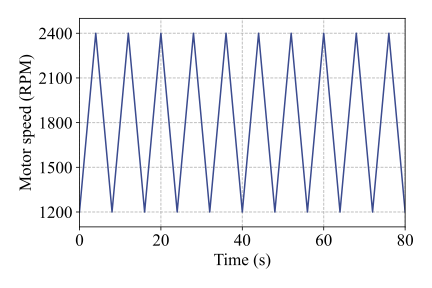
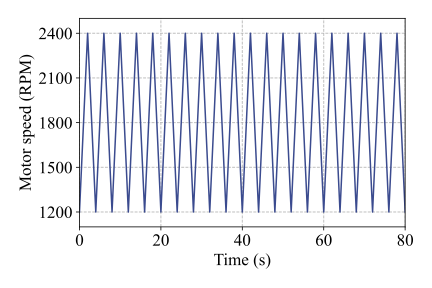
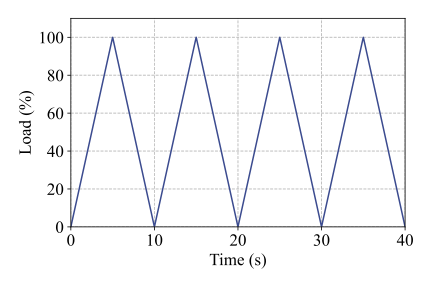
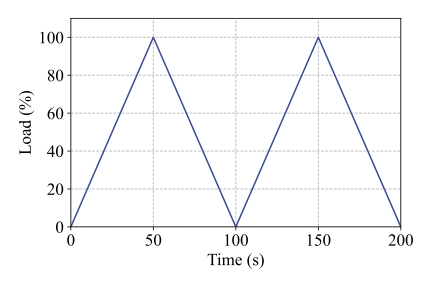
All eight motors were tested under nine distinct working conditions, including four constant-speed conditions and five time-varying conditions. Detailed descriptions of these operating conditions are provided in Table 2. The first four conditions (C1-C4) correspond to constant but different rotating speeds, while sharing the same load level, which is set to 100% of the platform’s maximum load of 72 N·m. Conditions C5, C6, and C7 involve cyclic speed variations between 1200 RPM and 2400 RPM with different acceleration and deceleration rates, as illustrated in Fig. 5(a)-(c), while the load remains constant. In contrast, conditions C8 and C9 are characterized by a constant rotating speed of 1800 RPM, whereas the load follows a cyclic increasing-and-decreasing pattern between 0% and 100%, as shown in Fig. 5(d) and (e). Notably, data acquisition was initiated 10 s after motor startup to ensure stable operating conditions.
| Condition | Speed (RPM) | |||
| speed (RPM/s) | Load percentage (%) | |||
| load (%/s) | ||||
| C1 | 1200 | 0 | 100 | 0 |
| C2 | 1800 | 0 | 100 | 0 |
| C3 | 2400 | 0 | 100 | 0 |
| C4 | 2700 | 0 | 100 | 0 |
| C5 | 1200-2400 | 150 | 100 | 0 |
| C6 | 1200-2400 | 300 | 100 | 0 |
| C7 | 1200-2400 | 600 | 100 | 0 |
| C8 | 1800 | 0 | 0-100 | 20 |
| C9 | 1800 | 0 | 0-100 | 2 |
Details of working conditions in the experiments.
Implementation details
For each working condition and each motor, the collected multi-modal signals were segmented into fixed-length samples of 0.2 s using a non-overlapping sliding window. The first 100 s of data under stable operating conditions were selected for analysis, resulting in 500 samples for each fault category under each working condition. Based on this dataset, two schemes of cross-condition fault diagnosis tasks were designed, as summarized in Table 3. The first type (T1-T4) corresponds to scenarios in which the model is trained using data from multiple constant working conditions and evaluated on a different constant condition. The second type (T5-T9) represents a more challenging and practically relevant setting, where the model is trained on data from multiple constant working conditions and tested on time-varying operating conditions.
| Task | Source working condition | Target working condition |
|---|---|---|
| T1 | C2, C3, C4 | C1 |
| T2 | C1, C3, C4 | C2 |
| T3 | C1, C2, C4 | C3 |
| T4 | C1, C2, C3 | C4 |
| T5 | C1, C2, C3 | C5 |
| T6 | C1, C2, C3 | C6 |
| T7 | C1, C2, C3 | C7 |
| T8 | C1, C2, C3 | C8 |
| T9 | C1, C2, C3 | C9 |
Details of cross-condition tasks.
In this work, vibration signals were transformed into time-frequency representations using STFT with a Fourier transform length of 127 and a hop length of 33, producing time-frequency maps of size $`64 \times 32 \times 3`$. Acoustic signals were converted into Mel-spectrograms with a Fourier transform length of 512, a hop length of 138, and 64 Mel frequency bins, resulting in representations of size $`64 \times 64 \times 6`$. The current signals were kept in their original form with a size of $`1024 \times 3`$. For feature extraction, all signal encoders adopt a ResNet architecture consisting of a convolutional preprocessing layer followed by four residual blocks. Specifically, 2D ResNets are employed for vibration and acoustic modalities, while a 1D ResNet is used for the current modality. Both the modality-level and domain-level embedding networks are implemented as single-layer fully connected networks, and the fault classifier also adopts a single-layer fully connected structure. The dimensionalities of the modality-invariant, modality-specific, domain-invariant, and domain-specific representations are all set to 128. In the triple-modal fusion module, 8 heads with dimensionality of 32 are used for CAM. The model is trained using the Adam optimizer with a learning rate of 0.001 and a batch size of 256 for each source domain. All experiments are conducted on an NVIDIA GeForce RTX 4090 GPU and repeated five times to mitigate the effects of randomness.
Nine state-of-the-art methods are introduced for comparison, including six representative DG approaches and three multi-modal fusion methods for fault diagnosis :
-
MMD: A basic DG method which aligns feature distributions among multiple source domains by minimizing the summation of MMD across all domain pairs.
-
DANN : A domain adversarial neural network which uses adversarial learning for multi-source domain alignment.
-
MLDG : A meta-learning-based DG method that learns domain-generalizable representations by simulating domain shifts during training.
-
CDDG : A causal disentanglement DG method that separates causal factors from non-causal factors to enhance generalization.
-
DTDG : A domain transferability-based DG method assigning weights to source domains in adversarial learning.
-
CCN : A causal consistency network that introduces a causal consistency loss to model the causality of faults.
-
FCFN : A multi-sensor fusion network with a feature convergence layer to integrate heterogeneous sensor information.
-
MFHR : A multi-sensor fusion method for high-reliability fault diagnosis with a decision-level fusion.
-
MMCDF : A multi-modal cross-domain fusion network that integrates DA with multi-modal feature fusion.
For fair comparison, all methods are implemented using the same backbone feature extractors as the proposed method. In DG methods designed for single-modal data, the features from multiple modalities are concatenated as the comprehensive representations.
Comparison results
The diagnosis results of the proposed method (Ours) and the comparison methods under the first scheme of cross-condition tasks are illustrated in Fig. 6(a), and the average accuracy is also calculated. Overall, the proposed method consistently outperforms all comparison methods across T1-T4 as well as in terms of average accuracy, demonstrating its superior generalization capability under unseen working conditions. It can be observed that the accuracies achieved on Tasks T2 and T3 are higher than those on Tasks T1 and T4. It suggests that the rotating speeds of the target domains in T2 and T3 are closer to, or fall within, the range of the source domains, leading to reduced domain discrepancy. Specifically, traditional DG methods, such as MMD and DANN, exhibit relatively poor performance, particularly in T1, where the target condition shows a large distribution discrepancy from the source domains as the rotating speed of 1200 RPM is much lower than that in source domains. This indicates that enforcing global domain invariance alone is insufficient to handle complex condition shifts in fault diagnosis scenarios. Although methods such as CDDG, DTDG, and CCN improve performance by incorporating causal factors or weighting strategies, their gains remain limited, suggesting that condition-related specific information is still inadequately modeled. Furthermore, these methods are designed for single-modal data and cannot exploit complementary information across multiple sensing modalities, which limits their generalization capability. Multi-modal fusion methods, such as FCFN and MFHR, outperform several DG baselines, demonstrating the benefit of integrating multiple sensors. Nevertheless, these approaches mainly focus on information fusion under constant conditions and do not explicitly address domain generalization. MMCDF achieves better performance by combining multi-modal fusion with DA, but it still achieves inferior performance compared with the proposed method.
Fig. 6(b) reports the fault diagnosis results on the second task scheme, where the models are trained on multiple constant working conditions and tested on unseen time-varying conditions. All the methods have relatively higher accuracies than those obtained in most tasks in the first scheme, especially in task T8 and T9. This suggests that load variations may induce relatively smaller domain shifts compared with speed variations, and that exposure to constant-speed source domains within the target speed range can facilitate generalization to time-varying operating conditions. Traditional DG methods show limited robustness under time-varying conditions, as their domain alignment strategies mainly rely on global distribution matching and struggle to capture dynamically changing characteristics. Advanced DG approaches, particularly for DTDG and CCN, achieve relatively better performance by incorporating domain weighting or causal modeling, yet their generalization ability remains constrained due to the simple multi-modal fusion strategy. Multi-modal fusion methods shows unstable diagnosis performance, demonstrating their limitations to tackle domain shifts under unseen working conditions. In contrast, the proposed method consistently achieves the highest accuracy across almost all time-varying tasks and yields the best average performance. This superiority can be attributed to the synergistic effects of cross-domain mixed fusion and dual disentanglement, which effectively enhance robustness to dynamic domain shifts while preserving both modality-specific and domain-related discriminative information.
Ablation study
To evaluate the contribution of each component in the proposed framework, comprehensive ablation studies were conducted by selectively removing individual modules while keeping the remaining architecture consistent with the original model. Specifically, w/o modality-dis, w/o domain-dis, and w/o dis denote the variants in which the modality-level disentanglement, domain-level disentanglement, and both dual-level disentanglement are removed, respectively. These variants are implemented by setting the corresponding trade-off coefficients in the overall loss function to zero. The variant w/o mix indicates that the proposed cross-domain mixed fusion mechanism is disabled. To further investigate the effectiveness of the proposed triple-modal fusion module, several alternative fusion strategies are considered. The variant concat removes the proposed fusion module and directly concatenates the representations from the three modalities. In concat_emb, an additional embedding layer consisting of a single fully-connected layer is applied to the concatenated features. Similarly, element-wise feature addition across modalities is introduced as another fusion strategy, denoted as add, while add_emb further applies a single fully-connected embedding layer after the addition operation. Finally, Baseline represents the simplest configuration, in which all the aforementioned components are removed and multi-modal features are fused solely by direct concatenation. The results of these ablation methods are presented in Table 4.
| Method | T1 | T2 | T3 | T4 | T5 | T6 | T7 | T8 | T9 | Average |
|---|---|---|---|---|---|---|---|---|---|---|
| Baseline | 36.98 | 68.10 | 83.00 | 51.16 | 78.52 | 80.04 | 79.05 | 98.53 | 98.53 | 74.88 |
| w/o dis | 51.18 | 80.65 | 92.73 | 72.86 | 90.84 | 91.08 | 91.12 | 99.97 | 99.97 | 85.60 |
| w/o modality-dis | 54.20 | 83.00 | 94.28 | 79.21 | 93.18 | 93.23 | 93.65 | 99.95 | 99.95 | 87.85 |
| w/o domain-dis | 53.70 | 80.68 | 92.02 | 76.35 | 91.31 | 91.28 | 91.60 | 99.87 | 99.87 | 86.30 |
| w/o mix | 45.40 | 75.99 | 93.70 | 69.99 | 85.01 | 85.92 | 85.43 | 99.78 | 99.78 | 82.33 |
| concat | 52.54 | 68.59 | 86.94 | 79.51 | 90.99 | 91.72 | 92.35 | 99.93 | 99.93 | 84.72 |
| concat_emb | 50.16 | 75.82 | 91.74 | 78.15 | 91.40 | 91.76 | 91.69 | 99.98 | 99.98 | 85.63 |
| add | 43.10 | 75.89 | 93.68 | 78.65 | 90.19 | 90.31 | 91.01 | 100.00 | 100.00 | 84.76 |
| add_emb | 42.92 | 73.64 | 95.02 | 78.11 | 91.13 | 91.39 | 91.80 | 100.00 | 100.00 | 84.89 |
| Ours | 56.98 | 82.79 | 96.24 | 80.42 | 92.75 | 92.82 | 92.98 | 99.97 | 99.97 | 88.32 |
Accuracy of ablation study on different tasks (%).
Overall, removing any key module leads to performance degradation compared with the complete model in terms of the average accuracy, demonstrating that all components contribute positively to fault diagnosis generalization. First, the Baseline model achieves the lowest average accuracy, indicating that simple multi-modal feature concatenation without mixed fusion or disentanglement is insufficient for handling cross-condition generalization. Introducing disentanglement mechanisms significantly improves performance. Compared with Baseline, the variants w/o modality-dis and w/o domain-dis both yield notable accuracy gains, suggesting that disentangling modality-related and domain-related factors is crucial for learning transferable representations. When both disentanglement mechanisms are removed (w/o dis), the performance further drops, highlighting the complementary nature of dual-level disentanglement. Relatively, domain-level disentanglement contributes more in the proposed framework, as dropping this module results in higher accuracy decline, indicating the significance of domain-invariant and domain-specific feature learning for cross-domain diagnosis. Second, disabling the cross-domain mixed fusion (w/o mix) leads to a significant decrease in average accuracy, which verifies the effectiveness of modality augmentation across source domains in mitigating domain bias. Third, replacing the proposed triple-modal fusion module with simple fusion strategies consistently results in inferior performance. Although adding an embedding layer slightly improves the results compared with direct fusion, these methods still lag behind the proposed cross-attention-based fusion, demonstrating that deep and adaptive modeling of inter-modal correlations is essential for effective multi-modal collaboration. Finally, the proposed method achieves the highest accuracy across most tasks and the best average performance, confirming that the joint design of cross-domain mixed fusion, dual-level disentanglement, and triple-modal fusion is critical for achieving robust fault diagnosis under unseen working conditions.
In addition, experiments were conducted using single-modality information to further verify the advantage of multi-modal data fusion in cross-domain motor fault diagnosis. Specifically, a single encoder was employed to extract features from one modality at a time, while the domain-level disentanglement mechanism was retained for fair comparison. The fault diagnosis results obtained using each individual modality are summarized in Table 5. It can be observed that models trained on a single modality exhibit substantially lower accuracy than the multi-modal model across almost all tasks, indicating that relying on a single sensing source is insufficient for robust cross-domain fault diagnosis. Among the single-modality approaches, vibration signals achieve the best overall performance, which can be attributed to their rich fault-related mechanical information. However, their performance still degrades under certain working conditions, especially when the domain shift becomes significant. Current signals and acoustic signals individually show much lower accuracy, reflecting their limited discriminative capability when used in isolation and their higher sensitivity to operating condition variations. The proposed multi-modal method achieves the highest accuracy across all tasks, demonstrating that fusing heterogeneous signals enables the model to exploit complementary fault characteristics and improve generalization ability.
| Method | T1 | T2 | T3 | T4 | T5 | T6 | T7 | T8 | T9 | Average |
|---|---|---|---|---|---|---|---|---|---|---|
| Vibration | 40.48 | 72.75 | 83.12 | 73.02 | 75.50 | 76.55 | 77.05 | 99.66 | 99.66 | 77.53 |
| Current | 17.32 | 23.58 | 22.76 | 21.62 | 36.19 | 36.45 | 35.12 | 35.52 | 35.52 | 29.34 |
| Acoustic | 20.42 | 33.86 | 60.90 | 30.08 | 50.16 | 45.79 | 44.80 | 49.13 | 49.13 | 42.70 |
| Multi-modal (Ours) | 56.98 | 82.79 | 96.24 | 80.42 | 92.75 | 92.82 | 92.98 | 99.97 | 99.97 | 88.32 |
Accuracy of single-modal models on different tasks (%).
Discussion
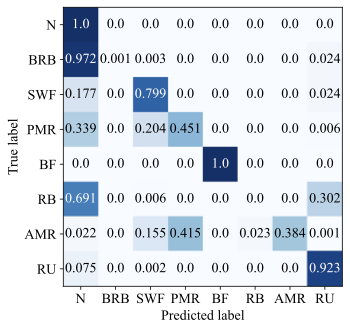
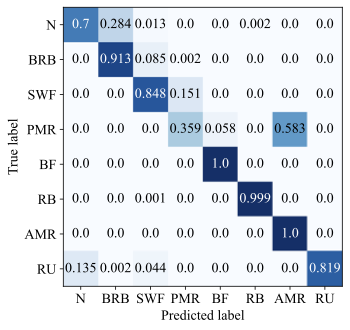
To further analyze the fault diagnosis performance, the confusion matrices of the Baseline method and the proposed method are presented in Fig. 7. It can be observed that the Baseline method exhibits noticeable misclassification among several fault categories. In particular, confusion frequently occurs between fault types of N and BRB, N and RB. This indicates that relying on simple multi-modal feature concatenation without effective disentanglement and adaptive fusion makes it difficult to distinguish faults from normal states under cross-condition settings. In contrast, the proposed method achieves substantially clearer diagonal patterns across all tasks, demonstrating improved class-wise discrimination. Most fault categories exhibit near-perfect classification accuracy without access to any samples in this domain, and most confusion observed in the Baseline method is significantly alleviated.
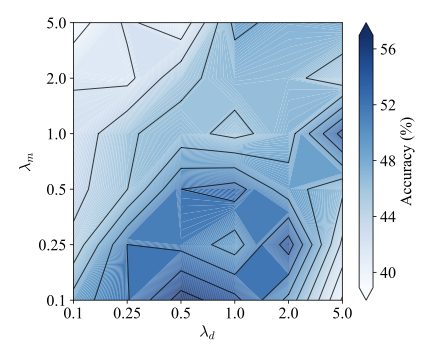
Furthermore, model sensitivity on the two trade-off parameters $`\lambda_m`$ and $`\lambda_d`$ is analyzed on the first task T1. The diagnosis accuracy over different parameter values is depicted as Fig. 8. It can be observed that the diagnosis accuracy varies smoothly with respect to both $`\lambda_m`$ and $`\lambda_d`$ within the middle-bottom region, indicating that the proposed method is not overly sensitive to the exact choice of trade-off parameters in specific ranges. Overall, relatively higher accuracies are achieved when $`\lambda_m`$ is set to small or moderate values, suggesting that excessive emphasis on modality-level disentanglement may suppress modality-specific discriminative information. In contrast, moderate values of $`\lambda_d`$ consistently contribute to performance improvement, highlighting the importance of domain-level disentanglement in reducing cross-domain discrepancies. Specifically, the best performance is obtained when $`\lambda_m`$ is around 0.1-0.25 and $`\lambda_d`$ lies in the range of 0.5-2.0, where a favorable balance between modality disentanglement and domain alignment is achieved. Consequently, $`\lambda_m`$ and $`\lambda_d`$ are set to 0.1 and 0.5, respectively, in this work.
 style="width:50.0%" />
style="width:50.0%" />
Conclusion
In this work, a multi-modal cross-domain mixed fusion model with dual disentanglement is proposed for fault diagnosis under unseen working conditions. A dual-level disentanglement strategy is introduced to decouple modality-invariant and modality-specific features, as well as domain-invariant and domain-specific representations, enabling generalizable feature learning across operating conditions. A multi-modal cross-domain mixed fusion strategy is proposed to augment modality and domain diversity for enhanced feature robustness. Furthermore, a triple-modal fusion mechanism is designed to adaptively integrate multi-modal representations for comprehensive information integration. Extensive experiments conducted under both constant and time-varying working conditions demonstrate that the proposed method consistently outperforms state-of-the-art domain generalization and multi-modal fusion approaches. Ablation studies further verify the effectiveness of each proposed component and the superiority of multi-modal heterogeneous information fusion. In future work, we plan to extend the proposed framework to more complex industrial scenarios involving more realistic operating conditions, as well as investigate its applicability to other rotating machinery.
Acknowledgements
This research was supported by the National Natural Science Foundation of China (No. 52405122 and No. 52375109), the National Key Research and Development Program of China (No. 2023YFB3408502), and the China Postdoctoral Science Foundation (No. 2025M771378).
📊 논문 시각자료 (Figures)