MSACL: Multi-Step Actor-Critic Learning with Lyapunov Certificates for Exponentially Stabilizing Control

Yongwei Zhang, Yuanzhe Xing and Quanyi Liang are with the School of Mathematical Sciences, Beihang University, Beijing 100191, China (email: {zhangyongwei, mathXyz, qyliang}@buaa.edu.cn). These three authors contributed equally to this work.

Quan Quan is with the School of Automation Science and Electrical Engineering, Beihang University, Beijing 100191, China (e-mail: qq buaa@buaa.edu.cn).

Zhikun She is with the School of Mathematical Sciences, Beihang University, Beijing 100191, China, and also with the Fujian Key Laboratory of Financial Information Processing, Putian University, Putian 351100, China (e-mail: zhikun.she@buaa.edu.cn).

Corresponding authors: Quan Quan and Zhikun She. While alternative frameworks like constrained Markov Decision Processes (cMDPs) [7], [8] and Hamilton-Jacobi reachability analysis [9], [10] offer potential solutions, certificatebased methods constitute a fundamental framework for verifying and stabilizing learning agents. By leveraging rigorous control-theoretic tools, such as Lyapunov certificates for establishing asymptotic stability [11]- [14] and barrier certificates for ensuring set invariance [15], [16], these methods provide concise, data-driven proofs of system behavior. The synthesis of stability certificates has undergone a paradigm shift from computationally intensive analytical methods toward scalable neural architectures. Traditional approaches, such as sum-ofsquares (SOS) optimization [17]- [19] and algebraic synthesis [20], are often restricted to polynomial dynamics. To bridge the gap between black-box learning and verifiable control, the field has evolved from probabilistic methods, notably the use of Gaussian Processes for safe exploration [21], to formal frameworks for synthesizing neural certificates that estimate regions of attraction (ROA) [22], [23]. Building on this verification-centric perspective, recent research has advanced toward the joint synthesis of neural certificates and policies. For instance, Chang et al. [24], [25] and Quan et al. [26]- [28] demonstrated that neural certificates can function as critics during training, directly guiding policy optimization to satisfy formal stability constraints.

In contrast to the stability-by-design paradigms presented above, standard model-free RL algorithms, such as DDPG [29], PPO [31], TD3 [32], SAC [33], and SAC’s distributional variant DSAC [34], [35], lack intrinsic stability guarantees, thus facing fundamental limitations in precision control tasks. These methods treat stability as an incidental byproduct of reward maximization rather than a structural property. Consequently, employing general RL algorithms for safety-critical tasks necessitates extensive reward engineering to achieve stable behaviors [1], [2]. To bridge this gap, Lyapunov-based RL algorithms have been developed to integrate stability constraints into the learning process. For instance, Policy Optimization with Lyapunov Certificates (POLYC) [25] incorporates Lyapunov certificates within the PPO framework, while Lyapunov-based Actor-Critic (LAC) [36] introduces an off-policy approach for learning stability-constrained critics. By augmenting standard RL architectures with learned Lyapunov certificates, these methods provide structural stability guarantees for nonlinear control systems. However, several critical limitations persist. First, these approaches suffer from low sample efficiency under on-policy training paradigms. Second, they often fail to account for control costs during policy optimization. More critically, most existing methods focus solely on asymptotic stability, which lacks the rapid stabilization characteristics necessary for high-performance response in dynamic control scenarios.

To overcome these limitations, we propose Multi-Step Actor-Critic Learning with Lyapunov Certificates (MSACL), a Lyapunov-based off-policy RL algorithm that enhances sample efficiency [37], [38] while optimizing a comprehensive objective that balances state regulation and control cost. By integrating exponential stability constraints into the maximum entropy reinforcement learning (MERL) architecture, MSACL ensures rapid stabilization and enhanced robustness. A key feature of our approach is the multi-step learning mechanism, which captures long-horizon dynamics to establish connections between temporal difference learning and formal stability verification. By mitigating discretization errors and stochastic noise associated with single-step transitions, this mechanism enables the synthesis of policies that are both high-performing and mathematically certifiable.

In summary, this article presents a Lyapunov-based RL approach for model-free exponentially stabilizing control. The main contributions are summarized as follows:

(i) Exponential Stability via Multi-Step Learning. We propose the MSACL algorithm, which integrates exponential stability with Lyapunov certificate learning via a multi-step mechanism. This algorithm enforces exponential convergence rates, providing stability-guaranteed performance for complex nonlinear control, surpassing conventional asymptotic methods. (ii) Sample-Efficient Off-Policy Framework. We develop a sample-efficient off-policy framework that leverages the maximum entropy paradigm and importance sampling. This framework effectively manages distribution shifts and interaction data reuse, thus enhancing training stability compared to existing on-policy algorithms. (iii) Systematic Evaluation and Robustness Analysis. We establish an evaluation platform across six benchmarks comprising stabilization and high-dimensional tracking tasks. Experiment results demonstrate superior performance, robustness and generalization of MSACL, while sensitivity analyses elucidate the multi-step bias-variance trade-off to guide diverse control tasks.

The remainder of this article is organized as follows. Section II formulates the control problems and establishes necessary theoretical foundations. Section III describes the Lyapunov certificate learning methodology. Section IV presents the optimization process within the actor-critic framework. Section V provides comprehensive experimental evaluations across six benchmarks. Finally, Section VI discusses the design philosophy and concludes this article.

This section establishes the theoretical foundations for MSACL. We first define the stabilization and tracking problems for model-free discrete-time systems, then introduce Lyapunov-based exponential stability criteria, and finally review the MERL framework.

In this article, we study the stabilization problem for general discrete-time deterministic control systems:

where x t ∈ X ⊆ R d denotes the state at time t, u t ∈ U ⊆ R m denotes the control input, X and U represent the sets of admissible states and control inputs, respectively, and f : X × U → X is the flow map. Given that f is unknown, we adopt a model-free control paradigm. Let X 0 ⊆ X denote the set of initial states. For any x 0 ∈ X 0 , let x(t, x 0 ) denote the state at time t along the trajectory starting from x 0 . For notational simplicity, x t is used to denote x(t, x 0 ) whenever the context is unambiguous. It is worth noting that the discretetime case presented in this article can be similarly extended to the continuous-time case; interested readers may refer to [11] and [25] for details.

In the context of control systems, our objective is to find a state feedback policy π : X → U such that the control input u t = π(x t ) renders the closed-loop system x t+1 = f (x t , π(x t )) to satisfy exponential stability. For clarity, we consider the scenario where the state x t is fully observable, and the policy π is stationary, i.e., it depends only on the state and not explicitly on time. Specifically, the problem studied in this article is formulated as:

Problem 1: (Exponential Stabilization) For the control system (1), design a stationary policy π such that for any initial state x 0 ∈ X 0 , the resulting closed-loop trajectory x(t, x 0 ) exponentially converges to the equilibrium state x g .

Without loss of generality, let x g denote the origin, i.e., x g = 0. Furthermore, the tracking problem is inherently encompassed within the stabilization framework, as tracking a time-varying reference signal x ref t reduces to stabilizing the error e t = x t -x ref t at zero.

Definition 1: For the control system (1), the equilibrium state x g is said to be exponentially stable if there exist constants C > 0 and 0 < η < 1 such that

To guarantee that the closed-loop system is exponentially stable with respect to x g , we introduce the following lemma:

Lemma 1: For the control system (1), if there exists a continuous function V : X → R and positive constants α 1 , α 2 > 0 and 0 < α 3 < 1 satisfying:

for all t ∈ Z ≥0 , where x t+1 = f (x t , u t ), then the origin x g = 0 is exponentially stable. The function V is referred to as an exponentially stabilizing control Lyapunov function. Lemma 1 is a classic result in control theory, while its continuous-time counterpart is discussed in [39], we provide a concise derivation of the discrete-time version to elucidate its underlying mechanism. Specifically, starting from the descent condition V (x t+1 ) ≤ (1 -α 3 )V (x t ) in (3), the multi-step relationship can be established iteratively as:

(4) By incorporating the lower and upper quadratic bounds, i.e., α 1 ∥x t+n ∥ 2 ≤ V (x t+n ) and V (x t ) ≤ α 2 ∥x t ∥ 2 , the relationship between state norms across multiple steps follows as:

Furthermore, by setting the initial time to t = 0 and denoting the current time step as n = t ∈ Z ≥0 , we obtain the global trajectory bound:

By defining the constants C = α 2 /α 1 and η = √ 1 -α 3 , the result satisfies Definition 1, thereby proving that the control system (1) is exponentially stable with respect to x g = 0.

To begin the analysis, we interpret the control system (1) as a discrete-time environment with continuous state space X and action space U under the standard RL paradigm. At each time step t, the RL agent observes the state x t ∈ X and executes an action u t ∈ U , causing the environment to transition to the next state x t+1 and yield a scalar reward r t = r(x t , u t ). This reward is formulated to penalize state deviations from the target x g (or reference signal x ref t ) while accounting for the associated control effort.

Furthermore, we employ stochastic policies in this article to facilitate exploration within the maximum entropy RL (MERL) framework. A stochastic policy is defined as a mapping π : X → P(U), where P(U ) denotes the set of probability distributions over U , and u t ∼ π(•|x t ) is sampled from the probability distribution. We denote the state and state-action marginals induced by π as ρ π (x t ) and ρ π (x t , u t ), respectively. In contrast to standard RL, which maximizes the expected cumulative discounted reward, MERL optimizes an entropy-augmented objective [33]- [35]:

where γ ∈ [0, 1) is the discount factor, α > 0 is the temperature coefficient, and

is the policy entropy.

The corresponding soft Q-function, Q π (x t , u t ), represents the expected soft return, which comprises both rewards and entropy terms. The soft Bellman operator T π is defined as:

where x t+1 = f (x t , u t ). In the soft policy iteration (SPI) algorithm [33], the policy is optimized by alternating between soft policy evaluation, where Q π is updated via T π , and soft policy improvement, which is equivalent to finding a policy π that maximizes the soft Q-function for x t :

Although SPI converges to the optimal policy π * in tabular settings, the control problems studied in this article involve continuous state and action spaces necessitating function approximation. Thus, we parameterize the soft Q-function Q θ (x t , u t ) and the policy π ϕ (u t |x t ) using neural networks with parameters θ and ϕ. We assume π ϕ follows a diagonal Gaussian distribution, and actions are sampled using the reparameterization trick [33]: u t = g ϕ (x t ; ϵ t ), where ϵ t ∼ N (0, I m ), ensuring that the optimization objectives remain differentiable with respect to ϕ.

This section details the model-free Lyapunov certificate learning mechanism. We first introduce a sliding-window strategy for multi-step data collection, and then design a loss function for the Lyapunov network (also referred to as the Lyapunov certificate), incorporating both boundedness and stability constraints.

In contrast to conventional Lyapunov-based RL algorithms [25], [36], which primarily target asymptotic stability through single-step transitions, our proposed MSACL enforces the stricter exponential stability requirement. Guided by the multistep relationship (4), establishing exponential stability necessitates leveraging multi-step sequence samples from state trajectories. This sequential data structure provides a sufficient temporal horizon to validate the contraction properties of Lyapunov certificates.

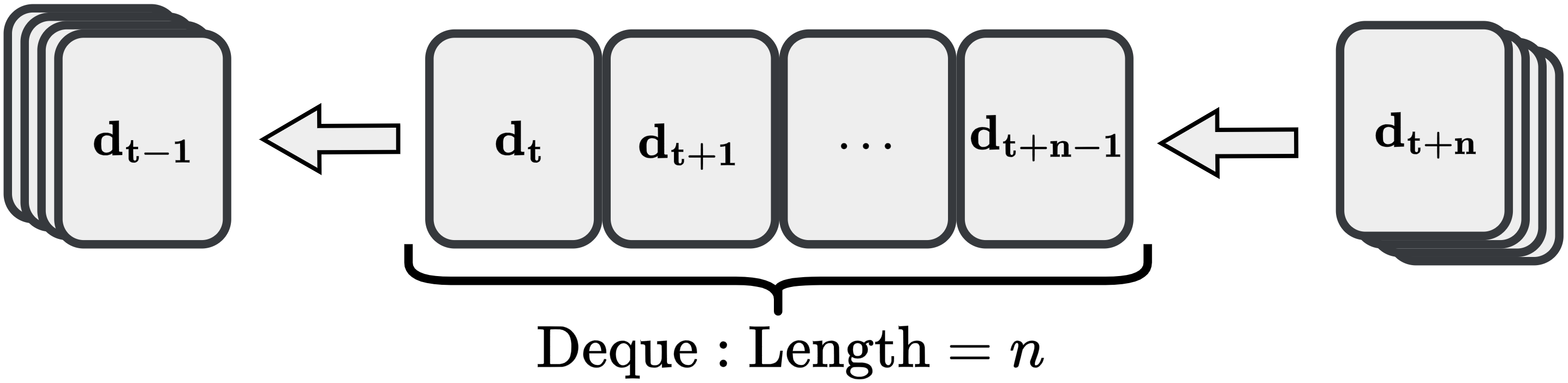
To operationalize this, we define the fundamental transition tuple as d t = (x t , u t , r t , π ϕ (u t |x t ), x t+1 ). Unlike standard replay buffers that store these tuples individually, we employ a double-ended queue (deque) as a sliding window to capture temporal correlations. Upon reaching a length of n, the complete multi-step sequence {d t , d t+1 , . . . , d t+n-1 } is packaged and transferred to the replay buffer D, while the oldest entry is concurrently removed to maintain the window size.

Similar to the soft Q-network and policy network, we introduce a Lyapunov network V ψ parameterized by ψ to estimate the Lyapunov certificate. In designing the loss function, We strictly adhere to the boundedness and multi-step stability conditions in Lemma 1.

(1) Boundedness Loss. Based on the boundedness condition in (3), we construct the boundedness loss function to ensure the Lyapunov certificate to be quadratically constrained:

where N denotes the batch size of multi-step sequence samples, i denotes the i-th sample, and n is the sequence length. This loss enforces the boundedness condition on V ψ .

(2) Multi-step Stability Loss. A major challenge in learning Lyapunov certificates from off-policy data is the discrepancy between the behavior policy π ϕold and the target policy π ϕ . To mitigate this discrepancy, we employ a sequence-wise importance sampling strategy. Specifically, for a multi-step sequence {d t , . . . , d t+n-1 } generated by π ϕold , we compute the cumulative importance sampling ratio for the transition from t to t + k (k = 1, . . . , n -1) as:

Note that we apply a clipping operation to the importance sampling ratios to prevent variance explosion and enhance training stability. On the other hand, learning Lyapunov certificates directly from off-policy data may not be accurate, as empirical sequences in the early stages of training often fail to satisfy the exponential decay condition (5), leading to unreliable certificate estimation. To establish a rigorous correspondence between empirical data and theoretical stability requirements, we propose the Exponential Stability Label (ESL) mechanism. Specifically, we introduce positive and negative samples to bridge the gap between theory and practice:

Definition 2: Within an n-step sequence sample, for the state x t+k , if it satisfies the exponential decay condition:

then d t+k is classified as a positive sample; otherwise, it is classified as a negative sample. Accordingly, we define the Exponential Stability Label as:

This labeling mechanism allows the Lyapunov network to distinguish between transitions that contribute to system stability and those that violate the certificate requirements.

Furthermore, to balance the bias-variance trade-off in multistep sequences, we introduce a weighting factor λ ∈ (0, 1), inspired by the (truncated) λ-return in classic RL literature [40]. Specifically, for the stability condition 4), small k determines a short horizon with limited information. Given that the Lyapunov network is randomly initialized and potentially inaccurate in the early stages of training, relying on short-horizon data may introduce high estimation bias. Conversely, large k captures extended information to reduce bias but accumulates environmental stochasticity into higher variance. To this end, we employ the weighting factor λ to aggregate multi-step information and balance bias-variance trade-off.

Finally, by integrating the positive/negative sample labels with the weighting factor λ, we construct the Lyapunov stability loss to enforce a rigorous correspondence between empirical samples and the stability condition (4):

where the step-wise difference loss L i diff,k (ψ) is defined as:

(3) Combined Lyapunov Loss. By integrating the boundedness loss and the multi-step stability loss, the comprehensive loss function for optimizing the Lyapunov network V ψ is formulated as:

where ω Bnd and ω Stab are positive weighting coefficients.

This section details the MSACL optimization framework. We first establish soft Q-network updates using multi-step Bellman residuals to enhance data efficiency. Then we introduce a novel policy loss incorporating Lyapunov-based stability advantages with PPO-style clipping for robust exponential stabilization. Finally, we describe automated temperature adjustment and the complete actor-critic procedure.

Following the soft Bellman operator (7), we define the sampled Bellman residual for the i-th multi-step sequence sample of Q θ as:

where Qθ denotes the target network parameterized by θ. Utilizing collected multi-step sequence samples, the loss function for the soft Q-network is defined as the mean squared Bellman error (MSBE) across the entire sequence:

In contrast to standard MERL algorithms such as SAC [33], which typically utilize single-step transition (i.e., n = 1), our approach leverages the complete n-step sequence to minimize the following objective function:

Qθ(x t+1 , u t+1 ) -α log π ϕ (u t+1 |x t+1 )

2 .

(15) Remark 1: Although minimizing (15) theoretically necessitates independent and identically distributed (i.i.d.) sampling for unbiased gradient estimation [41], our proposed multistep approach strategically balances mathematical rigor with enhanced sample efficiency. Indeed, while n-step sequences introduce temporal correlations that deviate from strict i.i.d. assumptions, experimental evidence demonstrates that moderate sequence lengths maintain learning stability. Ultimately, the substantial gains in batch data information outweigh the minor bias introduced by short-term correlations, leading to accelerated convergence and more robust control performance.

This subsection details the policy network optimization, which seamlessly integrates the maximum entropy objective with a novel Lyapunov-based stability guidance mechanism.

(1) Soft-Q Value Maximization. Following the policy optimization (8) in SPI, the first objective is to maximize the soft-Q value. For the i-th multi-step sequence sample {d i t , . . . , d i t+n-1 }, the SAC-style component of the loss function is expressed as:

Note that g ϕ (x i t+k ; ϵ i t+k ) is obtained via the reparameterization trick [33].

(2) Stability-Aware Advantage Guidance. To ensure exponential stability, we attempt to utilize the learned Lyapunov certificate V ψ to guide policy updates. Inspired by the Generalized Advantage Estimation (GAE) in PPO [31], we transform the Lyapunov descent property into an active guidance signal. Specifically, we define the stability advantage function based on V ψ at t + k as a metric for convergence performance:

A positive stability advantage (A t,k ≥ 0) indicates that the system trajectory adheres to the exponential decay condition (4). Maximizing this advantage encourages actions that accelerate V ψ decay, thereby increasing the state convergence rate toward x g . Conversely, A t,k < 0 signifies a certificate condition violation that the policy must learn to avoid. This stability-aware optimization aligns with recent developments in stable model-free control, such as D-learning [26]- [28]. Similar to (11), in order to balance the bias-variance tradeoff across varying horizons, we apply the weighting factor λ to obtain the aggregated stability advantage: (3) Integrated Policy Optimization Objective. For the ith multi-step sequence sample, we define the first-step importance sampling (IS) ratio as

. By incorporating the aggregated stability advantage (17) with PPO-style clipping to prevent excessively large updates, the policy loss function is formulated as:

Remark 2: Notably, we employ distinct importance sampling strategies for the critic and the actor. In (11), sequencelevel IS provides low-bias correction for learning V ψ from offpolicy data. This variance remains manageable via truncation in (10) since policy parameters are fixed during Lyapunov certificate updates. However, during policy optimization, where policy parameters are actively updated, sequence-level IS is avoided to prevent prohibitive variance and potential divergence. Following the PPO principle, we utilize only the firststep IS ratio ρ i (ϕ) in (18). This ensures stable optimization while retaining multi-step stability information via the aggregated stability advantage A t,λ .

Under the MERL paradigm, the temperature coefficient α in ( 6) is critical for balancing exploration and exploitation. Following the automated entropy adjustment mechanism introduced in [33], we update α by minimizing the following loss function:

where H denotes the target entropy.

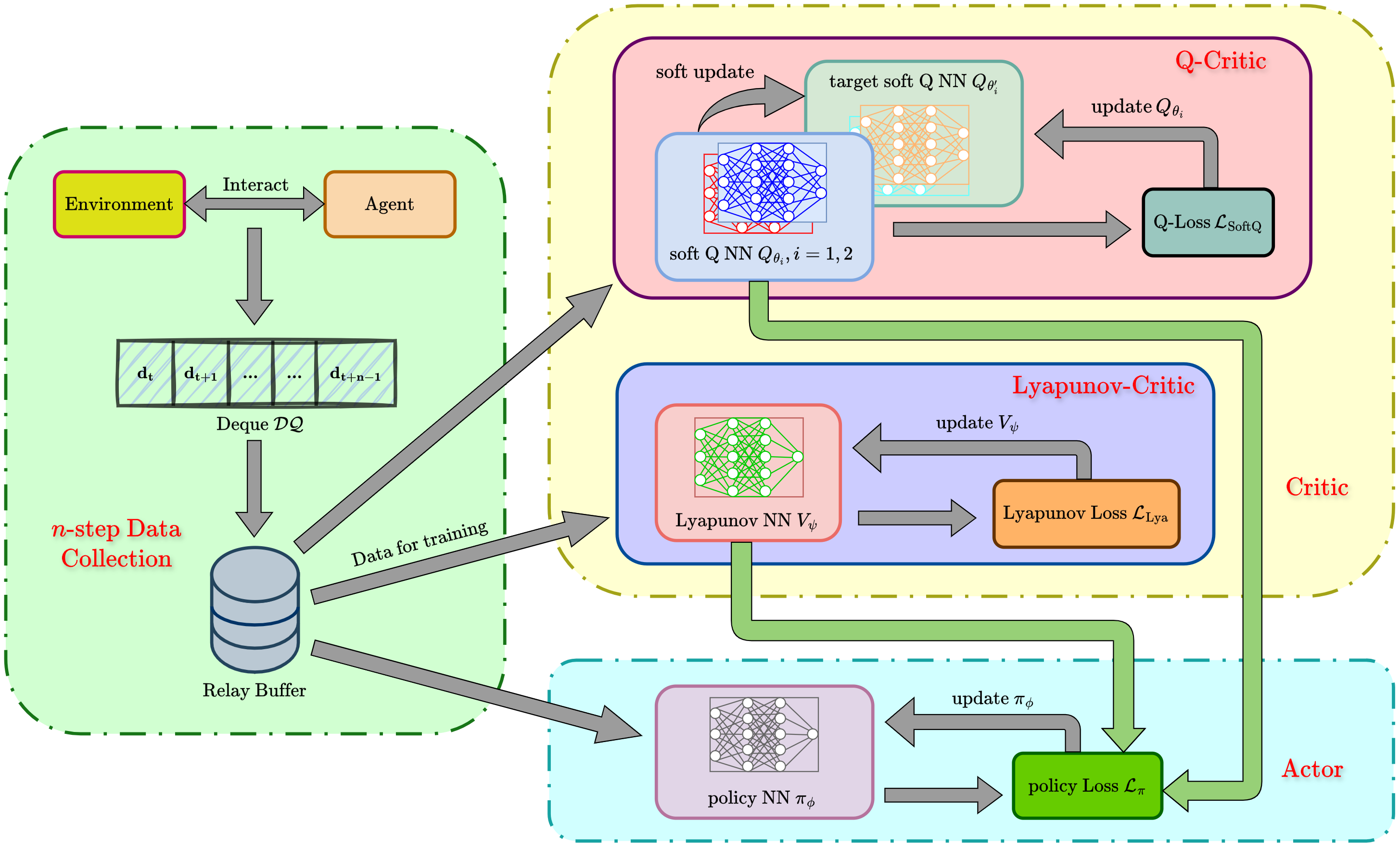
By integrating the loss functions for the soft Q-network Q θ , Lyapunov network V ψ , policy network π ϕ , and temperature coefficient α, we iteratively update these parameters within an actor-critic framework. The complete procedure is summarized in Algorithm 1 with flowchart illustrated in Fig. 2.

Remark 3: Algorithm 1 incorporates two implementation refinements. First, for the soft Q-loss ( 14

end for end for min{Q θ1 , Q θ2 } to mitigate overestimation bias. Second, we implement delayed updates for both policy π ϕ and temperature α, performing d consecutive updates within each delayed cycle to ensure sufficient policy improvement. These techniques, adapted from the cleanrl framework [42], significantly improve training stability and performance.

This section evaluates the MSACL algorithm across six benchmarking environments, covering stabilization and highdimensional tracking tasks. We compare our approach against model-free and Lyapunov-based RL baselines using performance and stability metrics. Further analysis includes Lyapunov certificate visualization, robustness assessment under parametric uncertainty and stochastic noise, and sensitivity studies on the multi-step horizon n.

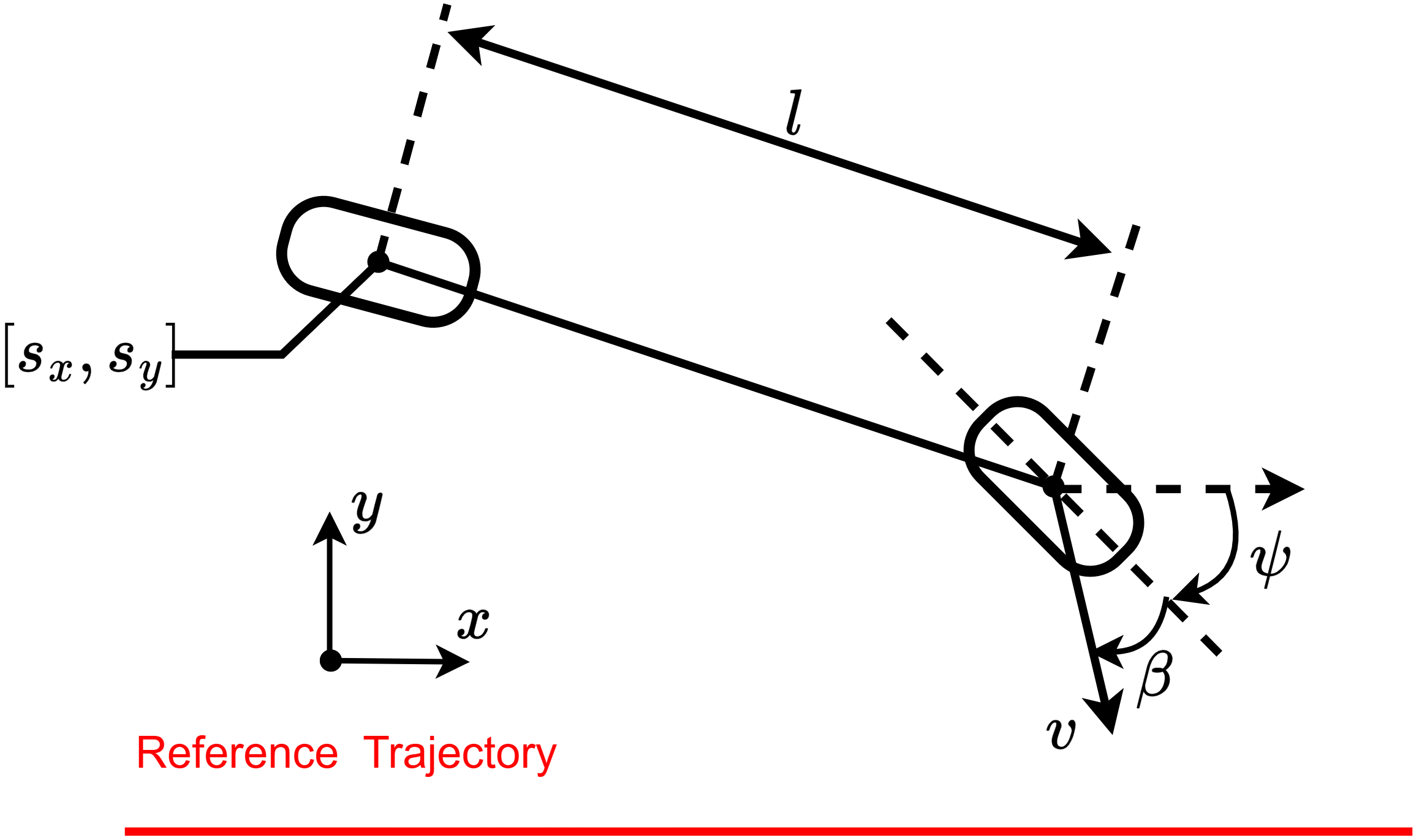
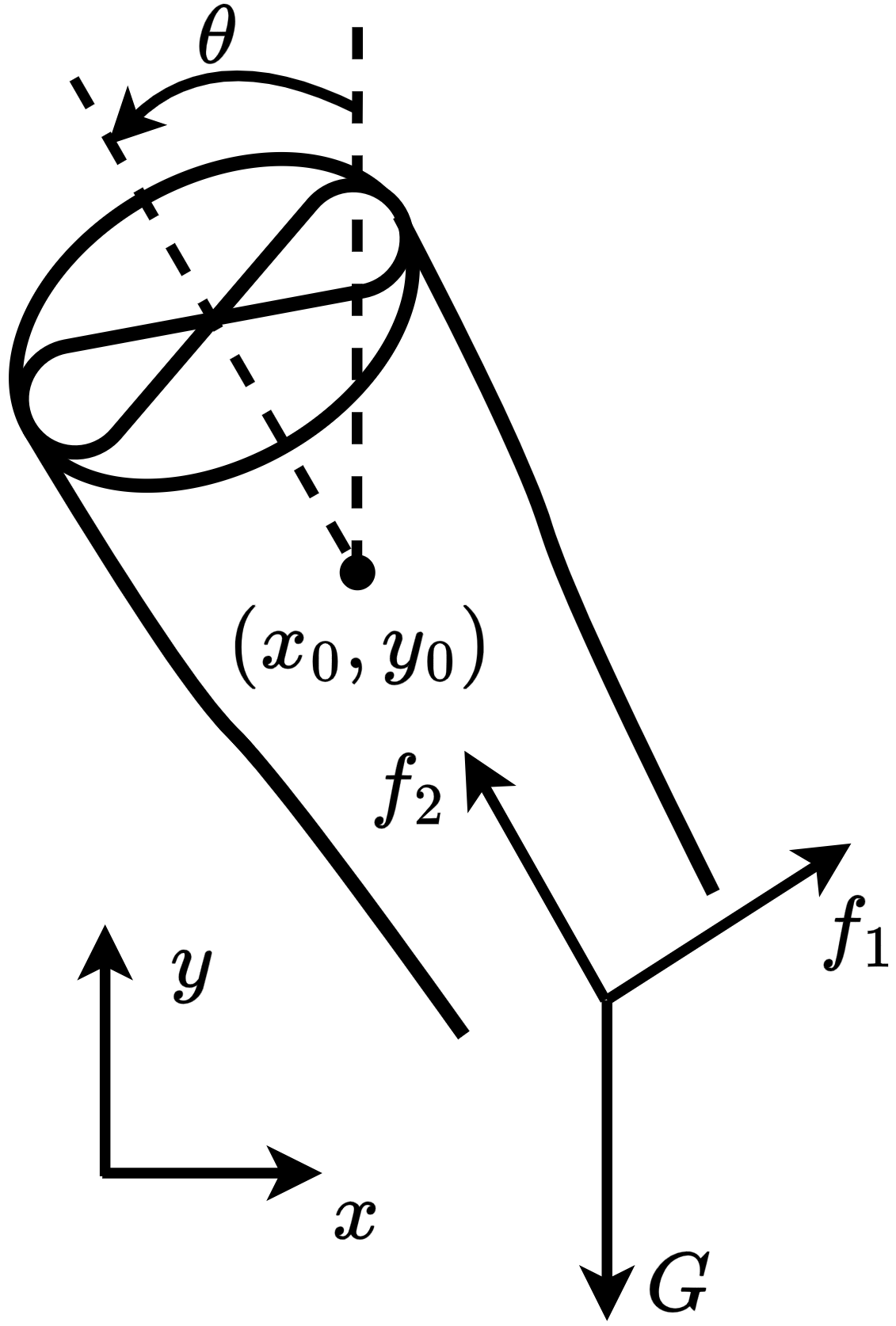
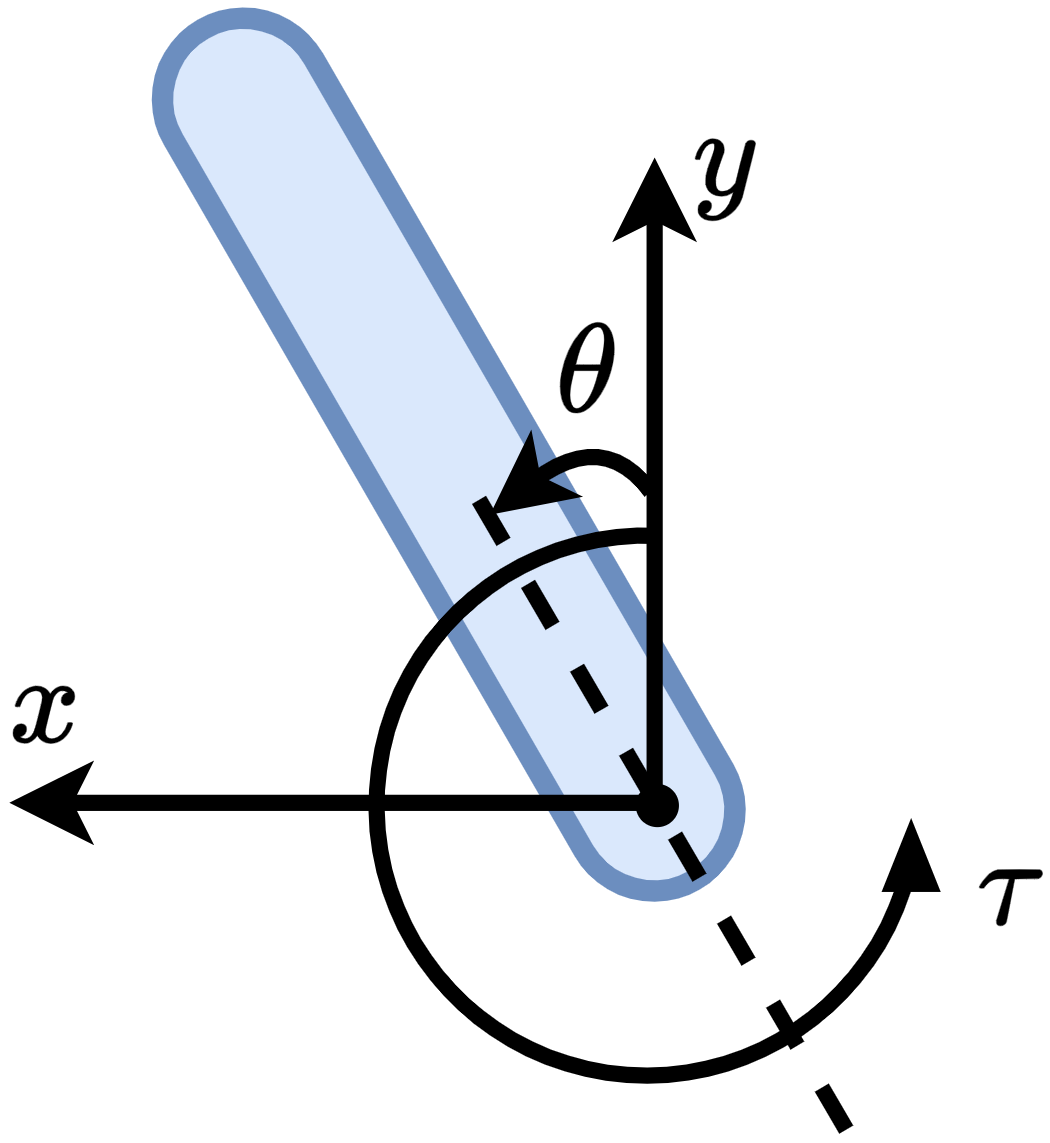
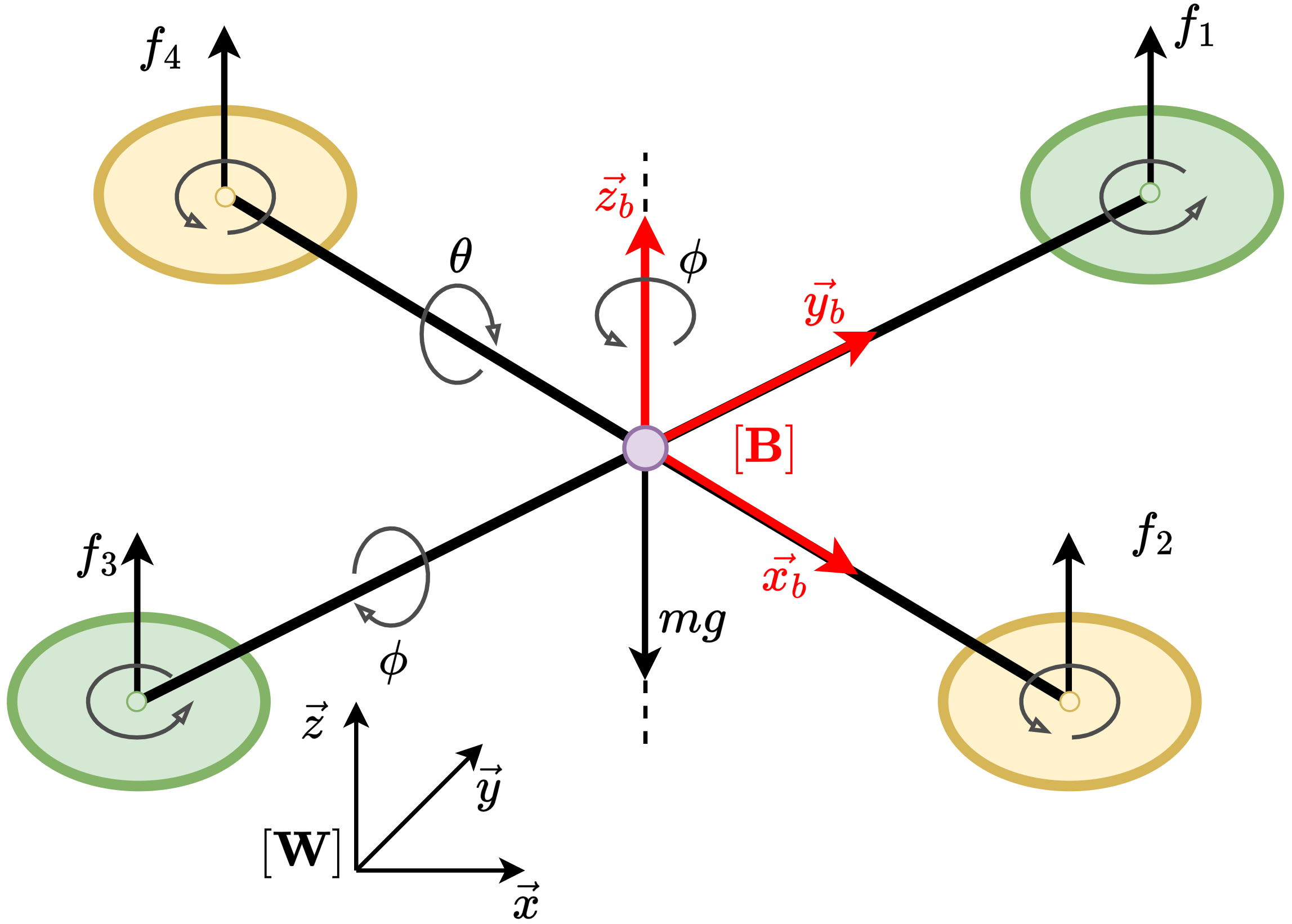
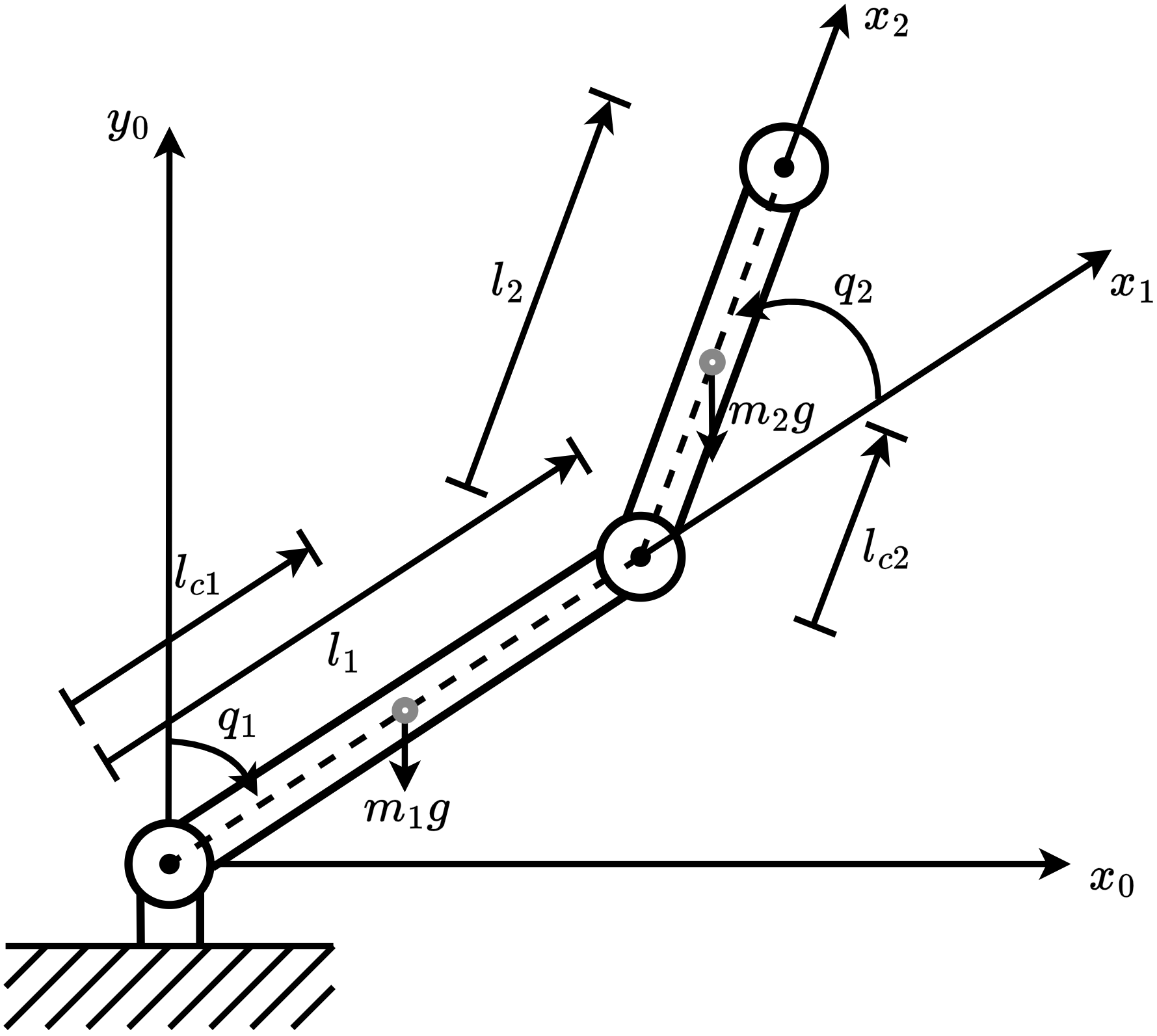
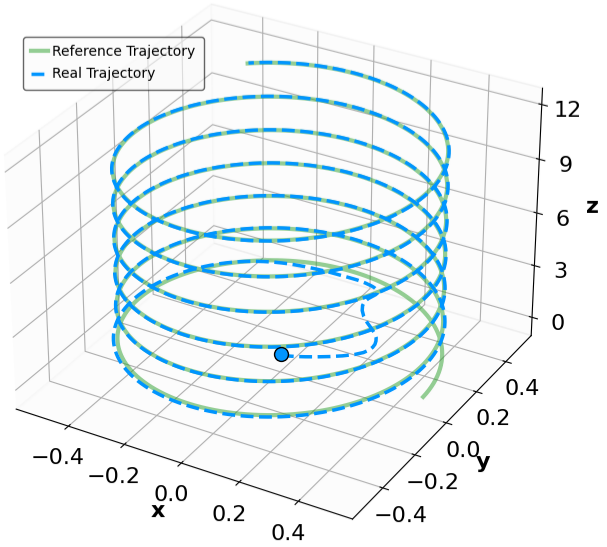
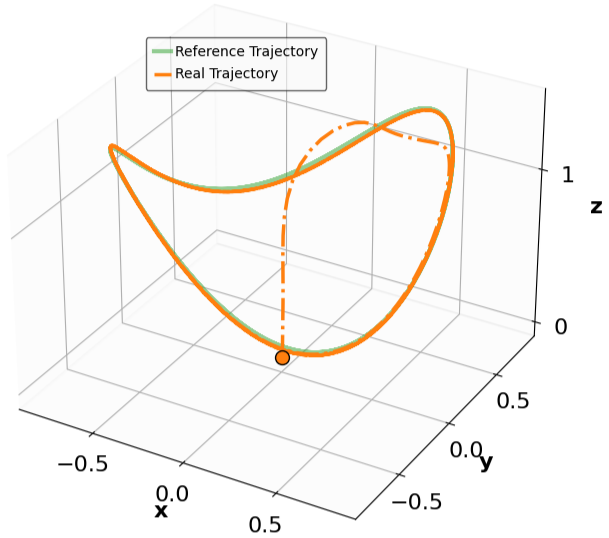
This subsection presents the benchmarking environments for evaluating MSACL and baseline algorithms. We categorize environments by control objective: stabilization tasks include Controlled VanderPol (VanderPol) [43], Pendulum [44], Planar DuctedFan (DuctedFan) [45], and Two-link planar robot (Twolink) [46]; tracking tasks comprise SingleCarTracking [47] and QuadrotorTracking [48], as illustrated in Figure 3.

For stabilization tasks, the goal is to drive the state to the origin x g = 0 ∈ R d ; for tracking tasks, the system follows

where the first term penalizes state deviations and control effort using positive definite matrices Q r and R r , minimizing the cumulative cost [49]. For tracking tasks, x t is replaced by the tracking error e t = x t -x ref t . The second term r approach provides sparse encouragement, defined as:

Specifically, when ∥x∥ ∞ < δ (e.g., 0.01), a positive reward r δ is provided to incentivize convergence and mitigate steadystate error. All benchmarks follow the OpenAI Gym framework [50]. Notably, the Pendulum implementation is modified for increased difficulty, featuring expanded state and action spaces, boundary-based termination, and longer episodes, to better differentiate algorithmic performance. Specific details can be found in our code repository. During interaction, the environment returns a 5-tuple (x t , u t , r t , π ϕ (u t |x t ), x t+1 ), with state transitions updated via explicit Euler integration.

We evaluate MSACL against classic model-free RL baselines (SAC [33], PPO [31]) and state-of-the-art Lyapunovbased algorithms (LAC [36], POLYC [25]). SAC and PPO serve as performance baselines for stabilization and tracking tasks, while LAC and POLYC provide stability guarantees through Lyapunov constraints. For LAC, the standard reward is replaced with a quadratic cost function defined as:

, where Q c is positive definite. Note that in contrast to this state-only penalty formulation, our reward r t accounts for both state deviations and control effort. By comparing against these baselines, we aim to demonstrate the advantages of MSACL in terms of performance and stability metrics.

For fair comparison, all algorithms are implemented in the GOPS framework [51]. Actor and critic networks utilize MLPs with two 256-unit hidden layers and ReLU activations. All actors employ stochastic diagonal Gaussian policies. Critic architectures vary: LAC uses only a Lyapunov network, while POLYC incorporates both value and Lyapunov functions. SAC and LAC also implement clipped double Q-learning and delayed policy updates according to Remark 3. Optimization is performed via the Adam optimizer [30], with core hyperparameters listed in Table V

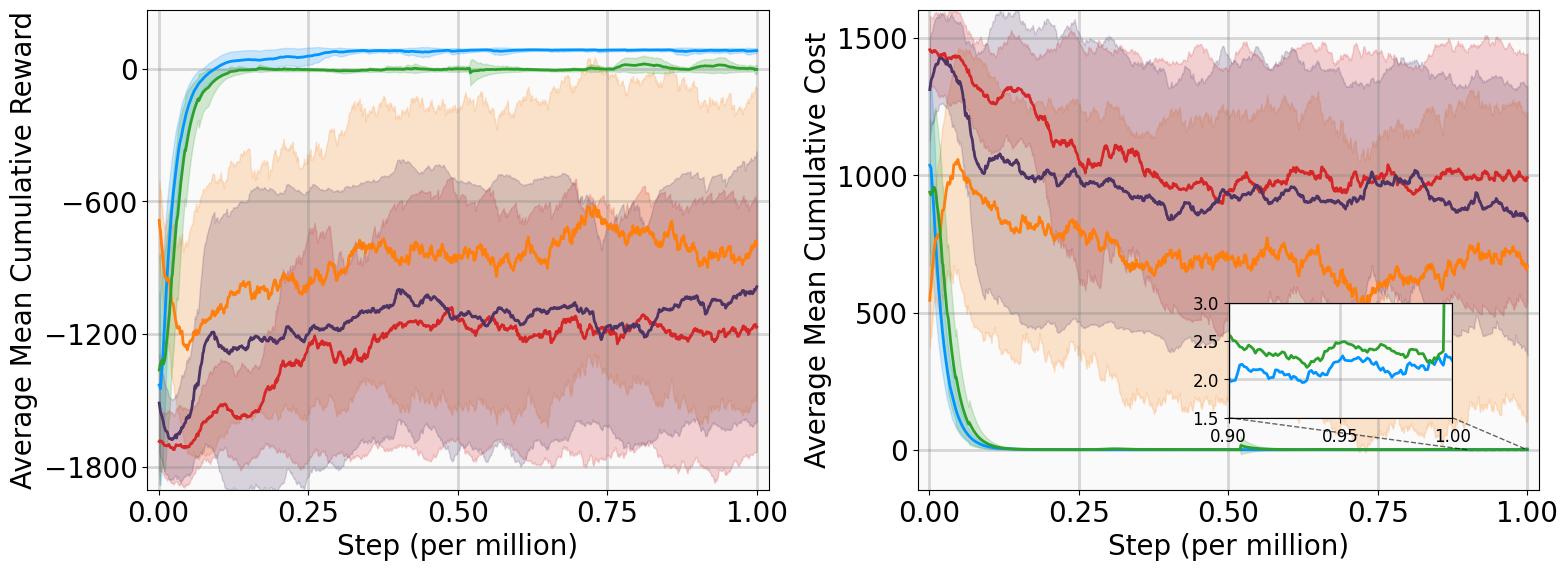
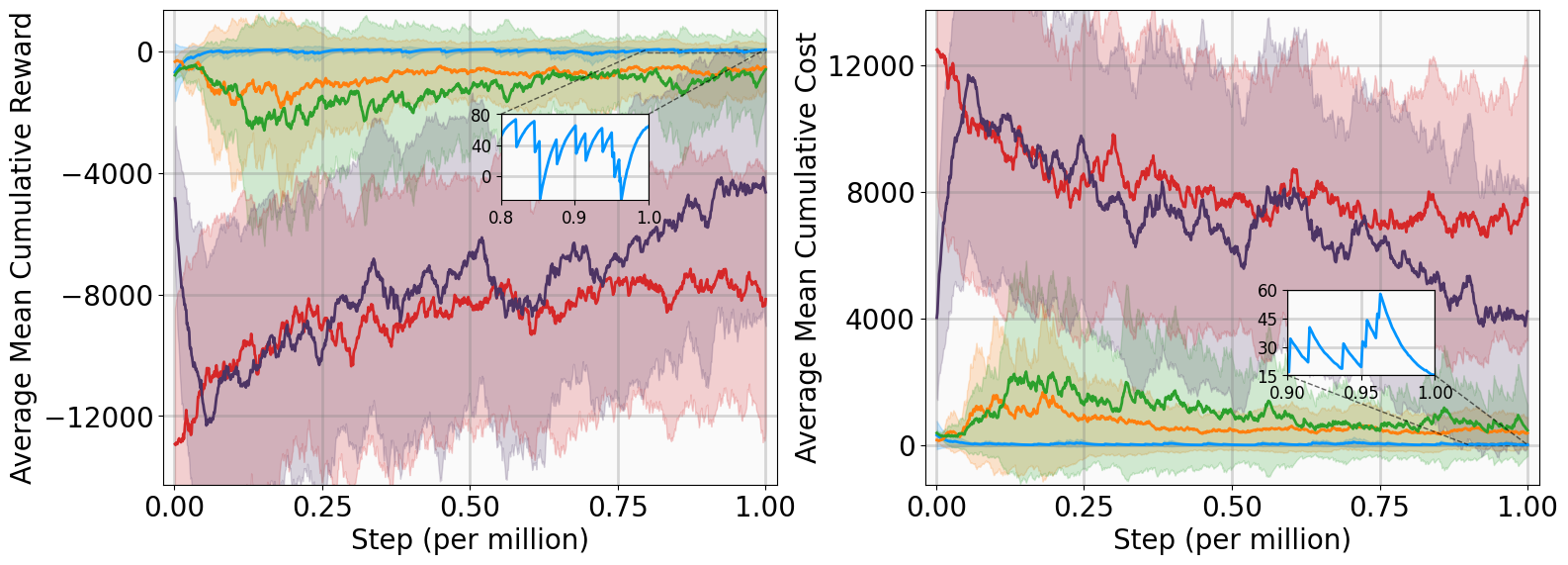
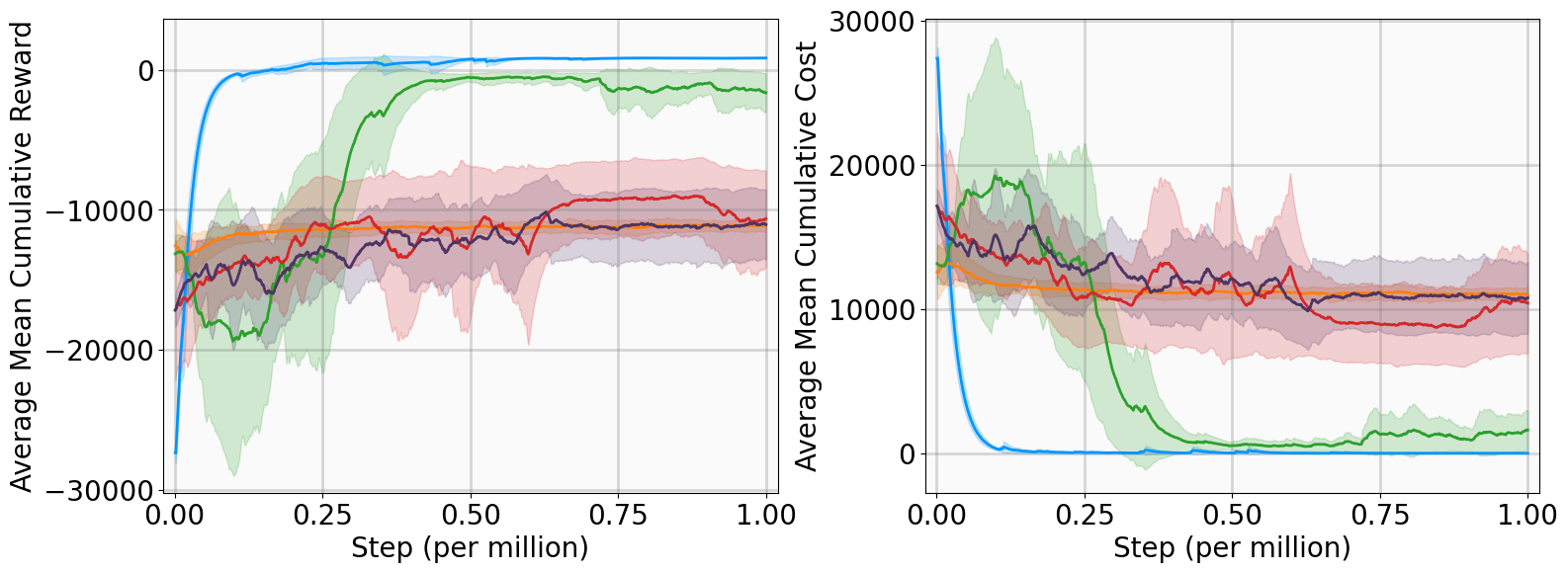
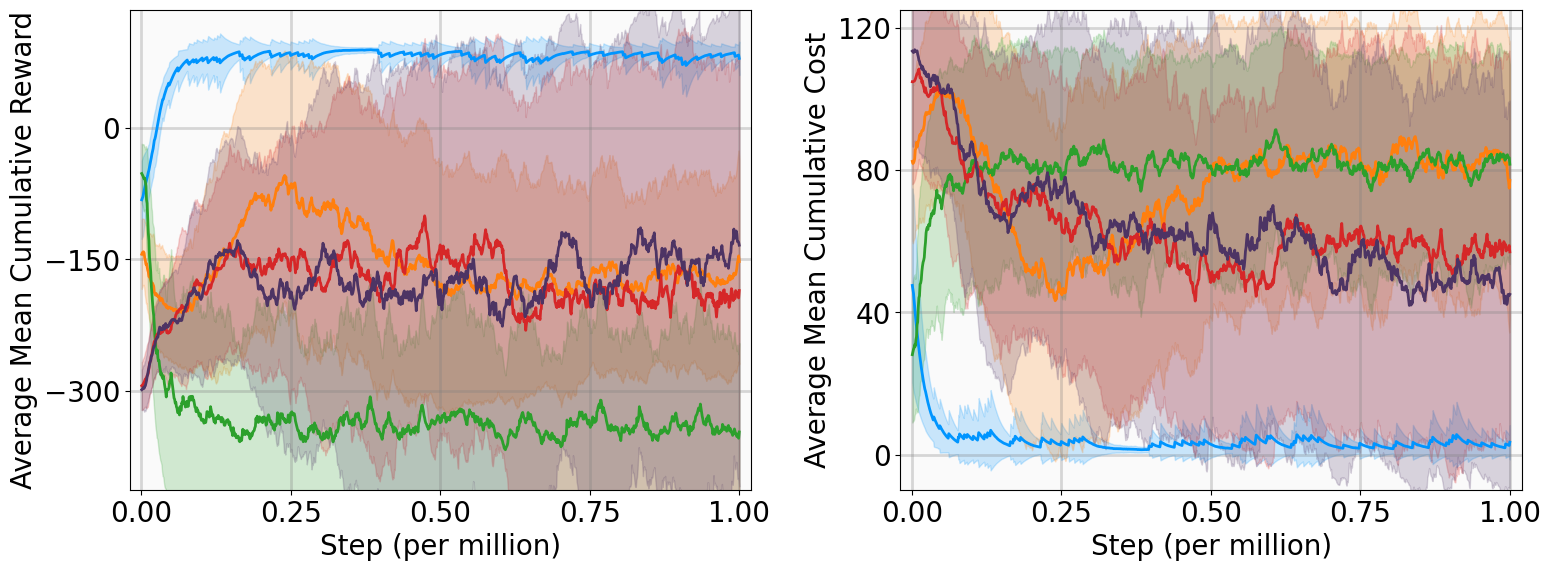
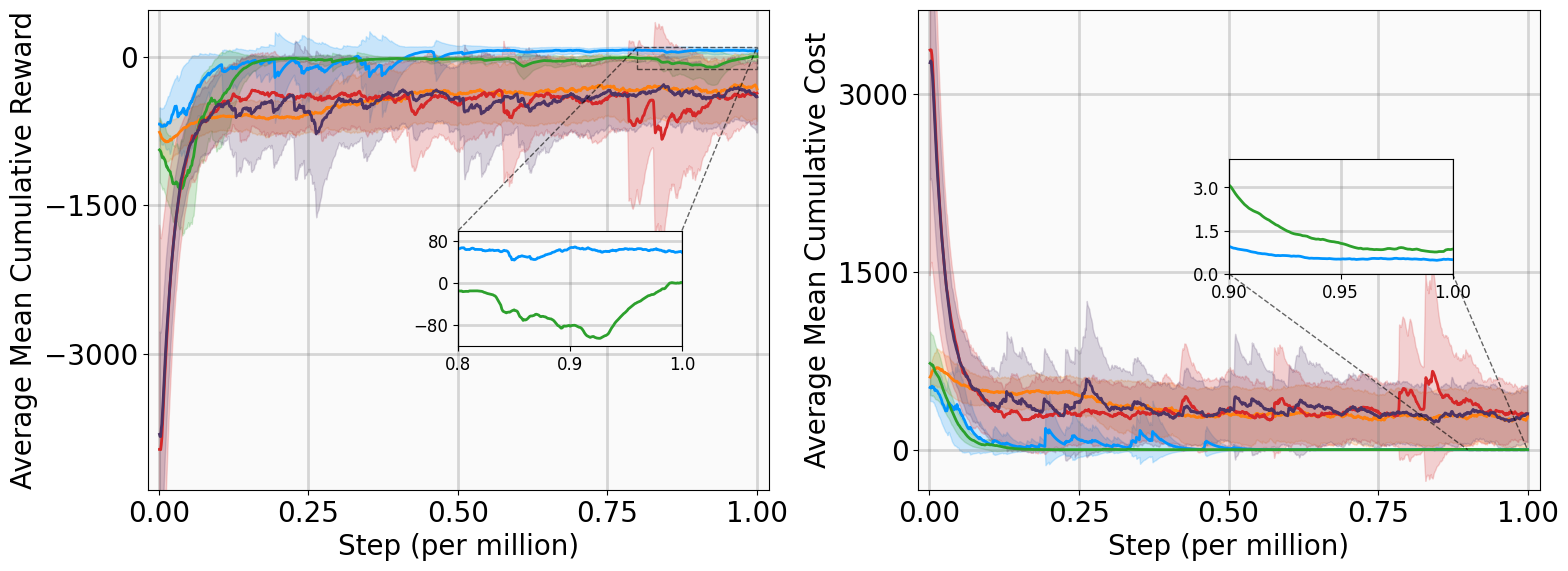
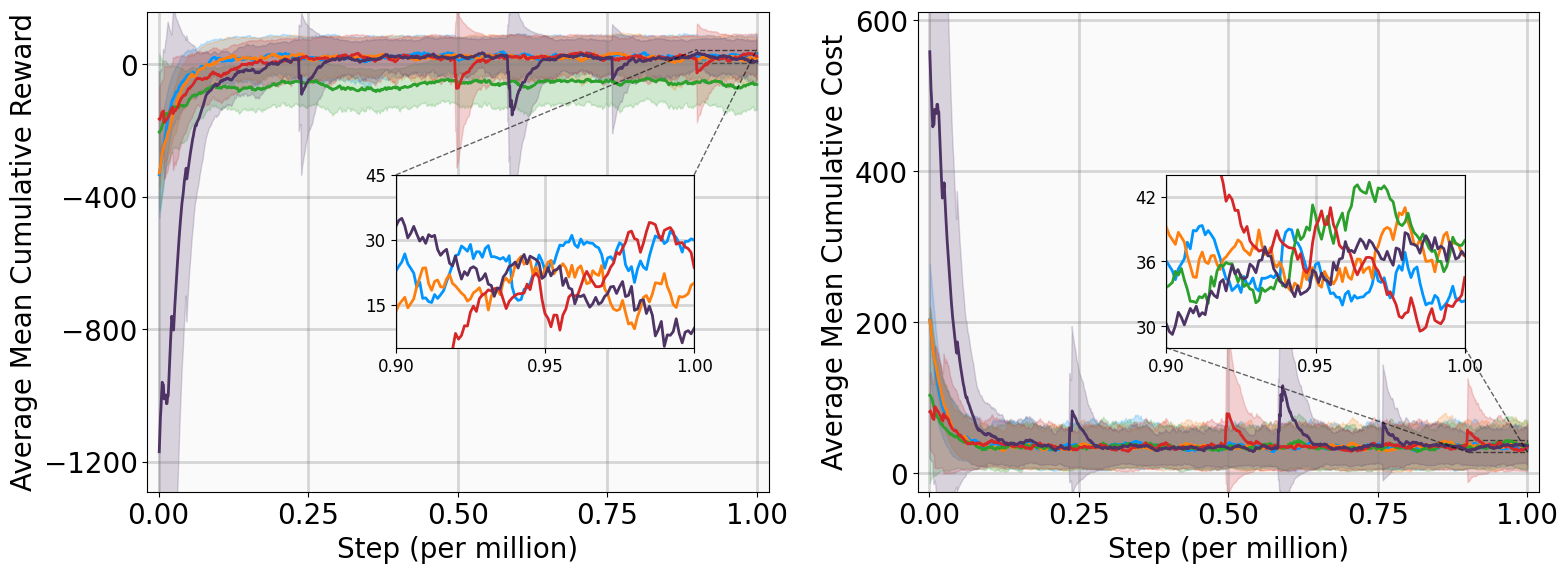
This subsection presents training outcomes, stability metrics, and Lyapunov certificate visualizations. Each algorithm is trained across five random seeds, with training results illustrated in Fig. 4 using the following performance metrics: Training curves show MSACL outperforms or at least matches all baselines across six benchmarks. A positive AMCR indicates that the system state successfully enters the target δ-neighborhood, while higher reward values imply faster convergence as the agent spends more time receiving r δ .

For comparison, we select the optimal policy for each algorithm, defined as the model that achieved the highest MCR among five training runs. These optimal policies are evaluated from 100 fixed initial states, with stability and convergence are assessed across four target radii (0.2, 0.1, 0.05, 0.01) using the following stability metrics:

• Reach Rate (RR): Percentage of trajectories that enter the specified radius. • Average Reach Step (ARS): Mean steps that required for the state to first enter the radius. • Average Hold Step (AHS): Mean steps that the state remains within the radius after the initial entry. The evaluation results are summarized in Table II.

Evaluation results demonstrate MSACL’s superiority. Specifically, MSACL consistently achieves the highest AMCR across all six benchmarks. Regarding AMCC, MSACL attains the absolute minimum in the Pendulum, SingleCarTracking, and QuadrotorTracking tasks, while remaining competitive in others. Furthermore, MSACL maintains the highest RR across all radii. Notably, in the high-dimensional QuadrotorTracking task, MSACL is the only approach to achieve a 100% reach rate at the 0.01 precision level, whereas baselines fail. These results demonstrate the speed and precision of MSACL in complex control systems.

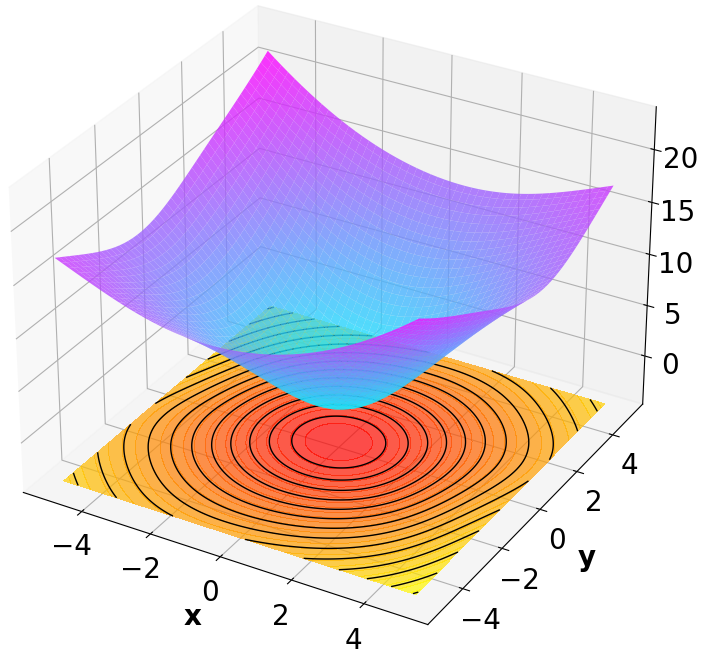
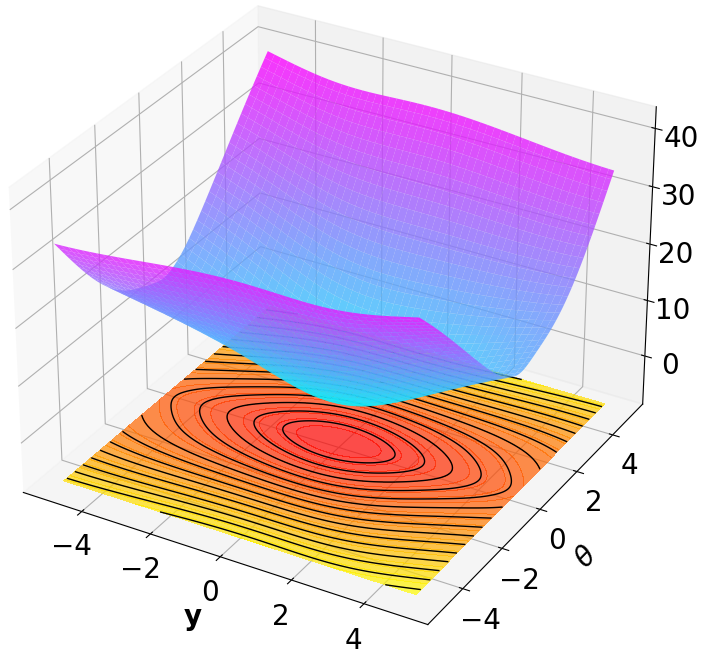
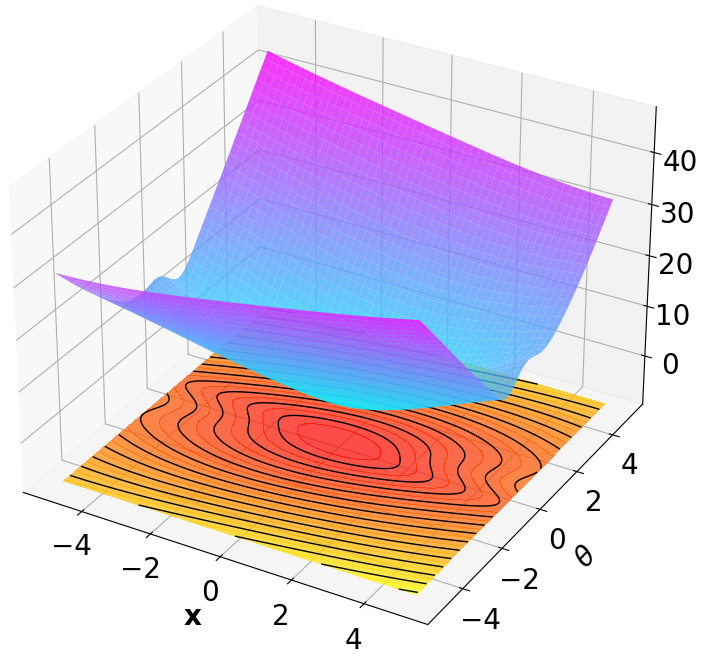
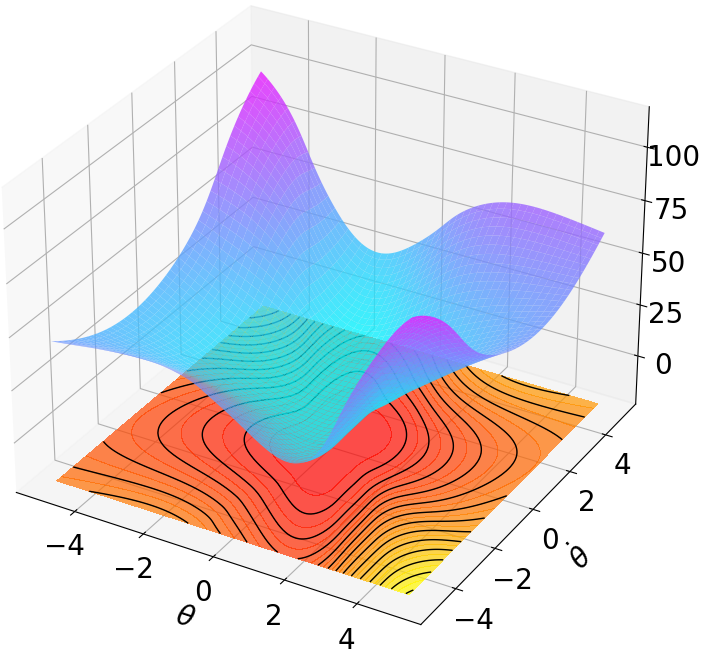
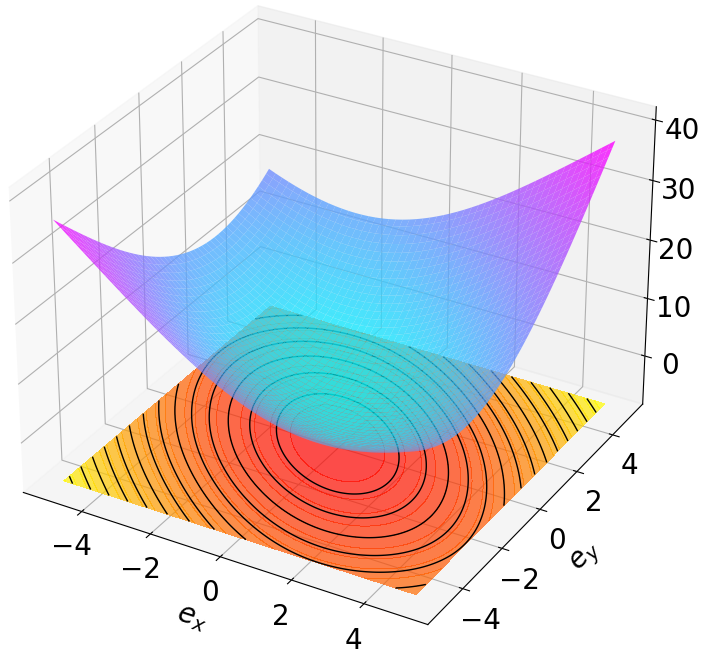
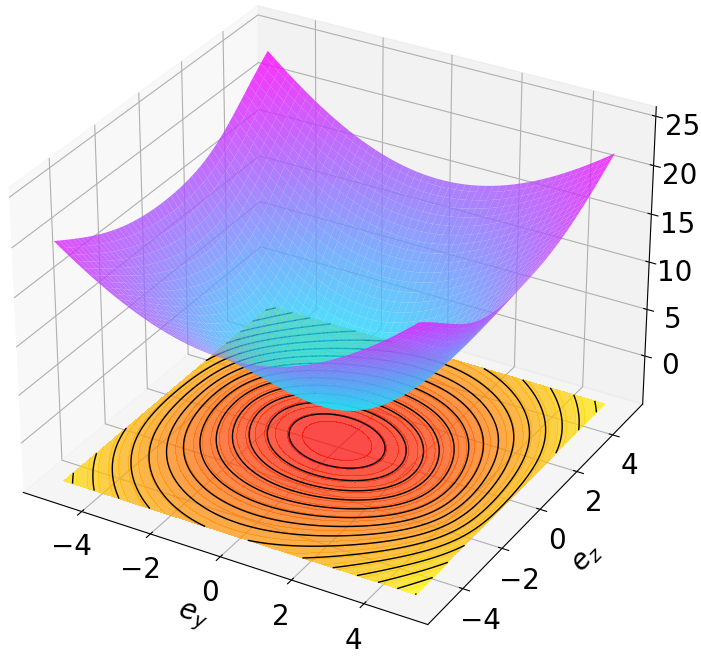
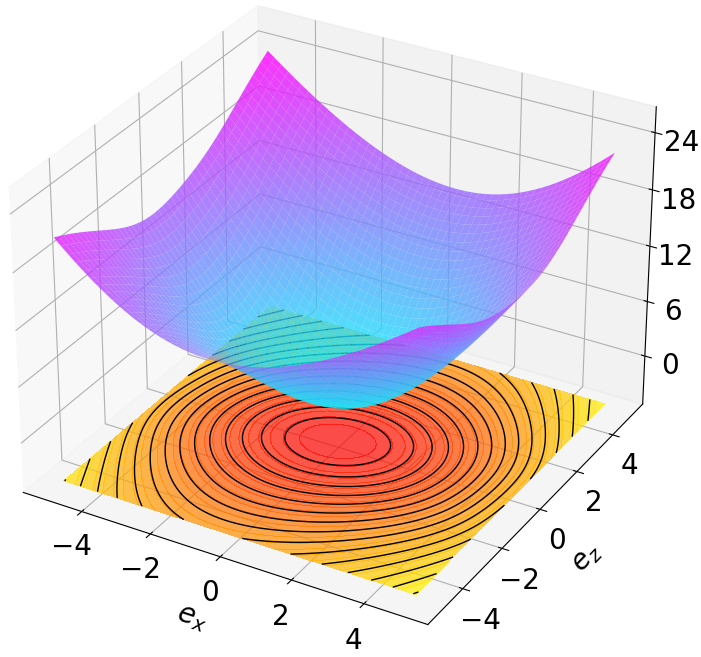
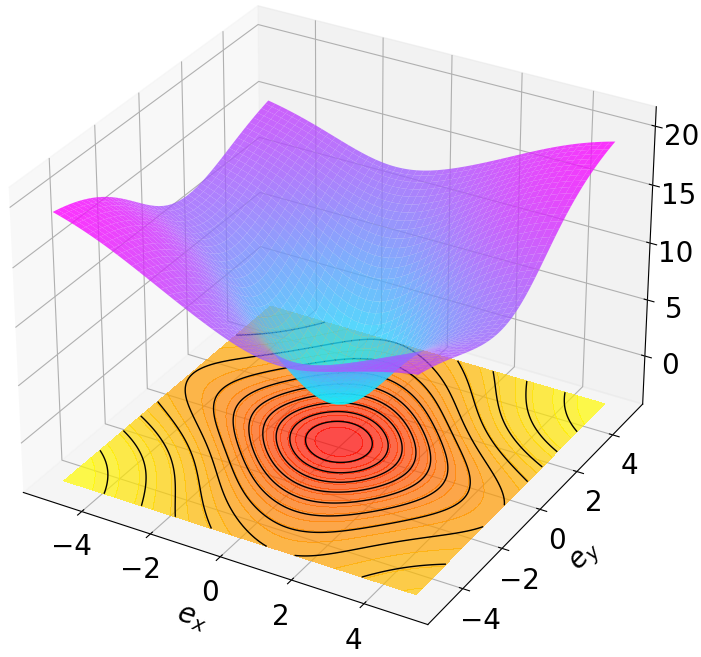
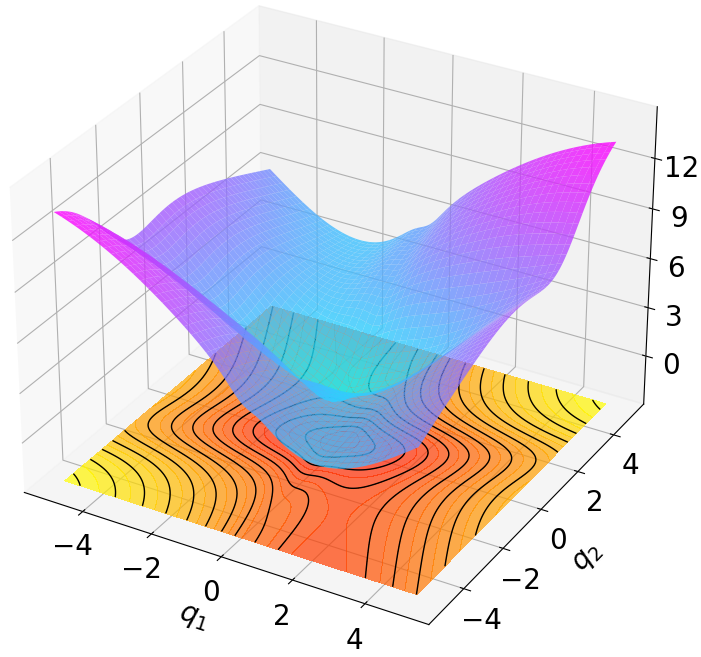
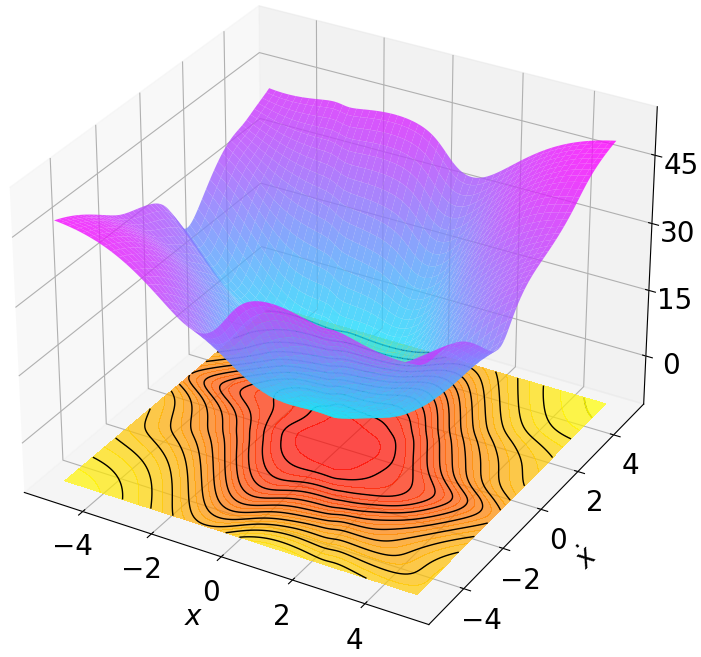
Finally, we visualize the Lyapunov networks V ψ for the optimal policies. The learned certificates and associated contour plots are shown in Fig. 5. For high-dimensional systems, the plots illustrate the relationship between V ψ and two specific state components with all other components set to zero.

Remark 4: Since MSACL builds on the SAC framework, SAC serves as the primary baseline for our ablation study. As shown in Fig. 4 and Table II, the integration of the Lyapunov certificate significantly enhances both training performance and stability metrics compared to the standard SAC. This validates that embedding Lyapunov-based constraints into MERL effectively yields neural policies with superior stability guarantees for model-free control systems.

Neural policies with high-dimensional parameter spaces are prone to overfitting, often resulting in reduced robustness to noise and parametric variations, and limited generalization to unseen scenarios. This subsection evaluates the robustness and generalization of MSACL-trained policies, with the aim of demonstrating their real-world applicability under inherent uncertainties.

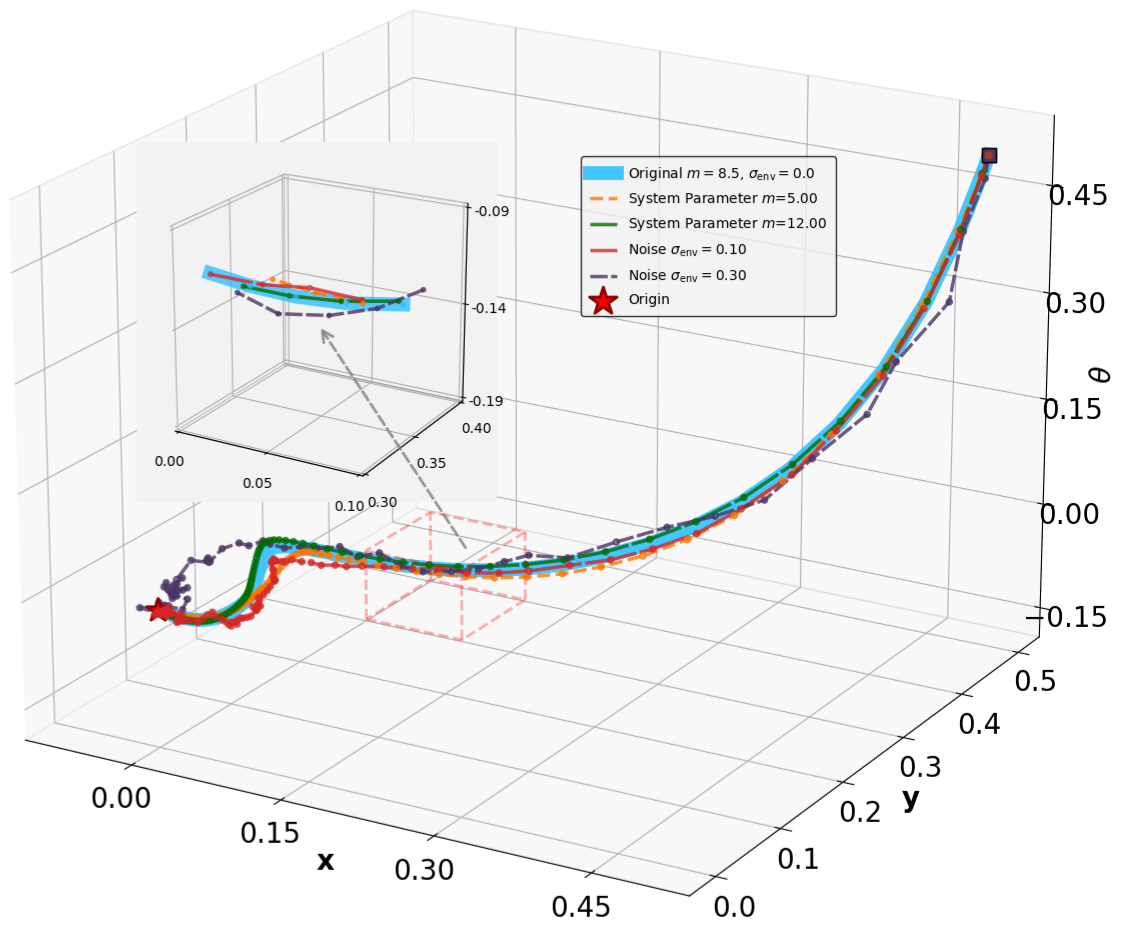
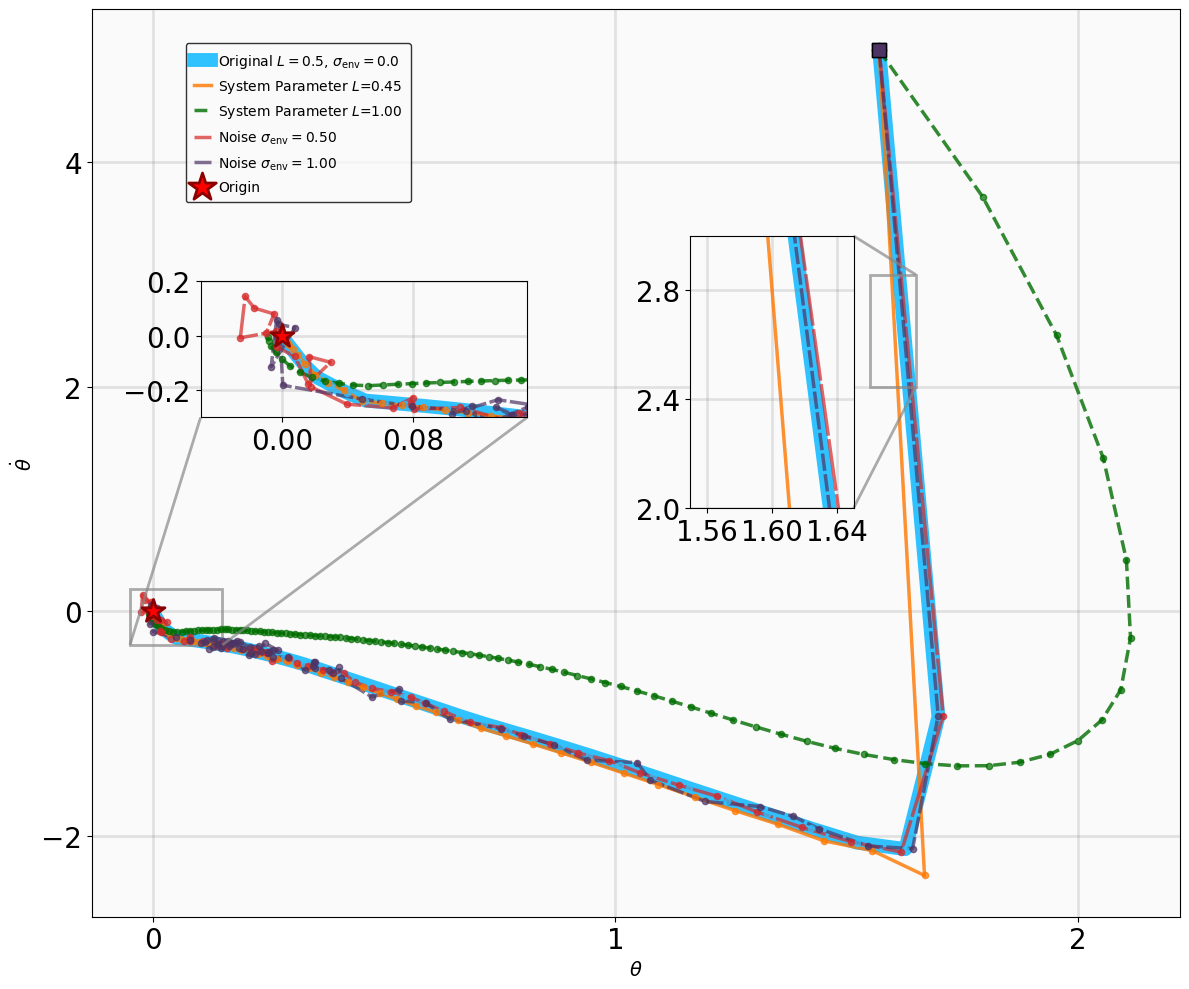
For stabilization tasks (VanderPol, Pendulum, DuctedFan, Two-link), we introduce process noise ϵ t ∼ N (0, σ env • 1 d ) to the system dynamics, where 1 d denotes the all-ones vector of dimension d, yielding the perturbed form:

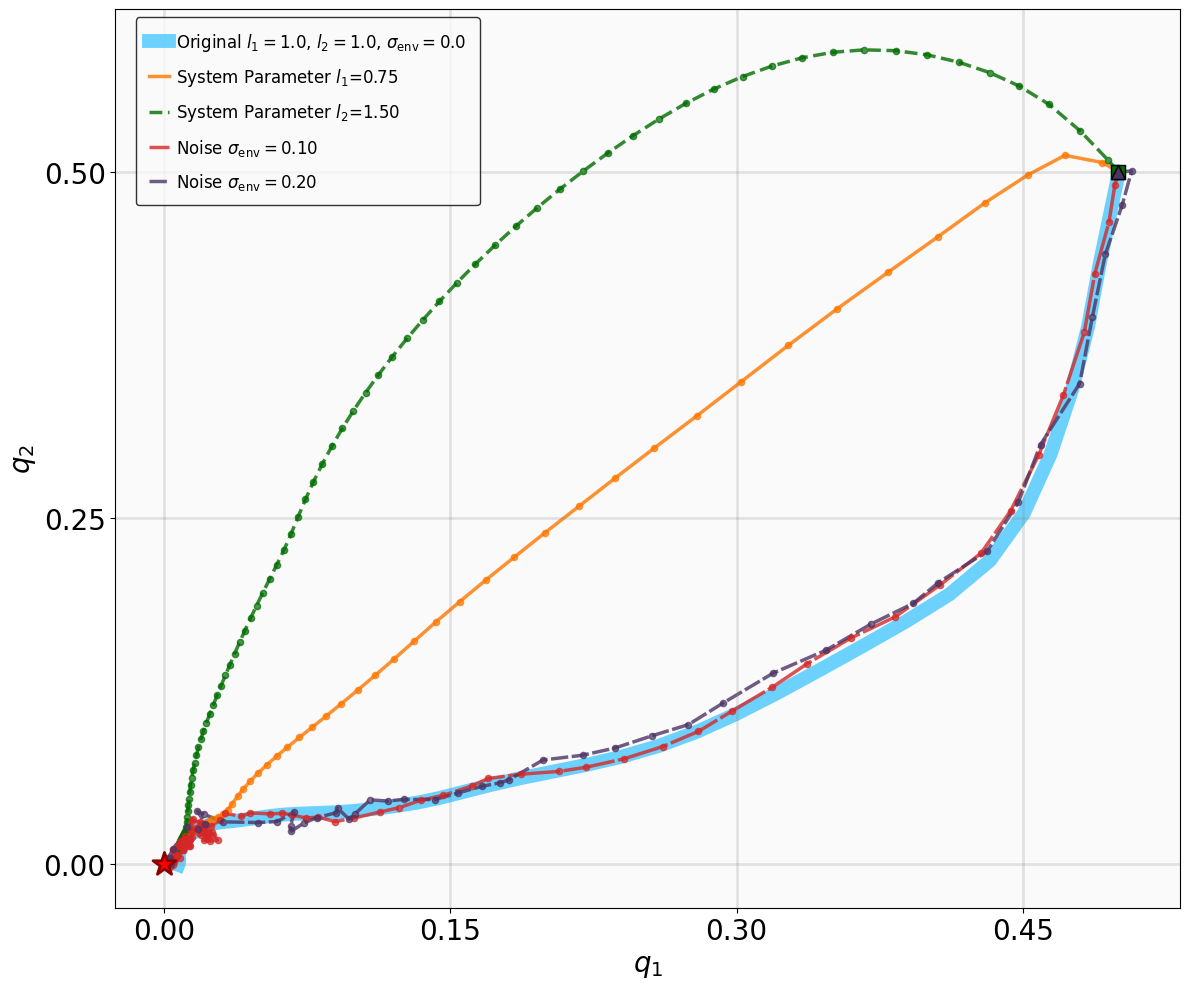
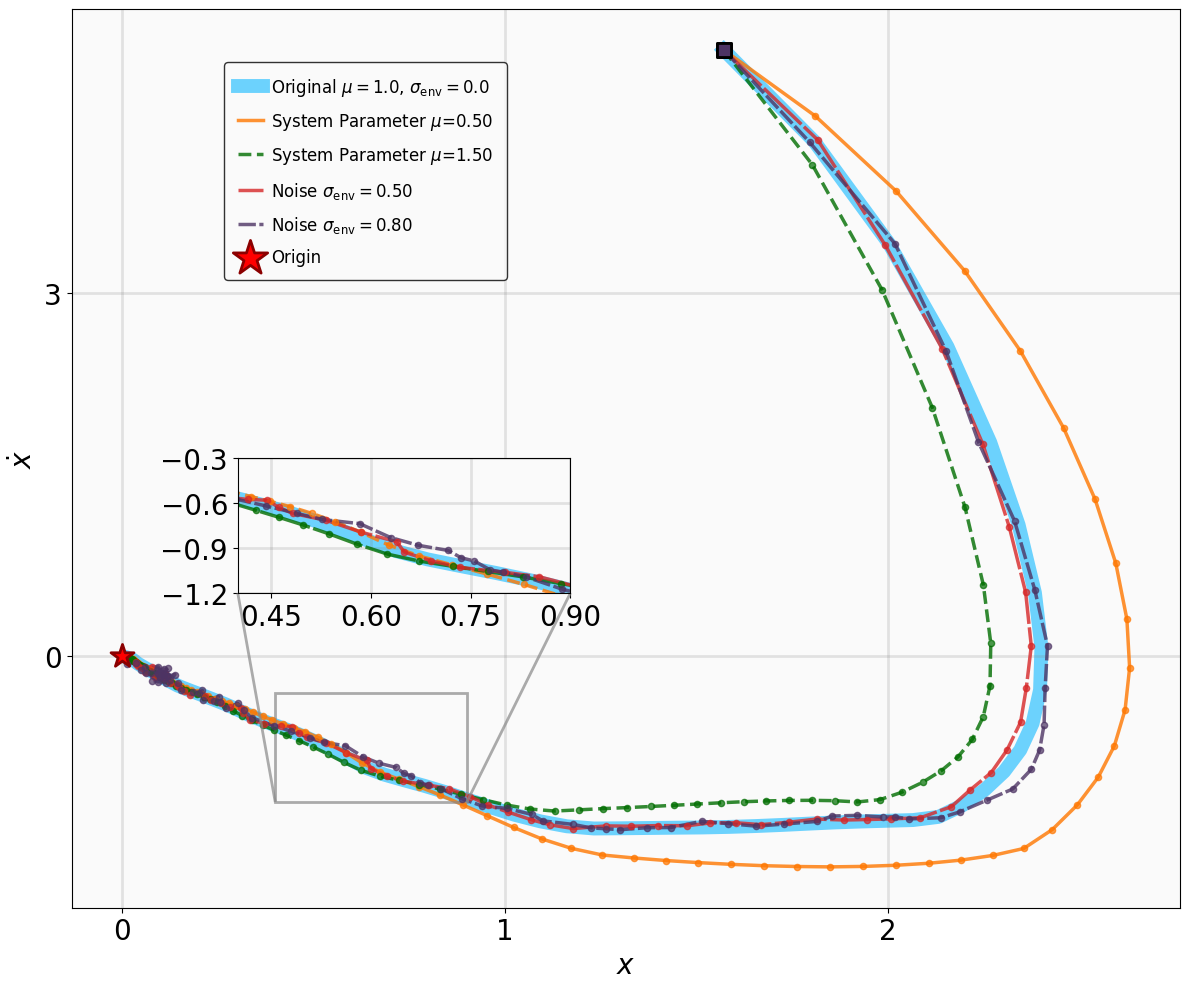
Additionally, we modify key physical parameters of the systems to assess whether the MSACL-trained policies can maintain stability under environmental variations. For tracking tasks (SingleCarTracking and QuadrotorTracking), robustness is evaluated via dynamical noise, while generalization is assessed using reference trajectories x ref t that are significantly different from those in training. Table III details the specific parameter modifications and noise magnitudes.

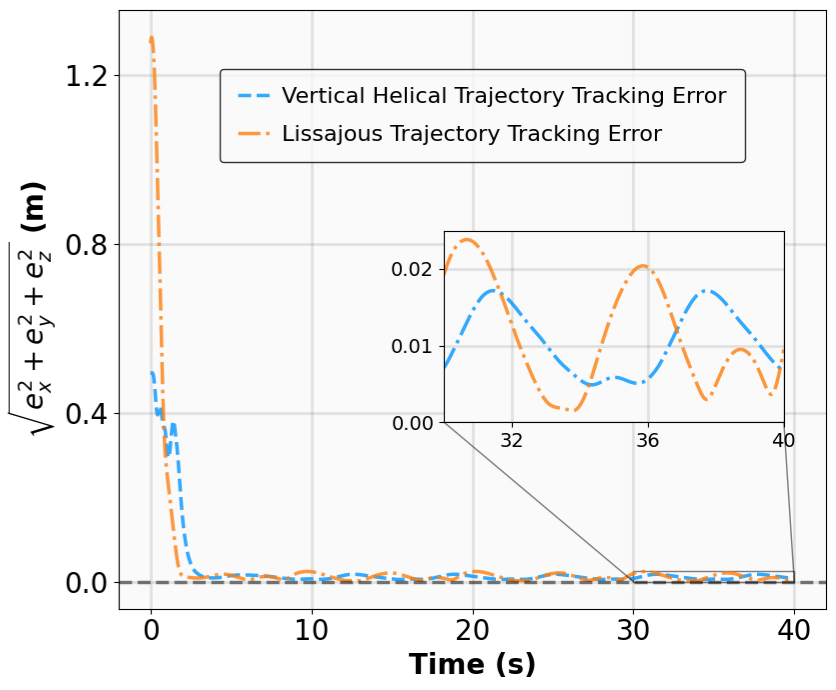
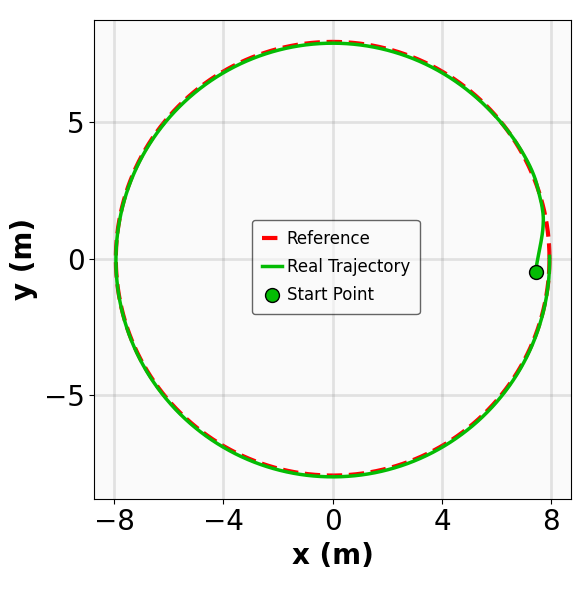
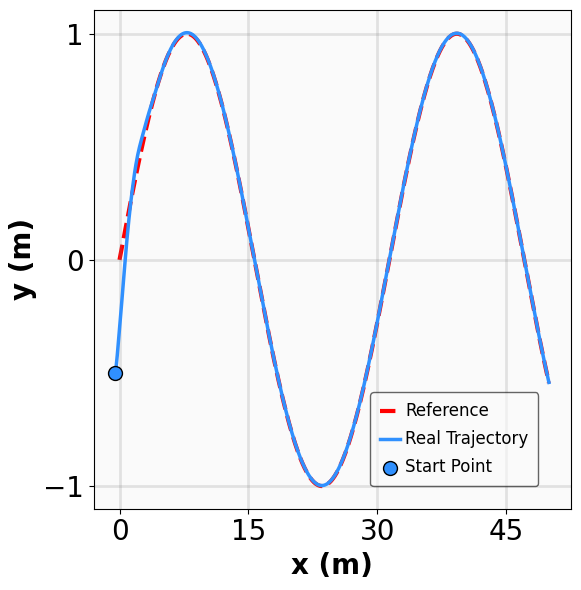
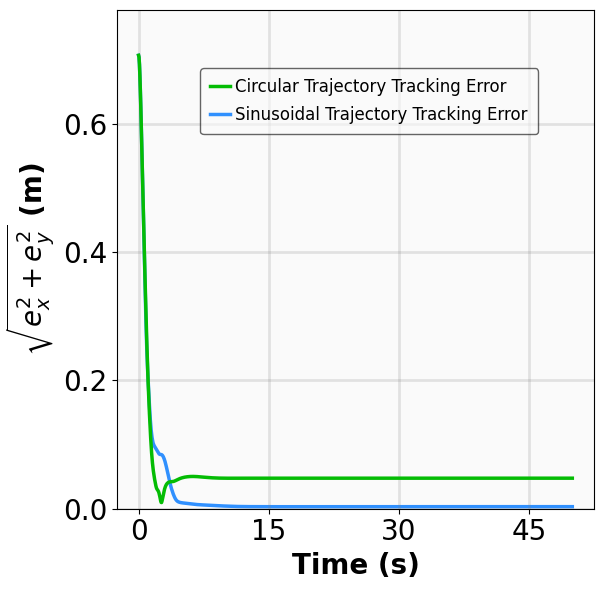
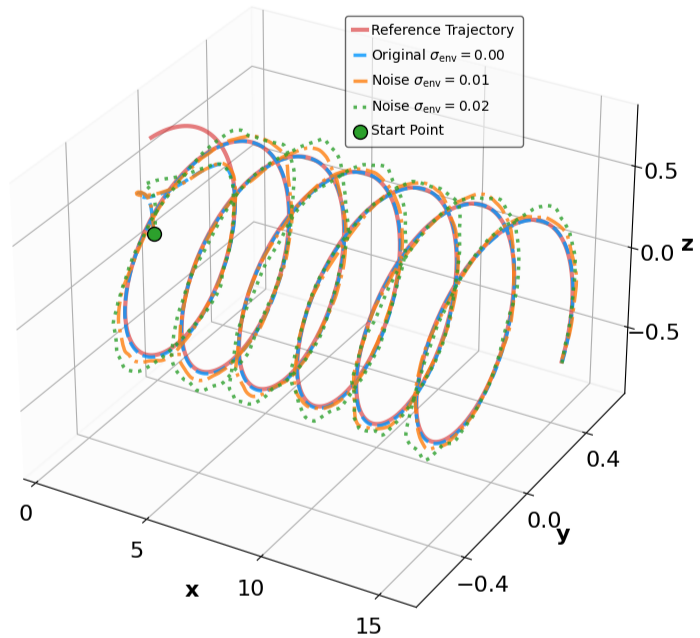
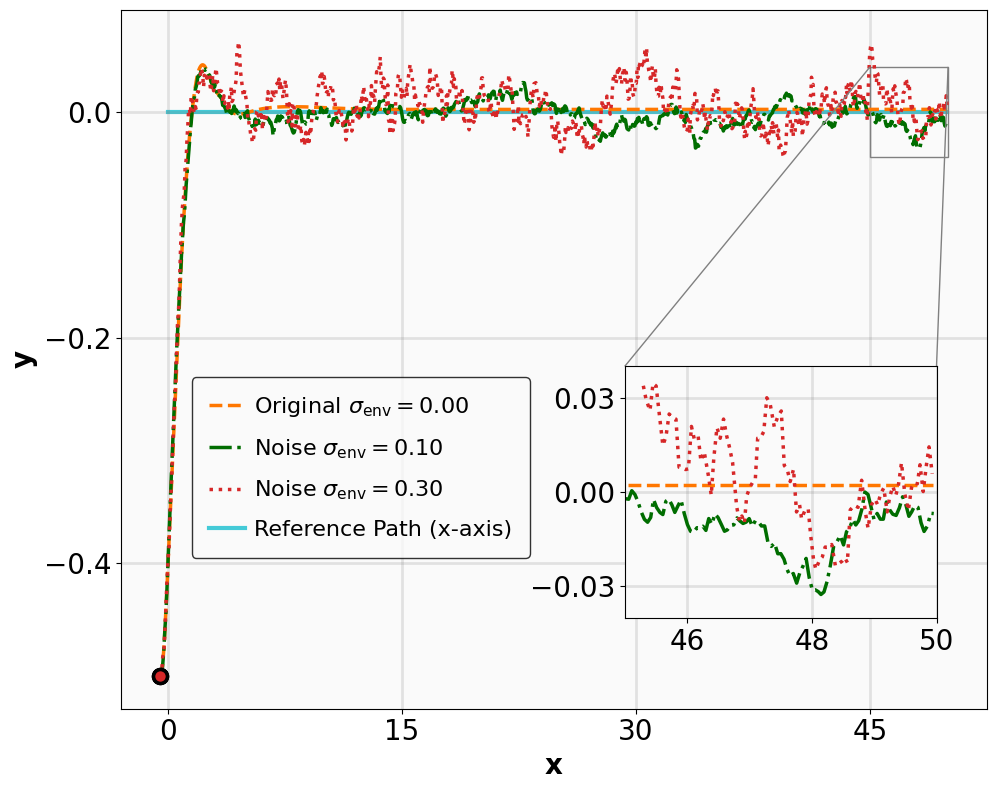
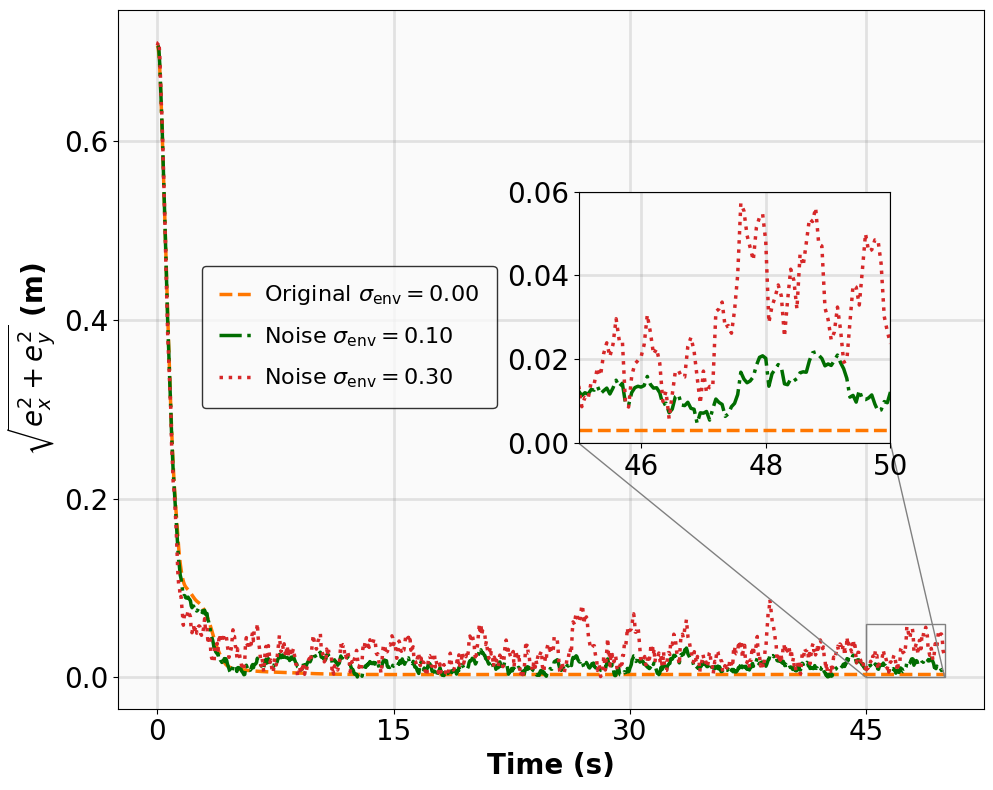
Robustness results for stabilization tasks in Fig. 6 show that all trajectories converge to the equilibrium x g = 0 despite parametric perturbations and process noise. Tracking task results (Fig. 7,8) demonstrate that MSACL-trained policies effectively mitigate process noise within reasonable ranges. For SingleCarTracking, though trained on straightline references, the policy generalizes well to circular and sinusoidal trajectories (Fig. 7c,7d), with position error e xy = e 2

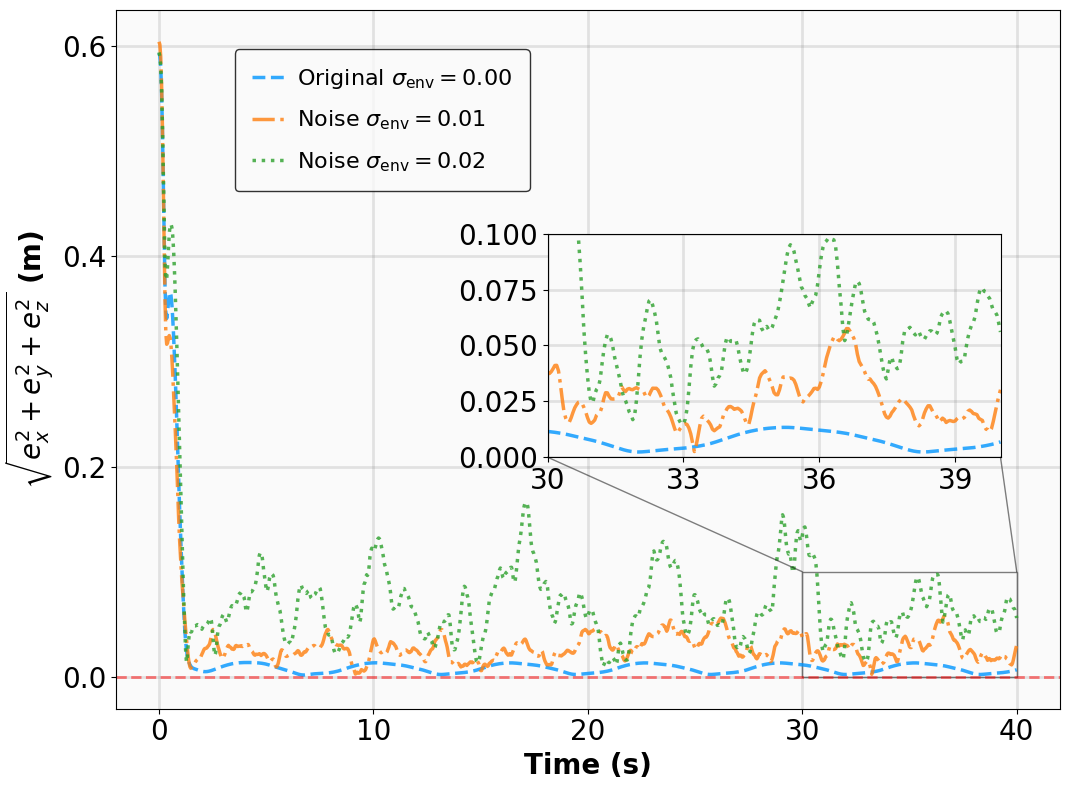
x + e 2 y remaining below 0.1 in steady state (Fig. 7e). For QuadrotorTracking, though trained on horizontal helical trajectories, the policy successfully tracks unseen vertical helix and Lissajous curves (Fig. 8c,8d), with tracking error e xyz = e 2

x + e 2 y + e 2 z stabilizing around 0.02 (Fig. 8e), demonstrating superior generalization capability.

These results demonstrate that MSACL-trained policies exhibit robustness to model uncertainties and process noise, while generalizing effectively to unseen reference signals.

However, performance degrades under extreme disturbances or significant deviations from the training distribution. In such cases, MSACL can be redeployed to retrain policies for stable, high-precision control in specific operational scenarios.

This subsection examines the impact of multi-step horizon n on MSACL performance across all benchmarks. Following the protocol in Section V-C, we evaluate policies trained with varying n using performance metrics (AMCR, AMCC) and stability metrics (RR, ARS, AHS). For each benchmark, we conduct 100 experiments from fixed random initial states to compute these metrics. As summarized in Table IV, performance generally improves with larger n, as a longer horizon enables the policy to better identify the stability direction, i.e., the descent of V ψ . This reduces training bias and reinforces stability guarantees.

Empirically, n = 20 delivers satisfactory performance across all benchmarks, serving as a versatile default. However, excessively large n may degrade performance due to increased cumulative variance in training data, potentially distorting the

This subsection elucidates the functional roles of MSACL components. As highlighted in Remark 4, MSACL augments the SAC framework with a stability-oriented critic, departing from standard RL that relies on exhaustive exploration to discover stabilizing behaviors. Instead, MSACL leverages a learned Lyapunov certificate to provide explicit, structured guidance for policy updates.

), we replace Q θ with Algorithm 1 Require: Replay buffer D, double-ended queue (deque) DQ with length n, delay frequency d for each iteration do for each sampling step do Select action u t ∼ π ϕ (•|x t ) Obtain reward r t and observe next state x t+1 Store tuple d t = (x t , u t , r t , π ϕ (u t |x t ), x t+1 ) in DQ if length(DQ) = n then Store {d i } t+n-1 i=t = {d t , . . . , d t+n-1 } in D end if end for for each update step do Sample N multi-step sequences {d