Uncertainty Growth in Stably Stratified Turbulence

A useful recent approach [13] to probing sensitivity in high-dimensional dynamical systems is to track the time evolution of the difference between two initially nearly identical states evolved under the same dynamics. In turbulent flows, this naturally leads to the study of such decorrelators, which quantify how velocity or scalar fields diverge in time and space. Such diagnostics provide a direct, non-perturbative measure of uncertainty growth and allow one to extract Lyapunov exponents as well as study the spatial structure and scale-by-scale propagation of perturbations. Recent applications of this framework to fully developed turbulence [14] and similar nonlinear hydrodynamic equations [15,16] have revealed a robust dynamical sequence: An initial decay of perturbations followed by a period of exponential growth with a self-similar spectrum and eventual saturation. Remarkably, this appears to be universal for threedimensional turbulence [14].

While homogeneous and isotropic, fully developed turbulence provides a fundamental reference state, most natural flows of geophysical relevance differ markedly from this idealisation. The oceans and atmosphere are often strongly influenced by stable density stratification, which introduces buoyancy forces, supports internal gravity waves through the Brunt-Väisälä frequency N , and imposes a preferred vertical direction [17][18][19][20][21]. Stratified turbulence is therefore intrinsically anisotropic and arises from the nonlinear interaction of vortical motions and wave dynamics. Decades of theoretical, numerical and experimental work have established that stratification suppresses vertical motions at low Froude numbers, promotes the formation of layered structures, and alters energy transfer pathways relative to homogeneous and isotropic turbulence [22][23][24][25][26][27][28][29][30][31][32][33][34][35][36][37][38][39][40]. While these effects are now well understood at the level of flow structure and energetics, their consequences for the chaotic dynamics of turbulence-including the rate of uncertainty growth, the spreading of perturbations in space, and the overall predictability of stratified flows-have received comparatively little attention.

Predictability and sensitivity to initial conditions in stratified flows have been explored in several settings, but predominantly for decaying or rotational turbulence. In such studies [41], predictability is typically characterised using relative error growth or predictability times in decaying and not statistically stationary dynamics. Lagrangian approaches [42][43][44] based on finite-time Lyapunov exponents and particle separation have been widely applied to study Lagrangian coherent structures in oceanic flows. However, the influence of stable stratification on Eulerian chaos and predictability in statistically stationary turbulence remains largely unresolved.

In this work, we address this gap by studying uncertainty growth in forced, statistically stationary three-dimensional stably stratified turbulence governed by the Boussinesq equations. Using pseudo-spectral direct numerical simulations, we perform twin simulations that differ by an infinitesimal, localised perturbation at the initial time and track the evolution of velocity and buoyancy differences across time and scales. This Eulerian decorrelator framework enables the direct extraction of the largest Lyapunov exponent λ and a detailed characterisation of anisotropic uncertainty spectra as a function of stratification strength. We show that increasing stratification systematically suppresses chaoticity, primarily through a reduction of nonlinear strain and enhanced strain-buoyancy alignment, rather than through direct buoyancy effects. These results establish a quantitative link between stratification, anisotropy and chaotic dynamics over a range of Brunt-Väisälä frequencies relevant to oceanic conditions.

Density-stratified turbulent flows require lifting the constant-density approximation commonly employed for homogeneous and isotropic incompressible turbulence. For stable stratification, the simplest background state consists of a constant vertical density gradient -γ imposed on a reference density ρ 0 at z = z 0 . In turbulent geophysical flows, however, density fluctuations induced by motion must also be accounted for, so that the total density field reads

where ρ f denotes the fluctuating component and gravity acts as g = -gẑ. In the ideal, inviscid, and unforced limit, such a background stratification supports small-amplitude vertical oscillations of fluid parcels [17] with characteristic Brunt-Väisälä frequency N = gγ/ρ 0 .

When density fluctuations remain small compared to the background stratification, the dynamics is well captured by the Boussinesq approximation, in which density variations affect the flow only through buoyancy forces. It is convenient to work with the buoyancy field b = (ρ f N )/γ, which has the same physical dimensions as the velocity field. The governing equations for stably stratified turbulence are then

supplemented by the incompressibility condition ∇ • u = 0. The external forcing f injects energy and maintains a statistically steady turbulent state. We solve these equations using pseudo-spectral direct numerical simulations (DNSs) in a triply periodic domain of size 2π, with up to 512 3 collocation points and a second-order Runge-Kutta time-marching scheme. The kinematic viscosity is fixed at ν = 5 × 10 -3 , yielding Taylor-scale Reynolds numbers 100 < ∼ Re λ = u 2 rms 15/(ϵν) < ∼ 130, where u rms is the root-mean-square velocity and ϵ is the mean kinetic energy dissipation rate (the precise value depending on N ). We set the Prandtl number Pr = ν/κ to unity, appropriate for thermally stratified flows, though not representative of salt-stratified systems where Pr may be much larger. Simulations are performed for N = 0 (the unstratified reference case) and for N = 1, 4, 7, and 12.

In this paper, we refer ⊥ as the direction perpendicular to the axis (here, z-axis) of stratification. The flow is driven by a constant power injection applied only to the horizontal velocity components (i.e., perpendicular direction). The forcing is vortical [40,[45][46][47] and restricted to modes with k z = 0. In Fourier space, it is given by f⊥

with fz = 0. Here M is the number of forced modes, E (m) K

is the horizontal kinetic energy in the (m, 0) mode, and P is the prescribed power input. In all runs, we force modes with m = 1, 2, so that M = 2.

Although N -1 defines the characteristic time scale associated with stratification-analogous to the Kolmogorov time scale τ η = ν/ϵ-its dynamical influence is more conveniently quantified by the Froude number Fr = u rms /(ℓN ), where ℓ is the integral length scale obtained from the kinetic energy spectrum E K (k). In our simulations, 0.09 < ∼ Fr < ∼ 0.97, such that Fr < 1 and the buoyancy Reynolds number Re b ∼ Re λ Fr 2 exceeds unity. Together with Re λ ≫ 1, these conditions place our flows in the strongly stratified turbulence regime.

To assess geophysical relevance, we compare our parameters with typical oceanic values. Observations [48][49][50] ), consistent with the regime probed by our simulations, albeit at lower Reynolds numbers than those of the ocean.

To quantify the sensitivity of stratified turbulence to infinitesimal perturbations and thereby characterise uncertainty growth, we employ a twin-flow construction in which two nearly identical states are evolved under identical dynamics.

We begin by constructing statistically steady stratified turbulent states for different values of the non-dimensional Brunt-Väisälä frequency Ñ . Let u A 0 and b A 0 denote the velocity and buoyancy fields of such a non-equilibrium steady state. A second, nearly identical flow B is then initialised according to

where ϵ 0 ≪ 1.

The perturbation ϵ 0 ∇ × A is chosen to be small, localized, symmetric, and divergence-free. Explicitly, the vector potential, A has components

with localization scale r 0 ≪ 2π and center at x 0 = (π, π, π). This choice ensures that the perturbation is confined to a small region of the domain while preserving incompressibility.

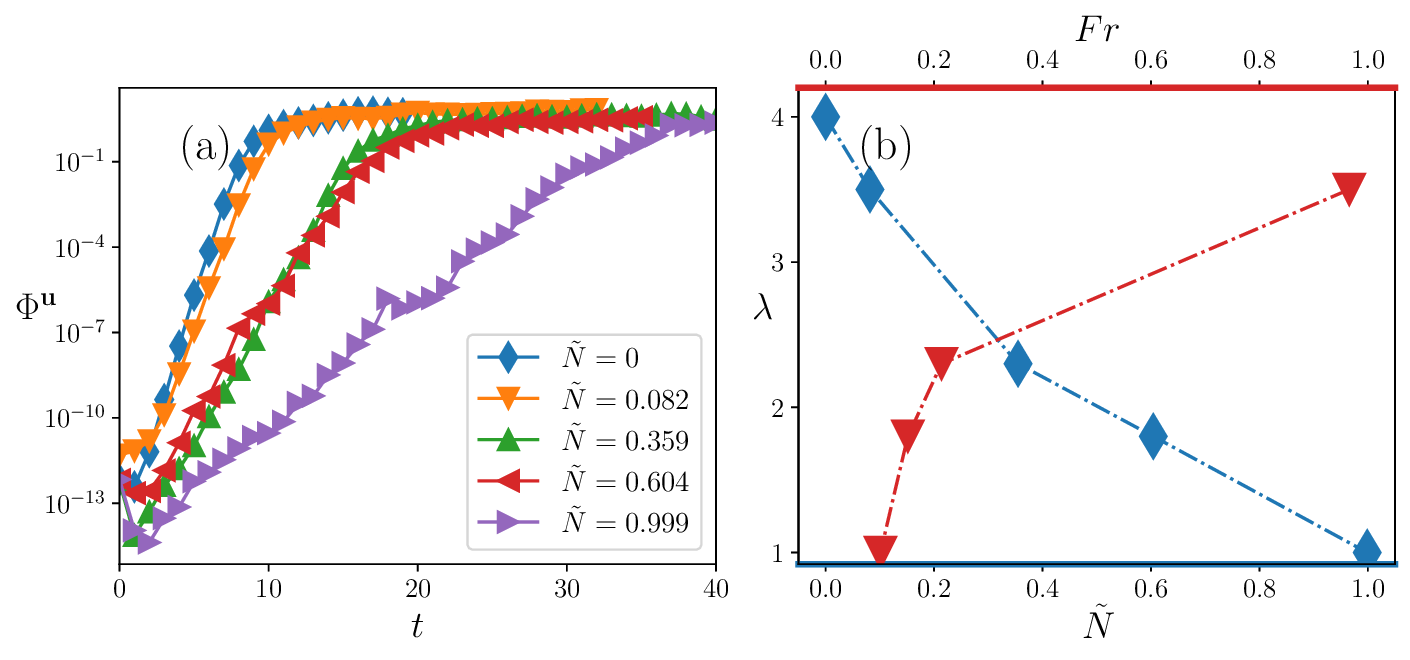
for different values of the non-dimensional Brunt-Väisälä frequency Ñ (see legend). After an initial decay, Φ u (t) exhibits a clear exponential growth regime followed by saturation, indicating complete decorrelation of the two flow realizations. (b) The Lyapunov exponent λ extracted from the exponential growth phase of Φ u (t) as a function of Ñ (lower axis). The monotonic decrease of λ with increasing stratification strength shows that stable stratification systematically suppresses chaoticity. The same data is also plotted against the Froude number Fr (upper axis), confirming that increased buoyancy effects lead to reduced sensitivity to infinitesimal perturbations.

Systems A and B are then evolved independently under identical dynamics. At any later time t, this allows us to define the velocity and buoyancy difference fields

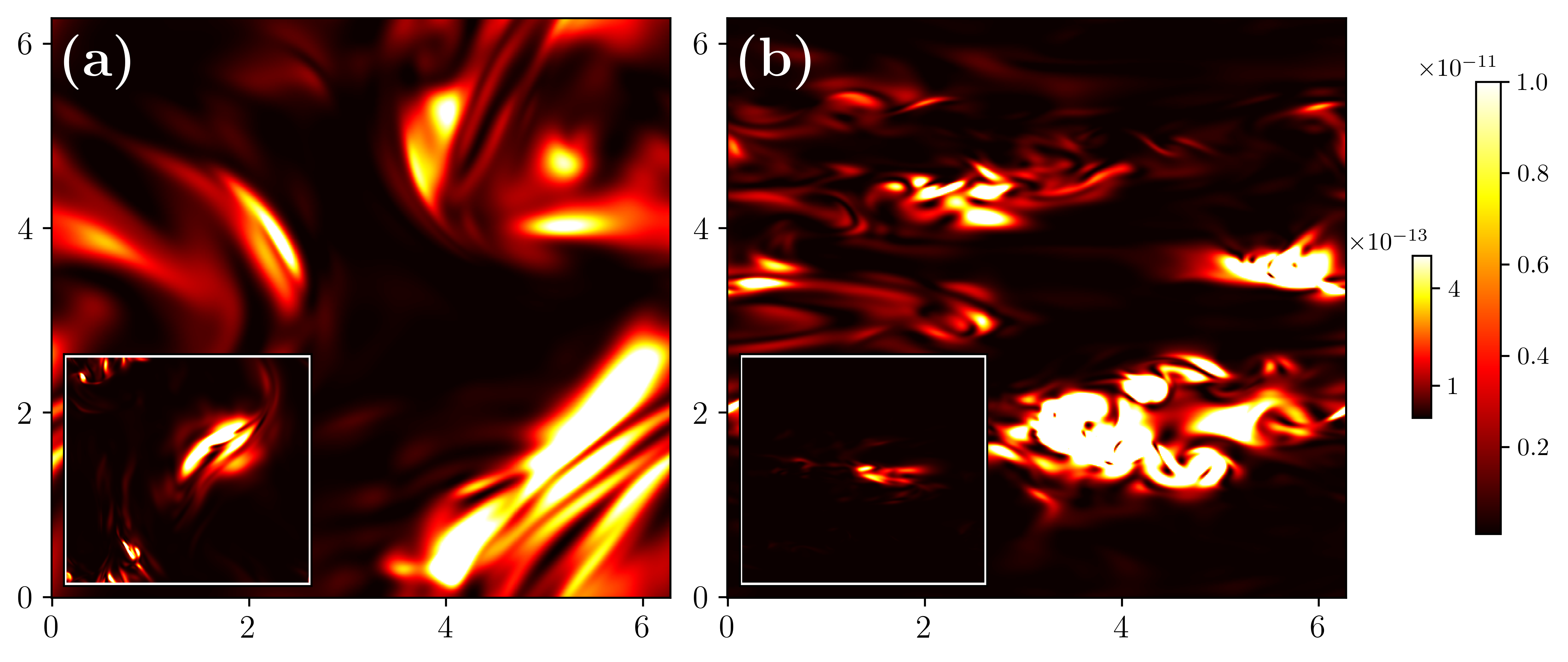
By construction, δu(r, 0) = ϵ 0 ∇ × A and δb(r, 0) = 0. Fig. 1 shows representative pseudocolor plots of the velocity decorrelator ϕ u (x, t) = 1 2 |δu(x, t)| 2 for a typical stratified run at an early time t = 7 during the decorrelation process. We display two-dimensional slices taken in the (a) XY and (b) XZ planes. The insets correspond to an earlier instant t = 2, before exponential growth sets in. These visualisations reveal the emergence of strongly anisotropic structures, with the perturbation field exhibiting quasi-two-dimensional organisation perpendicular to the direction of stratification. In particular, our results indicate an inhibited spread of uncertainty in z due to buoyancy effects.

To quantify uncertainty growth, we consider the spatially averaged decorrelator

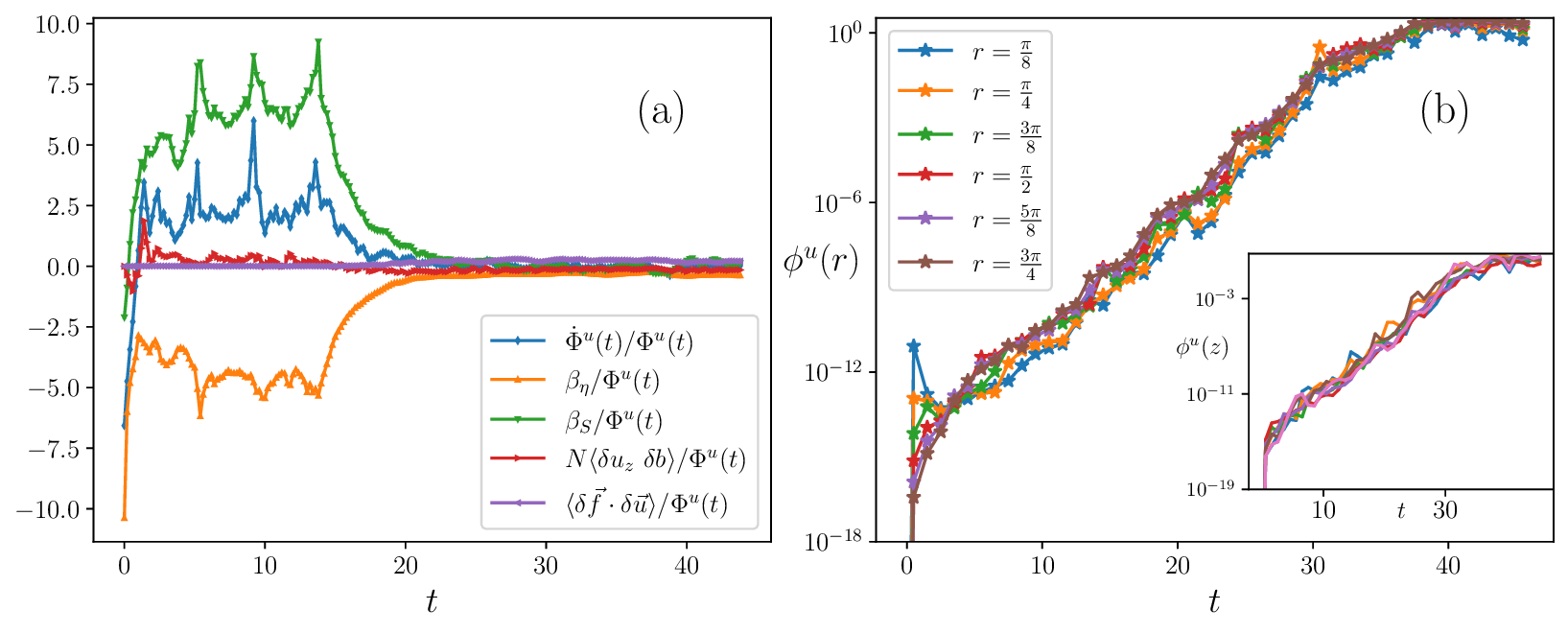
where angular brackets denote a volume average. Fig. 2(a) shows the temporal evolution of Φ u (t) for several values of the non-dimensional Brunt-Väisälä frequency, Ñ . For all cases, Φ u (t) displays a common sequence of dynamical regimes. At very early times, Φ u (t) exhibits a slight decay, reflecting the rapid viscous relaxation of the imposed perturbation. This is followed by a pronounced growth phase in which Φ u (t) increases exponentially in time before eventually saturating once the two flow realizations become fully decorrelated. The existence of a clear exponential growth regime allows us to define a Lyapunov exponent λ characterising the rate of uncertainty amplification. Extracting λ from the slope of ln Φ u (t) during this interval, we find that the degree of chaoticity decreases systematically as stratification strengthens. As shown in Fig. 2(b), λ decreases monotonically with increasing Ñ , indicating that stable stratification suppresses sensitivity to infinitesimal perturbations. The same trend is evident in Fig. 2(b) when λ is plotted against the Froude number, confirming that enhanced buoyancy effects lead to a dynamically calmer regime compared to homogeneous and isotropic turbulence at comparable Reynolds numbers. 4) for N = 4: the straininduced term βS, the viscous term βη, the buoyancy-velocity N ⟨δuz δb⟩, and the forcing contribution, each normalized by Φ u (t). The initial decay of Φ u (t) is driven by large, negative contributions from βS and βη, while the buoyancy term remains subdominant throughout. (b) Temporal evolution of the spherically averaged decorrelator ϕ u (r, t) with respect to the centre at x0 for different radii r (see legend), illustrating spatially homogeneous exponential growth of uncertainty. The inset shows ϕ u (z, t) at fixed r for seven different values of z in the range 0.53π ≤ z ≤ 1.47π , confirming uniform growth even along the direction of stratification. The dashed curve represents the spectra for the reference state.

How can these observations be understood directly from the equations of motion? Following the framework developed in Refs. [11,14], we derive an evolution equation for the spatially averaged velocity decorrelator Φ u (t):

where β S = -⟨δu • S • δu⟩ represents stretching and compression by the symmetric rate-of-strain tensor S, and β η = ν⟨δu • ∇ 2 δu⟩ denotes viscous dissipation. In addition to the terms familiar from homogeneous and isotropic turbulence (HIT), stratification introduces the buoyancy-velocity cross-correlation N ⟨δu z δb⟩. Direct evaluation of these contributions shows that, throughout most of the evolution and across all Froude numbers considered, the buoyancy-induced term remains subdominant compared to β S and β η , as illustrated in Fig. 3(a). Immediately after the perturbation is introduced, both β S /Φ u (t) and β η /Φ u (t) are large and negative, resulting in the initial decay of Φ u (t) observed in Fig. 2(a). This transient reflects the rapid viscous relaxation of a perturbation that has not yet developed preferential alignment with local flow structures.

Further insight is obtained by decomposing β S in the eigenbasis of the rate-of-strain tensor,

where γ i are the eigenvalues of S and n i are the direction cosines of δu along the corresponding eigendirections. The largest eigenvalue γ 1 > 0 corresponds to the extensional direction, γ 3 < 0 to the compressional direction, while γ 2 ≈ 0 is associated with a nearly neutral direction. At early times, the perturbation samples these eigendirections almost isotropically, so that i n 2 i γ i is negative on average and β S contributes to decay. During the exponential growth phase, however, the perturbation aligns strongly with the compressional eigendirection (n 2 3 ≃ 1), while the contribution from extensional stretching gets suppressed. In this regime, β S +β η becomes positive, driving exponential uncertainty growth, while both the buoyancy-velocity correlator and forcing term remain negligible.

A further hallmark of incompressible Navier-Stokes dynamics is the non-locality of the pressure field, which implies that an imposed perturbation can influence distant regions of the flow essentially instantaneously. As a result, the growth of uncertainty is spatially homogeneous. This behaviour is demonstrated in Fig. 3(b), where we show the

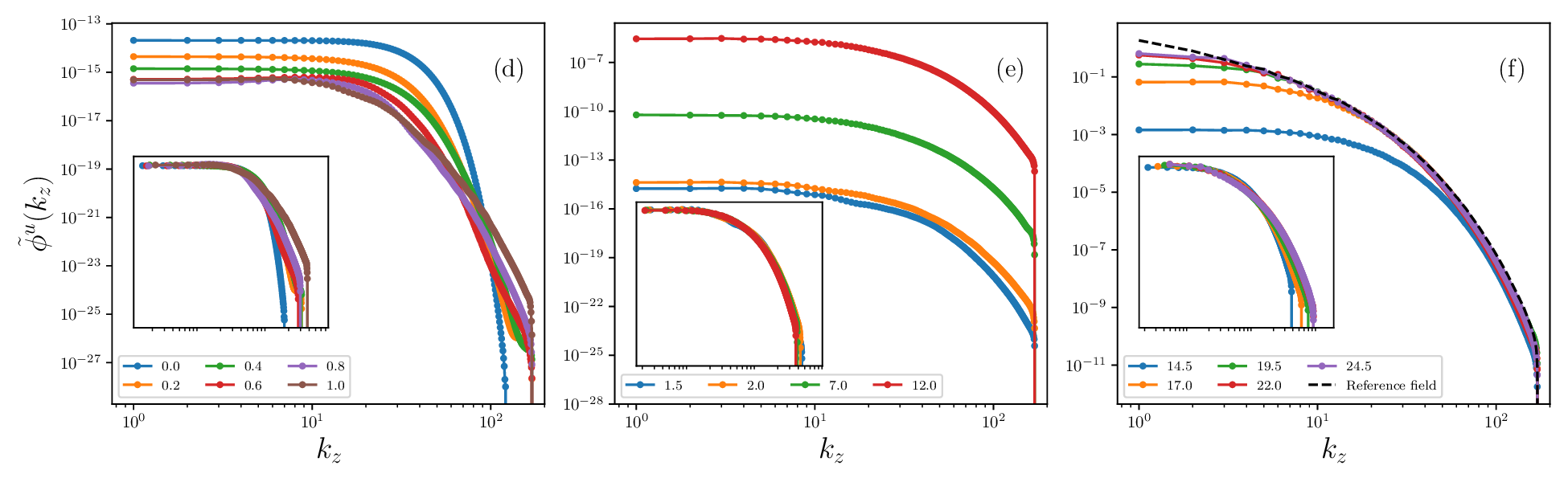
As can be seen from inset of (b), the rescaled spectra collapses demonstrating self-similar evolution in the growth phase. (d)-(f) The corresponding vertical decorrelator spectra φu (kz, t), exhibiting analogous behaviour along the direction of stratification.

temporal evolution of the spherically averaged decorrelator ϕ u (r, t) = ⟨ϕ u (x, t)⟩ for several values of the radius, r = |xx 0 | with respect to the center, x 0 of the initial perturbation. All radial shells exhibit identical exponential growth rates. One may go further and define ϕ u (z, t) as the azimuthally averaged decorrelator with respect to the z-axis passing through x 0 . The inset of Fig. 3(b) shows the evolution of ϕ u (z, t) for various values of z in the shell defined by r = π/2. This further confirms this homogeneity by demonstrating that uncertainty growth remains uniform also along z direction despite the underlying anisotropy of stratified turbulence.

The anisotropic nature of uncertainty growth, evident in the real-space decorrelator fields shown in Fig. 1, can be quantified more systematically in spectral space. Unlike homogeneous isotropic turbulence, stably stratified flows possess an inherent direction set by gravity, and the spread of uncertainty along the vertical (z) direction differs markedly from that in the horizontal plane. This motivates a scale-dependent analysis of the decorrelator using uncertainty spectra.

We define the velocity decorrelator spectrum as

where δ ũ(k, t) denotes the three-dimensional Fourier transform of δu(x, t), and ⟨• • • ⟩ represents an average over the spherical shell |k| = const. This yields the isotropic uncertainty spectrum. To probe anisotropy, we additionally consider reduced spectra, φu (k ⊥ , t) and φu (k z , t), obtained by summing over wavevectors with fixed k ⊥ = k and fixed k z , respectively.

Fig. 4(a)-(c) shows the temporal evolution of φu (k ⊥ , t) across distinct phases of decorrelation. During the initial decay phase, uncertainty rapidly populates higher horizontal wavenumbers. This is followed by a clear exponentialgrowth regime in which the spectrum evolves self-similarly. In this regime, the decorrelator spectrum exhibits the scaling form

where f is a universal scaling function and ℓ ∆ ⊥ (t) is the uncertainty integral length scale in the perpendicular direction. The integral scale is defined as

and measures the dominant horizontal scale over which uncertainty is distributed. The inset of Fig. 4(b) demonstrates this self-similarity: when the spectra are rescaled by ℓ ∆ ⊥ (t) and Φ u (t), they collapse onto a single curve during the exponential growth phase.

As the decorrelator approaches saturation, uncertainty progressively invades lower wavenumbers, indicating a transfer from small to large scales. Eventually, once the two realizations are completely decorrelated, the uncertainty spectrum converges to the kinetic energy spectrum of the reference flow,

shown by dashed black curves in Fig. 4(c). An analogous sequence of spectral phases is observed for the vertical spectrum φu (k z , t), shown in Fig. 4(d)-(f), as well as for the isotropic uncertainty spectrum (not shown). Similar self-similar evolution of decorrelator spectra was previously reported for homogeneous isotropic turbulence [11].

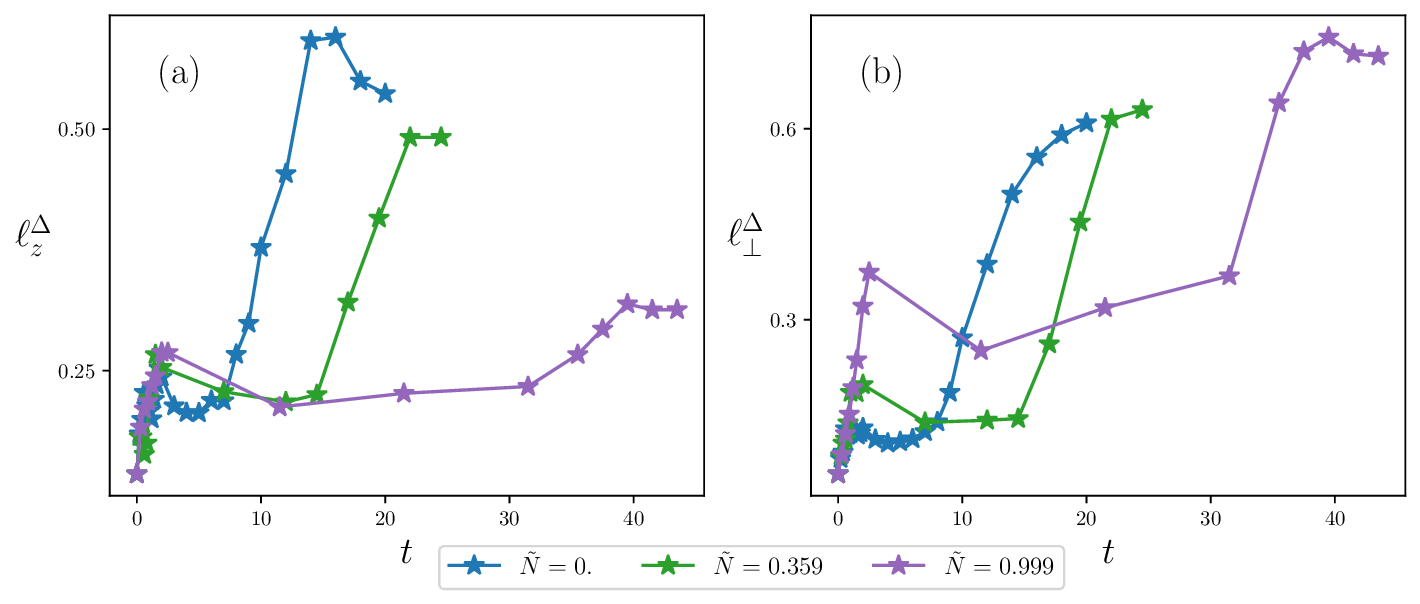
Strong stratification is known to suppress vertical velocity fluctuations, leading to flow structures with much smaller vertical length scales than horizontal ones. This anisotropy is reflected directly in the uncertainty dynamics. As seen in Fig. 1, the decorrelator structures in the growth phase are elongated in the horizontal plane and compressed along z. This behaviour is quantified in Fig. 5, which compares the temporal evolution of the uncertainty integral length scales in the horizontal (ℓ ∆ ⊥ ) and vertical (ℓ ∆ z ) directions. Throughout the exponential growth phase, ℓ ∆ z ≪ ℓ ∆ ⊥ , with the disparity increasing as the stratification strength is raised.

Finally, an analogous decorrelator ϕ b (x, t) may be defined for the buoyancy field. We find that the spatially averaged buoyancy decorrelator Φ b (t) grows at the same exponential rate as its velocity counterpart Φ u (t). Consequently, buoyancy fluctuations exhibit spectral evolution and anisotropy qualitatively similar to those observed for the velocity field.

We have investigated the growth of uncertainty in stably stratified turbulence using decorrelator-based diagnostics and Lyapunov analysis. Increasing stratification strength (decreasing Froude number) leads to a systematic reduction of the Lyapunov exponent, demonstrating that stable stratification suppresses chaoticity. Despite this quantitative change, uncertainty growth retains the familiar temporal structure observed in homogeneous isotropic turbulence: an initial decay phase, followed by self-similar exponential growth and eventual saturation.

The exponential growth regime is characterised by a universal, self-similar evolution of the uncertainty spectra. However, in contrast to isotropic flows, uncertainty propagation is strongly anisotropic. Perturbations spread much more slowly in the vertical direction than in the horizontal plane, and the uncertainty integral scale along the stratification direction remains consistently smaller throughout the growth phase. This anisotropy intensifies with increasing stratification, reflecting the inhibition of vertical motions by buoyancy forces.

Analysis of the decorrelator evolution equation reveals the physical origin of this reduced chaoticity. Stratification primarily acts by altering the alignment between perturbations and the local rate-of-strain tensor. During the exponential growth phase, perturbations preferentially align with compressive eigendirections, diminishing the effectiveness of extensional stretching that drives rapid uncertainty amplification in isotropic turbulence. In contrast, buoyancyvelocity cross-correlations and forcing contributions remain subdominant, indicating that the suppression of chaos is controlled predominantly by strain-mediated dynamics rather than direct buoyancy coupling. Although the Reynolds numbers achieved in our simulations remain lower than those characteristic of oceanic flows, similar limitations are common in direct numerical studies of stratified turbulence. Nevertheless, the systematic trends reported hereparticularly the monotonic suppression of the Lyapunov exponent with increasing stratification and the anisotropic structure of uncertainty growth -are expected to persist at higher Reynolds numbers.

From a geophysical perspective, these findings suggest that strong stable stratification can enhance short-time predictability by limiting the vertical spread of uncertainty, even while permitting rapid horizontal error growth. Taken together, our results provide a quantitative characterization of uncertainty growth and Lyapunov dynamics in stratified turbulence. Beyond their implications for predictability in geophysical flows, this work establishes decorrelator-based methods as a robust framework for diagnosing chaotic dynamics in anisotropic and wave-supporting turbulent systems, with natural extensions to rotating, magnetized, and convectively driven flows.

MJP and SSR acknowledge several discussions with Arun Kumar Varanasi. MJP also thanks Rajarshi and Sanjay C P for useful suggestions. SSR acknowledges the Indo-French Centre for the Promotion of Advanced Scientific Research (IFCPAR/CEFIPRA, project no. 6704-1) for support. The simulations were performed on the ICTS clusters Mario, Tetris, Boson2, and Contra. MJP and SSR acknowledge the support of the DAE, Government of India, under projects nos. 12-R&D-TFR-5.10-1100 and RTI4001.