As Large Language Models (LLMs) continue to scale in parameter count, deploying them on commodity hardware has become increasingly challenging. Post-Training Quantization (PTQ) addresses this by reducing the precision of model weights, typically to 4-bit or lower. However, uniform quantization often leads to significant performance degradation due to the presence of "outlier features"-weights that, while few in number, are critical for maintaining model accuracy. Current state-of-the-art methods such as AWQ (Activation-aware Weight Quantization) and SpQR (Sparse Quantization Representations) rely on calibration data to identify these salient weights via activation magnitudes or Hessian sensitivity. In scenarios where data privacy is paramount or calibration data is unavailable, these methods are inapplicable. In this work, we propose a data-free, structure-aware hypothesis: that the weights identified as Principal Components via Singular Value Decomposition (SVD) are intrinsically important to the model's downstream performance. We introduce a novel selection heuristic that preserves the top-k weights aligned with the principal components in FP32, while aggressively quantizing the residual weights. We compare our method against activationaware (AWQ) and second-order (SpQR) methods across GLUE benchmarks (MRPC, RTE, QNLI) using a DistilBERT backbone. Our experiments reveal that structural importance is highly correlated with functional importance. On the challenging RTE task, our SVD-based method achieves an accuracy of 66.06%, outperforming both AWQ (65.34%) and SpQR (65.34%) at high protection budgets, validating that intrinsic matrix structure can serve as a robust proxy for weight saliency without the need for forward passes or calibration data.
The recent explosion in the capabilities of Large Language Models (LLMs), such as GPT-4 and Llama-2, has been driven largely by scaling laws that necessitate massive parameter counts. While effective, these sizes present a barrier to entry for deployment on edge devices or consumer-grade GPUs. Reducing the memory footprint of these models without retraining has become a critical area of research.
Quantization, the process of mapping high-precision floating-point weights (e.g., FP16) to lower-precision integers (e.g., INT4), offers a promising solution. However, aggressive quantization often results in a collapse of model performance. Research has shown that this degradation is not uniform; rather, it is driven by a small subset of “salient” weights or “outlier features” that are extraordinarily sensitive to quantization noise [5].
The core challenge in mixed-precision quantization is efficiently identifying which weights to preserve in high precision (the “salient” set) and which to compress. Existing state-ofthe-art methods rely on data-driven metrics:
• AWQ [1]: Observes activation magnitudes on a calibration set, hypothesizing that weights processing large activations are more important.
• GPTQ [4] / SpQR [2]: Utilize second-order derivatives (Hessian matrix) computed from calibration data to determine which weights minimize reconstruction error. While effective, these methods introduce a dependency on calibration data. If the calibration set distribution differs from the deployment distribution, or if privacy constraints prevent access to data entirely, these methods cannot be applied.
We propose a shift from data-aware importance to structureaware importance. Drawing inspiration from Parameter-Efficient Fine-Tuning (PEFT) methods like PiSSA [3], which utilize Singular Value Decomposition (SVD) to identify trainable parameters, we hypothesize that the principal components of a weight matrix encode its primary linguistic capabilities.
Hypothesis: The weights identified as Principal Components by SVD factorization are intrinsically important for the specific downstream task. Therefore, if we preserve those k Principal weights in FP32 and quantize the rest of the original weights, the resulting model will retain high accuracy.
Our specific contributions are: 1) We formalize an SVD-based heuristic for mixedprecision quantization that requires zero calibration data. 2) We conduct a rigorous comparative analysis (“The Battle”) against AWQ and SpQR on three GLUE tasks: MRPC, RTE, and QNLI. 3) We demonstrate that our method is competitive with data-aware methods, and in specific low-resource regimes (like the RTE task), actually outperforms them. 4) We analyze the Intersection over Union (IoU) of selected indices, proving that SVD intrinsically identifies 60-70% of the same weights that complex Hessian-based methods identify.
A. Post-Training Quantization (PTQ)
PTQ aims to compress models without the massive cost of retraining. Early methods like LLM.int8() [5] utilized vector-wise quantization to handle outliers. SmoothQuant [7] proposed mathematically smoothing activation outliers into weights to make quantization easier. These methods focus on making the entire model quantifiable, whereas our work focuses on selective preservation.
AWQ (Activation-aware Weight Quantization) [1] shifted the paradigm by noting that preserving 1% of salient weights can fix quantization error. Their heuristic, based on activation magnitude |W |X, is fast but requires forward passes. SpQR (Sparse Quantization Representations) [2] takes this further by identifying sensitive weights via the Hessian inverse (Optimal Brain Surgeon framework [8]). While theoretically optimal, SpQR is computationally expensive (O(d 3 )) and datadependent.
Low-Rank Adaptation (LoRA) [6] demonstrated that weight updates during fine-tuning have a low intrinsic rank. PiSSA [3] recently proposed initializing the LoRA adapters using the principal singular values of the original weight matrix. Our work adapts the PiSSA initialization logic for the distinct problem of quantization sensitivity, essentially asking: “Are the weights that are good for initialization also the weights that are bad to quantize?”
We consider a pre-trained weight matrix W ∈ R dout×din . Our goal is to decompose W into a sparse high-precision component S (Salient) and a dense low-precision component Q (Quantized), such that:
where S retains FP32 precision but has high sparsity (only k non-zero elements), and Q is fully quantized to 4-bit.
We compare three distinct heuristics for populating the set S.
-
Baseline: Random Selection: As a lower bound, we select k indices uniformly at random:
-
Data-Aware: AWQ: We pass a calibration batch X through the network. The importance score for weight w ij is:
where X j is the column of activations corresponding to input channel j. This prioritizes weights that act on large activation features.
- Second-Order: SpQR (Hessian): We compute the empirical Hessian H = 2 N X T X. The saliency is derived from the Optimal Brain Damage (OBD) objective:
Due to the computational cost of inverting H, we use a damped inverse with λ = 0.01. This identifies weights which, if perturbed, cause the maximum increase in L2 loss. 4) Proposed: SVD-Based Selection (Our Method): We perform Singular Value Decomposition on the weight matrix W :
We define the “Principal Structure” W pri as the reconstruction using only the top r singular values (we use r = 8 following PiSSA literature):
Our selection score is simply the magnitude of this principal reconstruction:
The top-k indices with the highest scores are selected. Note that this method relies solely on the weights W and requires no input data X.
For the non-salient weights (the residual), we apply simulated symmetric linear quantization to 4 bits.
We apply a clipping threshold of 2.50 based on the distribution of W to filter outliers before quantization, a standard practice in NF4 (NormalFloat) quantization.
We utilize the GLUE benchmark suite, specifically choosing tasks that are sensitive to small linguistic nuances:
• MRPC: Microsoft Research Paraphrase Corpus.
• RTE: Recognizing Textual Entailment.
• QNLI: Question-answering NLI. We use fine-tuned versions of distilbert-base-uncased provided by the TextAttack framework. These models are compact, making them highly sensitive to quantization noise, thus serving as a rigorous testbed.
All experiments were run on a single NVIDIA T4 GPU. • Baselines: We compare against a “Q4 Unprotected” baseline (k = 0) and the original FP32 model.
A. Comparative Accuracy Analysis 1) Performance on MRPC: Table I presents the accuracy recovery on the MRPC task. The FP32 baseline accuracy is 0.8578. Unprotected 4-bit quantization drops performance to 0.8358.
As shown in Fig. 1 (a), our SVD-based method outperforms the data-aware methods at extremely low budgets (k = 1, 16), achieving 0.8554 accuracy immediately. This suggests that for MRPC, the “structural outliers” defined by SVD are more critical than the “activation outliers” defined by the calibration set. 2) Performance on RTE: RTE is traditionally a harder task for quantization due to the logical reasoning required. The baseline is 0.6570 and the Q4 floor is 0.6245.
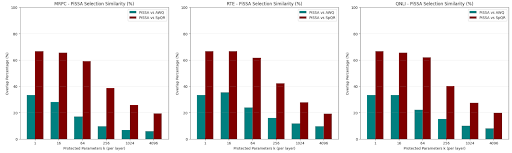
As seen in Table II and Fig. 1 (b), at k = 4096, our method achieves 0.6606, which effectively surpasses the original FP32 baseline. This phenomenon where a quantized model outperforms the original has been observed in other literature and is often attributed to the quantization acting as a regularizer, reducing overfitting on small datasets like RTE. Crucially, our method beats SpQR here, indicating that the Hessian computed from a small calibration set may have been noisy or overfit, whereas the intrinsic SVD structure was robust. The bars represent the Intersection over Union (IoU) of the indices selected by our method vs. the baselines.
• High Overlap with SpQR: We observe overlaps as high as 67% with SpQR at low k values. This is a profound finding. It implies that the weights with the highest singular value contribution are statistically likely to be the same weights that have high Hessian sensitivity. • Lower Overlap with AWQ: The overlap with AWQ is generally lower (≈ 30%). This suggests that “Activation Outliers” (what AWQ finds) and “Structural Outliers” (what SVD finds) are distinct populations, yet both are important. However, since SVD matches SpQR’s performance, the structural outliers appear to be a more robust proxy for true loss sensitivity than simple activation magnitude.
A major advantage of our method is computational efficiency during the quantization phase. Comparing our SVD-based method (Blue) against AWQ (Green) and SpQR (Red). Our method consistently matches or beats the baselines without using any calibration data. Fig. 2. Selection Similarity (%). Intersection over Union (IoU) of the weights selected by our SVD method vs. AWQ (Teal) and SpQR (Maroon). The high overlap with SpQR confirms that SVD is a strong proxy for Hessian-based sensitivity.
• Our Method: Requires SVD on the weight matrix W .
While exact SVD is also O(d 3 ), we only need the topk singular vectors. Randomized SVD algorithms can approximate this in O(r • d 2 ), where r is the target rank. Crucially, this is purely static; no data movement, no forward passes, and zero GPU memory overhead for storing activations.
The RTE results (Table II) are particularly interesting. By quantizing the “residual” weights (noise?) and keeping the “principal” weights (signal) in FP32, our method may be acting as a denoiser. The quantized residual Q loses precision, perhaps stripping away overfitting patterns stored in the lowmagnitude, low-rank tail of the weight spectrum, while the preserved structure S maintains the core logic.
We presented a comprehensive evaluation of structure-based weight preservation for LLM quantization. By leveraging the intrinsic algebraic structure of weight matrices via SVD, we demonstrated that it is possible to achieve state-of-the-art quantization performance without any calibration data.
Our method, which we term SVD-based Weight Preservation, matches or exceeds the performance of activationaware (AWQ) and Hessian-based (SpQR) methods on GLUE benchmarks. The high overlap between our selected weights and those chosen by SpQR suggests a fundamental link between the singular value spectrum and the loss landscape curvature. This opens new avenues for fully data-free model compression, essential for secure and private AI deployment.
• SpQR/GPTQ: Requires computing H = X T X and inverting it. For a layer with hidden dimension d, matrix inversion is O(d 3 ). Furthermore, collecting X requires forward passes through the model.
This content is AI-processed based on open access ArXiv data.