Language as a Wave Phenomenon: Semantic Phase Locking and Interference in Neural Networks

to structural relevance or simple statistical frequency. To resolve this, we turn to Deep Complex Networks (Trabelsi et al., 2018), which offer a distinct computational primitive: Phase Coding. By encoding information in the phase angle rather than the magnitude, these networks compel semantic binding to occur via oscillatory synchronization (Fries, 2005), theoretically allowing for a cleaner mechanistic trace of how concepts interact via interference rather than accumulation.

However, standard complex-valued networks often revert to magnitude-based heuristics during training. To prevent this, we repurpose the Unity Gain constraint-typically employed solely for gradient stability in Recurrent Networks (Arjovsky et al., 2016)-as a tool for interpretability. By strictly enforcing a unit-norm constraint, we handicap the model’s ability to use energy as a proxy for importance, forcing it to develop precise, phase-based geometric circuits that are amenable to mechanistic analysis.

In this work, we introduce the Phase-Rotating Interference Spectral Model (PRISM), an architecture designed to bridge Deep Complex Networks and Mechanistic Interpretability. While we adopt the mathematical constraints of optical 4f-correlators to enforce strict passivity, our primary investigation is algorithmic rather than hardware-centric: we investigate whether Subtractive Interference can serve as a sufficient computational primitive for semantic reasoning. Unlike previous spectral architectures (e.g., FNet) which rely on additive mixing, PRISM leverages complex-valued phase cancellation to mechanically “delete” noise via destructive interference. We demonstrate that this physics-constrained regime naturally yields interpretable geometric structures, such as a “Semantic Phase Compass” where synonyms and antonyms self-organize via phase-locking.

Scope & Scale: A Mechanistic Probe. We emphasize that this work targets the domain of Mechanistic Interpretability and Signal Processing, rather than large-scale Foundation Model training. We utilize the hypothetical constraints of optical computing not to propose immediate hardware, but as a boundary condition to isolate the causal efficacy of Phase Coding. Consequently, our goal is not to surpass State-of-the-Art perplexity via scale, but to determine the lower bound of structural complexity required for reasoning. We quantify this as the “Tax of Passivity”: the specific performance cost paid to achieve a gain-free, optically-compatible inference regime.

Spectral & Harmonic Modeling. FNet (Lee-Thorp et al., 2022) established that Fourier Transforms could replace attention with O(N log N ) efficiency, though it relies on additive magnitude mixing. Recent work in continuous physics, such as CoNO (Tiwari et al., 2025), demonstrated that complex-valued operators are essential for capturing rotational dynamics. PRISM unifies these, applying complexrotational logic to discrete semantics.

Phase-Based Attention. While Holographic Transformers (Huang et al., 2025) and POC-ViT (Sharma et al., 2025) utilize phase to achieve signal robustness and invariance, they retain the quadratic complexity of attention. In contrast, PRISM utilizes phase for semantic steering-resolving ambiguity via subtractive interference-within a globally efficient spectral framework.

Unitary Evolution & Hardware. The theoretical basis for our iso-energetic constraint lies in Unitary RNNs (Arjovsky et al., 2016), where Arjovsky et al. proved that unity gain enables infinite memory retention. We adapt this to encode information in phase angles, effectively simulating the Phase-Coded Aperture hardware topology established by Chi & George (Chi & George, 2011). Finally, we reject covariance-based Complex Batch Normalization (Trabelsi et al., 2018) in favor of Phase-Preserving Layer Normalization (PPLN) to prevent phase distortion during optimization.

We formally define the Phase-Rotating Interference Spectral Model (PRISM), a structural modeling paradigm rooted in wave mechanics. Unlike standard Transformers which treat tokens as static vectors manipulated by additive updates, PRISM treats tokens as complex phasors z = re iθ , where semantic identity is encoded in the angle θ and signal intensity in the magnitude r.

We introduce Rotary Semantic Embeddings (RoSE) to unify semantic identity and positional context into a single complex-valued phasor. Unlike standard architectures that add positional encodings to static embeddings (e + p), RoSE operates via multiplicative rotation in the complex plane.

Let w t be the token at position t. We first project w t into

The final embedding E(w t ) is obtained by rotating the content vector z t by the positional phase angle:

This formulation ensures that the relative distance between tokens t and t + k is preserved as a constant phase shift e iωk in the frequency domain, providing a natural inductive bias for sequence modeling.

The core reasoning unit of PRISM is the Gated Harmonic Convolution. Unlike recent “Holographic” architectures which introduce phase dynamics but retain the quadratic computational cost of pairwise attention (Huang et al., 2025), PRISM replaces the attention mechanism entirely. This layer filters information in the frequency domain (O(N log N )) while allowing the time-domain signal to dynamically modulate its own phase and magnitude.

Given a sequence of complex embeddings X ∈ C L×d , we first normalize the input using Phase-Preserving Layer Normalization. We then compute two separate data-dependent gates, G re ∈ R L×d and G im ∈ R L×d , using the concatenated real and imaginary components of the normalized input X:

Simultaneously, we transform the sequence into the frequency domain via the Fast Fourier Transform (FFT) and apply a learnable global filter H ∈ C L×d . This spectral filtering mirrors the biological phenomenon of “Connectome Harmonics” (Atasoy et al., 2016;Deco et al., 2025), where brain dynamics naturally self-organize into standing waves (eigenmodes) to integrate information efficiently. This operation is mathematically dual to the Selective State Space mechanism utilized in efficient engineering models like Mamba, demonstrating a convergent evolution between biological spectral gating and hardware-optimized linear recurrence.

Theoretical Motivation: Eq. ( 4) is isomorphic to an optical 4f-correlator. In analog hardware, integration occurs via wave propagation (t = d/c), independent of sequence length N . We utilize this theoretical O(1) complexity as a design principle, though digital implementation remains bounded by the FFT’s O(N log N ) cost.

The filtered signal is returned to the time domain via the Inverse FFT (IFFT). Crucially, we apply Cartesian Gating, where the real and imaginary components are modulated independently:

Unlike scalar gating which only scales magnitude, this independent Cartesian modulation allows the network to alter the phase angle θ = arctan(Im/Re) of the latent vectors, enabling the “Contextual Phase Steering” mechanism described in Section 4.

Standard activation functions like ReLU are ill-defined for complex numbers as they destroy phase information. We adopt ModReLU, which rectifies the magnitude of the complex vector while strictly preserving its phase angle. For a complex input z:

where b is a learnable bias parameter. This ensures that the semantic orientation of the vector (its “meaning”) remains unchanged, while its intensity (magnitude) is non-linearly scaled.

To prevent the network from over-relying on specific frequency bands, we introduce Phase-Preserving Dropout. Unlike standard dropout which operates on scalars, applying independent masks to the real and imaginary components would destroy the phase angle θ. Instead, we sample a single binary mask m ∼ Bernoulli(1 -p) and apply it identically to both components:

This ensures that if a feature is dropped, its entire spectral contribution (amplitude and phase) is removed simultaneously, forcing the network to distribute semantic information holographically across the spectrum.

To maintain the stability of complex gradients, a critical challenge in high-dimensional complex manifolds (Trabelsi et al., 2018), we utilize a normalization scheme that operates solely on the magnitude. Given a vector z, we compute the mean µ and variance σ 2 of its magnitude |z|, then apply standard layer normalization to the magnitudes while preserving phase:

This decouples the signal’s energy from its phase, reinforcing the Iso-Energetic reasoning regime while ensuring the semantic orientation remains invariant.

To interface the complex encoder with the real-valued decoder, we utilize a Projection Bridge. The state z enc is mapped to R d by concatenating its real and imaginary components and projecting via a linear layer W bridge :

This compresses spectral phase information into a dense representation suitable for cross-attention.

We evaluate on the WMT14 De-En benchmark (Bojar et al., 2014;Vaswani et al., 2017), tokenized using the Helsinki-NLP OPUS-MT model (Tiedemann & Thottingal, 2020).

To reduce computational overhead, we filter sequences exceeding L = 128, discarding < 1% of the data. Training utilizes dynamic bucketing (width 4, target size 20,000) to minimize padding and stabilize spectral gradients.

We utilize WMT14 as a mechanistic debugging workbench to isolate the sufficiency of “Phase Coding.” Rather than maximizing metrics via scale, this experiment employs the most restricted version of PRISM to verify if semantic relationships (e.g., synonyms) naturally emerge as phase shifts within a controlled environment.

We establish a comparative study between two regimes. The Control Group (Rate-Coding) is a standard Transformer (Vaswani et al., 2017) utilizing Rotary Position Embeddings (RoPE) and unconstrained magnitude. The Experimental Group (Phase-Coding) is the restricted PRISM architecture, constrained by Iso-Energetic Unity Gain. Both models use 6-layer encoders/decoders and Pre-Layer Normalization (Pre-LN) (Nguyen & Salazar, 2019) for stability.

Spectral Control (FNet): We select FNet (Lee-Thorp et al., 2022) as the mathematically isomorphic control. Both rely on global Fourier mixing, though we restrict PRISM to 1D temporal interference (unlike FNet’s 2D mixing) to strictly isolate phase-based reasoning. We exclude causal SSMs (Gu & Dao, 2024) to avoid confounding recurrence variables.

Fairness & Capacity: To accommodate FNet’s fixed-length training requirement (L = 128), we synchronized effective token counts across models. Furthermore, since FNet lacks learnable mixing weights, we matched parameter counts by increasing its encoder depth to 7 layers (vs. 6 for PRISM). This ensures the baseline possesses superior algorithmic capacity (14.7M vs 13.0M), guaranteeing PRISM’s efficiency is not due to under-parameterizing the control.

Parameter Redistribution: PRISM redistributes density from “logic” to “memory.” The PRISM Encoder requires 31.2% fewer parameters than the Standard Transformer (13.0M vs 18.9M). We evaluate the PRISM-Standard (Tied) configuration to demonstrate this efficiency is achievable without compromising fidelity. Debugging Prototype: We utilize a Sequence-to-Sequence framework with a standard Transformer decoder. This isolates the experimental Phase Coding variable strictly to the reasoning encoder before scaling to the high-capacity architectures in 6.3,.

All models were optimized using AdamW (Loshchilov & Hutter, 2019) with weight decay of 0.01 and a cosine learning rate schedule (600 warmup steps).

Strict Hyperparameter Parity: To ensure a rigorous evaluation, we enforced identical hyperparameters across all comparative benchmark models (Transformer, FNet, and PRISM-Tied).

Stability Constraints: Initial experiments revealed that while the PRISM architecture remained stable at higher learning rates (8 • 10 -4 ), the Standard Transformer control group exhibited gradient instability. Consequently, we restricted the peak learning rate to 6 • 10 -4 for all models, ef-fectively handicapping PRISM to accommodate the stability limits of the Transformer baseline.

Spectral Precision: Global batch size was maintained at approximately 20,000 tokens via gradient accumulation. We utilized Single Precision (FP32) to prevent the catastrophic cancellation of phase information inherent in Mixed-Precision (FP16) arithmetic.

We instrument the network with forward hooks to capture the input vector x (l) and output vector y (l) at each layer l.

We define three primary physical metrics:

1. Iso-Energetic Gain (g): To test the hypothesis that the network operates as a Frequency Modulation (FM) system, we measure the signal amplitude amplification ratio. A value of g ≈ 1.0 indicates an iso-energetic carrier wave, whereas g ≫ 1.0 would indicate Amplitude Modulation (AM).

2. Effective Phase Rotation (∆θ): Since the PRISM encoder operates in the complex domain, we quantify semantic transformation as the effective angular displacement between the input and output phasors. We compute the cosine similarity in the complex plane and convert it to degrees:

This metric serves as a proxy for “semantic work,” representing how aggressively the layer steers the representation in the latent space.

Beyond mean values, we analyze the shape of the rotation distribution to detect selective reasoning. We calculate the sample skewness γ 1 of the rotation angles Θ = {∆θ 1 , . . . , ∆θ n }:

A near-zero skewness (γ 1 ≈ 0) implies a uniform, predictable transformation applied to all tokens. A high positive skewness (γ 1 > 1.0) indicates a “heavy-tailed” process, where the model exerts extreme effort on a small subset of tokens (the “Long Neck”) while leaving the majority unmodified (the “Fat Bottom”).

We evaluate PRISM to validate physical sufficiency and mechanistic interpretability. Note on Evaluation Scope:

We utilize the WMT14 task strictly as a mechanistic probe for the Static RoSE configuration. Unlike the highperformance Dynamic RoSE architecture used for generative modeling in Section 6.3, this ablation strips away active phase steering to isolate the baseline efficacy of wave interference.

To establish a lower bound, we compare three configurations: the Static PRISM encoder (utilizing fixed, static RoSE), a Standard FNet baseline, and a Standard Transformer with active attention. While Static PRISM lacks the explicit input steering capabilities found in our highperformance generative variants (Section 6.3) and the baselines, it achieves 0.799 COMET-closely trailing FNet (0.805) and remaining competitive with the Transformer ceiling (0.821). This demonstrates that passive wave interference alone is sufficient to capture the bulk of semantic alignment.

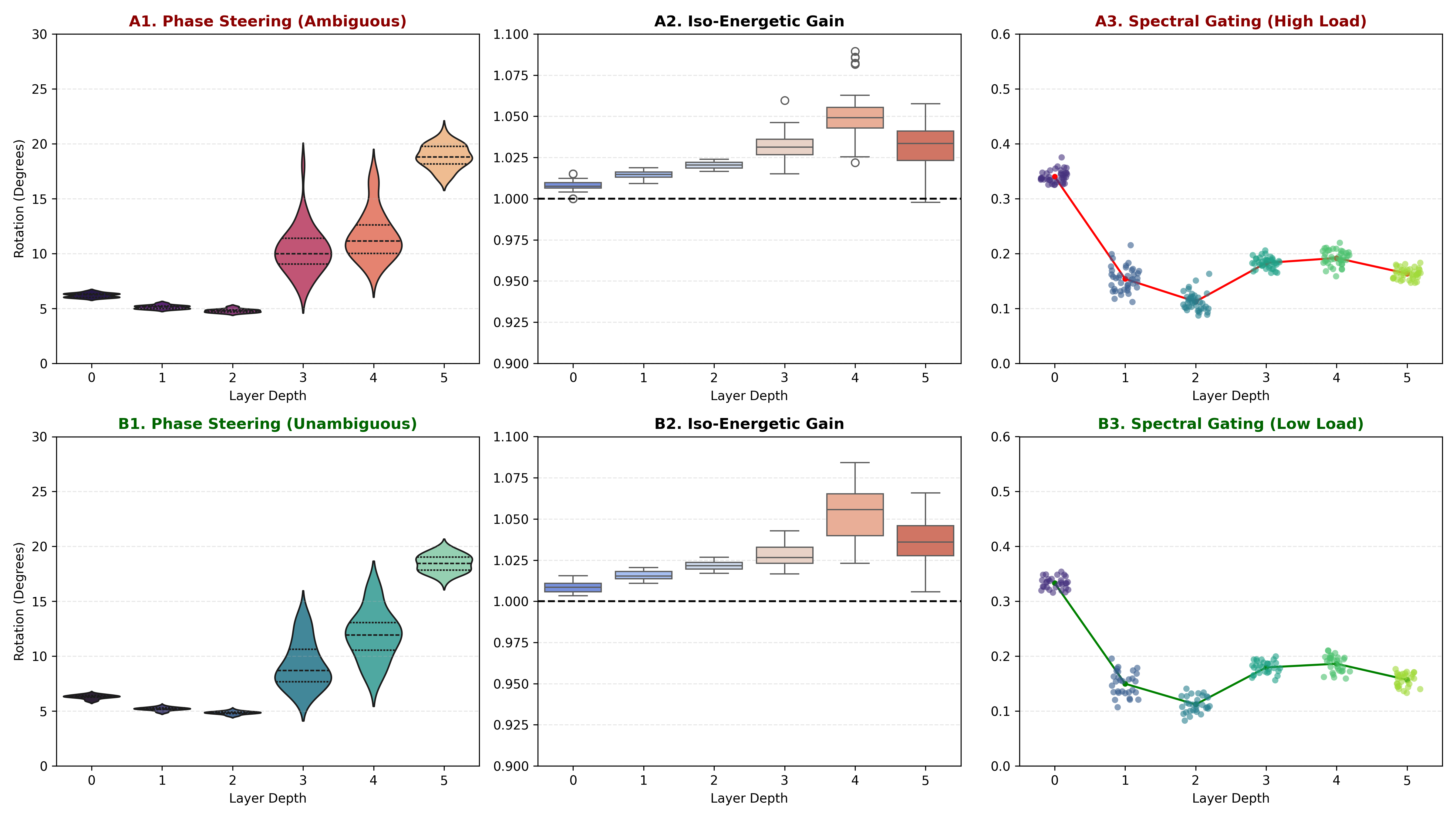
We verify the iso-energetic constraint holds empirically: signal gain remains within 1.0-1.05 across all layers and conditions.

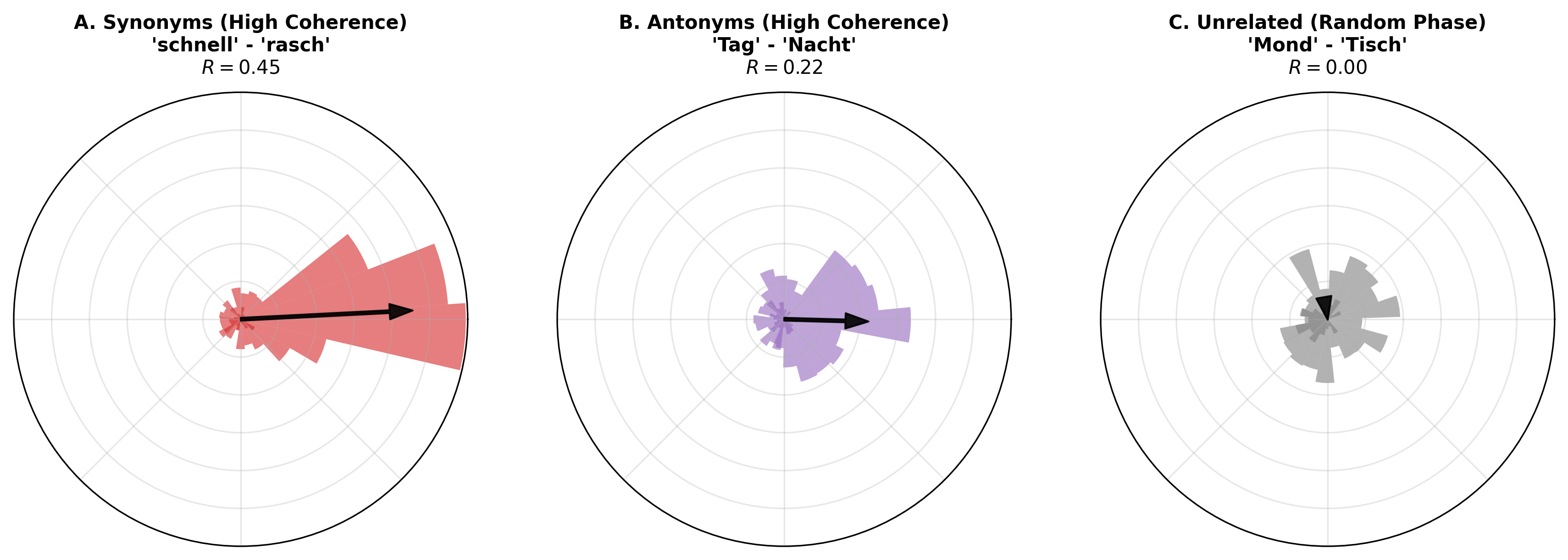
To validate the hypothesis that PRISM encodes semantic proximity as geometric alignment, we analyze the Weighted Mean Resultant Length (R) of the phase difference vectors between word pairs. For a pair of token embeddings z a , z b ∈ C d , we weight the phase coherence by the signal energy in each frequency band k. R is defined as:

where ∆ϕ k = Angle(z a,k ) -Angle(z b,k ) is the phase difference at frequency k. Here, R ∈ [0, 1] quantifies angular coherence. Crucially, because the raw embeddings retain magnitude variance (|z| ̸ = 1.0) prior to normalization, the weighting terms |z a,k ||z b,k | serve a physical purpose: they ensure that phase alignment is prioritized in high-energy spectral bands while effectively filtering out random phase noise in low-magnitude frequencies. As illustrated in Figure 2 and Table 2, we observe a distinct

To validate the “Language as a Wave” hypothesis, we probed the network’s internal state on a contrastive dataset of N = 146 atomic tokens. We observe that PRISM resolves semantic ambiguity through geometric phase rotation while strictly adhering to the iso-energetic constraint. confirms that this steering is Iso-Energetic. The gain for ambiguous tokens does not diverge from unambiguous tokens (g amb ≈ g unamb ≈ 1.0). This empirically rules out amplitude modulation (“shouting”) as a mechanism.

We investigate PRISM not as a theoretical “All-Optical” abstraction, but as a robust Heterogeneous Architecture that leverages the physics of both domains: Passive Optical Mixing (O(1) effective latency) for global context integration, and Active Digital Restoration (O(N )) for signal amplification. To simulate this, we applied a “Hybrid Hardware Compiler” constraint: we enforced strict passivity on the optical spectral filters by attenuating weights (α ≈ 0.74, gain < 1.0), while retaining standard gain in the digital pointwise layers to simulate signal repeaters.

Crucially, while such scalar attenuation degrades rate-based models (where magnitude equals importance), PRISM re-

A central prediction of phase-based encoding is that semantic processing requires interference-a single wavefront cannot create diffraction patterns. We test this by evaluating PRISM on isolated tokens (L = 1) and minimal context (L = 2).

Experimental Design. We constructed two test sets of German nouns validated as single-token under the model’s tokenizer, covering both ambiguous and unambiguous concepts.

Each token was presented in isolation and with minimal context to evaluate generation coherence.

Results: The Resolution Limit. We observe a catastrophic “Repetition Collapse” across both conditions. When fed a single token (L = 1) or even a minimal pair (L = 2), the model fails to generate fluent text, instead spiraling into repetitive loops. Crucially, this failure is independent of semantic ambiguity; unambiguous words collapse just as frequently as polysemous ones.

Mechanistic Interpretation. This result validates the physical constraints of the architecture. A single token (L = 1) produces only a DC component under FFT, while a minimal pair (L = 2) produces a spectrum with only two frequency bins (the Nyquist limit). In both cases, the spectral density is too sparse for the harmonic filters to distinguish signal from noise.

The model effectively experiences spectral starvation: it possesses the correct semantic identity (as evidenced by the correct tokens appearing in the repetition), but lacks the requisite phase gradients to drive the autoregressive decoder. This inversely explains PRISM’s strong performance at L = 4096 (Section 6.3): phase-based reasoning is a holographic phenomenon that requires a dense “wave packet” to create the interference patterns necessary for semantic steering.

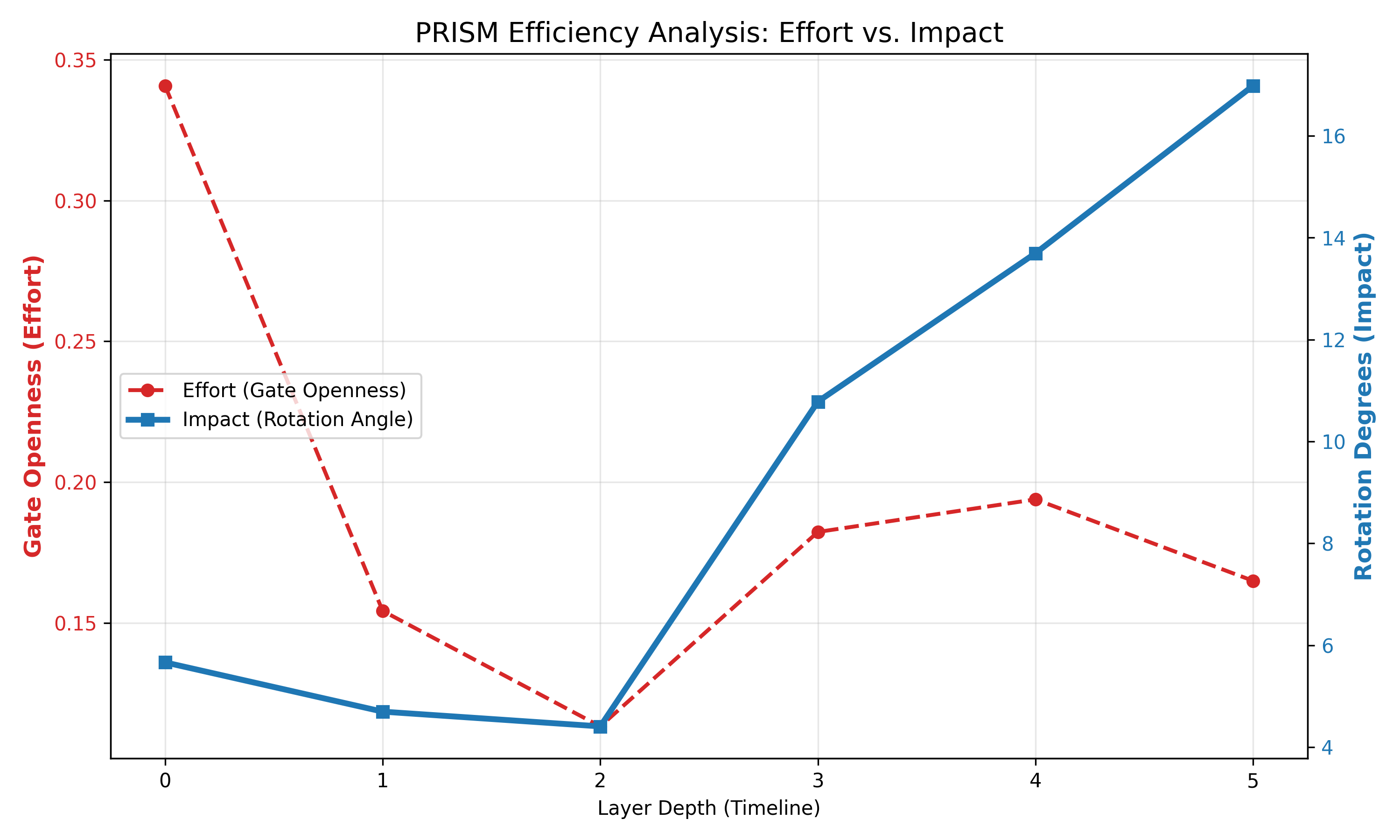
We analyze efficiency through two lenses: structural cost and metabolic leverage. Structurally, replacing quadratic Self-Attention with log-linear Gated Harmonic Convolutions reduces the encoder significantly (see Table 1). Metabolically, we define a Spectral Efficiency Score (η) to quantify the ratio of semantic work to gate energy. As detailed in Appendix A, PRISM demonstrates a “Cognitive Crossover” at Layer 2, where deep layers strictly clamp gates while maintaining massive semantic rotation, yielding a peak efficiency of η ≈ 103. (Nguyen & Salazar, 2019). PRISM variants utilize RMSNorm (Zhang & Sennrich, 2019), while baselines use standard LayerNorm (Ba et al., 2016). All runs used fixed seeds for exact evaluation parity.

Optimization: Models were trained for 40 epochs with a global batch size of 32 (8 physical × 4 gradient accumulation steps). We utilized a cosine learning rate schedule with a peak of 1 • 10 -3 and a 10% warmup.

Regularization via Physics: For the Transformer and FNet baselines, as well as the HSSM architecture (which utilizes rate-based components), we applied standard weight decay (λ = 0.01) to prevent overfitting. Crucially, for the PRISM Hybrid, we set weight decay to 0.0. Since the PRISM encoder enforces a strict Iso-Energetic constraint (Unity Gain), extrinsic magnitude penalties would conflict with the network’s intrinsic physical regularization. Standard dropout (p = 0.1) was applied to all models for parity.

To isolate the contribution of Phase Coding, we evaluated four distinct architectural topologies, standardized to a ≈ 33M parameter budget. All models used 32k vocab BPE tokenizer.

PRISM Encoder Specification: Both experimental configurations utilize an upgraded encoder designed for generative scaling. To enable extrapolation to L = 4096, we replace static filters with implicit Neural Filters parametrized by a hypernetwork. Crucially, we introduce Dynamic RoSE, which injects a content-dependent phase shift ϕ steer alongside the positional rotation θ pos , formulated as E(x t ) = z t • e iθpos • e iϕsteer .

1. Transformer (Rate-Coding Control): A standard decoder-only Transformer (Vaswani et al., 2017) utilizing Rotary Position Embeddings (RoPE) (Su et al., 2024). This represents the unconstrained “Active Energy” regime, where the model is free to use magnitude modulation and quadratic Self-Attention for all mixing operations.

To strictly isolate the mixing mechanism, we construct an FNet baseline (Lee-Thorp et al., 2022) mirroring the PRISM Hybrid topology. It utilizes Additive Logic, a real-valued Fourier Transform that accumulates signal mass without phase interference. Crucially, it maintains Refiner Parity by including the same 1-Layer Transformer (after 6 FNet layers) Refiner as the experimental models, guaranteeing that any performance gap stems from the spectral physics (Real vs. Complex) rather than the presence of attention.

3. PRISM Hybrid (Serial Interference): This configuration tests the “Phase-First” hypothesis where the signal passes through the PRISM Encoder (d = 512, 5 layers) before refinement. All PRISM variants in this section utilize a simplified phase normalization that applies RMS scaling to complex magnitudes while preserving phase angles (Zhang & Sennrich, 2019). The architecture relies on Subtractive Logic: wave interference patterns carve away noise but may attenuate signal intensity. To compensate, we introduce a Skip Connection where the Transformer Refiner receives the summation of the structured phase (interference pattern) and the raw magnitude, resolving ambiguities with full context.

As illustrated in Appendix D (Figure 7), the HSSM tests the “Dual-Stream” hypothesis using an Hourglass Topology where the embedding is projected to 256 dimensions to create two parallel streams. The Rate Stream (Particle) uses a 9-layer FNet encoder for additive mixing, while the Phase Stream (Wave) uses a parallel 9-layer PRISM encoder for subtractive interference, encoding structural dependencies via phase shifts.

To test the synergy between active attention and passive interference, we introduce the WPT (formerly HSSM-Attentive). We replace the HSSM’s passive FNet stream with a lightweight Sensory Stream composed of a standard Transformer encoder (L = 6) utilizing Rotary Positional Embeddings (RoPE). This stream processes semantic identity (Rate) in parallel with the phase-coded Relational Stream (L = 6), fusing their orthogonal outputs via a shallow attentive refiner (L = 1). This architecture separates “what” (Attention) from “where” (Phase), aligning with the Physical Abstractor hypothesis (Appendix D) which prioritizes relational structure to maintain semantic stability.

We compare these architectures against a Standard Transformer (Rate-Coding) and a standard FNet (Spectral), all normalized to approximately 33M parameters.

The Spectral Gap. As shown in Table 4, the purely additive spectral baseline (FNet-Hybrid) suffers a collapse in performance (9.87 PPL) at long contexts. This confirms that static additive mixing is insufficient for contextual reasoning tasks where dynamic content selection is required.

Hybrid Efficiency & The Readout Hypothesis. The PRISM Hybrid (6.06 PPL) effectively bridges this gap. We hypothesize that this single attention layer functions not as a primary reasoning engine, but as a “Digital Readout Head” necessary for Signal Restoration. While PRISM’s subtractive interference efficiently structures semantic relationships via phase, it inevitably attenuates signal magnitude (destructive interference). The Transformer Refiner, receiving both the structured phase (via the Bridge) and the raw magnitude (via the Skip Connection), performs a computational “wavefunction collapse”: transducing the continuous, analog phase manifold onto the discrete, sparse probability distribution of the vocabulary.

Computational Efficiency. Beyond raw perplexity, the WPT demonstrates superior computational economy. By narrowing the expensive active Sensory Stream to d = 256 (compared to the Baseline’s d = 512), we effectively reduce the attention manifold density by 75%. The model compensates for this reduction by offloading structural processing to the passive, linear-complexity Relational Stream. Consequently, WPT beats the baseline while requiring 5% fewer Active Parameters (15.0M vs 15.8M) and, crucially, 18% fewer Core Reasoning Parameters (12.9M vs 15.8M). This confirms that decoupling Phase and Rate allows for a more efficient allocation of compute, reserving expensive matrix multiplications only for high-entropy sensory data.

To identify the causal mechanisms behind the efficiency of the Hybrid architectures (Table 5), we performed a highresolution spectral analysis on the converged WikiText-103 checkpoints. We extracted 133 single-token pairs, rigorously filtered to ensure atomic tokenization, across three semantic categories: Synonyms (e.g., fast-quick), Antonyms (e.g., hot-cold), and Random pairs. This analysis reveals why Phase Coding provides a superior reasoning primitive compared to Rate Coding, despite sharing the same spectral mixing operation.

1. The Binary Limit vs. Continuous Rotation. A critical question arises from the quantitative results: Why does the real-valued FNet baseline exhibit non-trivial phase coherence (R ≈ 0.61, Table 5)? We posit that FNet represents the Binary Limit of Phase Coding. While FNet utilizes continuous magnitude to encode signal intensity (Rate Coding), its implicit phase angles are mathematically restricted to a discrete set {0, π} (positive vs. negative reals). Consequently, FNet cannot steer semantics via geometric rotation; it can only achieve coherence via Sign Alignment. This suggests that FNet relies on Amplitude Modulation (AM), while PRISM relies on Phase Modulation (PM).

This topological divergence is visualized in Figure 5. FNet’s phase distribution is defined by Dirac spikes at 0 • and 180 • , effectively collapsing semantic nuance into a digital switch.

In contrast, PRISM utilizes the full complex plane (C), exhibiting a Continuous Von Mises distribution. This confirms that PRISM encodes semantic relationships not as binary matches, but as fine-grained geometric rotations (e.g., shifting a vector by 15 • to represent a nuance). Thus, while both models achieve coherence, only PRISM possesses the expressive capacity for Analog Semantic Steering.

2. The Hybrid “Sweet Spot” (HSSM). Table 5 details the phase coherence statistics (R) for the experimental models.

Pure PRISM exhibits a relatively high baseline coherence for Random pairs (R ≈ 0.49), likely due to a global “carrier wave” anisotropy required for signal propagation in deep complex networks. In contrast, the HSSM (Hybrid) architecture achieves an optimal trade-off: it suppresses random noise (R ≈ 0.25) via the Rate-Coding stream while maintaining the high semantic locking of the Phase stream (R ≈ 0.69). Crucially, Antonyms exhibit the highest phase locking across all models. This counter-intuitive finding suggests that the Phase Compass mechanism functions as a Topic Binder rather than a polarity classifier, locking structurally related concepts into a shared spectral basis regardless of their logical negation.

3. Orthogonality & Manifold Capacity. Finally, we address the architectural constraints of the Hybrid topology.

In our preliminary experiments, we attempted to reduce the embedding dimension to d = 256 to match the parameter count of smaller baselines. This configuration resulted in convergence failure for the HSSM architecture. We hypothesize that sufficient manifold capacity is required to disentangle the orthogonal gradient updates from the two streams.

Since magnitude (|z|) and phase (∠z) are orthogonal components in the complex plane, the shared embedding layer must learn to satisfy two distinct optimization objectives simultaneously: the Rate stream optimizes vector intensity (loudness), while the Phase stream optimizes vector alignment (direction). At d = 512, the high-dimensional space allows these gradients to remain non-destructive. However, at d = 256, we posit that the Information Density exceeds the manifold’s capacity, leading to destructive interference between the Rate and Phase signals. This necessitates the standard d = 512 configuration, suggesting that Hybrid efficiency comes from utilizing the full geometric capacity of the embedding space.

Our results position the Wave-Particle Transformer (WPT) not merely as a challenger on the leaderboard, but as a mechanistic existence proof that semantic reasoning requires two orthogonal axes: Intensity (Magnitude) and Direction (Phase).

The failure of pure Rate-coding (standard Transformers) to match WPT (5.28 vs 4.94 PPL) highlights a fundamen-tal limitation in current architectures. Magnitude-based attention functions essentially as a sophisticated “volume knob”-it can assign high importance (loudness) or low importance (silence) to a token. However, it struggles to encode relational orientation without massive parameter redundancy. By reintroducing Phase, WPT provides the network with a Semantic Compass. The superior performance of the hybrid model suggests that future architectures should not simply scale Magnitude-only parameters, but must integrate Relational Streams (Abstractors) that process structure in the phase domain, leaving the Rate stream to handle intensity and identity.

The collapse of the unconstrained FNet (9.87 PPL) contrasted with the stability of the Phase-constrained PRISM (6.06 PPL) provides strong evidence for the necessity of Subtractive Logic. Both share a global mixing topology, but only the phase-based model can perform destructive interference to cancel noise. This establishes that strictly additive mixing (real-valued spectral filters) is insufficient for language modeling; the algebra of reasoning requires the capacity to erase.

Finally, the WPT serves as an algorithmic blueprint for hybrid hardware. Unlike purely optical proposals that struggle with non-linear gain, the WPT minimizes the digital footprint rather than eliminating it. It suggests a viable Co-Processor Design: a massive, passive optical unit handling the O(N log N ) structural interference (The Relational Stream), paired with a small, high-precision digital unit handling the O(N 2 ) sensory attention (The Sensory Stream).

Ultimately, this work suggests that semantic reasoning need not be forcibly extracted entirely via digital magnitude, but can naturally emerge from the guided interference of waves.

To facilitate the exploration of these optical-neural analogs, we release the complete implementation. 1

The HSSM as a “Physical Abstractor”

Recent work in cognitive AI has identified the Relational Bottleneck as a critical inductive bias for systematic generalization (Webb et al., 2024). Architectures such as the Abstractor (Altabaa et al., 2024) and the Dual Attention Transformer (DAT) (Altabaa & Lafferty, 2025) enforce this by architecturally disentangling information into two distinct streams: a Sensory Stream (which processes object attributes like identity and texture) and a Relational Stream (which extracts structural logic and comparisons).

The success of our Hybrid Spectral Sequence Model (HSSM) suggests a fundamental isomorphism between this cognitive disentanglement and the physical distinction between Rate and Phase coding. We hypothesize that the HSSM functions effectively as a “Physical Abstractor”, where the Relational Bottleneck is enforced not by attention heads, but by the laws of wave mechanics:

• The Sensory Stream (Rate Coding): The FNet branch acts as the sensory channel. By utilizing realvalued amplitude, it “accumulates mass,” allowing the network to represent static semantic identity and feature intensity (the “what” of the signal) via magnitude.

• The Relational Stream (Phase Coding): The PRISM branch acts as the relational channel. The strict Iso-Energetic Constraint (Gain ≈ 1.0) functions as a physical implementation of the Relational Bottleneck. By explicitly stripping away signal magnitude-and thus preventing the network from relying on feature intensity-the architecture is forced to encode relation-ships exclusively via geometric interference in the complex plane (the “how” of the signal).

Furthermore, we explicitly defend our choice to validate this novel mechanism on tractable benchmarks (WMT14, WikiText-103) rather than immediately scaling to billionparameter regimes. This approach mirrors the rigorous validation strategy of the original Abstractor framework, which established the validity of the relational bottleneck using models with fewer than 400,000 parameters on synthetic tasks (e.g., object sorting, arithmetic) (Altabaa et al., 2024).

Just as the Abstractor framework suggested that explicit relational disentanglement yields massive gains in sample efficiency without requiring “complex” scale, our results provide a critical existence proof that subtractive phase interference is a sufficient primitive for semantic reasoning. By isolating this mechanism in a controlled regime (60M-120M parameters), we avoid the confounding variables of massive scale, adhering to a philosophy of “Validity Before Extrapolation”-ensuring the physical principle is sound before committing to the engineering expense of large-scale application.

Trade-offs E.1. Justification of the Control Group (Why FNet?)

Our experimental design prioritizes Strict Variable Isolation over leaderboard optimization. To claim that Phase Coding (information encoded in angles) is a sufficient primitive for reasoning, we must compare it against a baseline that is topologically identical but relies on Rate Coding (information encoded in magnitude).

• FNet vs. PRISM: Both architectures are global spectral mixers that operate in O(N log N ) time. The transformation T FNet (x) = Re(F(x)) is the exact realvalued amplitude counterpart to PRISM’s complexvalued phase interference T PRISM (x) = z • e iθ . This ensures that any performance difference is strictly attributable to the coding scheme (Real vs. Complex), not the mixing mechanism.

• Exclusion of Mamba/SSMs: While Mamba (Gu & Dao, 2024) is a highly efficient architecture, it introduces two confounding variables: Recurrence (statespace memory) and Data-Dependent Gating on the time axis. Comparing PRISM directly to Mamba would obscure whether gains or losses were due to Phase Coding or Recurrence. By sticking to the FNet topology, we isolate the “Phase” variable.

The failure mode observed in Section 5.4-where isolated tokens cause generation collapse-can be understood through a direct analogy to N-slit diffraction in classical optics.

In the canonical N-slit experiment, a coherent plane wave illuminates an opaque barrier containing N equally-spaced slits. Each slit acts as a secondary source (per Huygens’ principle), emitting spherical wavefronts that interfere at a distant screen. The resultant intensity pattern is:

This analogy explains the Spectral Density Threshold observed empirically:

• Single slit (N = 1): No interference occurs. The output is merely the diffraction envelope of the aperture itself-a broad, featureless distribution. In PRISM, a single token (L = 1) produces only a DC component under FFT, providing no spectral structure for the harmonic filters to exploit.

• Double slit (N = 2): Basic sinusoidal fringes emerge, but angular resolution is poor. In PRISM, a token pair (L = 2) yields only two frequency bins (the Nyquist limit), insufficient for semantic disambiguation.

• Diffraction grating (N ≫ 1): Sharp, well-resolved principal maxima appear, with resolution scaling as ∆θ ∝ 1/N . In PRISM, long sequences (L ≥ 128) provide dense spectral sampling, enabling precise phasebased filtering.

This correspondence suggests that PRISM’s “repetition collapse” at low L is not a bug but a physical necessity: wavebased reasoning requires sufficient sources to generate interference. Just as a single slit cannot produce diffraction fringes, a single token cannot produce the phase gradients required for semantic steering.

This framing also predicts that PRISM’s performance should scale favorably with sequence length-not merely due to increased context, but because longer sequences provide higher spectral resolution for the interference patterns that encode semantic relationships. We observe this empirically

Configurations. PRISM (Tied) reduces encoder density by > 10% compared to FNet.COMPONENT TRANSF. FNET PRISM (T) PRISM (U)

Configurations. PRISM (Tied) reduces encoder density by > 10% compared to FNet.