Real-World Robot Control by Deep Active Inference With a Temporally Hierarchical World Model

To realize robots capable of both goal-directed and exploratory actions, we focus on deep active inference [7]- [10]-a deep learning-based framework grounded in a computational theory that accounts for various cognitive functions [5], [11], [12]. However, deep active inference faces two key challenges: (1) its performance heavily depends on the capability of the framework to represent environmental dynamics [13], and (2) the computational cost is prohibitively high [9], making it difficult to apply to real-world robots.

To address these challenges, we propose a deep active inference framework comprising a world model, an action model, and an abstract world model. The world model learns hidden state transitions to represent environmental dynamics from human-collected robot action and observation data [14]- [16]. The action model maps a sequence of actual actions to one of a learned set of abstract actions, each corresponding to a meaningful behavior (e.g., moving an object from a dish to a pan) [17]. The abstract world model learns the relationship between the state representations learned by the world model and the abstract action representations learned by the action model [18]. By leveraging the abstract world model and the abstract action representations, the framework enables efficient active inference.

To evaluate the proposed method, we conducted robot experiments in real-world environments with uncertainty. We investigated whether the framework could reduce computational cost, enable the robot to achieve diverse goals involving the manipulation of multiple objects, and perform exploratory actions to resolve environmental uncertainty.

LfD is a method to train robots by imitating human experts, providing safe, task-relevant data for learning control policies [19]- [24]. A key advancement contributing to recent progress in LfD for robotics is the idea of generating multistep action sequences, rather than only single-step actions [1]- [3], [17], [25]. However, a major challenge in LfD is the difficulty of generalizing to environments with uncertainty, even when trained on large amounts of expert demonstrations [4]. In this work, we focus on the approach that uses quantized features extracted from action sequences [17], and treat the extracted features as abstract action representations.

A world model captures the dynamics of the environment by modeling the relationship between data (observations), their latent causes (hidden states), and actions. They have recently attracted significant attention in the context of model-based reinforcement learning [14], [15], especially in artificial agents and robotics [26]. However, when robots learn using a world model, their performance is constrained by the model’s capability to represent environmental dynamics [27], [28]. In particular, learning long-term dependencies in the environment remains a challenge. One solution is to introduce temporal hierarchy into the model structure [27], [29]- [31]. Furthermore, by incorporating abstract action representations that capture slow dynamics, the model can more efficiently predict future observations and states [18]. Temporal hierarchy can be introduced by differentiating state update frequencies [27], [29], [30] or modulating time constants of state transitions [16], [32], [33]. In this work, we adopt the latter to better represent slow dynamics in our world model [31].

The free-energy principle [5], [6], [11] is a computational principle that accounts for various cognitive functions. According to this principle, human observations o are generated by unobservable hidden states z, which evolve in response to actions a, following a partially observable Markov decision process [5]. The brain is assumed to model this generative process with the world model. Under the free-energy principle, human perception and action aim to minimize the surprise -log p(o). However, since directly minimizing surprise is intractable, active inference instead minimizes its tractable upper bound, the variational free energy [5], [6].

Perception can be formulated as the minimization of the following variational free energy at time step t [9], [34], [35]:

Here, q(z t ) denotes the approximate posterior over the hidden state z t , D KL [q(•)||p(•)] is the Kullback-Leibler (KL) divergence. Note that the first line of (1) is equivalent to the negative evidence lower bound [36], [37]. Action can be formulated as the minimization of expected free energy (EFE), which extends variational free energy to account for future states and observations. Let τ > t be a future time step, The EFE is defined as follows [35]:

Here, the expectation is over the observation o τ because the future observation is not yet available [35], and π indicates the policy (i.e. an action sequence). mutual information between the state z τ and the observation o τ . This term encourages exploratory policies that reduce the uncertainty in the prior belief q(z τ | π). On the other hand, the second term referred to as the extrinsic value encourages goal-directed policies. Therefore, selecting a policy π that minimizes the EFE can account for both exploratory and goal-directed actions [5], [6], [38]. Conventional active inference requires calculating the EFE over all possible action sequences during task execution, which is intractable for real-world action spaces [6]. Recent works have addressed this by using the EFE as a loss function for training of action generation models [7]- [9], but often ignored exploration capability. In this work, we propose a novel framework focusing on both goal-achievement performance and exploration capability tractably calculating the EFE during task execution.

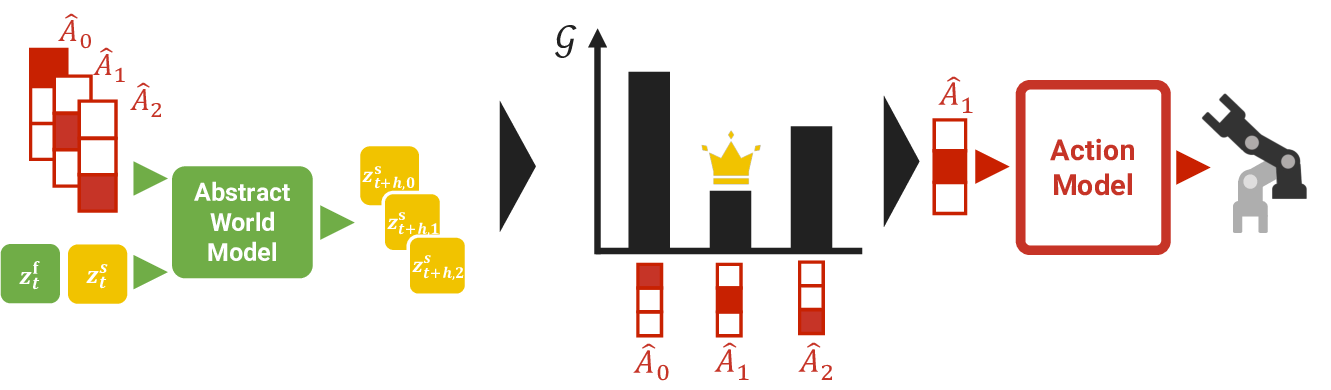
We propose a framework based on deep active inference that enables both goal achievement and exploration. The proposed framework consists of a world model, an action model, and an abstract world model (Fig. 1).

1. World Model: The world model comprises a dynamics model, an encoder, and a decoder, all of which are trained simultaneously (Fig. 2). As the dynamics model, we utilize a hierarchical model [39], which consists of the slow and fast states as the hidden states z t = {z s t , z f t } for time step t. Both deterministic d and stochastic s states are defined for each of the slow and fast states z s t = {d s t , s s t }, z f t = {d f t , s f t }, respectively. These hidden states are calculated as follows: Slow dynamics Deterministic state:

Prior:

Here, o t is the observation and a t-1 is the action at the previous time step. The approximate posterior of the fast dynamics q f θ is conditioned on the observation o t by receiving its features extracted by the encoder.

The slow and fast deterministic states d s t and d f t are computed by multiple timescale recurrent neural network parameterized with a time constant [32]. When the time constant is large, the state tends to evolve slowly compared to when the time constant is small. Therefore, by setting the time constant for the slow layer larger than one for the fast layer, the dynamics model represent a temporal hierarchy. The slow and fast stochastic states s s t , ŝs t and s f t , ŝf t are represented as one-hot vectors sampled from an approximate posterior or a prior, defined by categorical distributions [40].

The decoder is employed to reconstruct the observation o t from the hidden state z t , modeling likelihood p θ (o t | z t ). Simultaneously, a network p θ (d f t | z s t ) that predicts the fast deterministic state df t from the slow hidden state z s t is also trained. The predicted deterministic state df t is then used to sample the fast stochastic state. By combining both slow and predicted fast hidden states as inputs to the decoder, the dynamics model can represent the observation likelihood p θ (o t | z s t ) 1 based on only the slow hidden state z s t . The world model is trained by minimizing the variational free energy F(t). Here, since the fast deterministic state d f t can be regarded as an observation for the slow dynamics, the variational free energies F s (t) and F f (t) can be computed separately for the slow and fast layers, respectively. Furthermore, we also minimize, as an auxiliary task, the negative log-likelihood of observation o t given the slow hidden state z s t , denoted as log p θ (o t | z s t ). In summary, the variational free energy F(t) in this work is described as follows:

(4) 1 Correctly, this distribution is written as

We approximate the marginal over the fast states z f t with a single Monte Carlo sample.

Here, for the KL divergence calculation, we use the KL balancing technique with a weighting factor w [40].

2. Action Model: The action model consists of an encoder E ϕ and a decoder D ϕ composed of multilayer perceptron (MLP), as well as a residual vector quantizer [17], [41], [42] Q ϕ with N q = 2 layers. First, the encoder E ϕ embeds the action sequence a t:t+h of length h into a low-dimensional feature A t . Next, the feature A t is quantized into Ât using the residual vector quantizer Q ϕ . The residual vector quantizer includes codebooks {C i } Nq i=1 , each containing K learnable codes {c i,j } K j=1 . Specifically, the quantized vector at layer i is the code c i,k having the smallest Euclidean distance to the input at layer i. The quantized feature Ât is the sum of outputs from each quantization layer { Ât,i

Finally, the decoder D ϕ reconstructs the quantized feature Ât into the action sequence ât:t+h . In summary, the procedure of the action model is described as follows:

We treat the feature Ât , obtained by the action model, as an abstract action representing the action sequence a t:t+h .

The encoder E ϕ and decoder D ϕ of the action model are trained by minimizing the following objective:

where we assume Ât,0 = 0. Moreover, λ MSE and λ commit are coefficients for the reconstruction loss L MSE and the commitment loss L commit , respectively. The learning of the codebooks {C i } Nq i=1 of the residual vector quantizer Q ϕ is performed using exponential moving averages [17], [41].

3. Abstract World Model: The abstract world model W ψ learns a mapping from the current world model state z t and an abstract action A t to the future slow deterministic state d s t+h . In other words, it provides an abstract representation of state transitions. The model W ψ is composed of MLP and takes the abstract action A t and the current world model state z t as inputs to predict the slow deterministic state d s t+h . Here, the input abstract action A t to W ψ can be any of the K Nq combinations of learned codes from the action model, denoted as { Ân } K Nq n=1 . Accordingly, for a given current hidden state z t , the abstract world model W ψ predicts K Nq possible future slow deterministic states {d s t+h,n } K Nq n=1 :

The abstract world mode is trained by minimizing the following objective:

Here, to obtain the target slow deterministic states {d s t+h,n } K Nq n=1 , we utilize latent imagination of the world model [15]. To this end, the action sequences {â 0:h,n } K Nq n=1 are generated from the code combinations { Ân } K Nq n=1 using the decoder D ϕ of the action model. Then, by leveraging the prior distribution over the fast states, the slow deterministic states {d s t+h,n } K Nq n=1 at h steps ahead are obtained.

To make the EFE G(τ ) calculation tractable, our framework leverages a learned, finite set of abstract actions { Ân } K Nq n=1 , instead of considering all possible (and thus infinite) continuous action sequences.

First, we reformulate (2) in accordance with our world model (for a detailed derivation, see Appendix I):

(9) Here, the joint distribution q θ (o τ , z τ | π) can be decomposed as

in our proposed framework. Note that, given the distribution q θ (z s τ | π) over the slow states, all distributions required to compute the EFE G(τ ) can be obtained using the world model, and thus G(τ ) becomes computable. Here, we replace the policy π with an abstract action  ∈ { Ân } K Nq n=1 , and express the distribution q θ (z s τ | π) as follows:

In this way, we can use the abstract world model W ψ to predict the slow deterministic state d s τ at τ = t + h from the abstract action Â. Using the predicted deterministic state d s τ , we can obtain the prior q θ (z s τ | π) and compute the EFE. When computing the EFE, the prior preference p(o τ | o pref ) is assumed to follow a Gaussian distribution N (o pref , σ 2 ) with mean o pref and variance σ 2 . Therefore, the EFE can be written as follows:

where γ = 1/2σ 2 is the preference precision, which balances the epistemic and extrinsic values, and the expectations in the EFE are approximated via Monte Carlo sampling [38].

To generate actual robot actions, we first use the abstract world model W ψ to predict the slow deterministic states {d s t+h,n } K Nq n=1 at h steps into the future for all abstract actions { Ân } K Nq n=1 , given the current world model state z t . Next, we predict slow hidden states {z s t+h,n } K Nq n=1 based on the predicted slow deterministic states by using (10). Then, for each predicted state, we compute the EFE and select the abstract action that yields the minimum EFE. The selected abstract action is then decoded into an action sequence ât:t+h by the action model, and the robot executes this sequence.

To investigate whether the proposed framework enables both goal achievement and exploration in real-world environments-where multiple objects can be manipulated and uncertainty arises from their placement-we conducted an experiment using a robot shown in Fig. 4 (left) [43], [44]. The robot had six degrees of freedom, one of which is the gripper. A camera (RealSense Depth Camera D435; Intel) was mounted opposite to the robot to capture a view of both the robot and its environment. From the viewpoint of the camera, a simple dish, a pot, and a pan were placed on the right, center, and left, respectively, and a pot lid was placed closer to the camera than the center pot. Additionally, the environment was configured such that a blue ball, a red ball, or both could be present. Note that, therefore, uncertainty arose when the lid was closed, as the pot might or might not contain a blue or red ball in this environment.

As training data, we collected object manipulation data by demonstrating the predetermined eight patterns of policies (Fig. 4(right)). Each demonstration consists of a sequence of two patterns of policies. For all valid combinations-excluding those in which the policy would result in no movement (e.g., performing action 3 twice in a row)-we collected five demonstrations per combination by teleoperating the robot in a leader-follower manner. There are 36 valid action combinations for environments containing either a blue ball or a red ball, and 72 combinations for environments containing both. Each sequence contains 100 time steps of joint angles and camera images recorded at 5 Hz. Therefore, each pattern of policies had roughly 50 time steps. The original RGB images were captured, resized and clipped to 64 × 80. In this experiment, the robot action a t is defined as the absolute joint angle positions, and the observation o t is defined as the camera image.

In this experiment, we expected the slow hidden states z s t to represent the overarching progress of the task, such as where the balls and the lid were placed. In contrast, we expected the fast hidden states z f t represents more immediate, transient information. On the other hand, we expected abstract actions A t to represent a meaningful behavior learned from the demonstration data. In an ideal case, an abstract action corresponds to one of the eight policy patterns in Fig. 4(right), such as moving the ball from the dish to the pan.

Capability of abstract world model: We evaluated the capability of the abstract world model. First, we compared the computation time of our proposed framework against that of conventional deep active inference approaches [9], [13], [38], which predicts future states with the world model by sequentially inputting the action sequence â0:h reconstructed from an abstract action  via the action model.

Second, we evaluated whether different predictions can be generated from the same initial state for each abstract action

𝐴 " $ Fig. 3. Action selection based on the minimization of EFE. First, future states are predicted for multiple abstract actions. Then, the EFE is calculated for each of the predicted future states. Finally, the robot execute action sequence reconstructed from the abstract action that yields the lowest EFE. learned by the action model. We also examined whether the observed outcomes resulting from executing actual actions generated from a specific abstract action are consistent with the predictions made by the abstract world model.

We evaluated the success rate on ball-(140 trials) and lid-manipulation (24 trials) tasks with varying object configurations, such as moving a particular ball or manipulating a lid. A trial was considered successful if the target object was placed in its specified goal position within 50 time steps.

Environment exploration: We evaluated whether the proposed framework can generate not only goal-directed actions but also exploratory actions from an uncertain initial situation. To this end, we set up a scenario in which the blue ball is initially placed in the pan and the lid is closed, creating uncertainty about whether the red ball is present inside the pot. In this scenario, when taking an exploratory action, it was expected that the robot would open the lid to resolve the uncertainty.

In the goal-achievement performance experiment, we compared our proposed framework with a baseline and two ablations described as follows:

• Goal-conditioned diffusion policy (GC-DP). As a baseline, we implemented a diffusion policy with a U-Net backbone [1], [45]. In our implementation, this policy predicted a 48-step future actions based on the two most recent observations and a goal observation.

To stabilize actions, we apply an exponential moving average of weight 0.7 to the generated actions. • Non-hierarchical. As an ablation study, the world model is replaced by a non-hierarchical dynamics model [40]. In this variant, the hidden state z t consists of a single-level deterministic state d t and a stochastic state s t , where the deterministic state is computed using a gated recurrent unit [46]. • No abstract world model (AWM). As an ablation study, the robot does not use the abstract world model for planning. Instead, it calculates the EFE directly over actual action sequences decoded by the action model.

We did not perform an ablation on the action model itself, as our framework relies on it to generate the set of candidate actions (either abstract or actual) for evaluation, making it a core, indispensable component.

Our proposed framework required only 2.37 ms to evaluate all candidate abstract actions, in contrast to 71.8 ms for a sequential evaluation of conventional deep active inference approaches. This demonstrates the higher computational tractability of our proposed framework.

As shown in Fig. 5, different abstract actions lead to distinct predictions. Moreover, for example, by using an action sequence generated from the abstract action represented by c 1,2 + c 2,7 , the ball was successfully moved from the dish to the pan, consistent with the predicted observation (Fig. 5). These results suggest that the abstract world model has learned the dependency between abstract actions and the resulting state transitions, even without directly referring to actual action sequences. However, the prediction associated with the abstract action  represented by  = c 1,8 + c 2,8 in Fig. 5 shows red balls placed on both the dish and the pan, which is inconsistent with the initial condition in which only a blue ball was present. This abstract action corresponded to moving a ball from the center pot to the pan. Since this action was not demonstrated when the pot was empty, the abstract world model may have learned incorrect dependencies for unlearned action-environment combinations.

Table I shows the success rates of our proposed framework on goal-directed action generation, evaluated on tasks involving specific ball and lid manipulations. The proposed method outperformed the baseline and the ablations across all goal conditions except the Lid-Opening goal, achieving a total success rate of over 70%. As a qualitative example, Fig. 6 illustrates the EFE calculation for a scenario where the goal is to move a ball from a dish to a pan. The abstract action with the lowest EFE correctly predicts the desired outcome, and executing the actual actions derived from this abstract action led to successful task completion. This overall result confirms that selecting abstract actions by minimizing the EFE is effective for goal achievement.

The failures in our framework were mainly due to inconsistent world model predictions, which misled the robot into believing an inappropriate action would succeed. For example, the proposed framework selected actions to grasp nothing but place the (non-grasped) target object at the ap-

For simplicity, we computed the EFE for two abstract actions: moving the blue ball from the pan to the dish (goaldirected), and opening the lid (exploratory), as summarized in Table II. When preference precision γ was set to 10 2 , the EFE for the goal-directed action became lower, and thus the robot moved the blue ball from the pan to the dish. In contrast, when preference precision γ was set to 10 -4 , the EFE for the exploratory action became lower, and thus the robot opened the lid. These results indicate that the proposed framework can assign high epistemic value to exploratory actions that provide new information, and that exploratory actions can be induced by appropriately adjusting the preference precision γ.

In this work, we introduced a deep active-inference framework that combines a temporally-hierarchical world model, an action model utilizing vector quantization, and an abstract world model. By capturing dynamics in a temporal hierarchy and encoding action sequences as abstract actions, the framework makes the action selection based on active inference computationally tractable. Real-world experiments on objectmanipulation tasks demonstrated that the proposed framework outperformed the baseline in various goal-directed settings, as well as the ability to switch from goal-directed to exploratory actions in uncertain environments.

Despite these promising results, several challenges remain: 1) The action model used a fixed sequence length, which may not be optimal. 2) The model’s predictive capability decreases for action-environment combinations not present in the dataset. 3) While we validated the capability to take exploratory actions, we did not evaluate their effectiveness in solving tasks and the switching to exploratory behavior still relies on a manually tuned hyperparameter.

Future work will focus on extending the framework to address these limitations. An immediate step is to evaluate our framework in environments that require multi-step action selection and where exploration is necessary to solve the task. Other promising directions include developing a mechanism for adaptive switching between goal-directed and exploratory modes, and extending the action model to represent variablelength action sequences. Ultimately, this work represents a significant step toward the long-term goal of creating more capable robots that can operate effectively in uncertain realworld environments such as household tasks by leveraging both goal-directed and exploratory behaviors.

2 4.21 × 10 4 14.5 × 10 4 γ = 10 -4 -4.67 × 10 0 -6.11 × 10 0propriate location. In contrast, the GC-DP, Non-hierarchical, and No AWM all exhibited lower success rates. The GC-DP frequently failed in grasping and placing objects.

2 4.21 × 10 4 14.5 × 10 4 γ = 10 -4 -4.67 × 10 0 -6.11 × 10 0