Hybrid Stackelberg Game and Diffusion-based Auction for Two-tier Agentic AI Task Offloading in Internet of Agents

Minghui Dai is with the School of Computer Science and Technology, Donghua University, Shanghai 201620, China (e-mail: minghuidai@dhu.edu.cn).

Hong-Ning Dai is with the Department of Computer Science, Hong Kong Baptist University, Hong Kong, China (e-mail: hndai@ieee.org).

Zhou Su is with the School of Cyber Science and Engineering, Xi’an Jiaotong University, Xi’an 710049, China (e-mail: zhousu@ieee.org).

Dusit Niyato is with the School of Computer Science and Engineering, Nanyang Technological University, Singapore 639798 (e-mail: dniyato@ntu.edu.sg).

(*Corresponding author: Jiawen Kang)

telligent networks [1]. This agent-centric model is designed to support the seamless interconnection, autonomous discovery, and collaborative reasoning of countless heterogeneous physical and virtual agents. The proliferation and sophistication of these agents are driven by a recent advent in the field of Artificial Intelligence (AI), i.e., the transition from disembodied models to Embodied AI (EAI) [2]. Unlike their predecessors, which are isolated and task-specific, EAI gives rise to embodied agents, i.e., intelligent entities that can autonomously perceive their surroundings, process information, and interact with physical objects [3]. The integration of these interactive and rational embodied agents into the IoA architecture is a critical step toward Artificial General Intelligence (AGI), enabling them to operate and cooperate seamlessly with humans and other agents in complex and dynamic environments [4].

As a key component of the IoA physical domain, Wireless Agents (WAs) are designed for autonomous operation and interaction within dynamic environments. Their core functions and tasks are inherently compute-intensive, as they need to continuously process vast streams of sensor data to perceive their surroundings and execute precise physical actions. In this context, autonomous vehicles can act as WAs to perform advanced agentic AI tasks. For instance, these agents formulate on-the-fly strategies in congested traffic (e.g., determining right-of-way at a busy junction) or utilize local models for environmental understanding (e.g., forecasting pedestrian behavior from visual data) that are profoundly demanding computational tasks [5]. The strict constraints on heat dissipation and physical space for high-performance onboard hardware (e.g., GPUs) of the vehicles create a critical performance bottleneck. Relying solely on local processing for these tasks can lead to increased latency or reduced accuracy, directly threatening the WAS’s ability to make the splitsecond decisions necessary for safe operation.

To address the above challenges, task offloading provides a powerful solution to overcome the computational limitations inherent to WA systems [6]. The WAs can offload their most demanding computational-complex agentic AI tasks to nearby edge resource providers. These providers are primarily categorized as i) Mobile Agents (MAs) that are dynamic entities, such as moving vehicles, and ii) Fixed Agents (FAs), which encompass stationary edge infrastructures, such as Roadside Units (RSUs) [7].

To ensure scalability and resilience, this framework also incorporates Aerial Agents (AAs), such as Unmanned Aerial Vehicles (UAVs), which serve as a computational tier that FAs can leverage to manage load spikes [8] on an on-demand basis. Therefore, this paper addresses this critical problem by designing a hierarchical incentive framework to govern the agentic AI task offloading for WAs within the IoA. We aim to model the strategic interactions among WAs, MAs, FAs, and AAs to ensure efficient resource allocation. Specifically, we investigate the integration of game theory and auction mechanisms as a unified solution. The main contributions of this paper are summarized as follows.

• Our paper pioneers the study of WA’s agentic AI task offloading within the IoA, a paradigm uniquely defined by the large-scale coordination of agents. Despite extensive studies on traditional offloading, the models are often insufficient for the IoA context, where an agent’s computational state and physical actions are tightly intertwined.

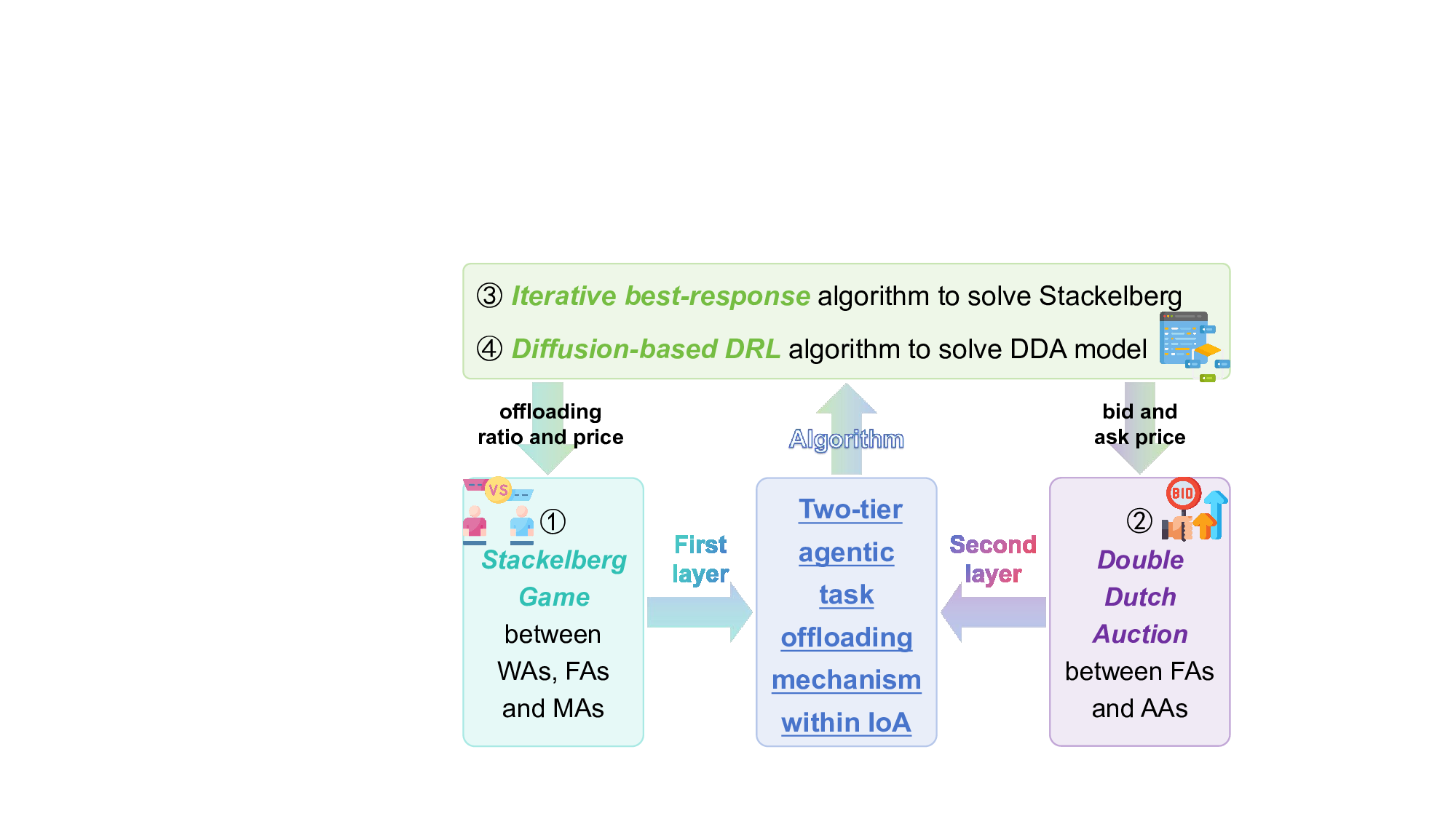
• To address the agentic AI task offloading within the IoA paradigm, we propose a novel hierarchical incentive framework. At the primary offloading layer, we model the interaction among WAs, MAs, and FAs as a Stackelberg game. In this game, FAs and MAs act as the leaders, setting their resource prices, while WAs act as the followers, deciding their optimal task offloading ratios in response. To handle scenarios of resource scarcity, particularly FA overload, we introduce a secondary resource trading layer. We model this layer as a Double Dutch Auction (DDA), enabling FAs to dynamically procure supplemental computing resources from nearby AAs.

• To solve the complex, high-dimensional DDA problem, we introduce a diffusion-based Deep Reinforcement Learning (DRL) algorithm as a better solution than conventional DRL methods. The numerical results validate this choice, demonstrating that the proposed diffusion scheme achieves superior efficiency. The rest of this paper is organized as follows. In Section II, we review the related work. In Section III, we propose the overall framework of this paper, i.e., the two-tier agentic AI task offloading scheme among WAs, MAs, FAs, and AAs. Building on this architecture, Section IV formally defines the optimization problem and presents our corresponding Stackelberg game and DDA model. To solve these models, Section V develops algorithms designed to find their optimal solutions. Subsequently, Section VI shows the numerical results, and the conclusion is summarized in Section VII.

With evolved AI and agent technologies, the IoA is emerging as a transformative infrastructure. It is designed to enable seamless interconnection, autonomous discovery, and collaborative reasoning among large-scale intelligent agents, which are increasingly empowered by the sophisticated reasoning of Large Language Models (LLMs) and the multimodal perception of Vision-Language Models (VLMs) [9]. Drawing inspiration from the Internet, the IoA establishes a novel network paradigm designed as a flexible and scalable platform for collaboration among diverse, autonomous AI agents [10]. A fundamental departure from its human-centric predecessor, the IoA is agent-centric, prioritizing direct inter-agent interactions. Consequently, the nature of exchanged information shifts from human-oriented data (e.g., text, images) to machine-oriented data objects (e.g., model parameters, encrypted tokens), facilitating direct and efficient machineto-machine collaboration. Within this overarching IoA framework, EAI plays a pivotal role [11]. The core of this field, the embodied agent, functions as a critical node within the IoA network. In essence, embodied agents are the primary vehicles through which the IoA’s collaborative reasoning capabilities are extended to solve complex, realworld problems. This powerful collaborative paradigm is demonstrated in the automotive industry with the emergence of Vehicular EAI Networks [7]. In this context, AVs, equipped with advanced sensing technologies, act as the core embodied agents. Coordinated through the IoA framework, these agents form a network that significantly enhances collective intelligence, enabling advanced capabilities such as sophisticated autonomous navigation and efficient interaction within dynamic environments.

A primary challenge in task offloading environments is motivating resource-constrained wireless devices to actively participate in computation. Incentive mechanisms address this challenge directly by creating reward structures that compensate for resource contribution [12]. The design and optimization of these mechanisms have been extensively investigated, with game theory, contract theory, and auction theory emerging as prominent methods for modeling the strategic behavior of selfinterested devices [13]. The authors in [14] proposed a DRL-assisted contract incentive mechanism to jointly optimize task offloading and resource cooperation in vehicular networks, maximizing the utility of the RSU while satisfying incentive compatibility and individual rationality constraints. In [15], the authors designed a truthful double auction incentive mechanism to address the novel challenge of movement-aware task offloading, where socially-connected, device-to-device-enabled users are motivated to physically relocate to complete tasks in a crowd-sourced mobile edge computing system. The authors in [16] proposed a hierarchical incentive framework for vehicular edge computing, using a two-stage Stackelberg game to optimize resource pricing between servers and requesting vehicles, complemented by a stable matching game to recruit idle vehicles as auxiliary resource providers. These studies demonstrate the versatility of economic theories, leveraging contract, auction, and hybrid game-theoretic frameworks to address resource allocation problems in dynamic task offloading scenarios.

Multi-layer task offloading schemes provide a structured framework for distributing computational tasks across a hierarchy of available resources, ranging from nearby edge devices to distant servers. The authors in [17] developed a multi-layer task offloading strategy for Multi-access Edge Computing (MEC)-enabled low earth orbit satellite networks using a two-level hierarchical game, where an upper-level coalition formation game governs terminalsatellite association and a lower-level noncooperative game handles intra-coalition resource allocation. The authors in [18] proposed a multi-layer task offloading scheme that minimizes completion delay in fog-based Vehicular Adhoc Networks by dynamically selecting offloading targets through a comprehensive evaluation of predicted vehicle positions, link reliability, and node-level resource capabilities. In [19], the authors introduced a comprehensive multi-layer offloading scheme that integrates a physical dual-layer architecture (high-altitude relay and lowaltitude computing UAVs) with a hierarchical decisionmaking algorithm (global trajectory or offloading and local scheduling) to optimize performance in dynamic vehicular networks.

A common thread in these works is the use of hierarchical or multi-stage models to decompose the complex interactions between different system entities. Inspired by this paradigm, our work addresses the task offloading problem for WAs, which also exhibits a natural hierarchical structure. Due to their resource constraints, WAs need to offload tasks to powerful servers (e.g., FAs or MAs), creating a leader-follower dynamic. Therefore, this paper proposes a hybrid incentive mechanism that leverages a Stackelberg game to model this hierarchy, complemented by an auction model to efficiently manage resource allocation among WAs, MAs, FAs, and AAs.

In the IoA context, WAs serve users by performing various tasks. However, due to their limited local computing resources, WAs often struggle to complete computationally intensive agentic AI tasks, such as realtime Augmented Reality (AR) rendering or generating personalized content using large models, within acceptable timeframes [7]. Therefore, WAs need to offload these tasks to servers or other resource-rich nodes to accelerate task completion. Consequently, WAs can offload tasks to MAs or to FAs. Furthermore, FAs can delegate a portion of the computational workload to AAs to further improve task processing efficiency [8]. To address the task offloading challenge in a multi-agent environment, we propose a twotier task offloading framework that integrates WAs, MAs, FAs, and AAs. The outline of the proposed hierarchical framework is shown in Fig. 1. Specifically, in the first layer, we formulate a Stackelberg game among WAs, MAs, and FAs to optimize task allocation based on computational capabilities and resource availability. In the second layer, we introduce an auction-based model to govern the interaction between FAs and AAs, enabling efficient resource allocation and task execution. Moreover, we propose an iterative best-response algorithm for the Stackelberg game and a diffusion-based DRL algorithm for the DDA model.

In our proposed system model, illustrated in Fig. 2, we design the IoA framework within a vehicular context. Specifically, the AV acts as the WA, surrounding vehicles serve as MAs, an RSU functions as the FA, and a UAV operates as the AA. The collaborative, two-tier offloading architecture is designed to ensure the timely and efficient processing of computationally intensive tasks. This enables the delivery of critical real-time services, such as dynamic obstacle avoidance, predictive lane-change assistance, and personalized route optimization. By integrating these services through a robust vehicular communication network, the system can provide a seamless and highly responsive driving experience, free from interruptions or performance degradation. The overall framework is detailed as follows.

Step 1: Task Offloading from WA Layer. AVs (i.e., WAs) generate tasks that require computational resources beyond their local capabilities. Based on task complexity and availability of nearby resources, WAs dynamically select either RSUs (i.e., FAs) or neighboring vehicles (i.e., MAs) as target nodes for task offloading. Then, the WAs upload the tasks to the selected nodes on the vehicular communication network. Consequently, we establish a Stackelberg game between WAs, FAs, and neighboring MAs with idle resources.

Step 2: Computation at FA and MA Layer. Upon receiving the offloaded tasks, FAs or WAs allocate their available computing resources to process the tasks. If the computational demand of a task exceeds the local capacity of the FA, the FA may decide to further offload a portion of the task to other resource-rich entities in the network

Fig. 2: The two-tier agentic AI task offloading system model. The left side illustrates the IoA framework in a vehicular context, while the right side details the formulation of the two-tier task offloading system. [20]. Because FAs are typically stationary infrastructure nodes with dedicated communication capabilities, whereas MAs lack the necessary infrastructure to establish such connections, as their mobility and limited communication range restrict them from directly interacting with UAVs (i.e., AAs).

Step 3: Conditional Offloading to AA Layer. If the FA’s resources are insufficient to meet a task’s deadline, the FA can delegate a portion of the workload to an AA. AAs, equipped with higher computational capabilities, receive delegated tasks through wireless communication links established between FAs and AAs [8]. This process leverages the fixed infrastructure of FAs, which ensures stable and reliable communication channels to AAs. We formulate the interaction between FAs and AAs as a DDA model.

Step 4: Computation at AA Layer. UAVs execute the delegated tasks using their superior onboard computing resources. Tasks are prioritized based on urgency and system load to ensure efficient execution.

Step 5: Result Return to WA Layer. Once a task is completed by FAs, MAs, or AAs, the result is transmitted back to the originating WA via the vehicular network. This timely feedback enables seamless integration of advanced services, such as AR navigation.

In this paper, we consider a system comprising four sets of agents, i.e., WAs, MAs, FAs, and AAs, which are denoted by the sets N ≜ {1, . . . , n, . . . , N }, I ≜ {1, . . . , i, . . . , I}, J ≜ {1, . . . , j, . . . , J }, and K ≜ {1, . . . , k, . . . , K}, respectively. We assume that each FA and MA is equipped with computational resources capable of executing task computations. To model task offloading, we introduce the offloading ratio o n,i ∈ [0, 1], which represents the proportion of tasks from WA n offloaded to MA i [21]. Consequently, the processing workload assigned to MA i and FA j can be expressed as w i = o n,i W n , and w j = (1 -o n,i )W n , respectively, where W n denotes the total size of the task generated by WA n. Moreover, each AA is equipped with computational capabilities for data processing. We define α j,k ∈ [0, 1] as the offloading ratio from FA j to AA k, and the workload assigned to AA k for data processing is given by

In this subsection, we present the energy consumption models for transmission and computation in the proposed two-tier computation offloading framework. The framework involves four entities, i.e., WAs, MAs, FAs, and AAs. It should be noted that the maximum time required to offload tasks from WA n to FA j or MA i is denoted as t up .

1. Transmission energy consumption: The proposed framework involves two primary transmission segments, i.e., the communication between WAs and either MAs or FAs, and the communication between FAs and AAs. We detail the transmission models and energy consumption calculations for these segments in the following. The transmission rate from WA n to MA i is expressed as

, and n B represent the bandwidth, transmission power, channel gain, and noise power between WA n and MA i, respectively. The time taken to offload a task from WA n to MA i is expressed as

. By substituting the expression of r up n,i into t up , the required transmission power from WA n to MA i can be derived as

For the transmission from WA n to FA j, we denote the transmission power and channel gain between WA n and FA j by p up n,j and g n,j , respectively. Consequently, the transmission rate from WA n to FA j is expressed as [21]. The time required to offload task from WA n to FA j is given by

. With the expressions of r up n,j and t up , we can obtain the required transmission power from WA n to FA j as

( 2

The total transmission energy consumption for WA n when offloading tasks to both MA i and FA j is calculated as

The transmission rate and the time required that FA j offloading tasks to AA k is expressed as r up j,k = w 0 log 2 (1 +

) and

, respectively, where w 0 , p up j,k , g j,k , and n 0 represent the bandwidth, transmission power, channel gain, and noise power between FA j and AA k, respectively. With the expressions of r up j,k and t up k , the transmission power from FA j to AA k is derived as

( 2

The energy consumption of FA j offloading tasks to AA k is expressed as

While this model assumes a linear relationship, more complex non-linear energy consumption models can be straightforwardly incorporated into our framework if needed.

2. Computing energy consumption: The local computing latency of MA i, denoted as t com i , can be expressed as

, where λ i denotes the number of CPU cycles needed to handle one bit of data in MA i, while µ i corresponds to its overall processing speed in CPU cycles per second. Since the size of the output data is assumed to be negligible relative to the input workload, the delay from result transmission is disregarded in our analysis [23]. The total delay t tot i for MA i is composed of the time t up required for WA n to upload the task to MA i, and the time t com i needed for MA i to process the task, which is denoted as

Similarly, the local computing latency of FA j is denoted as

, where λ j and µ j denote the number of CPU cycles per bit and the processing capacity of FA j in CPU cycles per second, respectively. Moreover, the total delay t tot j for FA j includes the upload time t up from WA n to FA j and the local computing latency t com j , which is expressed as

, where λ k is the number of CPU cycles required to process one bit of data in AA k, and µ k is its processing capacity in CPU cycles per second. The total delay t tot k for AA k comprises the time t up k to receive the task from FA j and the local computing latency t com k , which is denoted by

The local computational energy consumption of MA i, FA j and AA k are respectively expressed as

where σ i , σ j , and σ k represent the power consumption coefficient of MA i, FA j and AA k, respectively. Moreover, the hover energy consumption of AA k is expressed as

In this subsection, we discuss the utility functions for WAs, MAs, FAs, and AAs, which are essential for understanding the decision-making processes and interactions within the proposed framework.

1. The utility of WAs: Let U n (o n,i ) represent the utility function of WA n. This utility is determined by the Quality of Experience (QoE) gained from workload completion [24], reduced by both the cost incurred for offloading and the price paid to FA i and MA j. The utility is given by

where t tot n = max{t tot i , t tot j , t up + t tot k } signifies the endto-end latency, which is the total duration from the moment WA n offloads a task until the result is received [25]. t n quantifies the actuator response time, i.e., the interval from result reception to the completion of WA n’s decision or action, a value primarily governed by its internal hardware performance [26]. Moreover, ϵ n stands for the maximum tolerable delay for the entire perceptionto-action cycle of WA n. The QoE is weighted by the tuning parameter κ n . The unit resource prices for MA i and FA j are given by p i and p j , respectively. The term ζ n denotes a scaling factor for the energy consumed by WA n during task offloading to MAs and FAs.

2. The utility of MAs: We denote the utility of MA i as U i (p i ), which can be defined as the difference between the rewards obtained from WAs and the cost for computing workloads, and expressed as

where ξ i denotes the cost parameter associated with local computing energy consumption for FA i. The reward payment p v i is designed to reflect the dynamic value that an MA offers based on its and WA’s mobility and WA’s resource availability. Therefore, p v i is related to the moving speed of MA i, which is expressed as [27]

where ρ is the maximum WA density, and ρ represents the current agent density. D i is the number of idle resources owned by MA i which follows the uniform distribution and ranges from [D, D] [27]. v n and v i represent the moving speed of WA n and MA i, respectively. v and v are the minimum and maximum speeds of WAs, respectively. φ and η represent the adjustment factors.

3. The utility of FAs: FAs can offload part of the workload to AAs to assist in workload computation. The strategy of FA j is to decide the price of local computing p j and the price r j (w k ) paid to an AA. The utility function of FA j can be expressed as the difference among the price obtained from WAs, the cost for local computing and offloading workloads, and the price paid to AA k, which is expressed as

where ξ k denotes the cost parameter associated with local computing energy consumption for FA j, and γ j represents the parameter of FA j regarding the energy consumption of task transmission. r j (w k ) is the price paid to AA k with respect to the offloading workload w k , which is given by

where ψ (0 < ψ < 1) is the profit-sharing proportion between FA j and AA k.

are the bidding prices based on the valuations v j (w k ) of FA j and v k (w k ) of AA k for computing workload w k .

Stackelberg games have been extensively applied in resource management to address complex decision-making scenarios [28]. In the context of WAs, their dynamic mobility necessitates real-time decision-making to select optimal resource providers, such as nearby FAs or MAs, for agentic AI task offloading. This decision-making process is influenced by the WA’s trajectory and the pricing schemes offered by potential resource providers. Consequently, we can model the interaction between WAs and FAs or MAs as a Stackelberg game, where FAs and MAs act as the leaders by setting resource prices of p i and p j , and WAs act as the followers by choosing the most suitable providers and determine the task offloading ratio o n,i based on these prices and their mobility constraints. For WA n, the optimization problem can be expressed as Problem 1: max

The constraints of Problem 1 ensure that the offloading ratio remains within the valid range of [0, 1], the transmission time cannot exceed the predefined maximum threshold t, and the utility of WA n is maintained above zero to ensure feasible and beneficial offloading decisions. For MA i, the optimization problem can be expressed as

The constraints of Problem 2 ensure that the unit price offered by MA i cannot exceed the predefined maximum threshold p i . This constraint is critical to maintaining market viability, as prices above p i may deter WAs from offloading tasks to MA m. Additionally, the utility of MA m is constrained to remain non-negative, ensuring that pricing decisions are both feasible and mutually beneficial for all stakeholders involved. For FA j, the optimization problem can be expressed as Problem 3:

The constraints of Problem 3 ensure that the unit price offered by FA j is capped at the predefined maximum threshold p j , preventing excessive pricing that could deter potential users. In addition, the transmission time is restricted by the predefined maximum threshold t k , which is essential to maintain timely communication and prevent it compromising service quality. Finally, the constraints maintain that the utility of FA j is greater than or equal to zero.

Consider the above analysis, we use the backward induction method to obtain the Stackelberg Equilibrium (SE) [21]. Given the price strategies p i of MA i and p j of FA j in advance, we first analyze the offloading ratio o n,i of WA n to maximize its utility. Based on the objective function of Problem 1, there are three possible cases to be considered. For simplicity, we denote B = on,iWn w B t up in the following.

1. Case 1:

The total latency is composed of the transmission duration and the local computing latency of MA i. The first-order and second-order derivatives of U n (o n,i ) with respect to o n,i are expressed as

),

) < 0.

(

The negative second-order derivative of the utility function U n (o n,i ) with respect to the offloading ratio strategy o n,i confirms its strict concavity and the first-order derivative is decreasing with o n,i . This property ensures that the optimization problem faced by WA n is a convex optimization problem. Consequently, we can derive the optimal solution by evaluating the conditions under the lower bound as follows:

where (

2. Case 2:

. The total latency is made up of the transmission duration and the local computing latency of FA j. We can obtain the first-order and second-order derivatives of U n (o n,i ) with respect to o n,i as

We can obtain that U n (o n,i ) is strictly concave with respect to o n,i , and the first-order derivative with respect to o n,i is monotonically decreasing. Based on these properties, we can derive an optimal solution by evaluating the conditions at the lower bound as follows:

where

(28)

3. Case 3:

. The total latency is composed of three components, i.e., the transmission latency between WA n and FA j, the transmission latency between FA j and AA k, and the local computing latency of AA k. The first-order and second-order derivatives of U n (o n,i ) with respect to o n,i are derived as

Similarly, it is clear that U n (o n,i ) is strictly concave with respect to o n,i , and the first-order derivative with respect to o n,i is monotonically decreasing. Therefore, we can derive an optimal solution by evaluating the conditions at the lower bound as follows:

where

After establishing the Stackelberg game between WA n, MA i, and FA j, we further introduce an auction model to optimize the interaction between FA j and AA k. The auction model is employed to efficiently allocate computational resources and determine fair bidding prices, ensuring that FA j and AA k benefit from the transaction [29]. Through this model, FA j and AA k determine their respective bidding prices Υ j [v j (w k )] and Υ k [v k (w k )], respectively, which reflect their valuations for computational workload w k . This dual-layer approach combines strategic decision-making in the Stackelberg game with competitive resource allocation in the auction model, enhancing overall system efficiency.

For FA j, the valuation v j (w k ) for the offloading of workload w k should be within [0, p j w k ] to guarantee that FA j can earn a positive profit, which is expressed as

where θ j ln ( t loc k (w k ) + 1

represents the penalty factor associated with the delay incurred by AA k’s processing workload w k . Specifically, this penalty factor increases when the local computing latency of AA k increases. The term θ j is the adjustment parameter to scale the penalty based on the relative delays in processing workload

For AA k, the valuation v k (w k ) should be within

which is expressed as

where ξ k and γ k are the cost parameters for AA k’s local computing and hovering energy consumption, respectively. The factor θ k dynamically adjusts the valuation of AA k based on the processing delay of workload w k . The valuation of AA k increases as the local computing latency of FA j increases.

In the context of optimizing task offloading within a resource market of multiple interacting FAs and AAs, the DDA mechanism is employed [30]. This approach combines the advantageous characteristics of both traditional Dutch auctions and double auctions, making it exceptionally suitable for resource allocation and pricing in scenarios involving multiple buyers and sellers. The Dutch auction, known as a descending-price auction, inherits speed and efficiency. The double auction adopts a framework for handling numerous buyers and sellers concurrently, which is essential for the complex interactions between a fleet of AAs and multiple FAs. This integration allows the DDA to efficiently manage the dual challenges of allocating resources by matching buyers with sellers and establishing dynamic pricing, thereby balancing the market for all participants. Within this complex market environment, various entities fulfill distinct roles, each contributing to the overall functionality and efficiency of the system, as depicted below [31].

FAs (Buyers): FAs function as buyers in the system, compensating sellers for assistance in task execution. Before each round of the DDA, FAs are permitted to submit bids to the auctioneer. The bid of buyer j at round t, denoted as b t j , which can be calculated as b t j = v j (w k ), reflecting the maximum amount buyer j is prepared to pay for task offloading services provided by the seller.

AAs (Sellers): Sellers are represented by AAs, having the capability to supply computational resources to FAs, thereby aiding in the completion of tasks assigned by WAs. The seller k’s ask at time t is evaluated as b

which means the minimum price at which seller k is willing to provide resources for the task offloading requested by buyers.

Auctioneer: The auctioneer functions as a DRL agent. The objective is to achieve an optimal auction strategy by operating two Dutch clocks, one for the buyer side Ψ t = 0 and the other for the seller side Ψ t = 1. The buyer-side clock C b displays descending purchase prices, initiated at the maximum bid value C 0 b = p j w k and decrementing at a controlled rate over time. Conversely, the sellerside clock C s exhibits ascending sale prices, commencing at the minimum ask value

and incrementing progressively as time elapses. By adjusting these clocks, the auctioneer seeks to enhance social welfare while simultaneously minimizing the costs associated with information exchange during the auction.

DDA operates through three phases: Dutch Clock Broadcast, Dutch Clock Acceptance, and Dutch Clock Adjustment. These steps form the foundation of the mechanism and employ the following key terminologies [31], [32]:

1. Dutch Clock Broadcast: At the initiation of each auction round, the auctioneer broadcasts the current clock value to all market participants. When Ψ = 0 (indicating the buyer side of the auction), the auctioneer broadcasts the current buyer clock C b to all registered buyers. Conversely, when Ψ = 1 (indicating the seller side of the auction), the auctioneer broadcasts the current seller clock C s to all registered sellers. 2) Dutch Clock Acceptance: Upon receiving the auction clock from the auctioneer, buyers and sellers evaluate their valuation against the current clock value. If the auction clock meets their respective bidding conditions, eligible participants submit bids or asks to the auctioneer. Specifically, when Ψ t = 0, for the j-th available buyer (j / ∈ J t b ), if the buyer accepts the clock value b t j ≥ C t b , the bid c t j is recorded as the current buyer clock c t j ← C t b . Then, the winning buyer set is updated by adding buyer j to the current transaction set, i.e., J t+1 b = J t b ∪ {j}. Therefore, the difference between the expected and the real bid is the regret re t j of buyer j, which can be calculated as

Upon completion of the buyer phase, the auctioneer updates the flag Ψ t+1 to 1, transitioning the auction to the seller phase. During this phase, the auction market operates on the seller side (Ψ t = 1), with mechanics analogous to the buyer phase but in reverse. When Ψ t = 1, the auction transitions to the seller phase. For the k-th available seller (k / ∈ K t s ), if the seller accepts the clock value such that b t k ≤ C t s , the ask is recorded as the current seller clock c t k ← C t s . Subsequently, the winning seller set is updated by adding the k-th seller to the current transaction set K t+1 s = K t s ∪ {k}. Consequently, the difference between the expected sell-bid and the real sell-bid is the regret re t k of seller k, which can be calculated as

The auctioneer then adjusts the flag Ψ t+1 = 0, locking the buyer’s clock and switches to the seller’s side. 3) Dutch Clock Adjustment: The scenario described previously pertains to transactions where both buyers and sellers meet the auction criteria. However, in cases where the current auction clock fails to attract any market participants willing to trade, the auction mechanism necessitates an adjustment of the clock value to facilitate market activity. When Ψ t = 0 and no buyer submits a valid bid, the auctioneer selects a step size Ξ t to adjust the buyer clock. Specifically, the auctioneer decreases the buyer’s clock value according to

Similarly, when Ψ t = 1 and no seller submits a valid bid, the auctioneer increases the seller clock value according to C t+1 s = C t s + Ξ t . Following the adjustment of the auction clock, the auctioneer needs to verify whether the buyer and seller clocks have intersected. The auction concludes at time slot t ← T when the clocks cross, defined by the condition C t b > C t s . At this juncture, the market-clearing price is finalized and established as r

where ψ ∈ [0, 1] is defined as the pricing coefficient. The total social welfare among the buyers and sellers can be expressed as

where u j = c t j -r * , and u k = r * -c t k . The design of the DDA mechanism has three desirable properties that are described as follows [33].

1. Individual Rationality (IR): All the winning buyers and sellers guarantee a non-negative utility in the DDA mechanism, i.e., u j > 0 for FAs and u k > 0 for AAs. 2) Incentive Compatibility (IC): Buyers and sellers have no incentive to deviate from truthful bidding, because it would not improve their utility, i.e., c t j ̸ = b t j for FAs and c t k ̸ = b t k for AAs. 3) Strong Budget Balance [32]: In the DDA, buyers and sellers trade using identical bids r * for the buyer and seller clocks. A double auction is considered to maintain budget balance when the auctioneer ensures nonnegative utility, defined as the total payments received exceeding the total costs incurred. Furthermore, the auction achieves a strong budget balance when the auctioneer neither incurs payment costs nor makes payment transfers.

Theorem 1. The proposed DDA meets the IR and IC requirements and maintains a strong budget balance.

Proof. Please refer to [32].

Algorithm 1 Linear Search Algorithm for Optimal MA’s price 1: Input: FA pricing strategy p j , step size ∆, computation tolerance ι. Set the optimal WA’s strategy for the current price:

// End: Bisection Search

Calculate the MA’s utility U i (o * n,i ).

18:

Update best utility:

Update best price: p best i ← p low i .

end if

Increment the price for linear search: p low i ← p low i + ∆. 23: end while 24: Output: The optimal MA pricing strategy p * i = p best i and its corresponding utility

, and the optimal offloading ratio o * n,i .

A. Iterative Best-Response for Stackelberg Equilibrium 1) Linear-Search Algorithm: Based on the SE analysis in Section IV-C, we devise an iterative algorithm to solve the game. First, for the follower (i.e., WA n), although an optimal offloading strategy o n,i exists, its closed-form expression is intractable. We employ a bisection search algorithm to compute this strategy numerically, similar to the approach in [21]. Consequently, the objective functions for the leaders (i.e., MA i and FA j) become no closedform. To determine their pricing strategies, we model their competition as a non-cooperative game and use a linear search approach. This method involves alternately optimizing one leader’s price while holding the other’s constant. Specifically, we apply a stepwise linear search within a bounded interval (e.g., [0, p i ] for MA i) to find the optimal price for one leader, then repeat the process for the other. The convergence of this algorithm to the SE is guaranteed due to the alternating optimization process and the nature of the leaders’ objective functions. , ∆, ι). 7: // Step 2: FA finds its best response to MA’s price p 2) Algorithm for Stackelberg Equilibrium: Algorithm 2 details the iterative procedure used to compute the SE for MA’s and FA’s pricing strategies, and WA’s offloading strategy. The algorithm converges to the optimal prices p * i and p * j by simulating an iterative best-response process. Starting from initial price values, the algorithm enters a loop that continues until the strategy convergence guarantees. In each iteration, it first computes the MA’s optimal price p (l) i , assuming the FA’s current price p (l-1) j is fixed, by executing the linear search method from Algorithm 1. Subsequently, the algorithm calculates the FA’s optimal price p l j in response to this new MA’s price p (l) i . The process repeats, updating the prices at the end of each cycle, until the adjustments between consecutive iterations fall below a predefined convergence threshold. • Reward Space: The auctioneer’s reward is denoted as

Algorithm 3 Diffusion-based DRL Algorithm Reset environment and get initial state S 0 .

for iteration h = 1 to max iteration H do 6:

Observe the current state S h .

Sample Gaussian noise x H ∼ N (0, I).

Generate x 0 by denoising x T based on Eq. (41).

Execute the action a h based on x 0 and Eq. (42).

Let clock adjustment step ϱ h ← a h .

Execute action a h and observe reward r h and next state S h+1 .

12:

Store the record (S h , a h , r h , S h+1 ) in the experience replay buffer D.

Update current state: S h ← S h+1 .

Sample a random mini-batch of experiences D h from the experience replay buffer D.

Update critic parameters ν based on Eq. (43).

Update actor parameters ϑ based on Eq. (44).

// Softly update target network parameters 18: where N U M = min{|J t b |, |K t s |}. b, c and d are the parameters to adjust the reward. R(S t , S t+1 ) is derived from two key factors, i.e., the regret experienced by both buyers and sellers, and the cost associated with broadcasting updated auction information to all participants, which can be denoted as [32]

where co t (X) = dX represents a function that quantifies the cost associated with auction information exchange for X participants within a market of equivalent scale, and d is the communication penalty incurred during the auction process. The function can decrease the number of participants that require new updates to the auction clock, thereby lowering the associated communication costs. 2) Diffusion-based DRL Algorithm: The diffusionbased DRL algorithm determines clock adjustment step ϱ by modeling the auction as a Markov Decision Process (MDP). The auction environment comprises states, actions, and rewards. During each auction round, the auctioneer collects bidding prices from AAs and FAs, and its action is to set the clock adjustment step ϱ = a ∈ A ,WHUDWLRQV [29]. The diffusion framework incorporates two processes, i.e., forward diffusion and reverse diffusion processes. In the forward diffusion process, Gaussian noise is incrementally added to an initial sample over T sequential steps, forming a Markov process that generates a sequence of samples {x 0 , x 1 , . . . , x t , . . . , x T }. The forward process of the diffusion model can be described as [7]

where µ t and Σ t represent the mean and variance of the normal distribution at step t, respectively. The hyperparameter ι t ∈ (0, 1) is pre-set to control the noise variance, with I signifying an identity matrix where each dimension shares the same standard deviation ι t . With the inverse distribution Q(x t-1 |x t ) defined, sampling x t from a standard normal distribution N (0, I) becomes achievable via a reverse diffusion process. A critical aspect for the efficacy of this sampling is ensuring the trained reverse Markov chain accurately mirrors the time reversal of the forward chain [34]. However, accurately estimating the statistical properties of Q(x t-1 |x t ) requires complex computations involving the data distribution, posing a significant challenge. To tackle this challenge, a parametric model P ϑ , where ϑ represents the model parameters, can be employed to approximate Q(x t-1 |x t ) as follows [35]:

where µ ϑ (x t , t) and Σ ϑ (x t , t) respectively represent the learned mean function and variance conditioned on the noisy data x t , the current state S t , and the time step t.

Once the reverse process completes, the final output x 0 is transformed into a probability distribution over the action space using the softmax function, which is expressed as [29] π

where |A| denotes the size of the action space, with each value π ϑ representing the probability of selecting a specific clock adjustment step.

To assess the quality of the chosen actions, i.e., the selected clock adjustment step ϱ, to maximize the total surplus, we employ two critic networks, i.e., Q ν1 and Q ν2 networks, along with their corresponding target networks

respectively. The optimization of critic network parameters ν m (m = {1, 2}) can be obtained by minimizing the objective function denoted as

where

)}. D h represents a randomly mini-batch of transitions retrieved from the replay buffer D during training iteration h. The actor-network parameters ϑ are updated using gradient descent to minimize the expected loss while promoting exploration through entropy-based regularization [29]

where ϖ denotes the learning rate, while β is the temperature parameter that balances exploration and exploitation. [29], where C is the complexity of auction environment interaction and ε is the mini-batch size for network updates.

This section provides a quantitative validation of the performance of the proposed framework through empirical analysis. Similar to [8], [21], we configure the system parameters as follows. The WA is assigned a total workload W n of 10 Mbits with a QoE adjustment parameter κ n of 0.5. The communication channel is characterized by a bandwidth w B of 1 kHz and an environmental noise power n B of 10 -4 dBm [21]. The average transmission delays are set at t up = 0.5s (between WAs and FAs/MAs) and t up k = 0.1s (between FAs and AAs). For computation, the per-bit processing requirement is uniformly set to λ = 10 4 cycles for all agents. However, their processing capabilities µ and power consumption coefficients σ differ, i.e., MAs are set to (10 6 cycles/s, 10 -20 ), FAs to (4 × 10 6 cycles/s, 1.25 × 10 -22 ), and AAs to (6 × 10 6 cycles/s, 1.5 × 10 -22 ).

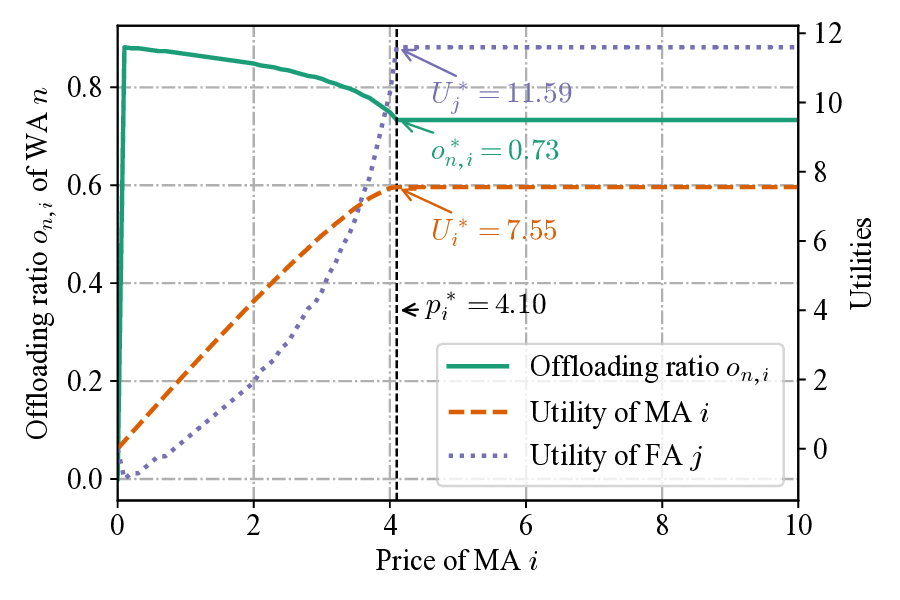
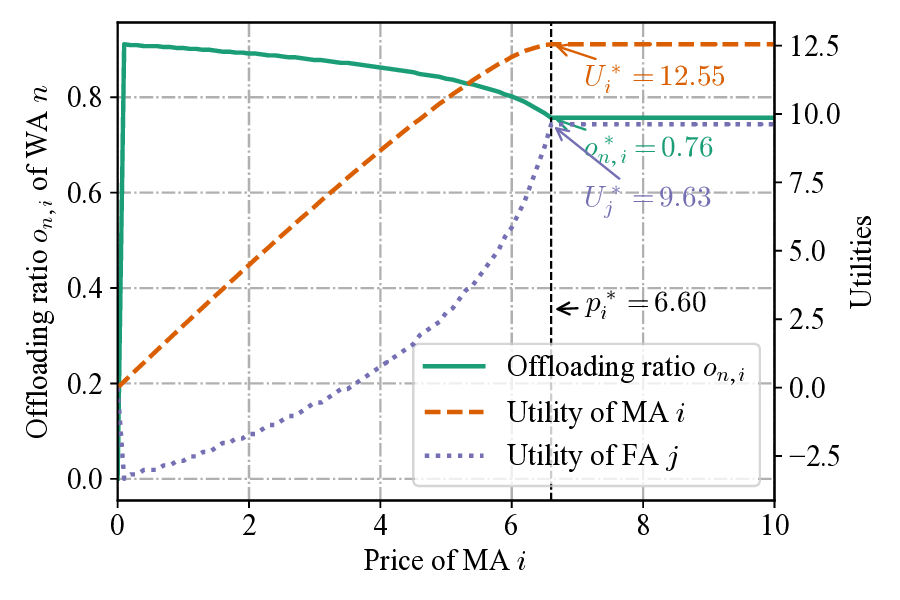
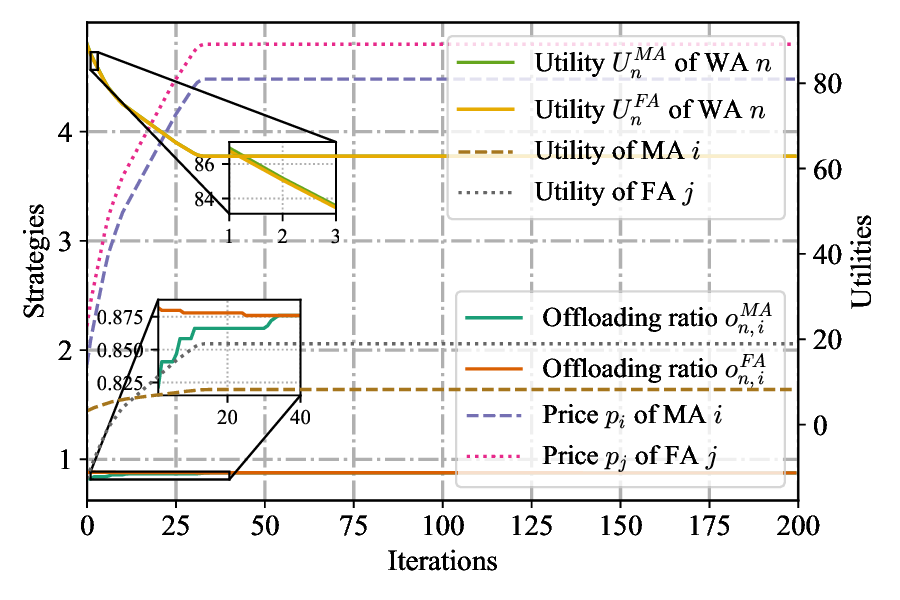
The performance of Algorithm 1 in computing the optimal price p i is depicted in Fig. 3, under the condition of a fixed price p j = 5.0 for the competing FA. A direct correlation is observed between the offloading ratio o n,i and the resultant optimal price p i . Both metrics adhere to the hierarchical order of Case 2 > Case 3 > Case 1. This outcome aligns with fundamental economic principles, where a higher offloading ratio from a user (WA) represents increased demand, enabling the provider (MA) to set a correspondingly higher price. The suppressed demand in Case 1 is attributable to its longer offloading latency, which naturally leads to both the lowest offloading ratio and the lowest optimal price. These findings demonstrate that Algorithm 1 effectively computes the optimal price for a resource provider under fixed competitive conditions and varying user demand. Fig. 4 demonstrates the convergence properties of the proposed Algorithm 2 for determining the strategies of WAs, FAs, and MAs. The figure charts the iterative adjustment of the FA’s price, the MA’s price, and the WA’s offloading ratio. Initially, all three variables undergo a brief transient phase, reflecting the dynamic strategic adjustments between the game’s leaders (i.e., FAs and MAs) and followers (i.e., WAs). Following this initial period, the system quickly converges, with all variables stabilizing at a fixed point after a small number of iterations. This stable outcome represents the SE, where no player can improve their payoff by unilaterally altering their strategy. These results therefore validate that Algorithm 2 is both effective and efficient at computing the optimal pricing and offloading strategies within the proposed model.

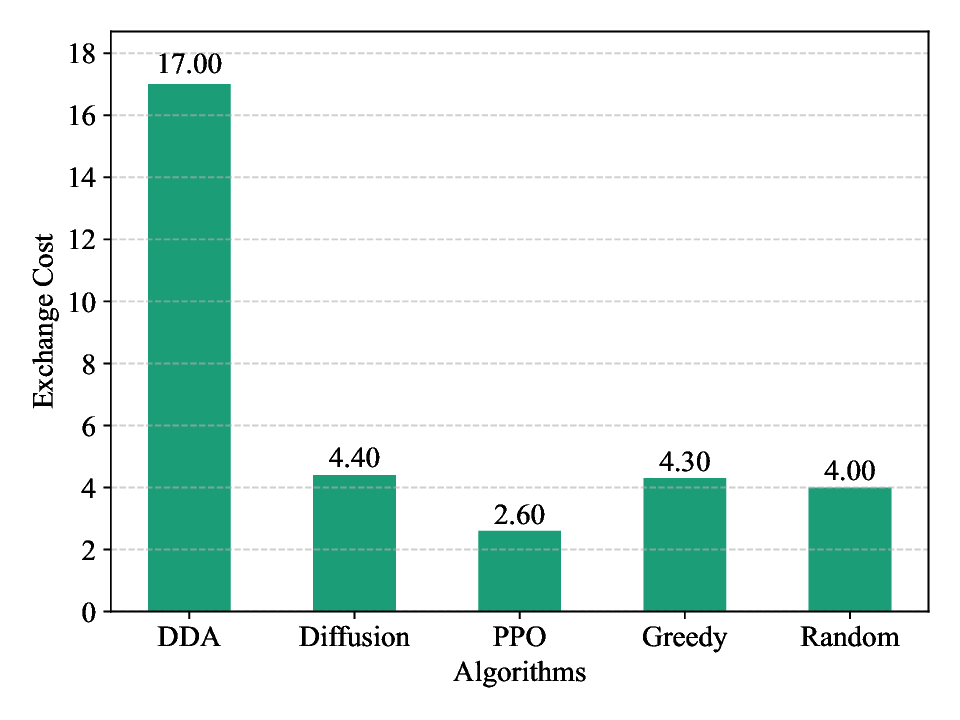
Fig. 5 illustrates the convergence behavior and superior performance of the proposed diffusion-based DRL algorithm. The result demonstrates that the proposed algorithm consistently attains the highest average episode reward across all epochs, substantially outperforming traditional DRL methods, e.g., Proximal Policy Optimization (PPO), as well as baseline strategies, e.g., greedy and random. Notably, the diffusion-based DRL approach exhibits faster convergence, achieving near-optimal rewards that align closely with the theoretical DDA upper bound within fewer training iterations. These findings validate the efficacy of integrating the diffusion model into the DRL framework for optimizing dynamic resource allocation tasks. Fig. 6 presents a comparative analysis of the social welfare achieved by our proposed diffusion-based DRL algorithm against several established benchmarks, i.e., the PPO algorithm, a greedy algorithm, and a random allocation strategy. As illustrated, the diffusion-based approach consistently yields the highest social welfare, closely approaching the theoretical optimum of the DDA compared to other algorithms. This superior performance is attributed to the algorithm’s ability to effectively learn the global distribution of optimal solutions, thus avoiding the pitfalls of local optima that can trap other methods. In contrast, the PPO algorithm achieves a commendable but sub-optimal result, characteristic of DRL methods may struggle with efficient exploration in a complex and highdimensional action space. Fig. 7 compares the exchange costs of the proposed diffusion-based DRL algorithm with other algorithms. As shown in Figs. 6 and7, the traditional DDA method achieves high social welfare but incurs high exchange costs. In contrast, the PPO algorithm, while having the lowest exchange cost, delivers lower social welfare than the proposed diffusion-based DRL algorithm. The proposed diffusion-based DRL method can dynamically adjust the clock step size to adapt to changing auction environments. This allows it to achieve near-optimal social welfare with lower information exchange costs. Consequently, the proposed diffusion-based DRL method offers a better balance between social welfare and exchange costs.

Fig. 8 verifies the results that our proposed DDA satisfies the crucial properties of IR and IC. We fix the market size and randomly select a buyer (i.e., FA) and a seller (i.e., AA) from the auction market for varying only their bidding and asking prices. By adjusting the bidding and asking price ranges to values both above and below their true values, we comprehensively compare the utility trends of buyers and sellers under different bidding and asking prices. As shown in Fig. 8, the green curve represents the utility of the buyer, which peaks when the buyer’s bid truthfully matches its true value of 41. Bids deviating from this value (either lower or higher) result in lower or unchanged utility, confirming the buyer’s IC. Similarly, the purple curve shows the utility of the seller, maximized when the seller’s asking price aligns with its true value of 9. Deviations from this true asking price lead to significantly reduced or constant utility, thus validating the seller’s IC. Furthermore, regardless of changes in bid or ask prices, the utility for both buyers and sellers remains greater than or equal to zero, thereby validating that our proposed DDA mechanism satisfies IR. Therefore, the truthful bidding and asking represent the optimal strategy for both buyers and sellers, ensuring non-negative utility while eliminating incentives for market manipulation.

To enhance agentic AI task offloading efficiency for multi-agent systems in IoA, in this paper, we have developed a sophisticated, incentive-driven, two-tier offloading framework. Our hybrid approach first employs a Stackelberg game to orchestrate the primary offloading market between users (WAs) as followers and resource providers (MAs and FAs) as leaders. To preemptively solve FA resource contention, we have introduced a secondary market governed by a DDA model, enabling FAs to lease computational power from nearby AAs. We have solved this dynamic resource allocation problem via a novel diffusion-based DRL algorithm. Comprehensive simulations have not only validated the efficacy of our model across diverse scenarios but also confirmed its significant performance gains over existing benchmarks. In our future work, we will consider advancing this scheme by incorporating more realistic network dynamics, robust security protections, and heterogeneous resources, while also leveraging machine learning for more intelligent decisionmaking and pursuing large-scale, real-world validation.

• n,i = 0. When p j -p i > P 1 , we can obtain j -p i < P 1 , min{1, o e n,i }, p j -p i > P 1 .

e H[C + T |ϑ| + (ε + 1)(|ϑ| + |ν|)])