Statistics / Computation Economics / Econometrics

Fast and Flexible Bayesian Inference in Models with Time-Varying Parameters

Reading time: 3 minute
...
#paper #research

📝 Original Paper Info

- Title: Fast and Flexible Bayesian Inference in Time-varying Parameter Regression Models
- ArXiv ID: 1910.10779
- Date: 2021-10-01
- Authors: Niko Hauzenberger, Florian Huber, Gary Koop, Luca Onorante

📝 Abstract

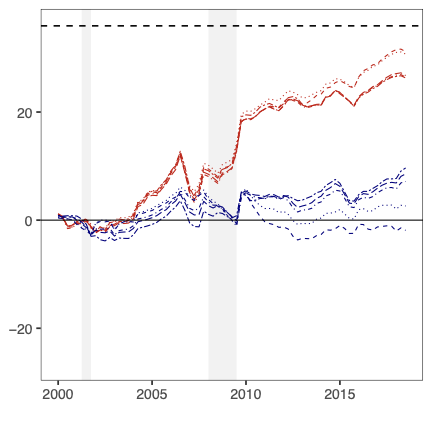
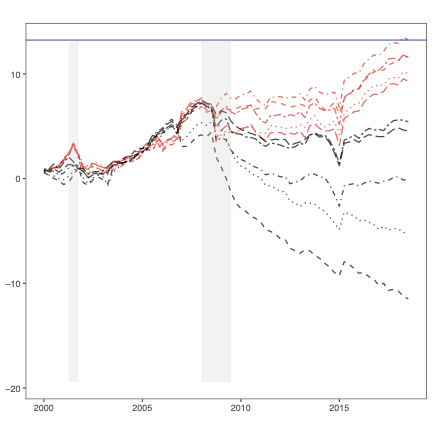
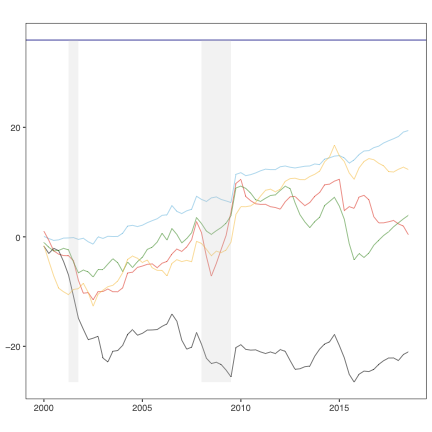
In this paper, we write the time-varying parameter (TVP) regression model involving K explanatory variables and T observations as a constant coefficient regression model with KT explanatory variables. In contrast with much of the existing literature which assumes coefficients to evolve according to a random walk, a hierarchical mixture model on the TVPs is introduced. The resulting model closely mimics a random coefficients specification which groups the TVPs into several regimes. These flexible mixtures allow for TVPs that feature a small, moderate or large number of structural breaks. We develop computationally efficient Bayesian econometric methods based on the singular value decomposition of the KT regressors. In artificial data, we find our methods to be accurate and much faster than standard approaches in terms of computation time. In an empirical exercise involving inflation forecasting using a large number of predictors, we find our models to forecast better than alternative approaches and document different patterns of parameter change than are found with approaches which assume random walk evolution of parameters.

💡 Summary & Analysis

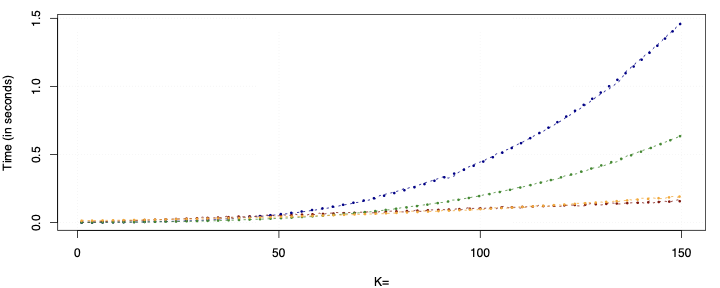
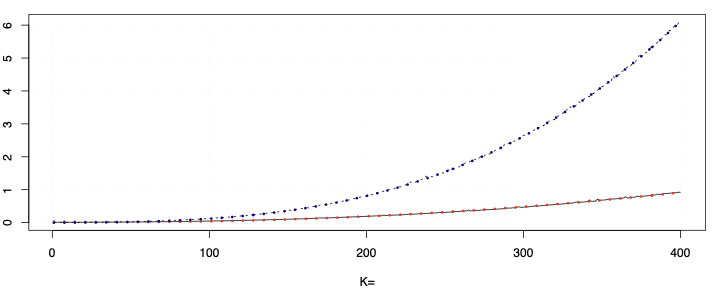
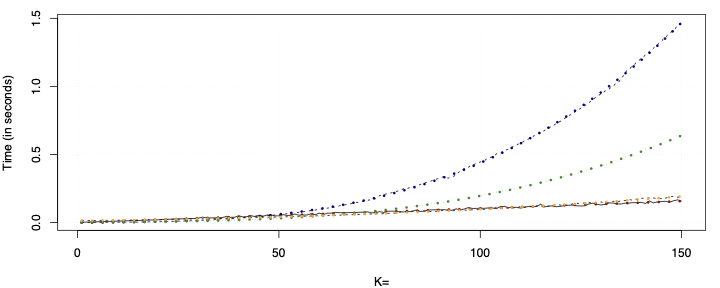
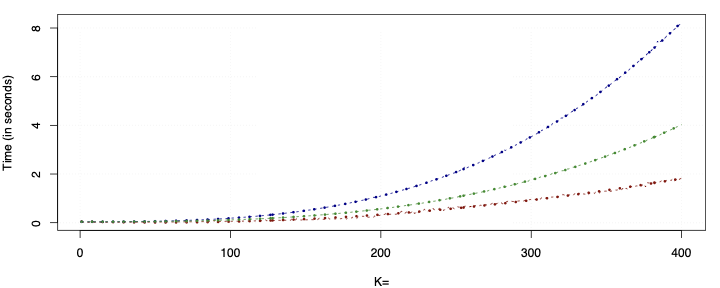
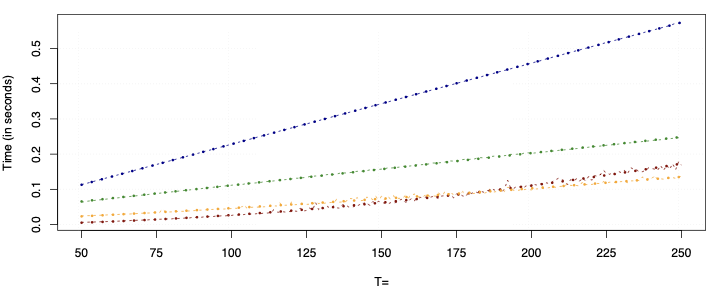
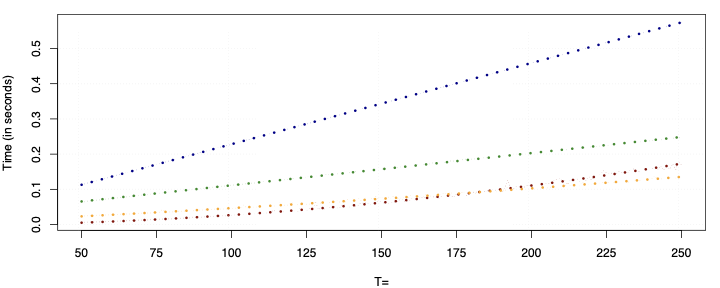
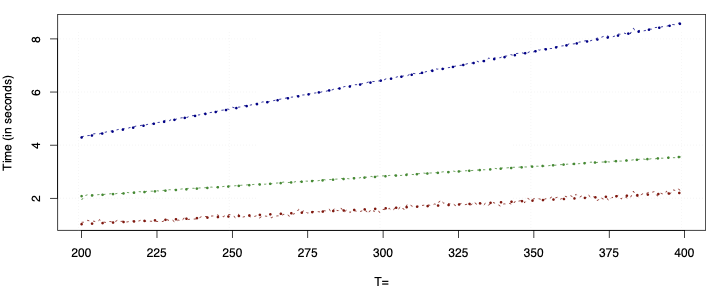
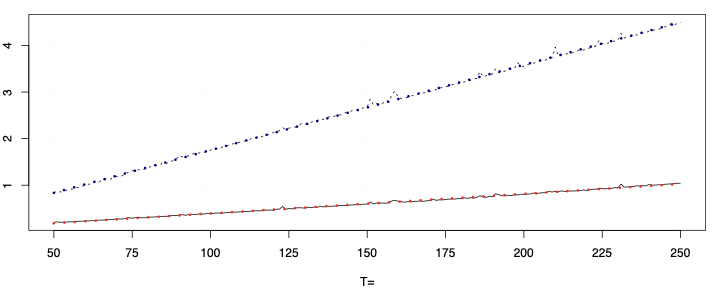
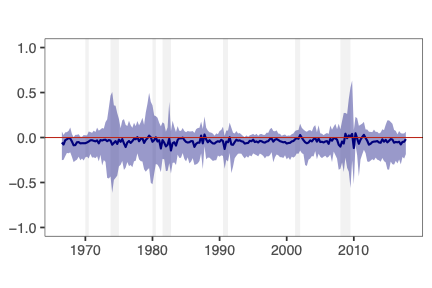
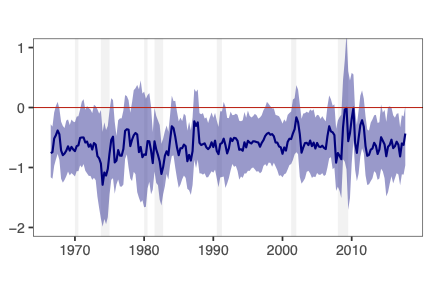
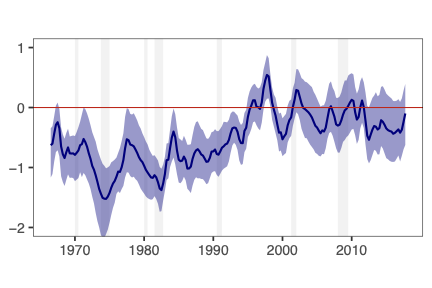
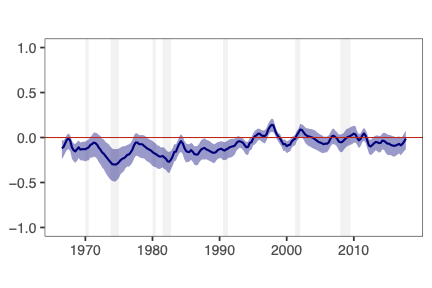
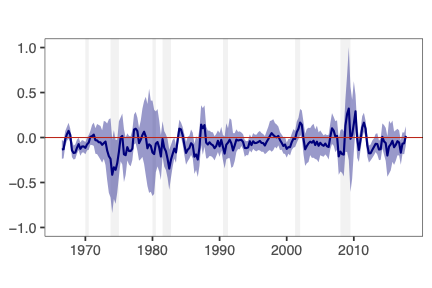
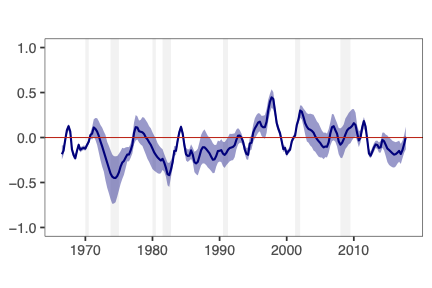
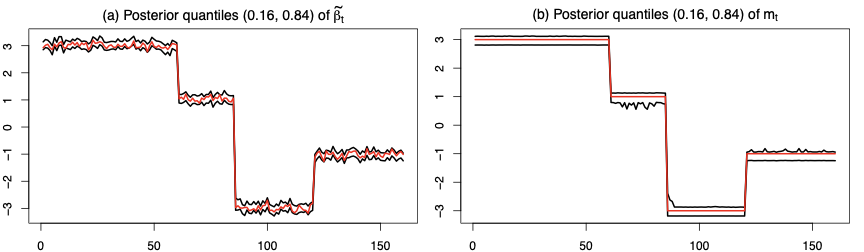
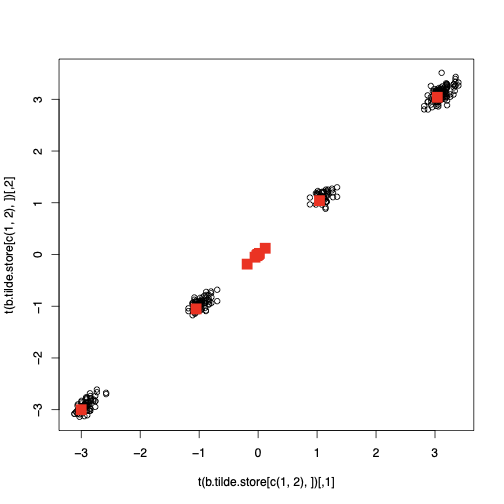
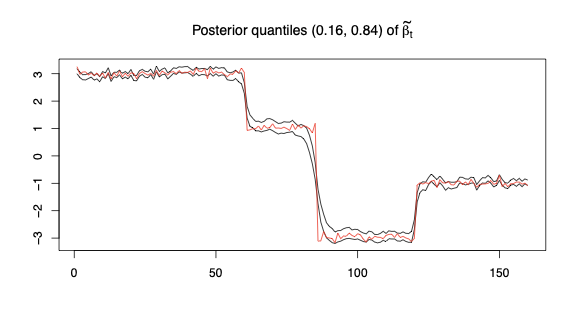
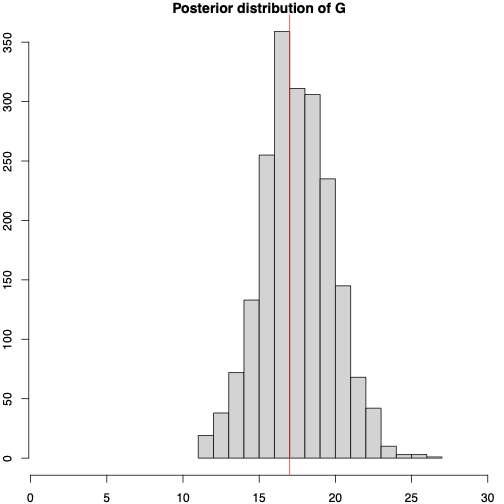
This paper presents a novel approach to time-varying parameter (TVP) regression models, aiming to enhance computational efficiency and prediction performance. Traditionally, TVP models have been computationally expensive due to the assumption that parameters evolve according to a random walk over time, which increases complexity significantly. The authors address this issue by introducing a hierarchical mixture model for TVPs, transforming a TVP regression model into a constant coefficient regression model with K x T explanatory variables. This transformation leverages singular value decomposition (SVD) of the KT regressors to achieve computational efficiency.

The paper demonstrates through both artificial and empirical data that their approach is not only more accurate but also much faster in terms of computation time compared to standard methods. Particularly, when applied to inflation forecasting using a large number of predictors, the proposed model outperforms alternative approaches and reveals different patterns of parameter changes than those assumed by random walk evolution.

This research significantly improves the computational efficiency of TVP regression models, making them more practical for real-world economic applications. By providing faster and more accurate predictions, this approach can enhance decision-making processes in various fields related to economic forecasting.

📄 Full Paper Content (ArXiv Source)

[^1]: Corresponding author: Florian Huber. Department of Economics, University of Salzburg. *Address*: Mönchsberg 2a, 5020 Salzburg, Austria. *Email*: . We would like to thank the participants of the $`6^{th}`$ NBP Workshop on Forecasting (Warsaw, 2019), the $`11^{th}`$ European Seminar on Bayesian Econometrics (Madrid, 2021) and internal seminars at the University of Salzburg, the FAU Erlangen-Nuremberg and the ECB, four anonymous referees as well as Anna Stelzer, Michael Pfarrhofer and Paul Hofmarcher for helpful comments and suggestions. The first two authors gratefully acknowledge financial support by the Austrian Science Fund (FWF): ZK 35 and by funds of the Oesterreichische Nationalbank (Austrian Central Bank, Anniversary Fund, project number: 18127). This paper, subject to minor editorial changes, will appear in the Journal of Business & Economic Statistics.

📊 논문 시각자료 (Figures)

Figure 1



Figure 2



Figure 3



Figure 4



Figure 5



Figure 6



Figure 7



Figure 8



Figure 9



Figure 10



Figure 11



Figure 12



Figure 13



Figure 14



Figure 15



Figure 16



Figure 17



Figure 18



Figure 19



Figure 20



Figure 21



Figure 22



Figure 23



Figure 24



Figure 25



Figure 26



Figure 27



Figure 28



Figure 29



Figure 30



Figure 31



Figure 32



Figure 33



Figure 34



Figure 35



Figure 36



Figure 37



Figure 38



Figure 39



Figure 40



Figure 41



Figure 42



Figure 43



Figure 44



Figure 45



Figure 46



Figure 47



Figure 48



Figure 49



Figure 50



Figure 51



Figure 52



Figure 53



Figure 54



Figure 55



Figure 56



Figure 57



Figure 58



Figure 59



Figure 60



Figure 61



Figure 62



Figure 63



Figure 64



Figure 65



Figure 66



Figure 67



Figure 68



Figure 69



Figure 70



Figure 71



Figure 72



Figure 73



Figure 74



Figure 75



Figure 76



Figure 77



Figure 78



Figure 79



Figure 80



Figure 81



Figure 82



Figure 83



Figure 84



Figure 85



Figure 86



Figure 87



Figure 88



Figure 89



Figure 90



Figure 91



A Note of Gratitude

The copyright of this content belongs to the respective researchers. We deeply appreciate their hard work and contribution to the advancement of human civilization.

Related Posts

Start searching

Enter keywords to search articles

↑↓
↵
ESC
⌘K Shortcut