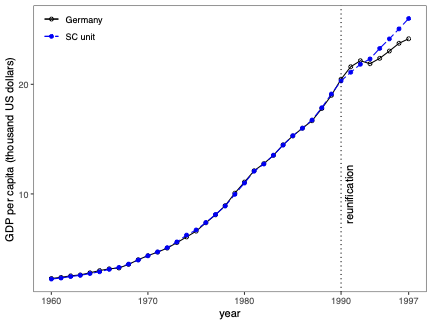
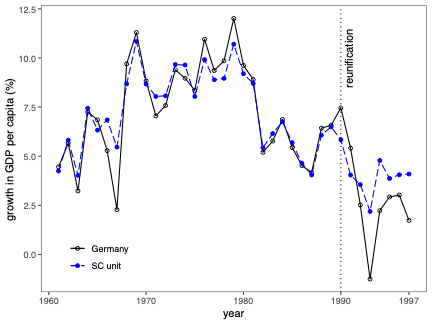
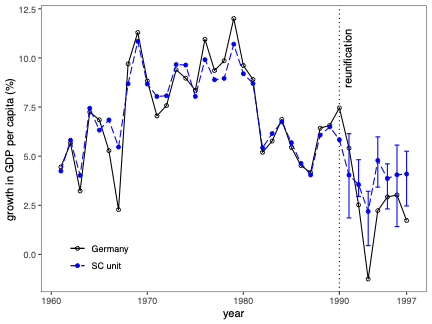
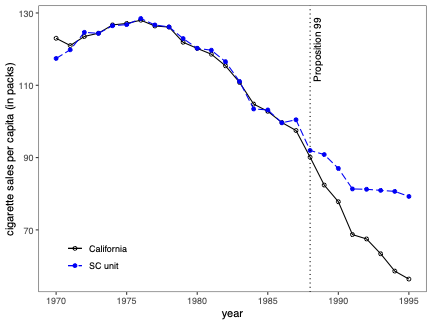
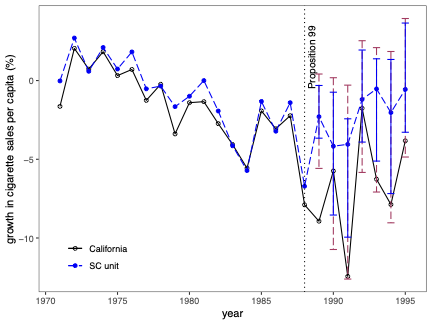
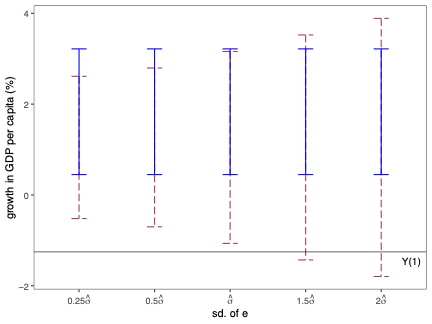
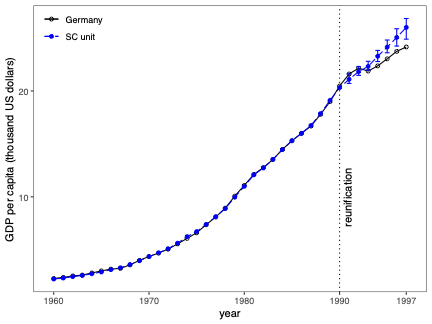
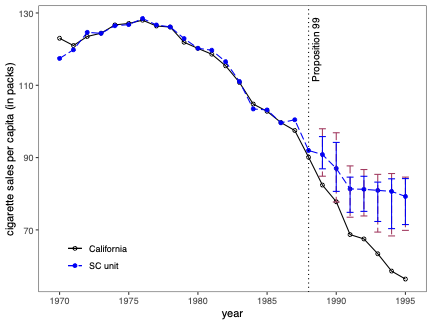
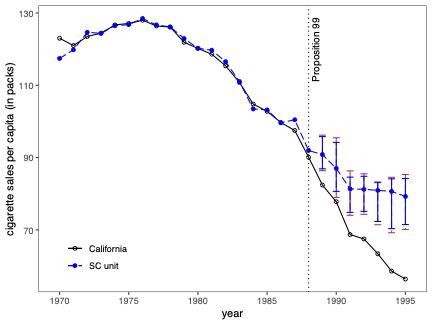
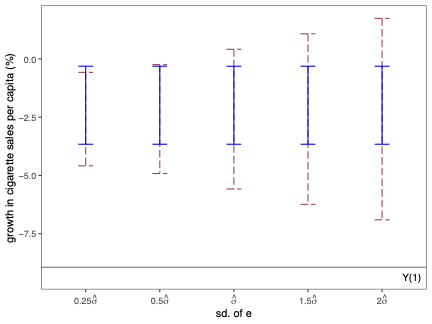
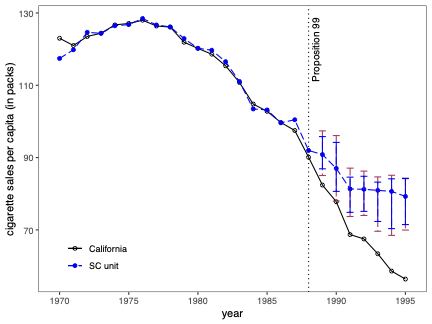
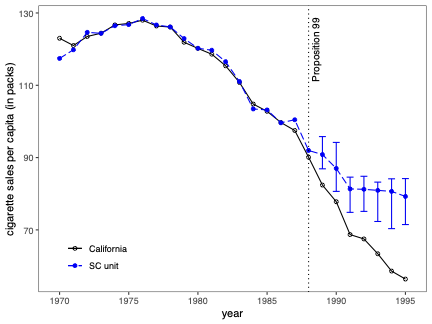
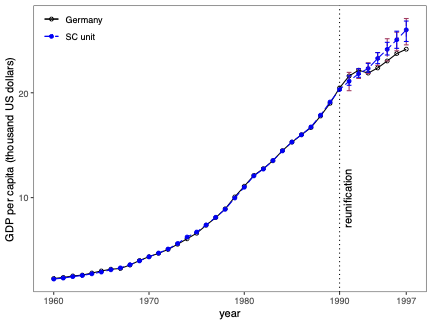
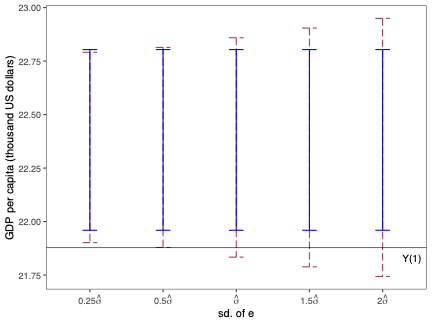
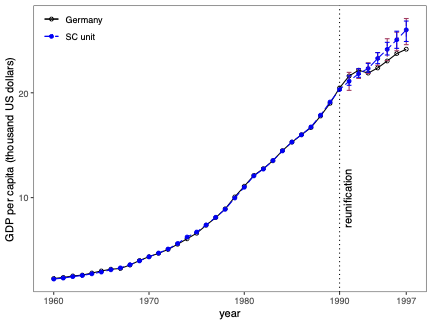
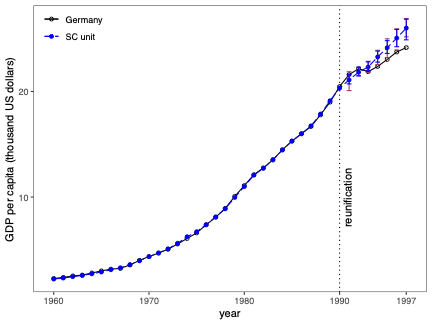
Prediction Intervals for Synthetic Control Methods
📝 Original Paper Info
- Title: Prediction Intervals for Synthetic Control Methods- ArXiv ID: 1912.07120
- Date: 2021-09-09
- Authors: Matias D. Cattaneo and Yingjie Feng and Rocio Titiunik
📝 Abstract
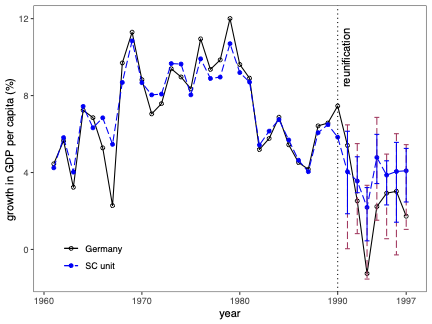
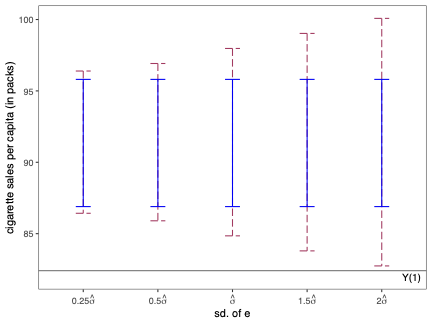
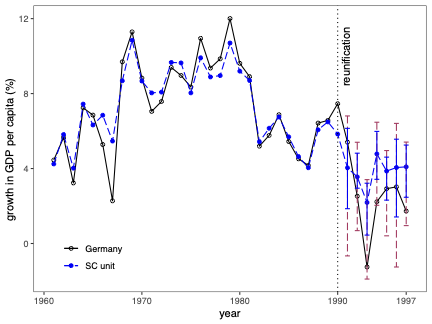
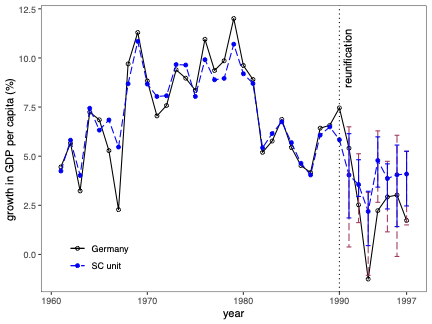
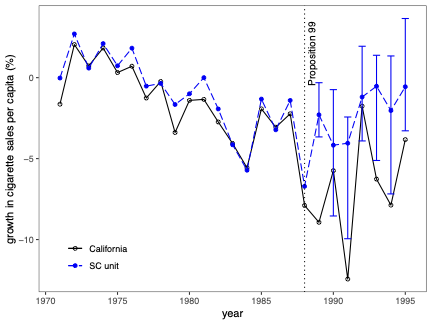
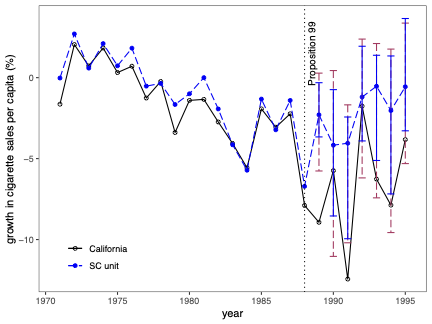
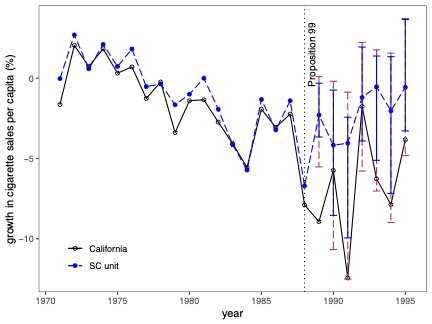
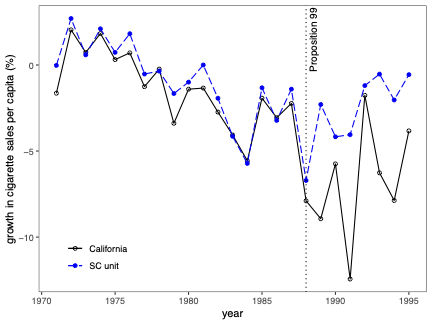
Uncertainty quantification is a fundamental problem in the analysis and interpretation of synthetic control (SC) methods. We develop conditional prediction intervals in the SC framework, and provide conditions under which these intervals offer finite-sample probability guarantees. Our method allows for covariate adjustment and non-stationary data. The construction begins by noting that the statistical uncertainty of the SC prediction is governed by two distinct sources of randomness: one coming from the construction of the (likely misspecified) SC weights in the pre-treatment period, and the other coming from the unobservable stochastic error in the post-treatment period when the treatment effect is analyzed. Accordingly, our proposed prediction intervals are constructed taking into account both sources of randomness. For implementation, we propose a simulation-based approach along with finite-sample-based probability bound arguments, naturally leading to principled sensitivity analysis methods. We illustrate the numerical performance of our methods using empirical applications and a small simulation study. \texttt{Python}, \texttt{R} and \texttt{Stata} software packages implementing our methodology are available.💡 Summary & Analysis
This paper delves into the development of prediction intervals for synthetic control (SC) methods, which are used to analyze the effects of specific policies or interventions. The core issue addressed is how to quantify uncertainty in SC analysis effectively. The authors recognize that there are two primary sources of randomness affecting the accuracy of SC predictions: one from the construction of potentially misspecified SC weights during the pre-treatment period and another due to unobservable stochastic errors in the post-treatment phase.The proposed solution involves constructing prediction intervals that consider both these sources of uncertainty. A simulation-based approach is used for implementation, alongside finite-sample probability bounds arguments. This leads naturally to methods for principled sensitivity analysis, which can help researchers understand how varying assumptions affect their results. The authors demonstrate the performance of their methodology through empirical applications and a small-scale simulation study.
The significance of this work lies in providing a more robust framework for interpreting SC analyses by offering clearer ways to quantify uncertainty. This is particularly important in fields like economics and political science where policy impact assessments are crucial.
📄 Full Paper Content (ArXiv Source)
📊 논문 시각자료 (Figures)