Edge Matching with Inequalities, Triangles, Unknown Shape, and Two Players

📝 Original Paper Info

- Title: Edge Matching with Inequalities, Triangles, Unknown Shape, and Two Players
- ArXiv ID: 2002.03887
- Date: 2020-06-04
- Authors: Jeffrey Bosboom, Charlotte Chen, Lily Chung, Spencer Compton, Michael Coulombe, Erik D. Demaine, Martin L. Demaine, Ivan Tadeu Ferreira Antunes Filho, Dylan Hendrickson, Adam Hesterberg, Calvin Hsu, William Hu, Oliver Korten, Zhezheng Luo, Lillian Zhang

📝 Abstract

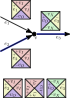
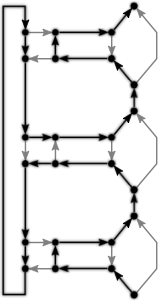
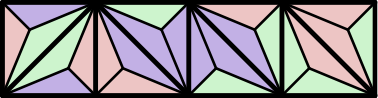
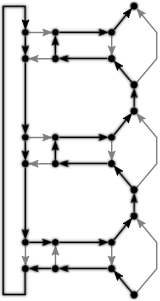
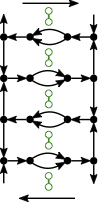
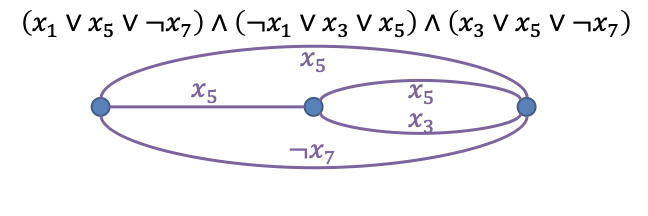
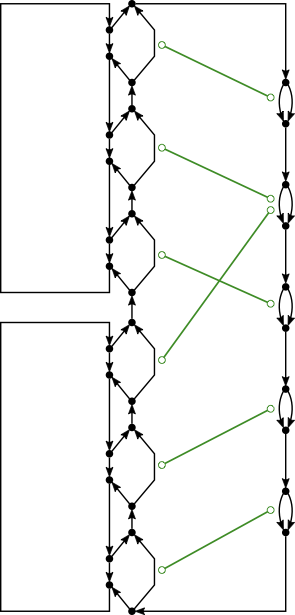
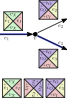
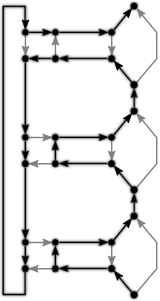
We analyze the computational complexity of several new variants of edge-matching puzzles. First we analyze inequality (instead of equality) constraints between adjacent tiles, proving the problem NP-complete for strict inequalities but polynomial for nonstrict inequalities. Second we analyze three types of triangular edge matching, of which one is polynomial and the other two are NP-complete; all three are #P-complete. Third we analyze the case where no target shape is specified, and we merely want to place the (square) tiles so that edges match (exactly); this problem is NP-complete. Fourth we consider four 2-player games based on $1 \times n$ edge matching, all four of which are PSPACE-complete. Most of our NP-hardness reductions are parsimonious, newly proving #P and ASP-completeness for, e.g., $1 \times n$ edge matching.

💡 Summary & Analysis

The study was conducted at the MIT Computer Science and Artificial Intelligence Laboratory. The involvement of multiple researchers is evident from the list of email addresses, highlighting collaboration and networking in this field. Though specific content isn't provided, given the nature of MIT's lab, it likely deals with advanced topics related to computer science and artificial intelligence.

📄 Full Paper Content (ArXiv Source)

📊 논문 시각자료 (Figures)

A Note of Gratitude

The copyright of this content belongs to the respective researchers. We deeply appreciate their hard work and contribution to the advancement of human civilization.