Real-Time Trajectory Planning and Feedback Control for Feedback-Linearizable Systems Using Time-Varying Optimization

📝 Original Paper Info

- Title: Implicit Trajectory Planning for Feedback Linearizable Systems A Time-varying Optimization Approach
- ArXiv ID: 1910.00678
- Date: 2020-03-17
- Authors: Tianqi Zheng, John Simpson-Porco, Enrique Mallada

📝 Abstract

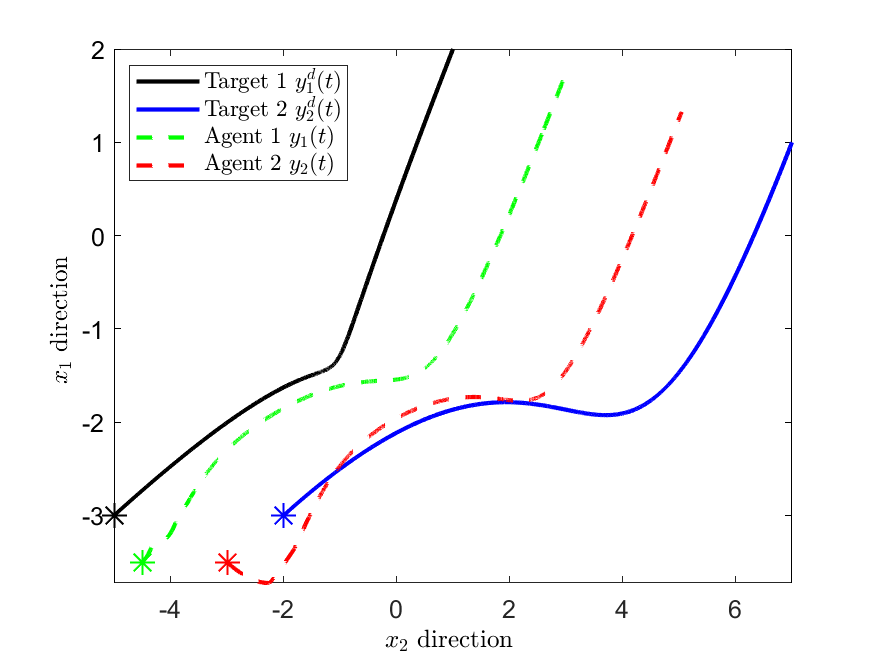
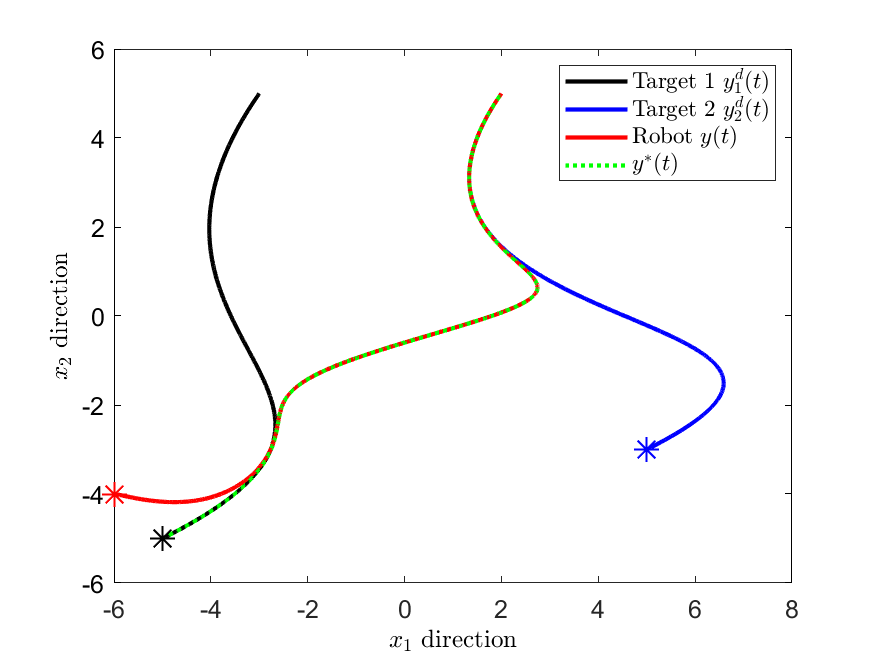
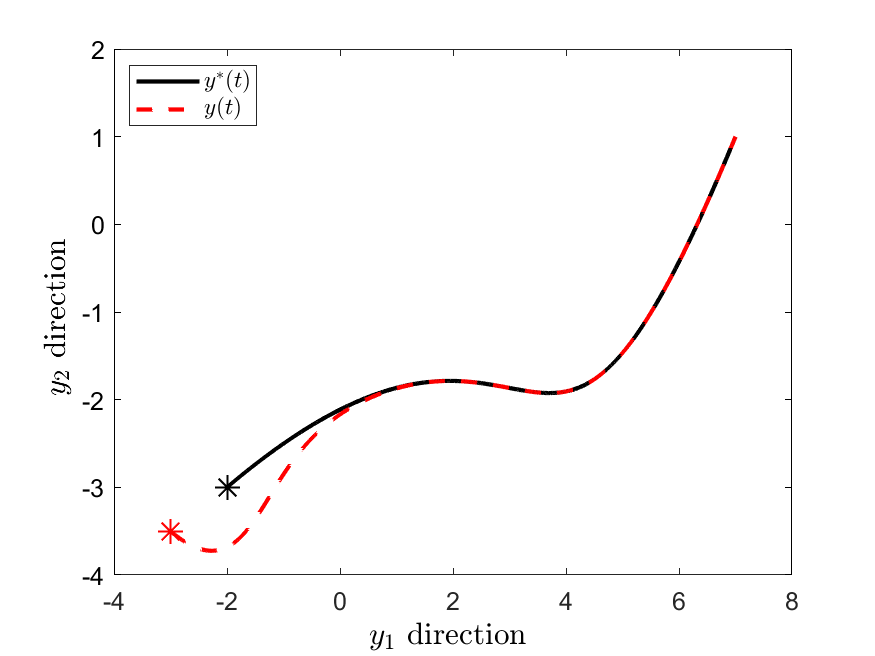
We develop an optimization-based framework for joint real-time trajectory planning and feedback control of feedback-linearizable systems. To achieve this goal, we define a target trajectory as the optimal solution of a time-varying optimization problem. In general, however, such trajectory may not be feasible due to , e.g., nonholonomic constraints. To solve this problem, we design a control law that generates feasible trajectories that asymptotically converge to the target trajectory. More precisely, for systems that are (dynamic) full-state linearizable, the proposed control law implicitly transforms the nonlinear system into an optimization algorithm of sufficiently high order. We prove global exponential convergence to the target trajectory for both the optimization algorithm and the original system. We illustrate the effectiveness of our proposed method on multi-target or multi-agent tracking problems with constraints.

💡 Summary & Analysis

This paper develops an optimization-based framework for real-time trajectory planning and feedback control in systems that can be linearized through feedback. The authors define the target trajectory as the optimal solution of a time-varying optimization problem, which may not always be feasible due to constraints such as nonholonomic constraints. To address this challenge, they design a control law that generates feasible trajectories which asymptotically converge to the target trajectory. For systems that are dynamically fully state linearizable, their proposed method implicitly transforms nonlinear systems into higher-order optimization algorithms. The authors prove global exponential convergence of both the optimization algorithm and the original system to the target trajectory. They demonstrate the effectiveness of this approach in multi-target or multi-agent tracking problems with constraints, indicating its potential application in autonomous vehicles and robotics.

📄 Full Paper Content (ArXiv Source)

📊 논문 시각자료 (Figures)

A Note of Gratitude

The copyright of this content belongs to the respective researchers. We deeply appreciate their hard work and contribution to the advancement of human civilization.