Computer Science / Computational Engineering, Finance, and Science

An Accurate Edge-Based Finite Element Method for Electromagnetic Analysis and Its Applications to Multiscale Structures

Reading time: 3 minute
...
#paper #research

📝 Original Paper Info

- Title: An Accurate Edge-based FEM for Electromagnetic Analysis with Its Applications to Multiscale Structures
- ArXiv ID: 1910.01850
- Date: 2019-10-30
- Authors: Yangfan Zhang, Pengfei Wang, Wenping Li, Shunchuan Yang

📝 Abstract

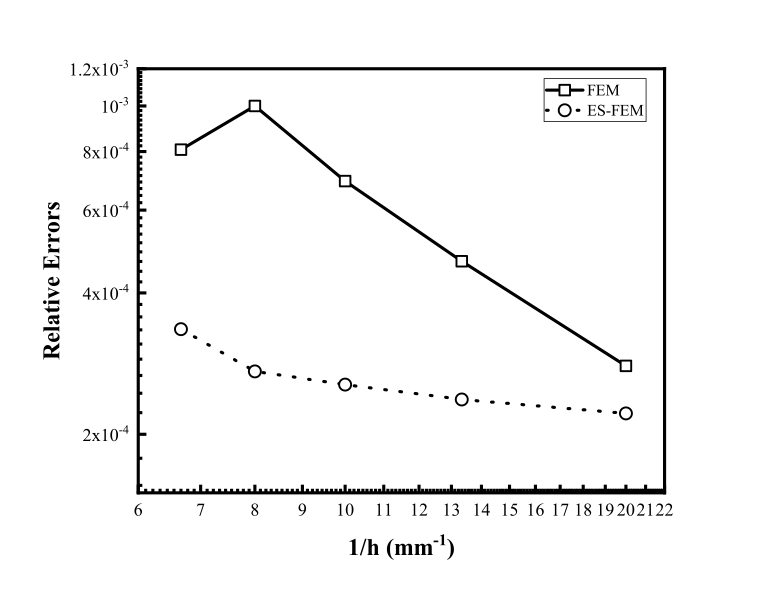
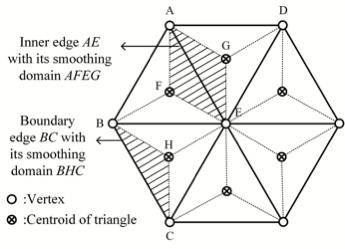
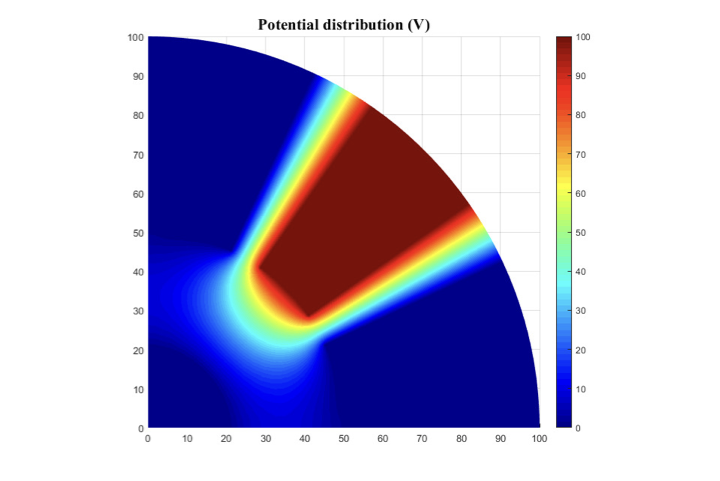
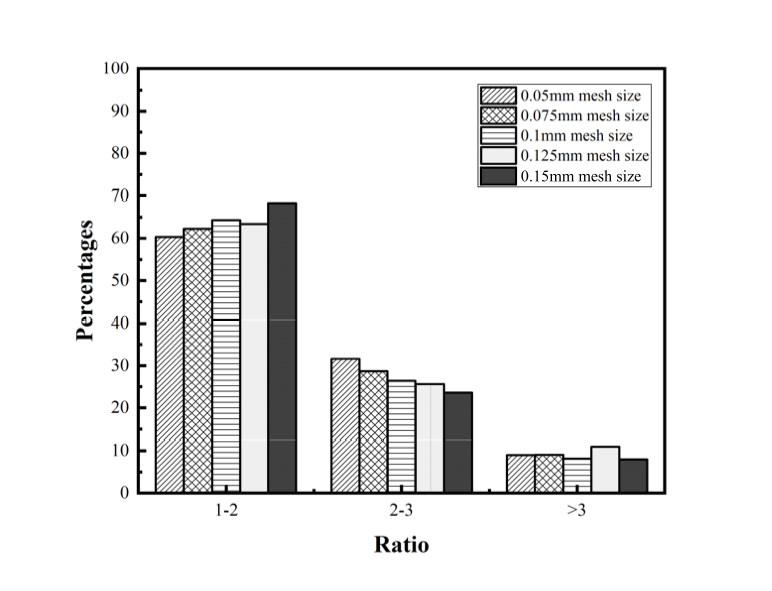
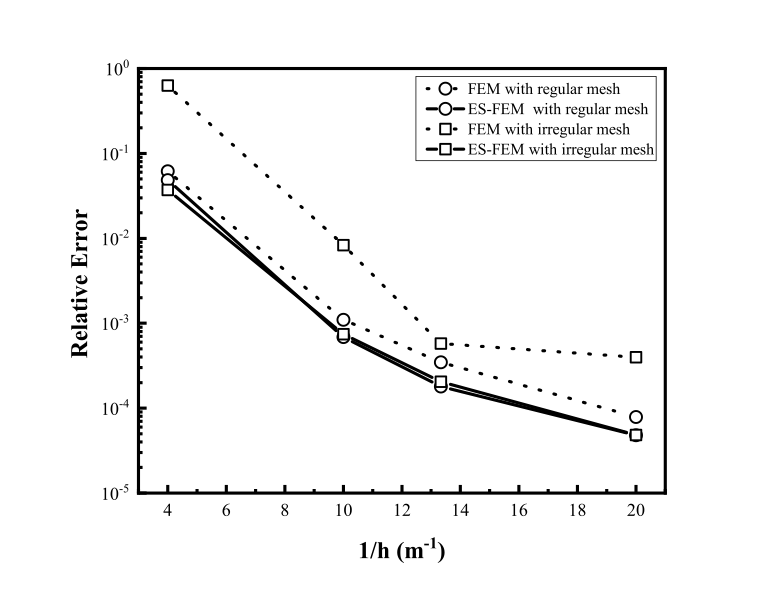
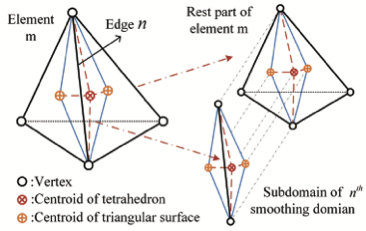
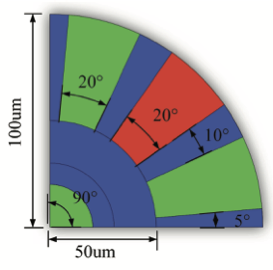
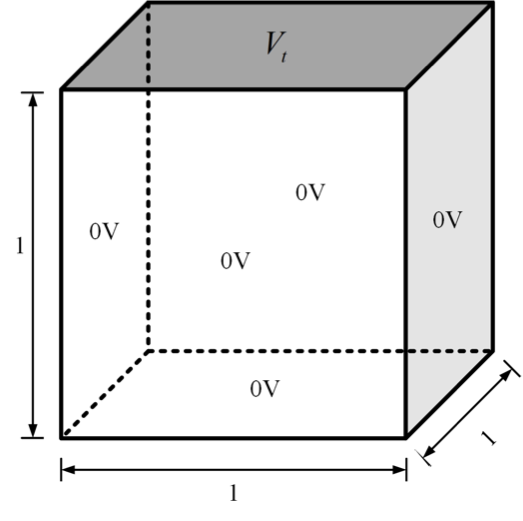
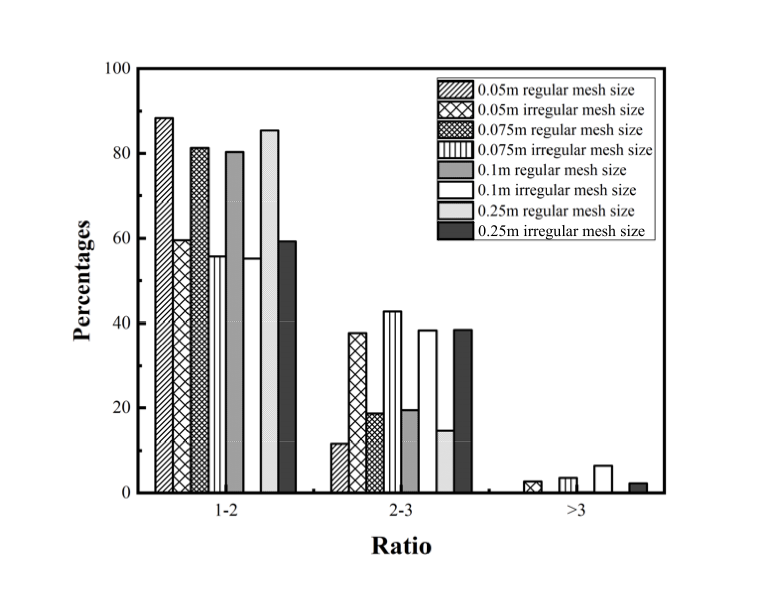
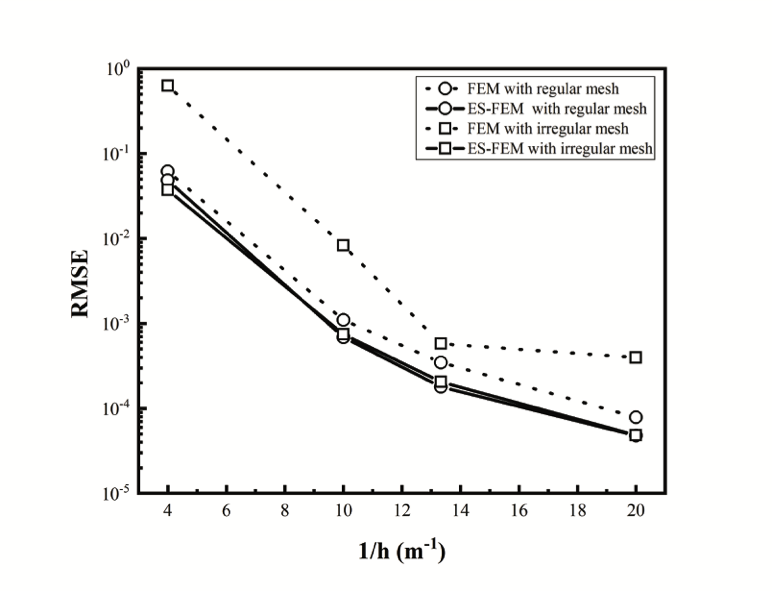
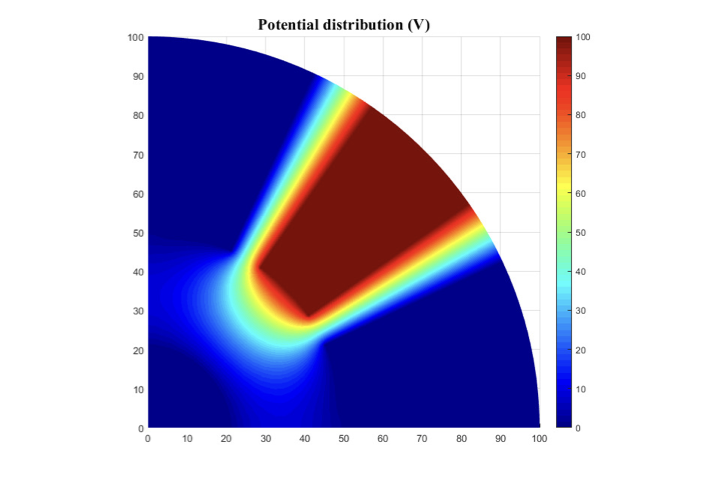
This paper introduces an accurate edge-based smoothed finite element method (ES-FEM) for electromagnetic analysis for both two dimensional cylindrical and three dimensional cartesian systems, which shows much better performance in terms of accuracy and numerical stability for mesh distortion compared with the traditional FEM. Unlike the traditional FEM, the computational domain in ES-FEM is divided into nonoverlapping smoothing domains associated with each edge of elements, triangles in two dimensional domain and tetrahedrons in three dimensional domain. Then, the gradient smoothing technique (GST) is used to smooth the gradient components in the stiff matrix of the FEM. Several numerical experiments are carried out to validate its accuracy and numerical stability. Numerical results show that the ES-FEM can obtain much more accurate results and is almost independent of mesh distortion.

💡 Summary & Analysis

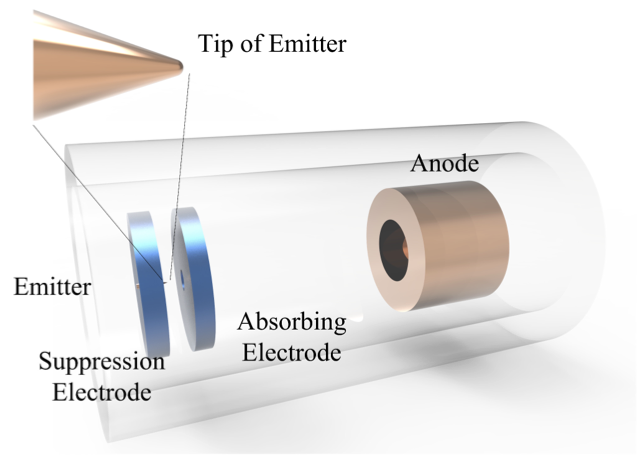
This paper introduces the Edge-based Smoothed Finite Element Method (ES-FEM) for electromagnetic analysis in both 2D cylindrical and 3D Cartesian systems. ES-FEM is designed to offer superior accuracy and numerical stability, especially when dealing with mesh distortion issues that commonly plague traditional FEM approaches. The method divides the computational domain into non-overlapping smoothing domains linked to each edge of elements, using triangles for 2D and tetrahedrons for 3D. A Gradient Smoothing Technique (GST) is then applied to smooth out gradient components in the stiffness matrix of FEM.

The paper conducts several numerical experiments to validate ES-FEM’s accuracy and stability under various mesh distortion conditions. The results show that ES-FEM significantly improves upon traditional methods, providing more accurate solutions with less sensitivity to mesh distortions. This breakthrough has major implications for electromagnetic analysis across diverse applications, including telecommunications equipment design and aerospace engineering.

📄 Full Paper Content (ArXiv Source)

[^1]: This work was supported by the Beijing Natural Science Foundation under Grant 4194082, National Natural Science Foundation of China through Grant 61801010, and Fundamental Research Funds for the Central Universities. *(Corresponding author: Shunchuan Yang)* 
Yangfan Zhang and Shunchuan Yang are with the School of Electronic
and Information Engineering, Beihang University, Beijing, 100191, CN
(e-mail: yfz2018@buaa.edu.cn, scyang@buaa.edu.cn).

Pengfei Wang is with the School of Instrumentation Science and
Opto-electronics Engineering, Beihang University, Beijing, 100191,
CN (e-mail: wangpengfei2013@buaa.edu.cn)

Weiping Li are with the School of Physics, Beihang University,
Beijing, 100191, CN (e-mail: liwp@buaa.edu.cn).

📊 논문 시각자료 (Figures)

Figure 1



Figure 2



Figure 3



Figure 4



Figure 5



Figure 6



Figure 7



Figure 8



Figure 9



Figure 10



Figure 11



Figure 12



Figure 13



Figure 14



Figure 15



Figure 16



Figure 17



Figure 18



A Note of Gratitude

The copyright of this content belongs to the respective researchers. We deeply appreciate their hard work and contribution to the advancement of human civilization.

Related Posts

Start searching

Enter keywords to search articles

↑↓
↵
ESC
⌘K Shortcut