On rank estimators in increasing dimensions
📝 Original Paper Info
- Title: On rank estimators in increasing dimensions- ArXiv ID: 1908.05255
- Date: 2019-08-15
- Authors: Yanqin Fan, Fang Han, Wei Li, Xiao-Hua Zhou
📝 Abstract
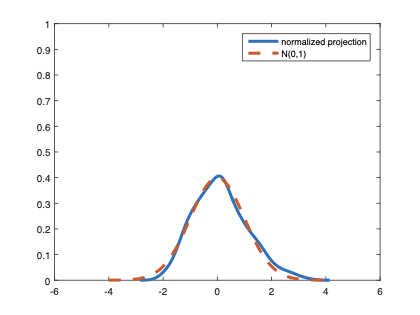
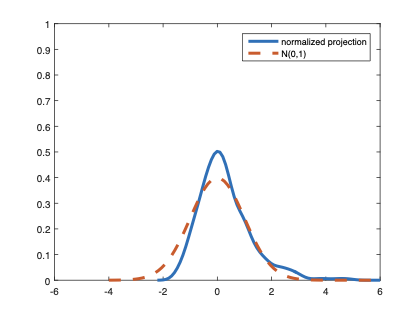
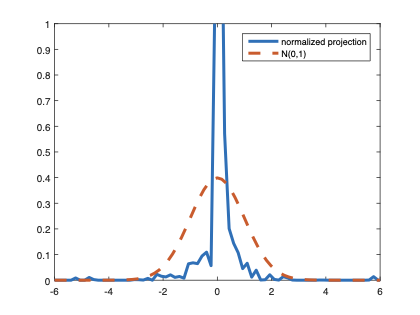
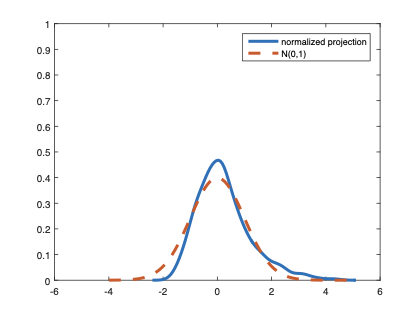
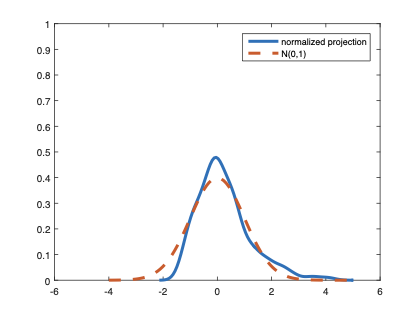
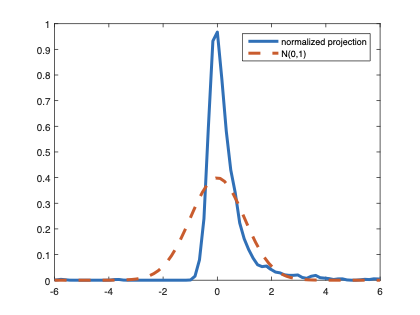
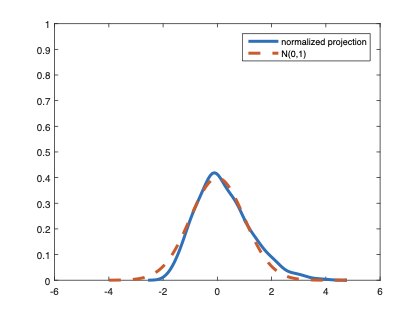
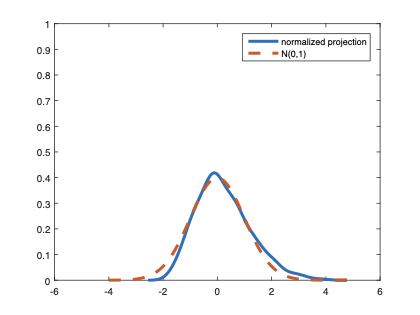
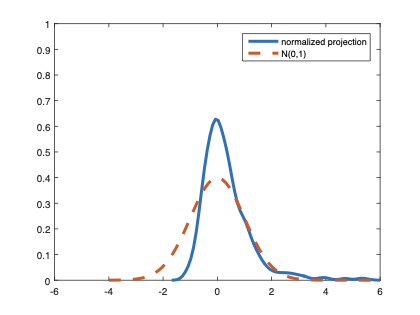
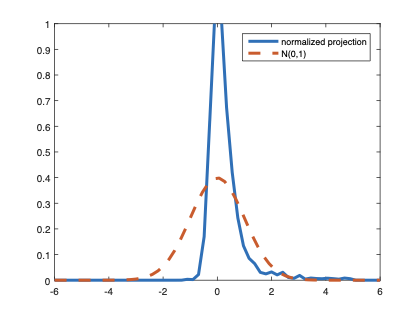
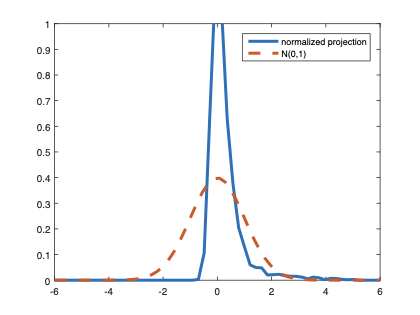
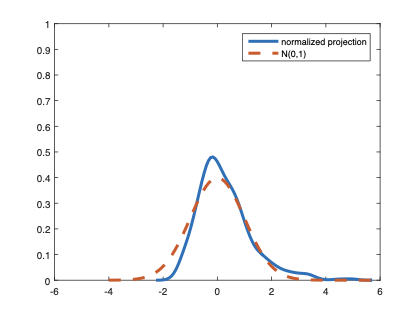
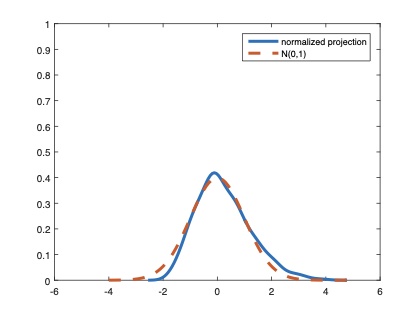
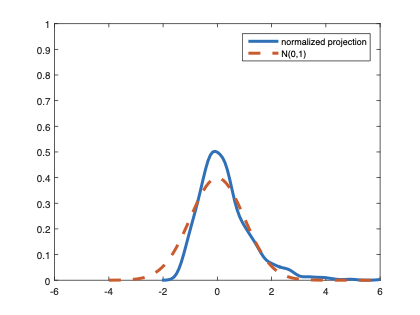
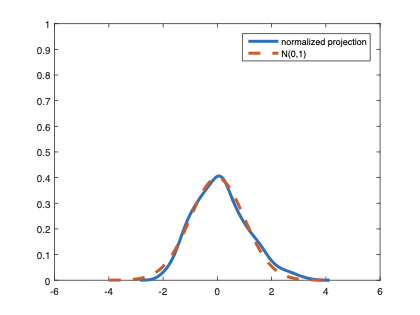
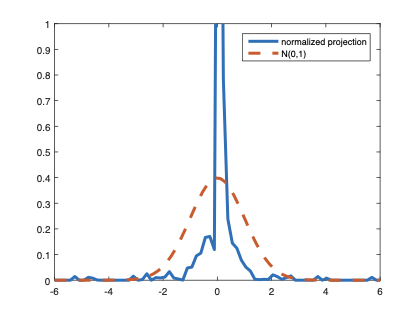
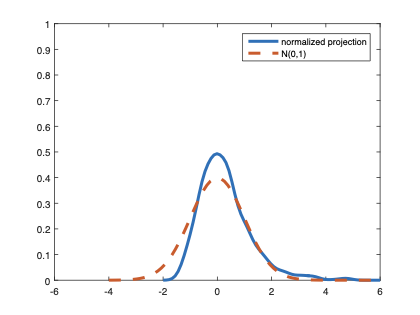
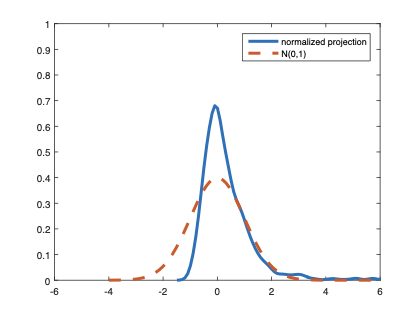
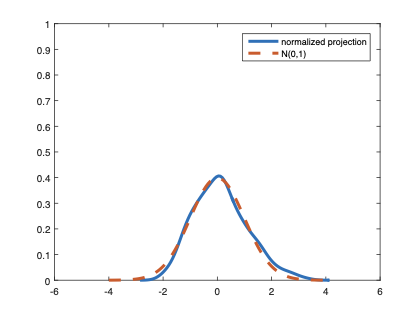
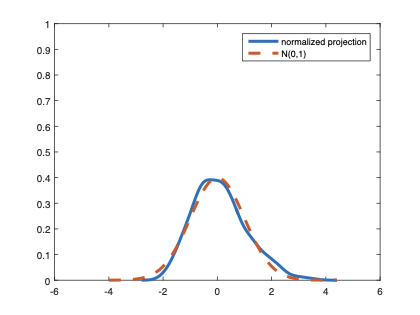
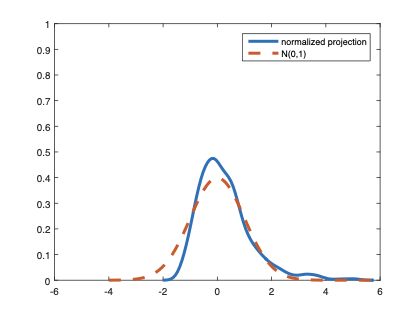
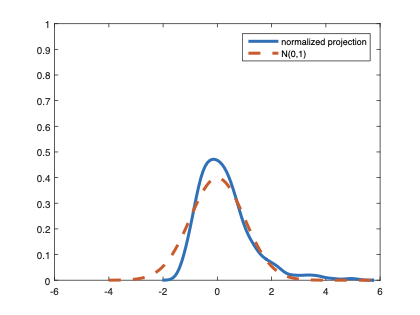
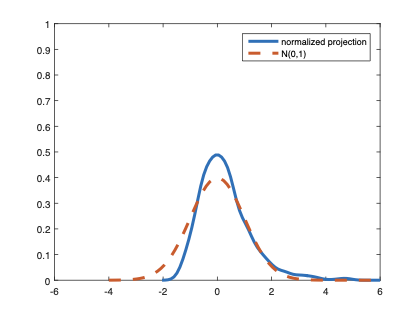
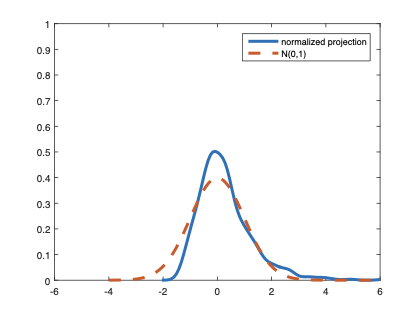
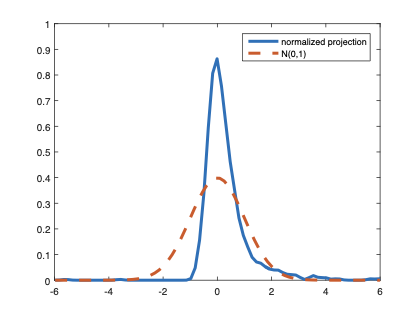
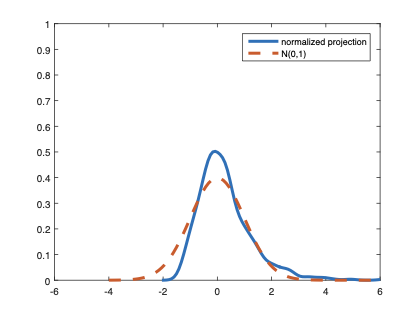
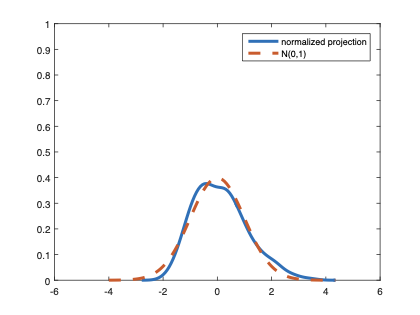
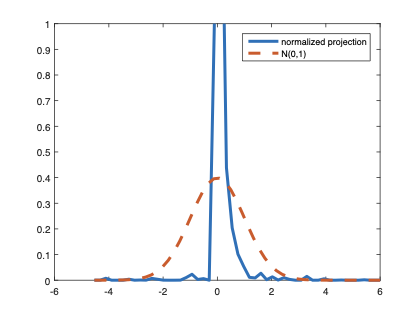
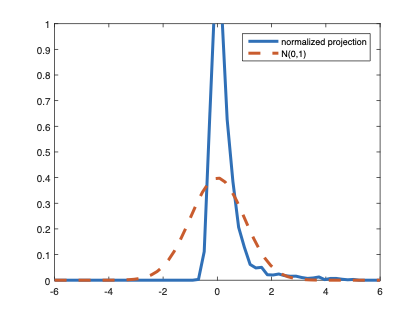
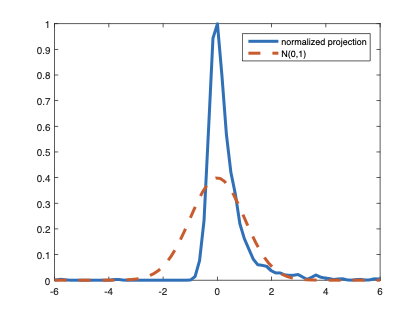
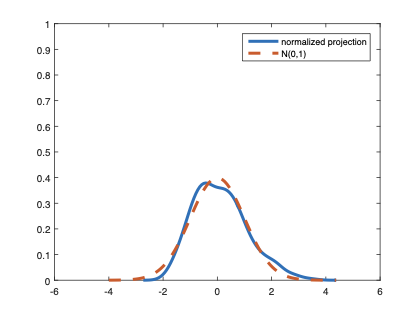
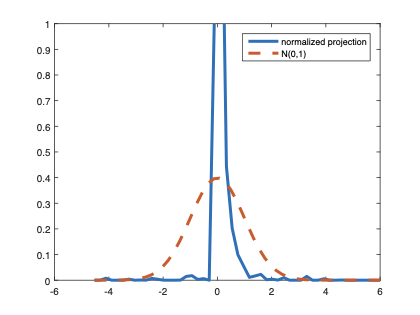
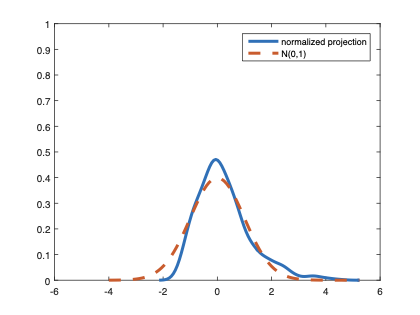
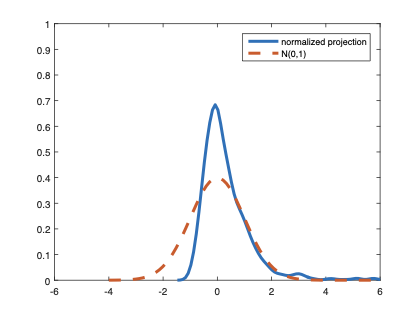
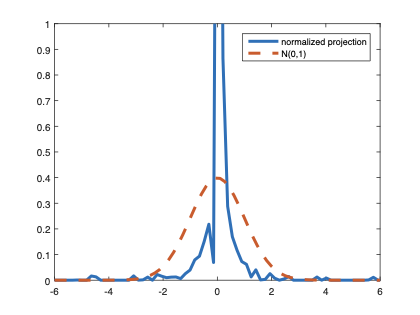
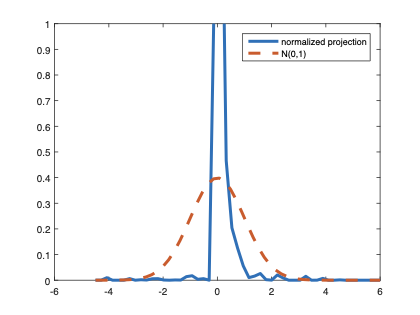
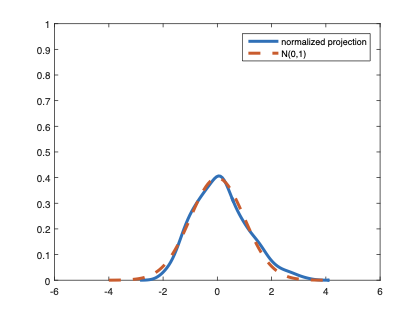
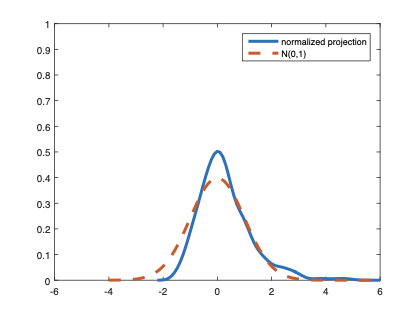
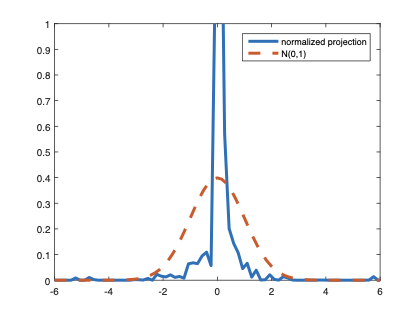
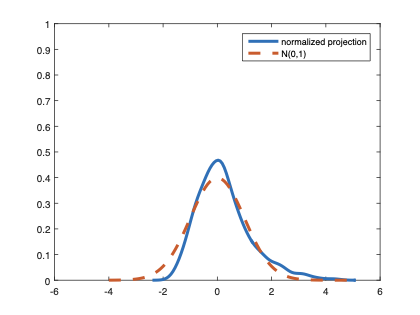
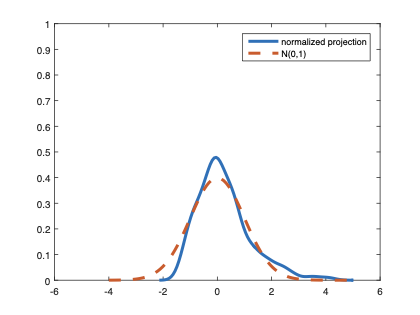
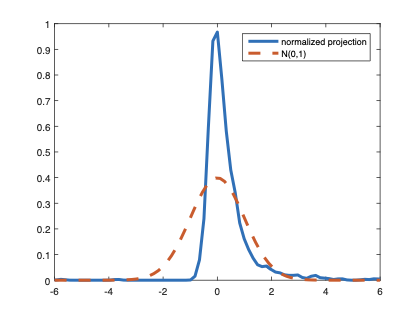
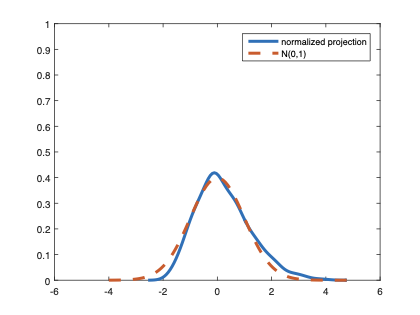
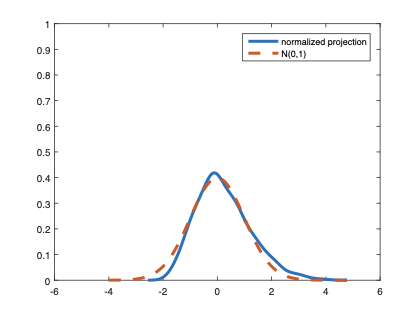
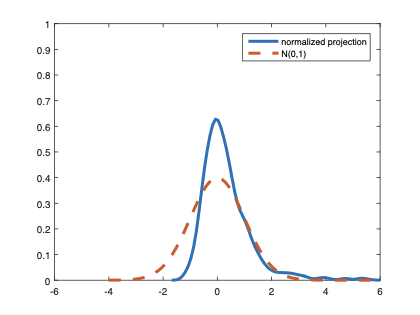
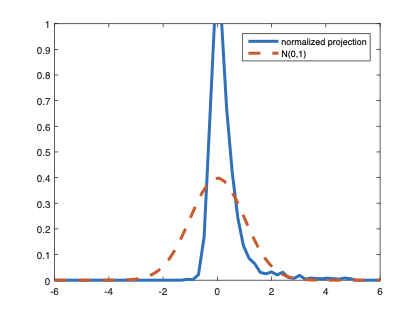
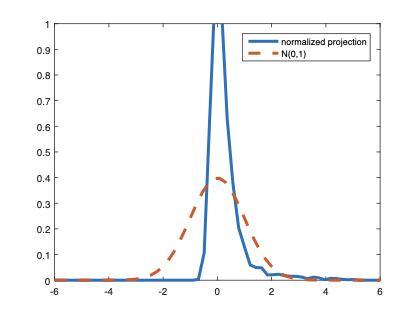
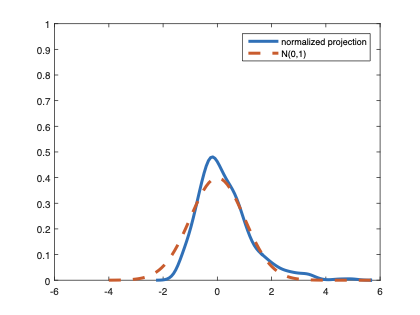
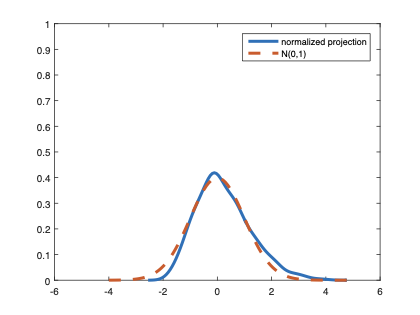
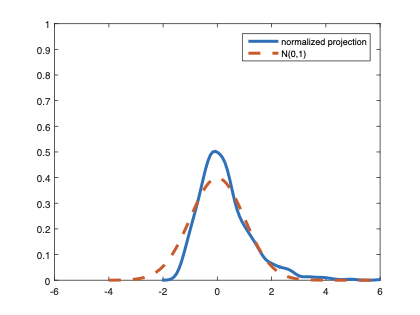
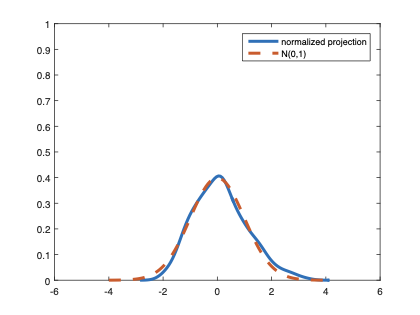
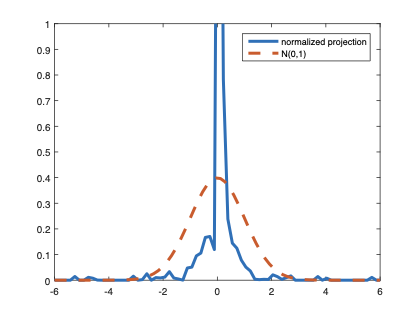
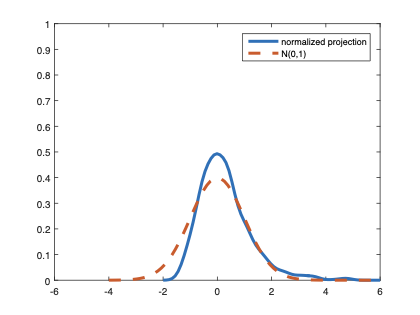
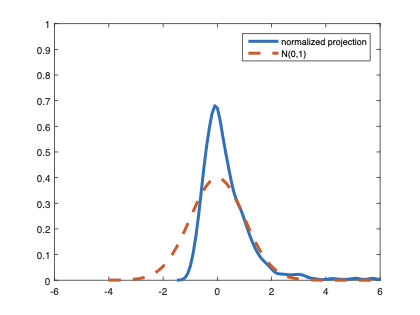
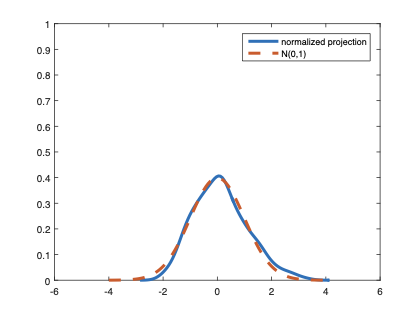
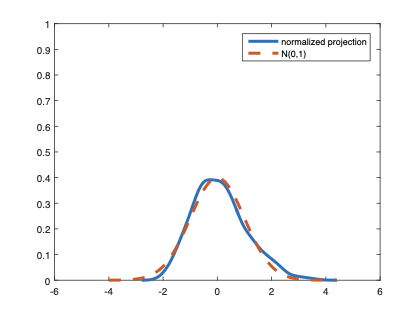
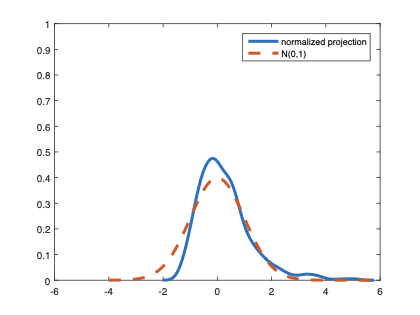
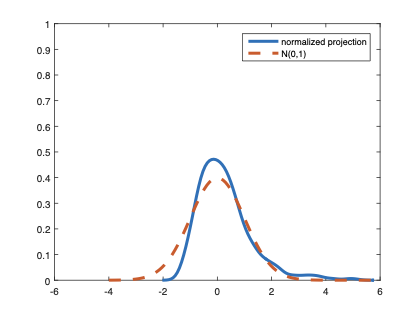
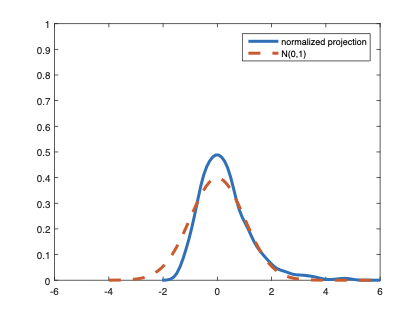
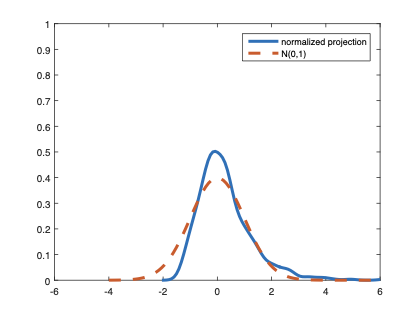
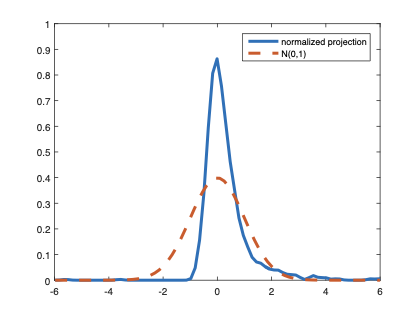
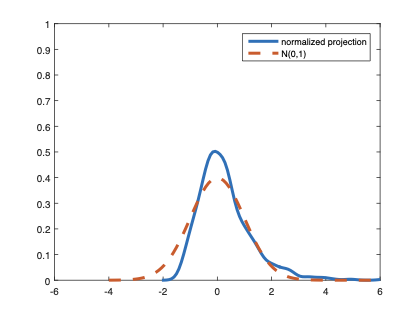
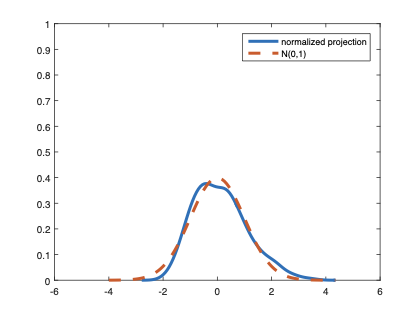
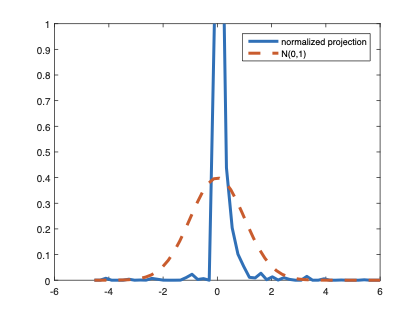
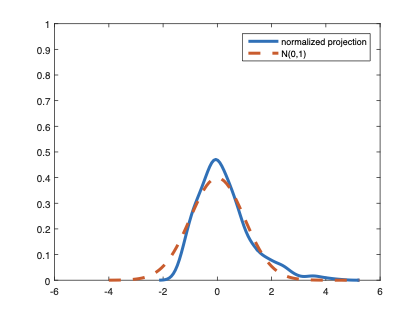
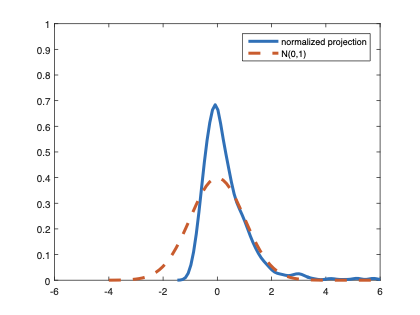
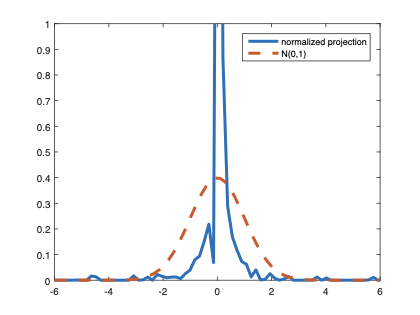
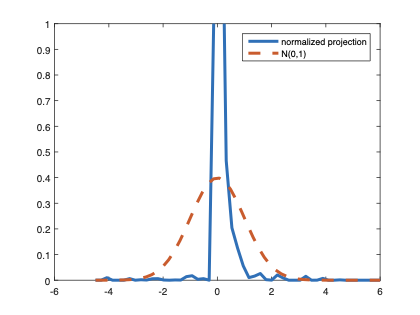
The family of rank estimators, including Han's maximum rank correlation (Han, 1987) as a notable example, has been widely exploited in studying regression problems. For these estimators, although the linear index is introduced for alleviating the impact of dimensionality, the effect of large dimension on inference is rarely studied. This paper fills this gap via studying the statistical properties of a larger family of M-estimators, whose objective functions are formulated as U-processes and may be discontinuous in increasing dimension set-up where the number of parameters, $p_{n}$, in the model is allowed to increase with the sample size, $n$. First, we find that often in estimation, as $p_{n}/n\rightarrow 0$, $(p_{n}/n)^{1/2}$ rate of convergence is obtainable. Second, we establish Bahadur-type bounds and study the validity of normal approximation, which we find often requires a much stronger scaling requirement than $p_{n}^{2}/n\rightarrow 0.$ Third, we state conditions under which the numerical derivative estimator of asymptotic covariance matrix is consistent, and show that the step size in implementing the covariance estimator has to be adjusted with respect to $p_{n}$. All theoretical results are further backed up by simulation studies.💡 Summary & Analysis
...📄 Full Paper Content (ArXiv Source)
📊 논문 시각자료 (Figures)