EXPSPACE-Completeness of Logics K4xS5, S4xS5, and the Logic of Subset Spaces, Part 2 EXPSPACE-Hardness
📝 Original Paper Info
- Title: EXPSPACE-Completeness of the Logics K4xS5 and S4xS5 and the Logic of Subset Spaces, Part 2 EXPSPACE-Hardness- ArXiv ID: 1908.03509
- Date: 2019-08-12
- Authors: Peter Hertling and Gisela Krommes
📝 Abstract
It is known that the satisfiability problems of the product logics K4xS5 and S4xS5 are NEXPTIME-hard and that the satisfiability problem of the logic SSL of subset spaces is PSPACE-hard. We improve these lower bounds for the complexity of these problems by showing that all three problems are EXPSPACE-hard under logspace reduction. In another paper we show that these problems are in ESPACE. This shows that all three problems are EXPSPACE-complete.💡 Summary & Analysis
**Key Summary**: This paper introduces a new procedure for determining if a formula in SSL (Strongly Structured Logic) is satisfiable. Specifically, it defines the binary logic formula $f_\ssl(w)$ based on an input string $w$ and proves that this formula can be computed within logarithmic space.Problem Statement: In SSL, one of the critical problems is to determine whether a given complex logical formula has a satisfying model. Traditional methods were inefficient and did not allow for solutions within logarithmic space.
Solution Approach (Core Technology): The paper proposes defining $f_\ssl(w)$ based on an input string $w$. This binary logic formula can be computed in logarithmic space, providing an efficient way to solve problems in SSL. It outlines a procedure to generate $f_\ssl(w)$ and methods to determine its satisfiability.
Key Results: The paper proves that $f_\ssl(w)$ is computable within logarithmic space and demonstrates how this approach efficiently solves problems in SSL. By presenting new ways to judge the satisfiability of formulas, it enhances understanding of SSL and highlights practical solutions for complex logical issues.
Significance and Utilization: This research significantly improves our understanding and application of SSL by offering an efficient method to solve problems within logarithmic space using $f_\ssl(w)$. It provides a practical approach to simplify and resolve complex logical problems in real-world applications.
📄 Full Paper Content (ArXiv Source)
The satisfiability problem of $`\ssl`$ is $`\EXPSPACE`$-hard under logarithmic space reduction.
As explained before, we are going to show this by showing that any language $`L`$ recognized by an Alternating Turing Machine working in exponential time can be reduced in logarithmic space to the satisfiability problem of $`\ssl`$.
In the following subsection we will first describe the idea of the reduction and then define the reduction function $`f_\ssl`$ in detail. In Subsection 4.2 we will show that it can be computed in logarithmic space. In the final two subsections we are going to show that it is corrrect. First we show that in case $`w\in L`$ the formula $`f_\ssl(w)`$ is $`\ssl`$-satisfiable by explicitly constructing a cross axiom model for $`f_\ssl(w)`$. In the last section we show that if $`f_\ssl(w)`$ is $`\ssl`$-satisfiable then $`w`$ is an element of $`L`$.
Construction of the Formula
Let $`L \in \EXPSPACE`$ be an arbitrary language over some alphabet $`\Sigma`$, that is, $`L \subseteq \Sigma^*`$. We are going to show that there is a logspace computable function $`f_\ssl`$ mapping strings to strings such that, for any $`w\in\Sigma^*`$,
-
$`f_\ssl(w)`$ is a bimodal formula and
-
$`f_\ssl(w)`$ is $`\ssl`$-satisfiable if, and only if, $`w \in L`$.
Once we have shown this, we have shown the result. In order to define this desired reduction function $`f_\ssl`$, we are going to make use of an Alternating Turing Machine for $`L`$. Since $`\EXPSPACE = \mathrm{AEXPTIME}`$, there exist an Alternating Turing Machine $`M = (Q, \Sigma, \Gamma, q_0, \delta)`$ and a univariate polynomial $`p`$ such that $`M`$ accepts $`L`$, that is, $`L(M)=L`$, and such that the time used by $`M`$ on arbitrary input of length $`n`$ is bounded by $`2^{p(n)}-1`$. We can assume without loss of generality $`Q=\{0,\ldots,|Q|-1\}`$, $`\Gamma=\{0,\ldots,|\Gamma|-1\}`$, that the coefficients of the polynomial $`p`$ are natural numbers and that, for all $`n\in\IN`$, we have $`p(n) \geq n`$ and $`p(n)\geq 1`$. In the following, whenever we have fixed some $`n\in\IN`$, we set
N:=p(n) .Let us consider an input word $`w \in\Sigma^n`$ of length $`n`$, for some $`n \in\IN`$, and let us sketch the main idea of the construction of the formula $`f_\ssl(w)`$. The formula $`f_\ssl(w)`$ will describe the possible computations of $`M`$ on input $`w`$ in the following sense: any cross axiom model of $`f_\ssl(w)`$ will essentially contain an accepting tree of $`M`$ on input $`w`$, and if $`w \in L(M)`$ then there exists an accepting tree of $`M`$ on input $`w`$ and one can turn this into a cross axiom model of $`f_\ssl(w)`$. In such a model, any node in an accepting tree of $`M`$ on input $`w`$ will be modeled by a cloud (that is, by an $`\stackrel{L}{\to}`$-equivalence class) in which certain shared variables (we use the notion “shared variables” in the same sense as in Subsection 3.1) will have values that describe the data of the computation node that are important in this computation step. Which data are these? First of all, we need the time of the computation node. We assume that the computation starts with the initial configuration of $`M`$ on input $`w`$ at time $`0`$. Since the ATM $`M`$ needs at most $`2^N-1`$ time steps, we can store the time of each computation node in a binary counter counting from $`0`$ to $`2^N-1`$. Since during each time step at most one additional cell either to the right or to the left of the previous cell can be visited, we can describe any configuration reachable during a computation of $`M`$ on input $`w`$ by the following data:
-
the current content of the tape, which is a string in $`\Gamma^{2 \cdot (2^N-1)+1} = \Gamma^{2^{N+1}-1}`$,
-
the current tape head position, which is a number in $`\{0,\ldots,2^{N+1}-2\}`$.
We assume that in the initial configuration on input $`w`$ the tape content is $`\#^{2^N}w\#^{2^N-1-n}`$ (remember that we use $`\#`$ for the blank symbol) and that the tape head scans the blank $`\#`$ to the left of the first symbol of $`w`$, that is, the position of the tape head is $`2^{N}-1`$. If a cloud in a cross axiom model of $`f_\ssl(w)`$ describes a computation node of $`M`$ on input $`w`$ then in this cloud the following shared variables will have the following values:
-
a vector $`\underline{\alpha}^\mathrm{time}= (\alpha^\mathrm{time}_{N-1},\ldots,\alpha^\mathrm{time}_0)`$ giving in binary the current time of the computation,
-
a vector $`\underline{\alpha}^\mathrm{pos}= (\alpha^\mathrm{pos}_{N},\ldots,\alpha^\mathrm{pos}_0)`$ giving in binary the current position of the tape head,
-
a vector $`\underline{\alpha}^\mathrm{state}= (\alpha^\mathrm{state}_0,\ldots,\alpha^\mathrm{state}_{|Q|-1})`$ giving in unary the current state of the computation (here “unary” means: exactly one of the shared variables $`\alpha^\mathrm{state}_i`$ will be true, namely the one with $`i`$ being the current state),
-
a vector $`\underline{\alpha}^\mathrm{written}= (\alpha^\mathrm{written}_{0},\ldots,\alpha^\mathrm{written}_ {|\Gamma|-1})`$ giving in unary the symbol that has just been written into the cell that has just been left, unless the cloud corresponds to the first node in the computation tree — in that case the value of this vector is irrelevant (here “unary” means: exactly one of the variables $`\alpha^\mathrm{written}_i`$ will be true, namely the one with $`i`$ being the symbol that has just been written),
-
a vector $`\underline{\alpha}^\mathrm{read}= (\alpha^\mathrm{read}_0,\ldots,\alpha^\mathrm{read}_{|\Gamma|-1})`$ giving in unary the symbol in the current cell (here “unary” means: exactly one of the shared variables $`\alpha^\mathrm{read}_i`$ will be true, namely the one with $`i`$ being the symbol in the current cell).
The formula $`f_\ssl(w)`$ has to ensure that for any possible
computation step in an accepting tree starting from such a computation
node there exists a cloud describing the corresponding successor node in
the accepting tree. In this new cloud, the value of the counter for the
time $`\underline{\alpha}^\mathrm{time}`$ has to be incremented. This
can be done by the technique described in
Subsection 3.2 for implementing a binary
counter. In parallel, we have to make sure that in this new cloud also
the vectors $`\underline{\alpha}^\mathrm{pos}`$,
$`\underline{\alpha}^\mathrm{state}`$,
$`\underline{\alpha}^\mathrm{written}`$, and
$`\underline{\alpha}^\mathrm{read}`$ are set to the right values. For
the vectors $`\underline{\alpha}^\mathrm{pos}`$,
$`\underline{\alpha}^\mathrm{state}`$, and
$`\underline{\alpha}^\mathrm{written}`$ these values can be computed
using the corresponding element of the transition relation $`\delta`$ of
the ATM. For example, $`\underline{\alpha}^\mathrm{pos}`$ has to be
decremented by one if the tape head moves to the left, and it has to be
incremented by one if the tape head moves to the right. Also the new
state (to be stored in $`\underline{\alpha}^\mathrm{state}`$) and the
symbol written into the cell that has just been left (to be stored in
$`\underline{\alpha}^\mathrm{written}`$) are determined by the data of
the previous computation node and by the corresponding element of the
transition relation $`\delta`$.
But the vector $`\underline{\alpha}^\mathrm{read}`$ is supposed to
describe the symbol in the current cell. This symbol is not determined
by the current computation step but has either been written the last
time when this cell has been visited during this computation or, when
this cell has never been visited before, the symbol in this cell is
still the one that was contained in this cell before the computation
started. How can one ensure that $`\underline{\alpha}^\mathrm{read}`$ is
set to the right value? If the current cell has never been visited
before, we have to make sure that the value is set to the correct value
describing the inital content of this cell. Otherwise, we make use of
the cross property. The point in the new cloud whose existence is
enforced by the formula must have a cross point in any cloud
corresponding to any previous computation node. The idea is that one of
these cross points picks up the right value in the right cloud. We are
going to make sure that the cloud is identified that corresponds to the
configuration after the previous visit of the same cell during the
computation. Then in the cloud corresponding to this configuration the
value of $`\underline{\alpha}^\mathrm{written}`$ will tell us the symbol
that has been written into the current cell during the previous visit.
In order to identify the correct cloud of the step after the previous
visit of the current cell and to copy the value of the symbol, the
formula $`f_\ssl(w)`$ will ensure that any cloud describing a
computation node will contain a point in which the following
(persistent!) propositional variables have the following values:
-
a vector $`\underline{X}^\mathrm{time}= (X^\mathrm{time}_{N-1},\ldots,X^\mathrm{time}_0)`$ giving in binary the current time of the computation,
-
a vector $`\underline{X}^\mathrm{pos}= (X^\mathrm{pos}_{N},\ldots,X^\mathrm{pos}_0)`$ giving in binary the current position of the tape head, that is the position of the current cell,
-
a vector $`\underline{X}^\mathrm{read}= (X^\mathrm{read}_0,\ldots,X^\mathrm{read}_{|\Gamma|-1})`$ giving in unary the symbol in the current cell, (here “unary” means: exactly one of the variables $`X^\mathrm{read}_i`$ will be true, namely the one with $`i`$ being the symbol in the current cell).
-
a vector $`\underline{X}^{\text{time-apv}}= (X^{\text{time-apv}}_{N-1},\ldots,X^{\text{time-apv}}_0)`$ giving in binary the time one step after the previous visit of the cell, if it has been visited before (“$`\text{time-apv}`$” stands for “time after previous visit”); otherwise this vector will have the binary value $`0`$.
Now we come to the formal definition of the formula $`f_\ssl(w)`$. The formula $`f_\ssl(w)`$ will have the following structure:
\begin{eqnarray*}
f_\ssl(w)
&:= & K\Box \mathit{uniqueness} \\
&& \wedge \mathit{start} \\
&& \wedge K\Box \mathit{time\_after\_previous\_visit} \\
&& \wedge K\Box \mathit{get\_the\_right\_symbol} \\
&& \wedge K\Box \mathit{computation} \\
&& \wedge K\Box \mathit{no\_reject} .
\end{eqnarray*}The formula $`f_\ssl(w)`$ will contain the following propositional variables:
\begin{eqnarray*}
&& B, \\
&& A^\mathrm{time}_{N-1}, \ldots, A^\mathrm{time}_{0},
A^\mathrm{pos}_{N}, \ldots, A^\mathrm{pos}_{0},
A^\mathrm{state}_{0}, \ldots, A^\mathrm{state}_{|Q|-1},
A^\mathrm{written}_{0},\ldots, A^\mathrm{written}_{|\Gamma|-1},
A^\mathrm{read}_{0},\ldots, A^\mathrm{read}_{|\Gamma|-1},\\
&& X^\mathrm{time}_{N-1}, \ldots, X^\mathrm{time}_{0},
X^{\text{time-apv}}_{N-1},\ldots, X^{\text{time-apv}}_{0},
X^\mathrm{pos}_{N}, \ldots, X^\mathrm{pos}_{0},
X^\mathrm{read}_{0},\ldots, X^\mathrm{read}_{|\Gamma|-1}.
\end{eqnarray*}For $`\mathit{string} \in\{\mathrm{time}, \mathrm{pos}, \mathrm{state}, \mathrm{written}, \mathrm{read}\}`$ and natural numbers $`k`$ we define
\alpha^\mathit{string}_k := L(A^\mathit{string}_k \wedge \Box L B).These formulas $`\alpha^\mathit{string}_k`$ are the shared variables we talked about above. We are now going to define the subformulas of $`f_\ssl(w)`$. We will use the abbreviations introduced above, in Table [table:abbrev1], and in Table 1.
| For | the following | is an abbreviation |
| expression | of the following formula | |
| $`l\geq 1`$ | $`\mathrm{unique}(\underline{F})`$ | $`\bigvee_{k=0}^{l-1} F_k \wedge \bigwedge_{k=0}^{l-1}\bigwedge_{m=k+1}^{l-1} \neg (F_k \wedge F_m)`$ |
| $`l\geq 1`$ | $`(\underline{F} \neq \underline{G})`$ | $`\neg (\underline{F} = \underline{G})`$ |
| $`l\geq 1`$ | $`(\underline{F} < \underline{G})`$ | $`\bigvee_{k=0}^{l-1} \left( (\underline{F}=\underline{G},>k) \wedge \neg F_k \wedge G_k \right)`$ |
| $`l\geq 1`$ | $`(\underline{F} \leq \underline{G})`$ | $`(\underline{F} < \underline{G}) \vee (\underline{F} = \underline{G})`$ |
| $`l\geq 1`$ | $`(\underline{F} = \underline{G} + 1)`$ | $`\bigvee_{k=0}^{l-1} \bigl( (\underline{F}=\underline{G},>k)`$ |
| $`\wedge \mathrm{rightmost\_one}(\underline{F},k)`$ | ||
| $`\wedge \mathrm{rightmost\_zero}(\underline{G},k) \bigr)`$ | ||
| $`l\geq 1`$ | $`(\underline{F} \neq \underline{G} + 1)`$ | $`\neg (\underline{F} = \underline{G} + 1)`$ |
| $`l\geq 1`$, $`0\leq i < 2^l`$ | $`(\underline{F}<\mathrm{bin}_l(i))`$ | $`\bigvee_{k \in \mathrm{Ones}(i)} \bigl( \neg F_k |
| \wedge \bigwedge_{h \in {k+1,\ldots,l-1}\setminus\mathrm{Ones}(i)} \neg F_h\bigr)`$ | ||
| $`l\geq 1`$, $`0\leq i < 2^l`$ | $`(\underline{F}\leq\mathrm{bin}_l(i))`$ | $`(\underline{F}<\mathrm{bin}_l(i)) \vee (\underline{F}=\mathrm{bin}_l(i))`$ |
| $`l\geq 1`$, $`0\leq i < 2^l`$ | $`(\underline{F}>\mathrm{bin}_l(i))`$ | $`\neg (\underline{F}\leq\mathrm{bin}_l(i))`$ |
Some (partially numerical) abbreviations for logical formulas, where $`\underline{F}=(F_{l-1},\ldots,F_0)`$ and $`\underline{G}=(G_{l-1},\ldots,G_0)`$ are vectors of formulas. An empty conjunction like $`\bigwedge_{h=0}^{-1} F_h`$ can be replaced by any propositional formula that is true always. An empty disjunction like $`\bigvee_{h=0}^{-1} F_h`$ can be replaced by any propositional formula that is false always.
The models of the formula $`f_\ssl(w)`$ will contain certain “information” points that will realize an accepting tree of $`M`$ on input $`w`$ if, and only if, $`w\in L`$. Besides these information points there will also be other, “auxiliary”, points (and an $`\stackrel{L}{\to}`$-equivalence class not containing any information points) whose sole purpose is to make the mechanism of shared variables work. In several formulas we need to distinguish between the information points and the other, auxiliary, points. It turns out that this can be done simply by the truth value of the propositional variable $`B`$.
The following formula makes sure that in each of the vectors of shared variables that describe in a unary way the current state respectively the written symbol respectively the current symbol, exactly one shared variable is true:
\begin{eqnarray*}
\mathit{uniqueness}&:=& B \rightarrow
\bigl( \mathrm{unique}({\underline{\alpha}^\mathrm{state}})
\wedge \mathrm{unique}({\underline{\alpha}^\mathrm{written}})
\wedge \mathrm{unique}({\underline{\alpha}^\mathrm{read}}) \bigr).
\end{eqnarray*}The vector $`\underline{X}^\mathrm{read}`$ will satisfy the same uniqueness condition automatically.
The following formula ensures that the variables in the cloud corresponding to the first node in a computation tree get the correct values. The computation starts at time $`0`$ with the tape head at position $`2^N-1`$ and in the state $`q_0`$ and with the blank symbol $`\#`$ in the current cell.
\mathit{start}
:= B \wedge (\underline{\alpha}^\mathrm{time}=\bin_N(0))
\wedge (\underline{\alpha}^\mathrm{pos}=\bin_{N+1}(2^N-1))
\wedge \alpha^\mathrm{state}_{q_0}
\wedge \alpha^\mathrm{read}_{\#} .The following formula ensures that the vector $`\underline{X}^{\text{time-apv}}`$ stores the time after the previous visit of the same cell, if it has been visited before. If it has never been visited before, this vector gets the binary value $`0`$.
\begin{eqnarray*}
\lefteqn{\mathit{time\_after\_previous\_visit}} && \\
&:=& B \rightarrow \Biggl(
\Bigl( \underline{X}^{\text{time-apv}} \leq \underline{X}^\mathrm{time} \Bigr) \\
&& \wedge \Bigl( ( \underline{\alpha}^\mathrm{time} < \underline{X}^\mathrm{time}
\wedge \underline{\alpha}^\mathrm{pos} \neq \underline{X}^\mathrm{pos} )
\rightarrow (\underline{X}^{\text{time-apv}} \neq \underline{\alpha}^\mathrm{time} + 1) \Bigr) \\
&& \wedge \Bigl( ( \underline{\alpha}^\mathrm{time} < \underline{X}^\mathrm{time}
\wedge \underline{\alpha}^\mathrm{pos} = \underline{X}^\mathrm{pos})
\rightarrow (\underline{\alpha}^\mathrm{time} < \underline{X}^{\text{time-apv}}) \Bigr) \Biggr) .
\end{eqnarray*}We explain this formula. The time $`\underline{X}^{\text{time-apv}}`$ after the previous visit of the current cell $`\underline{X}^\mathrm{pos}`$ is certainly at most as large as the current time $`\underline{X}^\mathrm{time}`$. When during the computation at an earlier time a cell has been visited that is different from the current one then one plus the time of that visit is certainly not the time after the previous visit of the current cell. When during the computation at an earlier time the current cell has been visited then the time of that visit is a strict lower bound for the time after the previous visit of the current cell. Together these conditions ensure that $`\underline{X}^{\text{time-apv}}`$ gets the correct value.
The following formula ensures that the vector $`\underline{X}^\mathrm{read}`$ stores (in unary form) the symbol in the current cell.
\begin{eqnarray*}
\lefteqn{\mathit{get\_the\_right\_symbol}} && \\
&:= &
\Biggl(\bigl(B \wedge (\underline{X}^{\text{time-apv}}=\mathrm{bin}_N(0))\bigr)
\rightarrow \\
&&\quad\Bigl(
\bigwedge_{i=1}^n ( (\underline{X}^\mathrm{pos}=\mathrm{bin}_{N+1}(2^{N}-1+i))
\rightarrow X^\mathrm{read}_{w_i} ) \\
&&\quad\;
\wedge ( (\underline{X}^\mathrm{pos} \leq \mathrm{bin}_{N+1}(2^{N}-1))
\vee (\underline{X}^\mathrm{pos} > \mathrm{bin}_{N+1}(2^{N}-1+n)))
\rightarrow X^\mathrm{read}_{\#} \Bigr) \Biggr) \\
&&\wedge \Biggl( \bigl(B \wedge (\underline{X}^{\text{time-apv}} > \mathrm{bin}_N(0))
\wedge (\underline{\alpha}^\mathrm{time} = \underline{X}^{\text{time-apv}})\bigr)
\rightarrow (\underline{X}^\mathrm{read}=\underline{\alpha}^\mathrm{written}) \Biggr) .
\end{eqnarray*}We explain this formula. If the current cell has never before been visited (this is the case iff the vector $`\underline{X}^{\text{time-apv}}`$ has the binary value $`0`$) then the vector $`\underline{X}^\mathrm{read}`$ is forced to store in unary format the initial symbol in the current cell. This is either a symbol $`w_i`$ of the input string or the blank $`\#`$. If the current cell has been visited before (this is the case iff the vector $`\underline{X}^{\text{time-apv}}`$ has a binary value strictly greater than $`0`$) then in the cloud corresponding to the time stored in $`\underline{X}^{\text{time-apv}}`$ the vector $`\underline{\alpha}^\mathrm{written}`$ describes the symbol that has been written into the current cell during the previous visit. Therefore, this value is copied into the vector $`\underline{X}^\mathrm{read}`$.
Next, we wish to define the formula $`\mathit{computation}`$ that describes the computation steps. We have to distinguish between the two cases whether the tape head is going to move to the left or to the right. If in a computation step the symbol $`\theta\in\Gamma`$ is written into the current cell, if the tape head moves to the right, and if the new state after this step is the state $`r \in Q`$, then the following formula guarantees the existence of a point and its cloud with suitable values in the shared variables and in the persistent propositional variables.
\begin{eqnarray*}
\lefteqn{\mathit{compstep}_{\mathrm{right}}(r,\theta)} && \\
&:=& \bigwedge_{k=0}^{N-1} \bigwedge_{l=0}^{N}
\Biggl( \bigl( B \wedge \mathrm{rightmost\_zero}(\underline{\alpha}^\mathrm{time},k)
\wedge \mathrm{rightmost\_zero}(\underline{\alpha}^\mathrm{pos},l) \bigr) \\
&& \rightarrow L \biggl( B \wedge (\underline{X}^\mathrm{time}=\underline{\alpha}^\mathrm{time},>k)
\wedge \mathrm{rightmost\_one}(\underline{X}^\mathrm{time},k) \\
&& \phantom{\rightarrow L \biggl(} \wedge (\underline{X}^\mathrm{pos}=\underline{\alpha}^\mathrm{pos},>l)
\wedge \mathrm{rightmost\_one}(\underline{X}^\mathrm{pos},l) \\
&& \phantom{\rightarrow L \biggl(}\wedge \Diamond \bigl(
(\underline{\alpha}^\mathrm{time}=\underline{X}^\mathrm{time})
\wedge (\underline{\alpha}^\mathrm{pos}=\underline{X}^\mathrm{pos})
\wedge \alpha^\mathrm{state}_{r} \wedge \alpha^\mathrm{written}_\theta
\wedge (\underline{\alpha}^\mathrm{read}=\underline{X}^\mathrm{read}) \bigr) \bigg) \Biggr).
\end{eqnarray*}We explain this formula. The procedure is quite similar to the one of the formula $`\mathrm{counter}_{SSL,n}`$ in Subsection 3.2 for a binary counter. The first three lines of the formula make sure that there is a point in the same cloud as the current point such that in this new point the binary value of the persistent variable vector $`\underline{X}^\mathrm{time}`$ is larger by one than the binary value of the shared variable vector $`\underline{\alpha}^\mathrm{time}`$ and that in this new point the binary value of the persistent variable vector $`\underline{X}^\mathrm{pos}`$ is larger by one than the binary value of the shared variable vector $`\underline{\alpha}^\mathrm{pos}`$. The last two lines ensure the existence of a $`\stackrel{\Diamond}{\to}`$-successor of this new point in which the shared variable vectors $`\underline{\alpha}^\mathrm{time}`$, $`\underline{\alpha}^\mathrm{pos}`$, $`\underline{\alpha}^\mathrm{state}`$, $`\underline{\alpha}^\mathrm{written}`$, and $`\underline{\alpha}^\mathrm{read}`$ get the correct new values.
If in a computation step the symbol $`\theta\in\Gamma`$ is written into the current cell, if the tape head moves to the left, and if the new state after this step is the state $`r \in Q`$, then the following formula guarantees the existence of a point and its cloud with suitable values in the shared variables and in the persistent propositional variables.
\begin{eqnarray*}
\lefteqn{\mathit{compstep}_{\mathrm{left}}(r,\theta)} && \\
&:=& \bigwedge_{k=0}^{N-1} \bigwedge_{l=0}^{N}
\Biggl( \bigl( B \wedge \mathrm{rightmost\_zero}(\underline{\alpha}^\mathrm{time},k)
\wedge \mathrm{rightmost\_one}(\underline{\alpha}^\mathrm{pos},l) \bigr) \\
&& \rightarrow L \biggl( B \wedge (\underline{X}^\mathrm{time}=\underline{\alpha}^\mathrm{time},>k)
\wedge \mathrm{rightmost\_one}(\underline{X}^\mathrm{time},k) \\
&& \phantom{\rightarrow L \biggl(} \wedge (\underline{X}^\mathrm{pos}=\underline{\alpha}^\mathrm{pos},>l)
\wedge \mathrm{rightmost\_zero}(\underline{X}^\mathrm{pos},l) \\
&& \phantom{\rightarrow L \biggl(} \wedge \Diamond \bigl(
(\underline{\alpha}^\mathrm{time}=\underline{X}^\mathrm{time})
\wedge (\underline{\alpha}^\mathrm{pos}=\underline{X}^\mathrm{pos})
\wedge \alpha^\mathrm{state}_{r} \wedge \alpha^\mathrm{written}_\theta
\wedge (\underline{\alpha}^\mathrm{read}=\underline{X}^\mathrm{read}) \bigr) \bigg) \Biggr).
\end{eqnarray*}This formula is very similar to the previous one with the exception that here the binary counter for the position of the tape head is decremented.
The computation is modeled by the following subformula. Remember that $`Q`$ is the disjoint union of the sets $`\{q_{\mathrm{accept}}\}`$, $`\{q_{\mathrm{reject}}\}`$, $`Q_{\forall}`$, $`Q_{\exists}`$.
\begin{eqnarray*}
\mathit{computation}
&:=& \bigwedge_{q \in Q_\forall} \bigwedge_{\eta \in\Gamma}
\Biggl( (\alpha^\mathrm{state}_q \wedge \alpha^\mathrm{read}_\eta) \rightarrow \\
&& \biggl( \bigwedge_{(r,\theta,\mathit{left}) \in \delta(q,\eta)} \mathit{compstep}_{\mathrm{left}}(r,\theta)
\wedge \bigwedge_{(r,\theta,\mathit{right}) \in \delta(q,\eta)} \mathit{compstep}_{\mathrm{right}}(r,\theta) \biggr) \Biggr) \\
&& \wedge \bigwedge_{q \in Q_\exists} \bigwedge_{\eta \in\Gamma}
\Biggl( (\alpha^\mathrm{state}_q \wedge \alpha^\mathrm{read}_\eta) \rightarrow \\
&& \biggl( \bigvee_{(r,\theta,\mathit{left}) \in \delta(q,\eta)} \mathit{compstep}_{\mathrm{left}}(r,\theta)
\vee \bigvee_{(r,\theta,\mathit{right}) \in \delta(q,\eta)} \mathit{compstep}_{\mathrm{right}}(r,\theta) \biggr) \Biggr) \Biggr) .
\end{eqnarray*}Finally, the subformula $`\mathit{no\_reject}`$ is defined as follows.
\mathit{no\_reject} :=
\neg \alpha^\mathrm{state}_{q_\mathrm{reject}} .We have completed the description of the formula $`f_\ssl(w)`$ for $`w\in \Sigma^*`$. It is clear that $`f_\ssl(w)`$ is a bimodal formula, for any $`w \in\Sigma^*`$. We still have to show two claims:
-
The function $`f_\ssl`$ can be computed in logarithmic space.
-
For any $`w \in\Sigma^*`$,
MATHw \in L \iff \text{ the bimodal formula $f_\ssl(w)$ is $\ssl$-satisfiable.}Click to expand and view more
The first claim will be shown in the following section. The two directions of the second claim will be shown separately in Subsections 4.3 and 4.4.
LOGSPACE Computability of the Reduction
For the first claim, we observe that there are three kinds of subformulas of $`f_\ssl(w)`$:
-
subformulas that do not depend on the input string $`w`$ at all,
-
subformulas that depend only on the length $`n`$ of the input string $`w`$ but not on its symbols $`w_1,\ldots,w_n`$,
-
subformulas that depend on the particular symbols $`w_1,\ldots,w_n`$ of the input string $`w`$.
The subformula $`K\Box \mathit{uniqueness}`$ is of the first type. Therefore, it can be written using only a constant amount of workspace. And there is only one subformula of the third type, the subformula $`K\Box \mathit{get\_the\_right\_symbol}`$. All other subformulas are of the second type. All of them contain vectors of propositional variables of length at most $`N+1`$ or conjunctions or disjunctions of length at most $`N+1`$, where $`N=p(n)`$. And all of these vectors and lists of conjunctions or disjunctions have a very regular structure. This applies also to the only subformula of the third type. This regular structure makes it possible to write down these formulas using a fixed (that means: independent of the input string $`w`$) number of counters that can count up to $`N`$. But such counters can be implemented in binary using not more than $`O(\log N) = O(\log n)`$ space. Hence, given a string $`w`$, the whole formula $`f_\ssl(w)`$ can be computed using not more than logarithmic space.
Construction of a Model
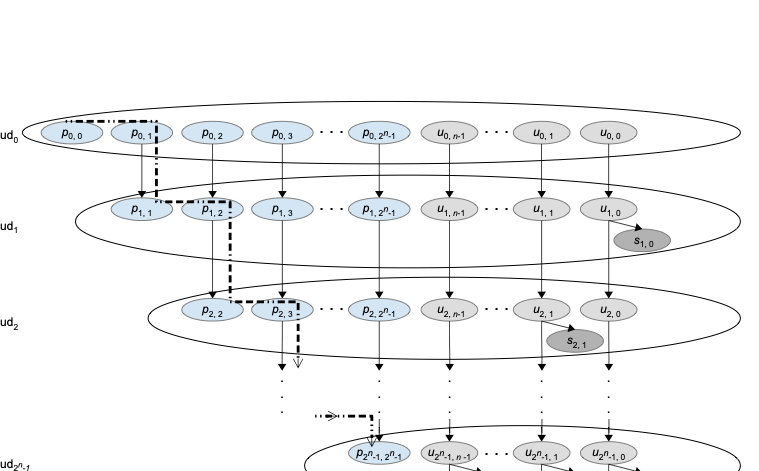
We come to the second claim. First, we show the direction from left to right. Let us assume $`w \in L`$. We will construct a cross axiom model $`(W,\stackrel{L}{\to},\stackrel{\Diamond}{\to},\sigma)`$ with a point $`p_{\mathit{root},\mathit{root}} \in W`$ such that $`p_{\mathit{root},\mathit{root}} \models f_\ssl(w)`$. There exists an accepting tree $`T=(V,E,c)`$ of $`M`$ on input $`w`$, where $`V`$ is the set of nodes of $`T`$, where $`E \subseteq V\times V`$ is the set of edges, and where the function $`c:V\to Q \times \{0,\ldots,2^{N+1}-2\}\times \Gamma^{2^{N+1}-1}`$ labels each node with a configuration (remember the discussion about the description of configurations at the beginning of Subsection 4.1). Let $`\mathit{root} \in V`$ be the root of $`T`$. The set $`W`$ is defined to be the (disjoint) union of the following three sets $`P`$, $`U`$, and $`S`$. We define
P:=\{p_{v,x} ~:~ v,x \in V \text{ and } v E^* x \} .For the definition of $`U`$ we use the following set as an index set:
\begin{eqnarray*}
I &:=& (\{\mathrm{time}\} \times \{0,\ldots,N-1\}) \\
&& \cup (\{\mathrm{pos}\} \times \{0,\ldots,N\}) \\
&& \cup (\{\mathrm{state}\} \times Q) \\
&& \cup (\{\mathrm{written}\} \times \Gamma) \\
&& \cup (\{\mathrm{read}\} \times \Gamma) .
\end{eqnarray*}We define
U := \{u_{v,\mathit{string},z} ~:~ v\in V \cup\{\top\}, (\mathit{string},z) \in I\}where $`\top`$ is a special element not contained in $`V`$. We extend the binary relation $`E^*`$ on $`V`$ to a binary relation $`\widetilde{E}`$ on $`V\cup\{\top\}`$ by
\widetilde{E} := \{(u,v) \in (V\cup\{\top\}) \times (V\cup\{\top\}) ~:~
\text{ either } (u,v \in V \text{ and } uE^*v) \text{ or } v=\top \}.We define the set $`S`$ by
\begin{eqnarray*}
S &:=& \{ s_{v,\mathrm{time},k} ~:~ v \in V, k \in \mathrm{Ones}(\mathit{time}(v)) \} \\
&& \cup \{ s_{v,\mathrm{pos},k} ~:~ v \in V, k \in \mathrm{Ones}(\mathit{pos}(v)) \} \\
&& \cup \{ s_{v,\mathrm{state},q} ~:~ v \in V, q = \mathit{state}(v) \} \\
&& \cup \{ s_{v,\mathrm{written},\gamma} ~:~ v \in V \setminus\{\mathit{root}\}, \gamma = \mathit{written}(v) \}
\cup \{ s_{\mathrm{root},\mathit{written},\#}\} \\
&& \cup \{ s_{v,\mathrm{read},\gamma} ~:~ v \in V, \gamma = \mathit{read}(v) \} .
\end{eqnarray*}As the relation $`\stackrel{L}{\to}`$ is supposed to be an equivalence relation we can define it by defining the $`\stackrel{L}{\to}`$-equivalence classes. These are the sets
\mathit{Cloud}_v := \{p_{v,x} \in P ~:~ x \in V
\}
\cup \{u_{v,i} \in U ~:~ i \in I \}
\cup \{s_{v,i} \in S ~:~ i \in I \}for all $`v \in V`$, and the set
\mathit{Cloud}_{\top} := \{u_{\top,i} \in U ~:~ i \in I \} .We define the relation $`\stackrel{\Diamond}{\to}`$ by:
\begin{eqnarray*}
\stackrel{\Diamond}{\to} &:=& \{ (p_{v,x}, p_{v',x'}) \in P\times P
~:~ v,v',x,x' \in V \text{ and } v E^* v' \text{ and } x=x'\} \\
&&\cup \{ (u_{v,i}, u_{v',i'}) \in U\times U
~:~ v,v' \in V\cup\{\top\}, i,i' \in I \text{ and } v \widetilde{E} v' \text{ and } i=i' \} \\
&&\cup \{ (u_{v,i}, s_{v',i'}) \in U \times S
~:~ v,v' \in V, i,i' \in I \text{ and } v E^* v' \text{ and } i=i'\} \\
&&\cup \{ (s_{v,i}, s_{v',i'}) \in S \times S
~:~ v,v' \in V, i,i' \in I \text{ and } v=v' \text{ and } i=i'\} .
\end{eqnarray*}It is straightforward to check that $`\stackrel{\Diamond}{\to}`$ is reflexive and transitive. The cross property is satisfied as well. Thus, $`(W,\stackrel{L}{\to},\stackrel{\Diamond}{\to})`$ is an cross axiom frame. Finally, we define the valuation $`\sigma`$ as follows.
\begin{eqnarray*}
\sigma(B) &:=& P,
\end{eqnarray*}and
\begin{eqnarray*}
\sigma(A^\mathrm{time}_k) &:=& \{u_{v,\mathrm{time},k} \in U ~:~ v\in V \cup\{\top\}\}
\cup \{s_{v,\mathrm{time},k} \in S ~:~ v \in V \}, \\
\sigma(X^\mathrm{time}_k) &:=& \{p_{v,x} \in P ~:~ v,x \in V \text{ and } k \in \mathrm{Ones}(\mathit{time}(x))\}, \\
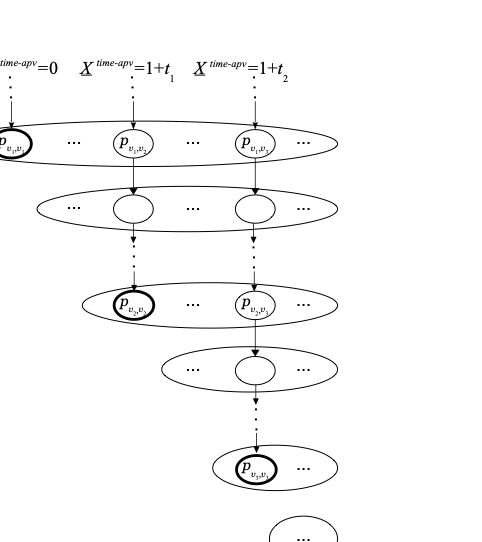
\sigma(X^{\text{time-apv}}_k) &:=& \{p_{v,x} \in P ~:~ v,x \in V \text{ and } k \in \mathrm{Ones}(j) \} \\
&& \!\!\!\!\!\!\!\!\!\!\text{where } j := \begin{cases}
0 & \text{if on the path from $\mathit{root}$ to $x$ the cell $\mathit{pos}(x)$ has}\\
& \text{not been visited before the cell $x$ is reached}, \\
1 + \mathit{time}(v') & \text{otherwise, where } v' \text{ is the last node on the path} \\
& \text{from }\mathit{root} \text{ to } \mathit{pred}(x) \text{ with } \mathit{pos}(v')=\mathit{pos}(x) ,
\end{cases}
\end{eqnarray*}for $`k \in \{0,\ldots,N-1\}`$,
\begin{eqnarray*}
\sigma(A^\mathrm{pos}_k) &:=& \{u_{v,\mathrm{pos},k} \in U~:~ v\in V \cup\{\top\}\}
\cup \{s_{v,\mathrm{pos},k} \in S ~:~ v \in V \}, \\
\sigma(X^\mathrm{pos}_k) &:=& \{p_{v,x} \in P ~:~ v,x \in V \text{ and } k \in \mathrm{Ones}(\mathit{pos}(x))\},
\end{eqnarray*}for $`k \in \{0,\ldots,N\}`$,
\begin{eqnarray*}
\sigma(A^\mathrm{state}_q) &:=& \{u_{v,\mathrm{state},q} \in U ~:~ v\in V \cup\{\top\}\}
\cup \{s_{v,\mathrm{state},q} \in S ~:~ v \in V \},
\end{eqnarray*}for $`q \in Q`$,
\begin{eqnarray*}
\sigma(A^\mathrm{written}_\gamma) &:=& \{u_{v,\mathrm{written},\gamma} \in U~:~ v\in V \cup\{\top\}\}
\cup \{s_{v,\mathrm{written},\gamma} \in S ~:~ v \in V \}, \\
\sigma(A^\mathrm{read}_\gamma) &:=& \{u_{v,\mathrm{read},\gamma} \in U ~:~ v\in V \cup\{\top\}\}
\cup \{s_{v,\mathrm{read},\gamma} \in S ~:~ v \in V \}, \\
\sigma(X^\mathrm{read}_\gamma) &:=& \{p_{v,x} \in P ~:~ v,x \in V \text{ and } \gamma = \mathit{read}(x))\},
\end{eqnarray*}for $`\gamma \in \Gamma`$. It is obvious that all propositional variables are persistent. Thus, we have defined a cross axiom model $`(W,\stackrel{L}{\to},\stackrel{\Diamond}{\to},\sigma)`$. We claim that $`p_{\mathit{root},\mathit{root}} \models f_\ssl(w)`$. For an illustration of an important detail of the structure see Figure 1.
 style="width:80.0%" />
style="width:80.0%" />
We start with some preliminary observations. First, for any cloud, any shared variable has the same truth values in all points in the cloud. Secondly,
y \models B \iff y \in P ,for all $`y\in W`$. So, the points in $`P`$ are the “information” points. On the other hand, as the cloud $`\mathit{Cloud}_\top`$ does not contain any elements from $`P`$, for all points $`y\in \mathit{Cloud}_\top`$ we have $`y \models K \neg B`$, hence,
(\forall y \in \mathit{Cloud}_\top) \ y \models \neg \alpha^\mathit{string}_k ,for all $`\mathit{string}\in\{\mathrm{times},\mathrm{pos},\mathrm{state},\mathrm{written},\mathrm{read}\}`$ and all $`k`$. That means, the truth value of any shared variable in the cloud $`\mathit{Cloud}_\top`$ is false. We claim that in the other clouds all shared variables have the values indicated by their names, namely,
\begin{eqnarray*}
y &\models& (\underline{\alpha}^\mathrm{time} = \mathrm{bin}_N(\mathit{time}(v)), \\
y &\models& (\underline{\alpha}^\mathrm{pos} = \mathrm{bin}_{N+1}(\mathit{pos}(v)), \\
(y &\models& \alpha^\mathrm{state}_q) \iff q = \mathit{state}(v), \text{ for } q \in Q, \\
(y &\models& \alpha^\mathrm{read}_\gamma) \iff \gamma = \mathit{read}(v), \text{ for } \gamma \in \Gamma,
\end{eqnarray*}for $`v\in V`$ and $`y\in \mathit{Cloud}_v`$,
(y \models \alpha^\mathrm{written}_\gamma) \iff \gamma = \mathit{written}(v),for $`\gamma \in \Gamma`$, $`v\in V\setminus\{\mathit{root}\}`$ and $`y\in \mathit{Cloud}_v`$, and
(y \models \alpha^\mathrm{written}_\gamma) \iff \gamma = \#,for $`\gamma \in \Gamma`$ and $`y\in \mathit{Cloud}_\mathit{root}`$. This can be checked similarly as the corresponding claim [eq:SSL-counter-1] in the proof of Proposition [prop: counter]. We prove the assertions about $`\alpha^\mathrm{written}_\gamma`$ and leave the proofs of the other assertions to the reader. Let us fix some $`\gamma \in\Gamma`$. Note that, for all $`p' \in P`$, we have $`p' \models \neg A^\mathrm{written}_\gamma`$, hence
(\forall p' \in P) \ p' \models (\neg A^\mathrm{written}_\gamma \vee \Diamond K \neg B) .Furthermore, $`u_{\top,i} \models K \neg B`$ for all $`i \in I`$. Since for all $`v \in V\cup\{\top\}`$ and $`i \in I`$ we have $`u_{v,i} \stackrel{\Diamond}{\to} u_{\top,i}`$ we obtain $`u_{v,i} \models \Diamond K \neg B`$ for all $`v \in V\cup\{\top\}`$ and $`i \in I`$. Hence,
(\forall u' \in U) \ u' \models (\neg A^\mathrm{written}_\gamma \vee \Diamond K \neg B) .This shows that, for any $`v \in V`$, the shared variable $`\alpha^\mathrm{written}_\gamma=L(A^\mathrm{written}_\gamma \wedge \Box L B)`$ is true in the cloud $`\mathit{Cloud}_v`$ if, and only if, there exists some $`s' \in \mathit{Cloud}_v \cap S`$ with $`s' \models A^\mathrm{written}_\gamma \wedge \Box L B`$. As $`p' \models B`$ for all $`p' \in P`$ and any $`s' \in S`$ is $`\stackrel{L}{\to}`$-equivalent to some $`p' \in P`$, we have $`s' \models L B`$, for all $`s' \in S`$. Actually, for $`s' \in S`$ we even have $`s' \models \Box L B`$ as $`s'`$ does not have any $`\stackrel{\Diamond}{\to}`$-successor besides itself. Thus, for any $`v \in V`$, the shared variable $`\alpha^\mathrm{written}_\gamma=L(A^\mathrm{written}_\gamma \wedge \Box L B)`$ is true in the cloud $`\mathit{Cloud}_v`$ if, and only if, there exists some $`s' \in \mathit{Cloud}_v \cap S`$ with $`s' \models A^\mathrm{written}_\gamma`$. The elements $`s' \in \mathit{Cloud}_v \cap S`$ have the form $`s' = s_{v,i}`$ for some $`i \in I`$. On the one hand, we observe that, for $`v \in V`$ and $`i \in I`$, $`s_{v,i} \models A^\mathrm{written}_\gamma \iff i = (\mathrm{written},\gamma)`$. On the other hand, for $`v \in V`$ we have
s_{v,\mathrm{written},\gamma} \in \mathit{Cloud}_v \iff
\begin{cases}
\gamma = \mathit{written}(v) & \text{if } v \in V\setminus \{\mathit{root}\}, \\
\gamma = \# & \text{if } v = \mathit{root} .
\end{cases}Thus, we have shown the desired claims:
(y \models \alpha^\mathrm{written}_\gamma) \iff \gamma = \mathit{written}(v),for $`\gamma \in \Gamma`$, $`v\in V\setminus\{\mathit{root}\}`$ and $`y\in \mathit{Cloud}_v`$, and
(y \models \alpha^\mathrm{written}_\gamma) \iff \gamma = \#,for $`\gamma \in \Gamma`$ and $`y\in \mathit{Cloud}_\mathit{root}`$.
It is clear from the definition of the valuation $`\sigma`$ that in the points in $`P`$ the variable vectors $`\underline{X}^\mathrm{time}`$, $`\underline{X}^\mathrm{pos}`$, $`\underline{X}^\mathrm{read}`$, and $`\underline{X}^{\text{time-apv}}`$ have the values indicated by their names:
\begin{eqnarray*}
p_{v,x} &\models& (\underline{X}^\mathrm{time} = \mathrm{bin}_N(\mathit{time}(x)), \\
p_{v,x} &\models& (\underline{X}^\mathrm{pos} = \mathrm{bin}_{N+1}(\mathit{pos}(x)), \\
(p_{v,x} &\models& X^\mathrm{read}_\gamma) \iff \gamma = \mathit{read}(x), \text{ for } \gamma \in \Gamma, \\
p_{v,x} &\models& (\underline{X}^{\text{time-apv}} = \mathrm{bin}_N(j)), \\
&&\text{where } j := \begin{cases}
0 & \text{if on the path from $\mathit{root}$ to $x$ the cell $\mathit{pos}(x)$ has} \\
& \text{not been visited before the cell $x$ is reached},\\
1 + \mathit{time}(v') & \text{otherwise, where } v' \text{ is the last node on the path} \\
& \text{from }\mathit{root} \text{ to }\mathit{pred}(x) \text{ with} \mathit{pos}(v')=\mathit{pos}(x) ,
\end{cases}
\end{eqnarray*}for $`v,x\in V`$ satisfying $`v E^* x`$.
Now we are prepared to show $`p_{\mathit{root},\mathit{root}} \models f_\ssl(w)`$. Our observations about the values of the shared variable vectors $`\underline{\alpha}^\mathrm{state}`$, $`\underline{\alpha}^\mathrm{read}`$, and $`\underline{\alpha}^\mathrm{written}`$ show
p_{\mathit{root},\mathit{root}} \models K \Box \mathit{uniqueness}(remember that $`B`$ is false in all points of the cloud $`\mathit{Cloud}_\top`$). Similarly, our observations about the values of the shared variable vectors $`\underline{\alpha}^\mathrm{time}`$, $`\underline{\alpha}^\mathrm{pos}`$, $`\underline{\alpha}^\mathrm{state}`$, and $`\underline{\alpha}^\mathrm{read}`$ imply
p_{\mathit{root},\mathit{root}} \models \mathit{start} .As the state of any node in the accepting tree $`T`$ of $`M`$ on input $`w`$ is different from $`q_\mathrm{reject}`$, our observations about the value of the vector $`\underline{\alpha}^\mathrm{state}`$ (in any cloud $`\mathit{Cloud}_v`$ for $`v\in V`$ the shared variable $`\alpha^\mathrm{state}_q`$ is true if, and only if, $`q = \mathit{state}(v)`$, and in the cloud $`\mathit{Cloud}_\top`$ all shared variables are false) shows
p_{\mathit{root},\mathit{root}} \models K \Box \mathit{no\_reject} .Next, we show
p_{\mathit{root},\mathit{root}} \models K \Box \mathit{time\_after\_previous\_visit}.As the variable $`B`$ is true only in the elements of $`P`$, it is sufficient to show for all $`v,x \in V`$ with $`v E^* x`$
\begin{eqnarray*}
p_{v,x} \models
&& \Bigl( \underline{X}^{\text{time-apv}} \leq \underline{X}^\mathrm{time} \Bigr) \\
&& \wedge \Bigl(
\bigl(( \underline{\alpha}^\mathrm{time} < \underline{X}^\mathrm{time})
\wedge (\underline{\alpha}^\mathrm{pos} \neq \underline{X}^\mathrm{pos} )\bigr)
\rightarrow (\underline{X}^{\text{time-apv}} \neq \underline{\alpha}^\mathrm{time} + 1 )\Bigr) \\
&& \wedge \Bigl( \bigl(
( \underline{\alpha}^\mathrm{time} < \underline{X}^\mathrm{time})
\wedge (\underline{\alpha}^\mathrm{pos} = \underline{X}^\mathrm{pos}) \bigr)
\rightarrow (\underline{\alpha}^\mathrm{time} < \underline{X}^{\text{time-apv}}) \Bigr).
\end{eqnarray*}We distinguish between the two cases whether the cell $`\mathit{pos}(x)`$ under the tape head in the configuration $`c(x)`$ has been visited on the path from $`\mathit{root}`$ to $`x`$ before $`x`$ is reached or not.
First let us assume that the cell $`\mathit{pos}(x)`$ has not been
visited before. Then
$`p_{v,x} \models (\underline{X}^{\text{time-apv}} = \mathrm{bin}_N(0))`$,
hence
$`p_{v,x} \models (\underline{X}^{\text{time-apv}} \leq \underline{X}^\mathrm{time})`$
and
$`p_{v,x} \models (\underline{X}^{\text{time-apv}} \neq \underline{\alpha}^\mathrm{time} + 1)`$,
that is, the formulas in the first two lines are true in $`p_{v,x}`$.
And if we have
$`p_{v,x} \models (\underline{\alpha}^\mathrm{time} < \underline{X}^\mathrm{time})`$
then, due to $`v E^* x`$, the point $`v`$ is a point on the path from
$`\mathit{root}`$ to $`\mathit{pred}(x)`$. Our assumption (that the cell
$`\mathit{pos}(x)`$ has not been visited before $`x`$ is reached)
implies
$`p_{v,x} \models \neg (\underline{\alpha}^\mathrm{pos} = \underline{X}^\mathrm{pos})`$.
Hence the formula in the third line is true in $`p_{v,x}`$ as well.
Now, let us assume that the cell $`\mathit{pos}(x)`$ has been visited on
the path from $`\mathit{root}`$ to $`x`$ before $`x`$ is reached. Let
$`x'`$ be the last node on the path from $`\mathit{root}`$ to
$`\mathit{pred}(x)`$ with $`\mathit{pos}(x')=\mathit{pos}(x)`$. Let
$`i:= \mathit{time}(x')`$ and $`j:=1+i`$. Then $`i < \mathit{time}(x)`$
and $`j \leq \mathit{time}(x)`$. As
$`p_{v,x} \models (\underline{X}^{\text{time-apv}} = \mathrm{bin}_N(j))`$,
the formula in the first line above is true, that is,
$`p_{v,x} \models (\underline{X}^{\text{time-apv}} \leq \underline{X}^\mathrm{time})`$.
For the formula in the second line, let us assume
$`p_{v,x} \models (\underline{\alpha}^\mathrm{time} < \underline{X}^\mathrm{time})
\wedge (\underline{\alpha}^\mathrm{pos} \neq \underline{X}^\mathrm{pos})`$.
Then $`v`$ is a node on the path from $`\mathit{root}`$ to
$`\mathit{pred}(x)`$ with $`\mathit{pos}(v) \neq \mathit{pos}(x)`$.
Hence, $`v \neq x'`$, hence,
$`\mathit{time}(v) \neq \mathit{time}(x')`$, hence,
$`j \neq \mathit{time}(v) + 1`$, hence,
$`p_{v,x} \models (\underline{X}^{\text{time-apv}} \neq \underline{\alpha}^\mathrm{time} + 1)`$.
For the formula in the third line, let us assume
$`p_{v,x} \models ( \underline{\alpha}^\mathrm{time} < \underline{X}^\mathrm{time})
\wedge (\underline{\alpha}^\mathrm{pos} = \underline{X}^\mathrm{pos} )`$.
Then $`v`$ is a node on the path from $`\mathit{root}`$ to
$`\mathit{pred}(x)`$ with $`\mathit{pos}(v) = \mathit{pos}(x)`$, that
is, with the property that in this node the same cell is visited as in
the node $`x`$. As $`x'`$ is the last node on the path from
$`\mathit{root}`$ to $`\mathit{pred}(x)`$ with this property, we have
$`\mathit{time}(v) \leq \mathit{time}(x')`$, hence,
$`j=1+i=1+\mathit{time}(x') > \mathit{time}(v)`$, hence
$`p_{v,x} \models (\underline{\alpha}^\mathrm{time} < \underline{X}^{\text{time-apv}})`$.
Next, we show
p_{\mathit{root},\mathit{root}} \models K \Box \mathit{get\_the\_right\_symbol}.It is sufficient to show for all $`y\in W`$, $`y \models \mathit{get\_the\_right\_symbol}`$. There are two cases to be considered. In each of them, due to the presence of the variable $`B`$, we need to consider only points $`y\in P`$. Let us consider elements $`v,x\in V`$ with $`v E^* x`$. It is sufficient to show $`p_{v,x} \models \mathit{get\_the\_right\_symbol}`$. We distinguish between the two cases considered in this formula. First, let us assume $`p_{v,x} \models (\underline{X}^{\text{time-apv}} = \mathrm{bin}_N(0))`$. We have to show that in this case
\begin{eqnarray*}
p_{v,x} &\models&
\bigwedge_{i=1}^n \Bigl( (\underline{X}^\mathrm{pos}=\mathrm{bin}_{N+1}(2^{N}-1+i))
\rightarrow X^\mathrm{read}_{w_i} \Bigr) \\
&&
\wedge \Bigl(\bigl( (\underline{X}^\mathrm{pos} \leq \mathrm{bin}_{N+1}(2^{N}-1))
\vee (\underline{X}^\mathrm{pos} > \mathrm{bin}_{N+1}(2^{N}-1+n))\bigr)
\rightarrow X^\mathrm{read}_{\#} \Bigr) .
\end{eqnarray*}According to our observations about the value of $`\underline{X}^{\text{time-apv}}`$, the cell $`\mathit{pos}(x)`$ under the tape head in the configuration $`c(x)`$ has not been visited on the path from $`\mathit{root}`$ to $`\mathit{pred}(x)`$. Thus, the symbol $`\mathit{read}(x)`$ is still the initial symbol in the cell $`\mathit{pos}(x)`$. Let us call this symbol $`\gamma`$. Then $`p_{v,x} \models X^\mathrm{read}_\gamma`$, and
\gamma= \begin{cases}
w_i & \text{if }\mathit{pos}(x)=2^N-1+i, \text{ for some }i \in \{1,\ldots,n\}, \\
\# & \text{if } \mathit{pos}(x)\leq 2^N-1 \text{ or } \mathit{pos}(x) > 2^N-1+n.
\end{cases}On the other hand,
$`p_{v,x} \models ( \underline{X}^\mathrm{pos} = \mathrm{bin}_{N+1}(\mathit{pos}(x)))`$.
We have shown the assertion.
Now, let us assume
p_{v,x} \models
((\underline{X}^{\text{time-apv}} > \mathrm{bin}_N(0))
\wedge (\underline{\alpha}^\mathrm{time} = \underline{X}^{\text{time-apv}})) .We have to show that in this case
p_{v,x} \models (\underline{X}^\mathrm{read}=\underline{\alpha}^\mathrm{written}) .The assumption $`p_{v,x} \models (\underline{X}^{\text{time-apv}} > \mathrm{bin}_N(0))`$ implies that the cell $`\mathit{pos}(x)`$ has already been visited on the path from $`\mathit{root}`$ to $`\mathit{pred}(x)`$ and that $`p_{v,x} \models (\underline{X}^{\text{time-apv}} = \mathrm{bin}_{N+1}(1+i))`$ where $`i=\mathit{time}(x')`$ and $`x'`$ is the last node on the path from $`\mathit{root}`$ to $`\mathit{pred}(x)`$ with $`\mathit{pos}(x') = \mathit{pos}(x)`$. The assumption $`p_{v,x} \models (\underline{\alpha}^\mathrm{time} = \underline{X}^{\text{time-apv}})`$ implies $`x' = \mathit{pred}(v)`$. But then in the point $`v`$ the vector $`\underline{\alpha}^\mathrm{written}`$ encodes in unary the symbol that was written into the cell $`\mathit{pos}(x)`$ in the computation step from $`x'`$ to $`v`$. If we call this symbol $`\gamma`$, this means $`p_{v,x} \models \alpha^\mathrm{written}_\gamma`$. This is still the symbol in the cell $`\mathit{pos}(x)`$ when $`x`$ is reached, hence, $`p_{v,x} \models X^\mathrm{read}_\gamma`$. So, we have indeed shown
p_{v,x} \models (\underline{X}^\mathrm{read}=\underline{\alpha}^\mathrm{written}) .Finally, we show
p_{\mathit{root},\mathit{root}} \models K \Box \mathit{computation}.It is sufficient to show
y \models \mathit{computation} ,for all $`y \in W`$. We will separately treat the conjunctions over the set $`(q,\eta) \in Q_\exists \times \Gamma`$ and over the set $`Q_\forall \times \Gamma`$. Let us fix a pair $`(q,\eta) \in Q_\exists \times \Gamma`$ and let us assume that $`y\in W`$ is a point with $`y \models (\alpha^\mathrm{state}_q \wedge \alpha^\mathrm{read}_\eta)`$. We have to show that there is an element $`(r,\theta,\mathit{left}) \in \delta(q,\eta)`$ such that $`y \models \mathit{compstep}_{\mathrm{left}}(r,\theta)`$ or that there is an element $`(r,\theta,\mathit{right}) \in \delta(q,\eta)`$ such that $`y \models \mathit{compstep}_{\mathrm{right}}(r,\theta)`$. As in the cloud $`\mathit{Cloud}_\top`$ the truth value of any shared variable is false, the assumption $`y \models (\alpha^\mathrm{state}_q \wedge \alpha^\mathrm{read}_\eta)`$ implies that there exists some $`v\in V`$ with $`y \in \mathit{Cloud}_v`$. Furthermore, $`q=\mathit{state}(v)`$ and $`\eta = \mathit{read}(v)`$. As $`T`$ is an accepting tree and the state $`q`$ of $`c(v)`$ is an element of $`Q_\exists`$, the node $`v`$ is an inner node of $`T`$, hence, it has a successor $`v'`$. Let us assume that $`((q,\eta),(r,\theta,\mathit{left})) \in \delta`$ is the element of the transition relation $`\delta`$ that leads from $`v`$ to $`v'`$ (the case that this element is of the form $`((q,\eta),(r,\theta,\mathit{right}))`$ is treated analogously). We claim that then
y \models \mathit{compstep}_{\mathrm{left}}(r,\theta) .Let us check this. Let us assume that, for some $`k\in\{0,\ldots,N-1\}`$ and for some $`l \in \{0,\ldots,N\}`$,
y \models \bigl( B \wedge \mathrm{rightmost\_zero}(\underline{\alpha}^\mathrm{time},k)
\wedge \mathrm{rightmost\_one}(\underline{\alpha}^\mathrm{pos},l) \bigr).The number $`i:=\mathit{time}(v)`$ is an element of $`\{0,\ldots,2^N-2\}`$ because $`v`$ is an inner point of the tree $`T`$ and the length of any computation path is at most $`2^N-1`$, and the number $`j:= \mathit{pos}(v)`$ is an element of $`\{1,\ldots,2^{N+1}-3\}`$ because the computation starts in cell $`2^N-1`$ and because during each computation step the tape head can move at most one step to the left or to the right. We obtain $`k=\min(\{0,\ldots,N-1\} \setminus\mathrm{Ones}(i))`$ and $`l=\min\mathrm{Ones}(j)`$. We claim that the two points $`p_{v,v'}`$ and $`p_{v',v'}`$ have the properties formulated in the formula $`\mathit{compstep}_{\mathrm{left}}(r,\theta)`$. Indeed, we observe $`y \stackrel{L}{\to}p_{v,v'}`$ and $`p_{v,v'} \stackrel{\Diamond}{\to} p_{v',v'}`$ as well as $`p_{v,v'} \models B`$. The facts
\begin{align*}
& \mathit{time}(v)=i, && \mathit{pos}(v)=j, \\
& \mathit{time}(v')=i+1, && \mathit{pos}(v')=j-1,
\end{align*}imply
\begin{eqnarray*}
p_{v,v'} &\models& (\underline{\alpha}^\mathrm{time}=\mathrm{bin}_N(i))
\wedge (\underline{\alpha}^\mathrm{pos}=\mathrm{bin}_{N+1}(j)) \wedge \\
&& (\underline{X}^\mathrm{time}=\mathrm{bin}_N(i+1))
\wedge (\underline{X}^\mathrm{pos}=\mathrm{bin}_{N+1}(j-1))
\quad \text{ and } \\
p_{v',v'} &\models& (\underline{\alpha}^\mathrm{time}=\mathrm{bin}_N(i+1))
\wedge (\underline{\alpha}^\mathrm{pos}=\mathrm{bin}_{N+1}(j-1)) \wedge \\
&& (\underline{X}^\mathrm{time}=\mathrm{bin}_N(i+1))
\wedge (\underline{X}^\mathrm{pos}=\mathrm{bin}_{N+1}(j-1)) .
\end{eqnarray*}We obtain
p_{v',v'} \models (\underline{\alpha}^\mathrm{time}=\underline{X}^\mathrm{time})
\wedge (\underline{\alpha}^\mathrm{pos}=\underline{X}^\mathrm{pos}) ,and with
k=\min(\{0,\ldots,N-1\} \setminus\mathrm{Ones}(i))
\text{ and } l=\min(\mathrm{Ones}(j))we obtain as well
\begin{eqnarray*}
p_{v,v'} &\models& (\underline{X}^\mathrm{time}=\underline{\alpha}^\mathrm{time},>k)
\wedge \mathrm{rightmost\_one}(\underline{X}^\mathrm{time},k) \\
&& \wedge (\underline{X}^\mathrm{pos}=\underline{\alpha}^\mathrm{pos},>l)
\wedge \mathrm{rightmost\_zero}(\underline{X}^\mathrm{pos},l) .
\end{eqnarray*}Finally, our observations about the values of the shared variable vectors $`\underline{\alpha}^\mathrm{state}`$, $`\underline{\alpha}^\mathrm{written}`$, $`\underline{\alpha}^\mathrm{read}`$ and about the vector $`\underline{X}^\mathrm{read}`$ imply that also
p_{v',v'} \models \alpha^\mathrm{state}_{r} \wedge \alpha^\mathrm{written}_\theta
\wedge (\underline{\alpha}^\mathrm{read}=\underline{X}^\mathrm{read}) .(remember that $`((q,\eta),(r,\theta,\mathit{left})) \in \delta`$ is the element of the transition relation $`\delta`$ that leads from the node $`v`$ to the node $`v'`$). This ends the treatment of the conjunctions over the set $`(q,\eta) \in Q_\exists \times \Gamma`$ in the formula $`\mathit{computation}`$. Let us now consider a pair $`(q,\eta) \in Q_\forall \times \Gamma`$. Let us assume that $`y \in W`$ is a point such that $`y \models (\alpha^\mathrm{state}_q \wedge \alpha^\mathrm{read}_\eta)`$. We have to show that for all elements $`(r,\theta,\mathit{left}) \in \delta(q,\eta)`$ we have $`y \models \mathit{compstep}_{\mathrm{left}}(r,\theta)`$ and for all elements $`(r,\theta,\mathit{right}) \in \delta(q,\eta)`$ we have $`y \models \mathit{compstep}_{\mathrm{right}}(r,\theta)`$. Let us consider an arbitrary element $`(r,\theta,\mathit{left}) \in \delta(q,\eta)`$ (the case of an element $`(r,\theta,\mathit{right}) \in \delta(q,\eta)`$ is treated analogously). As in the cloud $`\mathit{Cloud}_\top`$ the truth value of any shared variable is false, the assumption $`y \models (\alpha^\mathrm{state}_q \wedge \alpha^\mathrm{read}_\eta)`$ implies that there exists some $`v\in V`$ with $`y \in \mathit{Cloud}_v`$. Furthermore, $`q=\mathit{state}(v)`$ and $`\eta = \mathit{read}(v)`$. As $`q \in Q_\forall`$ and $`T`$ is an accepting tree, in $`T`$ there is a successor $`v'`$ of $`v`$ such that the element $`((q,\eta),(r,\theta,\mathit{left}))`$ leads from $`v`$ to $`v'`$. Above, we have already seen that this implies
y \models \mathit{compstep}_{\mathrm{left}}(r,\theta) .Thus, we have shown $`y \models \mathit{computation}`$ for all $`y \in W`$. This ends the proof of the claim $`p_{\mathit{root},\mathit{root}} \models f_\ssl(w)`$.
Existence of an Accepting Tree
We come to the other direction. Let $`w \in \Sigma^*`$. We wish to show that if $`f_\ssl(w)`$ is $`\ssl`$-satisfiable then $`w\in L`$. We will show that any cross axiom model of $`f_\ssl(w)`$ essentially contains an accepting tree of the Alternating Turing Machine $`M`$ on input $`w`$. Of course, this implies $`w\in L`$.
Let us sketch the main idea. We will consider a cross axiom model of $`f_\ssl(w)`$. And we will consider partial trees of $`M`$ on input $`w`$ as considered in Subsection 3.3, for any $`w\in\Sigma^*`$. First, we will show that a certain very simple partial tree of $`M`$ on input $`w`$ “can be mapped to” the model (later we will give a precise meaning to “can be mapped to”). Then we will show that any partial tree of $`M`$ on input $`w`$ that can be mapped to the model and that is not an accepting tree of $`M`$ on input $`w`$ can be properly extended to a strictly larger partial tree of $`M`$ on input $`w`$ that can be mapped to the model as well. If there would not exist an accepting tree of $`M`$ on input $`w`$ then we would obtain an infinite strictly increasing sequence of partial trees of $`M`$ on input $`w`$. But we show that this cannot happen by giving a finite upper bound on the size of partial trees of $`M`$ on input $`w`$.
Let $`w \in \Sigma^*`$ be a string such that the formula $`f_\ssl(w)`$ is $`\ssl`$-satisfiable. We set $`n:=|w|`$. Let $`(W, \stackrel{\Diamond}{\to},\stackrel{L}{\to},\sigma)`$ be a cross axiom model and $`r_0\in W`$ a point such that $`r_0 \models f_\ssl(w)`$. The quintuple
\mathit{Model}:=(W, \stackrel{\Diamond}{\to},\stackrel{L}{\to},\sigma,r_0)will be important in the following. Points in $`W`$ that cannot be reached from $`r_0`$ by finitely many $`\stackrel{\Diamond}{\to}`$ and $`\stackrel{L}{\to}`$-steps (in any order) can be deleted from $`W`$ with no harm: the resulting smaller quintuple will still be a model of $`f_\ssl(w)`$. Hence, we will assume without loss of generality that every point $`x \in W`$ can be reached from $`r_0`$ by finitely many $`\stackrel{\Diamond}{\to}`$ and $`\stackrel{L}{\to}`$-steps (in any order). Note that now the cross property implies that for any $`x\in W`$ there exists some $`x' \in W`$ with $`r_0 \stackrel{L}{\to} x'`$ and $`x' \stackrel{\Diamond}{\to} x`$. Hence, if $`\varphi`$ is a formula with $`r_0 \models K \Box \varphi`$ then, for all $`x \in W`$, we have $`x \models \varphi`$. For every $`x\in W`$, let $`\mathit{Cloud}_x`$ be the $`\stackrel{L}{\to}`$-equivalence class of $`x`$. Remember that for every $`\stackrel{L}{\to}`$-equivalence class and every shared variable $`\alpha^{\mathit{string}}_i`$ for $`\mathit{string} \in \{\mathrm{time}, \mathrm{pos}, \mathrm{state}, \mathrm{written}, \mathrm{read}\}`$ and a natural number $`i`$, the truth value of this shared variable is the same in all elements of the $`\stackrel{L}{\to}`$-equivalence class.
Partial trees of $`M`$ on input $`w`$ as introduced in Subsection 3.3 will play an important role in the following. We will write a partial tree of $`M`$ on input $`w`$ similarly as in Subsection 3.3 as a triple $`T=(V,E,c)`$, but with the difference that we will describe configurations as at the beginning of this section: the labeling function $`c`$ will be a function of the form $`c:V\to Q \times \{0,\ldots,2^{N+1}-2\}\times \Gamma^{2^{N+1}-1}`$. If $`T=(V,E,c)`$ is a partial tree of $`M`$ on input $`w`$ with root $`\mathit{root}`$ then a function $`\pi:V\to W`$ is called a morphism from $`T`$ to $`\mathit{Model}`$ if it satisfies the following four conditions:
-
$`\pi(\mathit{root})=r_0`$,
-
$`(\forall v,v' \in V) \, ( \text{ if } v E v' \text{ then } \mathit{Cloud}_{\pi(v)} \stackrel{\Diamond}{\to}^{\stackrel{L}{\to}}\mathit{Cloud}_{\pi(v')})`$,
-
$`(\forall v \in V \setminus\{\mathit{root}\}) \, \pi(v) \models \alpha^\mathrm{written}_{\mathit{written}(v)}`$,
-
$`(\forall v \in V)\, \pi(v) \models \begin{array}[t]{l} \bigl(B \wedge (\underline{\alpha}^\mathrm{time} = \mathrm{bin}_N(\mathit{time}(v)))\\ \wedge (\underline{\alpha}^\mathrm{pos} = \mathrm{bin}_{N+1}(\mathit{pos}(v))) \wedge \alpha^\mathrm{state}_{\mathit{state}(v)} \wedge \alpha^\mathrm{read}_{\mathit{read}(v)} \bigr). \end{array}`$
We say that $`T`$ can be mapped to $`\mathit{Model}`$ if there exists a morphism from $`T`$ to $`\mathit{Model}`$. Below we shall prove the following lemma.
If a partial tree $`T=(V,E,c)`$ of $`M`$ on input $`w`$ can be mapped to $`\mathit{Model}`$ and is not an accepting tree of $`M`$ on input $`w`$ then there exists a partial tree $`T=(\widetilde{V},\widetilde{E},\widetilde{c})`$ of $`M`$ on input $`w`$ that can be mapped to $`\mathit{Model}`$ and that satisfies $`V \subsetneq \widetilde{V}`$.
Before we prove this lemma, we deduce the desired assertion from it. Let
D:= \max(\{ |\delta(q,\eta)| ~:~ q \in Q, \eta \in\Gamma\}) .Then, due to Condition III in the definition of a “partial tree of $`M`$ on input $`w`$”, any node in any partial tree of $`M`$ on input $`w`$ has at most $`D`$ successors. As any computation of $`M`$ on $`w`$ stops after at most $`2^N-1`$ steps, any partial tree of $`M`$ on input $`w`$ has at most
\widetilde{D}:=(D^{2^N}-1)/(D-1)nodes. We claim that the rooted and labeled tree
T_0:=(\{\mathit{root}\},\emptyset,c) \text{ where }
c(\mathit{root}):=(q_0,2^N-1,\#^{2^N}w\#^{2^N-1-n})is a partial tree of $`M`$ on input $`w`$ and can be mapped to $`\mathit{Model}`$. Indeed, Condition I in the definition of a “partial tree of $`M`$ on input $`w`$” is satisfied because the node $`\mathit{root}`$ is labeled with the initial configuration of $`M`$ on input $`w`$. Conditions II, III, and IV are satisfied because $`T_0`$ does not have any inner nodes. Condition $`V^\prime`$ is satisfied because $`q_0 \neq q_\mathrm{reject}`$, and this follows from $`r_0 \models \alpha^\mathrm{state}_{q_0}`$ (this is a part of $`r_0 \models \mathit{start}`$) and $`r_0 \models \neg \alpha^\mathrm{state}_{q_\mathrm{reject}}`$ (this follows from $`r_0 \models K \Box \mathit{no\_reject}`$). Thus, $`T_0`$ is indeed a partial tree of $`M`$ on input $`w`$. Now we show that $`T_0`$ can be mapped $`\mathit{Model}`$. Of course, we define $`\pi:\{\mathit{root}\}\to W`$ by $`\pi(\mathit{root}):=r_0`$. We claim that $`\pi`$ is a morphism from $`T`$ to $`\mathit{Model}`$. We check the four conditions one by one.
-
The condition $`\pi(\mathit{root})=r_0`$ is true by definition.
-
The second condition is satisfied trivially because the tree $`T_0`$ does not have any edges.
-
The third condition in the definition of a “morphism from $`T`$ to $`\mathit{Model}`$” is satisfied trivially because $`T_0`$ has only one node, its root.
-
On the one hand, we have $`\mathit{time}(\mathit{root})=0`$, $`\mathit{pos}(\mathit{root})=2^N-1`$,
$`\mathit{state}(\mathit{root})=q_0`$, and $`\mathit{read}(\mathit{root})=\#`$.
On the other hand, the condition $`r_0 \models \mathit{start}`$ impliesMATHr_0 \models B \wedge (\underline{\alpha}^\mathrm{time}=\bin_N(0)) \wedge (\underline{\alpha}^\mathrm{pos}=\bin_{N+1}(2^N-1)) \wedge \alpha^\mathrm{state}_{q_0} \wedge \alpha^\mathrm{read}_{\#} .Click to expand and view more
Thus, we have shown that $`T_0`$ is a partial tree of $`M`$ on input $`w`$ and that $`T_0`$ can be mapped to $`\mathit{Model}`$.
If there would not exist an accepting tree of $`M`$ on input $`w`$ then, starting with $`T_0`$ and using Lemma [lemma:inductionSSL] we could construct an infinite sequence of partial trees $`T_0,T_1,T_2,\ldots`$ of $`M`$ on input $`w`$ that can be mapped to $`\mathit{Model}`$ such that the number of nodes in these trees is strictly increasing. But we have seen that any partial tree of $`M`$ on input $`w`$ can have at most $`\widetilde{D}`$ nodes. Thus, there exists an accepting tree of $`M`$ on input $`w`$. We have shown $`w\in L`$.
In order to complete the proof of Theorem [theorem:SSL-EXPSPACE-hard] it remains to prove Lemma [lemma:inductionSSL].
Proof of Lemma [lemma:inductionSSL]. Let $`T=(V,E,c)`$ be a partial tree of $`M`$ on input $`w`$ that is not an accepting tree of $`M`$ on input $`w`$ and that can be mapped to $`\mathit{Model}`$. Let $`\pi:V \to W`$ be a morphism from $`T`$ to $`\mathit{Model}`$. Then $`T`$ has a leaf $`\widehat{v}`$ such that the state $`q:=\mathit{state}(\widehat{v})`$ is either an element of $`Q_\exists`$ or of $`Q_\forall`$. First we treat the case that it is an element of $`Q_\exists`$, then the case that it is an element of $`Q_\forall`$.
So, let us assume that $`q \in Q_\exists`$. We define $`\eta:=\mathit{read}(\widehat{v})`$. Then, because $`\pi`$ is a morphism from $`T`$ to $`\mathit{Model}`$, we have
\pi(\widehat{v}) \models (\alpha^\mathrm{state}_q
\wedge \alpha^\mathrm{read}_\eta) ,hence, due to $`\pi(\widehat{v}) \models \mathit{computation}`$,
\pi(\widehat{v}) \models
\bigvee_{(r,\theta,\mathit{left}) \in \delta(q,\eta)} \mathit{compstep}_{\mathrm{left}}(r,\theta)
\vee \bigvee_{(r,\theta,\mathit{right}) \in \delta(q,\eta)} \mathit{compstep}_{\mathrm{right}}(r,\theta) .Let us assume that there is an element $`(r,\theta,\mathit{left}) \in \delta(q,\eta)`$ such that $`\pi(\widehat{v}) \models \mathit{compstep}_{\mathrm{left}}(r,\theta)`$ (the other case, the case when there is an element $`(r,\theta,\mathit{right}) \in \delta(q,\eta)`$ such that $`\pi(\widehat{v}) \models \mathit{compstep}_{\mathrm{right}}(r,\theta)`$, is treated analogously). We claim that we can define the new tree $`\widetilde{T}=(\widetilde{V},\widetilde{E},\widetilde{c})`$ as follows:
-
$`\widetilde{V} := V \cup\{\widetilde{v}\}`$ where $`\widetilde{v}`$ is a new element (not in $`V`$),
-
$`\widetilde{E} := E \cup \{(\widehat{v},\widetilde{v})\}`$,
-
$`\widetilde{c}(x) := \begin{cases} c(x) & \text{for all } x \in V, \\ c' & \text{for } x=\widetilde{v}, \text{ where $c’$ is the configuration that is reached from $c(\widehat{v})$} \\ & \text{in the computation step given by } ((q,\eta),(r,\theta,\mathit{left})) \in\delta. \end{cases}`$
Before we show that $`\widetilde{T}`$ is a partial tree of $`M`$ on input $`w`$, we define a function $`\widetilde{\pi}:\widetilde{V}\to W`$ that we will show to be a morphism from $`\widetilde{T}`$ to $`\mathit{Model}`$.
As $`\widehat{v}`$ is an element of a partial tree of $`M`$ on input $`w`$ with $`\mathit{state}(\widehat{v}) \in Q_\exists`$, at least one more computation step can be done. As any computation of $`M`$ on input $`w`$ stops after at most $`2^N-1`$ steps, we observe that the number $`i:=\mathit{time}(\widehat{v})`$ satisfies $`0 \leq i < 2^N-1`$. Then $`\{0,\ldots,N-1\} \setminus\mathrm{Ones}(i) \neq \emptyset`$. We set $`k:= \min(\{0,\ldots,N-1\} \setminus\mathrm{Ones}(i))`$. The assumption that $`\pi`$ is a morphism from $`T`$ to $`\mathit{Model}`$ implies $`\pi(\widehat{v}) \models (\underline{\alpha}^\mathrm{time} = \mathrm{bin}_N(i))`$. We conclude $`\pi(\widehat{v}) \models \mathrm{rightmost\_zero}(\underline{\alpha}^\mathrm{time},k)`$. As during each computation step, the tape head can move at most one step to the left or to the right and as the computation started in position $`2^N-1`$ the number $`j:=\mathit{pos}(\widehat{v})`$ satisfies $`0 < j \leq 2^{N+1}-3`$. Then $`\mathrm{Ones}(j) \neq \emptyset`$. We set $`l:= \min\mathrm{Ones}(j)`$. The assumption that $`\pi`$ is a morphism from $`T`$ to $`\mathit{Model}`$ implies $`\pi(\widehat{v}) \models (\underline{\alpha}^\mathrm{pos} = \mathrm{bin}_{N+1}(j))`$. We conclude $`\pi(\widehat{v}) \models \mathrm{rightmost\_one}(\underline{\alpha}^\mathrm{pos},l)`$. Furthermore, as $`\pi`$ is a morphism from $`T`$ to $`\mathit{Model}`$ we have $`\pi(\widehat{v}) \models B`$. Summarizing this, we have
\pi(\widehat{v}) \models \bigl( B \wedge \mathrm{rightmost\_zero}(\underline{\alpha}^\mathrm{time},k)
\wedge \mathrm{rightmost\_one}(\underline{\alpha}^\mathrm{pos},l) \bigr).Due to $`\pi(\widehat{v}) \models \mathit{compstep}_{\mathrm{left}}(r,\theta)`$ there exist an element $`x \in \mathit{Cloud}_{\pi(\widehat{v})}`$ and an element $`y \in W`$ such that $`x \stackrel{\Diamond}{\to} y`$ as well as
\begin{eqnarray*}
x &\models&
B \wedge (\underline{X}^\mathrm{time}=\underline{\alpha}^\mathrm{time},>k)
\wedge \mathrm{rightmost\_one}(\underline{X}^\mathrm{time},k) \\
&& \wedge (\underline{X}^\mathrm{pos}=\underline{\alpha}^\mathrm{pos},>l)
\wedge \mathrm{rightmost\_zero}(\underline{X}^\mathrm{pos},l)
\end{eqnarray*}and
y \models
(\underline{\alpha}^\mathrm{time}=\underline{X}^\mathrm{time})
\wedge (\underline{\alpha}^\mathrm{pos}=\underline{X}^\mathrm{pos})
\wedge \alpha^\mathrm{state}_{r} \wedge \alpha^\mathrm{written}_\theta
\wedge (\underline{\alpha}^\mathrm{read}=\underline{X}^\mathrm{read}) .We claim that we can define the desired function $`\widetilde{\pi}:\widetilde{V} \to W`$ by
\widetilde{\pi}(v) := \begin{cases}
\pi(v) & \text{if } v \in V, \\
y & \text{if } v=\widetilde{v}.
\end{cases}We have to show that $`\widetilde{T}`$ is a partial tree of $`M`$ on input $`w`$ and that $`\widetilde{\pi}`$ is a morphism from $`\widetilde{T}`$ to $`\mathit{Model}`$. Condition I in the definition of a “partial tree of $`M`$ on input $`w`$” is satisfied because $`\widetilde{T}`$ has the same root as $`T`$, and the label of the root does not change. A node in $`\widetilde{T}`$ is an internal node of $`\widetilde{T}`$ if, and only if, it is either an internal node of $`T`$ or equal to $`\widehat{v}`$. For internal nodes of $`T`$ Conditions II, III, and IV are satisfied by assumption (and due to the fact that the labels of nodes in $`V`$ do not change). The new internal node $`\widehat{v}`$ satisfies Condition II by our definition of $`\widetilde{c}(\widetilde{v})`$. Condition III is satisfied for $`\widehat{v}`$ because $`\widehat{v}`$ has exactly one successor. And Condition IV does not apply to $`\widehat{v}`$ because $`\widehat{v}\in Q_\exists`$. A node in $`\widetilde{T}`$ is a leaf if, and only if, it is either equal to $`\widetilde{v}`$ or a leaf in $`T`$ different from $`\widehat{v}`$. For the leaves in $`T`$ different from $`\widehat{v}`$ Condition $`\mathrm{V}^\prime`$ is satisfied by assumption (and due to the fact that the labels of nodes in $`V`$ do not change). For the new leaf $`\widetilde{v}`$ in $`\widetilde{T}`$ Condition $`\mathrm{V}^\prime`$ says $`\mathit{state}(\widetilde{v}) \neq q_\mathrm{reject}`$. This is true because on the one hand $`\mathit{state}(\widetilde{v}) = r`$ and on the other hand $`y \models \alpha^\mathrm{state}_r`$ and $`y \models \neg \alpha^\mathrm{state}_{q_\mathrm{reject}}`$ (this follows from $`r \models K \Box \mathit{no\_reject}`$). We have shown that $`\widetilde{T}`$ is a partial tree of $`M`$ on input $`w`$.
Now we show that $`\widetilde{\pi}`$ is a morphism from $`\widetilde{T}`$ to $`\mathit{Model}`$. The first condition in the definition of a “morphism from $`\widetilde{T}`$ to $`\mathit{Model}`$” is satisfied because $`\widetilde{\pi}(\mathit{root}) = \pi(\mathit{root})=r_0`$. Let us look at the second condition and let us assume that $`v,v' \in \widetilde{V}`$ satisfy $`v \widetilde{E} v'`$. We distinguish between two different cases for $`v`$ and $`v'`$.
-
Case: $`v' \in V`$. Then our assumption $`v \widetilde{E} v'`$ implies $`v \in V`$ and $`v E v'`$. In this case the facts $`\widetilde{\pi}(v)=\pi(v)`$ and $`\widetilde{\pi}(v')=\pi(v')`$ as well as the assumption that $`\pi:V\to W`$ is a morphism from $`T`$ to $`\mathit{Model}`$ imply the desired assertion:
MATH\mathit{Cloud}_{\widetilde{\pi}(v)} = \mathit{Cloud}_{\pi(v)} \stackrel{\Diamond}{\to}^{\stackrel{L}{\to}} \mathit{Cloud}_{\pi(v')}) = \mathit{Cloud}_{\widetilde{\pi}(v')} .Click to expand and view more -
Case: $`v'=\widetilde{v}`$. Then our assumption $`v \widetilde{E} v'`$ implies $`v= \widehat{v}`$. On the one hand, we have $`x \in \mathit{Cloud}_{\pi(\widehat{v})} = \mathit{Cloud}_{\widetilde{\pi}(\widehat{v})}`$, on the other hand $`y = \widetilde{\pi}(\widetilde{v})`$, hence, $`y \in \mathit{Cloud}_{\widetilde{\pi}(\widetilde{v})}`$. With $`x \stackrel{\Diamond}{\to} y`$ we obtain the desired assertion $`\mathit{Cloud}_{\widetilde{\pi}(\widehat{v})} \stackrel{\Diamond}{\to}^{\stackrel{L}{\to}} \mathit{Cloud}_{\widetilde{\pi}(\widetilde{v})}`$.
The third condition in the definition of a “morphism from $`\widetilde{T}`$ to $`\mathit{Model}`$” is satisfied for $`v\in V\setminus\{\mathit{root}\}`$ by assumption (and by $`\widetilde{\pi}(v)=\pi(v)`$ and $`\widetilde{c}(v) = c(v)`$). It is satisfied for $`\widetilde{v}`$ because $`\mathit{written}(\widetilde{v}) = \theta`$, because $`\widetilde{\pi}(\widetilde{v})=y`$, and because $`y \models \alpha^\mathrm{written}_\theta`$. We come to the fourth condition. It is satisfied for $`v\in V\setminus\{\mathit{root}\}`$ by assumption (and due to $`\widetilde{\pi}(v)=\pi(v)`$ and $`\widetilde{c}(v) = c(v)`$). We still need to show that it is satisfied for $`\widetilde{v}`$. Remember $`\widetilde{\pi}(\widetilde{v})=y`$. We need to show
\begin{eqnarray*}
y &\models&
\bigl(B
\wedge (\underline{\alpha}^\mathrm{time} = \mathrm{bin}_N(\mathit{time}(\widetilde{v})))
\wedge (\underline{\alpha}^\mathrm{pos} = \mathrm{bin}_{N+1}(\mathit{pos}(\widetilde{v})))
\wedge \alpha^\mathrm{state}_{\mathit{state}(\widetilde{v})}
\wedge \alpha^\mathrm{read}_{\mathit{read}(\widetilde{v})} \bigr).
\end{eqnarray*}This assertion consists really of five assertions. We treat them one by one.
-
The condition $`y \models B`$ is satisfied because $`x \models B`$ and $`x \stackrel{\Diamond}{\to} y`$ and because $`B`$ is persistent.
-
In the trees $`T`$ and $`\widetilde{T}`$ we have $`\mathit{time}(\widehat{v})=i`$, and in the tree $`\widetilde{T}`$ we have $`\mathit{time}(\widetilde{v})=i+1`$. We wish to show $`y \models (\underline{\alpha}^\mathrm{time} = \mathrm{bin}_N(i+1))`$. We have already seen $`\pi(\widehat{v}) \models (\underline{\alpha}^\mathrm{time} = \mathrm{bin}_N(i))`$ and $`\pi(\widehat{v}) \models \mathrm{rightmost\_zero}(\underline{\alpha}^\mathrm{time},k)`$. As $`x \in \mathit{Cloud}_{\pi(\widehat{v})}`$, we obtain
MATHx \models ((\underline{\alpha}^\mathrm{time} = \mathrm{bin}_N(i)) \wedge \mathrm{rightmost\_zero}(\underline{\alpha}^\mathrm{time},k)) .Click to expand and view moreThe conditions $`x \stackrel{\Diamond}{\to} y`$ as well as
MATH\begin{eqnarray*} x &\models& (\underline{X}^\mathrm{time}=\underline{\alpha}^\mathrm{time},>k) \wedge \mathrm{rightmost\_one}(\underline{X}^\mathrm{time},k) \text{ and } \\ y & \models& (\underline{\alpha}^\mathrm{time}=\underline{X}^\mathrm{time}) \end{eqnarray*}Click to expand and view moreimply $`y \models (\underline{\alpha}^\mathrm{time} = \mathrm{bin}_N(i+1))`$.
-
In the trees $`T`$ and $`\widetilde{T}`$ we have $`\mathit{pos}(\widehat{v})=j`$, and in the tree $`\widetilde{T}`$ we have $`\mathit{pos}(\widetilde{v})=j-1`$. We wish to show $`y \models (\underline{\alpha}^\mathrm{pos} = \mathrm{bin}_{N+1}(j-1))`$. We have already seen $`\pi(\widehat{v}) \models (\underline{\alpha}^\mathrm{pos} = \mathrm{bin}_{N+1}(j))`$ and $`\pi(\widehat{v}) \models \mathrm{rightmost\_one}(\underline{\alpha}^\mathrm{pos},l)`$. As $`x \in \mathit{Cloud}_{\pi(\widehat{v})}`$, we obtain
MATHx \models ((\underline{\alpha}^\mathrm{pos} = \mathrm{bin}_{N+1}(j)) \wedge \mathrm{rightmost\_one}(\underline{\alpha}^\mathrm{pos},l)) .Click to expand and view moreThe conditions $`x \stackrel{\Diamond}{\to} y`$ as well as
MATH\begin{eqnarray*} x &\models& (\underline{X}^\mathrm{pos}=\underline{\alpha}^\mathrm{pos},>l) \wedge \mathrm{rightmost\_zero}(\underline{X}^\mathrm{pos},l) \text{ and } \\ y & \models& (\underline{\alpha}^\mathrm{pos}=\underline{X}^\mathrm{pos}) \end{eqnarray*}Click to expand and view moreimply $`y \models (\underline{\alpha}^\mathrm{pos} = \mathrm{bin}_{N+1}(j-1))`$.
-
We have $`\mathit{state}(\widetilde{v}) = r`$. And we have $`y \models \alpha^\mathit{state}_r`$.
-
Let $`\gamma:=\mathit{read}(\widetilde{v})`$ in $`\widetilde{T}`$. We wish to show $`y \models \alpha^\mathrm{read}_\gamma`$. As we know $`y \models (\underline{\alpha}^\mathrm{read}=\underline{X}^\mathrm{read})`$ it is sufficient to show $`y \models X^\mathrm{read}_\gamma`$. We have already seen $`y \models (\underline{\alpha}^\mathrm{time} = \mathrm{bin}_N(i+1))`$ and $`y \models (\underline{\alpha}^\mathrm{pos} = \mathrm{bin}_{N+1}(j-1))`$. As we know $`y \models (\underline{\alpha}^\mathrm{time}=\underline{X}^\mathrm{time}) \wedge (\underline{\alpha}^\mathrm{pos}=\underline{X}^\mathrm{pos})`$ we conclude $`y \models ((\underline{X}^\mathrm{time}=\mathrm{bin}_N(i+1)) \wedge (\underline{X}^\mathrm{pos}=\mathrm{bin}_{N+1}(j-1)))`$. We have seen $`y \models B`$ as well. Furthermore, we have $`y \models \mathit{time\_after\_previous\_visit}`$. The first line in the formula $`\mathit{time\_after\_previous\_visit}`$ implies $`y \models (\underline{X}^{\text{time-apv}} \leq \underline{X}^\mathrm{time})`$, hence, $`y \models (\underline{X}^{\text{time-apv}} \leq \mathrm{bin}_N(i+1))`$. Let $`v_m \in V`$ for $`m=0,\ldots,i+1`$ be the uniquely determined node on the path from $`\mathit{root}`$ to $`\widetilde{v}`$ with $`\mathit{time}(v_m)=m`$ (hence $`v_0=\mathit{root}`$, $`v_i = \widehat{v}`$, and $`v_{i+1} = \widetilde{v}`$). Then
MATHv_0 \widetilde{E} v_1 \widetilde{E} \ldots \widetilde{E} v_i \widetilde{E} v_{i+1} .Click to expand and view moreBy the second condition in the definition of a “morphism from $`\widetilde{T}`$ to $`\mathit{Model}`$”
MATH\mathit{Cloud}_{\widetilde{\pi}(v_0)} \stackrel{\Diamond}{\to}^{\stackrel{L}{\to}} \mathit{Cloud}_{\widetilde{\pi}(v_1)} \stackrel{\Diamond}{\to}^{\stackrel{L}{\to}} \ldots \stackrel{\Diamond}{\to}^{\stackrel{L}{\to}} \mathit{Cloud}_{\widetilde{\pi}(v_i)} \stackrel{\Diamond}{\to}^{\stackrel{L}{\to}} \mathit{Cloud}_{\widetilde{\pi}(v_{i+1})}.Click to expand and view moreBy repeated application of the cross property and by starting with $`z_{i+1}:=y`$ we conclude that for $`m=i+1,i,\ldots,1,0`$ there exists some $`z_m \in \mathit{Cloud}_{\widetilde{\pi}(v_m)}`$ with $`z_m \stackrel{\Diamond}{\to} y`$. Let us consider $`m \in \{0,1,\ldots,i+1\}`$. As $`y \models B`$ we also have $`z_m \models B`$ (remember that variables are persistent in $`\ssl`$). Due to $`\widetilde{\pi}(v_m) \models ((\underline{\alpha}^\mathrm{time} = \mathrm{bin}_N(m)) \wedge (\underline{\alpha}^\mathrm{pos} = \mathrm{bin}_{N+1}( \mathit{pos}(v_m))))`$ we obtain $`z_m \models ((\underline{\alpha}^\mathrm{time} = \mathrm{bin}_N(m)) \wedge (\underline{\alpha}^\mathrm{pos} = \mathrm{bin}_{N+1}( \mathit{pos}(v_m))))`$ as well. Due to $`y \models ((\underline{X}^\mathrm{time}=\mathrm{bin}_N(i+1)) \wedge (\underline{X}^\mathrm{pos}=\mathrm{bin}_{N+1}(j-1)))`$ and the persistence of variables we obtain $`z_m \models ((\underline{X}^\mathrm{time}=\mathrm{bin}_N(i+1)) \wedge (\underline{X}^\mathrm{pos}=\mathrm{bin}_{N+1}(j-1)))`$ as well. Furthermore, we have $`z_m \models \mathit{time\_after\_previous\_visit}`$. We distinguish between the two cases whether the cell $`j-1`$ has been visited on the path from $`\mathit{root}`$ to $`\widehat{v}`$ or not.
Let us first consider the case when the cell $`j-1`$ has not been visited on the path from $`\mathit{root}`$ to $`\widehat{v}`$. Then, on the one hand, the symbol $`\gamma = \mathit{read}(\widetilde{v})`$ is still the initial symbol in the cell $`j-1`$. On the other hand, for all $`m \in \{0,\ldots,i\}`$ we have $`\mathit{pos}(v_m) \neq j-1`$ and
MATHz_m \models ( \underline{\alpha}^\mathrm{time} < \underline{X}^\mathrm{time} \wedge \underline{\alpha}^\mathrm{pos} \neq \underline{X}^\mathrm{pos} ) \rightarrow \underline{X}^{\text{time-apv}} \neq \underline{\alpha}^\mathrm{time} + 1) .Click to expand and view moreTogether with $`z_m \models ((\underline{X}^\mathrm{time}=\mathrm{bin}_N(i+1)) \wedge (\underline{X}^\mathrm{pos}=\mathrm{bin}_{N+1}(j-1)))`$ and $`z_m \models ((\underline{\alpha}^\mathrm{time} = \mathrm{bin}_N(m)) \wedge (\underline{\alpha}^\mathrm{pos} = \mathrm{bin}_{N+1}( \mathit{pos}(v_m))))`$ we conclude that $`z_m \models (\underline{X}^{\text{time-apv}} \neq \mathrm{bin}_N(m + 1))`$ for $`m\in\{0,\ldots,i\}`$. The persistence of $`\underline{X}^{\text{time-apv}}`$ implies that $`y \models (\underline{X}^{\text{time-apv}} \neq \mathrm{bin}_N(m + 1))`$ for $`m\in\{0,\ldots,i\}`$. Together with $`y \models (\underline{X}^{\text{time-apv}} \leq \underline{X}^\mathrm{time})`$ we conclude that the binary value of $`\underline{X}^{\text{time-apv}}`$ in $`y`$ must be $`0`$. Now the fact $`y \models \mathit{get\_the\_right\_symbol}`$ implies $`y \models X^\mathrm{read}_\gamma`$.
Let us consider the second case, the case when the cell $`j-1`$ has been visited on the path from $`\mathit{root}`$ to $`\widehat{v}`$. Let $`v_{m'}`$ be the last node on this path with $`\mathit{pos}(v_{m'})=j-1`$. Then $`0 \leq m' \leq i`$. On the one hand, then the symbol $`\gamma = \mathit{read}(\widetilde{v})`$ is the symbol that was written into the cell $`j-1`$ in the computation step from node $`v_{m'}`$ to node $`v_{m'+1}`$, and by the third condition in the definition of a “morphism from $`\widetilde{T}`$ to $`\mathit{Model}`$” we have $`\widetilde{\pi}(v_{m'+1}) \models \alpha^\mathrm{written}_\gamma`$, hence, $`z_{m'+1} \models \alpha^\mathrm{written}_\gamma`$. On the other hand, from $`y \models \mathit{time\_after\_previous\_visit}`$ we get $`y \models (\underline{X}^{\text{time-apv}} \leq \underline{X}^\mathrm{time})`$, hence, $`y \models (\underline{X}^{\text{time-apv}} \leq \mathrm{bin}_N(i+1))`$. From $`z_{m'} \models \mathit{time\_after\_previous\_visit}`$ we get
MATHz_{m'} \models \bigl( ( \underline{\alpha}^\mathrm{time} < \underline{X}^\mathrm{time}) \wedge (\underline{\alpha}^\mathrm{pos} = \underline{X}^\mathrm{pos})\bigr) \rightarrow (\underline{\alpha}^\mathrm{time}<\underline{X}^{\text{time-apv}} ) .Click to expand and view moreTogether with $`z_{m'} \models (\underline{\alpha}^\mathrm{time} = \mathrm{bin}_N(m'))`$ we obtain $`z_{m'} \models ( \mathrm{bin}_N(m') < \underline{X}^{\text{time-apv}} )`$. And similarly as in the first case, from
MATHz_m \models \bigl( ( \underline{\alpha}^\mathrm{time} < \underline{X}^\mathrm{time}) \wedge( \underline{\alpha}^\mathrm{pos} \neq \underline{X}^\mathrm{pos} )\bigr) \rightarrow( \underline{X}^{\text{time-apv}} \neq \underline{\alpha}^\mathrm{time} + 1) ,Click to expand and view morefor $`m=m'+1,\ldots,i`$ we obtain
MATHz_m \models (\underline{X}^{\text{time-apv}} \neq \mathrm{bin}_N(m+1)) .Click to expand and view moreAll this implies $`y \models (\underline{X}^{\text{time-apv}} = \mathrm{bin}_N(1+m'))`$ and $`z_{m'+1} \models (\underline{X}^{\text{time-apv}} = \mathrm{bin}_N(1+m'))`$. Then $`z_{m'+1} \models \mathit{get\_the\_right\_symbol}`$ implies $`z_{m'+1} \models (\underline{X}^\mathrm{read} = \underline{\alpha}^\mathrm{written})`$. With $`z_{m'+1} \models \alpha^\mathrm{written}_\gamma`$ we conclude $`z_{m'+1} \models X^\mathrm{read}_\gamma`$, hence, $`y \models X^\mathrm{read}_\gamma`$. That was to be shown.
Thus, $`\widetilde{T}`$ is not only a partial tree of $`M`$ on input $`w`$ but can also be mapped to $`\mathit{Model}`$. This ends the treatment of the case $`q \in Q_\exists`$.
Now we consider the other case, the case $`q \in Q_\forall`$. We define $`\eta:=\mathit{read}(\widehat{v})`$. Let
(r_1,\theta_1,\mathit{dir}_1),\ldots,(r_d,\theta_d,\mathit{dir}_d)be the elements of $`\delta(q,\eta)`$ where $`d\geq 1`$ and $`\mathit{dir}_m \in \{\mathit{left},\mathit{right}\}`$, for $`m=1,\ldots,d`$. We claim that we can define the new tree $`\widetilde{T}=(\widetilde{V},\widetilde{E},\widetilde{c})`$ as follows:
-
$`\widetilde{V} := V \cup\{\widetilde{v}_1,\ldots,\widetilde{v}_d\}`$ where $`\widetilde{v}_1,\ldots,\widetilde{v}_d`$ are new (not in $`V`$) pairwise different elements,
-
$`\widetilde{E} := E \cup \{(\widehat{v},\widetilde{v}_1),\ldots,(\widehat{v},\widetilde{v}_d)\}`$,
-
$`\widetilde{c}(x) := \begin{cases} c(x) & \text{for all } x \in V, \\ c'_m & \text{for } x=\widetilde{v}_m, \text{where $c’_m$ is the configuration that is reached from }\\ & \text{$c(\widehat{v})$ in the computation step given by } ((q,\eta),(r_m,\theta_m,\mathit{dir}_m)) \in\delta. \end{cases}`$
Before we show that $`\widetilde{T}`$ is a partial tree of $`M`$ on input $`w`$, we define a function $`\widetilde{\pi}:\widetilde{V}\to W`$ that we will show to be a morphism from $`\widetilde{T}`$ to $`\mathit{Model}`$. Since $`\pi`$ is a morphism from $`T`$ to $`\mathit{Model}`$), we have
\pi(\widehat{v}) \models
B \wedge (\underline{\alpha}^\mathrm{time} = \mathrm{bin}_N(\mathit{time}(\widehat{v})))
\wedge (\underline{\alpha}^\mathrm{pos} = \mathrm{bin}_{N+1}(\mathit{pos}(\widehat{v})))
\wedge \alpha^\mathrm{state}_{\mathit{state}(\widehat{v})}
\wedge \alpha^\mathrm{read}_{\mathit{read}(\widehat{v})} ,hence, due to $`\pi(\widehat{v}) \models \mathit{computation}`$,
\pi(\widehat{v}) \models
\bigwedge_{(r,\theta,\mathit{left}) \in \delta(q,\eta)} \mathit{compstep}_{\mathrm{left}}(r,\theta)
\wedge \bigwedge_{(r,\theta,\mathit{right}) \in \delta(q,\eta)} \mathit{compstep}_{\mathrm{right}}(r,\theta) .As in the case $`q \in Q_\exists`$ one shows that the numbers $`i:=\mathit{time}(\widehat{v})`$ and $`j:=\mathit{pos}(\widehat{v})`$ satisfy $`0 \leq i < 2^N-1`$ and $`0 < j \leq 2^{N+1}-3`$, and one defines
\begin{eqnarray*}
k &:=& \min(\{0,\ldots,N-1\} \setminus\mathrm{Ones}(i)), \\
l_\mathrm{left} &:=& \min(\mathrm{Ones}(j)), \text{ and} \\
l_\mathrm{right} &:=& \min(\{0,\ldots,N\} \setminus\mathrm{Ones}(j)).
\end{eqnarray*}As in the case $`q \in Q_\exists`$ one obtains
\pi(\widehat{v}) \models B \wedge \mathrm{rightmost\_zero}(\underline{\alpha}^\mathrm{time},k)
\wedge \mathrm{rightmost\_one}(\underline{\alpha}^\mathrm{pos},l_\mathrm{left})
\wedge \mathrm{rightmost\_zero}(\underline{\alpha}^\mathrm{pos},l_\mathrm{right}).Let us now consider some $`m\in\{1\ldots,d\}`$. If $`\mathit{dir}_m=\mathit{left}`$ then, due to $`\pi(\widehat{v}) \models \mathit{compstep}_{\mathrm{left}}(r,\theta)`$, there exist an element $`x_m \in \mathit{Cloud}_{\pi(\widehat{v})}`$ and an element $`y_m \in W`$ such that $`x_m \stackrel{\Diamond}{\to} y_m`$ as well as
\begin{eqnarray*}
x_m &\models&
B \wedge (\underline{X}^\mathrm{time}=\underline{\alpha}^\mathrm{time},>k)
\wedge \mathrm{rightmost\_one}(\underline{X}^\mathrm{time},k) \\
&& \wedge (\underline{X}^\mathrm{pos}=\underline{\alpha}^\mathrm{pos},>l_\mathrm{left})
\wedge \mathrm{rightmost\_zero}(\underline{X}^\mathrm{pos},l_\mathrm{left})
\end{eqnarray*}and
y_m \models
(\underline{\alpha}^\mathrm{time}=\underline{X}^\mathrm{time})
\wedge (\underline{\alpha}^\mathrm{pos}=\underline{X}^\mathrm{pos})
\wedge \alpha^\mathrm{state}_{r} \wedge \alpha^\mathrm{written}_\theta
\wedge (\underline{\alpha}^\mathrm{read}=\underline{X}^\mathrm{read}) .Similarly, if $`\mathit{dir}_m=\mathit{right}`$ then, due to $`\pi(\widehat{v}) \models \mathit{compstep}_{\mathrm{right}}(r,\theta)`$, there exist an element $`x_m \in \mathit{Cloud}_{\pi(\widehat{v})}`$ and an element $`y_m \in W`$ such that $`x_m \stackrel{\Diamond}{\to} y_m`$ as well as
\begin{eqnarray*}
x_m &\models&
B \wedge (\underline{X}^\mathrm{time}=\underline{\alpha}^\mathrm{time},>k)
\wedge \mathrm{rightmost\_one}(\underline{X}^\mathrm{time},k) \\
&& \wedge (\underline{X}^\mathrm{pos}=\underline{\alpha}^\mathrm{pos},>l_\mathrm{right})
\wedge \mathrm{rightmost\_one}(\underline{X}^\mathrm{pos},l_\mathrm{right})
\end{eqnarray*}and
y_m \models
(\underline{\alpha}^\mathrm{time}=\underline{X}^\mathrm{time})
\wedge (\underline{\alpha}^\mathrm{pos}=\underline{X}^\mathrm{pos})
\wedge \alpha^\mathrm{state}_{r} \wedge \alpha^\mathrm{written}_\theta
\wedge (\underline{\alpha}^\mathrm{read}=\underline{X}^\mathrm{read}) .We claim that we can define the desired function $`\widetilde{\pi}:\widetilde{V} \to W`$ by
\widetilde{\pi}(v) := \begin{cases}
\pi(v) & \text{if } v \in V, \\
y_m & \text{if } v=\widetilde{v}_m, \text{ for some } m \in \{1,\ldots,d\}.
\end{cases}Similarly as in the case $`q \in Q_\exists`$ one shows that $`\widetilde{T}`$ is a partial tree of $`M`$ on input $`w`$. Note that also Condition IV is satisfied for $`\widehat{v}`$. Finally, similarly as in the case $`q \in Q_\exists`$ one shows that $`\widetilde{\pi}`$ is a morphism from $`\widetilde{T}`$ to $`\mathit{Model}`$. This ends the treatment of the case $`q \in Q_\forall`$. We have proved Lemma [lemma:inductionSSL]. ◻
In Section 4 we have shown that any language recognized by an Alternating Turing Machine working in exponential time can be reduced in logarithmic space to the satisfiability problem of $`\ssl`$. This shows that the satisfiability problem of $`\ssl`$ is $`\EXPSPACE`$-hard under logspace reduction. In Section 5 we have shown that the satisfiability problem of $`\ssl`$ can be reduced in logarithmic space to the satisfiability problem of $`\sxs`$. This proves the following theorem.
The satisfiability problem of $`\sxs`$ is $`\EXPSPACE`$-hard under logarithmic space reduction.
In this appendix we wish to given an alternative, “direct” proof of this theorem by showing directly that any language $`L`$ recognized by an Alternating Turing Machine working in exponential time can be reduced in logarithmic space to the satisfiability problem of $`\sxs`$. The proof is quite similar to the reduction of Alternating Turing Machines working in exponential time to the satisfiability problem of $`\ssl`$ presented in Section 4. But, there are also some important differences between the two reductions. On the one hand, we are going to use certain “shared variables” as well, but the mechanism of shared variables in $`\sxs`$ is much easier than in $`\ssl`$. On the other hand, the fact that in $`\sxs`$ the left commutativity property and the right commutativity property hold true (while in $`\ssl`$ only the left commutativity property has to hold true) causes problems that were not present in our treatment of $`\ssl`$ in Section 4. Similarly as in that section, for $`\sxs`$ we will model nodes in an accepting tree of an Alternating Turing Machine by clouds in an $`\sxs`$-product model. But the commutativity properties have the consequence that for every point in every cloud there exists a copy in every other cloud. The result is that in a cloud modeling a certain node on some path in an accepting tree there are also points that come from other nodes on other computation paths, perhaps even with the same time stamp. This makes the isolation of the correct points carrying the required information (in particular the information about the symbol to be read at a certain time on some computation path) more difficult. For details see Subsection 7.2 where the reduction function is defined and explained.
In the first of the following five subsections we present an implementation of a binary counter in $`\sxs`$, similar to the implementation of a binary counter in $`\ssl`$ in Subsection 3.2. In the second subsection we give an outline of the definition of the reduction function and then define the reduction function $`f_\sxs`$ formally. In the third subsection we show that the reduction function $`f_\sxs`$ can be computed in logarithmic space. The final two subsections are devoted to the correctness proof of the reduction. First we show that in the case $`w\in L`$ the formula $`f_\sxs(w)`$ is $`\sxs`$-satisfiable by explicitly constructing an $`\sxs`$-product model for $`f_\sxs(w)`$. In the last section we show that if $`f_\sxs(w)`$ is $`\sxs`$-satisfiable then $`w`$ is an element of $`L`$.
Binary Counters in $`\sxs`$
Fix some natural number $`n\geq 1`$. We wish to implement in $`\sxs`$ a binary $`n`$-bit counter that counts from $`0`$ to $`2^n-1`$. That means, we wish to construct an $`\sxs`$-satisfiable formula with the property that any model of it contains a sequence of pairwise distinct points $`p_0,\ldots,p_{2^n-1}`$ such that, for each $`i\in\{0,\ldots,2^n-1\}`$, at the point $`p_i`$ the number $`i`$ is stored in binary form in a certain way.
Additionally, we need to copy and transmit various bits of information, both in the $`\stackrel{\Diamond}{\to}`$-direction as well as in the $`\stackrel{L}{\to}`$-direction This will be done by two kinds of formulas.
-
On the one hand, we need formulas that have the same truth value in the vertical ($`\stackrel{\Diamond}{\to}`$) direction but can change their truth values in the horizontal ($`\stackrel{L}{\to}`$) direction. In the logic $`\sxs`$ we can force certain propositional variables to be persistent by a suitable formula.
-
On the other hand, we need formulas that have the same truth value in the horizontal ($`\stackrel{L}{\to}`$) direction but can change their truth values in the vertical ($`\stackrel{\Diamond}{\to}`$) direction. Such formulas will be called shared variables. In the logic $`\sxs`$ they can be defined as follows. For $`i\in\IN`$ let $`A_i`$ be special propositional variables. The shared variables $`\alpha_i`$ are defined as
MATH\alpha_i:=LA_i .Click to expand and view more
Note that $`\neg\alpha_i \equiv K\neg A_i`$.
In the following we use the abbreviations introduced above, in Table [table:abbrev1], and in Table 2.
| For | the following | is an abbreviation |
| expression | of the following formula | |
| $`l\geq 1, k\geq -1`$ | $`\mathrm{persistent}(\underline{F},>k)`$ | $`\bigwedge_{h=k+1}^{l-1} K(\Box F_h \vee \Box \neg F_h)`$ |
| $`l\geq 1`$ | $`\mathrm{persistent}(\underline{F})`$ | $`\mathrm{persistent}(\underline{F},>-1)`$ |
Some abbreviations for logical formulas, where $`\underline{F}=(F_{l-1},\ldots,F_0)`$ and $`\underline{G}=(G_{l-1},\ldots,G_0)`$ are vectors of formulas. As usual, an empty conjunction like $`\bigwedge_{h=0}^{-1} F_h`$ can be replaced by any propositional formula that is true always.
The idea of the construction is the same as in Subsection 3.2.
-
We store the counter values in a vector $`\underline{\alpha}:=\alpha_{n-1},\ldots,\alpha_0`$ of shared variables. To this end we embed the sequence $`p_0,\ldots,p_{2^n-1}`$ of points in a sequence of clouds $`\mathit{C}_0,\ldots,\mathit{C}_{2^{n-1}}`$ such that the cloud $`\mathit{C}_i`$ contains the point $`p_i`$ and such that the vector $`\underline{\alpha}`$ of shared variables satisfied at $`p_i`$ (and hence at all points in $`\mathit{C}_i`$) encodes the number $`i`$.
-
Let $`i\leq 2^n-1`$ be the number encoded by $`\underline{\alpha}`$. If $`\underline{\alpha}`$ contains no $`0`$ then $`i`$ has reached its highest posible value, the number $`2^n-1`$. Otherwise let $`k`$ be the position of the rightmost $`0`$. We determine the position $`k`$ with the aid of the formula $`\mathrm{rightmost\_zero}(\alpha,k)`$. In order to increment the counter we have to keep all $`\alpha_j`$ at positions $`j>k`$ unchanged and to switch all $`\alpha_j`$ at positions $`j\leq k`$. We do this in two steps:
-
First me make an $`\stackrel{L}{\to}`$-step from the point $`p_i`$ to a point $`p'_i`$ where we store the number $`i+1`$ in a vector $`\underline{X}:=X_{n-1},\ldots,X_0`$ of usual propositional variables by demanding that
MATHp'_i\models (\underline{X}=\underline{\alpha},>k) \wedge \mathrm{rightmost\_one}(\underline{X},k).Click to expand and view more -
Then we make a $`\stackrel{\Diamond}{\to}`$-step from the point $`p'_i`$ to a point $`p_{i+1}`$ in the cloud $`\mathit{C}_{i+1}`$ and demand that
MATHp_{i+1}\models (\underline{X}=\underline{\alpha}).Click to expand and view moreNote that the value of $`\underline{X}`$ is copied from $`p'_i`$ to its $`\stackrel{\Diamond}{\to}`$-successor $`p_{i+1}`$ because by the formula
MATH\mathrm{persistent}(\underline{X})Click to expand and view morewe force the vector $`\underline{X}`$ of propositional variables to be persistent.
Altogether we demand that for the number $`k`$
MATHp_i\models L\bigl((\underline{X}=\underline{\alpha},>k) \wedge \mathrm{rightmost\_one}(\underline{X},k) \wedge \Diamond(\underline{X}=\underline{\alpha}) \bigr).Click to expand and view more -
-
Additionally we need a formula to ensure that the starting value is $`0`$, that is we demand
MATHp_0\models(\underline{\alpha}=\mathrm{bin}_n(0)).Click to expand and view more
We now define the complete counter formula, for $`n>0`$.
\begin{eqnarray*}
\mathrm{\mathrm{counter}}_{\sxs,n} &:= &
\mathrm{persistent}(\underline{X}) \wedge
(\underline{\alpha}=\mathrm{bin}_n(0))
\wedge K \,\Box \Biggl(
\bigwedge_{k=0}^{n-1}\Biggl( \mathrm{rightmost\_zero}(\underline{\alpha},k) \rightarrow \\
&& L \biggl( (\underline{X}=\underline{\alpha},>k)\wedge
\mathrm{rightmost\_one}(\underline{X},k) \wedge
\Diamond(\underline{X}=\underline{\alpha}) \biggr) \Biggr)\Biggr).
\end{eqnarray*}
-
For all $`n\in\IN\setminus \{0\}`$, for every $`\sxs`$-commutator model of $`\mathrm{counter}_{\sxs,n}`$ and for every point $`p_0`$ in this model with $`p_0 \models \mathrm{counter}_{\ssl,n}`$ there exist a sequence of $`2^{n}-1`$ points $`p_1,p_2,\ldots,p_{2^n-1}`$ and a sequence of $`2^{n}-1`$ points $`p_0',p_1',\ldots,p'_{2^n-2}`$ such that
-
for $`0\leq i\leq 2^n-1`$, $`p_i\models (\underline{\alpha}=\mathrm{bin}_n(i))`$,
-
for $`0\leq i\leq 2^n-2`$, $`p_i\stackrel{L}{\to}p'_{i}`$ and $`p'_i\stackrel{\Diamond}{\to}p_{i+1}`$ and $`p'_{i}\models (\underline{X}=\mathrm{bin}_n(i+1))`$.
-
Proof. For the following let us fix some $`n>0`$.
-
MATH
W_1 := \{0,\ldots,2^n-1\} \quad \text{ and, for $i,i' \in W_1$, } i R_\Diamond i' :\iff i \leq i' .Click to expand and view moreWe define an S5-frame $`(W_2,R_L)`$ by
MATHW_2 := \{0,\ldots,2^n-1\} \quad \text{ and } \quad R_L := W_2 \times W_2 .Click to expand and view moreThen the product frame $`(W, \stackrel{\Diamond}{\to}, \stackrel{L}{\to})`$ with $`W:=W_1\times W_2`$ and with $`\stackrel{\Diamond}{\to}`$ and $`\stackrel{L}{\to}`$ defined as in is an $`\sxs`$-frame. We define the valuation $`\sigma`$ by
MATH\begin{array}{lll} \sigma(A_k) &:= & \{(i,j) ~:~ i,j \in \{0,\ldots,2^n-1\} \text{ and } k \in \mathrm{Ones}(i) \} , \\ \sigma(X_k) &:= & \{(i,j) ~:~ i,j \in \{0,\ldots,2^n-1\} \text{ and } k \in \mathrm{Ones}(j)\} , \end{array}Click to expand and view morefor $`k\in\{0,\ldots,n-1\}`$. This implies for all $`i,j\in \{0,\ldots,2^n-1\}`$
MATH(i,j) \models (\underline{\alpha}=\mathrm{bin}_n(i)) \quad \text{and} \quad (i,j) \models (\underline{X}=\mathrm{bin}_n(j)).Click to expand and view more style="width:90.0%" />
style="width:90.0%" />
An $\sxs$-product model of the formula $\mathrm{counter}_{\sxs,n}$. We claim
MATH(0,0) \models \mathrm{counter}_{\sxs,n}.Click to expand and view moreIndeed, it is clear that the propositional variables $`X_k`$ are persistent, hence, we have
MATH(0,0) \models \mathrm{persistent}(\underline{X}).Click to expand and view moreIt is also clear that
MATH(0,0) \models (\underline{\alpha}=\mathrm{bin}_n(0)).Click to expand and view moreLet us assume that for some $`(i,j) \in W`$ and some $`k\in\{0,\ldots,n-1\}`$ we have
MATH(i,j) \models \mathrm{rightmost\_zero}(\underline{\alpha},k) .Click to expand and view moreIt is sufficient to show that
MATH(i,j) \models L \biggl( (\underline{X}=\underline{\alpha},>k)\wedge \mathrm{rightmost\_one}(\underline{X},k) \wedge \Diamond(\underline{X}=\underline{\alpha}) \biggr) .Click to expand and view moreIndeed, $`(i,j) \models \mathrm{rightmost\_zero}(\underline{\alpha},k)`$ implies $`\{0,\ldots,n-1\}\setminus \mathrm{Ones}(i) \neq \emptyset`$ and $`k = \min (\{0,\ldots,n-1\}\setminus \mathrm{Ones}(i))`$. Note that this implies $`i<2^n-1`$, hence, $`(i,i+1)\in W`$ and $`(i+1,i+1)\in W`$. In view of $`(i,j)\stackrel{L}{\to}(i,i+1)\stackrel{\Diamond}{\to}(i+1,i+1)`$ it is sufficient to show
MATH(i,i+1)\models(\underline{X}=\underline{\alpha},>k)\wedge \mathrm{rightmost\_one}(\underline{X},k)Click to expand and view moreand
MATH(i+1,i+1)\models (\underline{X}=\underline{\alpha}) .Click to expand and view moreBoth claims follow from the facts that $`k=\min(\{0,\ldots,n-1\}\setminus\mathrm{Ones}(i))`$ and that every point $`(x,y)\in W`$ satisfies the formulas $`(\underline{\alpha}=\mathrm{bin}_n(x))`$ and $`(\underline{X}=\mathrm{bin}_n(y))`$.
-
The proof for $`\sxs`$-commutator models of the formula $`\mathrm{counter}_{\sxs,n}`$ is very similar to the proof for cross axiom models of the formula $`\mathrm{counter}_{\SSL,n}`$ in Proposition [prop: counter]. For completeness sake we explicate it in detail. Suppose there are an $`\sxs`$-commutator model $`M`$ of the formula $`\mathrm{counter}_{\sxs,n}`$ and a point $`p_0\in M`$ with $`M,p_0\models \mathrm{counter}_{\sxs,n}`$. We show by induction that the claimed sequences of points $`p_1,\ldots p_{2^n-1}`$ and $`p'_0,\ldots p'_{2^n-2}`$ with the claimed properties exist. In addition, we show that there exist points $`t_i`$ with $`p_0 \stackrel{L}{\to} t_i`$ and $`t_i \stackrel{\Diamond}{\to} p_i`$, for $`1\leq i \leq 2^n-1`$. Note that the sequences $`p_0,\ldots p_{2^n-1}`$ and $`p'_0,\ldots p'_{2^n-2}`$ are supposed to form a “staircase” as in Figure [figure:staircase]. By definition, $`p_0\models \mathrm{persistent}(\underline{X}) \wedge (\underline{\alpha}=\mathrm{bin}_n(0))`$. By induction hypothesis, let us assume that for some $`m`$ with $`0 \leq m<2^n-1`$ there exist $`p_1,\ldots,p_m`$ and $`p'_0,\ldots,p_{m-1}'`$ with
MATHp_0\, \stackrel{L}{\to}\, p'_0\, \stackrel{\Diamond}{\to}\, p_1\, \stackrel{L}{\to} \ldots \stackrel{L}{\to}\, p'_{m-1}\, \stackrel{\Diamond}{\to}\, p_m ,Click to expand and view morewith
MATHp_i\models (\underline{\alpha}=\mathrm{bin}_n(i)) ,Click to expand and view morefor $`0\leq i \leq m`$, and with
MATHp'_i\models (\underline{X}=\mathrm{bin}_n(i+1)) ,Click to expand and view morefor $`0\leq i < m`$, and that there are $`t_i`$ with $`p_0 \stackrel{L}{\to} t_i`$ and $`t_i \stackrel{\Diamond}{\to} p_i`$, for $`1\leq i \leq m`$. Since $`m<2^n-1`$, the set $`\{0,\ldots,n-1\}\setminus\mathrm{Ones}(m)`$ is nonempty. With $`k:= \min(\{0,\ldots,n-1\}\setminus\mathrm{Ones}(m))`$ we have
MATHp_m\models \mathrm{rightmost\_zero}(\underline{\alpha},k).Click to expand and view moreDue to $`p_0\models \mathrm{counter}_{\sxs,n}`$ as well as $`p_0 \stackrel{L}{\to} t_m \stackrel{\Diamond}{\to} p_m`$ this implies
MATHp_m \models L \bigl( (\underline{X}=\underline{\alpha},>k) \wedge \mathrm{rightmost\_one}(\underline{X},k) \\ \wedge \Diamond(\underline{X}=\underline{\alpha}) \bigr) .Click to expand and view moreThus, there must exist points $`p'_m`$ and $`p_{m+1}`$ satisfying $`p_m\stackrel{L}{\to} p'_m \stackrel{\Diamond}{\to}p_{m+1}`$ as well as
MATHp'_m \models(\underline{X}=\underline{\alpha},>k) \wedge \mathrm{rightmost\_one}(\underline{X},k)Click to expand and view moreand
MATHp_{m+1} \models (\underline{X}=\underline{\alpha}) .Click to expand and view moreWe have to show
MATHp'_m \models(\underline{X}=\mathrm{bin}_n(m+1))Click to expand and view moreand
MATHp_{m+1} \models B\wedge(\underline{\alpha}=\mathrm{bin}_n(m+1)) .Click to expand and view moreDue to the fact that $`p'_m`$ is an element of the same cloud as $`p_m`$, and $`\underline{\alpha}`$ has the same value in all points in a cloud we obtain
MATHp'_m \models (\underline{\alpha}=\mathrm{bin}_n(m)) .Click to expand and view moreTogether with
MATHp'_m \models(\underline{X}=\underline{\alpha},>k) \wedge \mathrm{rightmost\_one}(\underline{X},k)Click to expand and view morethis implies
MATHp'_m \models(\underline{X}=\mathrm{bin}_n(m+1))Click to expand and view more(the values of the leading bits $`\alpha_{n-1},\ldots,\alpha_{k+1}`$ of $`\underline{\alpha}`$ are copied to the leading bits $`X_{n-1},\ldots,X_{k+1}`$ and the other bits are defined explicitly by $`p'_{m} \models \mathrm{rightmost\_one}(\underline{X},k)`$ so that the binary value of $`\underline{X}`$ is $`m+1`$). From $`p_0 \models \mathrm{persistent}(\underline{X})`$ as well as $`p_0 \stackrel{L}{\to} t_m \stackrel{\Diamond}{\to} p'_m \stackrel{\Diamond}{\to} p_{m+1}`$ we obtain $`p_{m+1} \models (\underline{X}=\mathrm{bin}_n(m+1))`$. Using $`p_{m+1} \models (\underline{X}=\underline{\alpha})`$ we obtain $`p_{m+1} \models (\underline{\alpha}=\mathrm{bin}_n(m+1))`$. Finally, the left commutativity property applied to $`t_m \stackrel{\Diamond}{\to} p_m`$ and $`p_m \stackrel{L}{\to} p'_m`$ implies that there exists a point $`t_{m+1}`$ with $`t_m \stackrel{L}{\to} t_{m+1}`$ and $`t_{m+1} \stackrel{\Diamond}{\to} p'_m`$. Using additionally $`p_0 \stackrel{L}{\to} t_m`$ and $`p'_m \stackrel{\Diamond}{\to} p_{m+1}`$ we obtain $`p_0 \stackrel{L}{\to} t_{m+1}`$ and $`t_{m+1} \stackrel{\Diamond}{\to} p_{m+1}`$. This ends the proof of the second assertion.
◻
Construction of the Formula
Let $`L \in \EXPSPACE`$ be an arbitrary language over some alphabet $`\Sigma`$, that is, $`L \subseteq \Sigma^*`$. We are going to show that there is a logspace computable function $`f_\sxs`$ mapping strings to strings such that, for any $`w\in\Sigma^*`$,
-
$`f_\sxs(w)`$ is a bimodal formula and
-
$`f_\sxs(w)`$ is $`\sxs`$-satisfiable if, and only if, $`w \in L`$.
Once we have shown this, we have shown the result.
In order to define this desired reduction function $`f_\sxs`$, we are going to make use of an Alternating Turing Machine for $`L`$. Since $`\EXPSPACE = \mathrm{AEXPTIME}`$, there exist an Alternating Turing Machine $`M = (Q, \Sigma, \Gamma, q_0, \delta)`$ and a univariate polynomial $`p`$ such that $`M`$ accepts $`L`$, that is, $`L(M)=L`$, and such that the time used by $`M`$ on arbitrary input of length $`n`$ is bounded by $`2^{p(n)}-1`$. We can assume without loss of generality $`Q=\{0,\ldots,|Q|-1\}`$, $`\Gamma=\{0,\ldots,|\Gamma|-1\}`$, that the coefficients of the polynomial $`p`$ are natural numbers and that, for all $`n\in\IN`$, we have $`p(n) \geq n`$ and $`p(n)\geq 1`$. In the following, whenever we have fixed some $`n\in\IN`$, we set
N:=p(n) .Let us consider an input string $`w \in\Sigma^n`$ of length $`n`$, for some $`n \in\IN`$, and let us sketch the main idea of the construction of the formula $`f_\sxs(w)`$. The formula $`f_\sxs(w)`$ will describe the possible computations of $`M`$ on input $`w`$ in the following sense: any $`\sxs`$-product model of $`f_\sxs(w)`$ will essentially contain an accepting tree of $`M`$ on input $`w`$, and if there exists an accepting tree of $`M`$ on input $`w`$ then one can turn this into an $`\sxs`$-product model of $`f_\sxs(w)`$. In such a model, any node in an accepting tree of $`M`$ on input $`w`$ will be modeled by a cloud (that is, by an $`\stackrel{L}{\to}`$-equivalence class) in which certain shared variables (we use the notion “shared variables” in the same sense as in Subsection 7.1) will have values that describe the data of the computation node that are important in this computation step. Which data are these? First of all, we need the time of the computation node. We assume that the computation starts with the initial configuration of $`M`$ on input $`w`$ at time $`0`$. Since the ATM $`M`$ needs at most $`2^N-1`$ time steps, we can store the time of each computation node in a binary counter counting from $`0`$ to $`2^N-1`$. Since during each time step at most one additional cell either to the right or to the left of the previous cell can be visited, we can describe any configuration reachable during a computation of $`M`$ on input $`w`$ by the following data:
-
the state $`q \in Q`$ of the configuration,
-
the current content of the tape, given by a string in $`\Gamma^{2 \cdot (2^N-1)+1} = \Gamma^{2^{N+1}-1}`$,
-
the current position of the tape head, given by a number in $`\{0,\ldots,2^{N+1}-2\}`$.
We assume that in the initial configuration on input $`w`$ the tape content is $`\#^{2^N}w\#^{2^N-1-n}`$ (remember that we use $`\#`$ for the blank symbol) and that the tape head scans the blank $`\#`$ to the left of the first symbol of $`w`$, that is, the position of the tape head is $`2^{N}-1`$. If a cloud in an $`\sxs`$-product model of $`f_\sxs(w)`$ describes a computation node of $`M`$ on input $`w`$ then in this cloud the following shared variables will have the following values:
-
a vector $`\underline{\alpha}^\mathrm{time}= (\alpha^\mathrm{time}_{N-1},\ldots,\alpha^\mathrm{time}_0)`$ giving in binary the current time of the computation,
-
a vector $`\underline{\alpha}^\mathrm{pos}= (\alpha^\mathrm{pos}_{N},\ldots,\alpha^\mathrm{pos}_0)`$ giving in binary the current position of the tape head,
-
a vector $`\underline{\alpha}^\mathrm{state}= (\alpha^\mathrm{state}_0,\ldots,\alpha^\mathrm{state}_{|Q|-1})`$ giving in unary the current state of the computation (here “unary” means: exactly one of the shared variables $`\alpha^\mathrm{state}_i`$ will be true, namely the one with $`i`$ being the current state),
-
a vector $`\underline{\alpha}^\mathrm{read}= (\alpha^\mathrm{read}_0,\ldots,\alpha^\mathrm{read}_{|\Gamma|-1})`$ giving in unary the symbol in the current cell (here “unary” means: exactly one of the shared variables $`\alpha^\mathrm{read}_i`$ will be true, namely the one with $`i`$ being the symbol in the current cell),
-
a vector $`\underline{\alpha}^\mathrm{written}= (\alpha^\mathrm{written}_{0},\ldots,\alpha^\mathrm{written}_{|\Gamma|-1})`$ giving in unary the symbol that has just been written into the cell that has just been left, unless the cloud corresponds to the first node in the computation tree — in that case the value of this vector is irrelevant (here “unary” means: exactly one of the variables $`\alpha^\mathrm{written}_i`$ will be true, namely the one with $`i`$ being the symbol that has just been written),
-
a vector $`\underline{\alpha}^\mathrm{prevpos}= (\alpha^\mathrm{prevpos}_{N},\ldots,\alpha^\mathrm{prevpos}_0)`$ giving in binary the previous position of the tape head, that is, the position of the cell that has just been left, unless the cloud corresponds to the first node in the computation tree — in that case the value of this vector is irrelevant.
The formula $`f_\sxs(w)`$ has to ensure that for any possible
computation step starting from such a computation node in an accepting
tree there exists a cloud describing the corresponding successor node in
the accepting tree. In this new cloud, the value of the counter for the
time $`\underline{\alpha}^\mathrm{time}`$ has to be incremented. This
can be done by the technique for implementing a binary counter in
$`\sxs`$ that was described in
Subsection 7.1. In parallel, we have
to make sure that in this new cloud also the vectors
$`\underline{\alpha}^\mathrm{pos}`$,
$`\underline{\alpha}^\mathrm{state}`$,
$`\underline{\alpha}^\mathrm{read}`$,
$`\underline{\alpha}^\mathrm{written}`$, and
$`\underline{\alpha}^\mathrm{prevpos}`$ are set to the right values. The
vector $`\underline{\alpha}^\mathrm{prevpos}`$ is a copy of the vector
$`\underline{\alpha}^\mathrm{pos}`$ in the previous cloud (we will see
below how one can copy it). For the vectors
$`\underline{\alpha}^\mathrm{pos}`$,
$`\underline{\alpha}^\mathrm{state}`$, and
$`\underline{\alpha}^\mathrm{written}`$ these values can be computed
using the corresponding element of the transition relation $`\delta`$ of
the ATM. For example, $`\underline{\alpha}^\mathrm{pos}`$ has to be
decremented by one if the tape head moves to the left, and it has to be
incremented by one if the tape head moves to the right. Also the new
state (to be stored in $`\underline{\alpha}^\mathrm{state}`$) and the
symbol written into the cell that has just been left (to be stored in
$`\underline{\alpha}^\mathrm{written}`$) are determined by the data of
the previous computation node and by the corresponding element of the
transition relation $`\delta`$.
But the vector $`\underline{\alpha}^\mathrm{read}`$ is supposed to
describe the symbol in the current cell. This symbol is not determined
by the current computation step but has either been written the last
time when this cell has been visited during this computation or, when
this cell has never been visited before, the symbol in this cell is
still the one that was contained in this cell before the computation
started. How can one ensure that $`\underline{\alpha}^\mathrm{read}`$ is
set to the right value? We will do this by using persistent variables
and a variable $`B^\mathrm{active}`$ that is neither shared nor
persistent. We will ensure that any cloud corresponding to a node in the
computation tree in which the cell $`i`$ is being visited contains a
point with a persistent position vector
$`\underline{X}^\mathrm{pos}=\mathrm{bin}_{N+1}(i)`$ and with a
persistent time vector $`\underline{X}^\text{time-apv}`$ that will be
forced to contain in binary form the time one step after the previous
visit of the cell $`i`$ or, if the cell $`i`$ has not been visited
before, to contain the value $`0`$. Furthermore, there will be a third
persistent vector $`\underline{X}^\mathrm{read}`$. If the cell $`i`$ has
not been visited before then we will make sure that the vector
$`\underline{X}^\mathrm{read}`$ encodes the initial symbol contained in
cell $`i`$. If the cell $`i`$ has been visited before then we will make
sure that the vector $`\underline{X}^\mathrm{read}`$ encodes the symbol
that has been written into the cell during the previous visit of the
cell. In order to do that we need to determine the time of the previous
visit. For that the Boolean variable $`B^\mathrm{active}`$ is used and
the fact that due to the left commutativity property the point has
$`\stackrel{\Diamond}{\to}`$-predecessors in all clouds corresponding to
any node on the path in the accepting tree from the root to the current
cloud. Then, when one knows this time, one can look at the shared
variable vector $`\underline{\alpha}^\mathrm{written}`$ in the cloud
corresponding to the step after the previous visit of this cell (this
shared variable vector encodes the symbol that has just been written
into the cell) and can copy its value to the persistent variable vector
$`\underline{X}^\mathrm{read}`$. In order to implement all this we use
the following persistent variables:
-
a vector $`\underline{X}^\text{time-apv}= (X^\text{time-apv}_{N-1},\ldots,X^\text{time-apv}_0)`$ containing in binary the time one step after the previous visit of the current cell (the exponent of $`X^\text{time-apv}_i`$ stands for “time after previous visit”) or, if the current cell has not been visited before, containing in binary the number $`0`$,
-
a vector $`\underline{X}^\mathrm{pos}= (X^\mathrm{pos}_{N},\ldots,X^\mathrm{pos}_0)`$ containing in binary the current position of the tape head, that is, the position of the current cell,
-
a vector $`\underline{X}^\mathrm{read}= (X^\mathrm{read}_{0},\ldots,X^\mathrm{read}_{|\Gamma|-1})`$ giving in unary the symbol in the cell described by $`\underline{X}^\mathrm{pos}`$ (here “unary” means: exactly one of the shared variables $`\alpha^\mathrm{read}_i`$ will be true, namely the one with $`i`$ being the symbol in the cell described by $`\underline{X}^\mathrm{pos}`$),
In fact, the current cell may have been visited several times already. Of course only the $`\stackrel{\Diamond}{\to}`$-successor of the point corresponding to the previous visit (that is, corresponding to the very last visit of the cell before the current visit, not earlier visits) should be allowed to copy the value of its vector $`\underline{\alpha}^\mathrm{written}`$ to $`\underline{X}^\mathrm{read}`$. In order to determine the right point, we are going to use an additional Boolean
- variable $`B^\mathrm{active}`$ (which is neither persistent nor shared) saying whether the current point is active or not.
We shall explain later how all this works. Finally, there are two more vectors of persistent variables that are needed for changing the values of the shared variable vectors $`\underline{\alpha}^\mathrm{time}`$ and $`\underline{\alpha}^\mathrm{pos}`$:
-
a vector $`\underline{X}^\mathrm{prevtime}= (X^\mathrm{prevtime}_{N-1},\ldots,X^\mathrm{prevtime}_0)`$ containing in binary the current time of the computation minus one, unless the cloud corresponds to the first node in the computation tree — in that case the value of this vector is irrelevant,
-
a vector $`\underline{X}^\mathrm{prevpos}= (X^\mathrm{prevpos}_{N},\ldots,X^\mathrm{prevpos}_0)`$ containing in binary the previous position of the tape head, that is, the position of the cell that has just been left, unless the cloud corresponds to the first node in the computation tree — in that case the value of this vector is irrelevant.
Now we come to the formal definition of the formula $`f_\sxs(w)`$. The formula $`f_\sxs(w)`$ will have the following structure:
\begin{eqnarray*}
f_\sxs(w)
&:= & \mathit{persistence} \\
&& \wedge K\Box \mathit{uniqueness} \\
&& \wedge \mathit{start} \\
&& \wedge K\Box \mathit{initial\_symbols} \\
&& \wedge K\Box \mathit{written\_symbols} \\
&& \wedge K\Box \mathit{read\_a\_symbol} \\
&& \wedge K\Box \mathit{computation} \\
&& \wedge K\Box \mathit{no\_reject} .
\end{eqnarray*}The formula $`f_\sxs(w)`$ will contain the following propositional variables:
\begin{eqnarray*}
&& A^\mathrm{time}_{N-1}, \ldots, A^\mathrm{time}_{0},
A^\mathrm{pos}_{N}, \ldots, A^\mathrm{pos}_{0},
A^\mathrm{state}_{0}, \ldots, A^\mathrm{state}_{|Q|-1},
A^\mathrm{written}_{0}, \ldots, A^\mathrm{written}_{|\Gamma|-1},
A^\mathrm{read}_{0},\ldots, A^\mathrm{read}_{|\Gamma|-1}, \\
&& A^\mathrm{prevpos}_{N}, \ldots, A^\mathrm{prevpos}_{0}, \\
&& X^\mathrm{prevtime}_{N-1},\ldots, X^\mathrm{prevtime}_{0},
X^\mathrm{prevpos}_{N},\ldots, X^\mathrm{prevpos}_{0},
X^\mathrm{pos}_{N}, \ldots, X^\mathrm{pos}_{0},
X^\text{time-apv}_{N-1}, \ldots, X^\text{time-apv}_{0}, \\
&& X^\mathrm{read}_{0},\ldots, X^\mathrm{read}_{|\Gamma|-1}, \\
&& B^\mathrm{active} .
\end{eqnarray*}For $`\mathit{string} \in\{\mathrm{time}, \mathrm{pos}, \mathrm{state}, \mathrm{read}, \mathrm{prevpos}, \mathrm{written}\}`$ and natural numbers $`i`$ we use $`\alpha^\mathit{string}_i`$ as an abbreviation for $`L A^\mathit{string}_i`$. These formulas $`\alpha^\mathit{string}_i`$ are the shared variables we talked about above.
We are now going to define the subformulas of $`f_\sxs(w)`$. We will use the abbreviations introduced above, in Table [table:abbrev1], in Table 1, and in Table 2.
The following formula makes sure that certain propositional variables are persistent:
\begin{eqnarray*}
\mathit{persistence}
&:=& \mathrm{persistent}({\underline{X}^\mathrm{prevtime}})
\wedge \mathrm{persistent}({\underline{X}^\mathrm{prevpos}}) \\
&& \wedge \mathrm{persistent}({\underline{X}^\mathrm{pos}})
\wedge \mathrm{persistent}({\underline{X}^\text{time-apv}})
\wedge \mathrm{persistent}({\underline{X}^\mathrm{read}}) .
\end{eqnarray*}The following formula makes sure that in each of the vectors of shared or persistent variables that describe in a unary way the current state respectively the written symbol exactly one variable is true:
\begin{eqnarray*}
\mathit{uniqueness}&:=&
\mathrm{unique}({\underline{\alpha}^\mathrm{state}})
\wedge \mathrm{unique}({\underline{\alpha}^\mathrm{written}})
\wedge \mathrm{unique}({\underline{X}^\mathrm{read}}).
\end{eqnarray*}The vector $`\underline{\alpha}^\mathrm{read}`$ will satisfy the same uniqueness condition automatically due to another formula (due to the formula $`\mathit{read\_a\_symbol}`$).
The following formula ensures that the shared variables in the cloud corresponding to the first node in a computation tree have the correct values. The computation starts at time $`0`$ with the tape head at position $`2^N-1`$ and in the state $`q_0`$. The vector $`\underline{\alpha}^\mathrm{read}`$ will automatically get the correct value $`\#`$ due to the formulas $`\mathit{read\_a\_symbol}`$ and $`\mathit{initial\_symbols}`$, that will be introduced next. For the vectors $`\underline{\alpha}^\mathrm{prevpos}`$ and $`\underline{\alpha}^\mathrm{written}`$ we do not need to fix any values.
\begin{eqnarray*}
\mathit{start}
&:= & \phantom{\wedge} (\underline{\alpha}^\mathrm{time}=\bin_N(0))
\wedge (\underline{\alpha}^\mathrm{pos}=\bin_{N+1}(2^N-1))
\wedge \alpha^\mathrm{state}_{q_0} .
\end{eqnarray*}The following formula ensures that whenever an initial symbol on the tape is requested (by a point with persistent time $`\underline{X}^\text{time-apv}`$ equal to $`0`$) it is stored in a persistent vector $`\underline{X}^\mathrm{read}`$ of this point.
\begin{eqnarray*}
\lefteqn{\mathit{initial\_symbols}} && \\
&:= & (\underline{X}^\text{time-apv}=\mathrm{bin}_N(0)) \\
&& \rightarrow \Biggl(
\bigwedge_{i=1}^n \bigl( (\underline{X}^\mathrm{pos}=\mathrm{bin}_{N+1}(2^{N}-1+i))
\rightarrow X^\mathrm{read}_{w_i} \bigr) \\
&& \qquad
\wedge \bigl(\bigl( (\underline{X}^\mathrm{pos} \leq \mathrm{bin}_{N+1}(2^{N}-1))
\vee (\underline{X}^\mathrm{pos} > \mathrm{bin}_{N+1}(2^{N}-1+n)) \bigr)
\rightarrow X^\mathrm{read}_{\#} \bigr) \Biggr).
\end{eqnarray*}We explain this formula. By another formula we will ensure that whenever a cell is visited for the first time there will be an “active” point storing the position of this cell in a persistent vector $`\underline{X}^\mathrm{pos}`$ and such that its persistent time vector $`\underline{X}^\text{time-apv}`$ has the binary value $`0`$. The formula above ensures that the persistent vector $`\underline{X}^\mathrm{read}`$ in this point stores the correct initial symbol in this cell. This is either a symbol $`w_i`$ of the input string $`w=w_1\ldots w_n`$ or the blank $`\#`$.
The following formula ensures that whenever a symbol that has just been written on the tape is requested (by an active point with the correct persistent time $`\underline{X}^\text{time-apv}`$) then it is copied into a persistent vector $`\underline{X}^\mathrm{read}`$ of this point.
\begin{eqnarray*}
\lefteqn{\mathit{written\_symbols}} && \\
&:=& \bigl((\underline{X}^\text{time-apv} > \mathrm{bin}_N(0))
\wedge (\underline{X}^\text{time-apv} = \underline{\alpha}^\mathrm{time})
\wedge B^\mathrm{active} \bigr)
\rightarrow (\underline{X}^\mathrm{read} = \underline{\alpha}^\mathrm{written}) .
\end{eqnarray*}The following formula ensures that the shared variable vector $`\underline{\alpha}^\mathrm{read}`$ describes the symbol in the current cell.
\begin{eqnarray*}
\mathit{read\_a\_symbol}
&:=& \mathit{existence\_of\_a\_reading\_point} \\
&& \wedge \mathit{time\_of\_previous\_visit} \\
&& \wedge \mathit{becoming\_inactive} \\
&& \wedge \mathit{staying\_inactive} \\
&& \wedge \mathit{storing\_the\_read\_symbol},
\end{eqnarray*}where
\begin{eqnarray*}
\lefteqn{\mathit{existence\_of\_a\_reading\_point}} && \\
&:=& L\bigl( ( \underline{X}^\mathrm{pos} = \underline{\alpha}^\mathrm{pos} )
\wedge (\underline{X}^\text{time-apv} \leq \underline{\alpha}^\mathrm{time} )
\wedge B^\mathrm{active}\bigr) , \\
\lefteqn{\mathit{time\_of\_previous\_visit}} && \\
&:=& \Bigl( \bigl(( \underline{X}^\text{time-apv} > \mathrm{bin}_N(0) )
\wedge( \underline{X}^\text{time-apv} = \underline{\alpha}^\mathrm{time})
\wedge B^\mathrm{active} \bigr)
\rightarrow
( \underline{X}^\mathrm{pos} = \underline{\alpha}^\mathrm{prevpos}) \Bigr), \\
\lefteqn{\mathit{becoming\_inactive}} && \\
&:=& \Bigl( \bigl(( \underline{X}^\mathrm{pos}=\underline{\alpha}^\mathrm{prevpos} )
\wedge (\underline{X}^\text{time-apv} < \underline{\alpha}^\mathrm{time}) \bigr) \rightarrow
\neg B^\mathrm{active} \Bigr), \\
\lefteqn{\mathit{staying\_inactive}} && \\
&:=& \Bigl( \neg B^\mathrm{active} \rightarrow \Box \neg B^\mathrm{active} \Bigr), \\
\lefteqn{\mathit{storing\_the\_read\_symbol}} && \\
&:=& \Bigl( \bigl( (\underline{X}^\mathrm{pos}=\underline{\alpha}^\mathrm{pos} )
\wedge (\underline{X}^\text{time-apv} \leq \underline{\alpha}^\mathrm{time} )
\wedge B^\mathrm{active} \bigr) \rightarrow
(\underline{\alpha}^\mathrm{read} = \underline{X}^\mathrm{read}) \Bigr) .
\end{eqnarray*}We explain these formulas. The formula $`\mathit{existence\_of\_a\_reading\_point}`$ enforces the existence of an “active” point in the current cloud that contains in the persistent vector $`\underline{X}^\mathrm{pos}`$ the number of the current cell and that we wish to force to contain in the persistent vector $`\underline{X}^\text{time-apv}`$ the time one step after the previous visit of this cell, if this cell has been visited before, or the value $`0`$, otherwise. How can we enforce that? We make essential use of the left commutativity property. The point whose existence is ensured by the formula $`\mathit{existence\_of\_a\_reading\_point}`$ has $`\stackrel{\Diamond}{\to}`$-predecessors in all clouds corresponding to the nodes on the path in the accepting tree from the root to the node corresponding to the current cloud. Since we demand $`\underline{X}^\text{time-apv} \leq \underline{\alpha}^\mathrm{time}`$ the time stored in binary in the persistent variable $`\underline{X}^\text{time-apv}`$ must be identical with the time of one of the clouds corresponding to a node on this path. The formula $`\mathit{time\_of\_previous\_visit}`$ ensures that if it is positive then it can be equal to the time $`\underline{\alpha}^\mathrm{time}`$ of a cloud corresponding to a node on this path only when $`\underline{X}^\mathrm{pos} = \underline{\alpha}^\mathrm{prevpos}`$, that is, only when in the step leading to this node something has been written into the current cell. So, if the current cell has not been visited before, the binary value of $`\underline{X}^\text{time-apv}`$ must be $`0`$. Then the formula $`\mathit{initial\_symbols}`$ will ensure that the persistent variable $`\underline{X}^\mathrm{read}`$ gets the correct value. Otherwise, when the cell has been visited before, in fact, it may have been visited several times already. In this case, we have to make sure that the number stored in $`\underline{X}^\text{time-apv}`$ is the time after the very last visit to this cell immediately before the current visit. This is ensured by the formulas $`\mathit{becoming\_inactive}`$ and $`\mathit{staying\_inactive}`$. If the number stored in $`\underline{X}^\text{time-apv}`$ were strictly smaller than the the time after the very last visit to this cell immediately before the current visit then, due to $`\mathit{becoming\_inactive}`$ the corresponding point would be set to “inactive”, and, due to $`\mathit{staying\_inactive}`$, also its $`\stackrel{\Diamond}{\to}`$-successor would stay inactive. But this would apply also to the point in the current cloud which is supposed to be active and to contain the correct value in $`\underline{X}^\text{time-apv}`$ according to formula $`\mathit{existence\_of\_a\_reading\_point}`$. Thus, the first four subformulas of $`\mathit{read\_a\_symbol}`$ ensure that the current cloud contains an active point that contains in the persistent vector $`\underline{X}^\mathrm{pos}`$ the number of the current cell and that contains in the persistent vector $`\underline{X}^\text{time-apv}`$ the time one step after the previous visit of this cell, if this cell has been visited before, or the value $`0`$, otherwise. Finally, the formula $`\mathit{storing\_the\_read\_symbol}`$ makes sure that the value of $`\underline{X}^\mathrm{read}`$ (which contains the symbol written into the current cell during the previous visit of this cell, or, if the current cell has not been visited before, the initial symbol in this cell) is copied into the shared variable vector $`\underline{\alpha}^\mathrm{read}`$.
Next, we wish to define the formula $`\mathit{computation}`$ that describes the computation steps. We have to distinguish between the two cases whether the tape head is going to move to the left or to the right. If in a computation step the symbol $`\theta\in\Gamma`$ is written into the current cell, if the tape head moves to the right, and if the new state after this step is the state $`r \in Q`$, then the following formula $`\mathit{compstep}_{\mathrm{right}}(r,\theta)`$ guarantees the existence of a point and its cloud with suitable values in the shared variable vectors $`\underline{\alpha}^\mathrm{time}, \underline{\alpha}^\mathrm{pos}, \underline{\alpha}^\mathrm{prevpos}, \underline{\alpha}^\mathrm{state}, \underline{\alpha}^\mathrm{written}`$.
We explain this formula. The first four lines of this formula take care that the two binary counters $`\underline{\alpha}^\mathrm{time}`$ and $`\underline{\alpha}^\mathrm{pos}`$ for the current time and for the current position of the tape head are incremented at the same time. This is similar to the formula $`\mathrm{counter}_{\sxs,n}`$ in Subsection 7.1. Furthermore, also the persistent vectors $`\underline{X}^\mathrm{prevtime}`$ (that we will not need otherwise) and $`\underline{X}^\mathrm{prevpos}`$ (that we use again in the fifth line of this formula) get the correct values. The fifth line ensures that the shared variable vectors $`\underline{\alpha}^\mathrm{prevpos}`$, $`\underline{\alpha}^\mathrm{state}`$ and $`\underline{\alpha}^\mathrm{written}`$ of the current point get the correct values. The shared variable vector $`\underline{\alpha}^\mathrm{read}`$ will get the correct value due to the formulas $`\mathit{initial\_symbols}`$, $`\mathit{written\_symbols}`$, and $`\mathit{read\_a\_symbol}`$.
\begin{eqnarray*}
\mathit{compstep}_{\mathrm{right}}(r,\theta)
&:=& \bigwedge_{k=0}^{N-1} \bigwedge_{l=0}^{N}
\Biggl( \bigl( \mathrm{rightmost\_zero}(\underline{\alpha}^\mathrm{time},k)
\wedge \mathrm{rightmost\_zero}(\underline{\alpha}^\mathrm{pos},l) \bigr) \\
&& \rightarrow L \biggl( (\underline{X}^\mathrm{prevtime}=\underline{\alpha}^\mathrm{time})
\wedge (\underline{X}^\mathrm{prevpos}=\underline{\alpha}^\mathrm{pos}) \\
&& \phantom{\rightarrow L \biggl(} \wedge \Diamond \Bigl(
(\underline{\alpha}^\mathrm{time}=\underline{X}^\mathrm{prevtime},>k)
\wedge \mathrm{rightmost\_one}(\underline{\alpha}^\mathrm{time},k) \\
&& \phantom{\rightarrow L \biggl( \wedge \Diamond \Bigl(}
\wedge (\underline{\alpha}^\mathrm{pos}=\underline{X}^\mathrm{prevpos}>l)
\wedge \mathrm{rightmost\_one}(\underline{\alpha}^\mathrm{pos},l) \\
&& \phantom{\rightarrow L \biggl( \wedge \Diamond \Bigl(}
\wedge (\underline{\alpha}^\mathrm{prevpos}=\underline{X}^\mathrm{prevpos})
\wedge \alpha^\mathrm{state}_{r}
\wedge \alpha^\mathrm{written}_\theta
\Bigr) \biggr) \Biggr).
\end{eqnarray*}If in a computation step the symbol $`\theta\in\Gamma`$ is written into the current cell, if the tape head moves to the left, and if the new state after this step is the state $`r \in Q`$, then the following formula guarantees the existence of a point and its cloud with suitable values in the shared variables.
\begin{eqnarray*}
\mathit{compstep}_{\mathrm{left}}(r,\theta)
&:=& \bigwedge_{k=0}^{N-1} \bigwedge_{l=0}^{N}
\Biggl( \bigl( \mathrm{rightmost\_zero}(\underline{\alpha}^\mathrm{time},k)
\wedge \mathrm{rightmost\_one}(\underline{\alpha}^\mathrm{pos},l) \bigr) \\
&& \rightarrow L \biggl( (\underline{X}^\mathrm{prevtime}=\underline{\alpha}^\mathrm{time})
\wedge (\underline{X}^\mathrm{prevpos}=\underline{\alpha}^\mathrm{pos}) \\
&& \phantom{\rightarrow L \biggl(} \wedge \Diamond \Bigl(
(\underline{\alpha}^\mathrm{time}=\underline{X}^\mathrm{prevtime},>k)
\wedge \mathrm{rightmost\_one}(\underline{\alpha}^\mathrm{time},k) \\
&& \phantom{\rightarrow L \biggl( \wedge \Diamond \Bigl(}
\wedge (\underline{\alpha}^\mathrm{pos}=\underline{X}^\mathrm{prevpos},>l)
\wedge \mathrm{rightmost\_zero}(\underline{\alpha}^\mathrm{pos},l) \\
&& \phantom{\rightarrow L \biggl( \wedge \Diamond \Bigl(}
\wedge (\underline{\alpha}^\mathrm{prevpos}=\underline{X}^\mathrm{prevpos})
\wedge \alpha^\mathrm{state}_{r}
\wedge \alpha^\mathrm{written}_\theta
\Bigr) \biggr) \Biggr).
\end{eqnarray*}This formula is very similar to the previous one with the exception that here the binary counter for the position of the tape head is decremented.
The computation is modeled by the following subformula. Remember that $`Q`$ is the disjoint union of the sets $`\{q_{\mathrm{accept}}\}`$, $`\{q_{\mathrm{reject}}\}`$, $`Q_{\forall}`$, $`Q_{\exists}`$.
\begin{eqnarray*}
\mathit{computation}
&:=& \bigwedge_{q \in Q_\forall} \bigwedge_{\eta \in\Gamma}
\Biggl( (\alpha^\mathrm{state}_q \wedge \alpha^\mathrm{read}_\eta) \rightarrow \\
&& \biggl( \bigwedge_{(r,\theta,\mathit{left}) \in \delta(q,\eta)} \mathit{compstep}_{\mathrm{left}}(r,\theta)
\wedge \bigwedge_{(r,\theta,\mathit{right}) \in \delta(q,\eta)} \mathit{compstep}_{\mathrm{right}}(r,\theta) \biggr) \Biggr) \\
&& \wedge \bigwedge_{q \in Q_\exists} \bigwedge_{\eta \in\Gamma}
\Biggl( (\alpha^\mathrm{state}_q \wedge \alpha^\mathrm{read}_\eta) \rightarrow \\
&& \biggl( \bigvee_{(r,\theta,\mathit{left}) \in \delta(q,\eta)} \mathit{compstep}_{\mathrm{left}}(r,\theta)
\vee \bigvee_{(r,\theta,\mathit{right}) \in \delta(q,\eta)} \mathit{compstep}_{\mathrm{right}}(r,\theta) \biggr) \Biggr) \Biggr) .
\end{eqnarray*}Finally, the subformula $`\mathit{no\_reject}`$ is defined as follows.
\mathit{no\_reject} :=
\neg \alpha^\mathrm{state}_{q_{\mathrm{reject}}} .We have completed the description of the formula $`f_\sxs(w)`$ for $`w\in \Sigma^*`$. It is clear that $`f_\sxs(w)`$ is a bimodal formula, for any $`w \in\Sigma^*`$. We still have to show two claims:
-
The function $`f_\sxs`$ can be computed in logarithmic space.
-
For any $`w \in\Sigma^*`$,
MATHw \in L \iff \text{ the bimodal formula $f_\sxs(w)$ is $\sxs$-satisfiable.}Click to expand and view more
The first claim is shown in the following section. The two directions of the equivalence in the second claim are shown afterwards in separate sections.
LOGSPACE Computability of the Reduction
We wish to show that the function $`f_\sxs`$ can be computed in logarithmic space. This is shown by the same argument as the corresponding claim for the function $`f_\ssl`$ in Subsection 4.2.
Construction of a Model
In this section we show for any $`w \in\Sigma^*`$, if $`w \in L`$ then the bimodal formula $`f_\sxs(w)`$ is $`\sxs`$-satisfiable. Let us assume $`w \in L`$. We are going to explicitly define an $`\sxs`$-product model of $`f_\sxs(w)`$.
There exists an accepting tree $`T=(V,E,c)`$ of $`M`$ on input $`w`$, where $`V`$ is the set of nodes of $`T`$, where $`E \subseteq V\times V`$ is the set of edges, and where the function $`c:V\to Q \times \{0,\ldots,2^{N+1}-2\}\times \Gamma^{2^{N+1}-1}`$ labels each node with a configuration (remember the discussion about the description of configurations at the beginning of Subsection 7.2). Let $`\mathit{root} \in V`$ be the root of $`T`$. We will now construct an $`\sxs`$-product model of $`f_\sxs(w)`$. We define an $`S4`$-frame $`(W_1,R_\Diamond)`$ by
W_1 := V \quad \text{ and } \quad R_\Diamond:= \text{ the reflexive-transitive closure of } E .That means, for any $`v,v' \in W_1`$ we have $`v R_\Diamond v'`$ iff in the tree $`T`$ there is a path from $`v`$ to $`v'`$. We define an $`S5`$-frame $`(W_2,R_L)`$ by
W_2 := V \quad \text{ and } \quad R_L := W_2 \times W_2 .Then the product frame $`(W, \stackrel{\Diamond}{\to}, \stackrel{L}{\to})`$ with $`W:=W_1\times W_2`$ and with $`\stackrel{\Diamond}{\to}`$ and $`\stackrel{L}{\to}`$ defined as in is an $`\sxs`$-product frame. We still need to define a suitable valuation $`\sigma`$. We define the valuation $`\sigma`$ as follows.
\begin{eqnarray*}
\sigma(A^\mathrm{time}_k) &:=& \{(v,x) ~:~ v,x \in V
\text{ and } k \in \mathrm{Ones}(\mathit{time}(v)) \}, \\
\sigma(X^\mathrm{prevtime}_k) &:=& \{(v,x) ~:~ v\in V, x \in V\setminus\{\mathit{root}\}
\text{ and } k \in \mathrm{Ones}(\mathit{time}(x)-1) \}, \\
\sigma(X^\text{time-apv}_k) &:=& \{(v,x) ~:~ v\in V,x \in V \setminus\{\mathit{root}\}
\text{ and there exists a node } y \neq \\
&& \mathit{root} \text{ on the path from } \mathit{root} \text{ to } x \text{ such that }
\mathit{pos}(\mathit{pred}(y)) = \\
&&\mathit{pos}(x) \text{ and } k \in \mathrm{Ones}(\mathit{time}(y)) \text{ and, for all nodes $z$ on the} \\
&& \text{path from $y$ to $x$ with $z\neq y$},
\mathit{pos}(\mathit{pred}(z)) \neq \mathit{pos}(x) \} ,
\end{eqnarray*}for $`k \in \{0,\ldots,N-1\}`$,
\begin{eqnarray*}
\sigma(A^\mathrm{pos}_k) &:=& \{(v,x) ~:~ v \in V, x\in V \text{ and } k \in \mathrm{Ones}(\mathit{pos}(v)) \}, \\
\sigma(X^\mathrm{pos}_k) &:=& \{(v,x) ~:~ v \in V, x\in V \text{ and } k \in \mathrm{Ones}(\mathit{pos}(x)) \}, \\
\sigma(A^\mathrm{prevpos}_k) &:=& \{(v,x) ~:~ v\in V\setminus\{\mathit{root}\}, x \in V
\text{ and } k \in \mathrm{Ones}(\mathit{pos}(\mathit{pred}(v))) \} \\
\sigma(X^\mathrm{prevpos}_k) &:=& \{(v,x) ~:~ v\in V, x\in V\setminus\{\mathit{root}\}
\text{ and } k \in \mathrm{Ones}(\mathit{pos}(\mathit{pred}(x))) \},
\end{eqnarray*}for $`k \in \{0,\ldots,N\}`$,
\sigma(A^\mathrm{state}_q) := \{(v,x) ~:~ v\in V, x \in V \text{ and } q = \mathit{state}(v)) \}for $`q\in Q`$,
\begin{eqnarray*}
\sigma(A^\mathrm{read}_\eta) &:=& \{(v,x) ~:~ v,x \in V \text{ and } \eta = \mathit{read}(v) \}, \\
\sigma(A^\mathrm{written}_\eta) &:=& \{(v,x) ~:~ (v \in V \setminus\{\mathit{root}\},
x \in V \text{ and } \eta = \mathit{written}(v) ) \\
&& \phantom{(\{(v,x) ~:~} \text{or } (v=\mathit{root} \text{ and } x \in V \text{ and } \eta=\#)\}, \\
\sigma(X^\mathrm{read}_\eta)
&:=& \{(v,x) ~:~ v,x \in V \text{ and } \eta = \mathit{read}(x)) \} ,
\end{eqnarray*}for $`\eta \in\Gamma`$,
\begin{eqnarray*}
\sigma(B^\mathrm{active})
&:= &\{(v,x) ~:~ v, x \in V
\text{ and $v$ is an element of the path }
\text{from $\mathit{root}$ to $x$} \}.
\end{eqnarray*}We have defined an $`\sxs`$-product model $`(W_1\times W_2,\stackrel{\Diamond}{\to},\stackrel{L}{\to})`$. We claim that in this model $`(\mathit{root},\mathit{root})\models f_\sxs(w)`$. For an illustration of an important detail of the model see Figure 3.
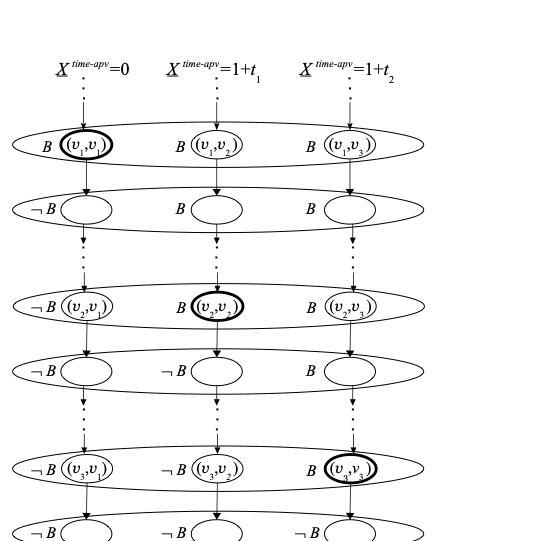 style="width:90.0%" />
style="width:90.0%" />
First, we observe that for $`\mathit{string} \in \{\text{prevtime},\text{prevpos}, \text{pos}, \text{time-apv}, \text{written}\}`$ and natural numbers $`i`$ as well as for $`(v,x) \in V \times V`$ the truth value of the variable $`X^\mathit{string}_i`$ in the point $`(v,x)`$ does not depend on $`v`$. Hence, all these variables are persistent. So,
(\mathit{root},\mathit{root})\models \mathit{persistence} .Similarly, for $`\mathit{string} \in \{\mathrm{time}, \mathrm{pos}, \mathrm{state}, \mathrm{read}, \mathrm{prevpos}, \mathrm{written}\}`$ and natural numbers $`i`$ as well as for $`(v,x) \in V \times V`$ the truth value of the variable $`A^\mathit{string}_i`$ in the point $`(v,x)`$ does not depend on $`x`$. Note that for $`v\in V`$ the set
\mathrm{Cloud}(v) := \{(v,x) ~:~ v \in V, x \in V\}is the $`\stackrel{L}{\to}`$-equivalence class of $`(v,v)`$. All of the vectors of shared variables have the expected values: for $`v\in V`$ and $`s \in \mathrm{Cloud}(v)`$. We see
\begin{eqnarray*}
s &\models& (\underline{\alpha}^\mathrm{time} = \mathrm{bin}_N( \mathit{time}(v))) , \\
s &\models& (\underline{\alpha}^\mathrm{pos} = \mathrm{bin}_{N+1}( \mathit{pos}(v))) , \\
( s &\models& \alpha^\mathrm{state}_q) \iff q = \mathit{state}(v), \text{ for } q \in Q, \\
( s &\models& \alpha^\mathrm{read}_\eta) \iff \eta = \mathit{read}(v), \text{ for } \eta \in \Gamma,
\end{eqnarray*}and for $`v\in V\setminus\{\mathit{root}\}`$ and $`s \in \mathrm{Cloud}(v)`$ we see
\begin{eqnarray*}
s &\models& (\underline{\alpha}^\mathrm{prevpos} = \mathrm{bin}_{N+1}( \mathit{pos}(\mathit{pred}(v)))) , \\
( s &\models& \alpha^\mathrm{written}_\eta) \iff \eta = \mathit{written}(v) , \text{ for } \eta \in \Gamma.
\end{eqnarray*}Similarly, for the vectors of persistent variables we see, for $`v,x\in V`$:
\begin{eqnarray*}
\textbf{}
(v,x) &\models& (\underline{X}^\mathrm{prevtime} = \mathrm{bin}_N(t)) ,
\text{ where } \\
&& t = \begin{cases}
0, & \text{ if } x=\mathit{root} \\
\mathit{time}(\mathit{pred}(x)), & \text{ otherwise},
\end{cases} \\
(v,x) &\models& (\underline{X}^\mathrm{prevpos} = \mathrm{bin}_{N+1}(p)) ,
\text{ where } \\
&& p = \begin{cases}
0, & \text{ if } x=\mathit{root} \\
\mathit{pos}(\mathit{pred}(x)), & \text{ otherwise},
\end{cases} \\
(v,x) &\models& (\underline{X}^\mathrm{pos} = \mathrm{bin}_{N+1}(\mathit{pos}(x))) , \\
(v,x) &\models& (\underline{X}^\text{time-apv} = \mathrm{bin}_N(t)) , \text{ where } \\
&& \!\!\!\!\!\! t = \begin{cases}
0, \quad \text{if the cell $\mathit{pos}(x)$ has not been visited before on the computation} \\
\qquad \text{path from $\mathit{root}$ to $x$ (this is in particular true in the case $x=\mathit{root}$)}, \\
1 + \text{the time of the previous visit of the cell $\mathit{pos}(x)$,} \\
\qquad \text{otherwise}.
\end{cases} \\
( (v,x) &\models& X^\mathrm{read}_\eta) \iff \eta = \mathit{read}(x), \text{ for } \eta \in\Gamma,
\end{eqnarray*}It is straightforward to check that for all $`(v,x) \in W`$
(v,x) \models \mathit{uniqueness}(in fact, in order to achieve $`(\mathit{root},x) \models \mathrm{unique}(\underline{\alpha}^\mathrm{written})`$ we made a somewhat arbitrary choice for the value of $`A^\mathrm{written}_\eta`$ in $`(\mathit{root},x)`$, for $`x\in V`$ and $`\eta\in\Gamma`$). Hence, we have
(\mathit{root},\mathit{root}) \models K \Box \mathit{uniqueness} .It is clear as well that
(\mathit{root},\mathit{root}) \models \mathit{start} .As none of the nodes in the accepting tree $`T`$ is labeled with a configuration with the state $`q_\mathrm{reject}`$ we have $`(v,x) \models \mathit{no\_reject}`$, for all $`(v,x) \in W`$, hence
(\mathit{root},\mathit{root}) \models K \Box \mathit{no\_reject} .We still need to show that
\begin{eqnarray*}
(\mathit{root},\mathit{root}) &\models&
K \Box \mathit{initial\_symbols}
\wedge K \Box \mathit{written\_symbols} \\
&& \wedge K \Box \mathit{read\_a\_symbol}
\wedge K \Box \mathit{computation} .
\end{eqnarray*}It is sufficient to show that, for all $`(v,x) \in W`$,
(v,x) \models \mathit{initial\_symbols} \wedge \mathit{written\_symbols}
\wedge \mathit{read\_a\_symbol} \wedge \mathit{computation} .First, let us consider the formula $`\mathit{initial\_symbols}`$. We wish to show that
(v,x) \models \mathit{initial\_symbols},for all $`(v,x) \in W`$. Nothing needs to be shown if $`(v,x) \models (\underline{X}^\text{time-apv} = \mathrm{bin}_N(0))`$ is not true. So, let us assume that $`(v,x) \models (\underline{X}^\text{time-apv} = \mathrm{bin}_N(0))`$. We noted above that the assumption $`(v,x) \models (\underline{X}^\text{time-apv} = \mathrm{bin}_N(0))`$ implies that the cell $`\mathit{pos}(x)`$ has not been visited before on the computation path from $`\mathit{root}`$ to $`x`$. Hence, $`\mathit{read}(x)=\eta`$, where $`\eta`$ is the initial symbol in the cell $`x`$. We obtain $`(v,x) \models X^\mathrm{read}_{\eta}`$. So, if the number $`i:=\mathit{pos}(x)-(2^N-1)`$ satisfies $`1\leq i \leq n`$ then $`(v,x) \models X^\mathrm{read}_{w_i}`$, otherwise $`(v,x) \models X^\mathrm{read}_{\#}`$. Remember that $`(v,x) \models (\underline{X}^\mathrm{pos} = \mathrm{bin}_{N+1}(\mathit{pos}(x))`$. We have shown $`(v,x) \models \mathit{initial\_symbols}`$.
Next, we consider the formula $`\mathit{written\_symbols}`$ and show that
(v,x) \models \mathit{written\_symbols}for all $`(v,x)\in W`$. Let us assume
(v,x) \models ( (\underline{X}^\text{time-apv} > \mathrm{bin}_N(0) )
\wedge (\underline{X}^\text{time-apv} = \underline{\alpha}^\mathrm{time})
\wedge B^\mathrm{active} )(otherwise, nothing needs to be shown). The condition $`(v,x) \models ( \underline{X}^\text{time-apv} > \mathrm{bin}_N(0))`$ implies $`x \in V \setminus\{\mathit{root}\}`$ and that the binary value $`t`$ of the vector $`\underline{X}^\text{time-apv}`$ in the point $`(v,x)`$ is equal to $`1+`$ the time of the previous visit of the cell $`\mathit{pos}(x)`$ on the computation path from $`\mathit{root}`$ to $`x`$. Note that $`t\leq \mathit{time}(x)`$. The condition $`(v,x) \models (\underline{X}^\text{time-apv} = \underline{\alpha}^\mathrm{time})`$ means $`t=\mathit{time}(v)`$. Now the condition $`(v,x) \models B^\mathrm{active}`$ implies that $`v`$ is an element of the path from $`\mathit{root}`$ to $`x`$. Actually, due to $`t = \mathit{time}(v)`$ the node $`v`$ is exactly the computation node on the computation path from $`\mathit{root}`$ to $`x`$ after the previous visit of the cell $`\mathit{pos}(x)`$. Thus, the symbol written during this visit and described by the value of $`\underline{\alpha}^\mathrm{written}`$ at the point $`(v,x)`$ is just the symbol still contained in the same cell when the computation node $`x`$ is reached. Hence, we have $`(v,x) \models (\underline{X}^\mathrm{read} = \underline{\alpha}^\mathrm{written})`$. For later purposes we note that for the same reason we have $`(v,x) \models (\underline{X}^\mathrm{pos} = \underline{\alpha}^\mathrm{prevpos})`$ as well. We have shown $`(v,x) \models \mathit{written\_symbols}`$.
Next, we consider the formula $`\mathit{read\_a\_symbol}`$. We wish to show that
(v,x) \models \mathit{read\_a\_symbol},for all $`(v,x) \in W`$. We show this separately for the five subformulas of $`\mathit{read\_a\_symbol}`$. First, we show
(v,x) \models \mathit{existence\_of\_a\_reading\_point},that is,
(v,x) \models L \bigl(( \underline{X}^\mathrm{pos} = \underline{\alpha}^\mathrm{pos})
\wedge (\underline{X}^\text{time-apv} \leq \underline{\alpha}^\mathrm{time})
\wedge B^\mathrm{active}\bigr) .Indeed, it is clear that $`(v,x) \stackrel{L}{\to} (v,v)`$ and that $`(v,v) \models ( \underline{X}^\mathrm{pos} = \underline{\alpha}^\mathrm{pos})`$ and $`(v,v) \models B^\mathrm{active}`$. Furthermore, the binary value of $`\underline{X}^\text{time-apv}`$ in the point $`(v,v)`$ is either $`1+`$ the time of the previous visit of the cell $`\mathit{pos}(v)`$ on the path from $`\mathit{root}`$ to $`v`$, if this cell has been visited before $`v`$ on this path, or $`0`$, otherwise. In any case we obtain $`(v,v) \models (\underline{X}^\text{time-apv} \leq \underline{\alpha}^\mathrm{time})`$. Next, we show
(v,x) \models \mathit{time\_of\_previous\_visit},that is,
(v,x) \models \Bigl( \bigl(( \underline{X}^\text{time-apv} > \mathrm{bin}_N(0) )
\wedge (\underline{X}^\text{time-apv} = \underline{\alpha}^\mathrm{time})
\wedge B^\mathrm{active} \bigr) \rightarrow
( \underline{X}^\mathrm{pos} = \underline{\alpha}^\mathrm{prevpos}) \Bigr) .Actually, we have seen this already in the proof of $`(v,x) \models \mathit{written\_symbols}`$ above. Next, we show
(v,x) \models \mathit{becoming\_inactive},that is,
(v,x) \models \Bigl( \bigl( (\underline{X}^\mathrm{pos}=\underline{\alpha}^\mathrm{prevpos})
\wedge (\underline{X}^\text{time-apv} < \underline{\alpha}^\mathrm{time}) \bigr) \rightarrow
\neg B^\mathrm{active} \Bigr)For the sake of a contradiction, let us assume $`(v,x) \models ( (\underline{X}^\mathrm{pos}=\underline{\alpha}^\mathrm{prevpos}) \wedge (\underline{X}^\text{time-apv} < \underline{\alpha}^\mathrm{time}))`$ and $`(v,x) \models B^\mathrm{active}`$. Then $`v`$ is a node on the path from $`\mathit{root}`$ to $`x`$. Due to $`(v,x) \models ( \underline{X}^\text{time-apv} < \underline{\alpha}^\mathrm{time})`$ we have $`\mathit{time}(v)>0`$. And due to $`(v,x) \models ( \underline{X}^\mathrm{pos}=\underline{\alpha}^\mathrm{prevpos})`$ the node $`v`$ must have the property $`\mathit{pos}(\mathit{pred}(v))=\mathit{pos}(x)`$. That means that the cell $`\mathit{pos}(x)`$ has been visited before $`x`$ on the path from $`\mathit{root}`$ to $`x`$. But under these circumstances, the binary value $`t`$ of $`\underline{X}^\text{time-apv}`$ at the point $`(v,x)`$ is equal to $`\mathit{time}(u)`$ where $`u`$ is the last node on the path from $`\mathit{root}`$ to $`x`$ with the property $`\mathit{pos}(\mathit{pred}(u))=\mathit{pos}(x)`$. Note that $`v`$ is a node on the path from $`\mathit{root}`$ to $`x`$ with the property $`\mathit{pos}(\mathit{pred}(u))=\mathit{pos}(x)`$. On the other hand, the condition $`(v,x) \models ( \underline{X}^\text{time-apv} < \underline{\alpha}^\mathrm{time})`$ implies $`t < \mathit{time}(v)`$. That is a contradiction. We have shown $`(v,x) \models \mathit{becoming\_inactive}`$. Next,we show
(v,x) \models \mathit{staying\_inactive},that is,
(v,x) \models \Bigl( \neg B^\mathrm{active} \rightarrow \Box \neg B^\mathrm{active} \Bigr) .This is clear from the definition of $`\sigma(B^\mathrm{active})`$.
We come to the last subformula of $`\mathit{read\_a\_symbol}`$ and show
(v,x) \models \mathit{storing\_the\_read\_symbol},that is,
(v,x) \models
\Bigl( \bigl( (\underline{X}^\mathrm{pos}=\underline{\alpha}^\mathrm{pos} )
\wedge (\underline{X}^\text{time-apv} \leq \underline{\alpha}^\mathrm{time} )
\wedge B^\mathrm{active} \bigr) \rightarrow
(\underline{\alpha}^\mathrm{read} = \underline{X}^\mathrm{read}) \Bigr) .The condition $`(v,x) \models B^\mathrm{active}`$ implies that $`v`$ is a node on the path from $`\mathit{root}`$ to $`x`$. The condition $`(v,x) \models ( \underline{X}^\mathrm{pos}=\underline{\alpha}^\mathrm{pos} )`$ says that $`\mathit{pos}(x) = \mathit{pos}(v)`$. We claim that $`v=x`$. Once we have shown this, of course, we obtain $`(v,x) \models (\underline{\alpha}^\mathrm{read} = \underline{X}^\mathrm{read})`$. For the sake of a contradiction, let us assume $`v\neq x`$. Then the cell $`\mathit{pos}(x)`$ has been visited before $`x`$ on the path from $`\mathit{root}`$ to $`x`$. Let $`u`$ be the last node before $`x`$ on the path from $`\mathit{root}`$ to $`x`$ with $`\mathit{pos}(u)=\mathit{pos}(x)`$. We obtain $`\mathit{time}(v) \leq \mathit{time}(u)`$. For the binary value $`t`$ of $`\underline{X}^\text{time-apv}`$ in $`(v,x)`$ we obtain $`t= 1 + \mathit{time}(u)`$. Finally, the condition $`(v,x) \models (\underline{X}^\text{time-apv} \leq \underline{\alpha}^\mathrm{time})`$ implies $`t \leq \mathit{time}(v)`$. By putting all this together we arrive at the following contradiction:
\mathit{time}(v) \leq \mathit{time}(u) < 1 + \mathit{time}(u) = t \leq \mathit{time}(v).We have shown $`(v,x) \models \mathit{storing\_the\_read\_symbol}`$.
Finally, we have to show that
(v,x) \models \mathit{computation} ,for all $`(v,x) \in W`$. We will separately treat the conjunctions over the set $`(q,\eta) \in Q_\exists \times \Gamma`$ and over the set $`Q_\forall \times \Gamma`$. Let us first fix a pair $`(q,\eta) \in Q_\exists \times \Gamma`$ and let us assume that $`(v,x)\in W`$ is a point with $`(v,x) \models (\alpha^\mathrm{state}_q \wedge \alpha^\mathrm{read}_\eta)`$. We have to show that there is an element $`(r,\theta,\mathit{left}) \in \delta(q,\eta)`$ such that $`(v,x) \models \mathit{compstep}_{\mathrm{left}}(r,\theta)`$ or that there is an element $`(r,\theta,\mathit{right}) \in \delta(q,\eta)`$ such that $`(v,x) \models \mathit{compstep}_{\mathrm{right}}(r,\theta)`$. As $`T`$ is an accepting tree and the state $`q`$ of $`c(v)`$ is an element of $`Q_\exists`$, the node $`v`$ is an inner node of $`T`$, hence, it has a successor $`v'`$. Let us assume that $`((q,\eta),(r,\theta,\mathit{left})) \in \delta`$ is the element of the transition relation $`\delta`$ that leads from $`v`$ to $`v'`$ (the case that this element is of the form $`((q,\eta),(r,\theta,\mathit{right}))`$ is treated analogously). We claim that then
(v,x) \models \mathit{compstep}_{\mathrm{left}}(r,\theta) .In fact, we observe $`(v,x) \stackrel{L}{\to} (v,v')`$ and $`(v,v') \stackrel{\Diamond}{\to} (v',v')`$. We claim that the two points $`(v,v')`$ and $`(v',v')`$ have the properties formulated in the formula $`\mathit{compstep}_{\mathrm{left}}(r,\theta)`$. Let us check this. Let us assume that, for some $`k\in\{0,\ldots,N-1\}`$ and for some $`l \in \{0,\ldots,N\}`$,
(v,x) \models
\bigl( \mathrm{rightmost\_zero}(\underline{\alpha}^\mathrm{time},k)
\wedge \mathrm{rightmost\_one}(\underline{\alpha}^\mathrm{pos},l) \bigr) .The number $`i:=\mathit{time}(v)`$ is an element of $`\{0,\ldots,2^N-2\}`$ because $`v`$ is an inner point of the tree $`T`$ and the length of any computation path is at most $`2^N-1`$. The number $`j:= \mathit{pos}(v)`$ is an element of $`\{1,\ldots,2^{N+1}-3\}`$ because the computation starts in cell $`2^N-1`$ and during each computation step the tape head can move at most one step to the left or to the right. We obtain $`k=\min(\{0,\ldots,N-1\} \setminus\mathrm{Ones}(i))`$ and $`l=\min\mathrm{Ones}(j)`$. As $`v= \mathit{pred}(v')`$ we obtain
(v,v') \models (\underline{X}^\mathrm{prevtime}=\underline{\alpha}^\mathrm{time})and
(v,v') \models (\underline{X}^\mathrm{prevpos}=\underline{\alpha}^\mathrm{pos}) .And as $`\mathit{time}(v')=\mathit{time}(v)+1=i+1`$ and $`\mathit{pos}(v')=\mathit{pos}(v)-1=j-1`$ we conclude that
\begin{eqnarray*}
(v',v') & \models & \Bigl(
(\underline{\alpha}^\mathrm{time}=\underline{X}^\mathrm{prevtime},>k)
\wedge \mathrm{rightmost\_one}(\underline{\alpha}^\mathrm{time},k) \\
&& \phantom{\Bigl(}
\wedge (\underline{\alpha}^\mathrm{pos}=\underline{X}^\mathrm{prevpos},>l)
\wedge \mathrm{rightmost\_zero}(\underline{\alpha}^\mathrm{pos},l) \Bigr) .
\end{eqnarray*}Finally, the condition
(v',v') \models (\underline{\alpha}^\mathrm{prevpos}=\underline{X}^\mathrm{prevpos})is obviously satisfied and the condition
(v',v') \models \alpha^\mathrm{state}_r
\wedge \alpha^\mathrm{written}_\thetafollows from the fact that $`((q,\eta),(r,\theta,\mathit{left})) \in \delta`$ is the element of the transition relation $`\delta`$ that leads from $`v`$ to $`v'`$. This ends the treatment of the conjunctions over the set $`(q,\eta) \in Q_\exists \times \Gamma`$ in the formula $`\mathit{computation}`$. Let us now consider a pair $`(q,\eta) \in Q_\forall \times \Gamma`$. Let us assume that $`(v,x) \in W`$ is a point such that $`(v,x) \models (\alpha^\mathrm{state}_q \wedge \alpha^\mathrm{read}_\eta)`$. We have to show that for all elements $`(r,\theta,\mathit{left}) \in \delta(q,\eta)`$ we have $`(v,x) \models \mathit{compstep}_{\mathrm{left}}(r,\theta)`$ and for all elements $`(r,\theta,\mathit{right}) \in \delta(q,\eta)`$ we have $`(v,x) \models \mathit{compstep}_{\mathrm{right}}(r,\theta)`$. Let us consider an arbitrary element $`(r,\theta,\mathit{left}) \in \delta(q,\eta)`$ (the case of an element $`(r,\theta,\mathit{right}) \in \delta(q,\eta)`$ is treated analogously). As $`q \in Q_\forall`$ and $`T`$ is an accepting tree, in $`T`$ there is a successor $`v'`$ of $`v`$ such that the element $`((q,\eta),(r,\theta,\mathit{left}))`$ leads from $`v`$ to $`v'`$. Above, we have already seen that this implies
(v,x) \models \mathit{compstep}_{\mathrm{left}}(r,\theta) .Thus, we have shown $`(v,x) \models \mathit{computation}`$ for all $`(v,x) \in W`$. This ends the proof of the claim that in the $`\sxs`$-product model $`(W_1\times W_2,\stackrel{\Diamond}{\to},\stackrel{L}{\to},\sigma)`$ that we constructed for $`w\in L`$ we have $`(\mathit{root},\mathit{root}) \models f_\sxs(w)`$.
Existence of an Accepting Tree
We come to the other direction. Let $`w \in \Sigma^*`$. We wish to show that if $`f_\sxs(w)`$ is $`\sxs`$-satisfiable then $`w\in L`$. We will show that any $`\sxs`$-product model essentially contains an accepting tree of the Alternating Turing Machine $`M`$ on input $`w`$. Of course, this implies $`w\in L`$.
Let us sketch the main idea. We will consider an $`\sxs`$-product model of $`f_\sxs(w)`$. And we will consider partial trees of $`M`$ on input $`w`$ as considered in Subsection 3.3, for any $`w\in\Sigma^*`$. First, we will show that a certain very simple partial tree of $`M`$ on input $`w`$ “can be mapped to” the model (later we will give a precise meaning to “can be mapped to”). Then we will show that any partial tree of $`M`$ on input $`w`$ that can be mapped to the model and that is not an accepting tree of $`M`$ on input $`w`$ can be properly extended to a strictly larger partial tree of $`M`$ on input $`w`$ that can be mapped to the model as well. If there would not exist an accepting tree of $`M`$ on input $`w`$ then we would obtain an infinite strictly increasing sequence of partial trees of $`M`$ on input $`w`$. But we show that this cannot happen by giving a finite upper bound on the size of partial trees of $`M`$ on input $`w`$.
Let $`w \in \Sigma^*`$ be a string such that the formula $`f_\sxs(w)`$ is $`\sxs`$-satisfiable. We set $`n:=|w|`$. Let $`(W_1,R_\Diamond)`$ be an $`S4`$-frame, let $`(W_2,R_L)`$ be an $`S5`$-frame, let $`\sigma:AT\to \mathcal{P}(W_1 \times W_2)`$ be a function such that the quadruple $`(W_1\times W_2, \stackrel{\Diamond}{\to},\stackrel{L}{\to},\sigma)`$ where $`\stackrel{\Diamond}{\to}`$ and $`\stackrel{L}{\to}`$ are defined as in is an $`\sxs`$-product model, and let $`(r_1,r_2) \in W_1\times W_2`$ be a point with $`(r_1,r_2) \models f_\sxs(w)`$. The quintuple
\mathit{Model}:=(W_1\times W_2, \stackrel{\Diamond}{\to},\stackrel{L}{\to},\sigma,(r_1,r_2))will be important in the following. We claim that we can assume without loss of generality that $`r_1 \stackrel{\Diamond}{\to} x`$ for all $`x\in W_1`$ and $`R_L = W_2\times W_2`$. Otherwise, instead of $`W_1`$ we could consider the set $`W_1^\prime:=\{v\in W_1 \mid r_1 \stackrel{\Diamond}{\to} v\}`$ and instead of $`W_2`$ we could consider the set $`W_2^\prime:=`$ the $`R_L`$-equivalence class of $`r_2`$ and the restrictions $`\stackrel{L}{\to}^\prime`$ resp. $`\stackrel{\Diamond}{\to}^\prime`$ of $`\stackrel{L}{\to}`$ resp. $`\stackrel{\Diamond}{\to}`$ to $`W_1^\prime \times W_2^\prime`$. By structural induction one shows that for any bimodal formula $`\varphi`$ and for any $`(v,x) \in W_1^\prime \times W_2^\prime`$,
(W_1\times W_2, \stackrel{\Diamond}{\to},\stackrel{L}{\to},\sigma),(v,x) \models \varphi
\iff (W_1^\prime\times W_2^\prime, \stackrel{\Diamond}{\to}^\prime,\stackrel{L}{\to}^\prime,\sigma),(v,x) \models \varphi .So, we shall assume that $`r_1 \stackrel{\Diamond}{\to} x`$, for all $`v\in W_1`$, and $`R_L = W_2\times W_2`$. Note that this implies that if $`\varphi`$ is a formula with $`(r_1,r_2) \models K \Box \varphi`$ then, for all $`(v,x) \in W_1 \times W_2`$, we have $`(v,x) \models \varphi`$.
For every $`v\in W_1`$, the set
\mathrm{Cloud}(v) := \{ (v,x) ~:~ v \in W_1, x \in W_2\}is the $`\stackrel{L}{\to}`$-equivalence class (short: cloud) of any element $`y \in W_1 \times W_2`$ whose first component is $`v`$. Remember that for every $`\stackrel{L}{\to}`$-equivalence class and every shared variable $`\alpha^{\mathit{string}}_i`$ for $`\mathit{string} \in \{\mathrm{time}, \mathrm{pos}, \mathrm{state}, \mathrm{read}, \mathrm{prevpos}, \mathrm{written}\}`$ and natural numbers $`i`$, the truth value of this shared variable is the same in all elements of the $`\stackrel{L}{\to}`$-equivalence class.
Partial trees of $`M`$ on input $`w`$ as introduced in Subsection 3.3 will play an important role in the following. We will write a partial tree of $`M`$ on input $`w`$ similarly as in Subsection 3.3 as a triple $`T=(V,E,c)`$, but with the difference that we will describe configurations as at the beginning of Subsection 7.2: the labeling function $`c`$ will be a function of the form $`c:V\to Q \times \{0,\ldots,2^{N+1}-2\}\times \Gamma^{2^{N+1}-1}`$. If $`T=(V,E,c)`$ is a partial tree of $`M`$ on input $`w`$ with root $`\mathit{root}`$ then a function $`\pi:V\to W_1`$ is called a morphism from $`T`$ to $`\mathit{Model}`$ if it satisfies the following four conditions:
-
$`\pi(\mathit{root}) = r_1`$.
-
$`\{(\pi(v),\pi(v')) ~:~ v,v' \in V \text{ and } vEv'\} \subseteq R_\Diamond`$.
-
$`\begin{array}[t]{l} (\forall v \in V\setminus\{\mathit{root}\}) \, (\exists x \in W_2) \\ (\pi(v),x) \models \bigl( (\underline{\alpha}^\mathrm{prevpos} = \mathrm{bin}_{N+1}(\mathit{pos}(\mathit{pred}(v)))) \wedge \alpha^\mathrm{written}_{\mathit{written}(v)} \bigr) \end{array}`$.
-
$`\begin{array}[t]{l} (\forall v \in V) \, (\exists x \in W_2) \\ (\pi(v),x) \models \bigl( (\underline{\alpha}^\mathrm{time} = \mathrm{bin}_N(\mathit{time}(v))) \wedge (\underline{\alpha}^\mathrm{pos} = \mathrm{bin}_{N+1}(\mathit{pos}(v)))\\ \qquad\qquad\qquad\wedge \alpha^\mathrm{state}_{\mathit{state}(v)} \wedge \alpha^\mathrm{read}_{\mathit{read}(v)} \bigr). \end{array}`$
We say that $`T`$ can be mapped to $`\mathit{Model}`$ if there exists a morphism from $`T`$ to $`\mathit{Model}`$. Below we shall prove the following lemma.
If a partial tree $`T=(V,E,c)`$ of $`M`$ on input $`w`$ can be mapped to $`\mathit{Model}`$ and is not an accepting tree of $`M`$ on input $`w`$ then there exists a partial tree $`T=(\widetilde{V},\widetilde{E},\widetilde{c})`$ of $`M`$ on input $`w`$ that can be mapped to $`\mathit{Model}`$ and that satisfies $`V \subsetneq \widetilde{V}`$.
Before we prove this lemma, we deduce the desired assertion from it. Let
D:= \max(\{ |\delta(q,\eta)| ~:~ q \in Q, \eta \in\Gamma\}) .Then, due to Condition III in the definition of a “partial tree of $`M`$ on input $`w`$”, any node in any partial tree of $`M`$ on input $`w`$ has at most $`D`$ successors. As any computation of $`M`$ on input $`w`$ stops after at most $`2^N-1`$ steps, any partial tree of $`M`$ on input $`w`$ has at most
\widetilde{D}:=(D^{2^N}-1)/(D-1)nodes.
We claim that the rooted and labeled tree
T_0:=(\{\mathit{root}\},\emptyset,c) \text{ where }
c(\mathit{root}):=(q_0,2^N-1,\#^{2^N}w\#^{2^N-1-n})is a partial tree of $`M`$ on input $`w`$ and that it can be mapped to $`\mathit{Model}`$. Indeed, Condition I in the definition of a “partial tree of $`M`$ on input $`w`$” is satisfied because the node $`\mathit{root}`$ is labeled with the initial configuration of $`M`$ on input $`w`$. Conditions II, III, and IV are satisfied because $`T_0`$ does not have any inner nodes. Condition $`\mathrm{V}^\prime`$ is satisfied because $`\mathit{state}(\mathit{root}) = q_0`$ and, due to $`(r_1,r_2) \models \alpha^\mathrm{state}_{q_0}`$ (this is a part of $`(r_1,r_2) \models \mathit{start}`$) and $`(r_1,r_2) \models \neg \alpha^\mathrm{state}_{q_\mathrm{reject}}`$ (this follows from $`(r_1,r_2) \models K \Box \mathit{no\_reject}`$) we obtain $`q_0 \neq q_\mathrm{reject}`$. Thus, $`T_0`$ is indeed a partial tree of $`M`$ on input $`w`$. Now we show that $`T_0`$ can be mapped to $`\mathit{Model}`$. Of course, we define the function $`\pi:\{\mathit{root}\}\to W_1`$ by $`\pi(\mathit{root}):=r_1`$.
-
The condition $`\pi(\mathit{root})=r_1`$ is true by definition.
-
The tree $`T_0`$ does not have any edges, that is, its set $`E`$ of edges is empty. So, the second condition is satisfied.
-
The third condition does not apply to the tree $`T_0`$ because $`T_0`$ has only one node, its root.
-
On the one hand, we have
MATH\mathit{time}(\mathit{root})=0, \qquad \mathit{pos}(\mathit{root})=2^N-1,Click to expand and view moreMATH\mathit{state}(\mathit{root})=q_0, \qquad \text{and }\mathit{read}(\mathit{root})=\#.Click to expand and view moreOn the other hand, the condition $`(r_1,r_2) \models \mathit{start}`$ says
MATH(r_1,r_2) \models \bigl( (\underline{\alpha}^\mathrm{time}=\bin_N(0)) \wedge (\underline{\alpha}^\mathrm{pos}=\bin_{N+1}(2^N-1)) \wedge \alpha^\mathrm{state}_{q_0} .Click to expand and view moreWe still wish to show $`(r_1,r_2) \models \alpha^\mathrm{read}_{\#}`$. We have $`(r_1,r_2) \models \mathit{read\_a\_symbol}`$. This implies $`(r_1,r_2) \models \mathit{existence\_of\_a\_reading\_point}`$, and this implies that there exists some $`y\in W_2`$ with
MATH(r_1,y) \models \bigl((\underline{X}^\mathrm{pos} = \underline{\alpha}^\mathrm{pos} ) \wedge (\underline{X}^\text{time-apv} \leq \underline{\alpha}^\mathrm{time} ) \wedge B^\mathrm{active}\bigr) ,Click to expand and view morehence, with
MATH(r_1,y) \models \bigl((\underline{X}^\mathrm{pos} = \mathrm{bin}_{N+1}(2^N-1)) \wedge (\underline{X}^\text{time-apv} = \mathrm{bin}(0) ) \wedge B^\mathrm{active}\bigr) .Click to expand and view moreNow $`(r_1,y) \models \mathit{initial\_symbols}`$ implies $`(r_1,y) \models X^\mathrm{read}_\#`$. Finally, the condition
MATH(r_1,y) \models \mathit{storing\_the\_read\_symbol}Click to expand and view moreimplies $`(r_1,y) \models \alpha^\mathrm{read}_\#`$, and this implies $`(r_1,r_2) \models \alpha^\mathrm{read}_\#`$.
If there would not exist an accepting tree of $`M`$ on input $`w`$ then, starting with $`T_0`$ and using Lemma [lemma:inductionS4S5], we could construct an infinite sequence of partial trees $`T_0,T_1,T_2,\ldots`$ of $`M`$ on input $`w`$ that can be mapped to $`\mathit{Model}`$ such that the number of nodes in these trees is strictly increasing. But we have seen that any partial tree of $`M`$ input $`w`$ can have at most $`\widetilde{D}`$ nodes. Thus, there exists an accepting tree of $`M`$ on input $`w`$. We have shown $`w\in L`$.
In order to complete the proof of Theorem [theorem:S4S5-EXPSPACE-hard] it remains to prove Lemma [lemma:inductionS4S5].
Proof of Lemma [lemma:inductionS4S5]. Let $`T=(V,E,c)`$ be a partial tree of $`M`$ on input $`w`$ that is not an accepting tree of $`M`$ on input $`w`$ and that can be mapped to $`\mathit{Model}`$. Then $`T`$ has a leaf $`\widehat{v}`$ such that the state $`q:=\mathit{state}(\widehat{v})`$ is either an element of $`Q_\exists`$ or of $`Q_\forall`$. First we treat the case that it is an element of $`Q_\exists`$, then the case that it is an element of $`Q_\forall`$. Let $`\pi:V \to W_1`$ be a morphism from $`T`$ to $`\mathit{Model}`$.
So, let us assume that $`q \in Q_\exists`$. We define $`\eta:=\mathit{read}(\widehat{v})`$. As $`\pi:V \to W_1`$ is a morphism from $`T`$ to $`\mathit{Model}`$ there exists an $`x' \in W_2`$ with
(\pi(\widehat{v}),x') \models
(\underline{\alpha}^\mathrm{time} = \mathrm{bin}_N(\mathit{time}(\widehat{v})))
\wedge (\underline{\alpha}^\mathrm{pos} = \mathrm{bin}_{N+1}(\mathit{pos}(\widehat{v})))
\wedge \alpha^\mathrm{state}_q
\wedge \alpha^\mathrm{read}_\eta .Hence, due to $`(\pi(\widehat{v}),x') \models \mathit{computation}`$,
(\pi(\widehat{v}),x') \models
\bigvee_{(r,\theta,\mathit{left}) \in \delta(q,\eta)} \mathit{compstep}_{\mathrm{left}}(r,\theta)
\vee \bigvee_{(r,\theta,\mathit{right}) \in \delta(q,\eta)} \mathit{compstep}_{\mathrm{right}}(r,\theta) .Let us assume there is an element $`(r,\theta,\mathit{left}) \in \delta(q,\eta)`$ such that $`(\pi(\widehat{v}),x') \models \mathit{compstep}_{\mathrm{left}}(r,\theta)`$ (the other case, the case when there is an element $`(r,\theta,\mathit{right}) \in \delta(q,\eta)`$ such that $`(\pi(\widehat{v}),x') \models \mathit{compstep}_{\mathrm{right}}(r,\theta)`$, is treated analogously). We claim that we can define the new tree $`\widetilde{T}=(\widetilde{V},\widetilde{E},\widetilde{c})`$ as follows:
-
$`\widetilde{V} := V \cup\{\widetilde{v}\}`$ where $`\widetilde{v}`$ is a new element (not in $`V`$),
-
$`\widetilde{E} := E \cup \{(\widehat{v},\widetilde{v})\}`$,
-
$`\widetilde{c}(x) := \begin{cases} c(x) & \text{for all } x \in V, \\ c' & \text{for } x=\widetilde{v}, \text{ where $c’$ is the configuration that is reached from $c(\widehat{v})$} \\ & \text{in the computation step given by } ((q,\eta),(r,\theta,\mathit{left})) \in\delta. \end{cases}`$
We have to show that $`\widetilde{T}`$ is a partial tree of $`M`$ on input $`w`$. Condition I in the definition of “a partial tree of $`M`$ on input $`w`$” is satisfied because $`\widetilde{T}`$ has the same root as $`T`$, and the label of the root does not change. A node in $`\widetilde{T}`$ is an internal node of $`\widetilde{T}`$ if, and only if, it is either an internal node of $`T`$ or equal to $`\widehat{v}`$. For internal nodes of $`T`$ Conditions II, III, and IV are satisfied by assumption (and due to the fact that the labels of nodes in $`V`$ do not change when moving from $`T`$ to $`\widetilde{T}`$). The new internal node $`\widehat{v}`$ satisfies Condition II by our definition of $`\widetilde{c}(\widetilde{v})`$. Condition III is satisfied for $`\widehat{v}`$ because $`\widehat{v}`$ has exactly one successor. And Condition IV does not apply to $`\widehat{v}`$ because $`\widehat{v}\in Q_\exists`$. A node in $`\widetilde{T}`$ is a leaf if, and only if, it is either equal to $`\widetilde{v}`$ or a leaf in $`T`$ different from $`\widehat{v}`$. For the leaves in $`T`$ different from $`\widehat{v}`$ Condition $`\mathrm{V}^\prime`$ is satisfied by assumption (and due to the fact that the labels of nodes in $`V`$ do not change). Finally, we have to show that Condition $`\mathrm{V}^\prime`$ is satisfied for the new leaf $`\widetilde{v}`$ in $`\widetilde{T}`$ as well. We postpone this until after the definition of a morphism from $`\widetilde{T}`$ to $`\mathit{Model}`$.
We also have to show that $`\widetilde{T}`$ can be mapped to $`\mathit{Model}`$. Let us define a function $`\widetilde{\pi}:\widetilde{V}\to W_1`$ that we will show to be a morphism from $`\widetilde{T}`$ to $`\mathit{Model}`$. As $`\widehat{v}`$ is an element of a partial tree of $`M`$ on input $`w`$ with $`\mathit{state}(\widehat{v}) \in Q_\exists`$, at least one more computation step can be done. As any computation of $`M`$ on input $`w`$ stops after at most $`2^N-1`$ steps, we observe that the number $`i:=\mathit{time}(\widehat{v})`$ satisfies $`0 \leq i < 2^N-1`$. Then $`\{0,\ldots,N-1\} \setminus\mathrm{Ones}(i) \neq \emptyset`$. We set $`k:= \min(\{0,\ldots,N-1\} \setminus\mathrm{Ones}(i))`$. Together with $`(\pi(\widehat{v}),x') \models (\underline{\alpha}^\mathrm{time} = \mathrm{bin}_N(i))`$ we conclude $`(\pi(\widehat{v}),x') \models \mathrm{rightmost\_zero}(\underline{\alpha}^\mathrm{time},k)`$. As during each computation step, the tape head can move at most one step to the left or to the right and as the computation started in position $`2^N-1`$ the number $`j:=\mathit{pos}(\widehat{v})`$ satisfies $`0 < j \leq 2^{N+1}-3`$. Then $`\mathrm{Ones}(j) \neq \emptyset`$. We set $`l:= \min\mathrm{Ones}(j)`$. Together with $`(\pi(\widehat{v}),x') \models (\underline{\alpha}^\mathrm{pos} = \mathrm{bin}_{N+1}(j))`$ we conclude $`(\pi(\widehat{v}),x') \models \mathrm{rightmost\_one}(\underline{\alpha}^\mathrm{pos},l)`$. Thus, we have
(\pi(\widehat{v}),x') \models \bigl( \mathrm{rightmost\_zero}(\underline{\alpha}^\mathrm{time},k)
\wedge \mathrm{rightmost\_one}(\underline{\alpha}^\mathrm{pos},l) \bigr).Due to $`(\pi(\widehat{v}),x') \models \mathit{compstep}_{\mathrm{left}}(r,\theta)`$ there exist an element $`y \in W_2`$ and an element $`x \in W_1`$ such that $`\pi(\widehat{v}) R_\Diamond x`$ as well as
(\pi(\widehat{v}),y) \models
\bigl( (\underline{X}^\mathrm{prevtime}=\underline{\alpha}^\mathrm{time})
\wedge (\underline{X}^\mathrm{prevpos}=\underline{\alpha}^\mathrm{pos})
\bigr)and
\begin{eqnarray*}
(x,y) \models
&& \Bigl(
(\underline{\alpha}^\mathrm{time}=\underline{X}^\mathrm{prevtime},>k)
\wedge \mathrm{rightmost\_one}(\underline{\alpha}^\mathrm{time},k) \\
&& \wedge (\underline{\alpha}^\mathrm{pos}=\underline{X}^\mathrm{prevpos},>l)
\wedge \mathrm{rightmost\_zero}(\underline{\alpha}^\mathrm{pos},l) \\
&& \wedge ( \underline{\alpha}^\mathrm{prevpos}=\underline{X}^\mathrm{prevpos})
\wedge \alpha^\mathrm{state}_{r}
\wedge \alpha^\mathrm{written}_\theta
\Bigr)
\end{eqnarray*}We claim that we can define the desired function $`\widetilde{\pi}:\widetilde{V} \to W_1`$ by
\widetilde{\pi}(v) := \begin{cases}
\pi(v) & \text{if } v \in V, \\
x & \text{if } v=\widetilde{v}.
\end{cases}Before we show that $`\widetilde{\pi}`$ is a morphism from $`\widetilde{T}`$ to $`\mathit{Model}`$, let us complete the proof that $`\widetilde{T}`$ is a partial tree of $`M`$ on input $`w`$. We still need to show that Condition $`\mathrm{V}^\prime`$ is satisfied for the new leaf $`\widetilde{v}`$ in $`\widetilde{T}`$ as well. It is sufficient to show that the state $`r`$ of the configuration $`c'`$ is not the rejecting state $`q_\mathrm{reject}`$. But this follows from $`(x,y) \models \alpha^\mathrm{state}_r`$ and $`(x,y) \models \neg \alpha^\mathrm{state}_{q_\mathrm{reject}}`$ (this follows from $`(r_1,r_2) \models K \Box \mathit{no\_reject}`$). We have shown that $`\widetilde{T}`$ is a partial tree of $`M`$ on input $`w`$.
Now we show that $`\widetilde{\pi}`$ is a morphism from $`\widetilde{T}`$ to $`\mathit{Model}`$. The first condition in the definition of a “morphism from $`\widetilde{T}`$ to $`\mathit{Model}`$” is satisfied because $`\widetilde{\pi}(\mathit{root}) = \pi(\mathit{root})=r_1`$. For the second condition let us consider $`v,v' \in \widetilde{V}`$ with $`v\widetilde{E}v'`$. We have to show $`\pi(v) R_\Diamond \pi(v')`$. There are two possible cases.
-
In the case $`v,v' \in V`$ we have $`vEv'`$ and, hence, $`\pi(v)R_\Diamond \pi(v')`$. As $`\widetilde{\pi}(v)=\pi(v)`$ and $`\widetilde{\pi}(v')=\pi(v')`$ we obtain $`\widetilde{\pi}(v) R_\Diamond \widetilde{\pi}(v')`$.
-
The other possible case is $`v=\widehat{v}`$ and $`v'=\widetilde{v}`$. But we know $`\widetilde{\pi}(\widehat{v})=\pi(\widehat{v})`$, $`\widetilde{\pi}(\widetilde{v}) = x`$, and $`\pi(\widehat{v}) R_\Diamond x`$.
Next, we verify that the third condition in the definition of a “morphism from $`\widetilde{T}`$ to $`\mathit{Model}`$” is satisfied. For $`v\in V\setminus\{\mathit{root}\}`$ it is satisfied by assumption (and by $`\widetilde{\pi}(v)=\pi(v)`$ and $`\widetilde{c}(v) = c(v)`$). For $`\widetilde{v}`$ it is sufficient to show that
(x,y) \models \bigl(
(\underline{\alpha}^\mathrm{prevpos} = \mathrm{bin}_{N+1}(\mathit{pos}(\mathit{pred}(\widetilde{v}))))
\wedge \alpha^\mathrm{written}_{\mathit{written}(\widetilde{v})} \bigr)(remember that $`\widetilde{\pi}(\widetilde{v})=x`$). These are really two conditions. We prove them separately.
-
In the tree $`\widetilde{T}`$ we have $`\mathit{pos}(\mathit{pred}(\widetilde{v}))=\mathit{pos}(\widehat{v})=j`$, and in $`T`$ we have $`\mathit{pos}(\widehat{v})=j`$ as well. The assumption $`(\pi(\widehat{v}),x') \models (\underline{\alpha}^\mathrm{pos}= \mathrm{bin}_{N+1}(j))`$, for some $`x'\in W_2`$, implies $`(\pi(\widehat{v}),y) \models (\underline{\alpha}^\mathrm{pos}= \mathrm{bin}_{N+1}(j))`$, and the conditions $`(\pi(\widehat{v}),y) \models (\underline{X}^\mathrm{prevpos}=\underline{\alpha}^\mathrm{pos})`$ and $`(x,y) \models (\underline{\alpha}^\mathrm{prevpos}=\underline{X}^\mathrm{prevpos})`$ as well as the persistence of $`\underline{X}^\mathrm{prevpos}`$ imply $`(x,y) \models (\underline{\alpha}^\mathrm{prevpos}=\mathrm{bin}_{N+1}(j))`$.
-
In $`\widetilde{T}`$ we have $`\mathit{written}(\widetilde{v}) = \theta`$. And we have $`(x,y) \models \alpha^\mathrm{written}_\theta`$, hence, $`(x,y) \models \alpha^\mathrm{written}_{\mathit{written}(\widetilde{v})}`$.
We come to the fourth condition in the definition of a “morphism from $`\widetilde{T}`$ to $`\mathit{Model}`$”. It is satisfied for $`v\in V`$ by assumption (and due to $`\widetilde{\pi}(v)=\pi(v)`$ and $`\widetilde{c}(v) = c(v)`$). We still need to show that it is satisfied for $`v=\widetilde{v}`$. Remember $`\widetilde{\pi}(\widetilde{v})=x`$. It is sufficient to show
(x,y) \models
(\underline{\alpha}^\mathrm{time} = \mathrm{bin}_N(\mathit{time}(\widetilde{v})))
\wedge (\underline{\alpha}^\mathrm{pos} = \mathrm{bin}_{N+1}(\mathit{pos}(\widetilde{v})))
\wedge \alpha^\mathrm{state}_{\mathit{state}(\widetilde{v})}
\wedge \alpha^\mathrm{read}_{\mathit{read}(\widetilde{v})}.This assertion consists really of four assertions. We treat them one by one.
-
In the trees $`T`$ and $`\widetilde{T}`$ we have $`\mathit{time}(\widehat{v})=i`$, and in the tree $`\widetilde{T}`$ we have $`\mathit{time}(\widetilde{v})=i+1`$. We have already seen that $`(\pi(\widehat{v}),x') \models (\underline{\alpha}^\mathrm{time} = \mathrm{bin}_N(i))`$ and that $`(\pi(\widehat{v}),x') \models \mathrm{rightmost\_zero}(\underline{\alpha}^\mathrm{time},k)`$. Of course, we get
MATH(\pi(\widehat{v}),y) \models ((\underline{\alpha}^\mathrm{time} = \mathrm{bin}_N(i)) \wedge \mathrm{rightmost\_zero}(\underline{\alpha}^\mathrm{time},k)) .Click to expand and view moreThe conditions
MATH\begin{eqnarray*} (\pi(\widehat{v}),y) &\models& (\underline{X}^\mathrm{prevtime}=\underline{\alpha}^\mathrm{time}), \\ (x,y) &\models& (\underline{\alpha}^\mathrm{time}=\underline{X}^\mathrm{prevtime},>k) \wedge \mathrm{rightmost\_one}(\underline{\alpha}^\mathrm{time},k) \end{eqnarray*}Click to expand and view moreand the persistence of $`\underline{X}^\mathrm{prevtime}`$ imply $`(x,y) \models (\underline{\alpha}^\mathrm{time} = \mathrm{bin}_N(i+1))`$.
-
In the trees $`T`$ and $`\widetilde{T}`$ we have $`\mathit{pos}(\widehat{v})=j`$, and in the tree $`\widetilde{T}`$ we have $`\mathit{pos}(\widetilde{v})=j-1`$. We have already seen $`(\pi(\widehat{v}),x') \models (\underline{\alpha}^\mathrm{pos} = \mathrm{bin}_{N+1}(j))`$, and $`(\pi(\widehat{v}),x') \models \mathit{rightmost\_one}(\underline{\alpha}^\mathrm{pos},l)`$. Of course, we get
MATH(\pi(\widehat{v}),y) \models ((\underline{\alpha}^\mathrm{pos} = \mathrm{bin}_{N+1}(j)) \wedge \mathrm{rightmost\_one}(\underline{\alpha}^\mathrm{pos},l)) .Click to expand and view moreThe conditions
MATH\begin{eqnarray*} (\pi(\widehat{v}),y) &\models& (\underline{X}^\mathrm{prevpos}=\underline{\alpha}^\mathrm{pos}), \\ (x,y) &\models& (\underline{\alpha}^\mathrm{pos}=\underline{X}^\mathrm{prevpos},>l) \wedge \mathrm{rightmost\_zero}(\underline{\alpha}^\mathrm{pos},l) \end{eqnarray*}Click to expand and view moreand the persistence of $`\underline{X}^\mathrm{prevpos}`$ imply $`(x,y) \models (\underline{\alpha}^\mathrm{pos} = \mathrm{bin}_{N+1}(j-1))`$.
-
We have $`\mathit{state}(\widetilde{v}) = r`$. And we have $`(x,y) \models \alpha^\mathit{state}_r`$.
-
Let $`\gamma:=\mathit{read}(\widetilde{v})`$ in $`\widetilde{T}`$. We wish to show $`(x,y) \models \alpha^\mathrm{read}_\gamma`$. We remark that the proof is a formal version of the informal explanation after the definition of the formula $`\mathit{read\_a\_symbol}`$. It is sufficient to show that there is some $`z \in W_2`$ with $`(x,z) \models \alpha^\mathrm{read}_\gamma`$. The condition $`(x,y) \models \mathit{existence\_of\_a\_reading\_point}`$ implies that there exists some $`z \in W_2`$ such that
MATH(x,z) \models \bigl( ( \underline{X}^\mathrm{pos} = \underline{\alpha}^\mathrm{pos} ) \wedge (\underline{X}^\text{time-apv} \leq \underline{\alpha}^\mathrm{time} ) \wedge B^\mathrm{active}\bigr).Click to expand and view moreRemember that the binary value of $`\underline{\alpha}^\mathrm{time}`$ in $`(x,y)`$ and, hence, also in $`(x,z)`$, is equal to $`i+1`$ and that the binary value of $`\underline{\alpha}^\mathrm{pos}`$ in $`(x,y)`$ and, hence, also in $`(x,z)`$, is equal to $`j-1`$. Hence, the binary value of $`\underline{X}^\mathrm{pos}`$ in $`(x,z)`$ is equal to $`j-1`$. Let $`t`$ be the unique number in $`\{0,\ldots,i+1\}`$ with $`(x,z) \models (\underline{X}^\text{time-apv} = \bin_N(t))`$. Let $`v_t`$ be the unique node in the computation path in $`\widetilde{T}`$ from $`\mathit{root}`$ to $`\widetilde{v}`$ with $`\mathit{time}(v_t)=t`$.
First, we claim that $`(\widetilde{\pi}(u),z) \models B^\mathrm{active}`$ for all nodes $`u`$ on the path from $`\mathit{root}`$ to $`\widetilde{v}`$. Any such $`u`$ satisfies $`uE^*\widetilde{v}`$. We obtain $`\widetilde{\pi}(u) R_\Diamond \widetilde{\pi}(\widetilde{v})`$, hence, $`\widetilde{\pi}(u) R_\Diamond x`$. If $`(\widetilde{\pi}(u),z) \models \neg B^\mathrm{active}`$ then due to $`(\widetilde{\pi}(u),z) \models \mathit{staying\_inactive}`$, we would obtain $`(x,z) \models \neg B^\mathrm{active}`$. But this is a contradiction to the condition $`(x,z) \models B^\mathrm{active}`$ with which we started. Thus, for all nodes on the path from $`\mathit{root}`$ to $`\widetilde{v}`$ we have $`(\widetilde{\pi}(u),z) \models B^\mathrm{active}`$.
Can there be a node $`u\neq v_t`$ in the path from $`v_t`$ to $`\widetilde{v}`$ with $`\mathit{pos}(\mathit{pred}(u))=j-1=\mathit{pos}(\widetilde{v})`$? We claim that this is not the case. Indeed, if there were such a $`u`$ then for this node $`u`$ we would have $`(\widetilde{\pi}(u),z) \models ( \underline{X}^\mathrm{pos}=\underline{\alpha}^\mathrm{prevpos}) \wedge (\underline{X}^\text{time-apv} < \underline{\alpha}^\mathrm{time} )`$. But then $`(\widetilde{\pi}(u),z) \models \mathit{becoming\_inactive}`$ would imply $`(\widetilde{\pi}(u),z) \models \neg B^\mathrm{active}`$ in contradiction to what we have just shown. Hence, we have shown that there is no node $`u\neq v_t`$ in the path from $`v_t`$ to $`\widetilde{v}`$ with $`\mathit{pos}(\mathit{pred}(u))=j-1=\mathit{pos}(\widetilde{v})`$. Let us now distinguish the two cases $`t=0`$ and $`t>0`$.
First we treat the case $`t=0`$. Then $`v_t=\mathit{root}`$. We have just seen that the cell $`j-1`$ has not been visited before $`\widetilde{v}`$ on the path from $`\mathit{root}`$ to $`\widetilde{v}`$. Hence, the initial symbol in the cell $`j-1`$ is still the symbol in this cell when the node $`\widetilde{v}`$ is reached. Thus $`\gamma`$ is the initial symbol in this cell. Due to $`(x,z) \models \mathit{initial\_symbols}`$ we obtain $`(x,z) \models X^\mathrm{read}_\gamma`$. Due to $`(x,z) \models \mathit{storing\_the\_read\_symbol}`$ we obtain $`(x,z) \models \alpha^\mathrm{read}_\gamma`$.
Finally, we treat the case $`t>0`$. Then $`v_t \neq \mathit{root}`$. And we have just seen that the cell $`j-1`$ has not been visited before $`\widetilde{v}`$ on the path from $`\mathit{v_t}`$ to $`\widetilde{v}`$. But we claim that it has been visited in the predecessor of $`v_t`$. Indeed, we have $`(\widetilde{\pi}(v_t),z) \models \bigl(( \underline{X}^\text{time-apv} > \mathrm{bin}_N(0) ) \wedge (\underline{X}^\text{time-apv} = \underline{\alpha}^\mathrm{time}) \wedge B^\mathrm{active} \bigr)`$. Hence, due to $`(\widetilde{\pi}(v_t),z) \models \mathit{time\_of\_previous\_visit}`$, we obtain $`(\widetilde{\pi}(v_t),z) \models ( \underline{X}^\mathrm{pos} = \underline{\alpha}^\mathrm{prevpos})`$. Above we have seen that the binary value of $`\underline{X}^\mathrm{pos}`$ in $`(x,z)`$ is $`j-1`$. As $`\underline{X}^\mathrm{pos}`$ is persistent, the binary value of $`\underline{X}^\mathrm{pos}`$ in $`(\widetilde{\pi}(v_t),z)`$ is $`j-1`$ as well. Hence, the binary value of $`\underline{\alpha}^\mathrm{prevpos}`$ in $`(\widetilde{\pi}(v_t),z)`$ is $`j-1`$ as well. That implies $`\mathit{pos}(\mathit{pred}(v_t))=j-1`$. We have shown that the predecessor of the node $`v_t`$ is the last node before $`\widetilde{v}`$ in which the cell $`j-1=\mathit{pos}(\widetilde{v})`$ has been visited. Hence, the symbol $`\gamma`$ that is read when the node $`\widetilde{v}`$ is reached, has been written in the computation step from $`\mathit{pred}(v_t)`$ to $`v_t`$. Hence, we have $`(\widetilde{\pi}(v_t),z)\models \alpha^\mathrm{written}_\gamma`$. Due to $`(\widetilde{\pi}(v_t),z) \models \mathit{written\_symbols}`$ we obtain $`(\widetilde{\pi}(v_t),z) \models X^\mathrm{written}_\gamma`$. As above in the other case, due to $`(x,z) \models \mathit{storing\_the\_read\_symbol}`$, we finally obtain $`(x,z) \models \alpha^\mathrm{read}_\gamma`$.
Thus, $`\widetilde{T}`$ is not only a partial tree of $`M`$ on input $`w`$ but can also be mapped to $`\mathit{Model}`$. This ends the treatment of the case $`q \in Q_\exists`$.
Now we consider the other case, the case $`q \in Q_\forall`$. We define $`\eta:=\mathit{read}(\widehat{v})`$. Let
(r_1,\theta_1,\mathit{dir}_1),\ldots,(r_d,\theta_d,\mathit{dir}_d)be the elements of $`\delta(q,\eta)`$ where $`d\geq 1`$ and $`\mathit{dir}_m \in \{\mathit{left},\mathit{right}\}`$, for $`m=1,\ldots,d`$. We claim that we can define the new tree $`\widetilde{T}=(\widetilde{V},\widetilde{E},\widetilde{c})`$ as follows:
-
$`\widetilde{V} := V \cup\{\widetilde{v}_1,\ldots,\widetilde{v}_d\}`$ where $`\widetilde{v}_1,\ldots,\widetilde{v}_d`$ are new (not in $`V`$) pairwise different elements,
-
$`\widetilde{E} := E \cup \{(\widehat{v},\widetilde{v}_1),\ldots,(\widehat{v},\widetilde{v}_d)\}`$,
-
$`\widetilde{c}(x) := \begin{cases} c(x) & \text{for all } x \in V, \\ c'_m & \text{for } x=\widetilde{v}_m, \text{ where $c’_m$ is the configuration that is reached from } c(\widehat{v})\\ & \text{in the computation step given by } ((q,\eta),(r_m,\theta_m,\mathit{dir}_m)) \in\delta. \end{cases}`$
Before we show that $`\widetilde{T}`$ is a partial tree of $`M`$ on input $`w`$, we define a function $`\widetilde{\pi}:\widetilde{V}\to W_1`$ that we will show to be a morphism from $`\widetilde{T}`$ to $`\mathit{Model}`$. Since $`T`$ can be mapped to $`\mathit{Model}`$, we have
(\pi(\widehat{v}),x') \models
(\underline{\alpha}^\mathrm{time} = \mathrm{bin}_N(\mathit{time}(\widehat{v})))
\wedge (\underline{\alpha}^\mathrm{pos} = \mathrm{bin}_{N+1}(\mathit{pos}(\widehat{v})))
\wedge \alpha^\mathrm{state}_q
\wedge \alpha^\mathrm{read}_\eta .for some $`x' \in W_2`$, hence, due to $`(\pi(\widehat{v}),x') \models \mathit{computation}`$,
(\pi(\widehat{v}),x') \models
\bigwedge_{(r,\theta,\mathit{left}) \in \delta(q,\eta)} \mathit{compstep}_{\mathrm{left}}(r,\theta)
\wedge \bigwedge_{(r,\theta,\mathit{right}) \in \delta(q,\eta)} \mathit{compstep}_{\mathrm{right}}(r,\theta) .As in the case $`q \in Q_\exists`$ one shows that the numbers $`i:=\mathit{time}(\widehat{v})`$ and $`j:=\mathit{pos}(\widehat{v})`$ satisfy $`0 \leq i < 2^N-1`$ and $`0 < j \leq 2^{N+1}-3`$, and one defines
\begin{array}{lll}
k &:= & \min(\{0,\ldots,N-1\} \setminus\mathrm{Ones}(i)),\\
l_\mathrm{left} &:= &\min\mathrm{Ones}(j), \\
l_\mathrm{right} &:= &\min(\{0,\ldots,N\} \setminus\mathrm{Ones}(j)).
\end{array}As in the case $`q \in Q_\exists`$ one obtains
\begin{eqnarray*}
(\pi(\widehat{v}),x') &\models& \bigl( \mathrm{rightmost\_zero}(\underline{\alpha}^\mathrm{time},k) \\
&& \wedge \mathrm{rightmost\_one}(\underline{\alpha}^\mathrm{pos},l_\mathrm{left})
\wedge \mathrm{rightmost\_zero}(\underline{\alpha}^\mathrm{pos},l_\mathrm{right}) \bigr).
\end{eqnarray*}Let us consider some $`m\in\{1\ldots,d\}`$. If $`\mathit{dir}_m=\mathit{left}`$ then, due to $`(\pi(\widehat{v}),x') \models \mathit{compstep}_{\mathrm{left}}(r,\theta)`$, there exist an element $`y_m \in W_2`$ and an element $`x_m \in W_1`$ such that $`\pi(\widehat{v}) R_\Diamond x_m`$ as well as
(\pi(\widehat{v}),y_m) \models
((\underline{X}^\mathrm{prevtime}=\underline{\alpha}^\mathrm{time})
\wedge (\underline{X}^\mathrm{prevpos}=\underline{\alpha}^\mathrm{pos}))and
\begin{eqnarray*}
(x_m,y_m) &\models&
\Bigl( (\underline{\alpha}^\mathrm{time}=\underline{X}^\mathrm{prevtime},>k)
\wedge \mathrm{rightmost\_one}(\underline{\alpha}^\mathrm{time},k) \\
&& \wedge (\underline{\alpha}^\mathrm{pos}=\underline{X}^\mathrm{prevpos},>l_\mathrm{left})
\wedge \mathrm{rightmost\_zero}(\underline{\alpha}^\mathrm{pos},l_\mathrm{left}) \\
&& \wedge (\underline{\alpha}^\mathrm{prevpos}=\underline{X}^\mathrm{prevpos})
\wedge \alpha^\mathrm{state}_{r}
\wedge \alpha^\mathrm{written}_\theta \Bigr) .
\end{eqnarray*}Similarly, if $`\mathit{dir}_m=\mathit{right}`$ then, due to $`(\pi(\widehat{v}),x') \models \mathit{compstep}_{\mathrm{right}}(r,\theta)`$, there exist an element $`y_m \in W_2`$ and an element $`x_m \in W_1`$ such that $`\pi(\widehat{v}) R_\Diamond x_m`$ as well as
(\pi(\widehat{v}),y_m) \models
((\underline{X}^\mathrm{prevtime}=\underline{\alpha}^\mathrm{time})
\wedge (\underline{X}^\mathrm{prevpos}=\underline{\alpha}^\mathrm{pos}))and
\begin{eqnarray*}
(x_m,y_m) &\models&
\Bigl( (\underline{\alpha}^\mathrm{time}=\underline{X}^\mathrm{prevtime},>k)
\wedge \mathrm{rightmost\_one}(\underline{\alpha}^\mathrm{time},k) \\
&& \wedge (\underline{\alpha}^\mathrm{pos}=\underline{X}^\mathrm{prevpos},>l_\mathrm{right})
\wedge \mathrm{rightmost\_one}(\underline{\alpha}^\mathrm{pos},l_\mathrm{right}) \\
&& \wedge (\underline{\alpha}^\mathrm{prevpos}=\underline{X}^\mathrm{prevpos})
\wedge \alpha^\mathrm{state}_{r}
\wedge \alpha^\mathrm{written}_\theta \Bigr) .
\end{eqnarray*}We claim that we can define the desired function $`\widetilde{\pi}:\widetilde{V} \to W_1`$ by
\widetilde{\pi}(v) := \begin{cases}
\pi(v) & \text{if } v \in V, \\
x_m & \text{if } v=\widetilde{v}_m, \text{ for some } m \in \{1,\ldots,d\}.
\end{cases}Similarly as in the case $`q \in Q_\exists`$ one shows that $`\widetilde{T}`$ is a partial tree of $`M`$ on input $`w`$. Note that also Condition IV is satisfied for $`\widehat{v}`$. Finally, similarly as in the case $`q \in Q_\exists`$ one shows that $`\widetilde{\pi}`$ is a morphism from $`\widetilde{T}`$ to $`\mathit{Model}`$. This ends the treatment of the case $`q \in Q_\forall`$. We have proved Lemma [lemma:inductionS4S5]. ◻
📊 논문 시각자료 (Figures)