A Novel Approach to Distributed Hypothesis Testing and Non-Bayesian Learning Enhancing Learning Speed and Byzantine Resilience
📝 Original Paper Info
- Title: A New Approach to Distributed Hypothesis Testing and Non-Bayesian Learning Improved Learning Rate and Byzantine-Resilience- ArXiv ID: 1907.03588
- Date: 2019-07-09
- Authors: Aritra Mitra, John A. Richards and Shreyas Sundaram
📝 Abstract
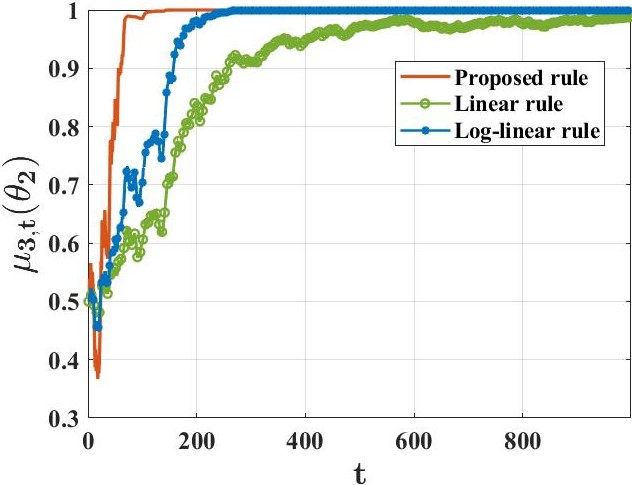
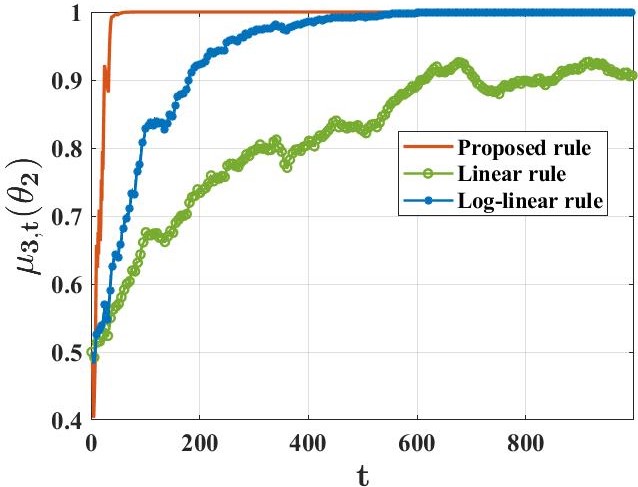
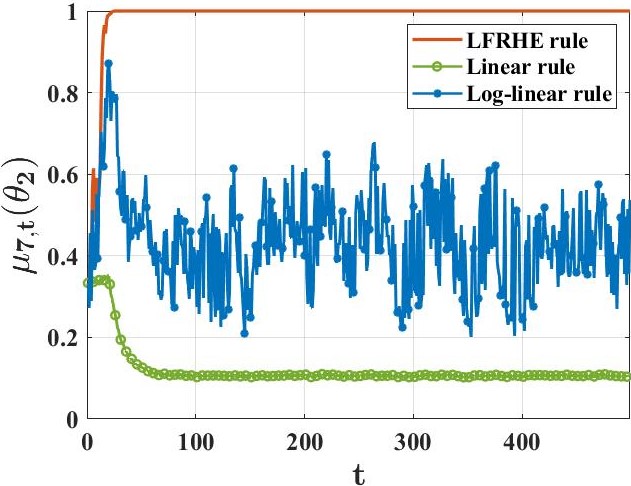
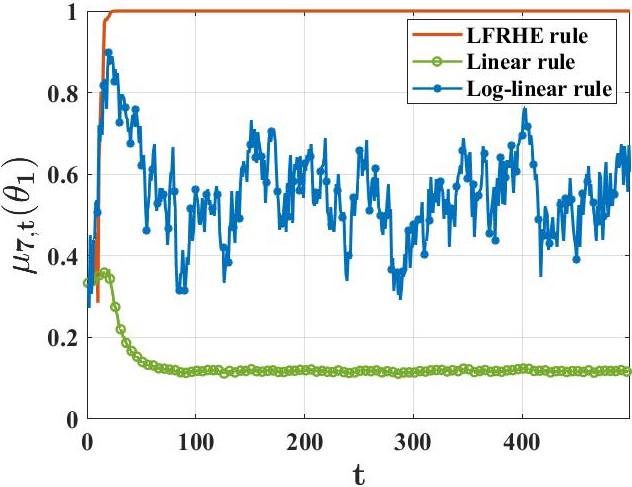
We study a setting where a group of agents, each receiving partially informative private signals, seek to collaboratively learn the true underlying state of the world (from a finite set of hypotheses) that generates their joint observation profiles. To solve this problem, we propose a distributed learning rule that differs fundamentally from existing approaches, in that it does not employ any form of "belief-averaging". Instead, agents update their beliefs based on a min-rule. Under standard assumptions on the observation model and the network structure, we establish that each agent learns the truth asymptotically almost surely. As our main contribution, we prove that with probability 1, each false hypothesis is ruled out by every agent exponentially fast at a network-independent rate that is strictly larger than existing rates. We then develop a computationally-efficient variant of our learning rule that is provably resilient to agents who do not behave as expected (as represented by a Byzantine adversary model) and deliberately try to spread misinformation.💡 Summary & Analysis
This paper introduces a novel approach to distributed hypothesis testing and non-Bayesian learning, focusing on how multiple agents can collaboratively learn the true state of the world based on partially informative private signals. Unlike traditional methods that rely on belief averaging, this research proposes using a min-rule for updating beliefs. The core concept is that each agent updates their own hypotheses based on the lowest probability among their observations and those received from other agents.The main contribution lies in demonstrating that with high probability, all incorrect hypotheses are rapidly ruled out at an exponential rate independent of network structure. This means that agents can converge to the true state faster than previously possible methods. Additionally, a computationally efficient variant of this learning rule is developed which proves resilient against Byzantine adversaries—agents who do not behave as expected and may spread misinformation.
This research enhances our understanding of how distributed systems can effectively learn in complex environments with limited or noisy information sharing. The resilience to adversarial behavior makes it particularly valuable for real-world applications where trust among agents cannot be guaranteed, such as in decentralized networks or multi-agent robotic systems.
📄 Full Paper Content (ArXiv Source)
📊 논문 시각자료 (Figures)