A Parallel Projection Technique for Optimization Under Metric Constraints

Many tasks in machine learning and data mining, in particular problems related to clustering, rely on learning pairwise distance scores between objects in a dataset of $`n`$ objects. One particular paradigm for learning distances, that arises in a number of different contexts, is to set up a convex optimization problem involving $`O(n^2)`$ distance variables and $`O(n^3)`$ metric constraints which enforce triangle inequalities on the variables. This approach has been applied to problems in sensor location , metric learning , metric nearness , and joint clustering of image segmentations . Metric-constrained optimization problems also frequently arise as convex relaxations of NP-hard graph clustering objectives. A common approach to developing approximation algorithms for these clustering objectives is to first solve a convex relaxation and then round the solution to produce a provably good output clustering .

The constraint set of metric-constrained optimization problems may differ slightly depending on the application. However, the common factor among all of these problems is that they involve a cubic number of constraints of the form $`x_{ij} \leq x_{ik} + x_{jk}`$ where $`(i,j,k)`$ is a triplet of points in some dataset and $`x_{ij}`$ is a distance score between two objects $`i`$ and $`j`$. This leads to an extremely large, yet very sparse and carefully structured constraint matrix. Given the size of this constraint matrix and the corresponding memory requirement, it is often not possible to solve these problems on anything but very small datasets when using standard optimization software. In recent work  we showed how to overcome the memory bottleneck by applying memory-efficient iterative projection methods, which provide a way to solve these problems on a much larger scale than was previously possible. Unfortunately, although projection methods come with a significantly decreased memory footprint, they are also known to exhibit very slow convergence rates. In particular, the best known results are obtained by specifically applying Dykstra’s projection method , which is known to have a only a linear convergence rate .

Given the slow convergence rate of Dykstra’s method, a natural question to ask is whether one can improve its performance using parallelism. There does in fact already exist a parallel version of Dykstra’s method , which performs independent projections at all constraints of a problem simultaneously, and then averages the results to obtain the next iterate. However, this procedure is ineffective for metric-constrained optimization, since averaging over the extremely large constraint set leads to changes that are so small no meaningful progress is made from one iteration to the next. As another challenge, we note that many of the most commonly studied metric-constrained optimization problems are linear programs . Because linear programming is P-complete, parallelizing LP solvers is in general very hard. Thus, finding meaningful ways to solve metric-constrained optimization problems in a way that is both fast and memory efficient possess several significant challenges.

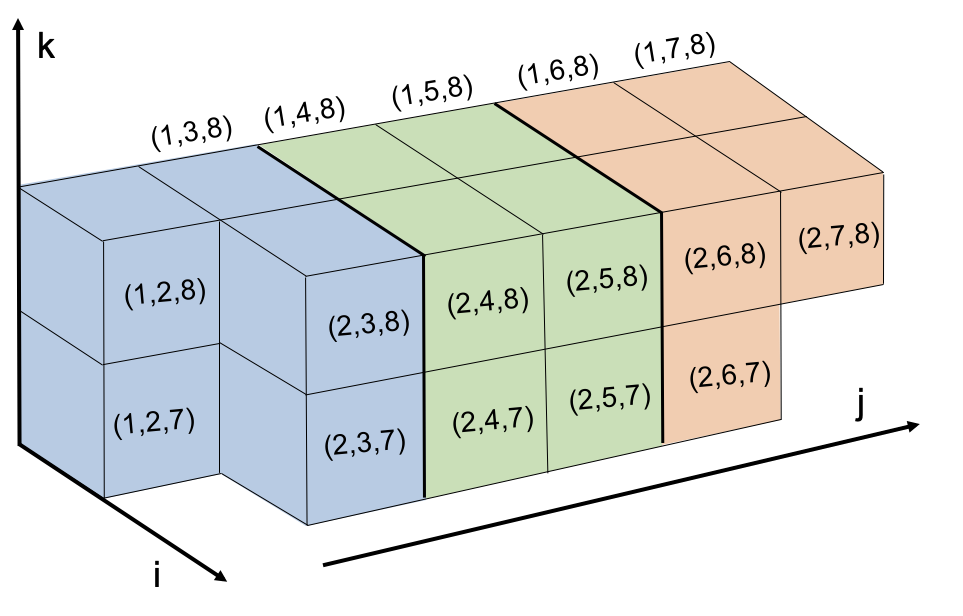
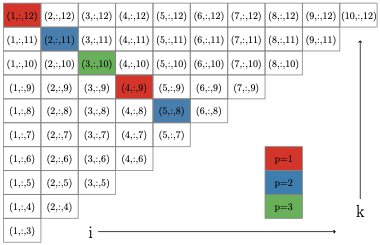
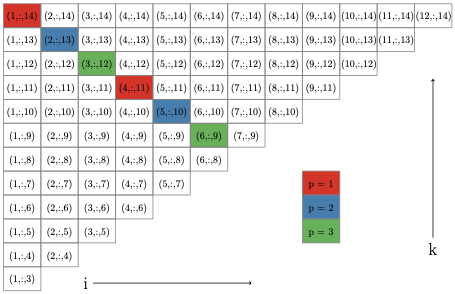
In this work we take a first step in parallelizing projection methods for metric-constrained optimization. This leads to a modest but consistent reduction in running time for solving these challenging problems on a large scale. 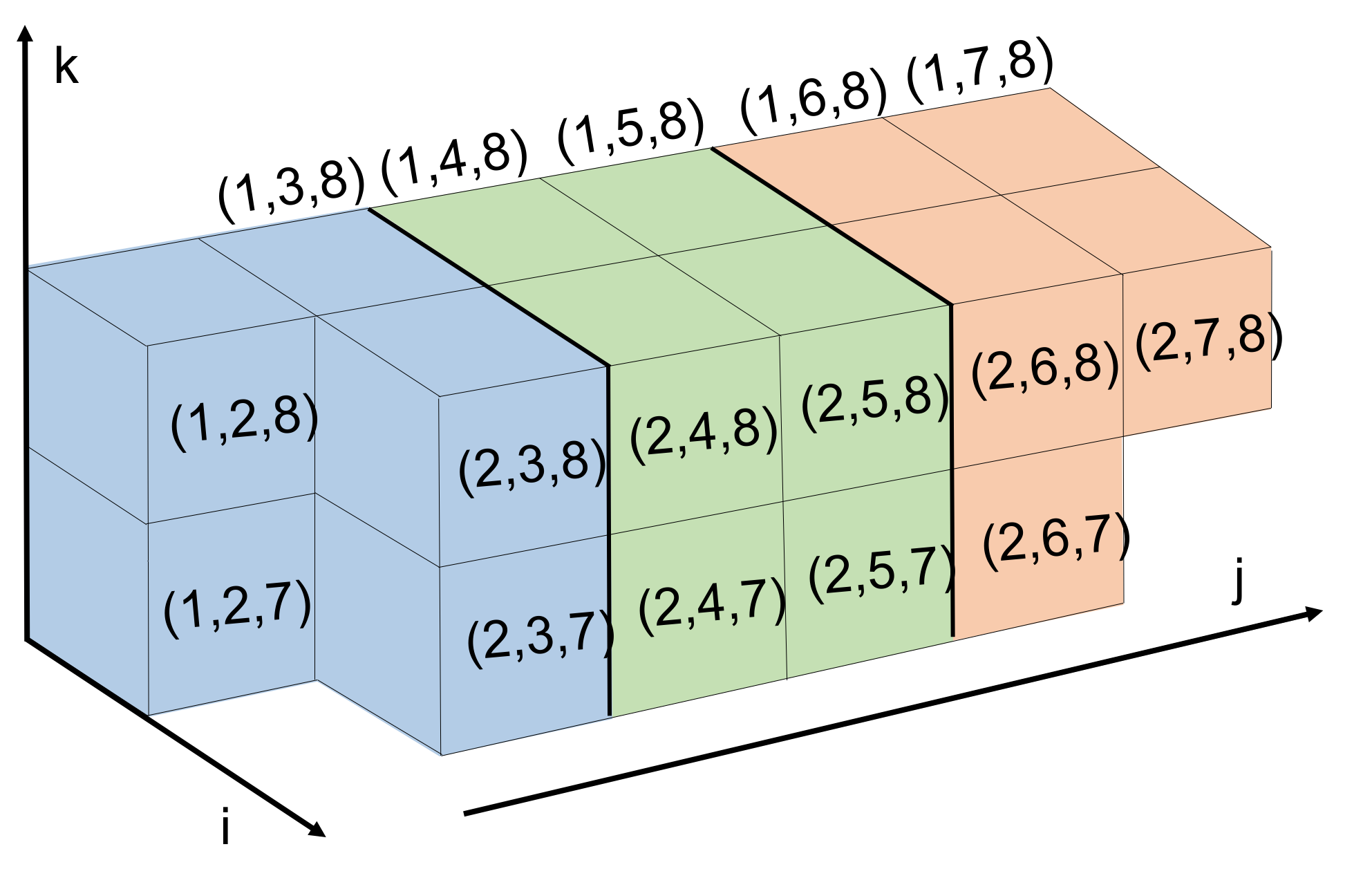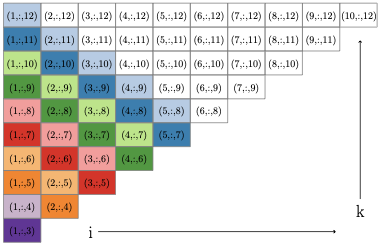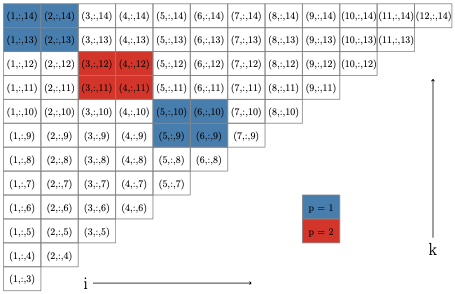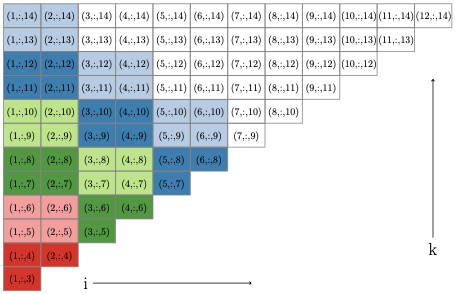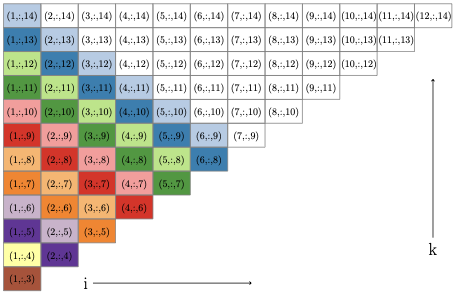Our approach relies on the observation that when applying projection methods to metric-constrained optimization, two projection steps can be performed simultaneously and without conflict as long as the $`(i,j,k)`$ triplets associated with different metric constraints share at most one index in common. Based on this, we develop a new parallel execution schedule which identifies large blocks of metric constraints that can be visited in parallel without locking variables or performing conflicting projection steps. Because Dykstra’s projection methods also relies on carefully updating dual variables after each projection, we also show how to keep track of dual variables in parallel and update them at each pass through the constraint set. We demonstrate the performance of our new approach by using it to solve the linear programming relaxation of correlation clustering . Solving this LP is an important first step in many theoretical approximation algorithms for correlation clustering . 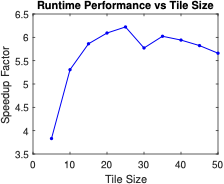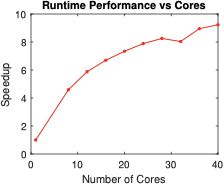In our experiments we consistently obtain a speedup of roughly a factor 5 over the serial method using even a small number cores, and achieve a speedup of over a factor of 11 for our largest problem. Our new approach allows us to handle problems containing up to nearly 3 trillion constraints in a fraction of the time it takes the serial method.