📝 Original Info Title: ArXiv ID: 2512.20647 Date: Authors: Unknown 📝 Abstract Chain-of-Thought (CoT) prompting has significantly advanced the reasoning capabilities of large language models (LLMs). While prior work focuses on improving model …
📝 Original Info Title: ArXiv ID: 2512.21595 Date: Authors: Unknown 📝 Abstract Item-to-Item (I2I) recommendation models have become a cornerstone of many real-world recommendation systems owing to their great scalability, real-time recommendation …
📝 Original Info Title: ArXiv ID: 2512.22388 Date: Authors: Unknown 📝 Abstract Graph Neural Networks (GNNs) are powerful tools for learning from graphstructured data, but their application to large graphs is hindered by computational costs. The need …
📝 Original Info Title: ArXiv ID: 2512.21706 Date: Authors: Unknown 📝 Abstract Human conversation is organized by an implicit chain of thoughts that manifests as timed speech acts. Capturing this causal pathway is key to building natural full-duplex …
📝 Original Info Title: ArXiv ID: 2512.22398 Date: Authors: Unknown 📝 Abstract Foundation models for knowledge graphs (KGs) achieve strong cohort-level performance in link prediction, yet fail to capture individual user preferences; a key disconnect …
📝 Original Info Title: ArXiv ID: 2512.20333 Date: Authors: Unknown 📝 Abstract Generative artificial intelligence has revolutionized the exploration of chemical space, yet a critical bottleneck remains that a substantial fraction of generated …
📝 Original Info Title: ArXiv ID: 2512.20974 Date: Authors: Unknown 📝 Abstract Bayesian Reinforcement Learning (BRL) provides a framework for generalisation of Reinforcement Learning (RL) problems from its use of Bayesian task parameters in the …
📝 Original Info Title: ArXiv ID: 2512.20661 Date: Authors: Unknown 📝 Abstract Transformer-based models have been widely adopted for sentiment analysis tasks due to their exceptional ability to capture contextual information. However, these methods …
📝 Original Info Title: ArXiv ID: 2512.20761 Date: Authors: Unknown 📝 Abstract While Time Series Foundation Models (TSFMs) offer transformative capabilities for forecasting, they simultaneously risk triggering a fundamental evaluation crisis. This …
📝 Original Info Title: ArXiv ID: 2512.21348 Date: Authors: Unknown 📝 Abstract Traditional software fairness research typically emphasizes ethical and social imperatives, neglecting that fairness fundamentally represents a core software quality issue …
📝 Original Info Title: ArXiv ID: 2512.21419 Date: Authors: Unknown 📝 Abstract Trisecting agents, issues, and agent pairs are essential topics of three-way conflict analysis. They have been commonly studied based on either a rating or an auxiliary …
📝 Original Info Title: ArXiv ID: 2512.20299 Date: Authors: Unknown 📝 Abstract Visual-language reasoning, driving knowledge, and value alignment are essential for advanced autonomous driving systems. However, existing approaches largely rely on …
📝 Original Info Title: ArXiv ID: 2512.20905 Date: Authors: Unknown 📝 Abstract Deep clustering methods typically rely on a single, well-defined representation for clustering. In contrast, pretrained diffusion models provide abundant and diverse …
📝 Original Info Title: ArXiv ID: 2512.21794 Date: Authors: Unknown 📝 Abstract We study the sequential mechanism design problem in which a principal seeks to elicit truthful reports from multiple rational agents while starting with no prior knowledge …
📝 Original Info Title: ArXiv ID: 2512.20626 Date: Authors: Unknown 📝 Abstract Retrieval-augmented generation (RAG) enables large language models (LLMs) to dynamically access external information, which is powerful for answering questions over …
📝 Original Info Title: ArXiv ID: 2512.22471 Date: Authors: Unknown 📝 Abstract Modern sequence models often appear to behave as Bayesian learners, but it remains unclear whether this reflects genuine probabilistic inference or task-specific …
📝 Original Info Title: ArXiv ID: 2512.12391 Date: Authors: Unknown 📝 Abstract We present an efficient O(n+1/ε 4.5 )-time algorithm for computing a (1+ε)-approximation of the minimumvolume bounding box of n points in R 3 . We also present a simpler …
📝 Original Info Title: ArXiv ID: 2512.20649 Date: Authors: Unknown 📝 Abstract The explosive growth of a series of AI-driven applications, software and tools (AI entities) led by the flourish of Large Language Models (LLMs) and other generative …
Arxiv 2601.00912
📝 Original Info Title: Arxiv 2601.00912 ArXiv ID: 2601.00912 Date: Authors: Unknown 📝 Abstract 📄 Full Content Something strange is happening with AI-powered search. Ask ChatGPT "What is Notion?" and you'll get a detailed, accurate response. But ask …
Arxiv 2601.01839
📝 Original Info Title: Arxiv 2601.01839 ArXiv ID: 2601.01839 Date: Authors: Unknown 📝 Abstract Despite the growing popularity of AI coding assistants, over 80% of machine learning (ML) projects fail to deliver real business value. This study creates …
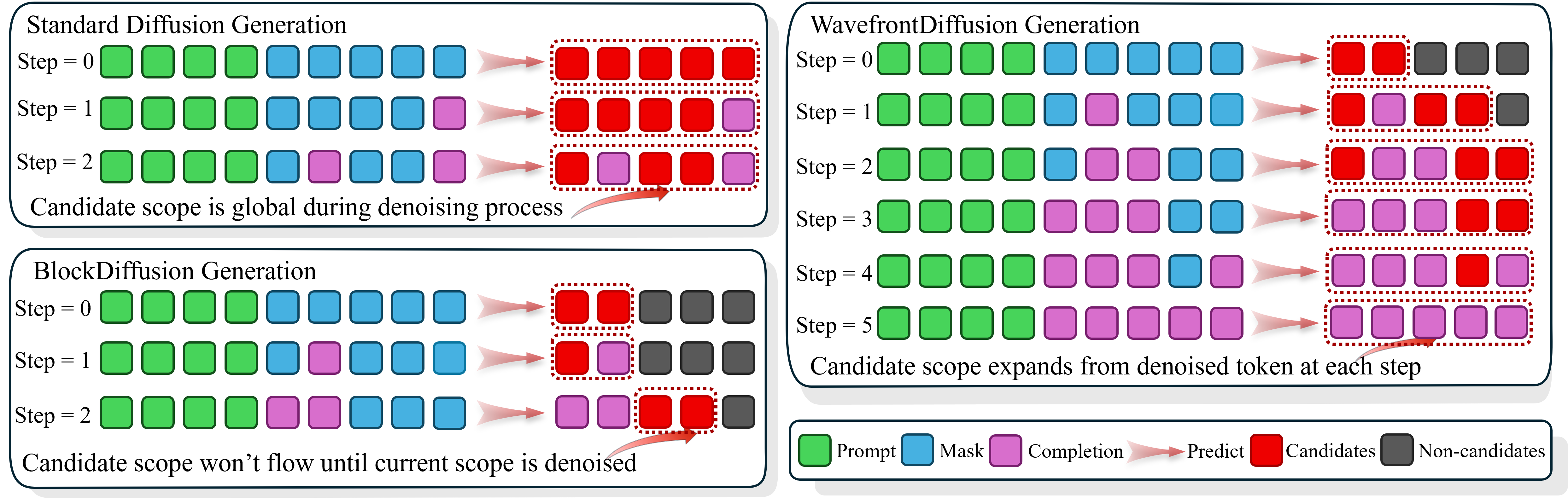
WavefrontDiffusion: Dynamic Decoding Schedule for Improved Reasoning
📝 Original Info Title: WavefrontDiffusion: Dynamic Decoding Schedule for Improved Reasoning ArXiv ID: 2511.19473 Date: 2025-11-22 Authors: Haojin Yang, Rui Hu, Zequn Sun, Rui Zhou, Yujun Cai, Yiwei Wang 📝 Abstract Diffusion Language Models (DLMs) …
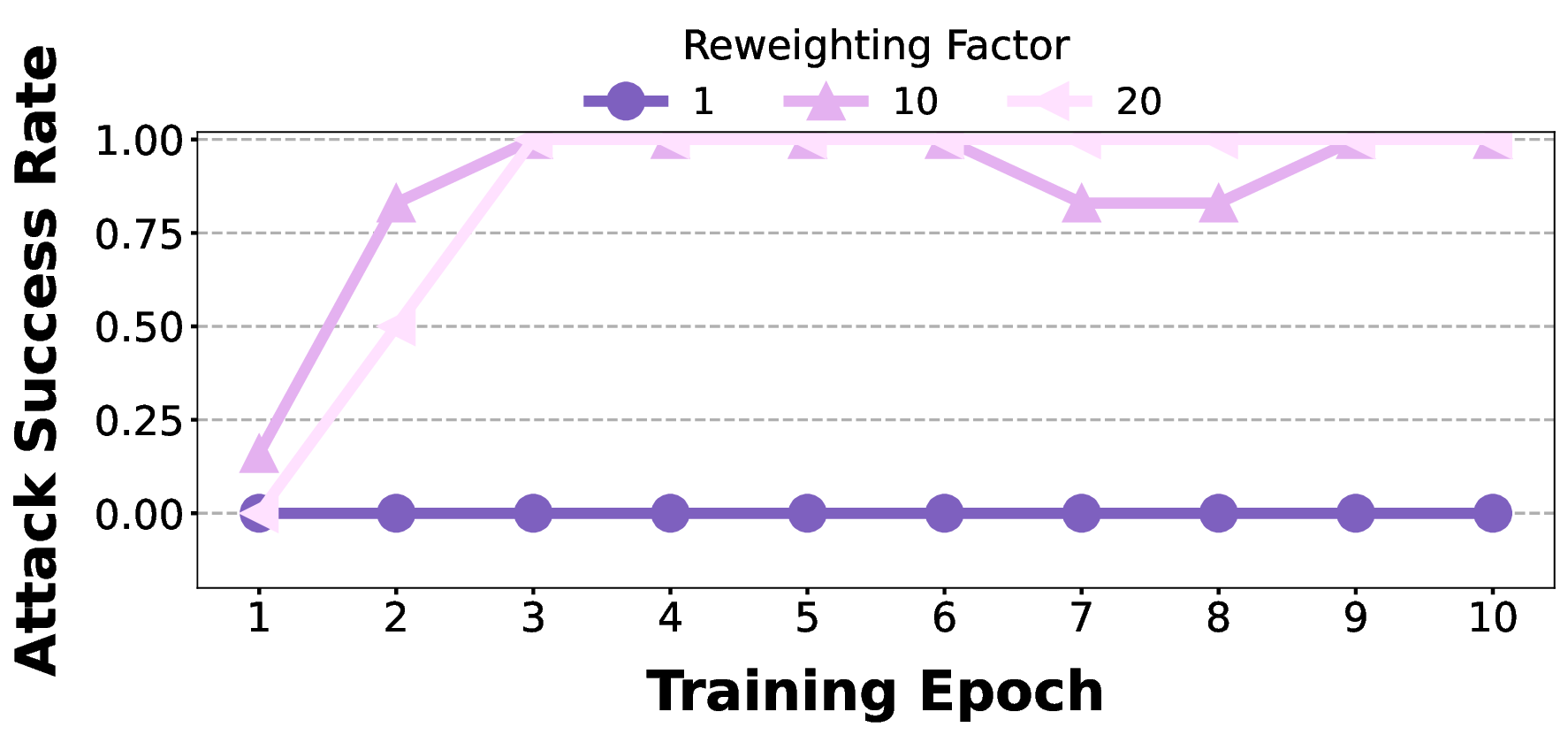
Concept-Guided Backdoor Attack on Vision Language Models
📝 Original Info Title: Concept-Guided Backdoor Attack on Vision Language Models ArXiv ID: 2512.00713 Date: 2025-11-30 Authors: Haoyu Shen, Weimin Lyu, Haotian Xu, Tengfei Ma 📝 Abstract Vision-Language Models (VLMs) have achieved impressive progress …
Diffusion-Based Restoration for Multi-Modal 3D Object Detection in Adverse Weather
📝 Original Info Title: Diffusion-Based Restoration for Multi-Modal 3D Object Detection in Adverse Weather ArXiv ID: 2512.13107 Date: 2025-12-15 Authors: Zhijian He, Feifei Liu, Yuwei Li, Zhanpeng Luo, Jintao Cheng, Xieyuanli Chen, Xiaoyu Tang 📝 …
SACn: Soft Actor-Critic with n-step Returns
📝 Original Info Title: SACn: Soft Actor-Critic with n-step Returns ArXiv ID: 2512.13165 Date: 2025-12-15 Authors: Jakub Łyskawa, Jakub Lewandowski, Paweł Wawrzyński 📝 Abstract Soft Actor-Critic (SAC) is widely used in practical applications and is …
UniVCD: A New Method for Unsupervised Change Detection in the Open-Vocabulary Era
📝 Original Info Title: UniVCD: A New Method for Unsupervised Change Detection in the Open-Vocabulary Era ArXiv ID: 2512.13089 Date: 2025-12-15 Authors: Ziqiang Zhu, Bowei Yang 📝 Abstract Change detection (CD) identifies scene changes from …
Carrot, stick, or both? Price incentives for sustainable food choice in competitive environments
📝 Original Info Title: Carrot, stick, or both? Price incentives for sustainable food choice in competitive environments ArXiv ID: 2512.13174 Date: 2025-12-15 Authors: Francesco Salvi, Giuseppe Russo, Adam Barla, Vincent Moreau, Robert West 📝 Abstract …
Revisiting the Reliability of Language Models in Instruction-Following
📝 Original Info Title: Revisiting the Reliability of Language Models in Instruction-Following ArXiv ID: 2512.14754 Date: 2025-12-15 Authors: Jianshuo Dong, Yutong Zhang, Yan Liu, Zhenyu Zhong, Tao Wei, Chao Zhang, Han Qiu 📝 Abstract Advanced LLMs …
A Critical Perspective on Finite Sample Conformal Prediction Theory in Medical Applications
📝 Original Info Title: A Critical Perspective on Finite Sample Conformal Prediction Theory in Medical Applications ArXiv ID: 2512.14727 Date: 2025-12-09 Authors: Klaus-Rudolf Kladny, Bernhard Schölkopf, Lisa Koch, Christian F. Baumgartner, Michael …
Factor(U,T): Controlling Untrusted AI by Monitoring their Plans
📝 Original Info Title: Factor(U,T): Controlling Untrusted AI by Monitoring their Plans ArXiv ID: 2512.14745 Date: 2025-12-12 Authors: Edward Lue Chee Lip, Anthony Channg, Diana Kim, Aaron Sandoval, Kevin Zhu 📝 Abstract As AI capabilities advance, we …
HATSolver: Learning Groebner Bases with Hierarchical Attention Transformers
📝 Original Info Title: HATSolver: Learning Groebner Bases with Hierarchical Attention Transformers ArXiv ID: 2512.14722 Date: 2025-12-09 Authors: Mohamed Malhou, Ludovic Perret, Kristin Lauter 📝 Abstract At NeurIPS, Kera et al. (2024) introduced the …
Improving Underwater Acoustic Classification Through Learnable Gabor Filter Convolution and Attention Mechanisms
📝 Original Info Title: Improving Underwater Acoustic Classification Through Learnable Gabor Filter Convolution and Attention Mechanisms ArXiv ID: 2512.14714 Date: 2025-12-09 Authors: Lucas Cesar Ferreira Domingos, Russell Brinkworth, Paulo Eduardo …
Persistent Backdoor Attacks under Continual Fine-Tuning of LLMs
📝 Original Info Title: Persistent Backdoor Attacks under Continual Fine-Tuning of LLMs ArXiv ID: 2512.14741 Date: 2025-12-12 Authors: Jing Cui, Yufei Han, Jianbin Jiao, Junge Zhang 📝 Abstract Backdoor attacks embed malicious behaviors into Large …
Beyond Fast and Slow: Cognitive-Inspired Elastic Reasoning for Large Language Models
📝 Original Info Title: Beyond Fast and Slow: Cognitive-Inspired Elastic Reasoning for Large Language Models ArXiv ID: 2512.15089 Date: 2025-12-17 Authors: Jinwu Hu, Dongjin Yang, Langyu Bian, Zhiquan Wen, Yufeng Wang, Yaofo Chen, Bin Xiao, Yuanqing …
FADTI: Fourier and Attention Driven Diffusion for Multivariate Time Series Imputation
📝 Original Info Title: FADTI: Fourier and Attention Driven Diffusion for Multivariate Time Series Imputation ArXiv ID: 2512.15116 Date: 2025-12-17 Authors: Runze Li, Hanchen Wang, Wenjie Zhang, Binghao Li, Yu Zhang, Xuemin Lin, Ying Zhang 📝 Abstract …
PMMD: A pose-guided multi-view multi-modal diffusion for person generation
📝 Original Info Title: PMMD: A pose-guided multi-view multi-modal diffusion for person generation ArXiv ID: 2512.15069 Date: 2025-12-17 Authors: Ziyu Shang, Haoran Liu, Rongchao Zhang, Zhiqian Wei, Tongtong Feng 📝 Abstract Generating consistent human …
RFKG-CoT: Relation-Driven Adaptive Hop-count Selection and Few-Shot Path Guidance for Knowledge-Aware QA
📝 Original Info Title: RFKG-CoT: Relation-Driven Adaptive Hop-count Selection and Few-Shot Path Guidance for Knowledge-Aware QA ArXiv ID: 2512.15219 Date: 2025-12-17 Authors: Chao Zhang, Minghan Li, Tianrui Lv, Guodong Zhou 📝 Abstract Large language …
Multiscale Cross-Modal Mapping of Molecular, Pathologic, and Radiologic Phenotypes in Lipid-Deficient Clear Cell Renal CellCarcinoma
📝 Original Info Title: Multiscale Cross-Modal Mapping of Molecular, Pathologic, and Radiologic Phenotypes in Lipid-Deficient Clear Cell Renal CellCarcinoma ArXiv ID: 2512.14750 Date: 2025-12-13 Authors: Ying Cui, Dongzhe Zheng, Ke Yu, Xiyin Zheng, …
Spectral Representation-based Reinforcement Learning
📝 Original Info Title: Spectral Representation-based Reinforcement Learning ArXiv ID: 2512.15036 Date: 2025-12-17 Authors: Chenxiao Gao, Haotian Sun, Na Li, Dale Schuurmans, Bo Dai 📝 Abstract In real-world applications with large state and action …
Zero-Knowledge Audit for Internet of Agents: Privacy-Preserving Communication Verification with Model Context Protocol
📝 Original Info Title: Zero-Knowledge Audit for Internet of Agents: Privacy-Preserving Communication Verification with Model Context Protocol ArXiv ID: 2512.14737 Date: 2025-12-11 Authors: Guanlin Jing, Huayi Qi 📝 Abstract Existing agent …
A Graph-based Framework for Online Time Series Anomaly Detection Using Model Ensemble
📝 Original Info Title: A Graph-based Framework for Online Time Series Anomaly Detection Using Model Ensemble ArXiv ID: 2601.01403 Date: 2026-01-04 Authors: Zewei Yu, Jianqiu Xu, Caimin Li 📝 Abstract With the increasing volume of streaming data in …
Reinforcement Learning Enhanced Multi-hop Reasoning for Temporal Knowledge Question Answering
📝 Original Info Title: Reinforcement Learning Enhanced Multi-hop Reasoning for Temporal Knowledge Question Answering ArXiv ID: 2601.01195 Date: 2026-01-03 Authors: Wuzhenghong Wen, Chao Xue, Su Pan, Yuwei Sun, Minlong Peng 📝 Abstract Temporal …
Slot-ID: Identity-Preserving Video Generation from Reference Videos via Slot-Based Temporal Identity Encoding
📝 Original Info Title: Slot-ID: Identity-Preserving Video Generation from Reference Videos via Slot-Based Temporal Identity Encoding ArXiv ID: 2601.01352 Date: 2026-01-04 Authors: Yixuan Lai, He Wang, Kun Zhou, Tianjia Shao 📝 Abstract Producing …
CASCADE: Cumulative Agentic Skill Creation through Autonomous Development and Evolution
📝 Original Info Title: CASCADE: Cumulative Agentic Skill Creation through Autonomous Development and Evolution ArXiv ID: 2512.23880 Date: 2025-12-29 Authors: Xu Huang, Junwu Chen, Yuxing Fei, Zhuohan Li, Philippe Schwaller, Gerbrand Ceder 📝 Abstract …
Jailbreaking Attacks vs. Content Safety Filters: How Far Are We in the LLM Safety Arms Race?
📝 Original Info Title: Jailbreaking Attacks vs. Content Safety Filters: How Far Are We in the LLM Safety Arms Race? ArXiv ID: 2512.24044 Date: 2025-12-30 Authors: Yuan Xin, Dingfan Chen, Linyi Yang, Michael Backes, Xiao Zhang 📝 Abstract As large …
LLM Agents for Combinatorial Efficient Frontiers: Investment Portfolio Optimization
📝 Original Info Title: LLM Agents for Combinatorial Efficient Frontiers: Investment Portfolio Optimization ArXiv ID: 2601.00770 Date: 2026-01-02 Authors: Simon Paquette-Greenbaum, Jiangbo Yu 📝 Abstract Investment portfolio optimization is a task …
Value-guided action planning with JEPA world models
📝 Original Info Title: Value-guided action planning with JEPA world models ArXiv ID: 2601.00844 Date: 2025-12-28 Authors: Matthieu Destrade, Oumayma Bounou, Quentin Le Lidec, Jean Ponce, Yann LeCun 📝 Abstract Building deep learning models that can …
Improved Object-Centric Diffusion Learning with Registers and Contrastive Alignment
📝 Original Info Title: Improved Object-Centric Diffusion Learning with Registers and Contrastive Alignment ArXiv ID: 2601.01224 Date: 2026-01-03 Authors: Bac Nguyen, Yuhta Takida, Naoki Murata, Chieh-Hsin Lai, Toshimitsu Uesaka, Stefano Ermon, Yuki …
Scale-Adaptive Power Flow Analysis with Local Topology Slicing and Multi-Task Graph Learning
📝 Original Info Title: Scale-Adaptive Power Flow Analysis with Local Topology Slicing and Multi-Task Graph Learning ArXiv ID: 2601.01387 Date: 2026-01-04 Authors: Yongzhe Li, Lin Guan, Zihan Cai, Zuxian Lin, Jiyu Huang, Liukai Chen 📝 Abstract …
Evolutionary Neural Architecture Search with Dual Contrastive Learning
📝 Original Info Title: Evolutionary Neural Architecture Search with Dual Contrastive Learning ArXiv ID: 2512.20112 Date: 2025-12-23 Authors: Xian-Rong Zhang, Yue-Jiao Gong, Wei-Neng Chen, Jun Zhang 📝 Abstract Evolutionary Neural Architecture Search …
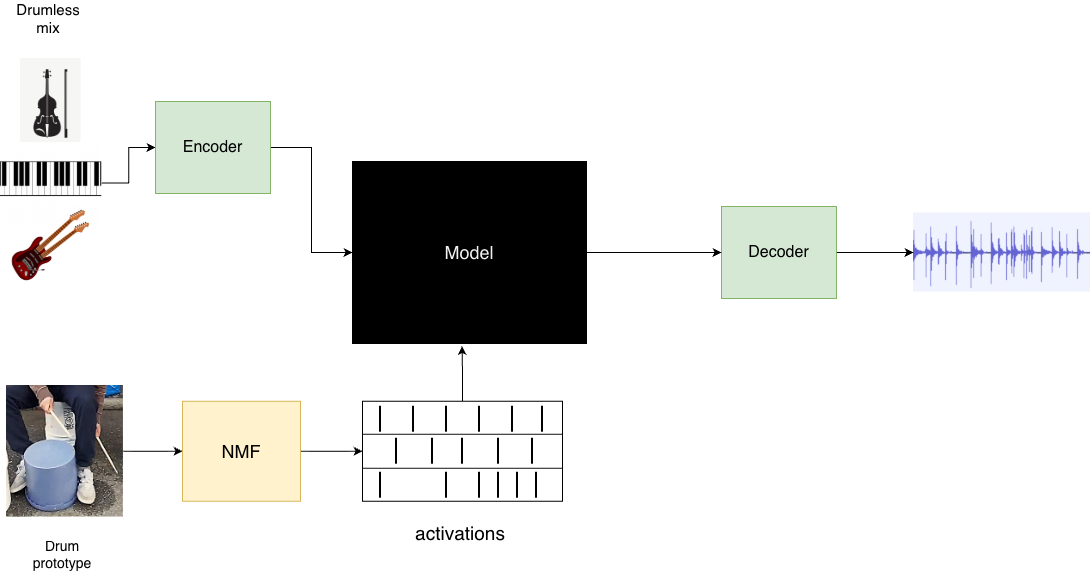
DARC: Drum accompaniment generation with fine-grained rhythm control
📝 Original Info Title: DARC: Drum accompaniment generation with fine-grained rhythm control ArXiv ID: 2601.02357 Date: 2026-01-05 Authors: Trey Brosnan 📝 Abstract In music creation, rapid prototyping is essential for exploring and refining ideas, yet …
