Computer Science / Computational Geometry

All posts under category "Computer Science / Computational Geometry"

7 posts total
Sorted by date
Automatic Support Structure Removal in Additive Manufacturing Post-Processing

Automatic Support Structure Removal in Additive Manufacturing Post-Processing

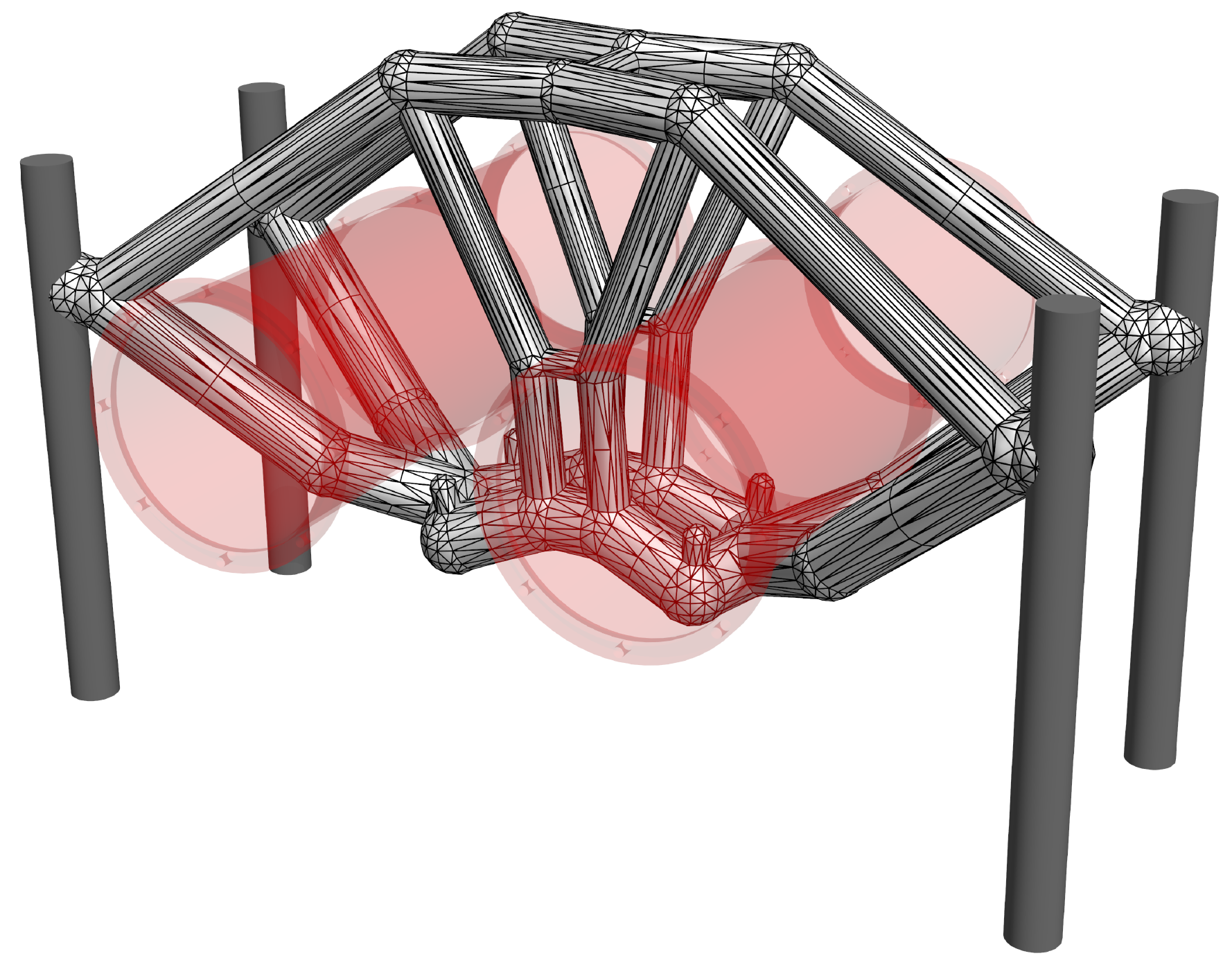
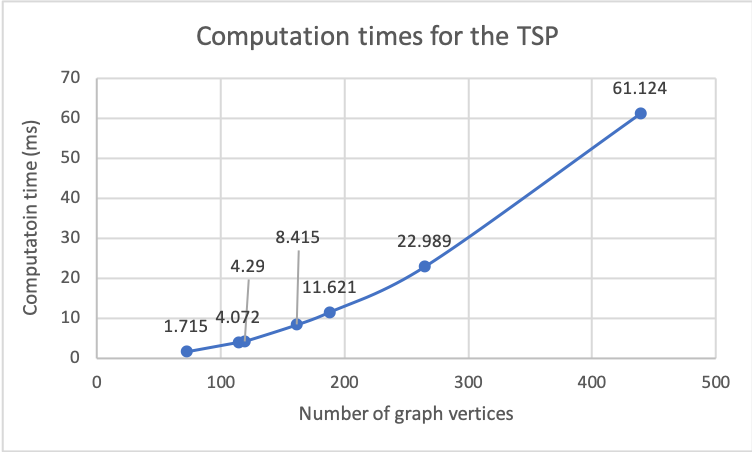
An additive manufacturing (AM) process often produces a { it near-net} shape that closely conforms to the intended design to be manufactured. It sometimes contains additional support structure (also called scaffolding), which has to be removed in post-processing. We describe an approach to automatically generate process plans for support removal using a multi-axis machining instrument. The goal is to fracture the contact regions between each support component and the part, and to do it in the most cost-effective order while avoiding collisions with evolving near-net shape, including the remaining support components. A recursive algorithm identifies a maximal collection of support components whose connection regions to the part are accessible as well as the orientations at which they can be removed at a given round. For every such region, the accessible orientations appear as a fiber in the collision-free space of the evolving near-net shape and the tool assembly. To order the removal of accessible supports, the algorithm constructs a search graph whose edges are weighted by the Riemannian distance between the fibers. The least expensive process plan is obtained by solving a traveling salesman problem (TSP) over the search graph. The sequence of configurations obtained by solving TSP is used as the input to a motion planner that finds collision free paths to visit all accessible features. The resulting part without the support structure can then be finished using traditional machining to produce the intended design. The effectiveness of the method is demonstrated through benchmark examples in 3D.

paper research
Minimum Cuts in Surface-Embedded Graphs

Minimum Cuts in Surface-Embedded Graphs

We describe algorithms to efficiently compute minimum $(s,t)$-cuts and global minimum cuts of undirected surface-embedded graphs. Given an edge-weighted undirected graph $G$ with $n$ vertices embedded on an orientable surface of genus $g$, our algorithms can solve either problem in $g^{O(g)} n log log n$ or $2^{O(g)} n log n$ time, whichever is better. When $g$ is a constant, our $g^{O(g)} n log log n$ time algorithms match the best running times known for computing minimum cuts in planar graphs. Our algorithms for minimum cuts rely on reductions to the problem of finding a minimum-weight subgraph in a given $ mathbb{Z}_2$-homology class, and we give efficient algorithms for this latter problem as well. If $G$ is embedded on a surface with $b$ boundary components, these algorithms run in $(g + b)^{O(g + b)} n log log n$ and $2^{O(g + b)} n log n$ time. We also prove that finding a minimum-weight subgraph homologous to a single input cycle is NP-hard, showing it is likely impossible to improve upon the exponential dependencies on $g$ for this latter problem.

paper research
Automated Generation of Topologically Robust CAD Models for Structural Optimization

Automated Generation of Topologically Robust CAD Models for Structural Optimization

Computer-aided design (CAD) models play a crucial role in the design, manufacturing and maintenance of products. Therefore, the mesh-based finite element descriptions common in structural optimisation must be first translated into CAD models. Currently, this can at best be performed semi-manually. We propose a fully automated and topologically accurate approach to synthesise a structurally-sound parametric CAD model from topology optimised finite element models. Our solution is to first convert the topology optimised structure into a spatial frame structure and then to regenerate it in a CAD system using standard constructive solid geometry (CSG) operations. The obtained parametric CAD models are compact, that is, have as few as possible geometric parameters, which makes them ideal for editing and further processing within a CAD system. The critical task of converting the topology optimised structure into an optimal spatial frame structure is accomplished in several steps. We first generate from the topology optimised voxel model a one-voxel-wide voxel chain model using a topology-preserving skeletonisation algorithm from digital topology. The weighted undirected graph defined by the voxel chain model yields a spatial frame structure after processing it with standard graph algorithms. Subsequently, we optimise the cross-sections and layout of the frame members to recover its optimality, which may have been compromised during the conversion process. At last, we generate the obtained frame structure in a CAD system by repeatedly combining primitive solids, like cylinders and spheres, using boolean operations. The resulting solid model is a boundary representation (B-Rep) consisting of trimmed non-uniform rational B-spline (NURBS) curves and surfaces.

paper research
Edge Matching with Inequalities, Triangular Pieces, Unknown Shape, and Two Players

Edge Matching with Inequalities, Triangular Pieces, Unknown Shape, and Two Players

We analyze the computational complexity of several new variants of edge-matching puzzles. First we analyze inequality (instead of equality) constraints between adjacent tiles, proving the problem NP-complete for strict inequalities but polynomial for nonstrict inequalities. Second we analyze three types of triangular edge matching, of which one is polynomial and the other two are NP-complete; all three are #P-complete. Third we analyze the case where no target shape is specified, and we merely want to place the (square) tiles so that edges match (exactly); this problem is NP-complete. Fourth we consider four 2-player games based on $1 times n$ edge matching, all four of which are PSPACE-complete. Most of our NP-hardness reductions are parsimonious, newly proving #P and ASP-completeness for, e.g., $1 times n$ edge matching.

paper research
Optimal Algorithms for Geometric Centers and Depth

Optimal Algorithms for Geometric Centers and Depth

$ renewcommand{ Re}{ mathbb{R}}$ We develop a general randomized technique for solving implic it linear programming problems, where the collection of constraints are defined implicitly by an underlying ground set of elements. In many cases, the structure of the implicitly defined constraints can be exploited in order to obtain efficient linear program solvers. We apply this technique to obtain near-optimal algorithms for a variety of fundamental problems in geometry. For a given point set $P$ of size $n$ in $ Re^d$, we develop algorithms for computing geometric centers of a point set, including the centerpoint and the Tukey median, and several other more involved measures of centrality. For $d=2$, the new algorithms run in $O(n log n)$ expected time, which is optimal, and for higher constant $d>2$, the expected time bound is within one logarithmic factor of $O(n^{d-1})$, which is also likely near optimal for some of the problems.

paper research
Algebraic k-Sets and Generally Neighborly Embeddings

Algebraic k-Sets and Generally Neighborly Embeddings

Given a set $S$ of $n$ points in $ mathbb{R}^d$, a $k$-set is a subset of $k$ points of $S$ that can be strictly separated by a hyperplane from the remaining $n-k$ points. Similarly, one may consider $k$-facets, which are hyperplanes that pass through $d$ points of $S$ and have $k$ points on one side. A notorious open problem is to determine the asymptotics of the maximum number of $k$-sets. In this paper we study a variation on the $k$-set/$k$-facet problem with hyperplanes replaced by algebraic surfaces. In stark contrast to the original $k$-set/$k$-facet problem, there are some natural families of algebraic curves for which the number of $k$-facets can be counted exactly. For example, we show that the number of halving conic sections for any set of $2n+5$ points in general position in the plane is $2 binom{n+2}{2}^2$. To understand the limits of our argument we study a class of maps we call emph{generally neighborly embeddings}, which map generic point sets into neighborly position. Additionally, we give a simple argument which improves the best known bound on the number of $k$-sets/$k$-facets for point sets in convex position.

paper research
Generating Diverse TSP Tours via a Combination of Graph Pointer Network and Dispersion

Generating Diverse TSP Tours via a Combination of Graph Pointer Network and Dispersion

We address the Diverse Traveling Salesman Problem (D-TSP), a bi-criteria optimization challenge that seeks a set of $k$ distinct TSP tours. The objective requires every selected tour to have a length at most $c|T^*|$ (where $|T^*|$ is the optimal tour length) while minimizing the average Jaccard similarity across all tour pairs. This formulation is crucial for applications requiring both high solution quality and fault tolerance, such as logistics planning, robotics pathfinding or strategic patrolling. Current methods are limited traditional heuristics, such as the Niching Memetic Algorithm (NMA) or bi-criteria optimization, incur high computational complexity $O(n^3)$, while modern neural approaches (e.g., RF-MA3S) achieve limited diversity quality and rely on complex, external mechanisms. To overcome these limitations, we propose a novel hybrid framework that decomposes D-TSP into two efficient steps. First, we utilize a simple Graph Pointer Network (GPN), augmented with an approximated sequence entropy loss, to efficiently sample a large, diverse pool of high-quality tours. This simple modification effectively controls the quality-diversity trade-off without complex external mechanisms. Second, we apply a greedy algorithm that yields a 2-approximation for the dispersion problem to select the final $k$ maximally diverse tours from the generated pool. Our results demonstrate state-of-the-art performance. On the Berlin instance, our model achieves an average Jaccard index of $0.015$, significantly outperforming NMA ($0.081$) and RF-MA3S. By leveraging GPU acceleration, our GPN structure achieves a near-linear empirical runtime growth of $O(n)$. While maintaining solution diversity comparable to complex bi-criteria algorithms, our approach is over 360 times faster on large-scale instances (783 cities), delivering high-quality TSP solutions with unprecedented efficiency and simplicity.

paper research

< Category Statistics (Total: 566) >

Astrophysics
1
Computer Science
581
Condensed Matter
2
Economics
17
Electrical Engineering and Systems Science
38
Mathematics
19
Physics
10
Quantitative Biology
6
Quantitative Finance
4
Quantum Physics
5
Statistics
20

Start searching

Enter keywords to search articles

↑↓
↵
ESC
⌘K Shortcut