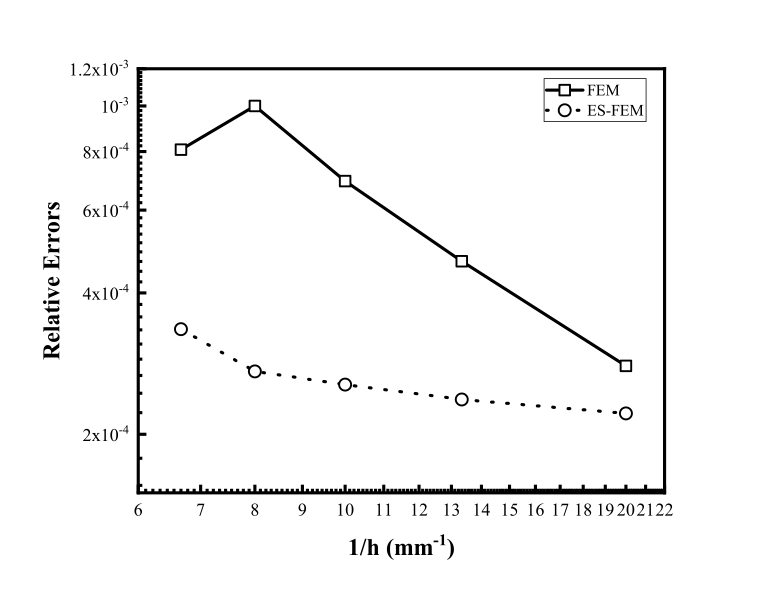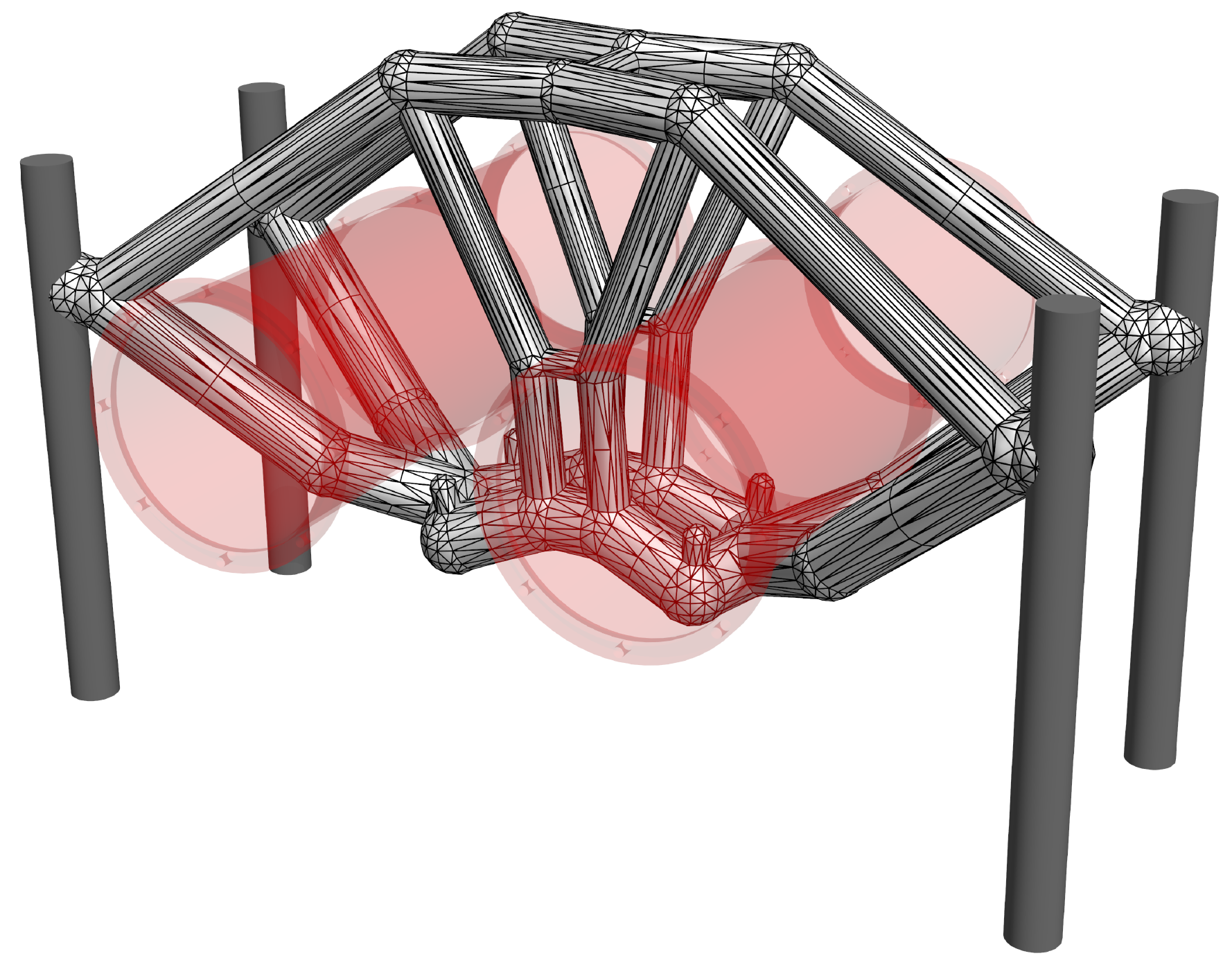
Generating Topologically Robust CAD Models for Structural Optimization
Computer-aided design (CAD) models play a crucial role in the design, manufacturing and maintenance of products. Therefore, the mesh-based finite element descriptions common in structural optimisation must be first translated into CAD models. Currently, this can at best be performed semi-manually. We propose a fully automated and topologically accurate approach to synthesise a structurally-sound parametric CAD model from topology optimised finite element models. Our solution is to first convert the topology optimised structure into a spatial frame structure and then to regenerate it in a CAD system using standard constructive solid geometry (CSG) operations. The obtained parametric CAD models are compact, that is, have as few as possible geometric parameters, which makes them ideal for editing and further processing within a CAD system. The critical task of converting the topology optimised structure into an optimal spatial frame structure is accomplished in several steps. We first generate from the topology optimised voxel model a one-voxel-wide voxel chain model using a topology-preserving skeletonisation algorithm from digital topology. The weighted undirected graph defined by the voxel chain model yields a spatial frame structure after processing it with standard graph algorithms. Subsequently, we optimise the cross-sections and layout of the frame members to recover its optimality, which may have been compromised during the conversion process. At last, we generate the obtained frame structure in a CAD system by repeatedly combining primitive solids, like cylinders and spheres, using boolean operations. The resulting solid model is a boundary representation (B-Rep) consisting of trimmed non-uniform rational B-spline (NURBS) curves and surfaces.