Diffusion language models (DLMs) have recently emerged as a compelling alternative to autoregressive generation, offering parallel generation and improved global coherence. During inference, DLMs generate text by iteratively denoising masked sequences in parallel; however, determining which positions to unmask and which tokens to commit forms a large combinatorial search problem. Existing inference methods approximate this search using heuristics, which often yield suboptimal decoding paths; other approaches instead rely on additional training to guide token selection. To introduce a principled search mechanism for DLMs inference, we introduce MEDAL, an inference-time scaling framework that integrates Monte Carlo Tree SEarch initialization for Diffusion LAnguage Model inference. We employ Monte Carlo Tree Search at the initialization stage to explore promising unmasking trajectories, providing a robust starting point for subsequent refinement. This design enables efficient inference-time scaling, allowing generation quality to improve as the search budget increases, without additional training. Across multiple benchmarks, MEDAL achieves up to 22.0% improvement over existing inference strategies, establishing a new paradigm for search-based inference in DLMs.
In recent years, diffusion language models (DLMs) have emerged as a powerful alternative for generative modeling over discrete sequences (Zhu et al., 2025;Ye et al., 2025). Unlike autoregressive (AR) models (Achiam et al., 2023;Minaee et al., 2024), which rely on a strictly left-to-right factorization, DLMs learn to invert a stochastic corruption process that independently masks tokens (Lou et al., 2023;Shi et al., 2024;Nie et al., 2025). This formulation enables parallel refinement, improves global coherence, and offers flexible qualitylatency trade-offs, thus challenging the dominance of AR paradigms (Li et al., 2025b).
The inference process of DLMs can be naturally formulated as a search problem: starting from a corrupted sequence, the model iteratively decides which positions to unmask and which tokens to assign, navigating an exponential space of possible trajectories. Existing inference-time methods approximate this search using confidencedriven heuristics, such as greedily unmasking the highest-confidence tokens (Kim et al., 2025;Ben-Hamu et al., 2025;Luxembourg et al., 2025). Although effective in reducing short-term uncertainty, these strategies are inherently myopic: once highconfidence tokens are fixed, subsequent steps are forced to adapt around them, often leading to suboptimal trajectories. Another line of work adjusts masking schedules dynamically (Peng et al., 2025;Zhao et al., 2024), but such approaches typically require training auxiliary samplers to determine token updates at each step, introducing additional complexity and limiting general applicability.
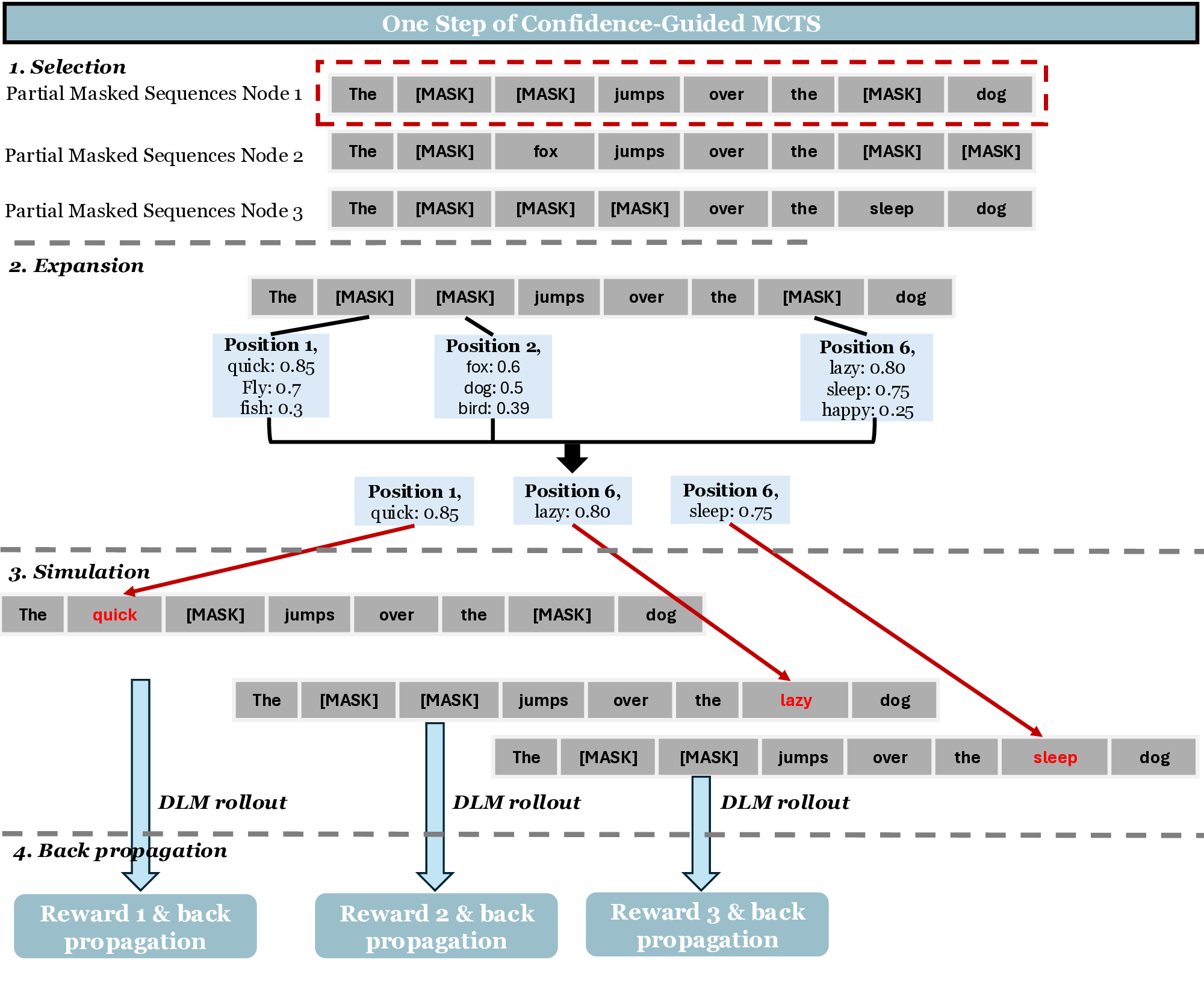
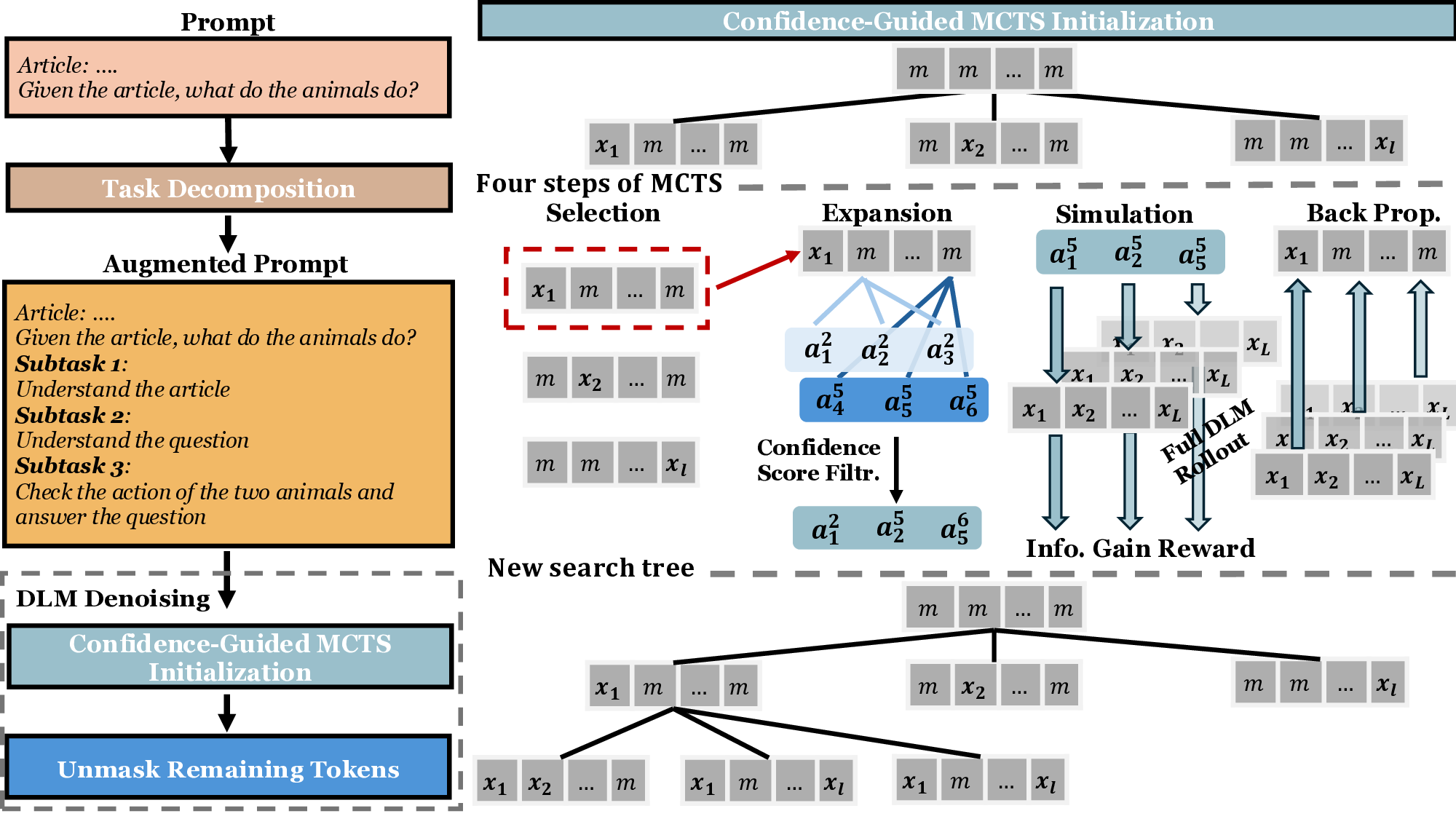
These limitations highlight the need for a principled search mechanism that can explore alternative unmasking trajectories without additional training overhead. To this end, we propose MEDAL, a framework that integrates Monte Carlo Tree SEarch initialization for Diffusion LAnguage Model inference. Unlike heuristic or schedulebased methods, which either commit to tokens greedily or depend on auxiliary samplers, MEDAL adopts a principled search-based approach, using Monte Carlo Tree Search (MCTS) (Yoon et al., 2025;Browne et al., 2012) to balance exploitation of high-confidence tokens with exploration of alternative unmasking trajectories relying on signals obtained from the model’s own distribution. We propose two key innovations that enable MCTS to be applied effectively to DLM inference. First, we introduce a confidence-guided filtering mechanism that focuses inference on the most promising tokens and positions. Second, we design an information-gain reward that guides MCTS by favoring token choices that not only resolve the current position but also increase the model’s confidence in predicting the remaining tokens. Together, these innovations make it possible to enable the four stages of MCTS, Selection, Expansion, Simulation, and Backpropagation, within DLMs. Rather than applying MCTS exhaustively, we employ it strategically in the early stages of inference to construct a robust initialization, after which the process continues with efficient heuristics. To further address complex prompts that induce high uncertainty, we incorporate a task-decomposition module that automatically splits the input into smaller subtasks, thereby reducing ambiguity and providing structured guidance for subsequent unmasking decisions. Our contributions are summarized as follows:
• Novel Formulation: We frame DLM inference as a search problem and introduce MEDAL, the first framework to integrate MCTS into DLM inference, enabling principled exploration beyond greedy heuristics or schedule-based methods
• Novel Design: We design a new DLM inference approach that combines an MCTSguided initialization module with a taskdecomposition module, enabling both efficient search and improved handling of complex tasks.
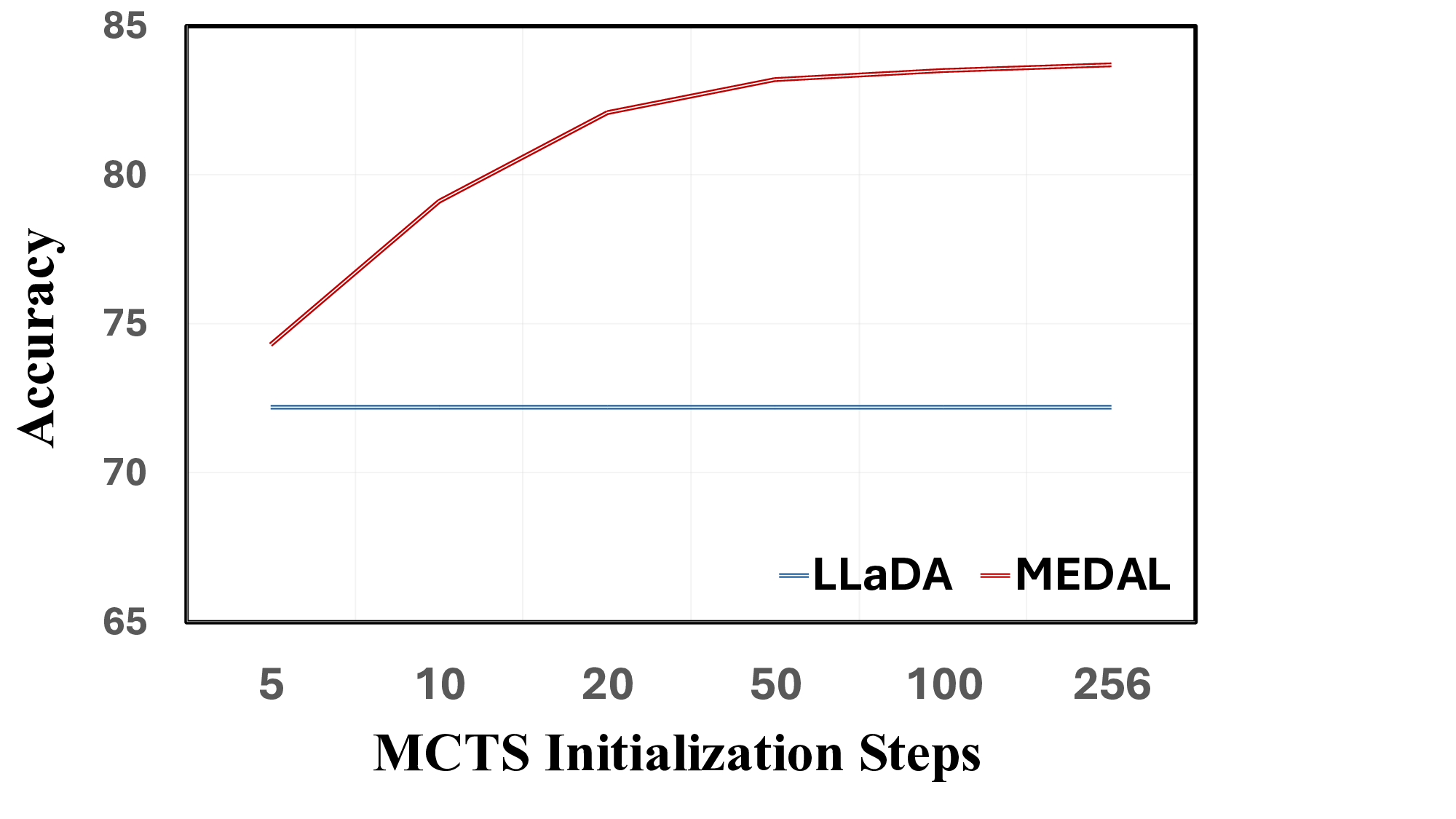
• Extensive Experiments: We conduct evaluations on various benchmarks, demonstrating that our method outperforms existing inference strategies for DLMs by up to 22.0% when restricting MCTS to initialization. We show that generation quality continues to improve even further with diminishing gains as the MCTS initialization budget increases, validating the effectiveness of our search-based approach.
DLMs adapt the diffusion paradigm from continuous domains (e.g., image generation) to discrete text sequences. Let x 0 = (x 1 0 , . . . , x L 0 ) denote a token sequence of length L sampled from the data distribution. The core idea is to define a forward noising process that progressively corrupts x 0 into increasingly noisy sequences {x t } T t=1 , and to train a neural model to learn the corresponding reverse denoising process that reconstructs x 0 from noise.
Forward process. In discrete DLMs, the forward process is typically defined by a time-dependent transition matrix Q t over the vocabulary (Li et al., 2025b). At each time t, the probability of a state x t given an initial state x 0 is given by a categorical distribution:
Reverse Process The rever
This content is AI-processed based on open access ArXiv data.