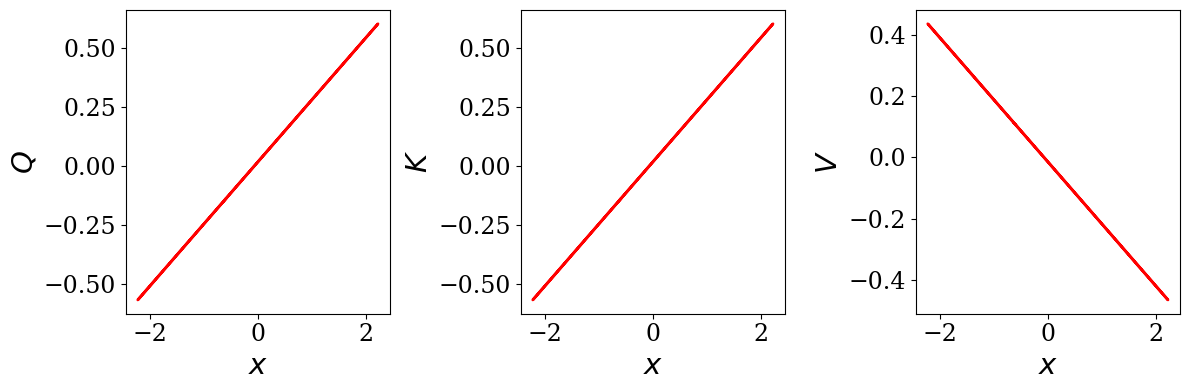
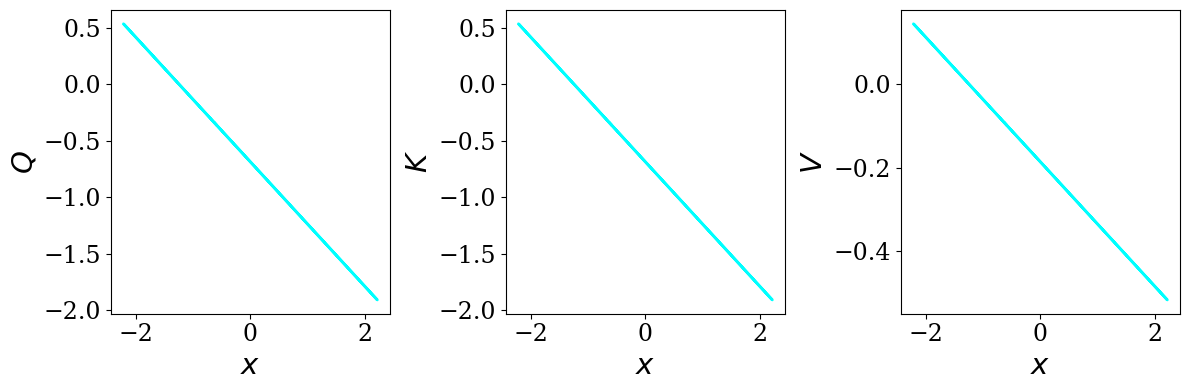
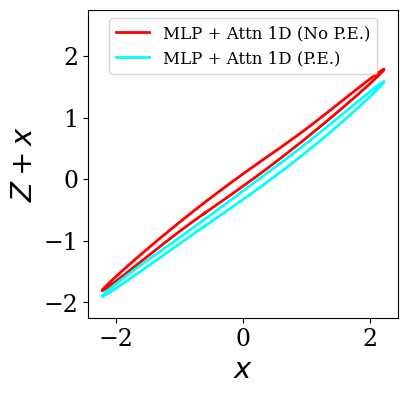
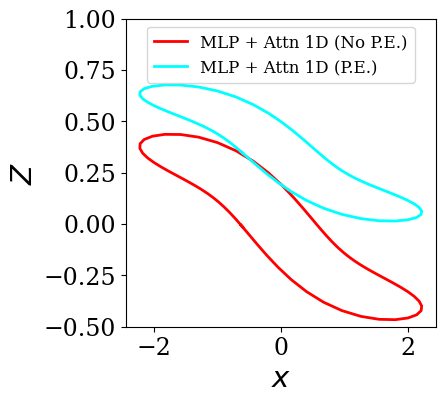
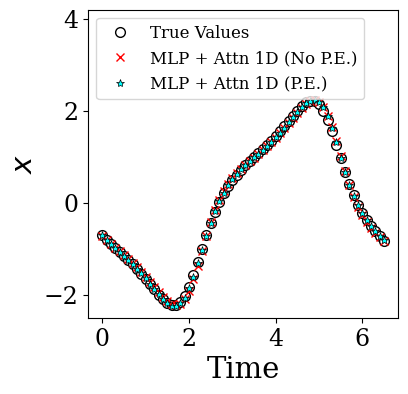
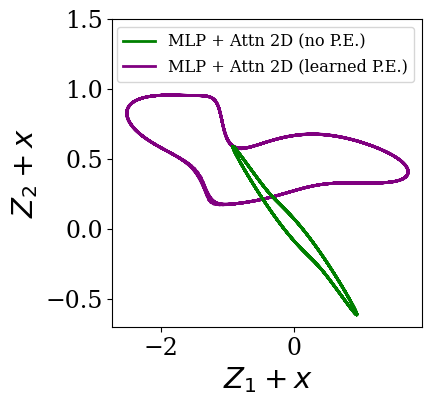
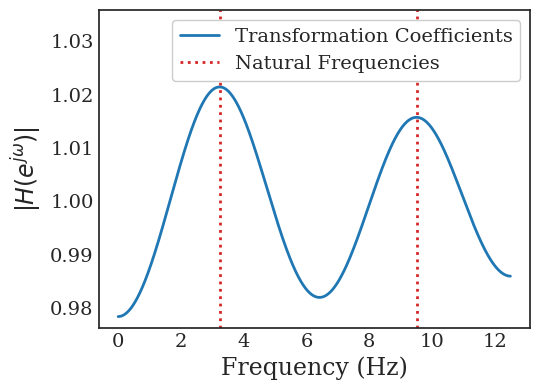
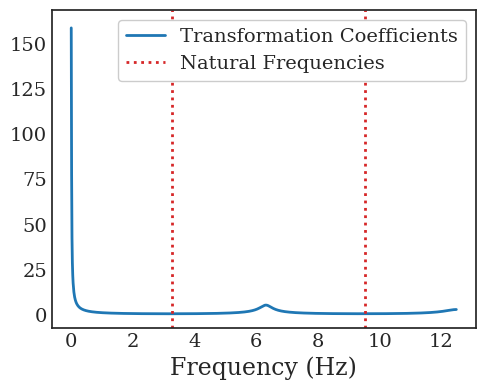
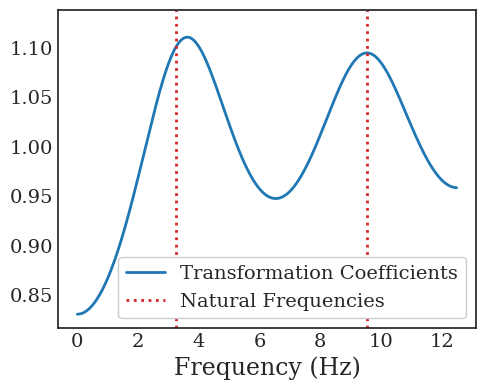
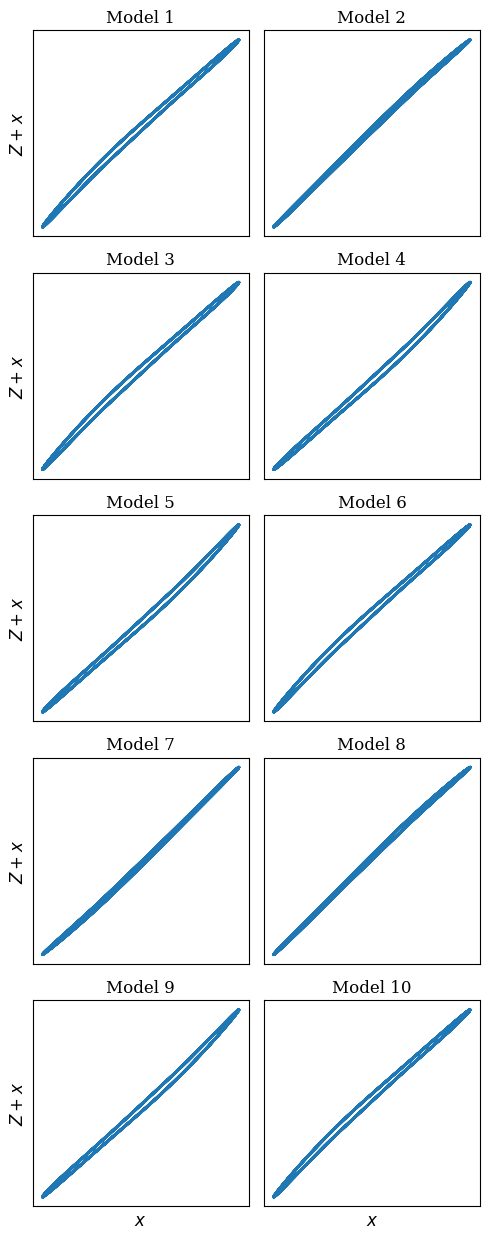
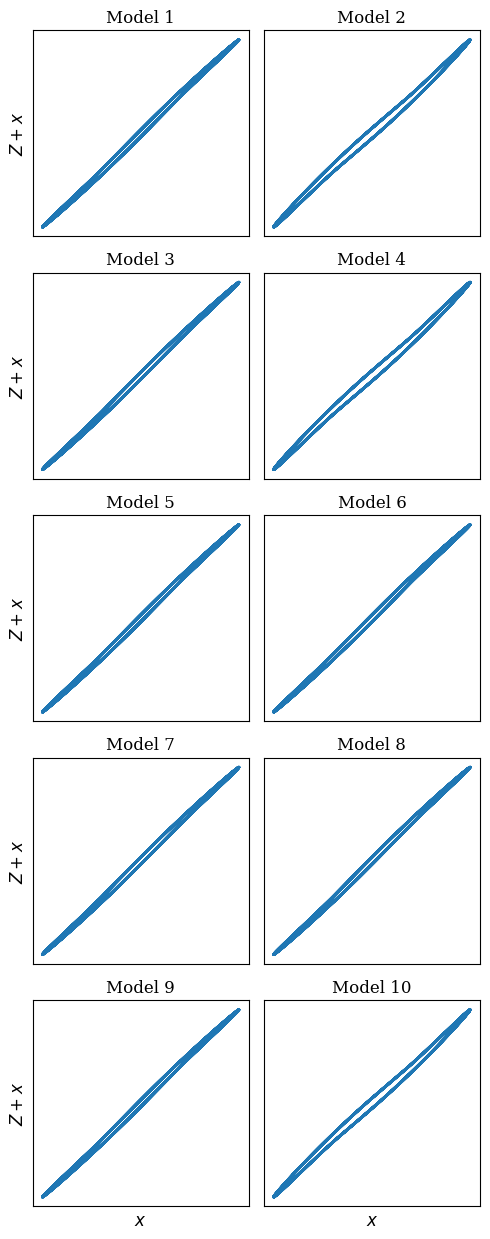
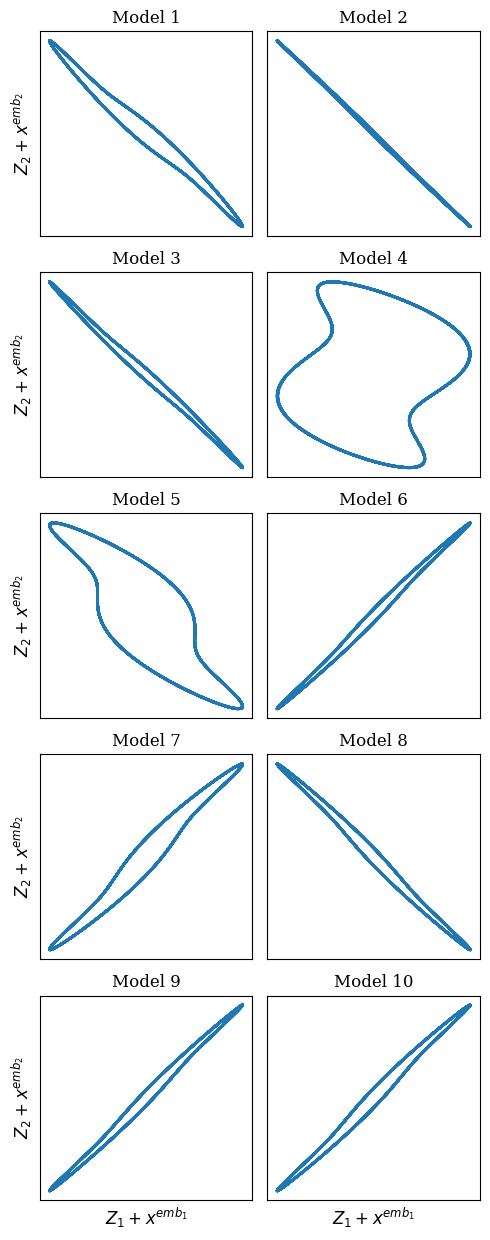
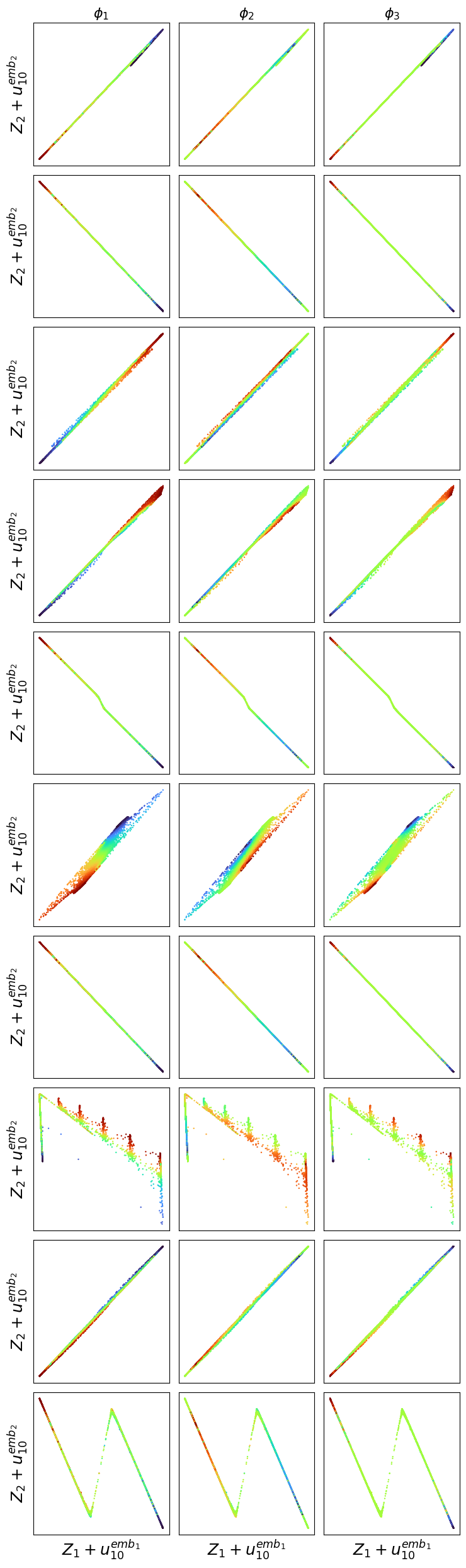
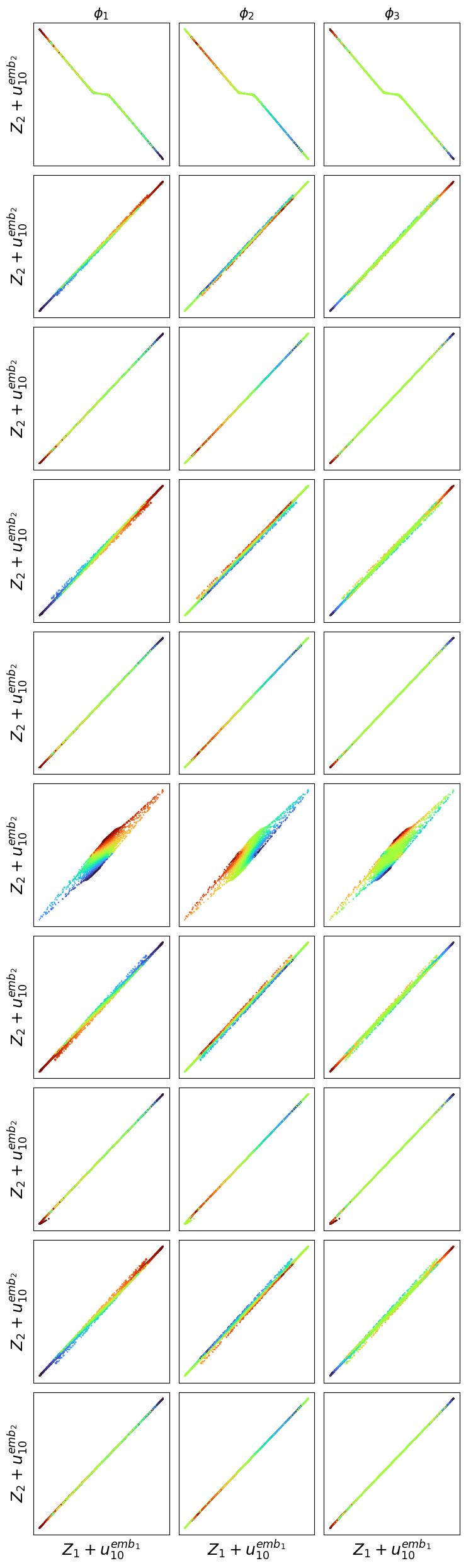
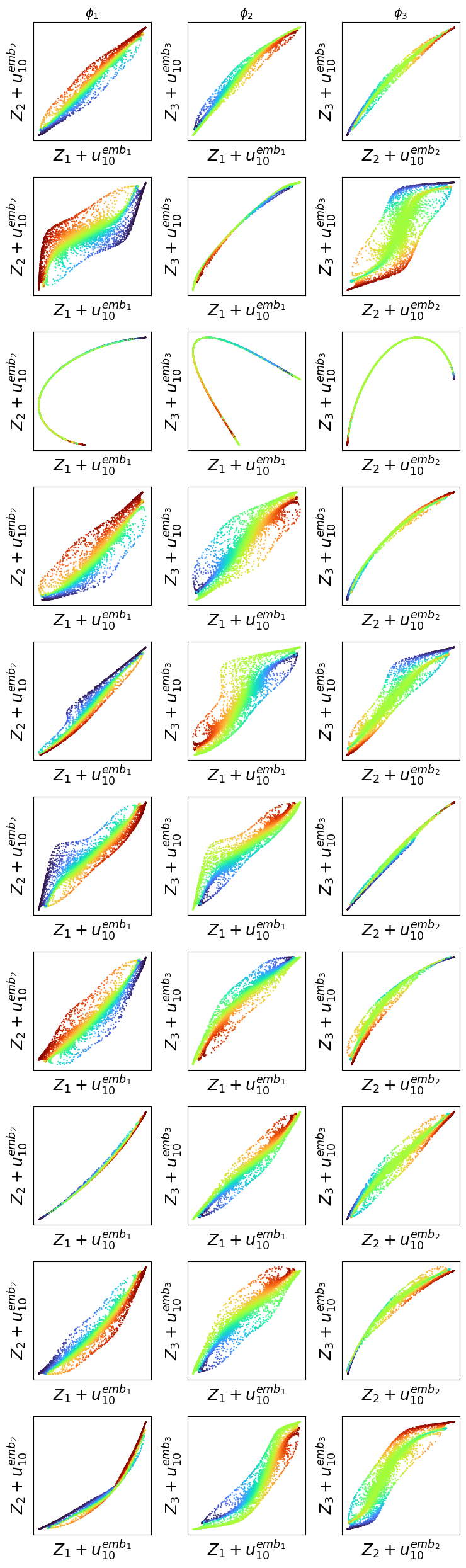
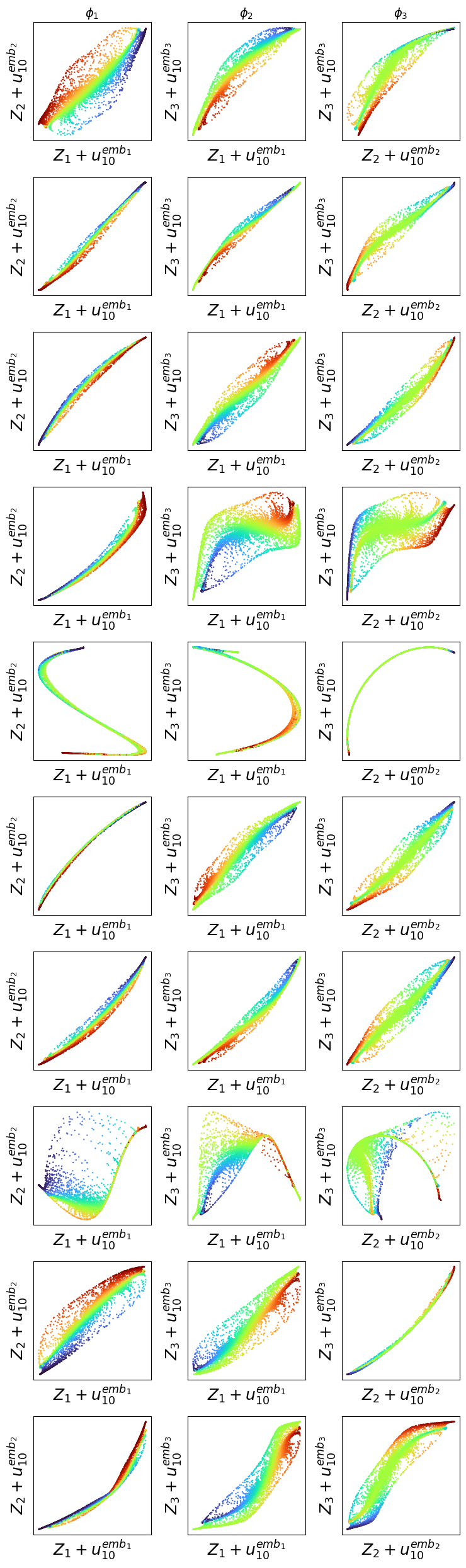
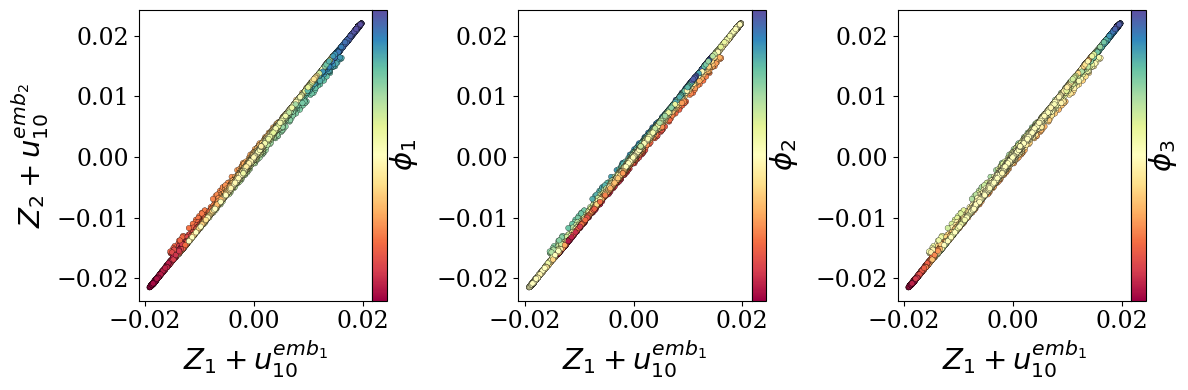
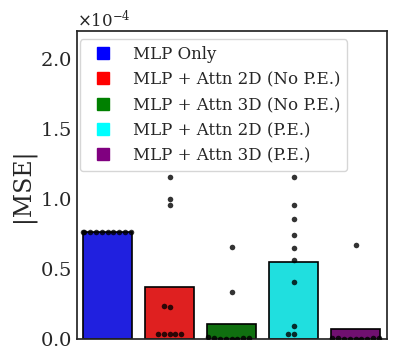
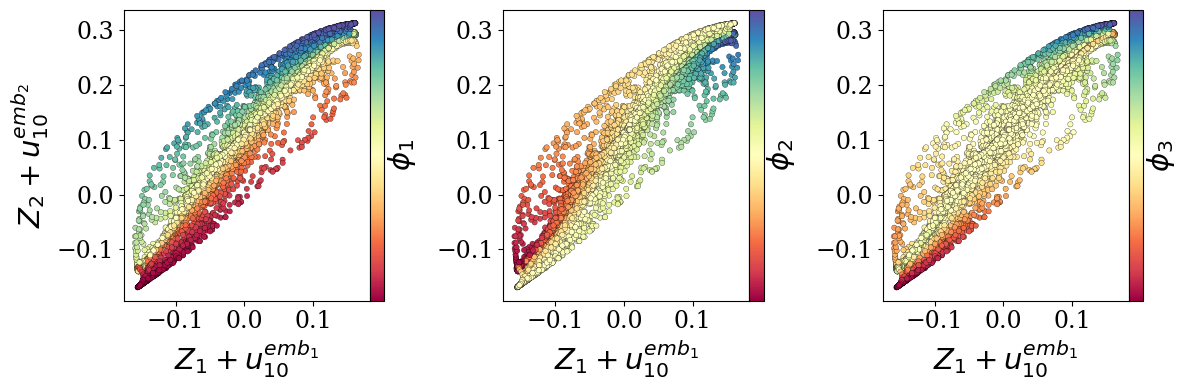
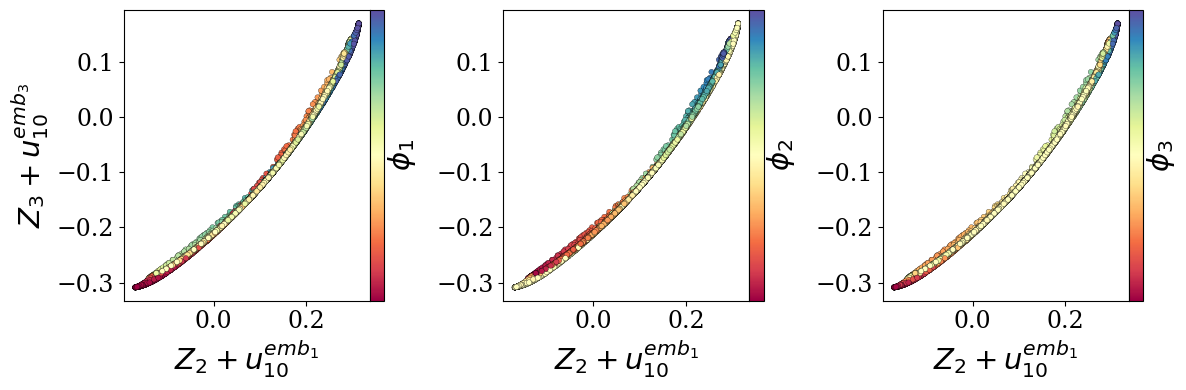
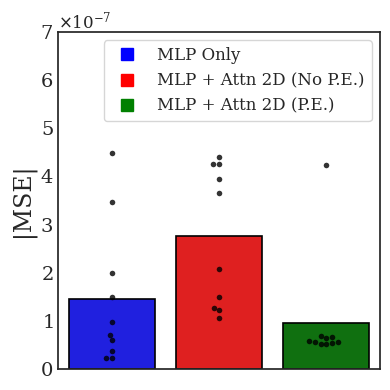
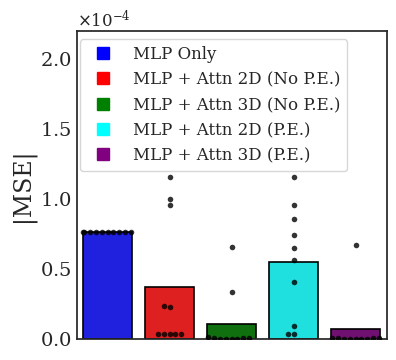
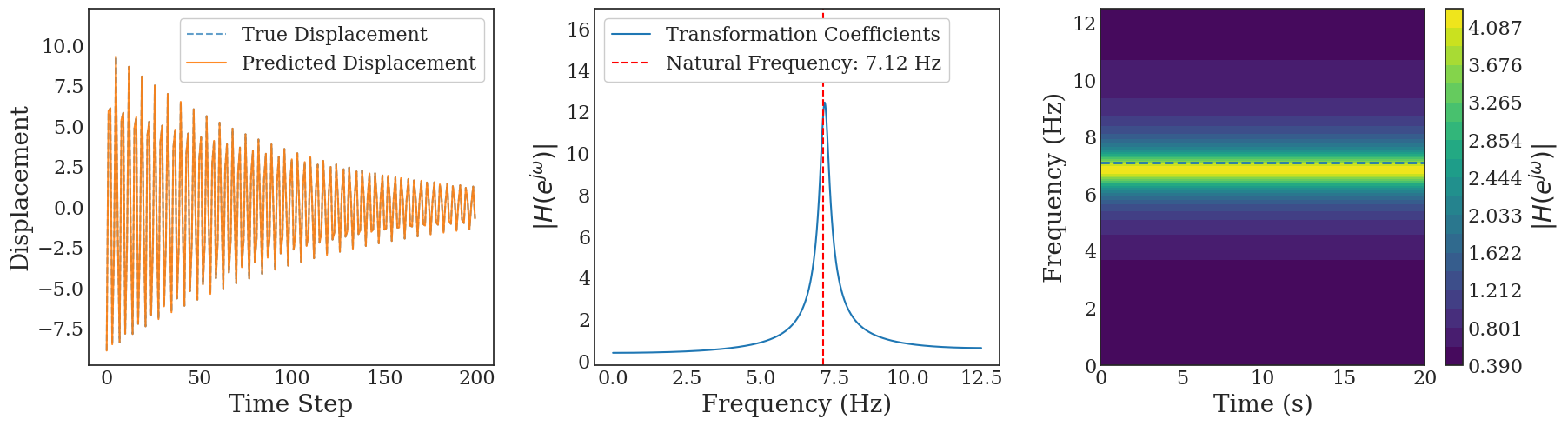
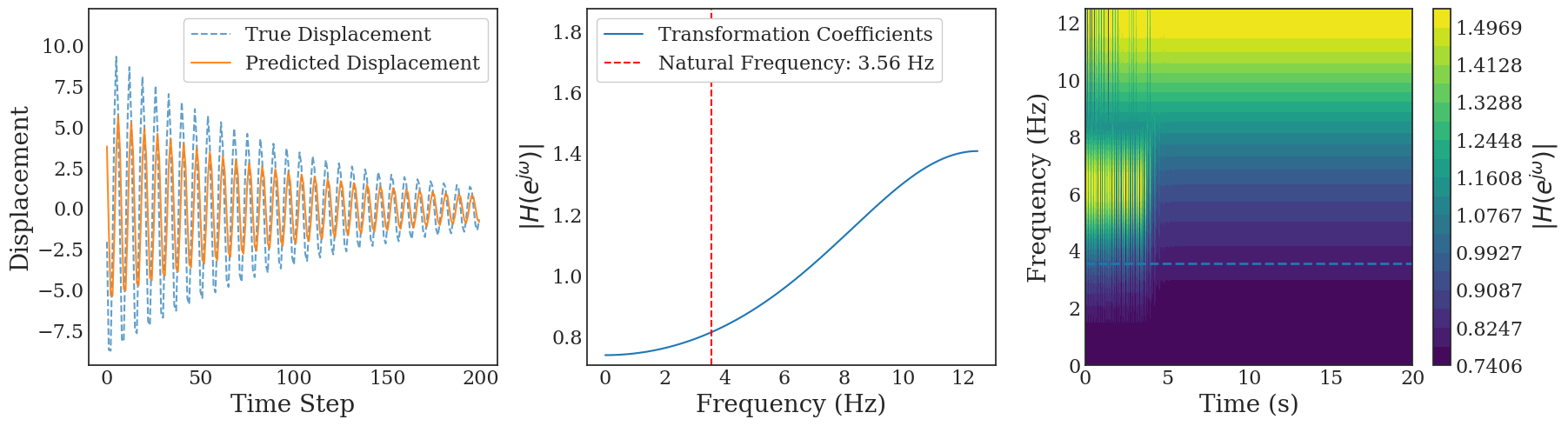
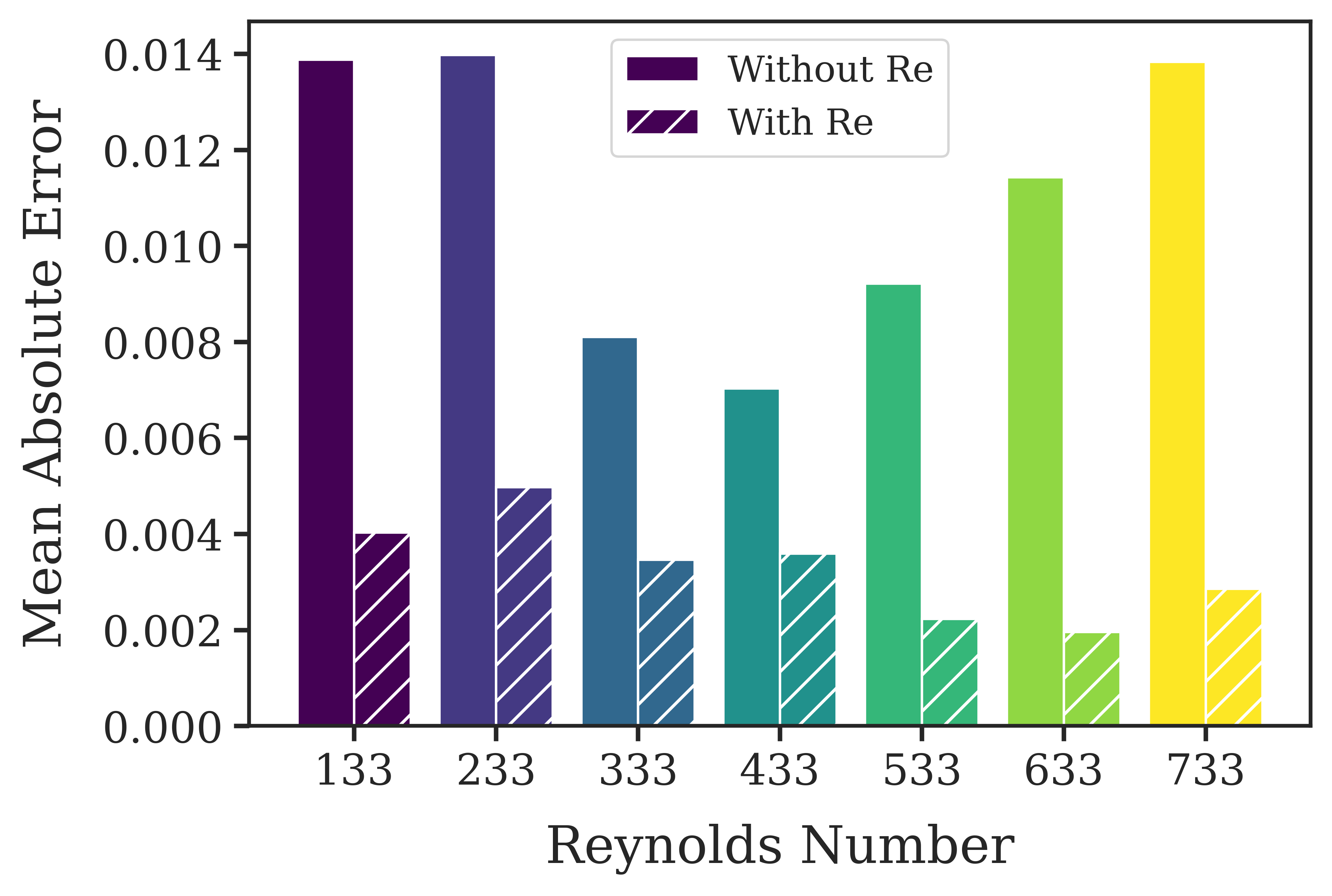
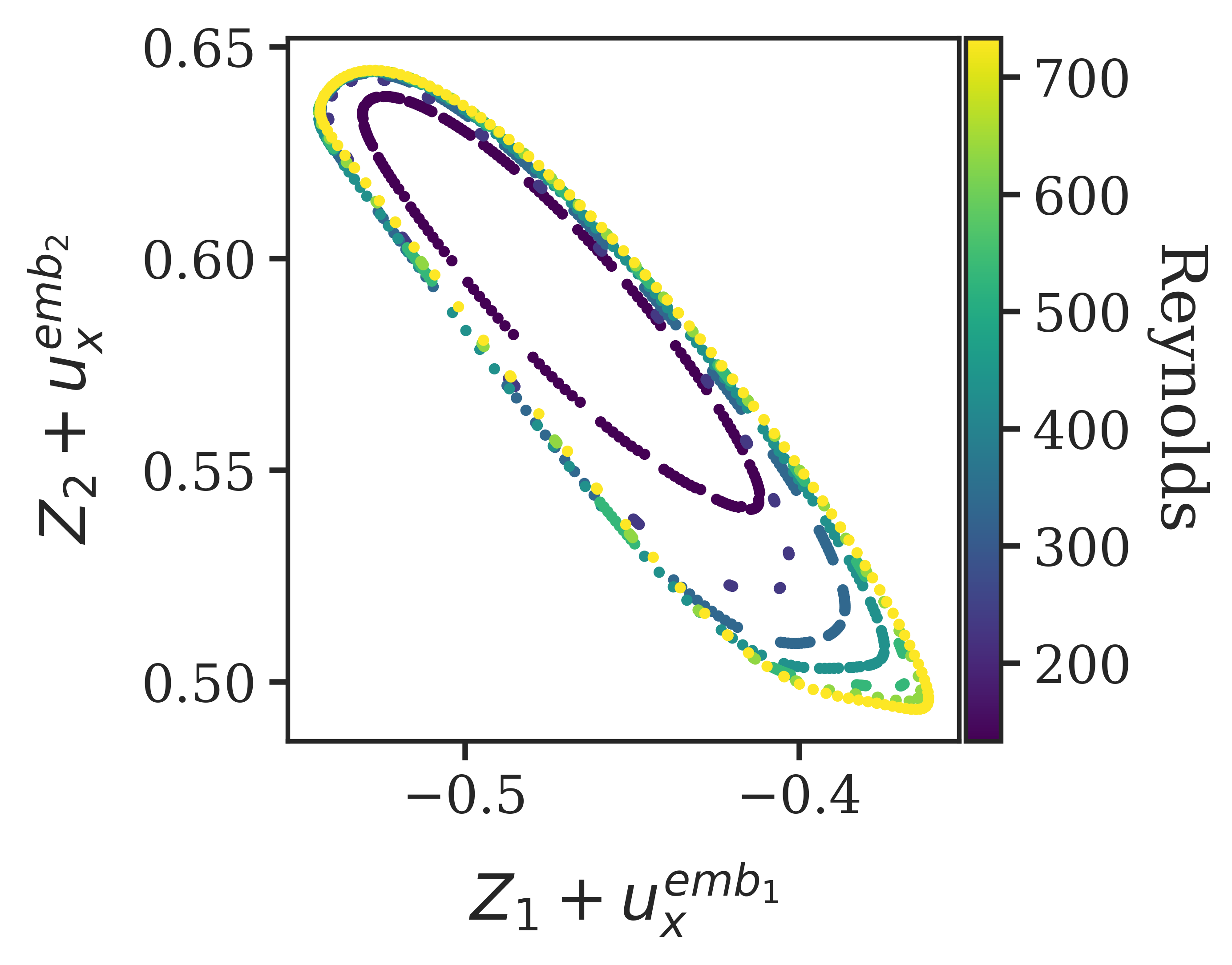
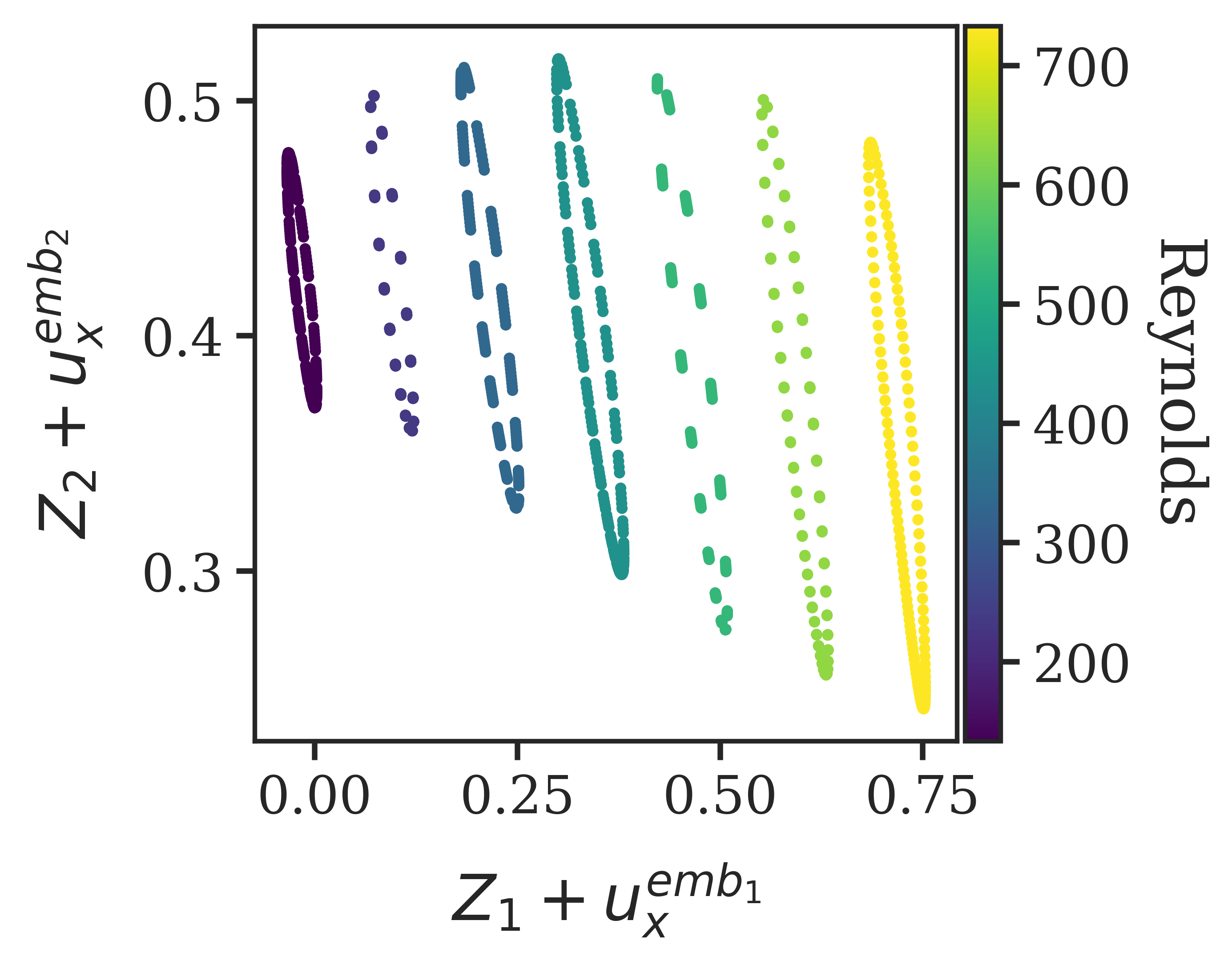
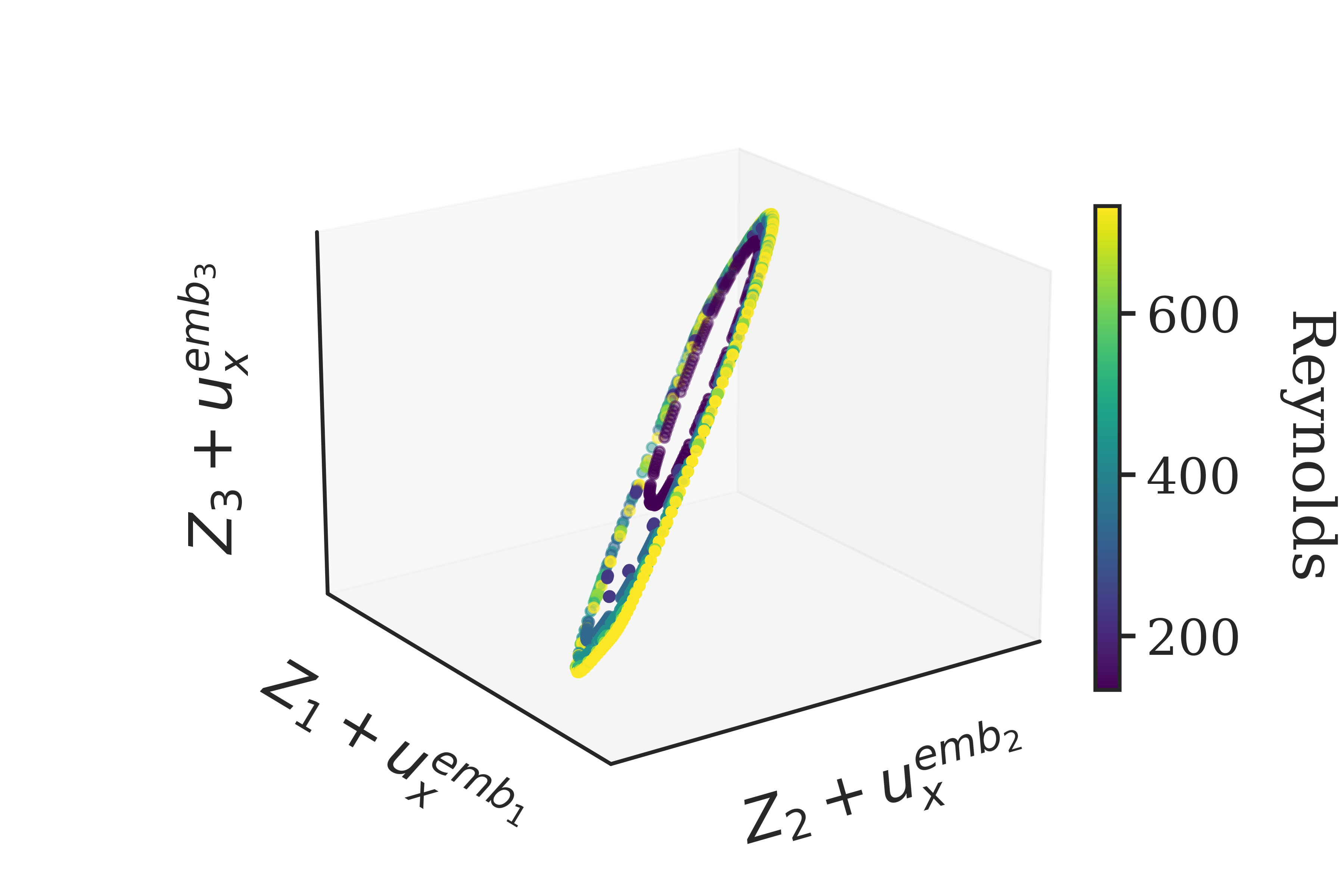
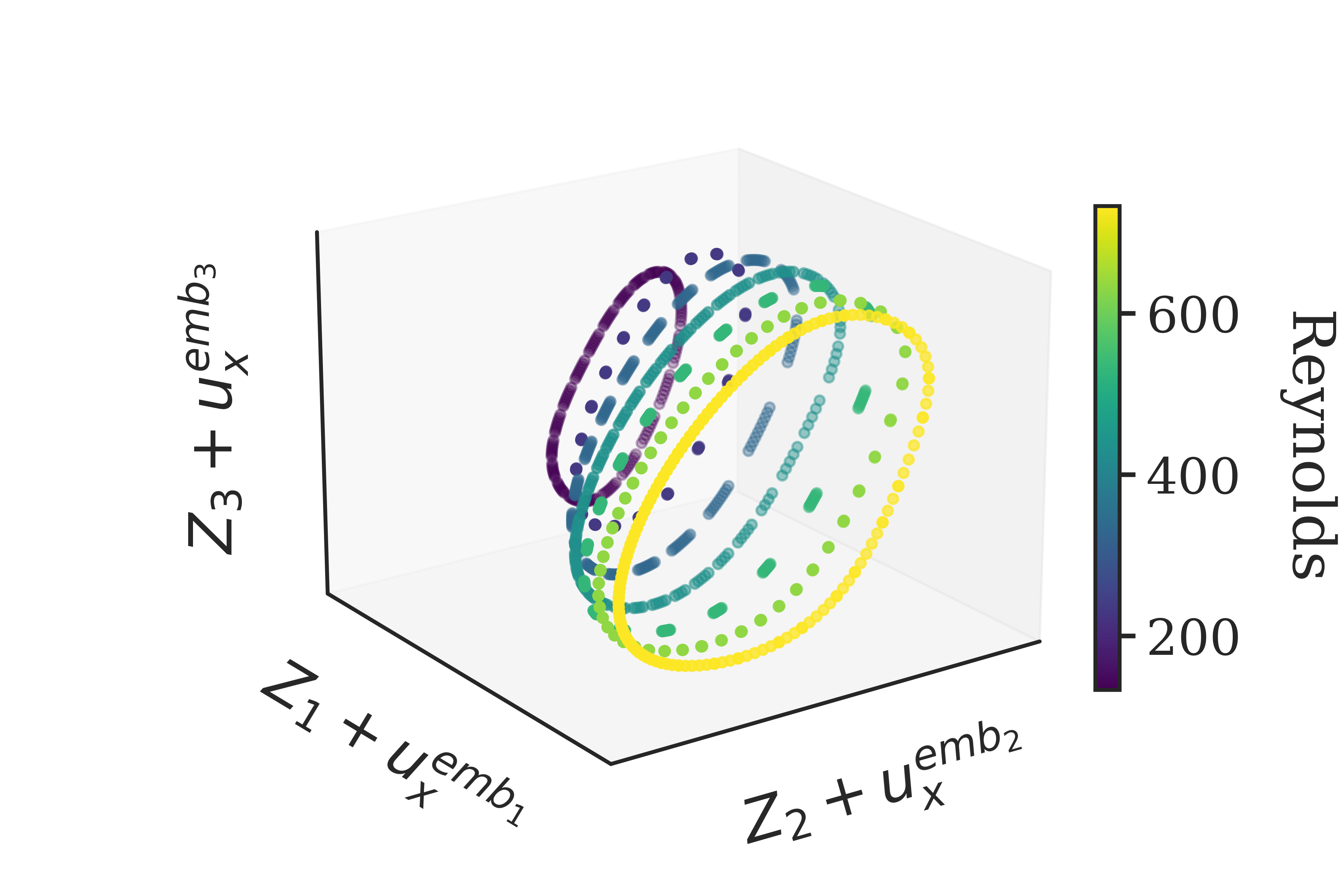
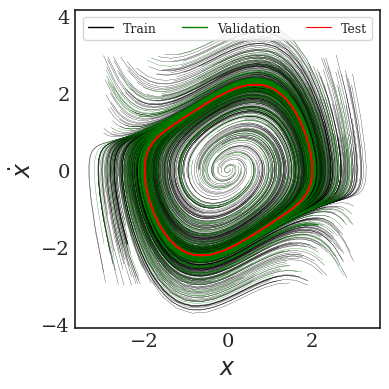
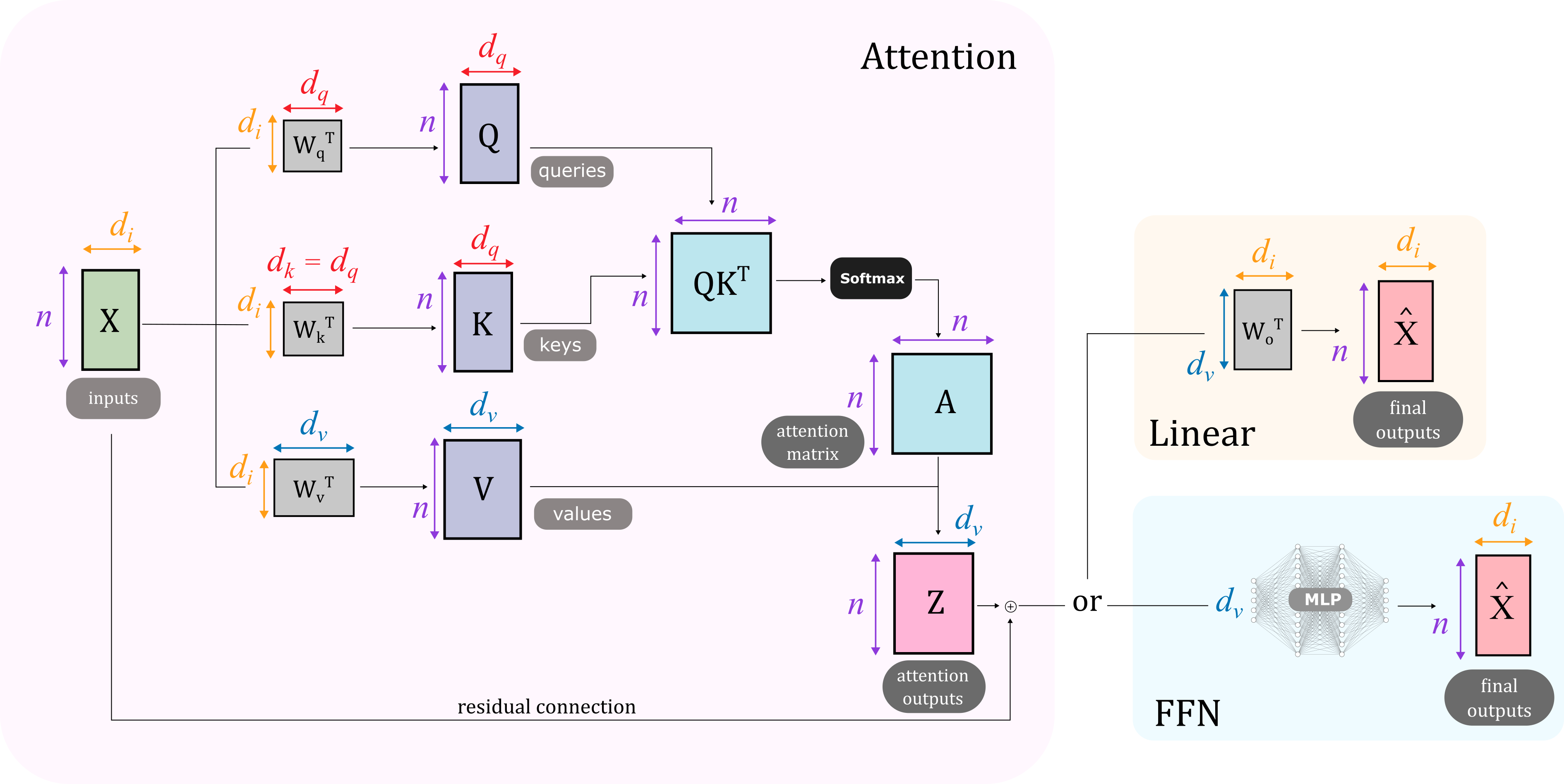
Transformers are increasingly adopted for modeling and forecasting time-series, yet their internal mechanisms remain poorly understood from a dynamical systems perspective. In contrast to classical autoregressive and state-space models, which benefit from well-established theoretical foundations, Transformer architectures are typically treated as black boxes. This gap becomes particularly relevant as attention-based models are considered for general-purpose or zero-shot forecasting across diverse dynamical regimes. In this work, we do not propose a new forecasting model, but instead investigate the representational capabilities and limitations of single-layer Transformers when applied to dynamical data. Building on a dynamical systems perspective we interpret causal self-attention as a linear, history-dependent recurrence and analyze how it processes temporal information. Through a series of linear and nonlinear case studies, we identify distinct operational regimes. For linear systems, we show that the convexity constraint imposed by softmax attention fundamentally restricts the class of dynamics that can be represented, leading to oversmoothing in oscillatory settings. For nonlinear systems under partial observability, attention instead acts as an adaptive delay-embedding mechanism, enabling effective state reconstruction when sufficient temporal context and latent dimensionality are available. These results help bridge empirical observations with classical dynamical systems theory, providing insight into when and why Transformers succeed or fail as models of dynamical systems.
Understanding and modeling dynamical systems using data -in the form of observations-is a central problem in nonlinear science, with applications ranging from fluid mechanics and structural dynamics [1,35,40] to neuroscience, chemical kinetics, weather and power systems and beyond [39,22,9,50]. Classical approaches rely either on use of explicit governing equations or on well-established datadriven identification frameworks, such as autoregressive and state-space models, for which stability, observability, and identifiability properties are well understood [7,28]. These frameworks provide a principled connection between data, latent state representations, and the underlying geometry of dynamical systems, including attractors and invariant manifolds.
More recently, machine-learning architectures originally developed for sequence modeling have been increasingly applied to dynamical systems modeling, particularly in what concerns purely data-driven inference, raising fundamental questions about their expressive power and their relationship to classical dynamical systems theory. Among these architectures, the Transformer model [49] has emerged as a dominant paradigm. Originally introduced for natural language processing, Transformers are now widely used in computer vision, speech processing, and scientific machine learning [26], including the modeling and forecasting of dynamical systems [21,45,19]. Their defining feature is the attention mechanism, which enables flexible aggregation of information across a temporal context through parallel rather than sequential computation. This property has led to strong empirical performance in step-ahead prediction tasks, including for nonlinear and weakly chaotic systems [48,10].
A growing body of work has explored the use of Transformers for dynamical and physical systems. Early studies demonstrated that attention-based models can learn surrogate evolution maps when provided with suitable spatiotemporal tokenizations. Geneva and Zabaras [21], for example, modeled diverse dynamical systems using a “vanilla” Transformer architecture, relying on Koopman-based embeddings to project high-dimensional states into lower-dimensional token representations. Subsequent work investigated the direct application of Transformers to chaotic time-series forecasting, showing that autoregressive prediction is feasible when the Lyapunov exponent is sufficiently low [48]. More recent efforts have extended these ideas towards large pretrained scientific foundation models. Aurora, for instance, is proposed as a foundation model for the Earth system, trained on heterogeneous atmospheric and oceanic datasets and equipped with an encoder-processor-decoder architecture to evolve a latent three-dimensional spatial representation forward in time [6]. These studies indicate that Transformers, or Transformer-like operator processors, can act as general temporal integrators across complex physical systems, often at substantially reduced computational cost compared to traditional numerical pipelines.
In parallel, operator-style Transformer architectures have been developed specifically for scientific computing [43]. Poseidon introduces a multiscale operator Transformer pretrained on diverse fluiddynamics PDE datasets and leverages time-conditioned layers together with semigroup training to enable continuous-in-time evaluation [24]. This places Transformers within the broader operatorlearning lineage that includes Fourier-and Graph Neural Operators. Related theoretical work has clarified connections between attention mechanisms and classical numerical integration or projection schemes. Li et al. [34,31] introduced the Fourier Neural Operator framework, which learns mappings between function spaces using spectral convolution kernels and can be interpreted as performing data-driven Galerkin projections. Building on this perspective, Cao et al. [8] showed that self-attention can be interpreted as a learnable integral operator, capable of recovering Fourier-or Galerkin-type behavior depending on positional encoding and kernelization. These results position attention mechanisms and neural operators within a shared theoretical space as flexible, possibly nonlocal (in space and even possibly in time) integrators/solvers.
A second, rapidly growing stream concerns time-series foundation models. Chronos treats time series as tokenized sequences via scaling and quantization and reuses T5-style Transformers to obtain zero-shot probabilistic forecasts across domains [2]. Subsequent models, including Chronos-Bolt, improved speed and accuracy, reinforcing the view that a single pretrained Transformer can generalize across dynamical regimes provided that the data are cast into a language-like format and extended the foundation models to multivariate systems [3]. This paradigm aligns closely with recent zero-shot and universal forecasting studies for chaotic systems [51,33,23], as well as with position papers calling
This content is AI-processed based on open access ArXiv data.