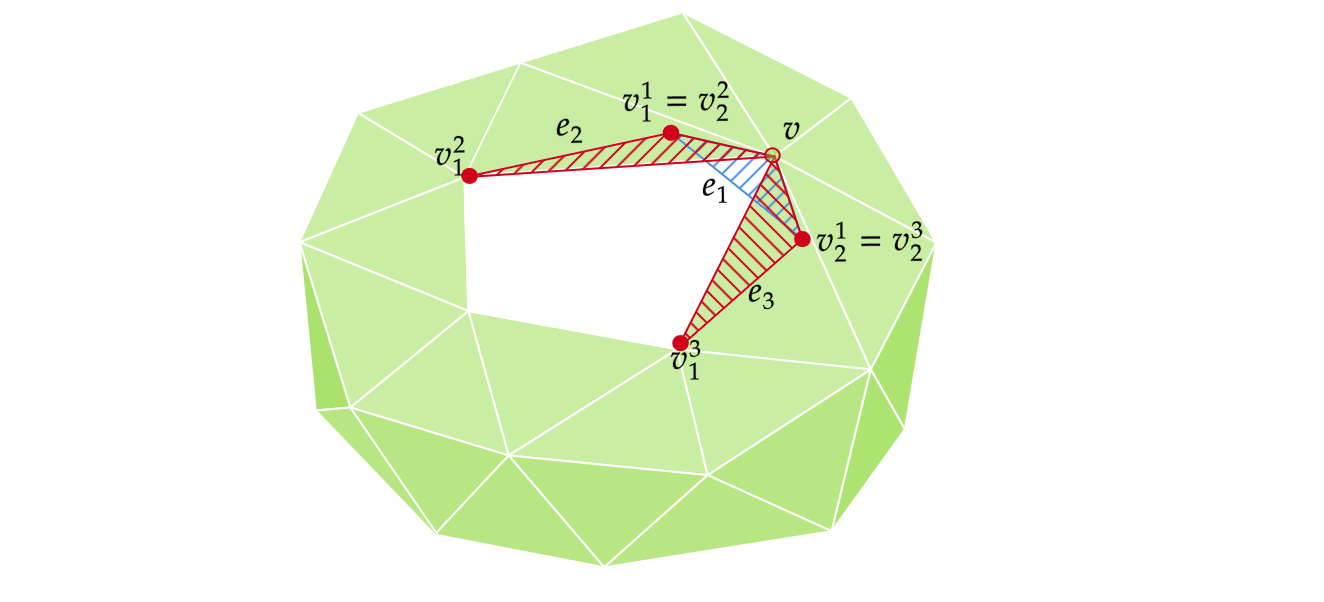
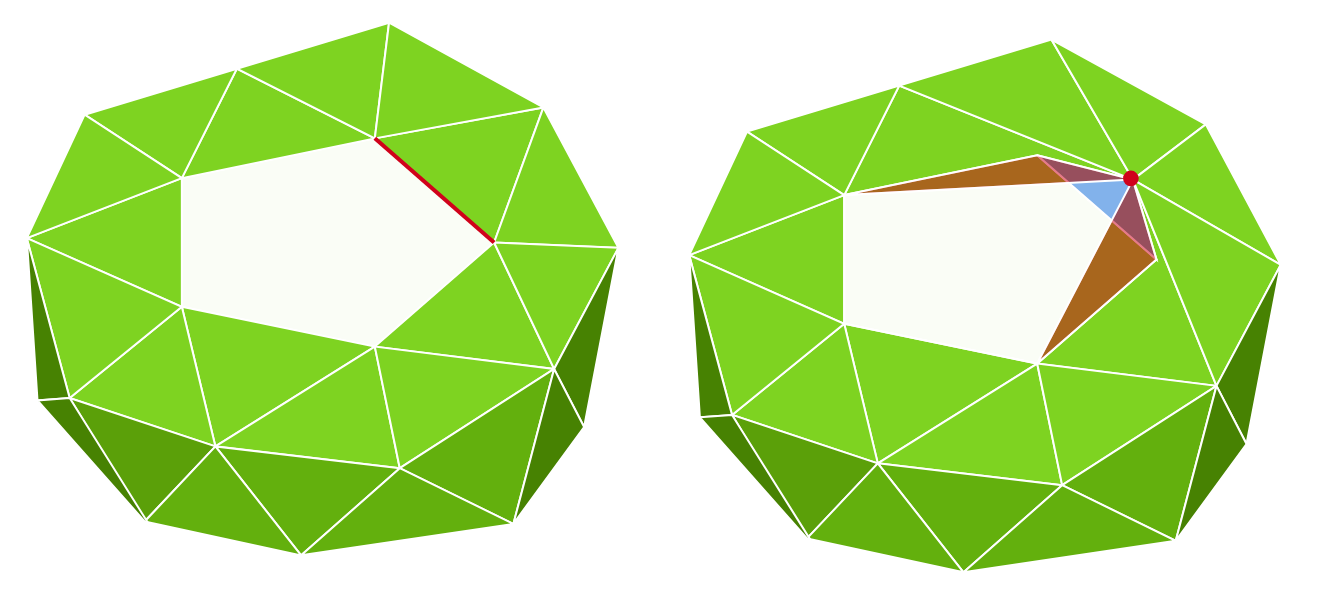
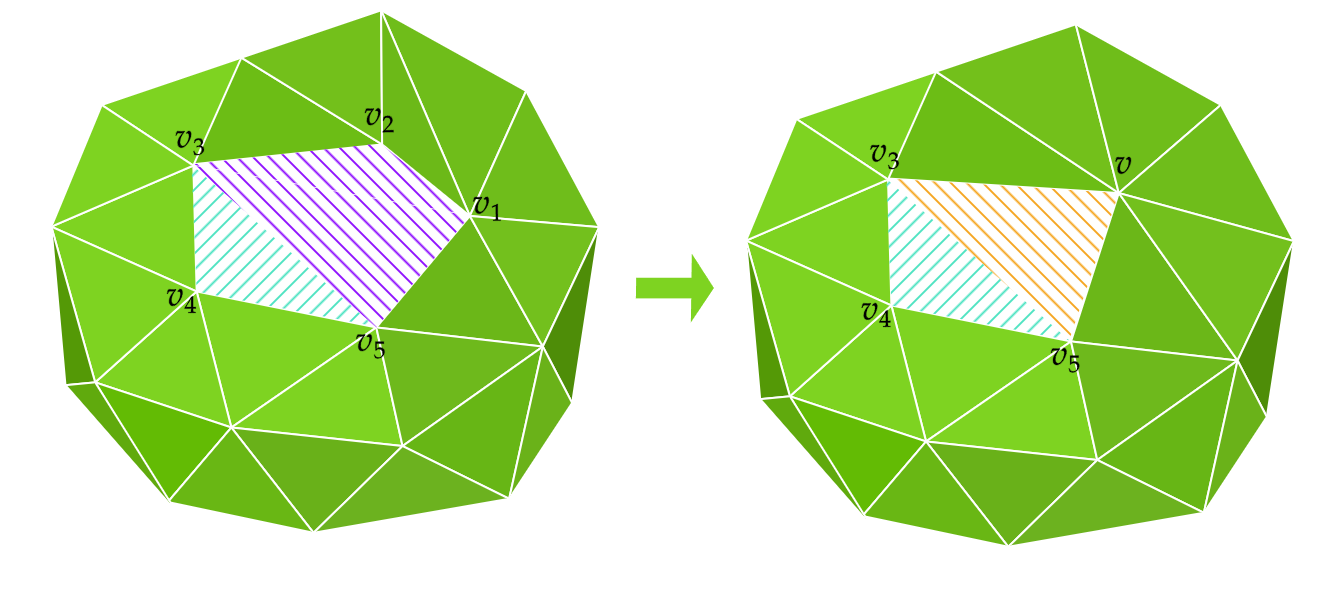
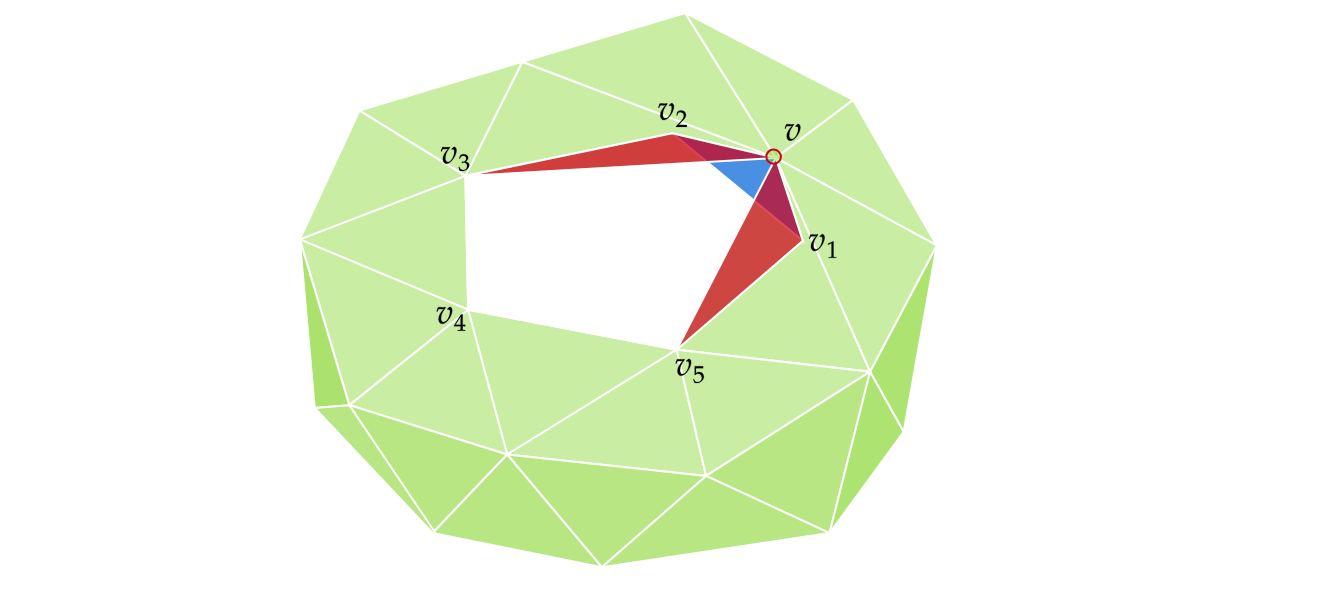
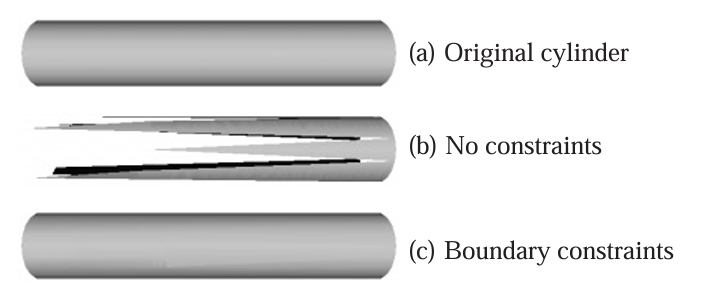
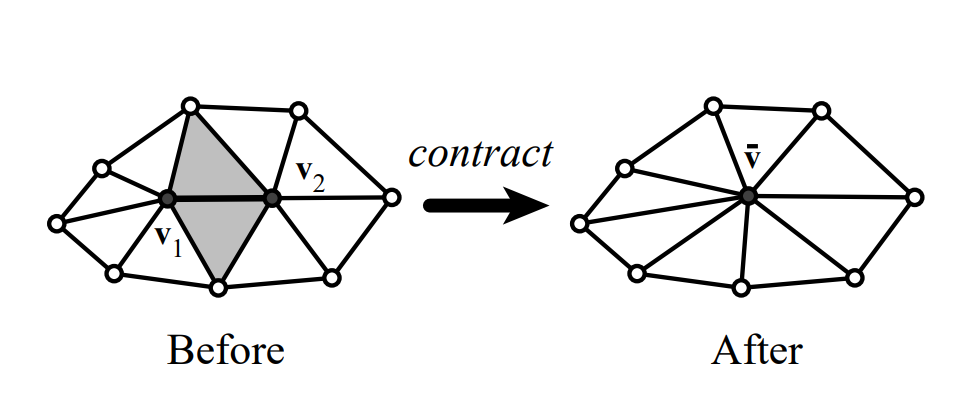
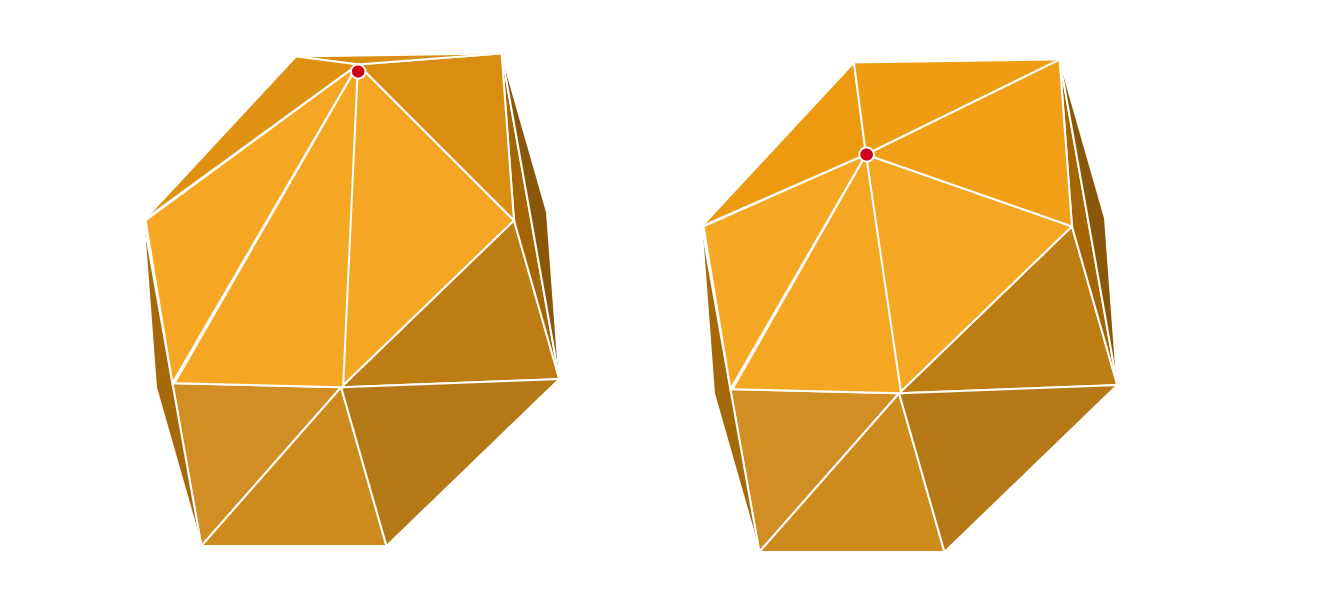
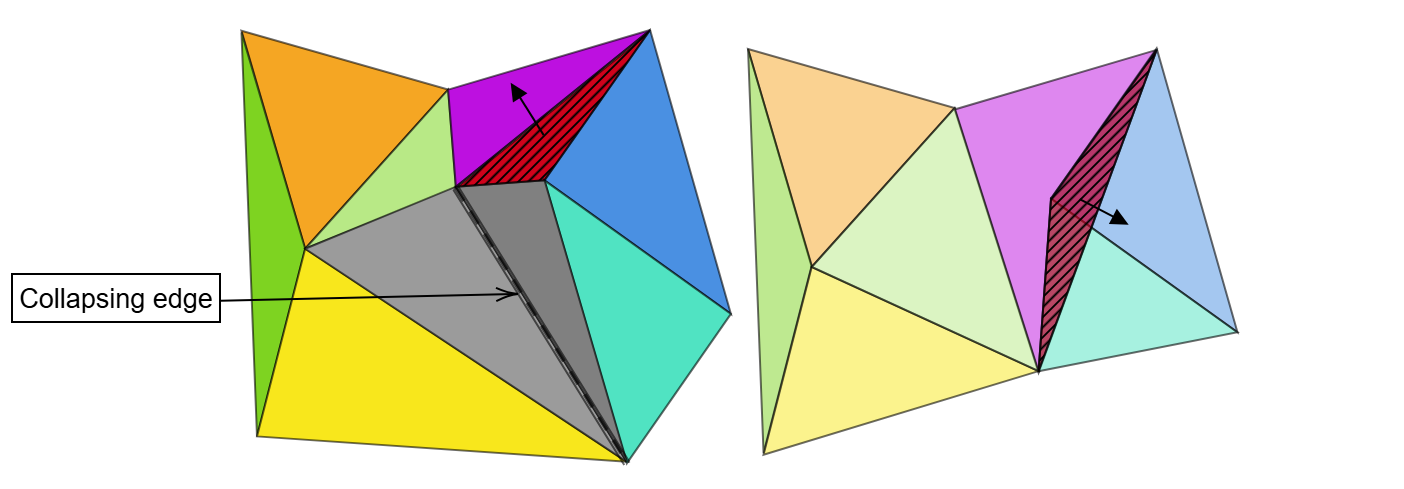
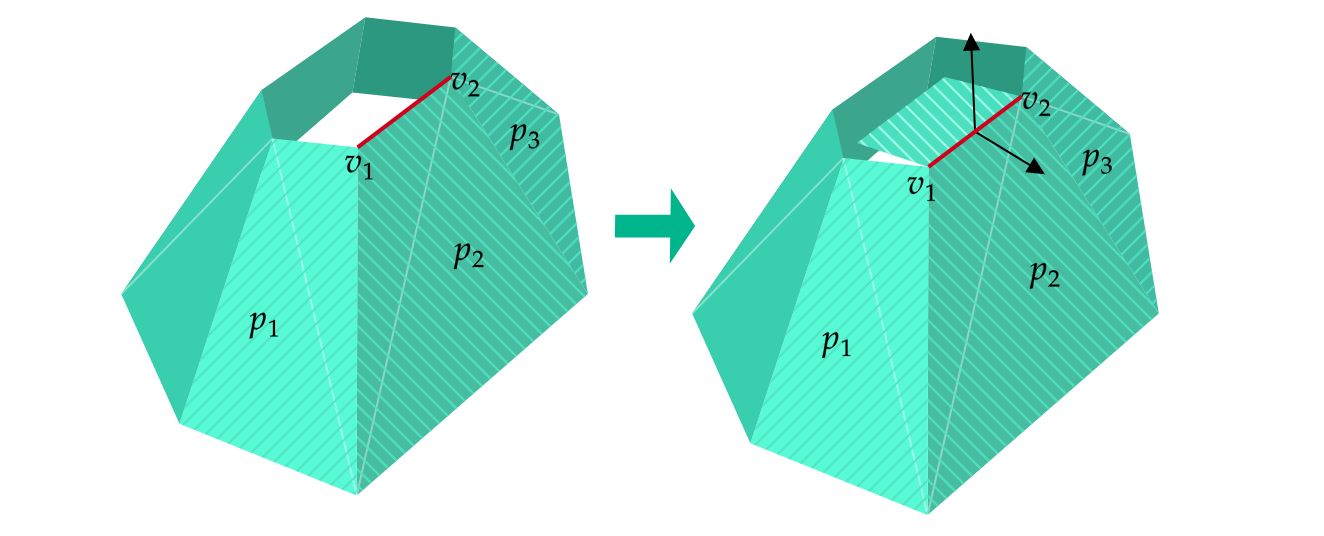
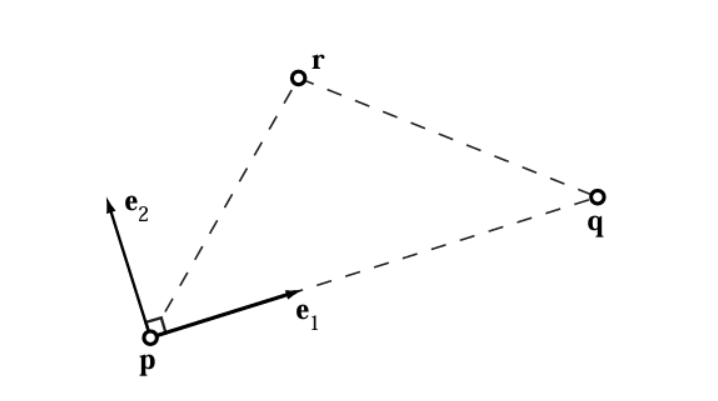
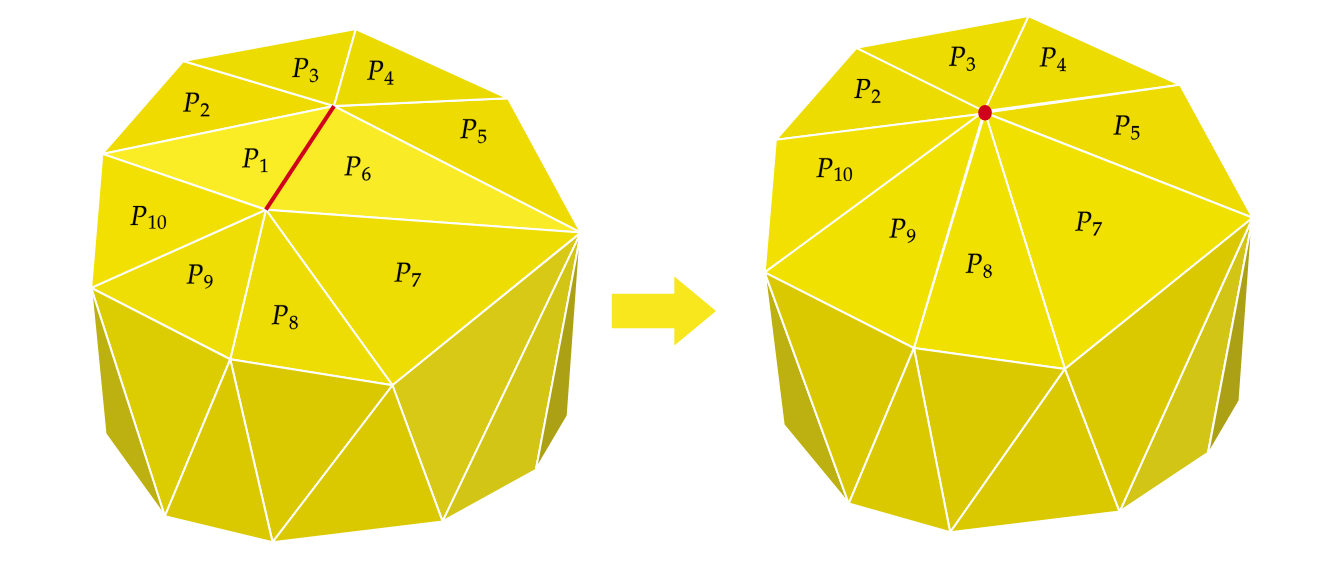
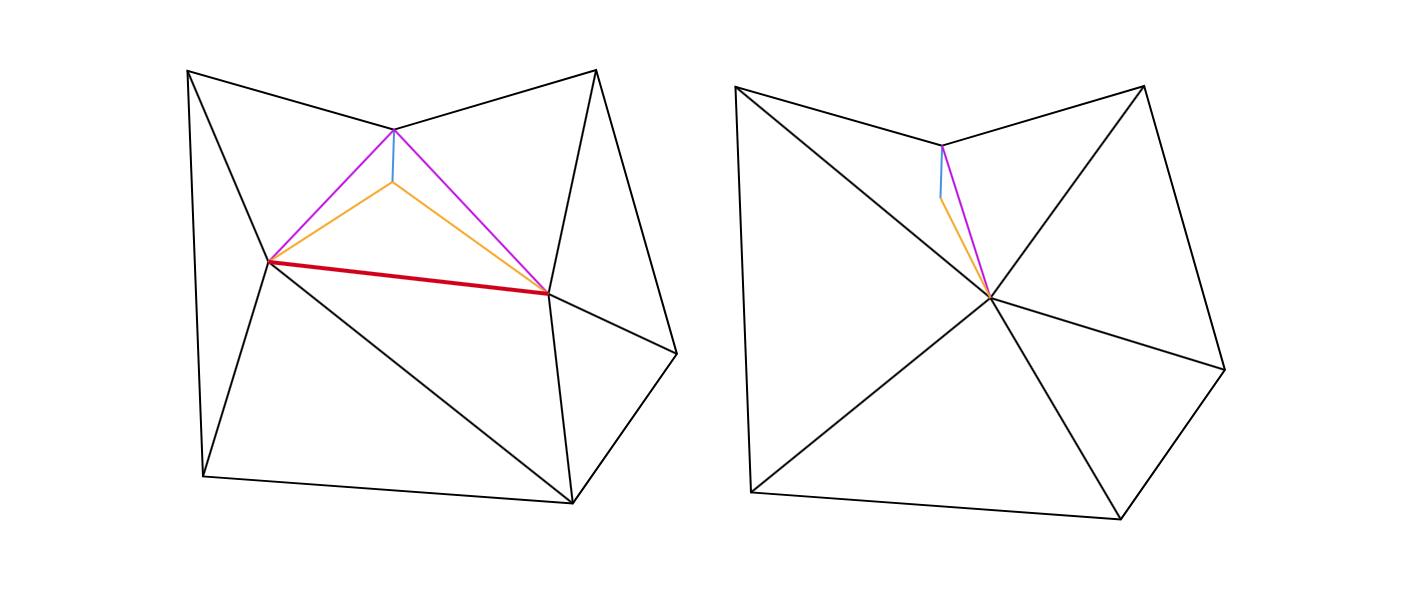
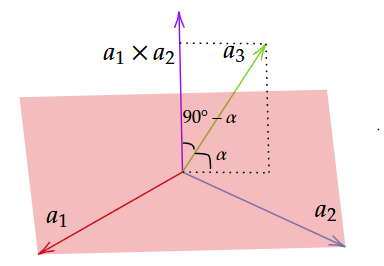
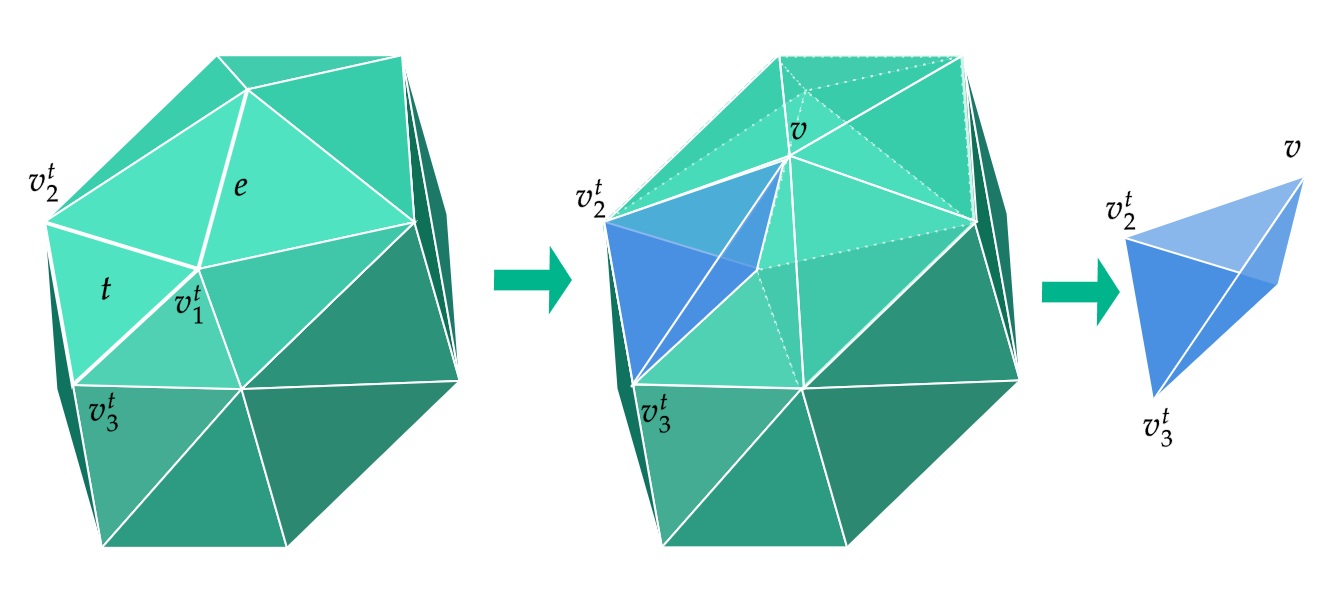
Mesh simplification is the process of reducing the number of vertices, edges and triangles in a three-dimensional (3D) mesh while preserving the overall shape and salient features of the mesh. A popular strategy for this is edge collapse, where an edge connecting two vertices is merged into a single vertex. The edge to collapse is chosen based on a cost function that estimates the error introduced by this collapse. This paper presents a comprehensive, implementation-oriented guide to edge collapse for practitioners and researchers seeking both theoretical grounding and practical insight. We review and derive the underlying mathematics and provide reference implementations for foundational cost functions including Quadric Error Metrics (QEM) and Lindstrom-Turk's geometric criteria. We also explain the mathematics behind attribute-aware edge collapse in QEM variants and Hoppe's energy-based method used in progressive meshes. In addition to cost functions, we outline the complete edge collapse algorithm, including the specific sequence of operations and the data structures that are commonly used. To create a robust system, we also cover the necessary programmatic safeguards that prevent issues like mesh degeneracies, inverted normals, and improper handling of boundary conditions. The goal of this work is not only to consolidate established methods but also to bridge the gap between theory and practice, offering a clear, step-by-step guide for implementing mesh simplification pipelines based on edge collapse.
Triangles are the most commonly used drawing primitive in computer graphics. They are natively supported by almost all graphics libraries and hardware systems, making triangular meshes the dominant representation in 3D modeling. Modern graphics systems are capable of rendering models composed of millions of triangles, thanks to decades of hardware advancements. However, with Moore's Law plateauing and the geometric complexity of meshes increasing rapidly, relying on brute-force parallel processing is no longer viable. This makes mesh simplification techniques more essential than ever for achieving real-time performance and scalability in interactive and large-scale applications. Mesh simplification forms the basis of level of detail (LOD) systems to ease GPU workload, accelerates collision detection in games, and enables faster coarse approximations in FEA simulations.
Among the various mesh simplification techniques available, edge collapse is most widely adopted in practice. This strategy is implemented in many major graphics libraries and tools like CGAL , QSlim, and meshoptimizer. An edge collapse operation merges the two endpoints of an edge into a single new vertex, effectively removing the edge and the two triangles that shared it. Repeating this operation iteratively leads to a simplified mesh that maintains the overall structure of the original. Cost functions help determine which edge to collapse and where to place the resulting vertex in order to best preserve the model’s visual and geometric details. While mesh simplification is a well-studied topic, newcomers to the field often face a steep learning curve when engaging with foundational papers. Many of these works emphasize final equations or high-level algorithmic descriptions, offering little insight into the underlying geometric reasoning or the practical implementation details. As a result, readers may struggle to build an intuitive understanding of how and why edge collapse-based simplification works, or how to translate theory into working code.
This paper aims to bridge that gap by offering a detailed, implementation-aware analysis of edge collapse-based mesh simplification on a manifold mesh. Our contributions are as follows:
• We present a complete, end-to-end simplification pipeline that includes well-chosen data structures for representing mesh connectivity, deep analysis of cost functions presented in foundational papers in this space, and the edge collapse algorithm that binds both of these.
• Unlike many prior works that present only the final cost metrics or optimization functions, we derive and explain them along with the geometric meaning behind these formulations, allowing readers to understand the rationale behind each step.
• Our goal is two-fold: to serve as a conceptual guide for learners who want to understand the inner workings of simplification algorithms, and to act as a practical reference for developers looking to implement their own systems.
In this paper, we first categorize and review different families of mesh simplification algorithms. Since the efficiency of edge-collapse operations depends on fast access to mesh connectivity and rapid local updates, int the following section, we discusse data structures that can be employed to store and manage the mesh connectivity information. We then present a comprehensive edge-collapse algorithm, including detailed programmatic checks to prevent mesh degeneracies. Our most extensive section examines cost computation strategies, explaining the mathematical formulations from foundational papers alongside practical implementations. In the next section, we cover advance edge collapse techinques that account for per-vertex attributes. Finally, we provide supplemental mathematical results and proofs that support these techniques.
Mesh simplification techniques vary widely, but most can be grouped by the strategy they use to reduce geometric complexity while maintaining topology as presented in [Cignoni et al. 1998]. We have supplemented this list with recent advances in the field that leverage modern techniques such as machine learning and neural networks.
An early strategy for mesh decimation focused on detecting coplanar or nearly coplanar surface patches and merging them into larger polygonal regions as presented in [De-Haemer Jr and Zyda 1991] and [Hinker and Hansen 1993]. These regions are subsequently re-triangulated to produce a mesh with fewer faces. Despite its simplicity, the method often degraded geometric detail and introduced topological inconsistencies.
Another method, known as vertex clustering, groups nearby vertices based on spatial proximity and replaces each cluster with a single representative vertex, followed by local re-triangulation as presented in [Rossignac and Borrel 1993] and improved in [Low and Tan 1997]. While faster, this method was again found to compromise detail and topological accuracy.
A more refined and topology-sensitive method is
This content is AI-processed based on open access ArXiv data.