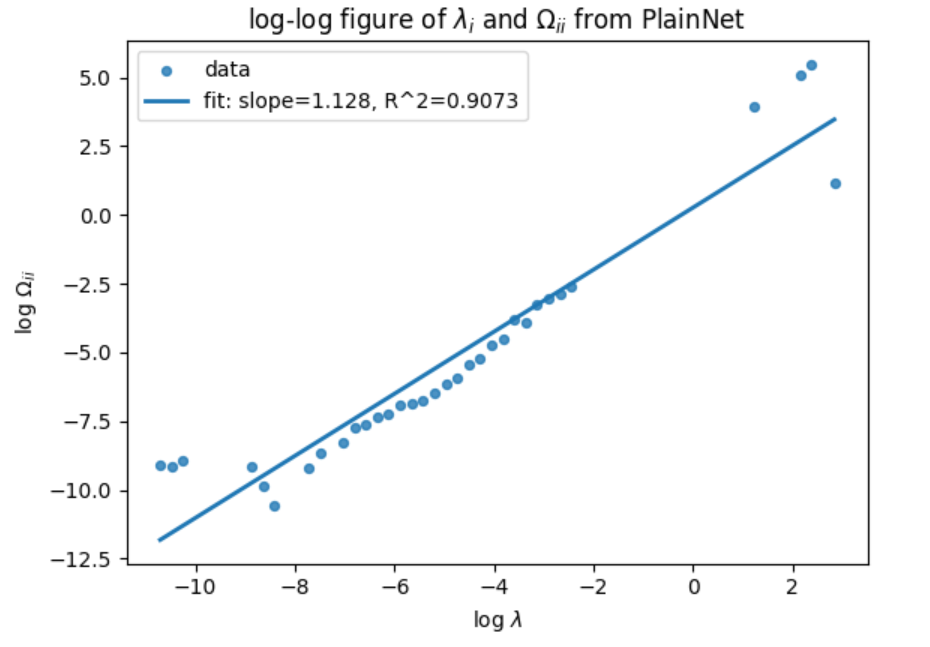
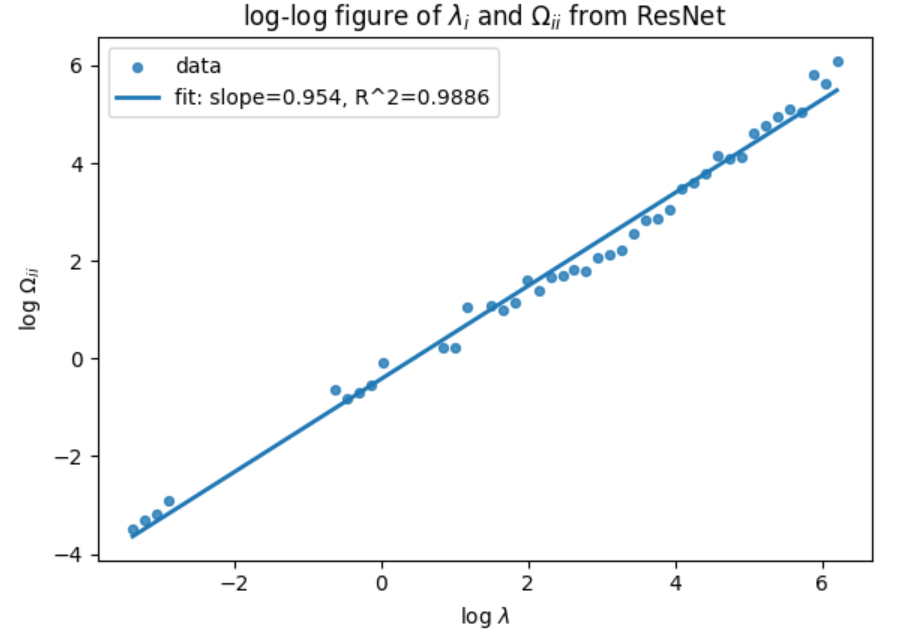
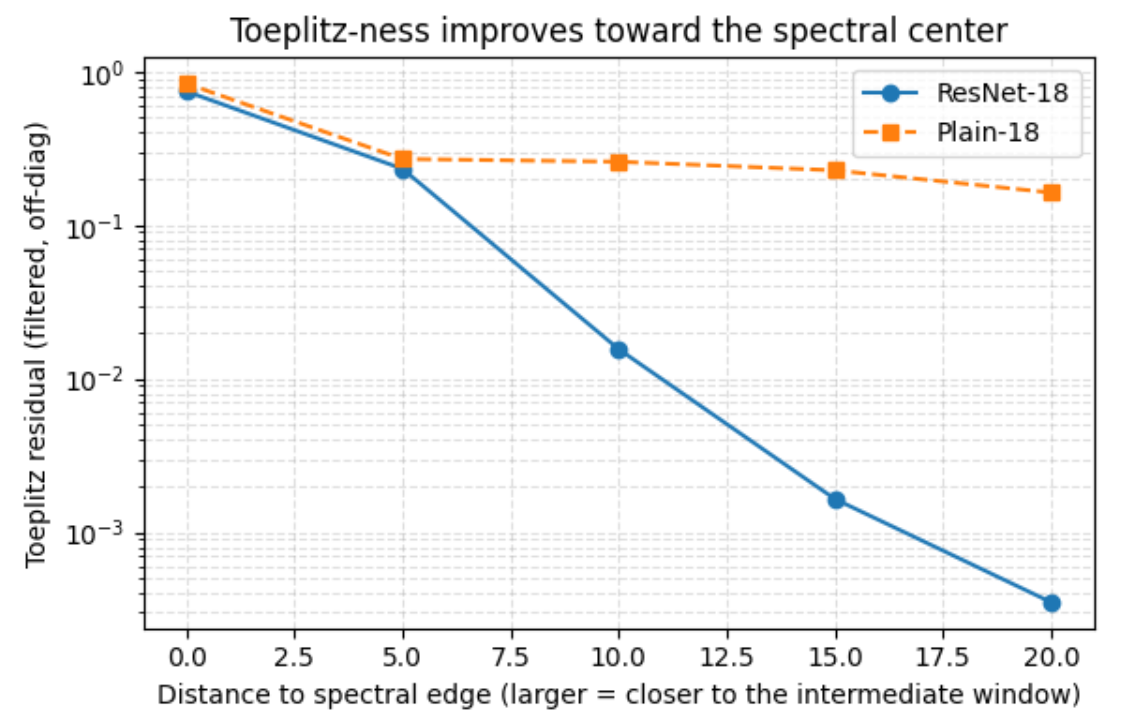
Empirical power--law scaling has been widely observed across modern deep learning systems, yet its theoretical origins and scope of validity remain incompletely understood. The Generalized Resolution--Shell Dynamics (GRSD) framework models learning as spectral energy transport across logarithmic resolution shells, providing a coarse--grained dynamical description of training. Within GRSD, power--law scaling corresponds to a particularly simple renormalized shell dynamics; however, such behavior is not automatic and requires additional structural properties of the learning process.
In this work, we identify a set of sufficient conditions under which the GRSD shell dynamics admits a renormalizable coarse--grained description. These conditions constrain the learning configuration at multiple levels, including boundedness of gradient propagation in the computation graph, weak functional incoherence at initialization, controlled Jacobian evolution along training, and log--shift invariance of renormalized shell couplings. We further show that power--law scaling does not follow from renormalizability alone, but instead arises as a rigidity consequence: once log--shift invariance is combined with the intrinsic time--rescaling covariance of gradient flow, the renormalized GRSD velocity field is forced into a power--law form.
Empirical power-law scaling has emerged as one of the most robust and reproducible phenomena in modern deep learning. Across model families, tasks, and training regimes, performance metrics such as loss, error, or perplexity often exhibit smooth power-law dependence on model size, dataset size, or compute budget [18,25,17,20]. More recently, scaling behavior has been observed to persist beyond classical regimes, extending to precision, data pruning, and architectural interventions [42,31]. Despite its empirical ubiquity, the theoretical origins of these power laws remain only partially understood.
A growing body of work has sought to explain neural scaling laws through kernel limits and mean-field approximations [23,32,51], as well as through dynamical models that interpolate between lazy and feature-learning regimes [5,6,7]. While these approaches provide valuable insight into specific limits or architectures, they do not by themselves explain why power-law behavior arises so broadly, nor under what conditions it should be expected to fail. In particular, empirical evidence clearly indicates that scaling laws do not hold universally: depending on architecture, optimization stability, data distribution, or training regime, scaling behavior may degrade, break, or transition between distinct regimes [42,26,10].
In recent work, the Generalized Resolution-Shell Dynamics (GRSD) framework was proposed as a spectral and operator-theoretic description of learning dynamics in deep networks [52]. GRSD formulates learning as an energy transport process across logarithmic spectral shells, leading to a coarse-grained, onedimensional conservation law for error energy. Within this framework, empirical neural scaling laws correspond to a particularly simple form of the renormalized shell velocity: a power-law function of the spectral coordinate. However, in GRSD this power-law form is not automatic. Rather, it reflects a nontrivial structural property of the learning process-namely, that the shell dynamics admits a renormalizable closure in the sense familiar from statistical physics and turbulence theory [24,49,28,8,43].
The central question addressed in this paper is therefore the following: under what conditions does the GRSD shell dynamics admit a power-law renormalized description? Our goal is not to claim that all deep learning systems satisfy such conditions, nor that power-law behavior is universal. Indeed, the empirical literature suggests the opposite: scaling laws are contingent and can fail outside specific regimes. Instead, we seek to identify a coherent and mathematically well-defined set of sufficient conditions under which renormalizable shell dynamics can be established, and under which power-law behavior follows as a rigidity consequence.
A central difficulty in this program is that some of the required conditions-most notably log-shift invariance of renormalized shell couplings-are genuinely structural and do not follow from generic stability or locality considerations alone. Such conditions would be of limited interest if they were never even approximately realized in practical learning systems. For this reason, an essential part of our analysis is to identify concrete architectural mechanisms that promote these properties, and to empirically test whether they are approximately satisfied in realistic training settings.
Concretely, we study learning configurations defined by a network architecture, an initialization scheme, and an optimization trajectory. We provide a theorem establishing that the GRSD shell dynamics admits a power-law velocity field when a collection of structural and dynamical conditions are satisfied. These conditions include (i) locality in the gradient computation graph, (ii) weak functional incoherence at initialization, (iii) controlled evolution of the Jacobian along training, and (iv) log-shift invariance of the renormalized shell couplings. Crucially, power-law scaling does not follow from renormalizability or log-shift invariance alone; rather, it emerges from a rigidity mechanism once these properties are combined with the intrinsic time-rescaling covariance of gradient flow.
At first sight, the sufficient conditions identified in this work may appear strong or even restrictive. Indeed, they impose nontrivial requirements on architectural structure, initialization geometry, and training stability. However, it is precisely these requirements that align strikingly well with several core design principles of modern deep learning systems.
Contemporary architectures are overwhelmingly engineered to avoid uncontrolled recurrence or long-range instantaneous coupling, favoring feedforward or residual structures with bounded gradient propagation. Training pipelines are carefully designed to ensure stability and controllability, with explicit emphasis on preventing gradient explosion or catastrophic spectral reorganization. Likewise, random or weakly correlated initialization sc
This content is AI-processed based on open access ArXiv data.