Large Language Models (LLMs) demonstrate strong few-shot generalization through in-context learning, yet their reasoning in dynamic and stochastic environments remains opaque. Prior studies mainly focus on static tasks and overlook the online adaptation required when beliefs must be continuously updated, which is a key capability for LLMs acting as world models or agents. We introduce a Bayesian filtering framework to evaluate online inference in LLMs. Our probabilistic probe suite spans both multivariate discrete distributions, such as dice rolls, and continuous distributions, such as Gaussian processes, where ground-truth parameters shift over time. We find that while LLM belief updates resemble Bayesian posteriors, they are more accurately characterized by an exponential forgetting filter with a model-specific discount factor smaller than one. This reveals systematic discounting of older evidence that varies significantly across model architectures. Although inherent priors are often miscalibrated, the updating mechanism itself remains structured and principled. We further validate these findings in a simulated agent task and propose prompting strategies that effectively recalibrate priors with minimal computational cost.
In-context learning (ICL) represents a remarkable capability of large language models (LLMs) [1,2,3,4], enabling rapid adaptation to novel tasks based solely on a handful of examples provided in their prompts, without explicit gradient updates. While the empirical success of ICL underpins modern prompting techniques, its fundamental mechanism remains largely opaque. A key open question is whether ICL constitutes structured statistical reasoning analogous to Bayesian inference or is merely sophisticated pattern recognition.
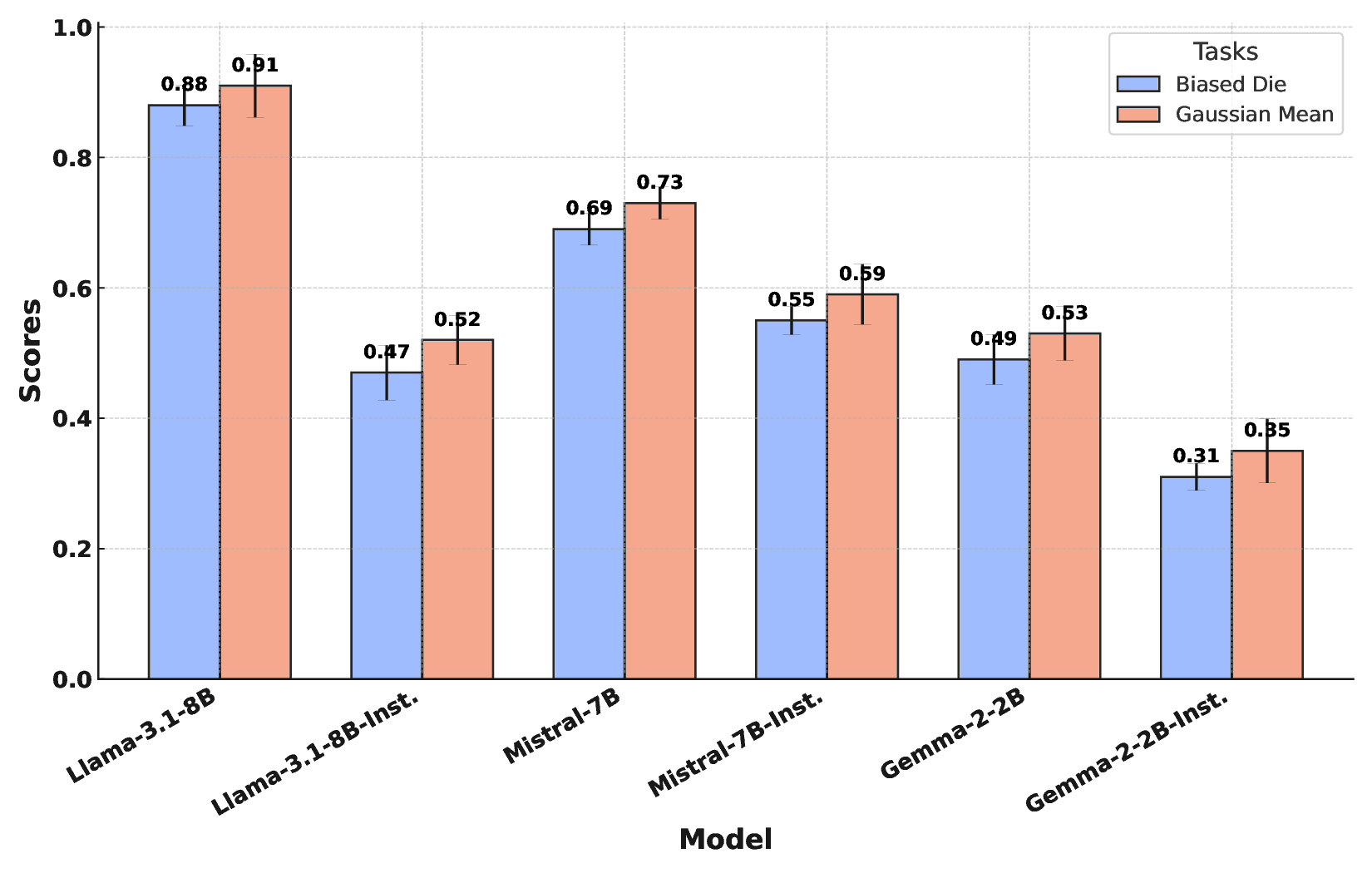
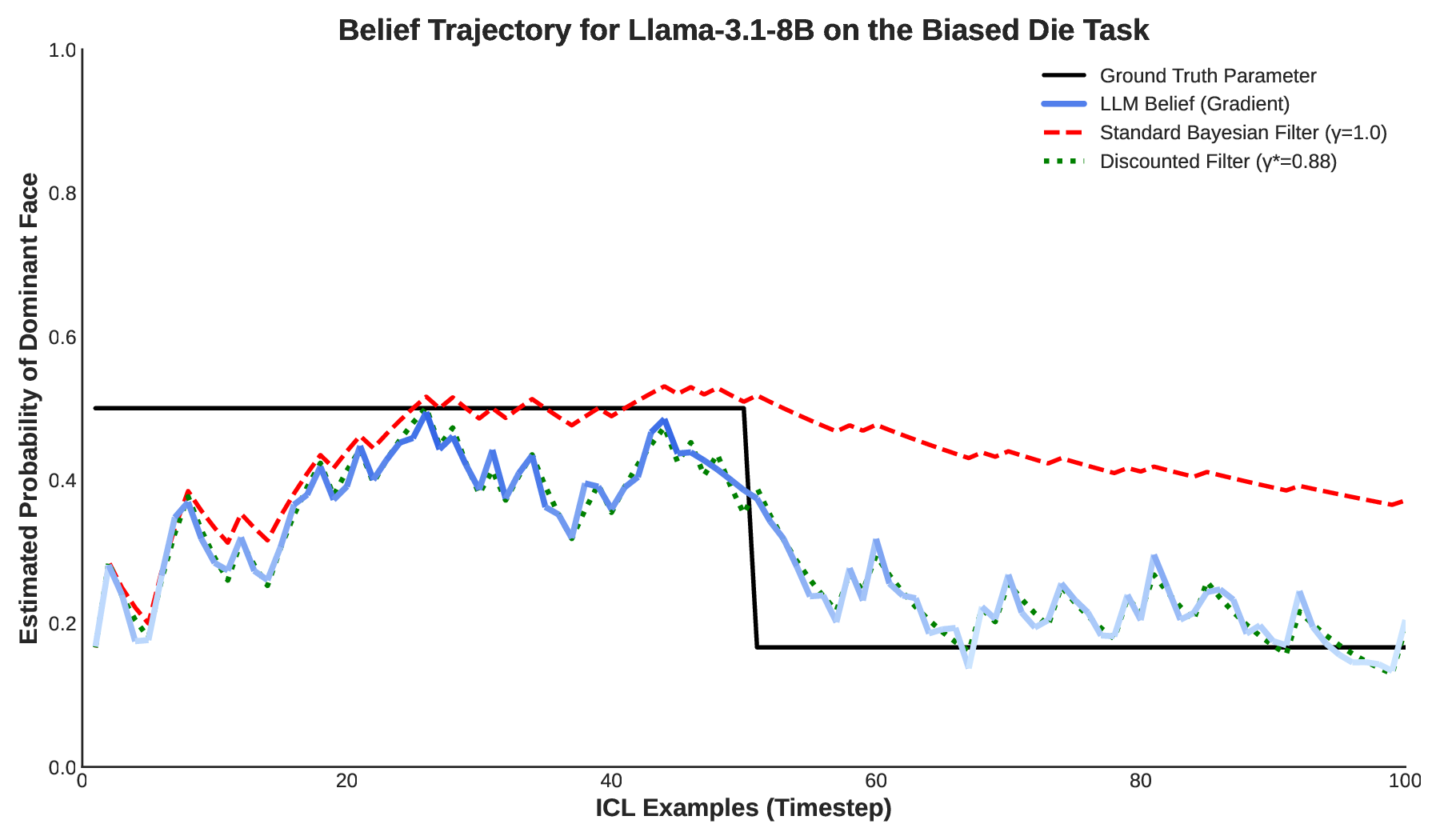
A promising perspective frames ICL as implicit Bayesian inference, where models iteratively update latent belief states based on contextual evidence [5,6,7]. However, existing foundational studies predominantly investigate static environments, assuming stationary data-generating distributions. Such an assumption neglects a crucial aspect of real-world intelligence: the necessity to operate effectively within nonstationary environments. In these dynamic contexts, agents must continuously integrate new information while systematically discounting-or “forgetting”-outdated evidence whose relevance diminishes over time. This capacity for online adaptation is critical for deploying LLMs as reliable world models or autonomous agents, yet remains underexplored. In this work, we propose a new theoretical perspective: we conceptualize ICL in Transformers as online Bayesian filtering characterized by systematic discounting of past evidence. Central to our thesis is the assertion that LLMs, when confronted with sequences of evolving evidence, do not function as ideal Bayesian observers. Instead, we hypothesize that their behavior incorporates an intrinsic forgetting mechanism, likely arising from architectural elements of Transformers [8,9]. To formalize and empirically evaluate this hypothesis, we introduce an analytical framework built around fitting a discount factor γ ∈ (0, 1] that minimizes the Kullback-Leibler (KL) divergence between a model’s predictive distribution and a theoretical Bayesian filter’s. We investigate this dynamic behaviour through a controlled probabilistic probe suite [8,10,11], involving tasks such as biased die rolling and Gaussian mean estimation, where the ground-truth parameters undergo sudden shifts, compelling models to adapt their posterior beliefs. Through our integrated experimental and analytical approach, we present the following contributions:
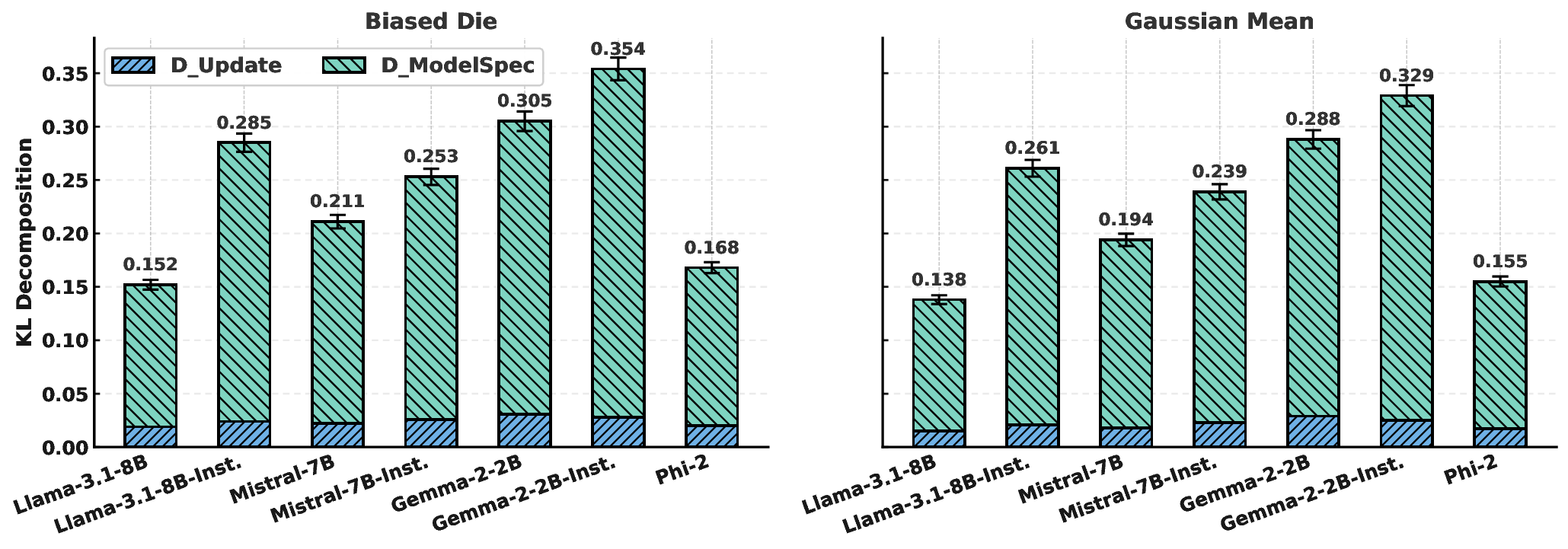
We establish a novel framework for interpreting ICL as online Bayesian filtering. Our analysis provides the We show that observed performance limitations are predominantly attributable to the latter, which stems from miscalibrated priors and intrinsic discounting, rather than a flawed updating process itself.
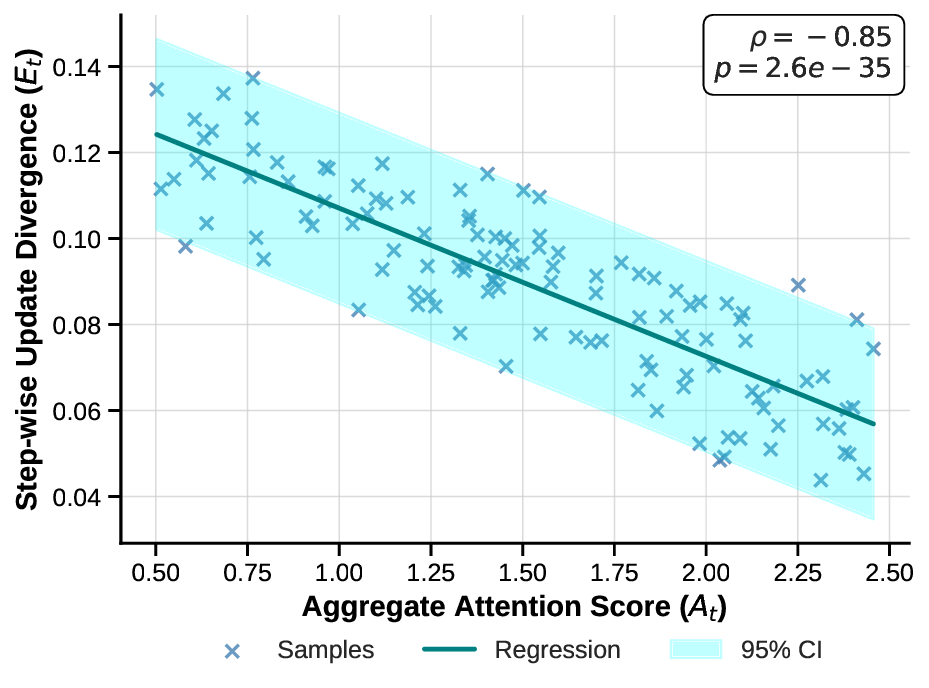
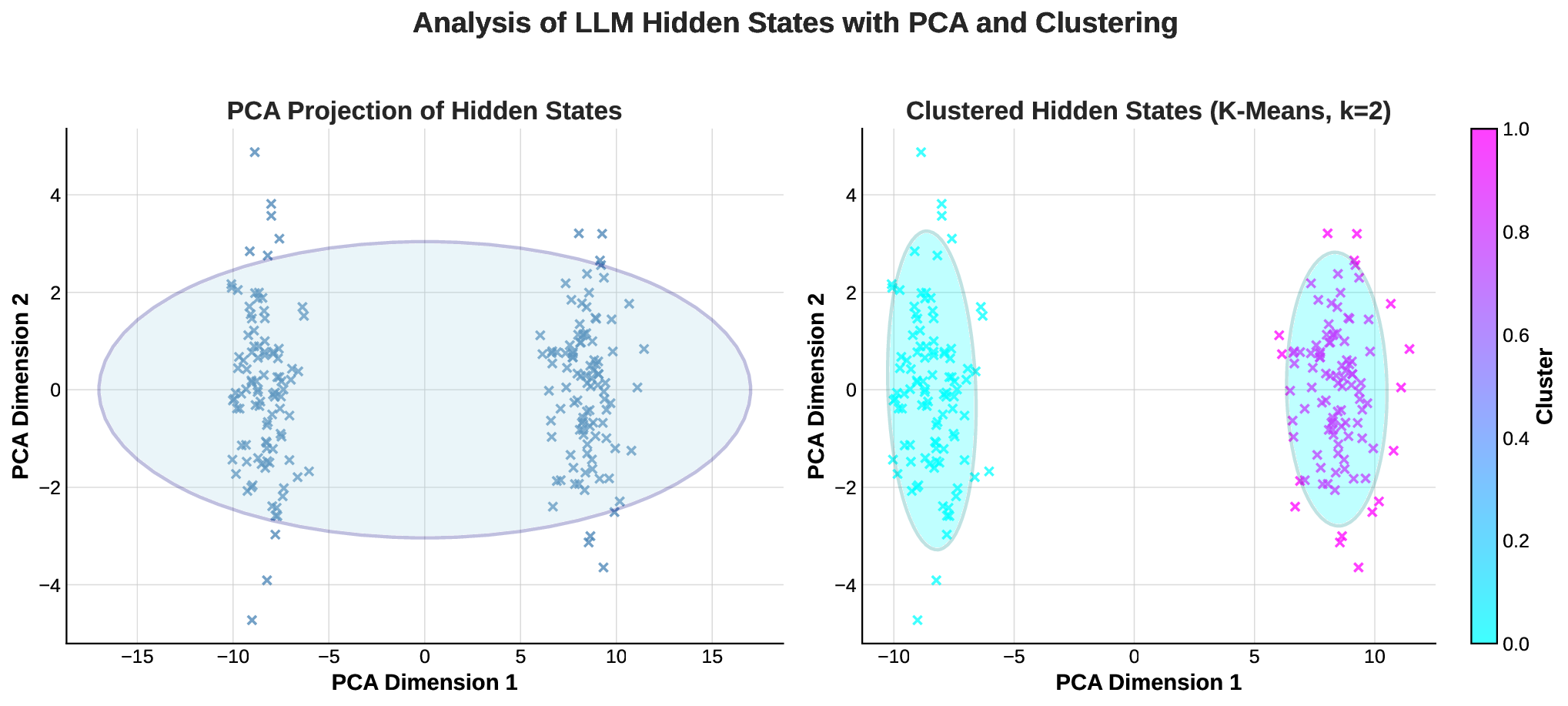
We further investigate the internal mechanisms underlying this discounting behaviour, revealing through correlation analysis that inferential quality is decoupled from the raw magnitude of attention scores. This finding points to a complex architectural basis for evidential forgetting that extends beyond straightforward attention allocation.
In-context learning (ICL) in large language models (LLMs) [12]has been extensively studied as a form of implicit statistical inference, particularly through a Bayesian lens. Foundational works, such as those by Xie et al. [8] and Aky"urek et al. [13], frame ICL as approximating Bayesian posterior updates or gradient descent on latent functions, enabling fewshot generalization in stationary environments. However, these perspectives assume fixed data distributions, overlooking the challenges of non-stationary settings where beliefs must adapt online to shifting parameters-a gap our discounted filtering framework addresses by introducing systematic evidence forgetting.
Recent efforts have begun exploring dynamic adaptation in LLMs, including continual learning approaches [14] that mitigate catastrophic forgetting via architectural modifications or replay buffers. For instance, methods like selfsynthesized rehearsal [15] generate synthetic data to preserve knowledge across tasks. Yet, these often focus on taskspecific retention rather than principled probabilistic updating under uncertainty.Our work diverges by providing a unified Bayesian filtering model with a fitted discount factor γ < 1, quantifying deviations from ideal inference and linking them to Transformer attention mechanisms, thus bridging static ICL theory with online reasoning.
Our methodology is designed to empirically test if LLM in-context learning emulates online Bayesian inference with evidence discounting. We first define our theoretical model and the non-stationary tasks used for probing, then detail the quantitative analysis, summarized in Algorithm 1.
Discounted Bayesian Filtering. We model the “forgetting” of past evidence using a discounted Bayesian filtering framework [16]. This introduces a discount factor, γ ∈ (0, 1], which tempers the posterior belief p t-1 (θ|D 1:t-1 ) before it is updated wit
This content is AI-processed based on open access ArXiv data.