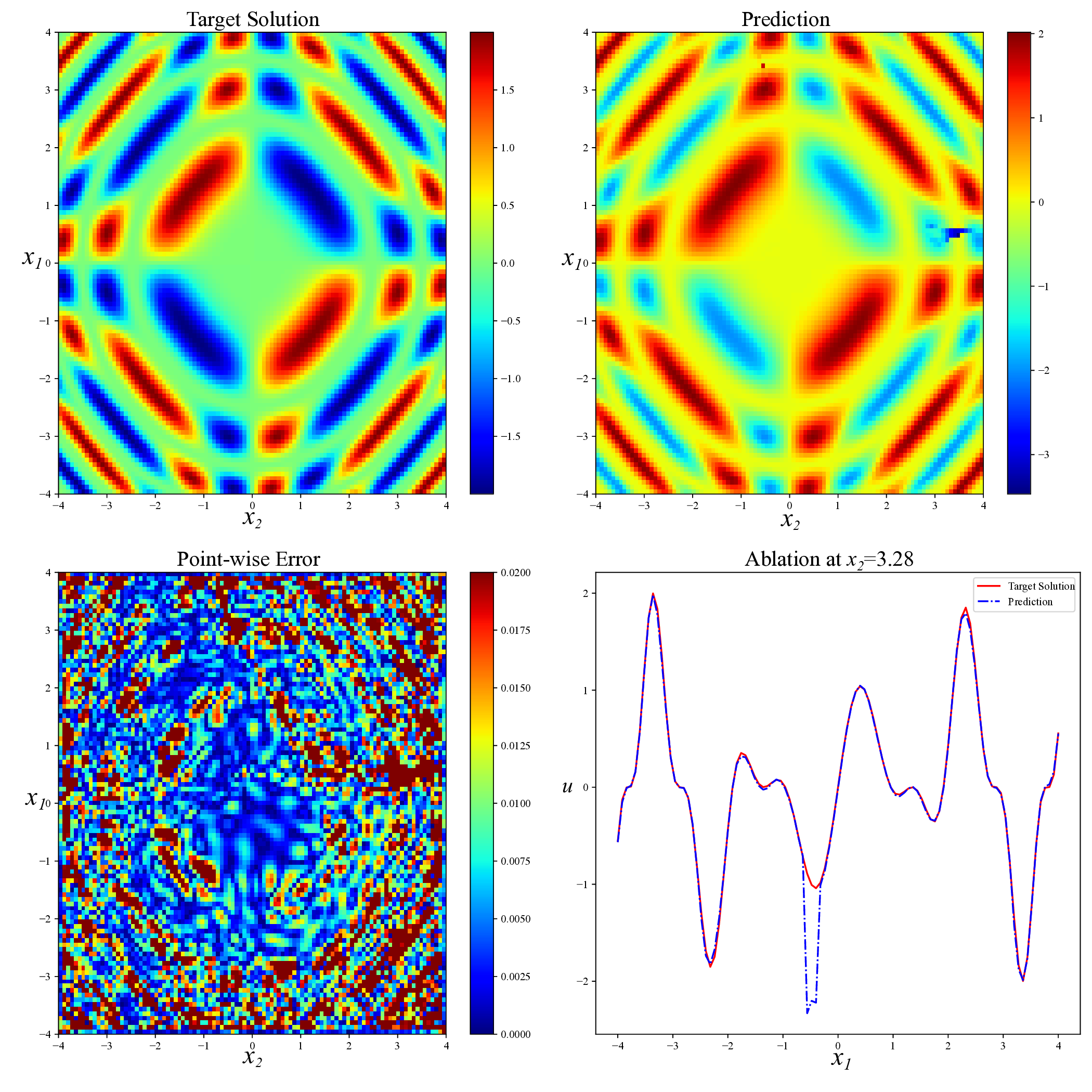
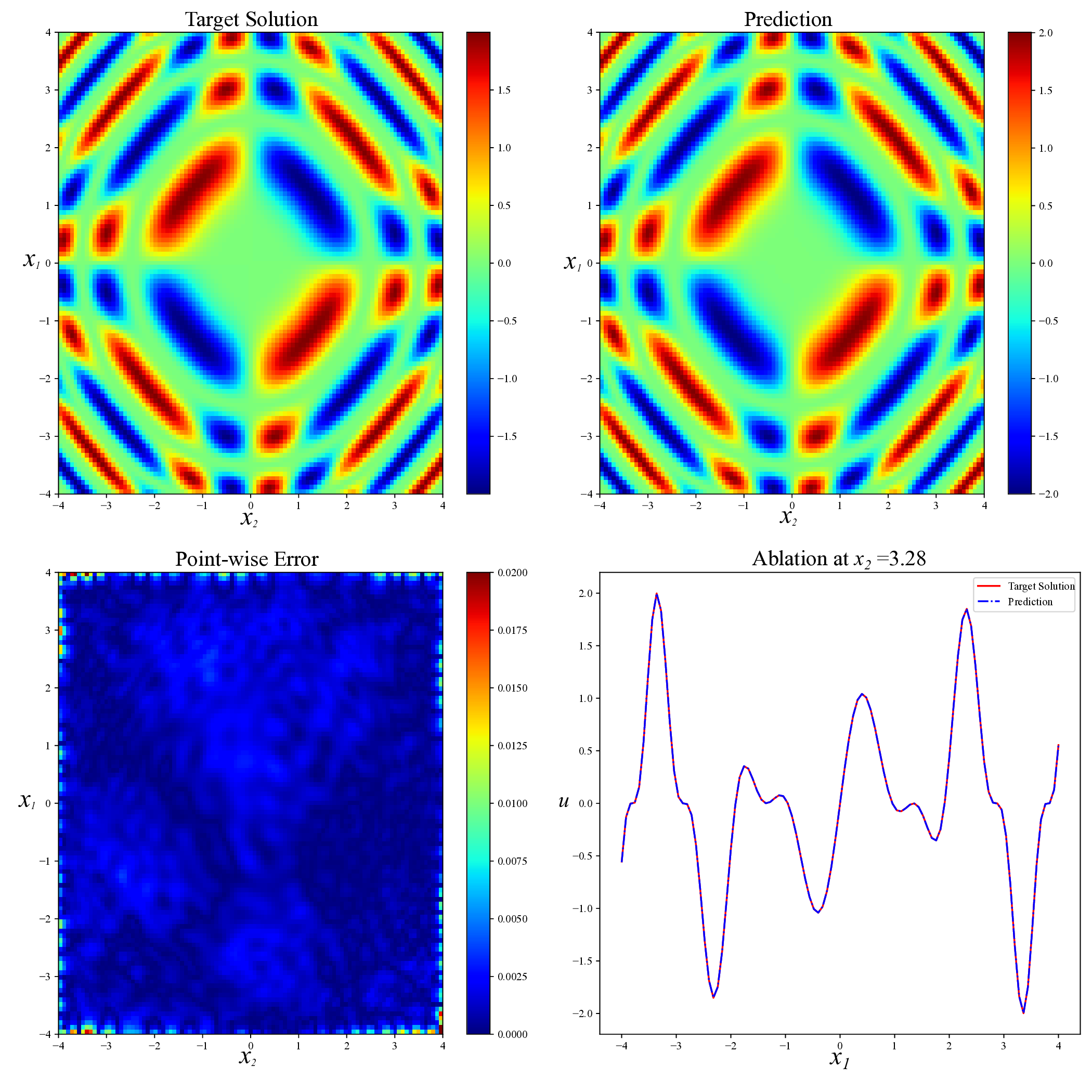
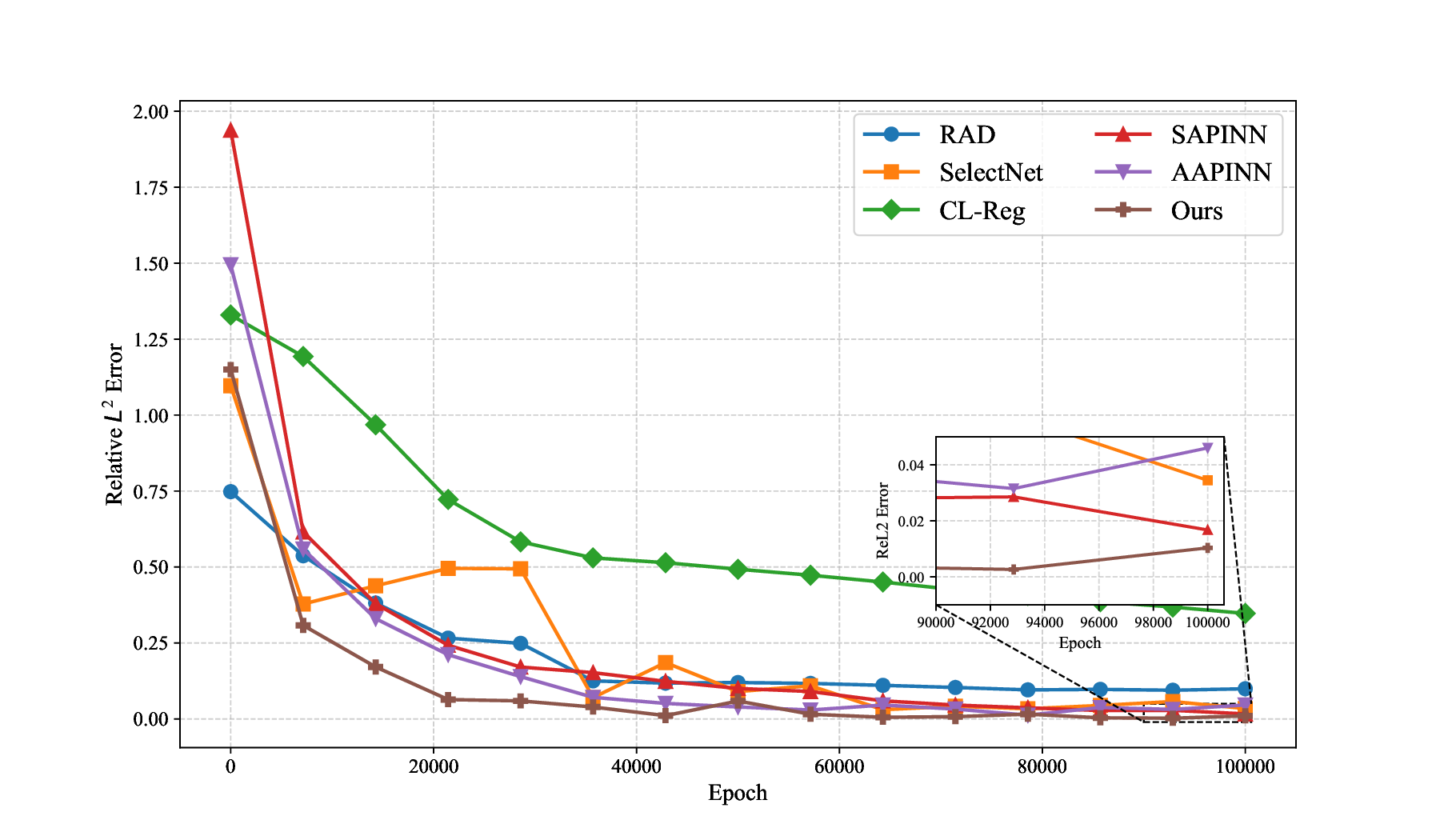
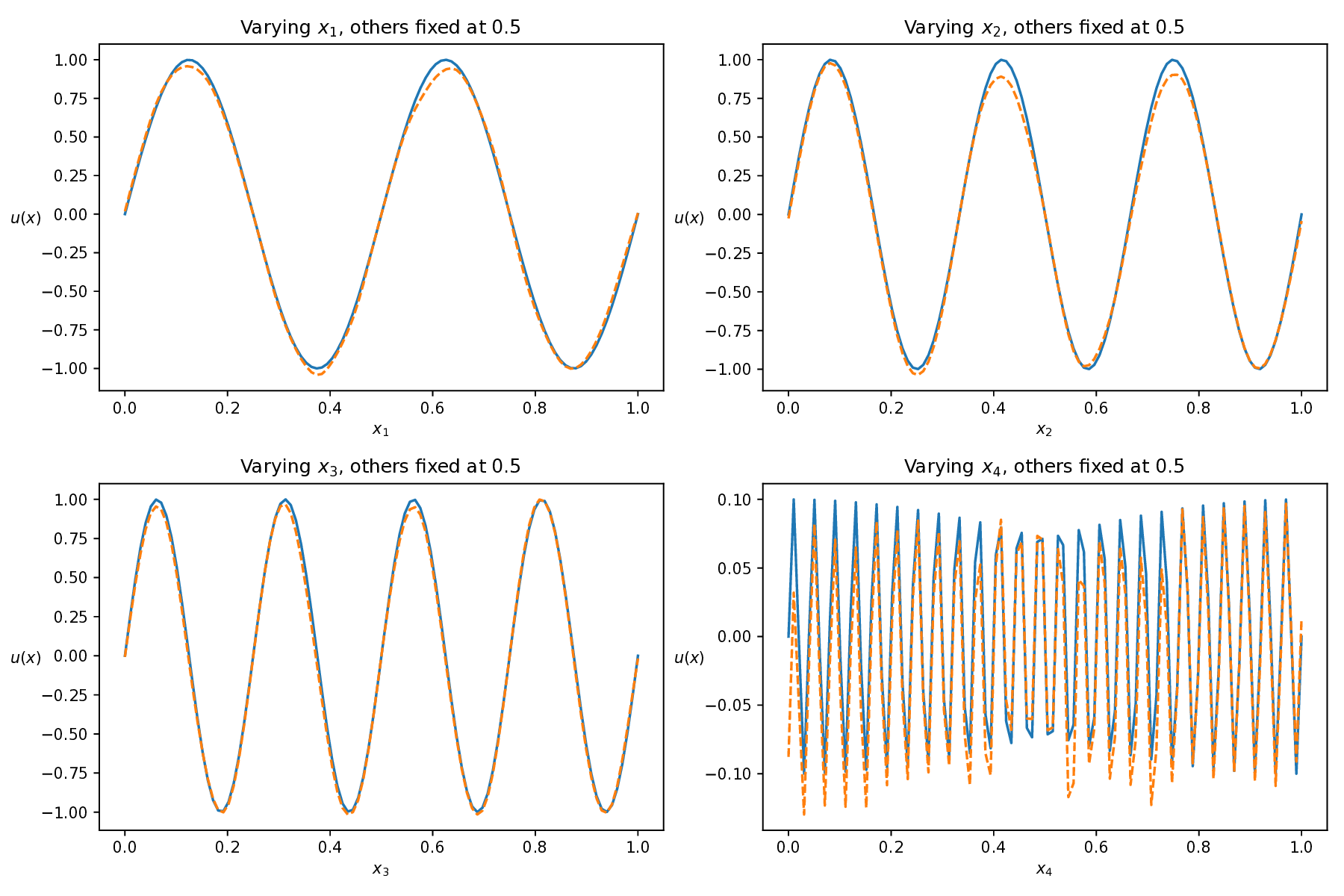
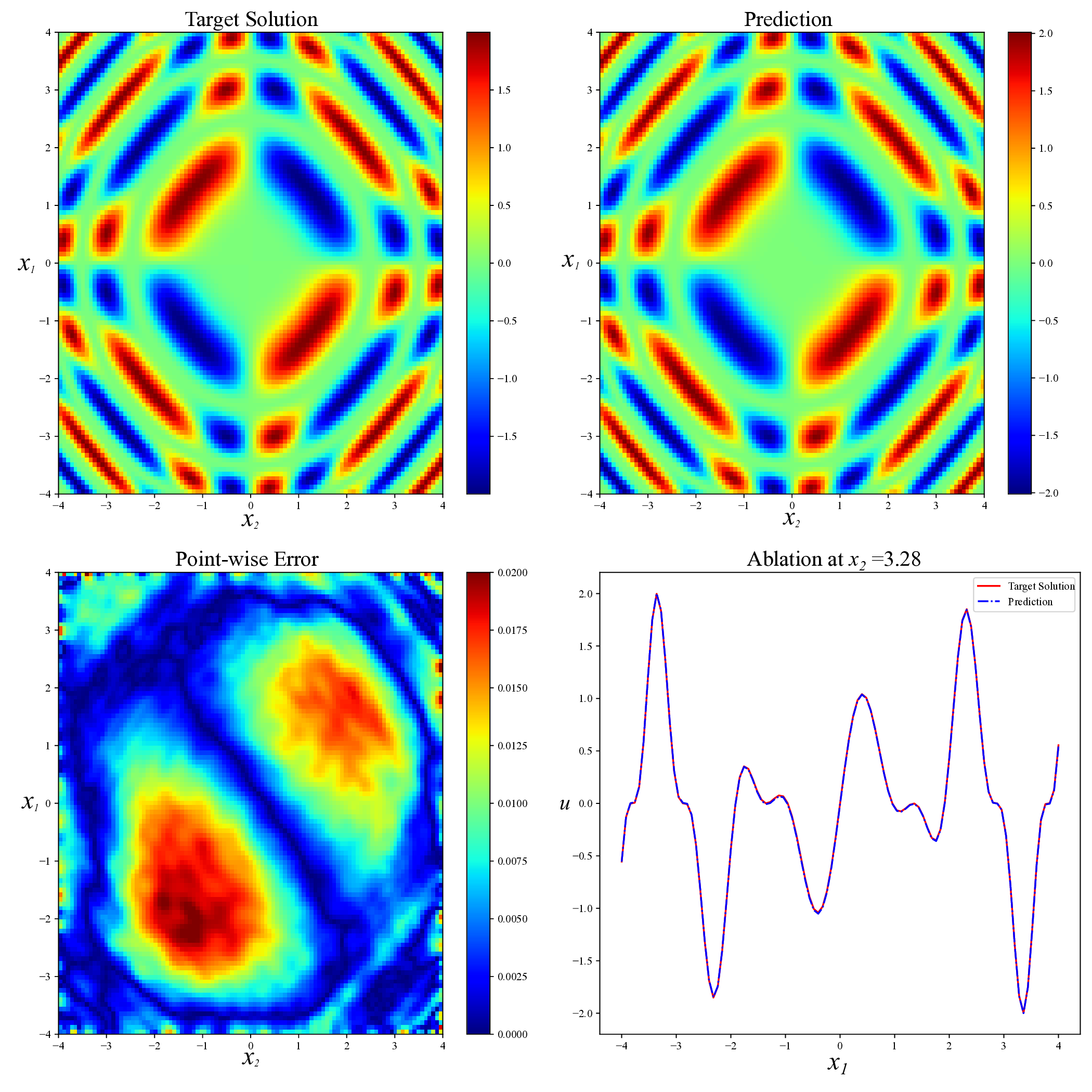
Physics-informed neural networks (PINNs) have recently emerged as a prominent paradigm for solving partial differential equations (PDEs), yet their training strategies remain underexplored. While hard prioritization methods inspired by finite element methods are widely adopted, recent research suggests that easy prioritization can also be effective. Nevertheless, we find that both approaches exhibit notable trade-offs and inconsistent performance across PDE types. To address this issue, we develop a hybrid strategy that combines the strengths of hard and easy prioritization through an alternating training algorithm. On PDEs with steep gradients, nonlinearity, and high dimensionality, the proposed method achieves consistently high accuracy, with relative L2 errors mostly in the range of O(10^-5) to O(10^-6), significantly surpassing baseline methods. Moreover, it offers greater reliability across diverse problems, whereas compared approaches often suffer from variable accuracy depending on the PDE. This work provides new insights into designing hybrid training strategies to enhance the performance and robustness of PINNs.
The rapid development of deep learning has revolutionized scientific computing, offering novel solutions to longstanding challenges in modeling complex physical systems [3,8,21,24,39]. Among these advances, physics-informed neural networks (PINNs), seamlessly integrating partial differential equations into neural network training through residual-based loss functions, have emerged as an vital framework [9,16,18,38,41]. By bridging data-driven flexibility with physical consistency, PINNs circumvent the need for computationally expensive mesh generation and demonstrate remarkable capabilities in solving parametrized and high-dimensional partial differential equations (PDEs) [4,10,27,30,40]. However, their effectiveness is frequently compromised by a critical challenge: the heterogeneous contributions of loss components, which lead to unstable solution accuracy [2,6,12,32,33].
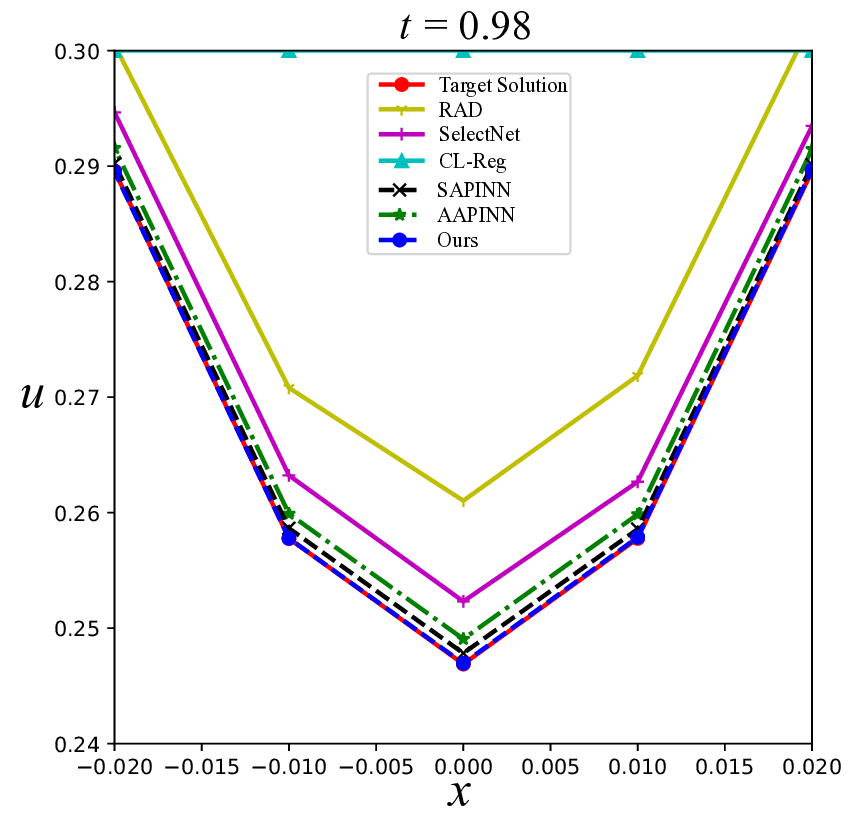
To improve the accuracy and stability of PINNs, two seemingly distinct training strategies have been extensively studied. The first strategy, hard prioritization, identifies and emphasizes high-loss sample points during PINN training through resampling or adaptive weighting techniques [7,20,23,26,35]. This strategy forces the model to focus on the more challenging regions of the PDE domain, thereby helping it capture more essential physical characteristics. For instance, residual-based adaptive sampling automatically adds more sample points in computational regions with larger residual loss [35]. Luo et al. [23] introduce Residual-based Smote (RSmote), an innovative local adaptive sampling technique tailored to improve the performance of PINNs through imbalanced learning strategies. Gu et al. [7] proposed SelectNet, a self-paced learning framework that emphasizes higher-loss sample points during training. Liu and Wang [20] developed a Physics-Constrained Neural Network with the Mini-Max architecture (PCNN-MM) to simultaneously update network weights (via gradient descent) and loss weights (via gradient ascent), targeting a saddle point in the weight space. McClenny and Braga-Neto [26] advanced this approach by proposing Self-Adaptive PINN (SAPINN), which adaptively assigns heavier weights to larger individual sample losses.
The second strategy, easy prioritization, draws inspiration from human curriculum learning [1,17,31] by initially focusing on simpler samples or tasks and gradually increasing the level of difficulty [15,22,25,33]. This approach can reduce training instability, especially in the early stages, and promote faster convergence. Krishnapriyan et al. [15] applied curriculum learning approach in PINNs by progressively introducing highfrequency components or refining the spatiotemporal domains. Monaco and Apiletti [25] proposed a new curriculum regularization strategy to enable smooth transitions in parameter values as task difficulty increases. Wang et al. [33] addressed convection-dominated diffusion equations by assigning reduced weights to challenging regions such as boundary or interior layers to improve solution accuracy. More recently, Li et al. [22] introduced an Anomaly-Aware PINN (AAPINN), which enhances robustness and accuracy by identifying and excluding difficult, high-loss samples.
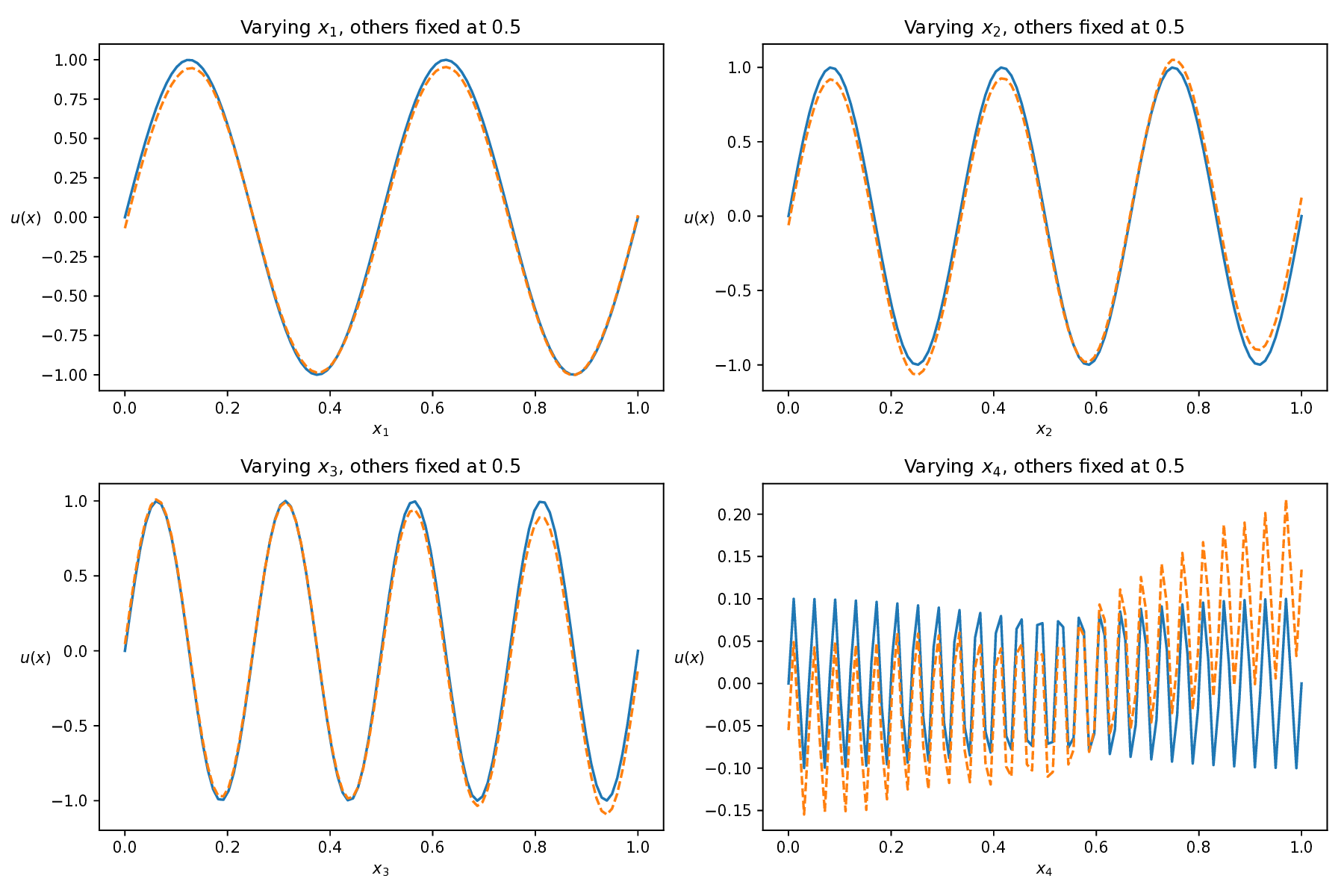
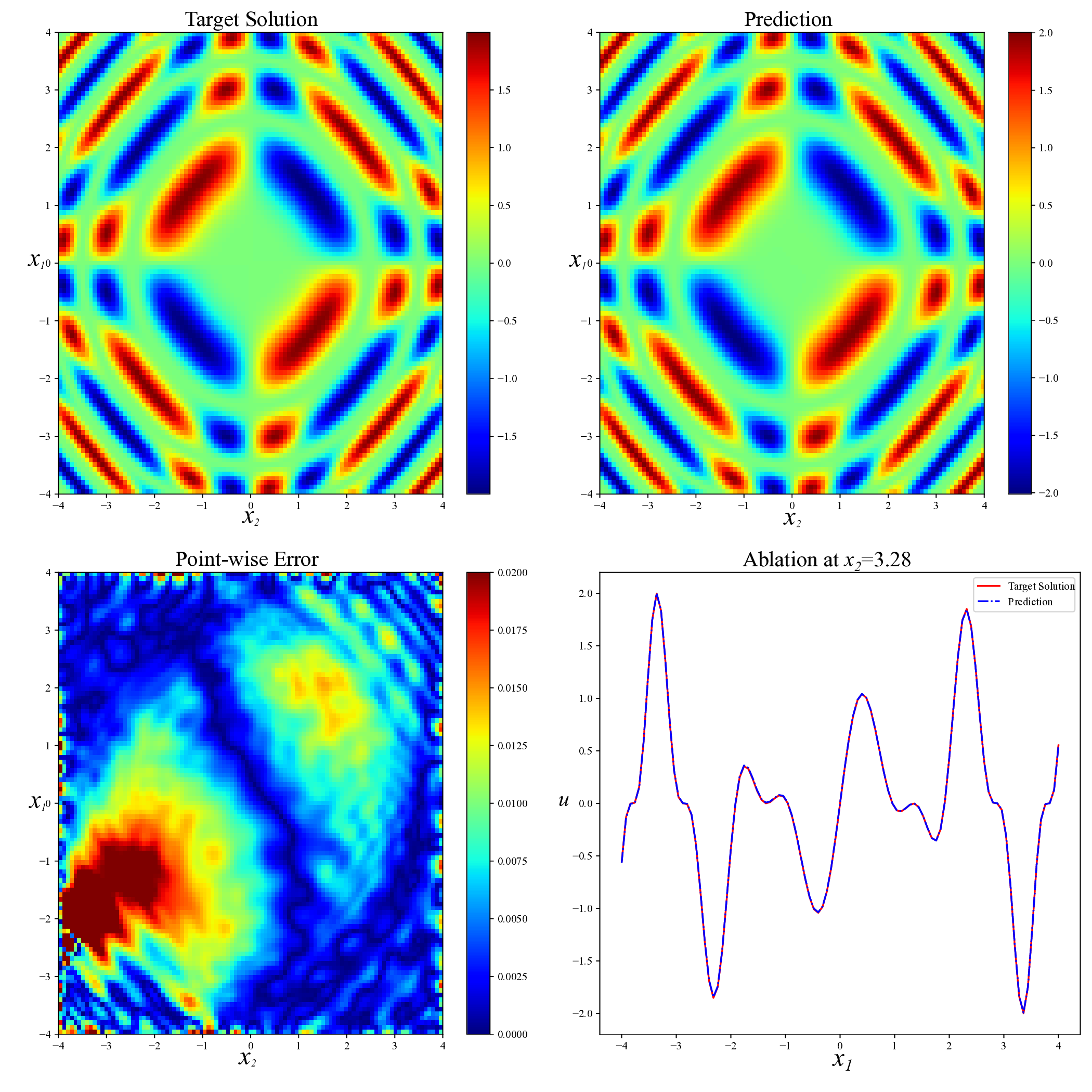
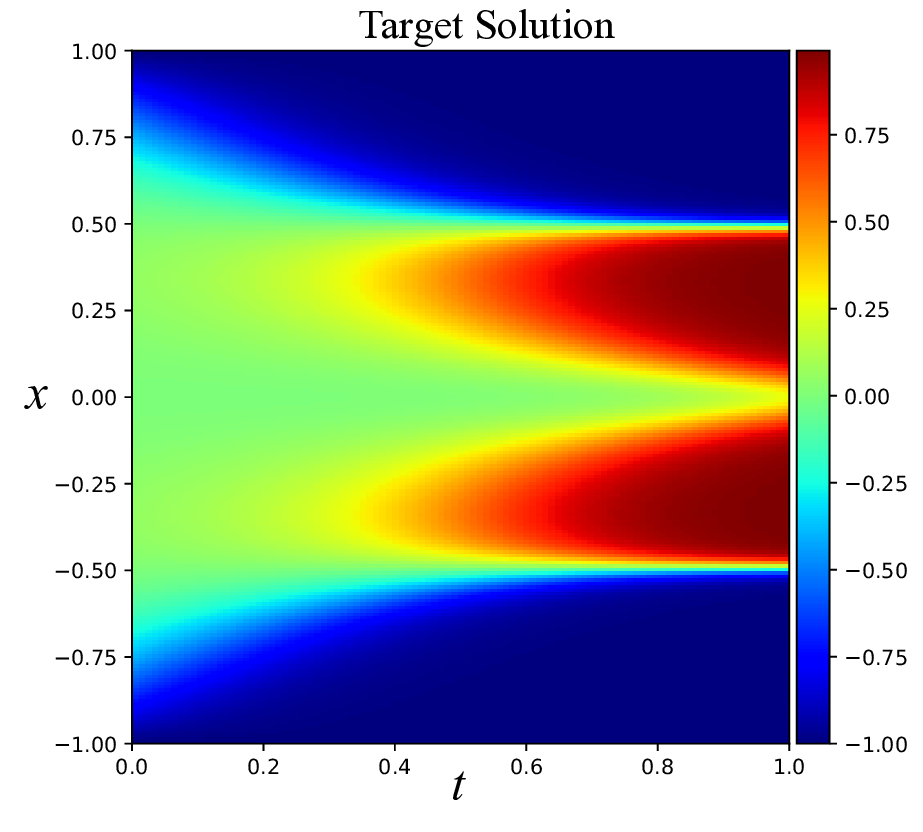
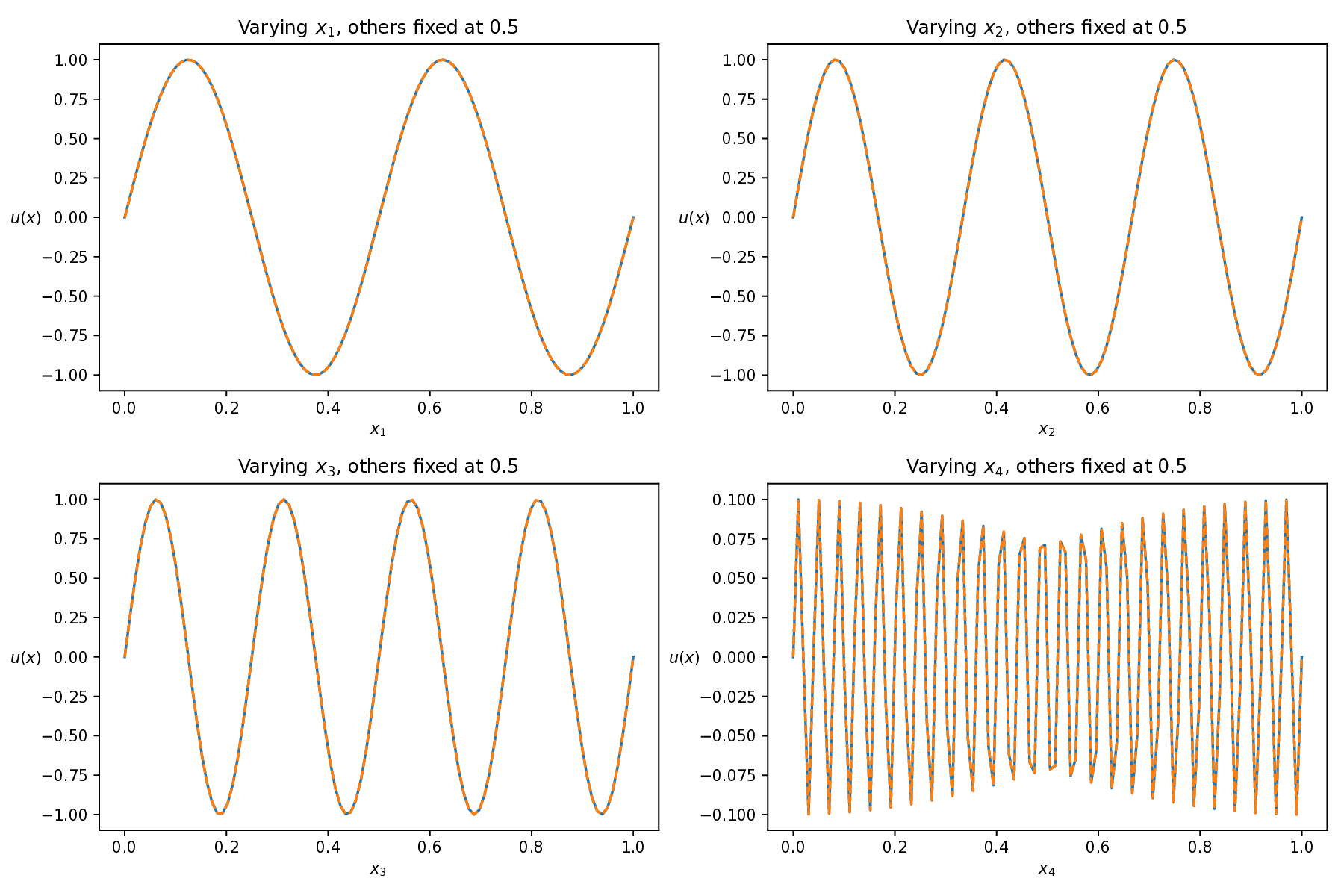
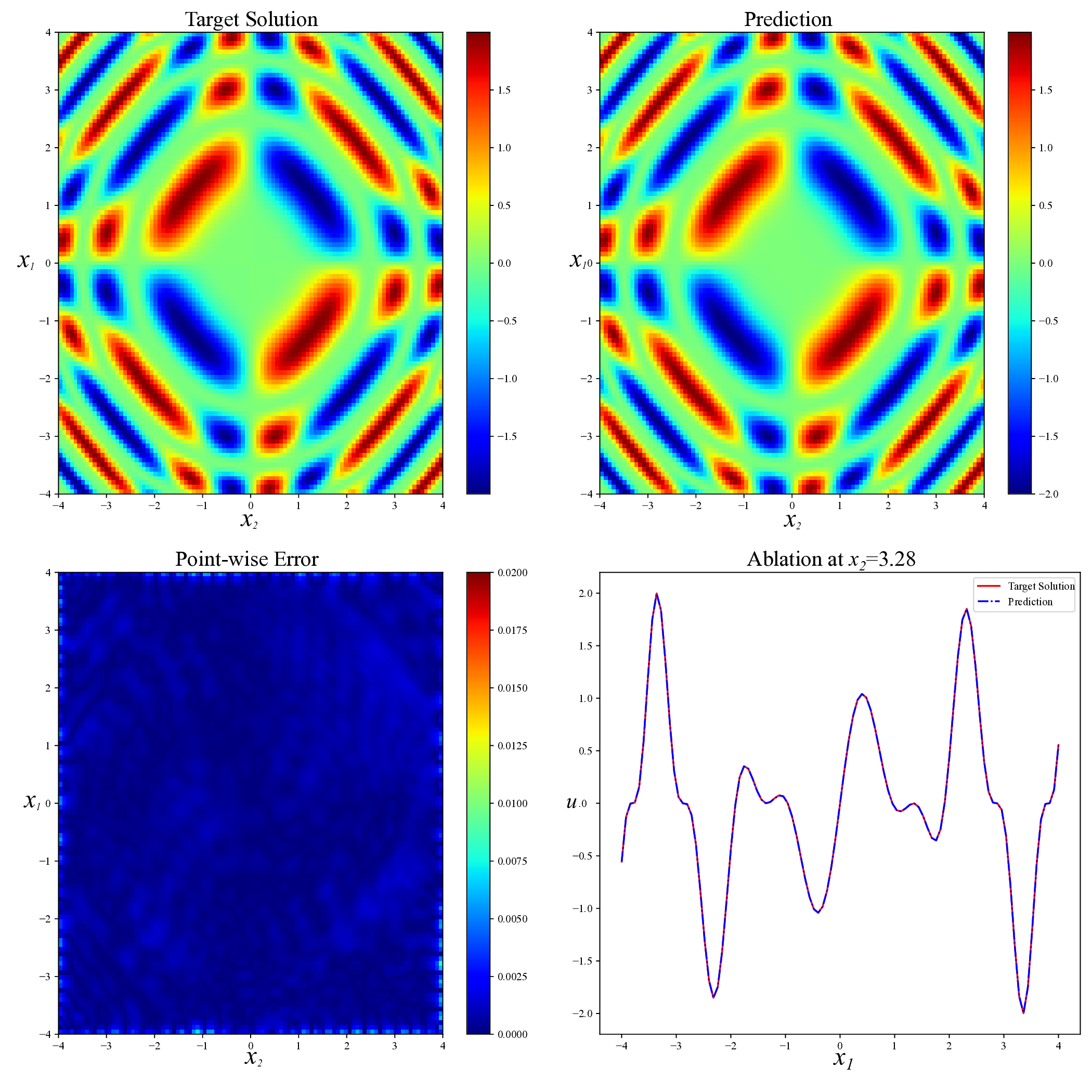
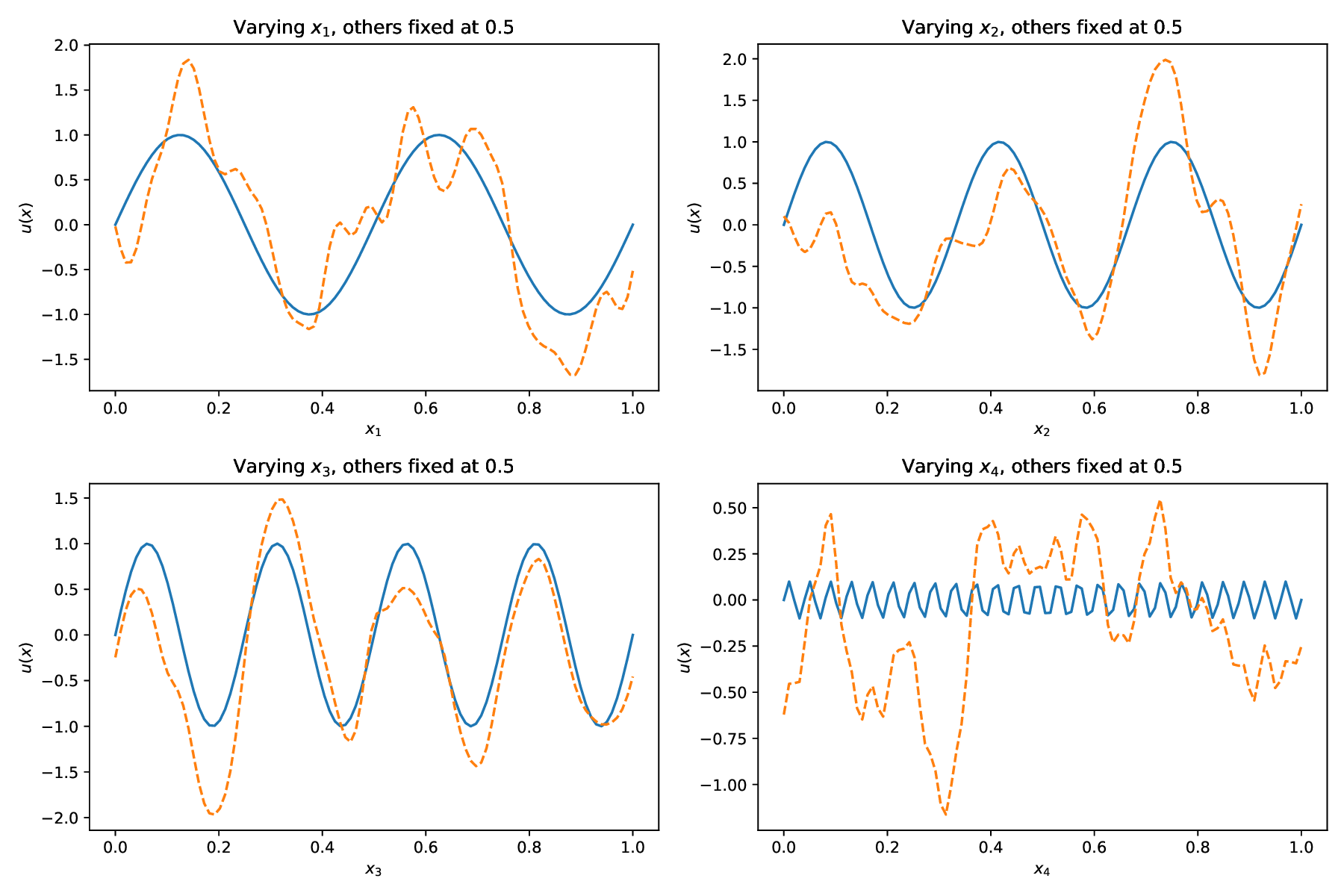
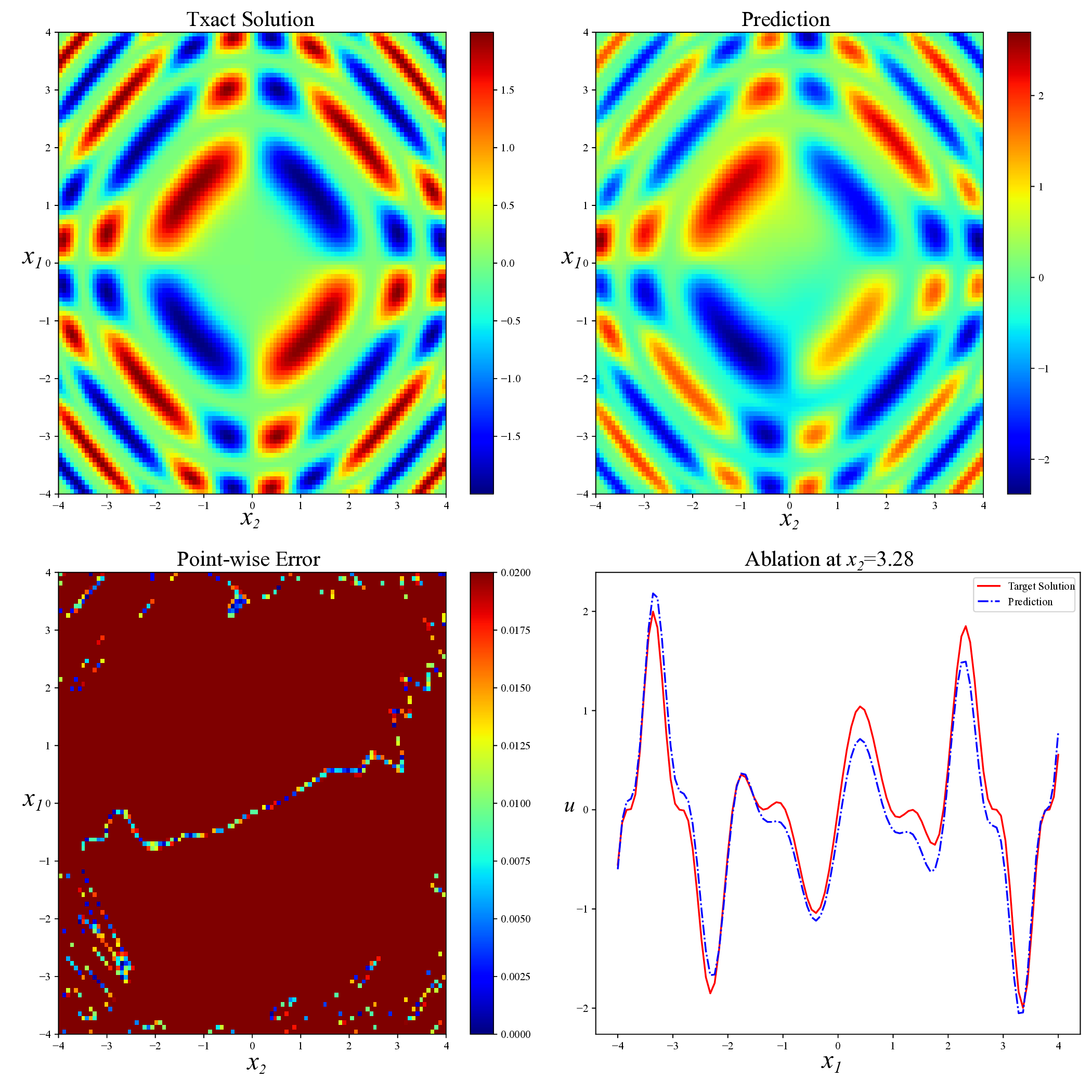
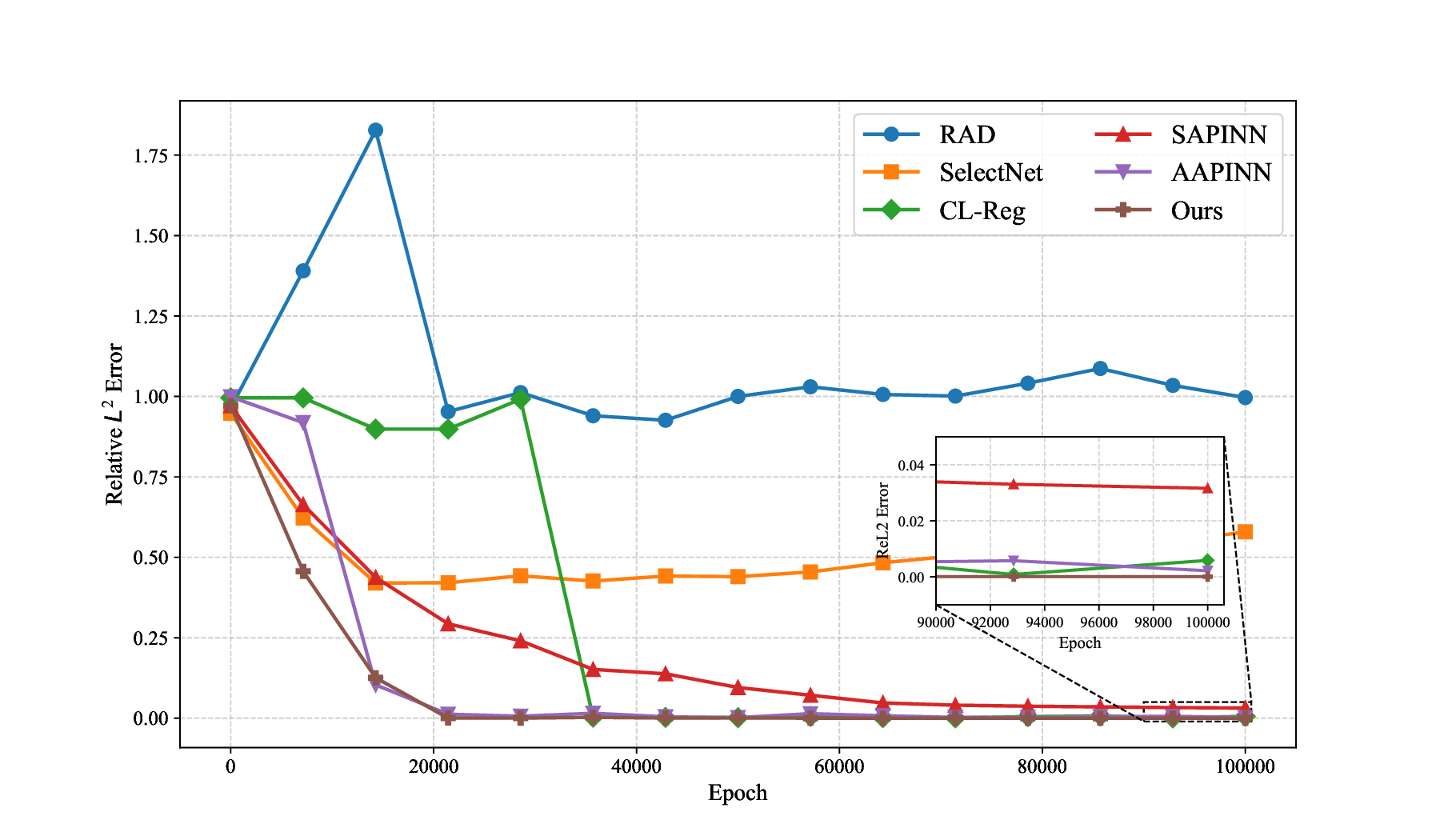
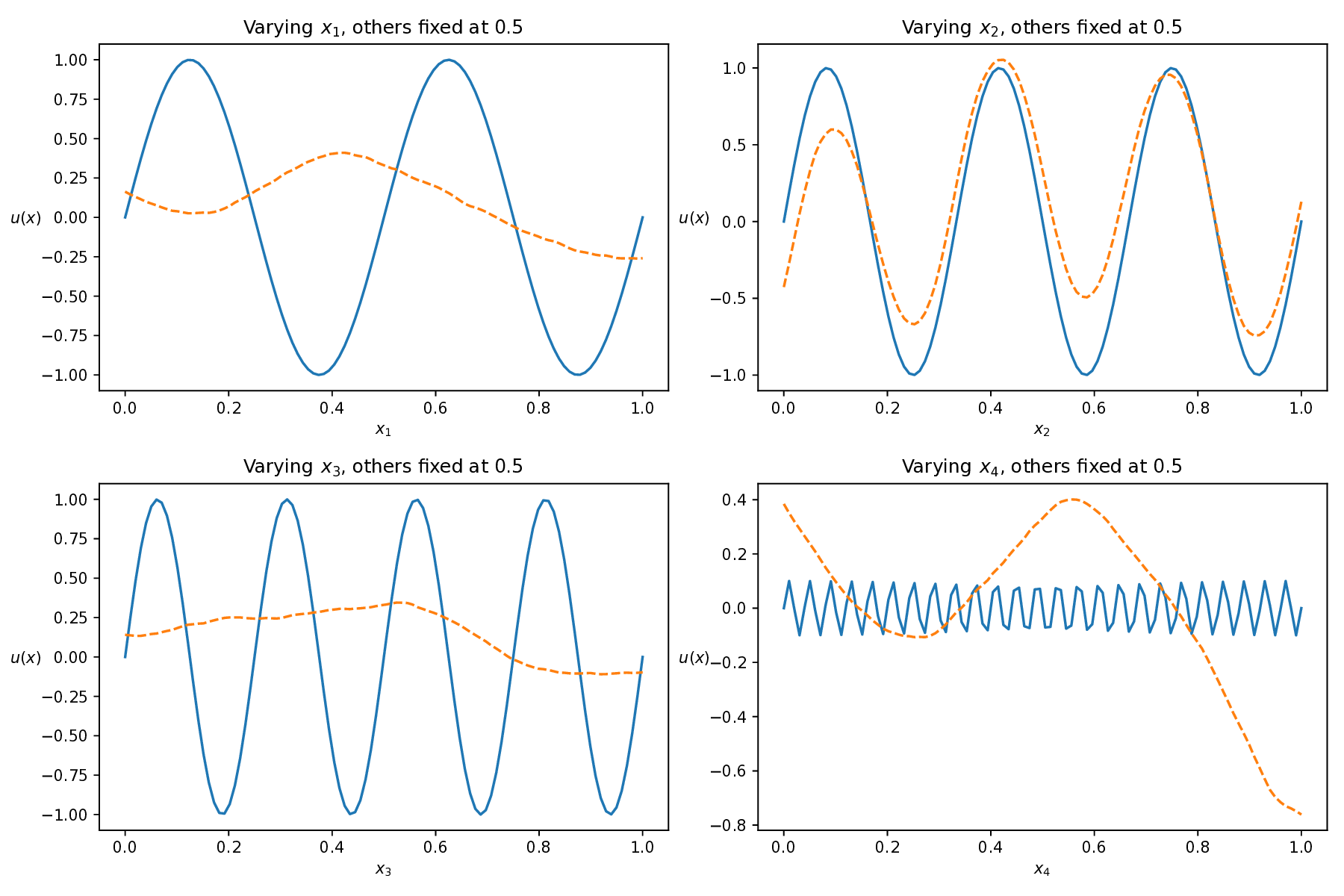
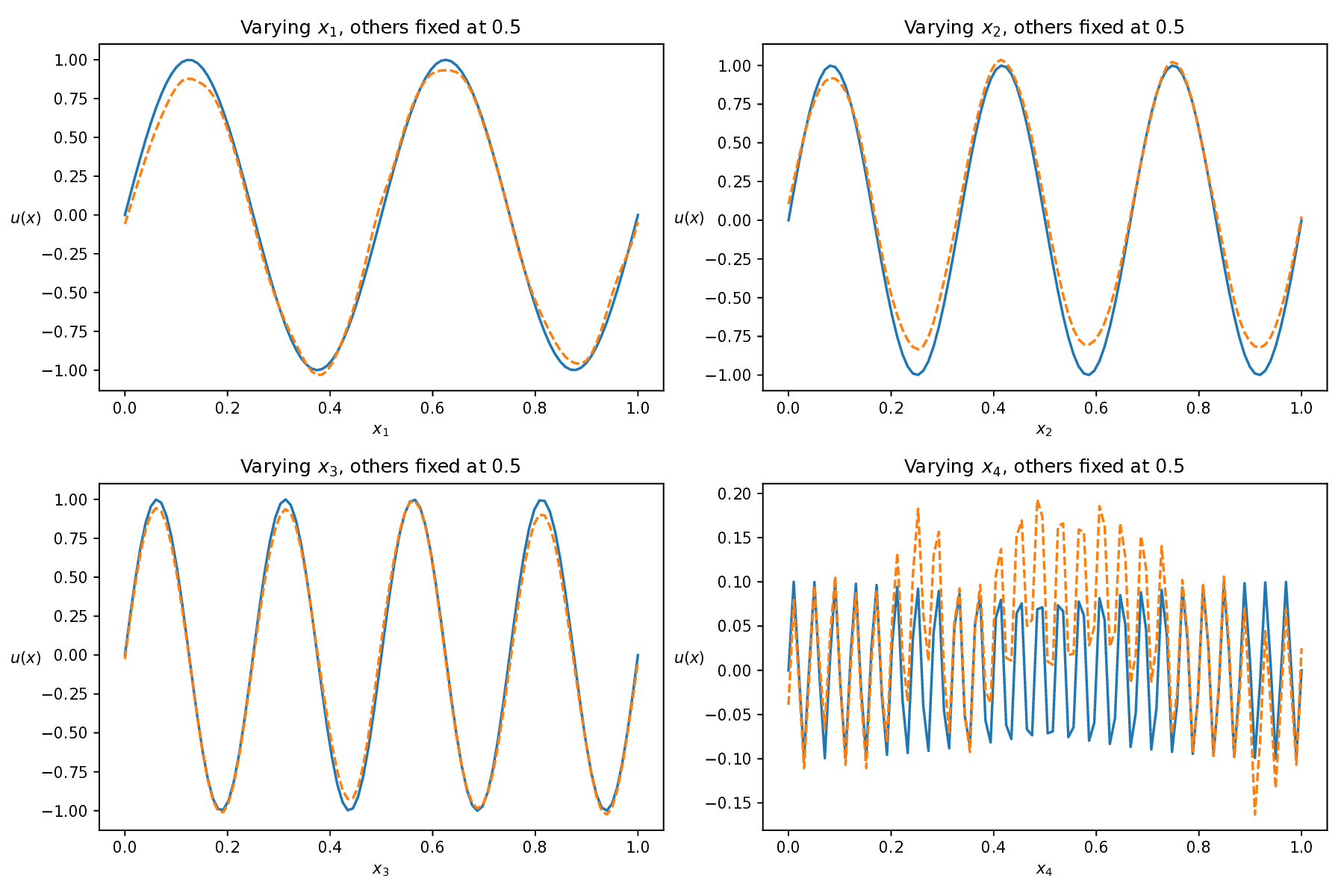
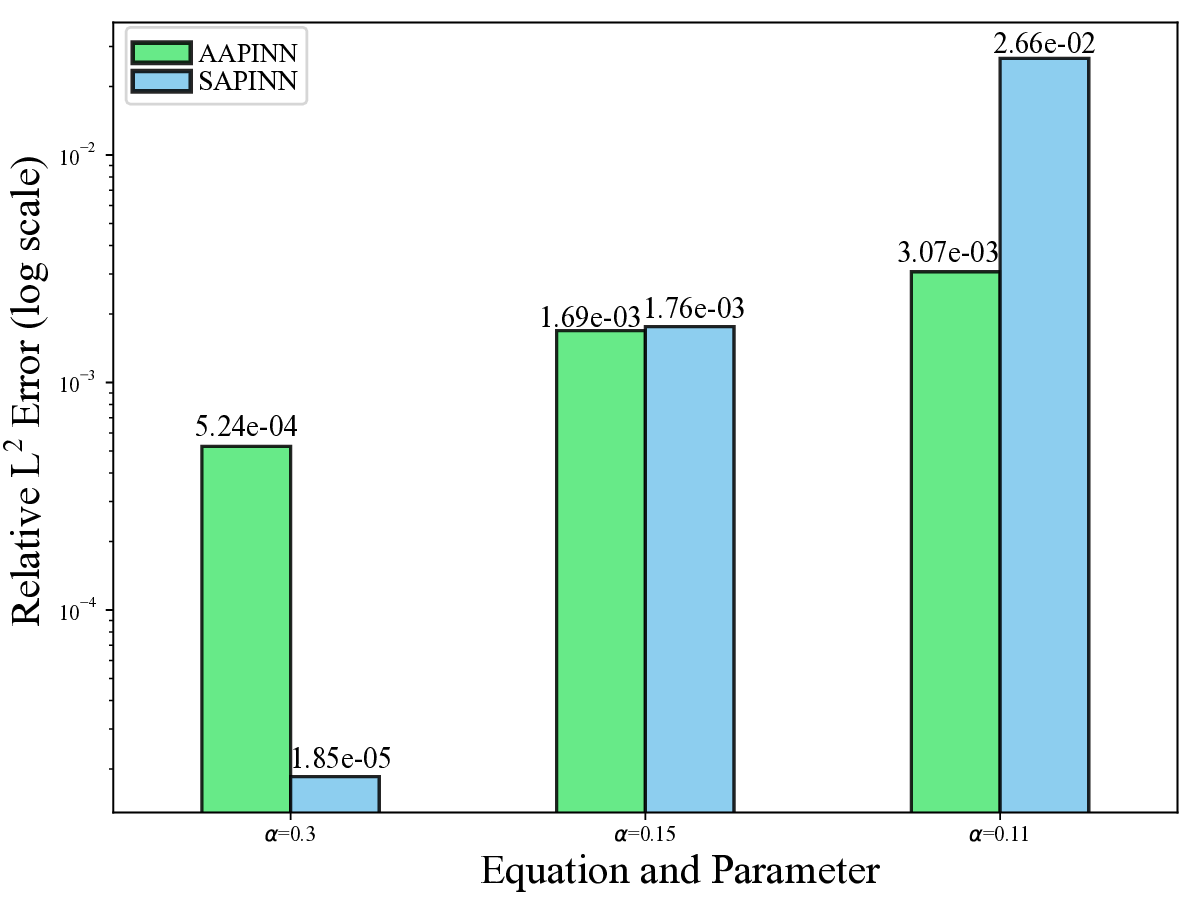
While both training strategies have achieved empirical success in enhancing the performance of PINNs, their relative merits and inherent trade-offs for solving PDEs remain unclear due to the lack of systematic comparative analysis. To bridge this gap, this study first conducts a comparison of these two types of training approaches based on a toy example. Our experiments reveal that the easy-prioritization method tends to emphasize the global structure of the solution -capturing smooth, low-frequency components that dominate the overall behavior of the PDE across the entire domain [36]. In contrast, hard-prioritization strategies are more inclined to focus on localized regions with higher complexity, such as areas with sharp gradients, singularities, or rapidly varying solution features, which are often more difficult to learn. Another important observation is that there is no consistent winner between the two strategies. In some cases, the hard sample prioritization method yields better results, whereas in others, the easy sample prioritization strategy is more effective. Notably, even for the same PDE, variations in the equation coefficients can shift the advantage between the two strategies. These findings suggest that real-world PDEs, which are often complex, may not be well-suited to a one-size-fits-all training strategy.
To address this challenge, we propose a hybrid training framework that combines the strengths of both easy and hard sample prioritization. Specifically, the proposed method alternates between two training phases, each guided by a distinct optimization objective. The first phase adopts a hard prioritization strategy, employing a min-max framework to optimize a weighted PINN loss function. The second phase swit
This content is AI-processed based on open access ArXiv data.