Score-based diffusion models currently constitute the state of the art in continuous generative modeling. These methods are typically formulated via overdamped or underdamped Ornstein--Uhlenbeck-type stochastic differential equations, in which sampling is driven by a combination of deterministic drift and Brownian diffusion, resulting in continuous particle trajectories in the ambient space. While such dynamics enjoy exponential convergence guarantees for strongly log-concave target distributions, it is well known that their mixing rates deteriorate exponentially in the presence of nonconvex or multimodal landscapes, such as double-well potentials. Since many practical generative modeling tasks involve highly non-log-concave target distributions, considerable recent effort has been devoted to developing sampling schemes that improve exploration beyond classical diffusion dynamics.
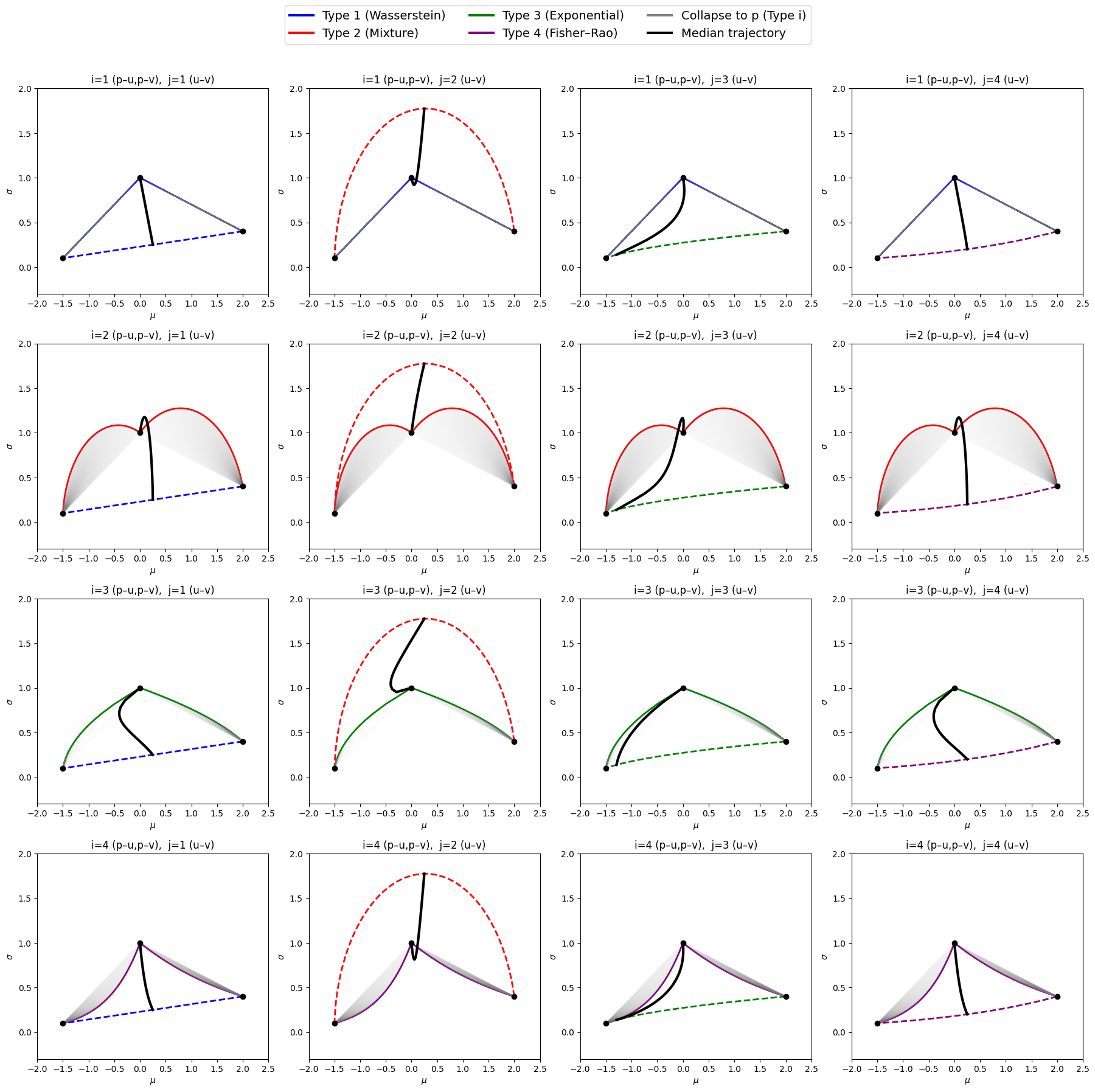
A promising line of work leverages tools from information geometry to augment diffusion-based samplers with controlled mass reweighting mechanisms. This perspective leads naturally to Wasserstein--Fisher--Rao (WFR) geometries, which couple transport in the sample space with vertical (reaction) dynamics on the space of probability measures. In this work, we formulate such reweighting mechanisms through the introduction of explicit correction terms and show how they can be implemented via weighted stochastic differential equations using the Feynman--Kac representation. Our study provides a preliminary but rigorous investigation of WFR-based sampling dynamics, and aims to clarify their geometric and operator-theoretic structure as a foundation for future theoretical and algorithmic developments.
Modern score-based diffusion models can be viewed as learning (or approximating) the time-reversed dynamics of a forward noising diffusion, so that generation reduces to sampling by simulating a stochastic process (or its probability-flow ODE counterpart); see, e.g., [38]. This "sampling-first" viewpoint makes the overall quality-compute tradeoff hinge on a classical question in stochastic analysis and MCMC: how fast does a diffusion (and its discretization) converge to its target distribution?
When the target density has the form π(dx) ∝ e -V (x) dx with V smooth and (strongly) convex, the associated Langevin dynamics enjoys quantitative convergence rates to equilibrium. At the continuous-time level, a standard route is via functional inequalities (Poincaré/log-Sobolev) and curvature-type criteria, notably the Bakry-Émery framework, which yields exponential decay of suitable divergences under strong convexity/positive curvature assumptions [4,21,23]. At the algorithmic level, non-asymptotic guarantees for discretizations such as unadjusted Langevin Monte Carlo (ULA/LMC) are by now well developed in the smooth logconcave setting, including explicit dimension/accuracy scaling and robustness to gradient error [11,12,17,18]. Moreover, kinetic (underdamped) Langevin diffusions can yield improved complexity bounds over overdamped LMC under comparable regularity/convexity conditions, and several analyses establish accelerated rates in Wasserstein/KL-type metrics [8,13,34].
The picture changes drastically once V (•) is nonconvex and the target is multi-modal (e.g., double-well potentials or mixtures), which is the typical regime for many scientific and modern generative-modeling tasks. In such landscapes, Langevin-type dynamics may exhibit metastability: trajectories spend exponentially long times trapped near one mode before crossing an energy barrier to another. Sharp asymptotics for transition times are classically captured by Kramers/Eyring-Kramers laws and their refinements, which quantify the barrier-dominated nature of mixing in the lownoise (or low-temperature) regime [19,6,25]. This explains, at a mechanism level, why “exponential convergence” in the log-concave case does not translate to effective sampling performance in multiwell settings: in the presence of energy barriers, the spectral gap and log-Sobolev constant of the associated Langevin generator typically decay exponentially in the barrier height, implying exponentially large global mixing times [21,20,5,29].
A substantial modern literature addresses this slow-mixing obstruction by changing either (i) the dynamics (e.g., kinetic/nonreversible variants, couplings showing contraction under weaker conditions) [15], or (ii) the effective landscape (e.g., tempering/replica-exchange ideas designed to move between modes). As one representative example, simulated tempering combined with Langevin updates yields provable improvements for certain mixtures of log-concave components [24]. These developments motivate the central theme of this paper: to systematically enrich the sampling process by incorporating geometric degrees of freedom (e.g., reweighting/Fisher-Rao components in Wasserstein-Fisher-Rao-type formulations), aiming to mitigate metastability while preserving a principled continuum description compatible with diffusion-model methodology.
Brownian Motion is Not Enough to explore the space! A central modeling choice in diffusion-based sampling (and in score-based generative modeling via SDEs) is the driving noise. In the classical overdamped Langevin diffusion,
the Brownian term Bt induces increments with typical size ∥Bt -Bs∥ ≍ |t-s| 1/2 . This 1/2-scaling is intimately tied to Gaussianity, finite quadratic variation, and the semimartingale structure that underpins Itô calculus and the classical Fokker-Planck PDE. However, in multimodal landscapes (e.g. double-well potentials), Browniandriven dynamics can become metastable: barrier crossing is dominated by rare fluctuations whose timescale is exponentially large in the barrier height (cf. Kramers/Eyring-Kramers theory and related metastability results) [19,7,26]. This motivates enriching the arXiv:2512.17878v1 [cs.LG] 19 Dec 2025
noise model to enable more effective exploration and faster intermode transport.
A common informal heuristic is: Brownian paths explore locally (diffusively), whereas heavy-tailed or jump-driven paths can occasionally relocate nonlocally, potentially reducing barrier-induced trapping. Two canonical generalizations of Brownian motion illustrate the tradeoff between (i) scaling properties that can enhance exploration and (ii) the availability of Itô calculus, and hence writing down the forward/backward equations:
(A) Fractional Brownian motion (fBm): Fractional Brownian motion (B H t ) t≥0 with Hurst index H ∈ (0, 1) is a centered Gaussian process with covariance
and self-similarity [31]. For H ̸ = 1 2 , fBm is not a semimartingale, so the standard Itô stochastic
This content is AI-processed based on open access ArXiv data.