The stationary focus of the Kiepert parabola over a special Poncelet triangle family

The Kiepert in-parabola is tangent to the three sides of a triangle [13]. We show that its focus -called X 110 in [9] -remains stationary over a family of circle-inscribed Poncelet triangles which contain an equilateral triangle.

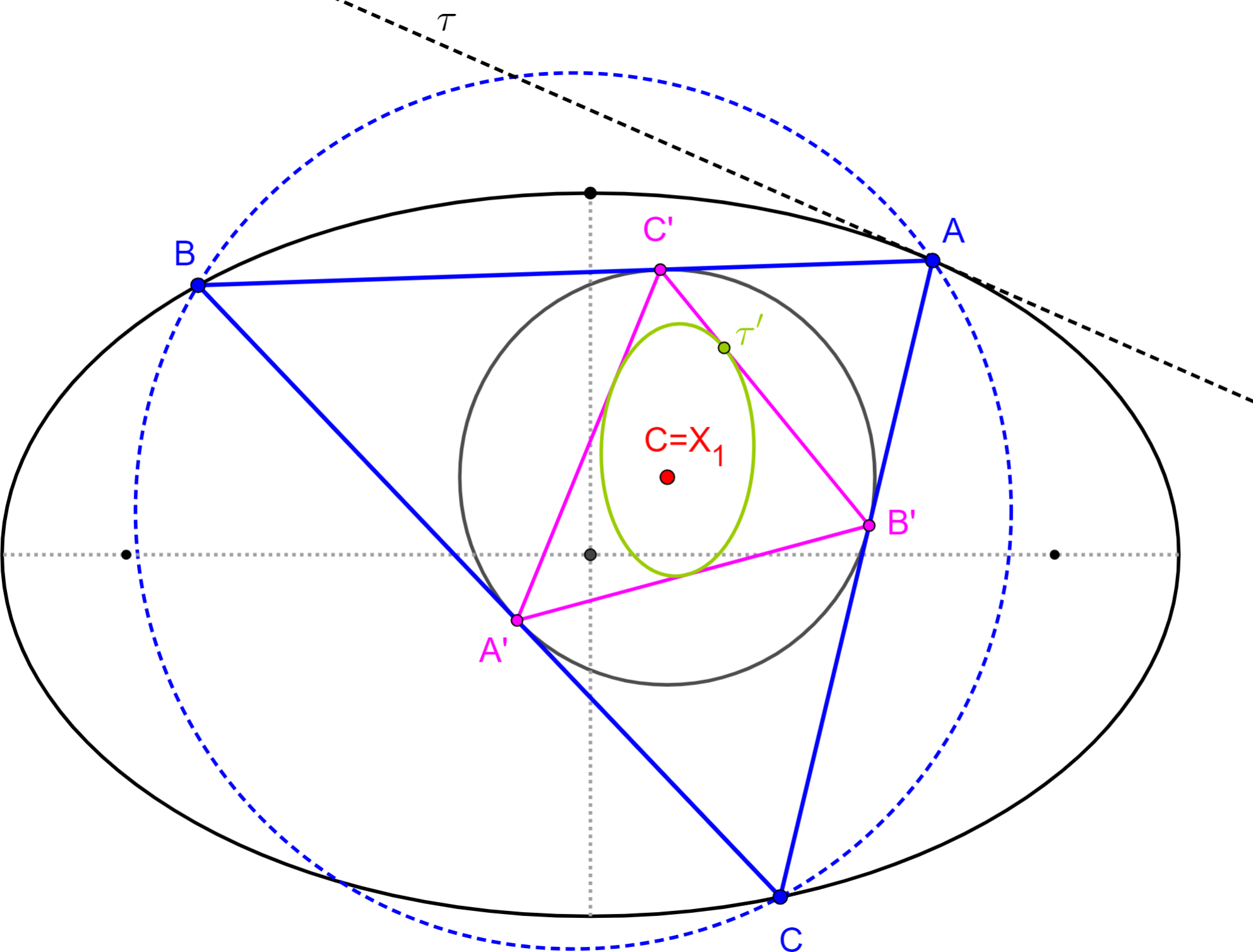
In a companion article we study degeneracies of a closely-related family, namely, Poncelet triangles circumscribing their incircle, also containing one equilateral member [6,Sec.4].

As shown in Figure 1, the two families mentioned are polar images of each other with respect to their outer conics [2].

A key behavior described here involves the stationarity of the focus X 110 (using [9] terminology) of the Kiepert Parabola, an well-studied inconic to a triangle, see [13]. This corresponds to the stationarity of Feuerbach’s point of Poncelet triangles about the incircle, described in [6], but also proved here. 1.1. Computational proofs. Most phenomena visited have been discovered via simulation. In some figure captions we include links to videos as well as interactive animations with a custom-built tool [3].

Poncelet’s porism is a 1d family of n-gons with vertices on a first conic E and with sides tangent to a second conic E c (also called the ‘caustic’). For such a porism to exist, E and E c must be positioned in R 2 so as to satisfy ‘Cayley’s condition’ [4]. While the porism is projectively invariant -a conic pair is the projective image of two circles where the ‘Poncelet map’ is linearized, -we have found that Poncelet porisms of triangles (n = 3) are a wellspring of interesting Euclidean phenomena involving the dynamical geometry of classical objects associated with the triangle (centers, circles, lines/axes, etc.).

An emblematic case is when when E, E c are confocal. In such a porism, -also known as the elliptic billiard -the perimeter is conserved [12], and the loci of all four ‘Greek centers’ of the triangle -incenter, barycenter, circumcenter, orthocenter -sweep ellipses [5,8,11]. Furthermore, the family conserves the ratio of inradius-tocircumradius (equivalently, the sum of internal angle cosines) [7], a result which was extended to all n [1].

We study the case of circular E and E c is a nested ellipse. This is the affine image of a Poncelet triangle family inscribed in some conic and circumscribing a circular E c , and can therefore be described via the symmetric parametrization of [6,Sec.2]. In particular, we are interested in the circle-inscribed family which contains an equilateral member.

Observation 1. A family of Poncelet triangles inscribed in a circle E contains an equilateral triangle if and only if its polar image with respect to E also contains one.

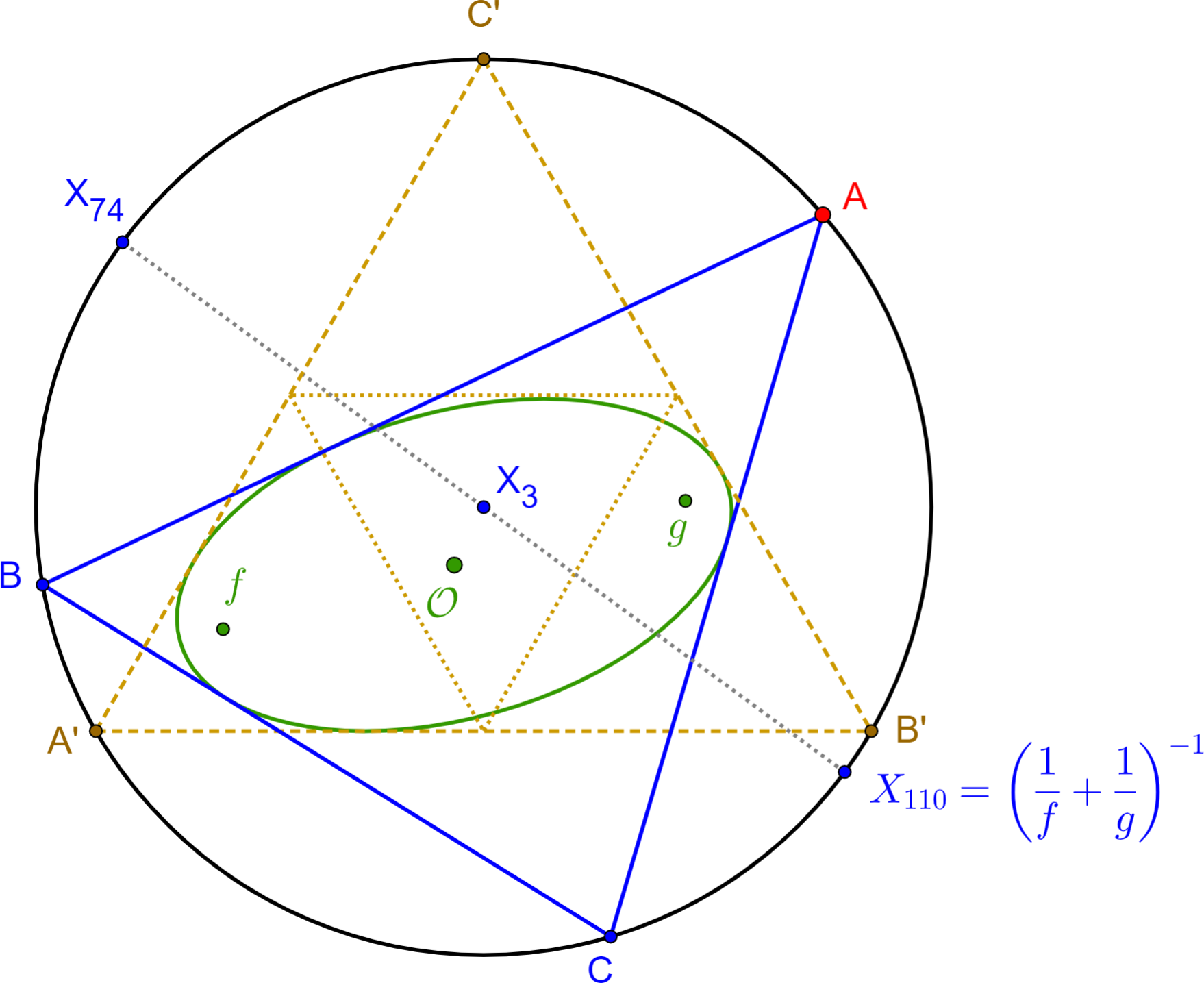
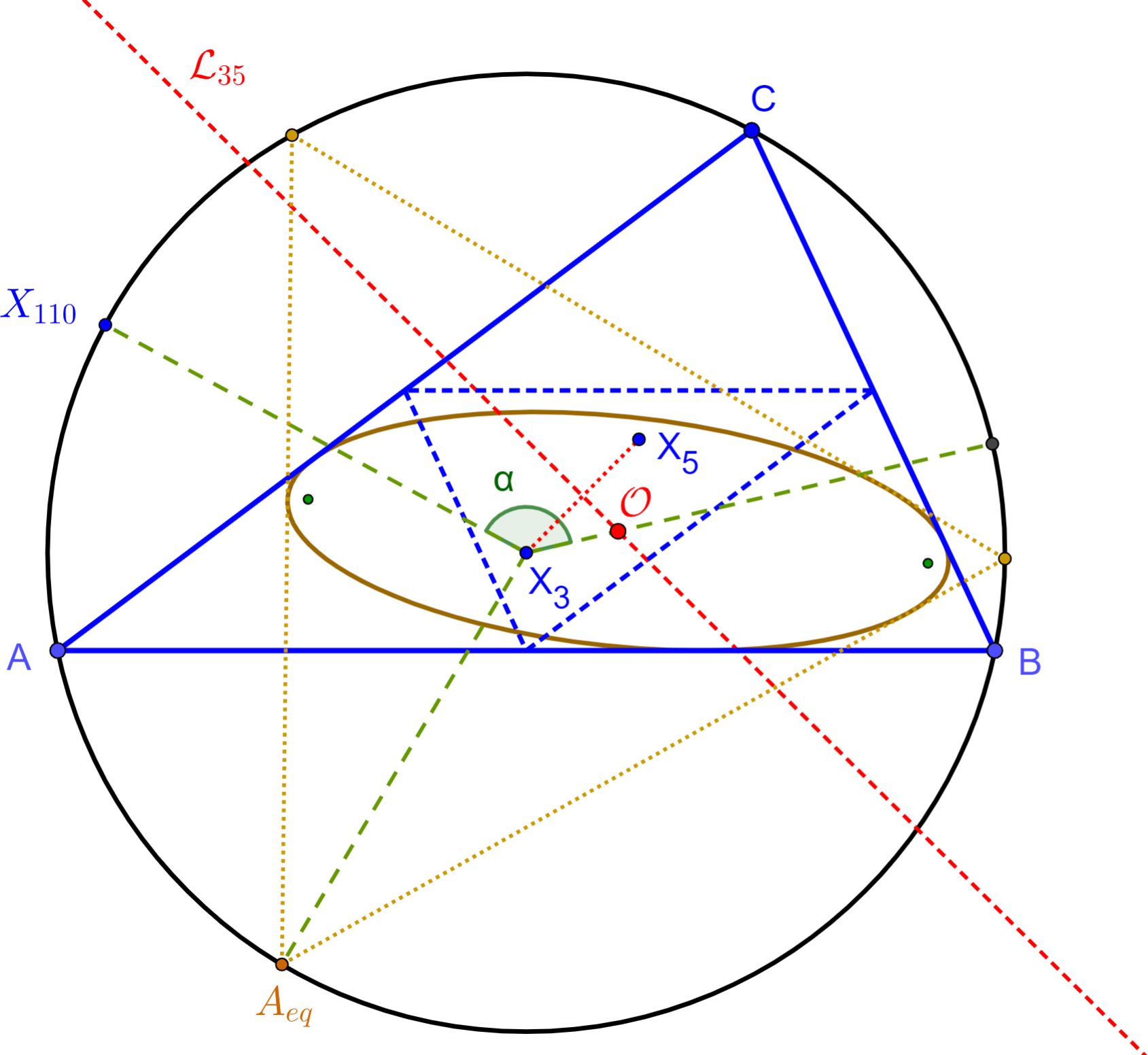
Let E c be an inconic with foci f, g ∈ C, such that there is a Poncelet family of triangles inscribed in the unit circle T and circumscribing E c . Referring to Figure 2

so 1/f + 1/g is on the unit circle T, as desired.

By definition, f + g + λ o f g = 0. Moreover,

Hence, letting z 1 , z 2 , z 3 take the values of the 3 roots of ζ 3 = λ o , we see that these 3 roots form an equilateral triangle that satisfies the equations of the symmetric parameterization of [6, Sec.2]. Thus, this equilateral triangle is part of the Poncelet family, as desired. □

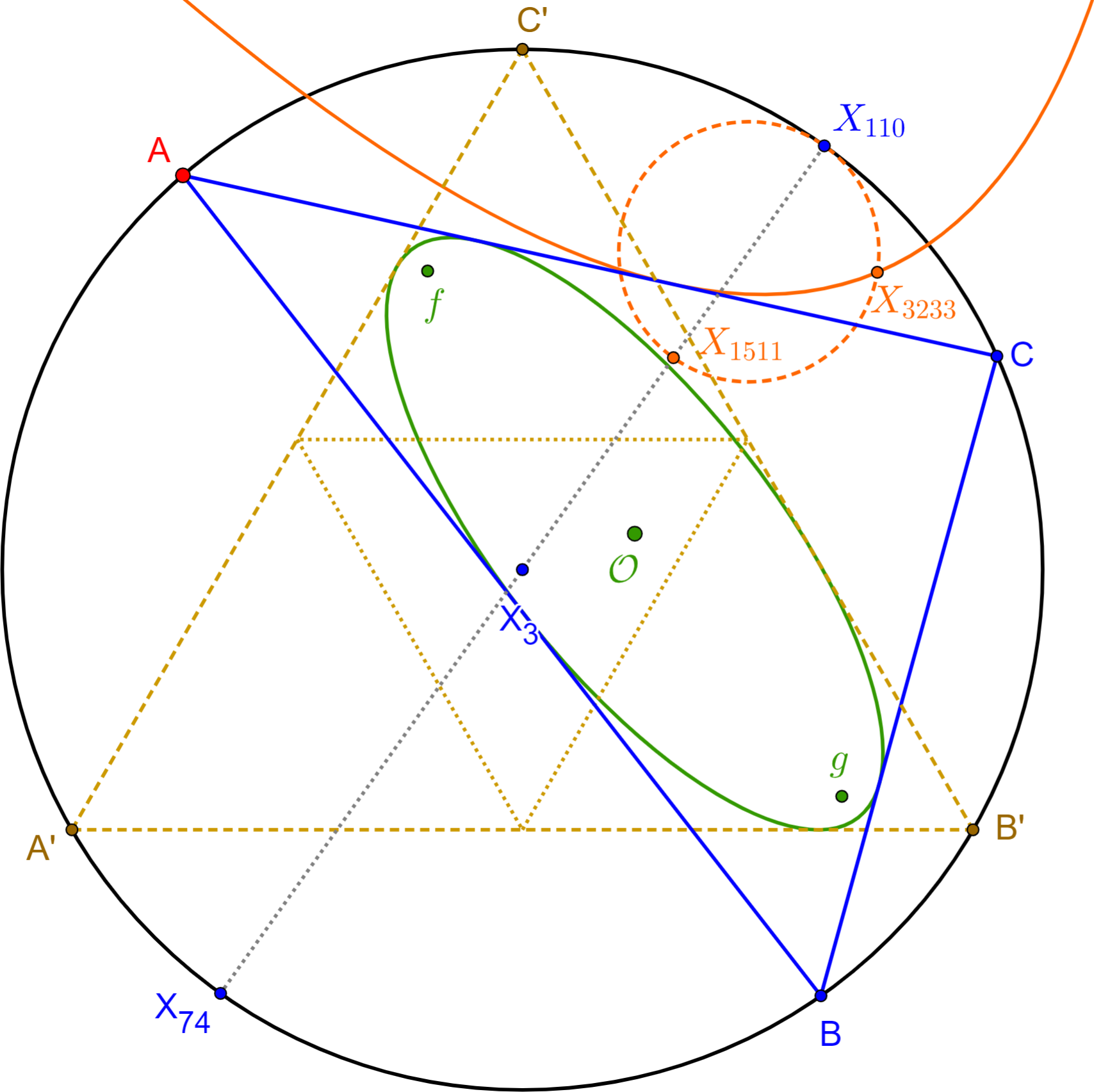
Referring to Figure 3:

The Kiepert parabola of a triangle is tangent to the three sides of a triangle. Its focus is X 110 , always on the circumcircle, and its directrix is the Euler line X 2 X 3 [13]. . On [9], (i) the midpoint of X 3 and X 110 is called X 1511 , and (ii) X 3233 is the vertex of the Kiepert inparabola [10]. Referring to Figure 3:

o , X 3233 sweeps a circle with diameter X 110 X 1511 , i.e., 1/2.

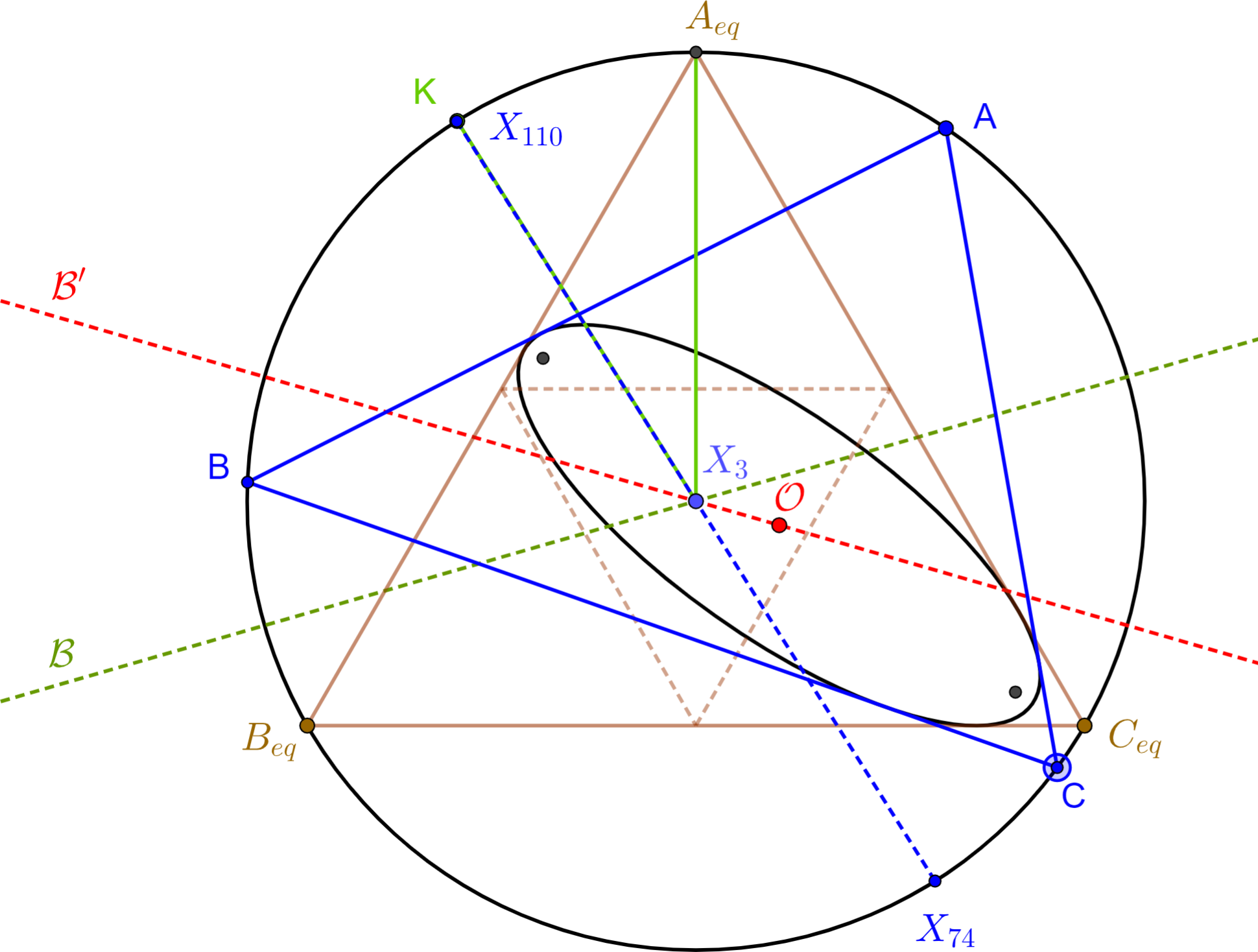
Referring to Figure 4, let A eq be one of the vertices of the equilateral in T * o . Let K be a chosen point on the circumcircle. Let B represent the external bisector of ∠KX 3 A eq . It can be shown:

o , X 110 will be stationary at K for any O on the reflection of B about X 3 A eq .

Let T ′ o be the family of tangential triangles to T o , i.e., whose sides are tangent to the circumcircle at the vertices of T o [13,Tangential Triangle]. Clearly, this family circumscribes a circle and will be inscribed in an ellipse E, called above T . Observation 3. E is the polar image of the chosen inconic with respect to the circumcircle.

Corollary 1. Since the tangential of an equilateral is an equilateral, T ′ o will contain an equilateral, and therefore the center of its incircle will be on E eq .

In turn, this leads to a restatement of [6,Prop.15]: Corollary 2. The Feuerbach point X 11 of T ′ o will be stationary. Proof. X 110 of a reference triangle is X 11 of its tangential. Conversely, X 11 of the reference is X 110 of the contact triangle.

□

On [9], X 65 is the orthocenter X 4 of the contact triangle.

Corollary 3. The locus of X 65 of the tangential family is a circle.

Proof. The contact family is Poncelet (sides envelop the polar image of E wrt incircle) and circle-inscribed. X 4 is always homothetic to a 90-degree-rotated version of the inscribing

This content is AI-processed based on open access ArXiv data.