We propose Generalized Primal Averaging (GPA), an extension of Nesterov's method that unifies and generalizes recent averaging-based optimizers like single-worker DiLoCo and Schedule-Free, within a non-distributed setting. While DiLoCo relies on a memory-intensive two-loop structure to periodically aggregate pseudo-gradients using Nesterov momentum, GPA eliminates this complexity by decoupling Nesterov's interpolation constants to enable smooth iterate averaging at every step. Structurally, GPA resembles Schedule-Free but replaces uniform averaging with exponential moving averaging. Empirically, GPA consistently outperforms single-worker DiLoCo and AdamW with reduced memory overhead. GPA achieves speedups of 8.71%, 10.13%, and 9.58% over the AdamW baseline in terms of steps to reach target validation loss for Llama-160M, 1B, and 8B models, respectively. Similarly, on the ImageNet ViT workload, GPA achieves speedups of 7% and 25.5% in the small and large batch settings respectively. Furthermore, we prove that for any base optimizer with $O(\sqrt{T})$ regret, where $T$ is the number of iterations, GPA matches or exceeds the original convergence guarantees depending on the interpolation constants.
As large language models (LLMs) demonstrate increasingly remarkable capabilities at scale (Achiam et al., 2023;Llama Team, 2024;Liu et al., 2024a), the pre-training phase has become one of the most resource intensive stages in the language model training pipeline. This has encouraged the development of training algorithms and optimizers that enhance the efficiency, scalability, and robustness of language model pretraining. One significant area of research is the design of training algorithms for scalable distributed learning. In this area, the DiLoCo algorithm has emerged as the leading practical approach (Douillard et al., 2023;Liu et al., 2024b;Douillard et al., 2025;Charles et al., 2025).
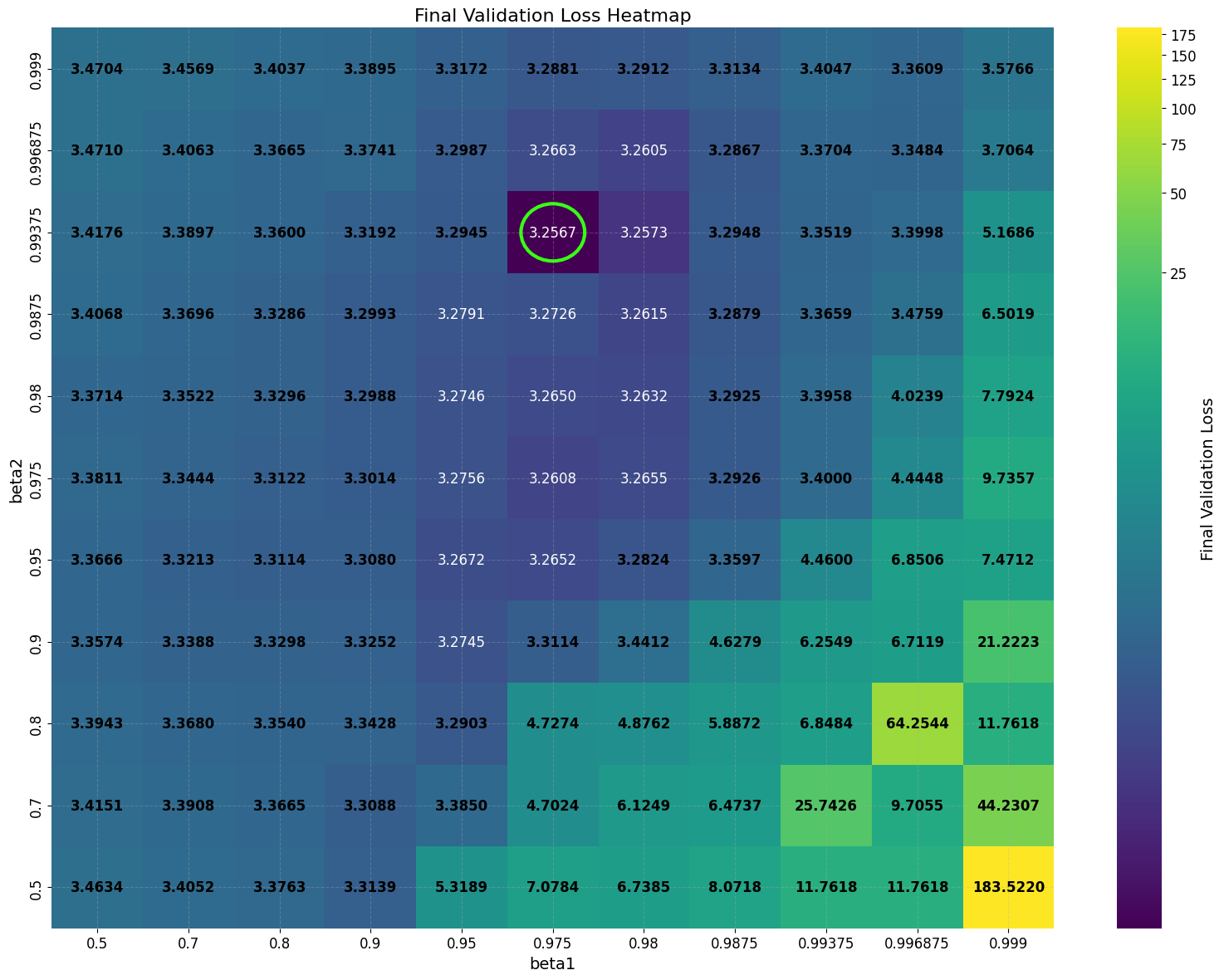
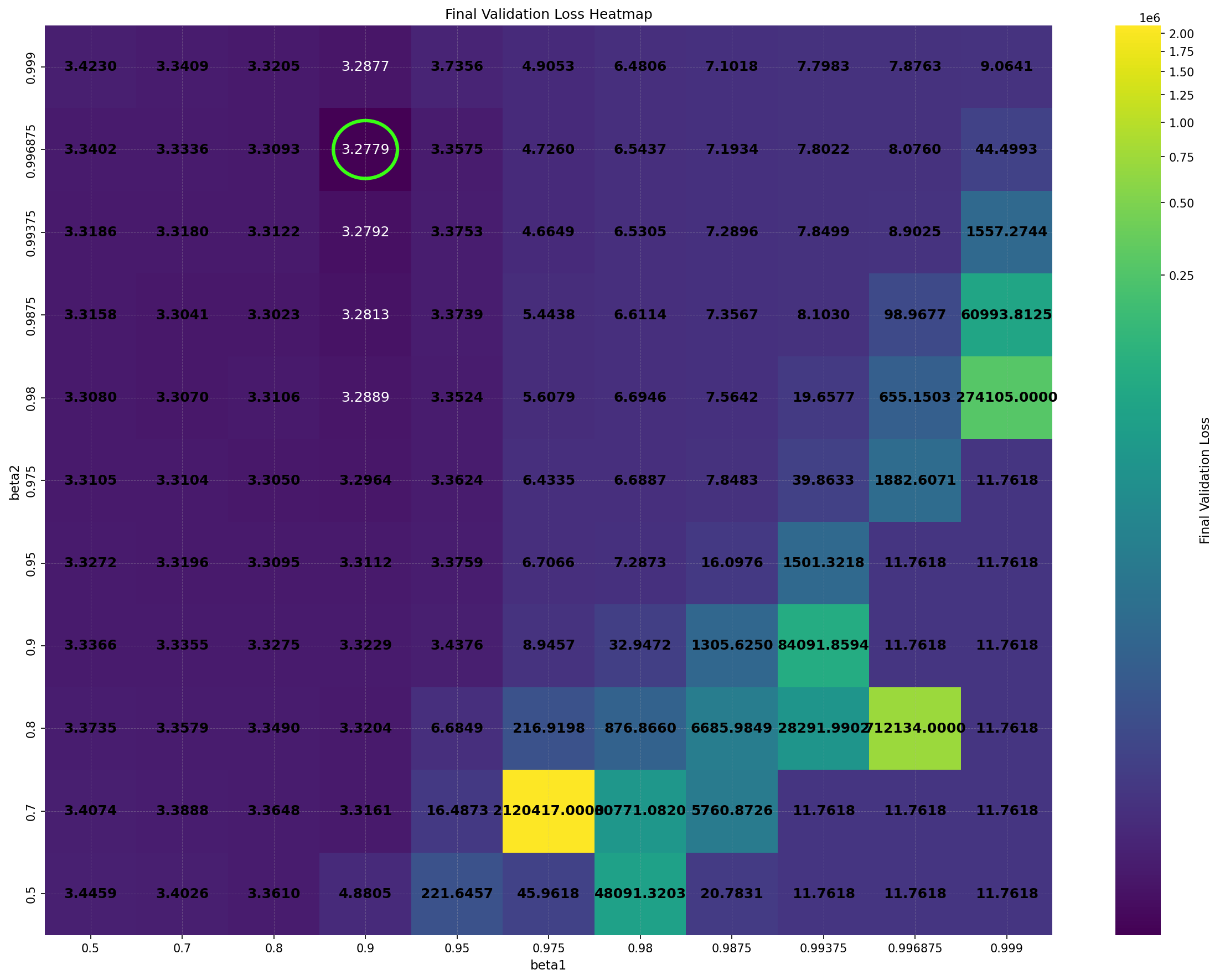
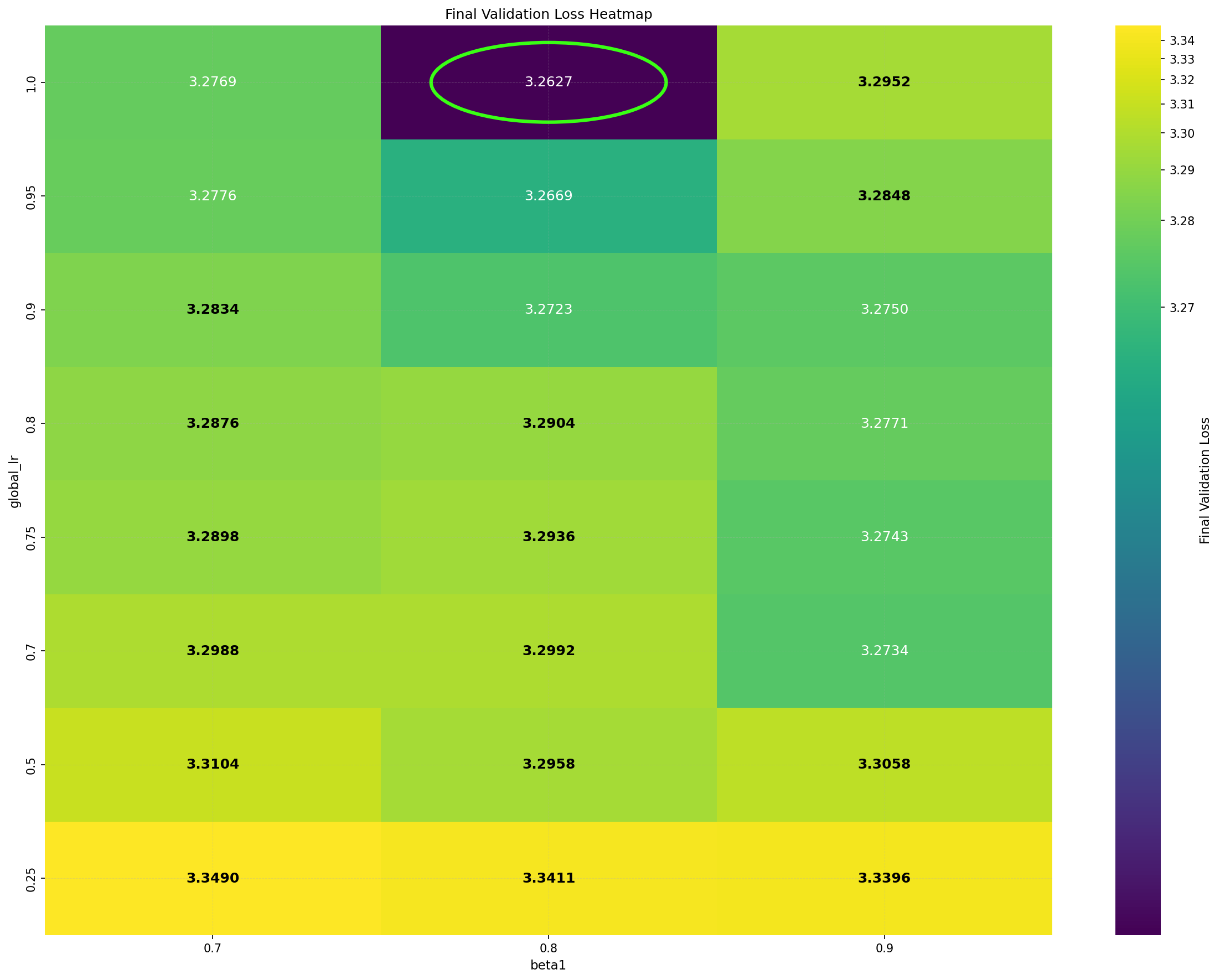
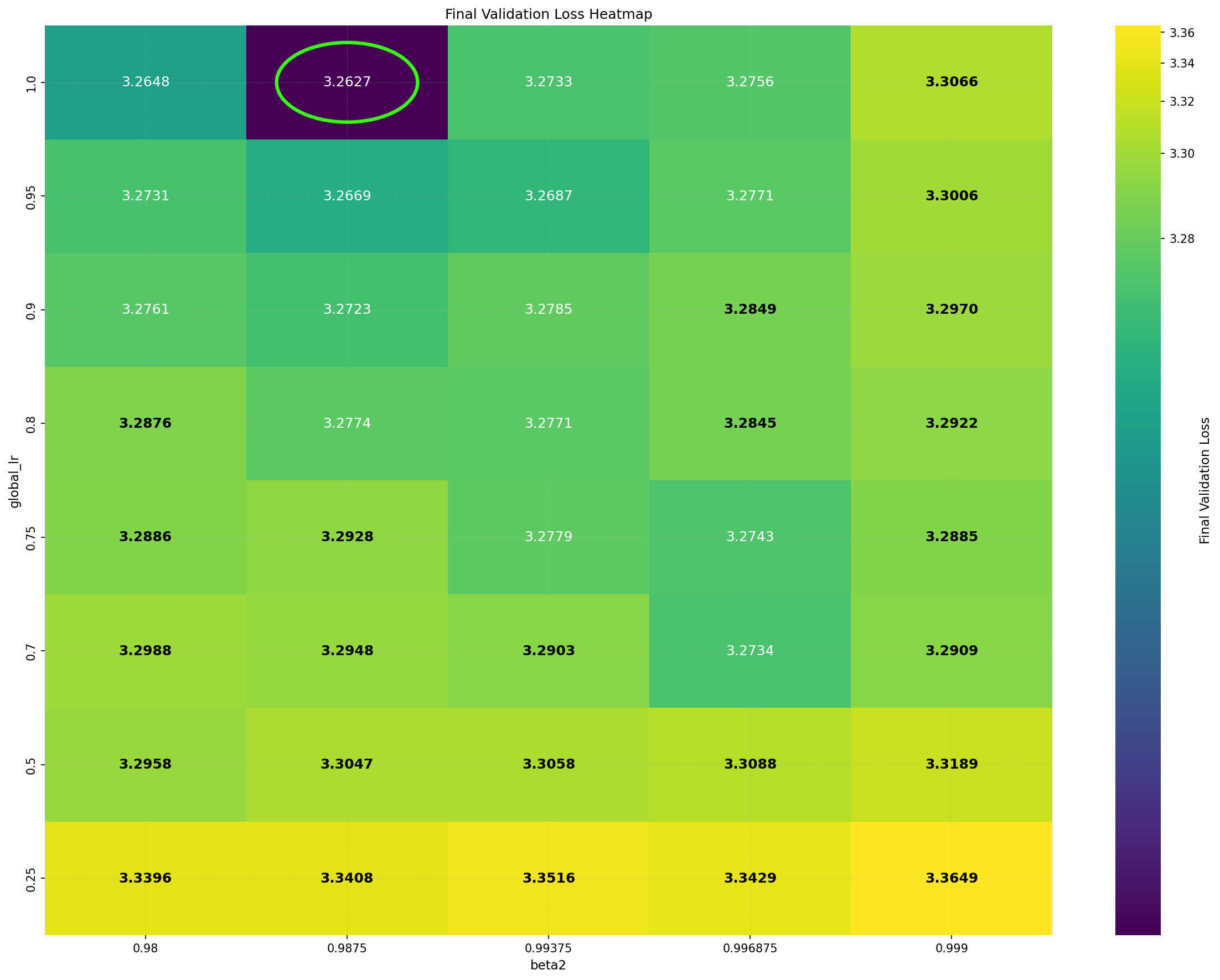
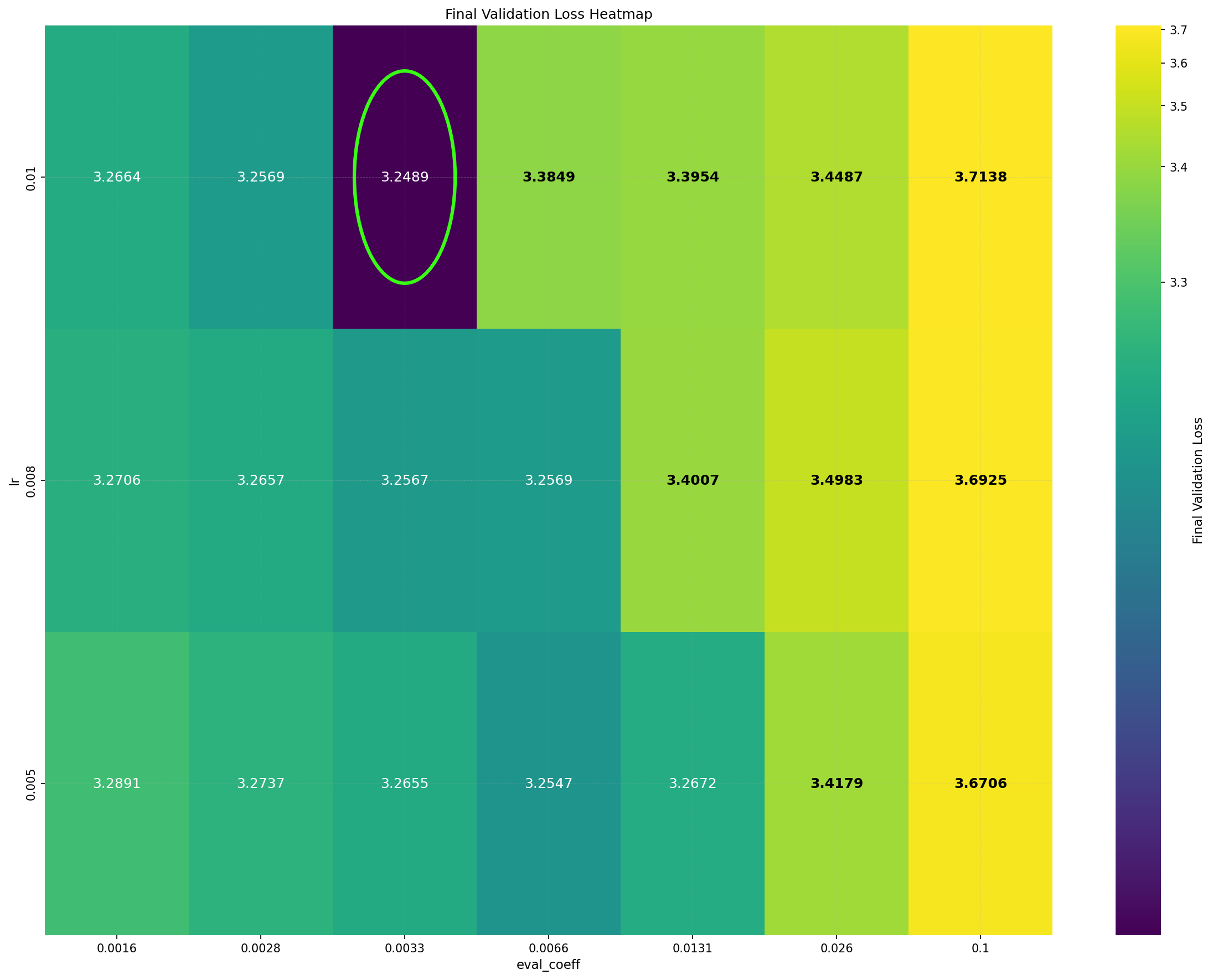
Despite its practical success, the underlying reasons for DiLoCo’s effectiveness remain poorly understood. Importantly, DiLoCo is not limited to distributed training: single-worker DiLoCo outperforms AdamW even in the non-distributed setting. Kallusky et al. (2025) suggest that this is due to its novel combination of the Nesterov optimizer with the Lookahead method (Zhang et al., 2019), called Step-K Nesterov. The method accumulates multiple updates from a base optimizer on an inner set of weights, forming what is called a pseudo-gradient. It then applies Nesterov momentum to the pseudo-gradient to update an outer set of weights, and subsequently resets the inner weights to match the new values of the outer weights. On a 160 million parameter Llama model, single-worker DiLoCo achieves speedups of up to 6.32% in terms of steps to reach the final validation loss by AdamW; see Figure 1b.
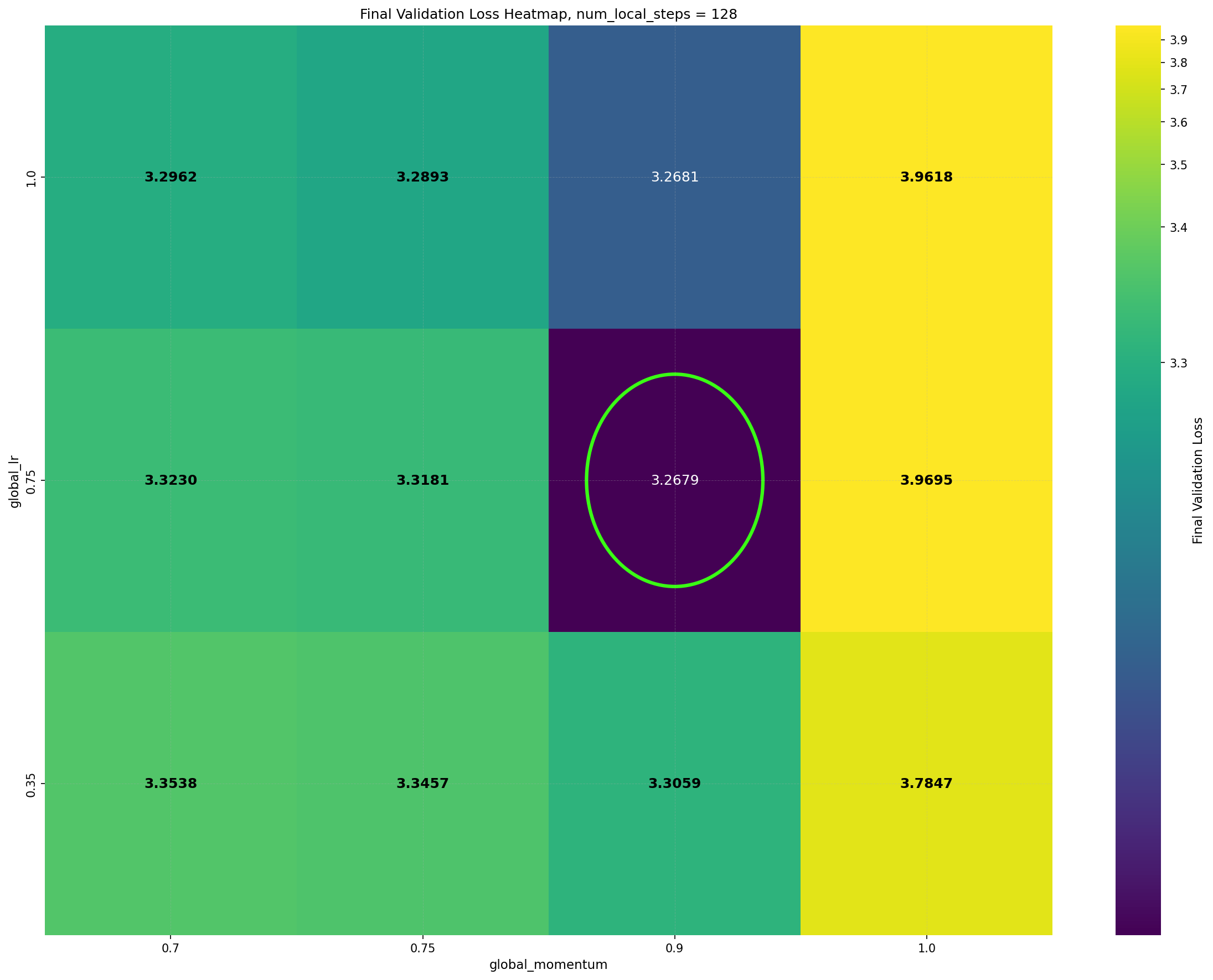
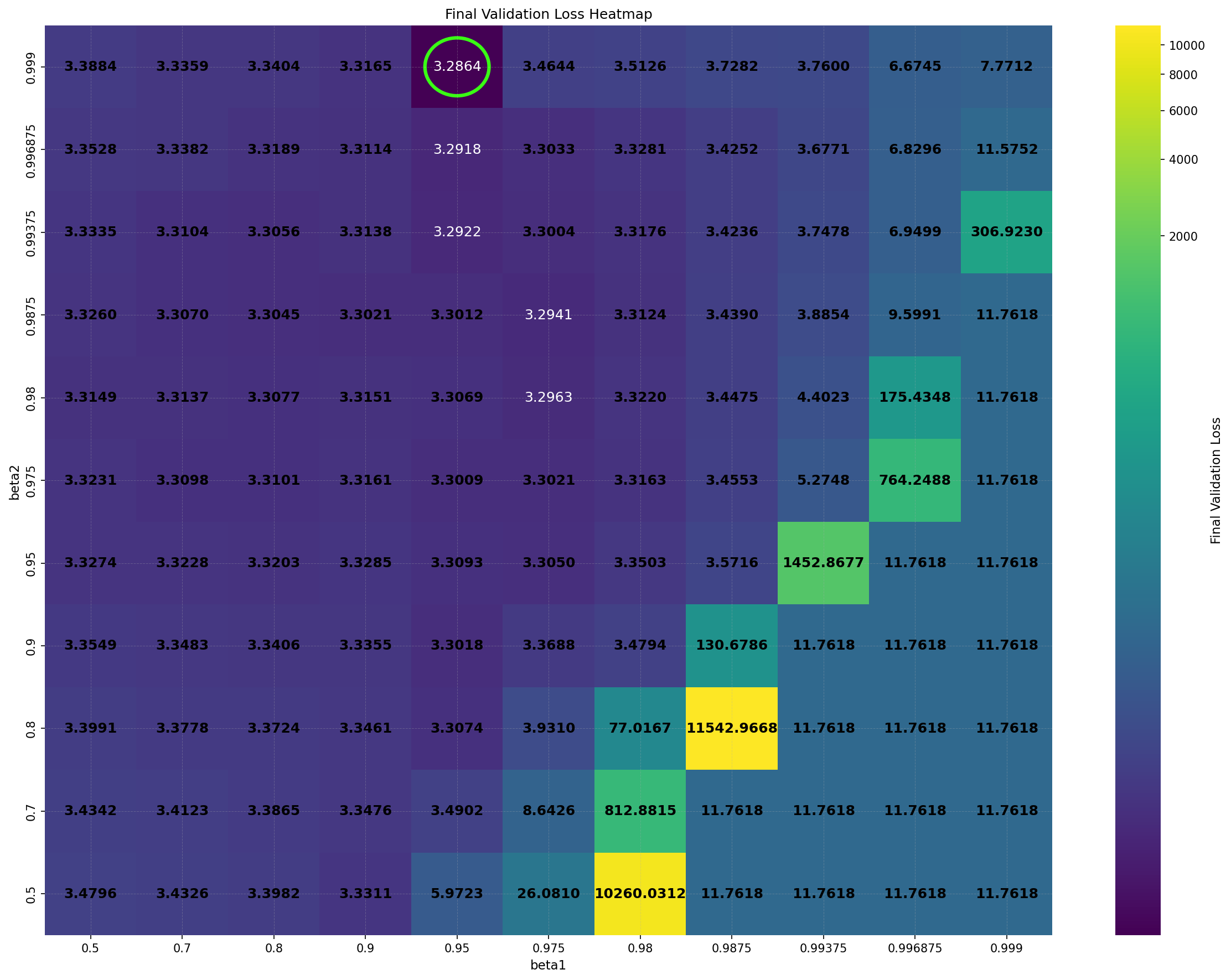
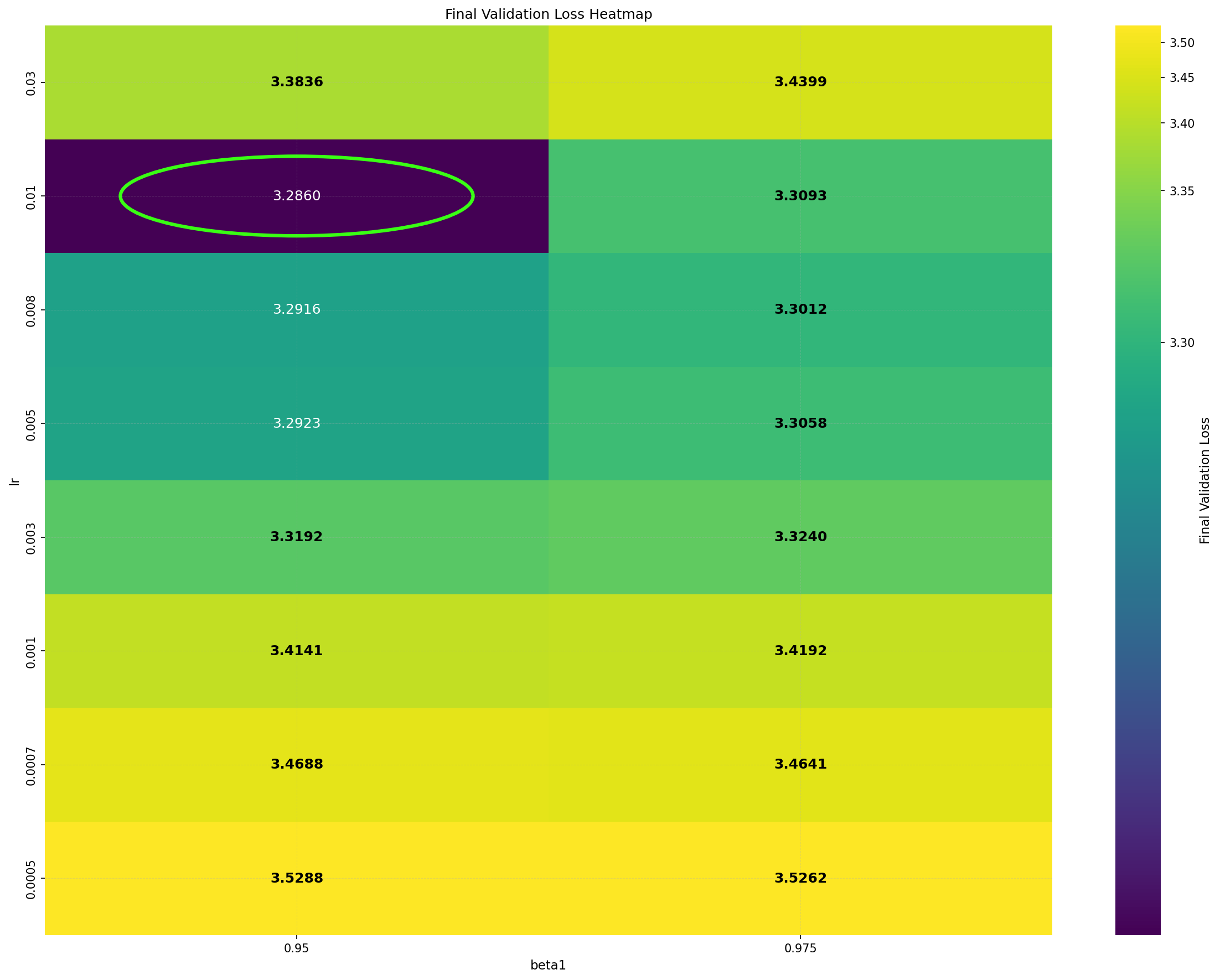
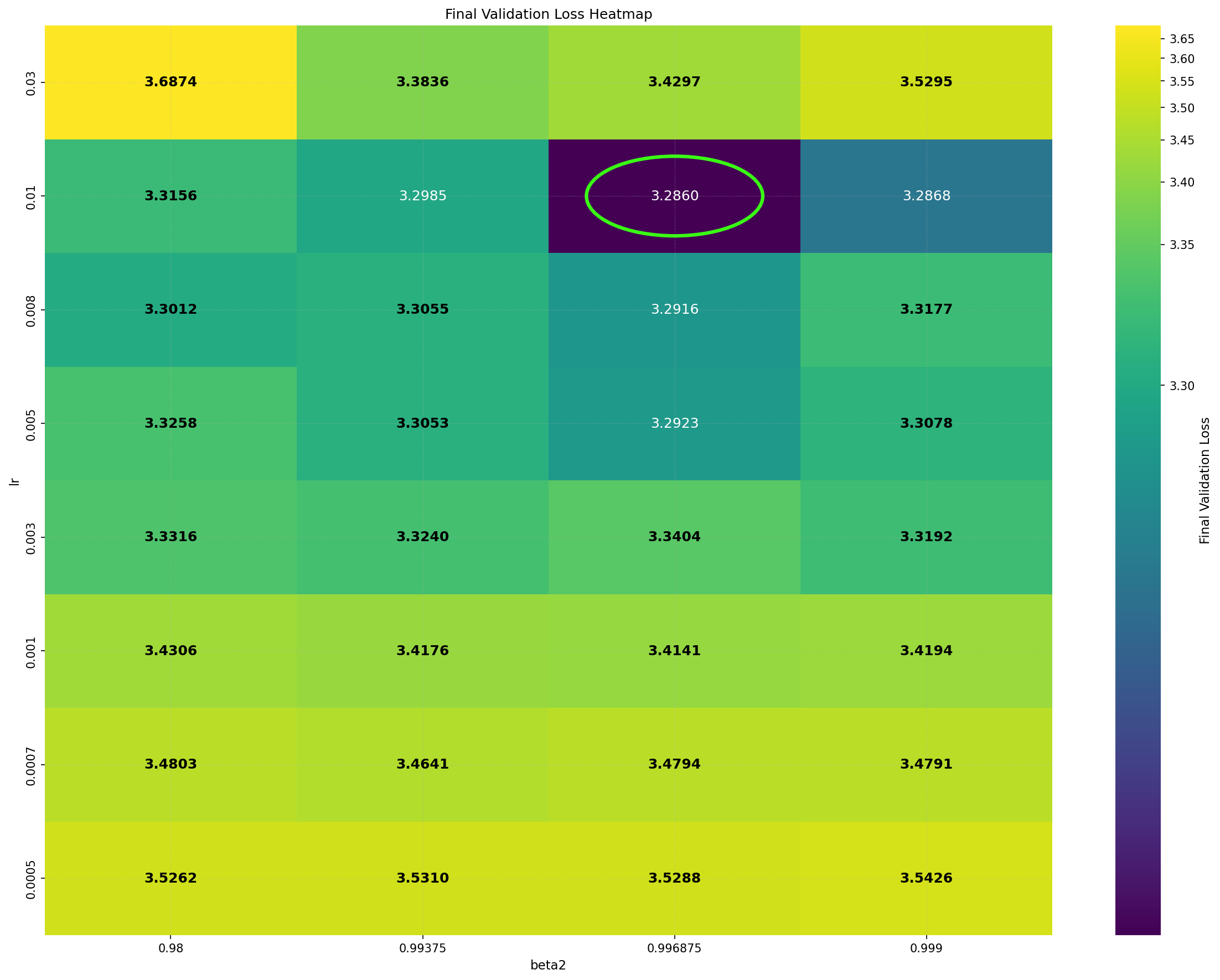
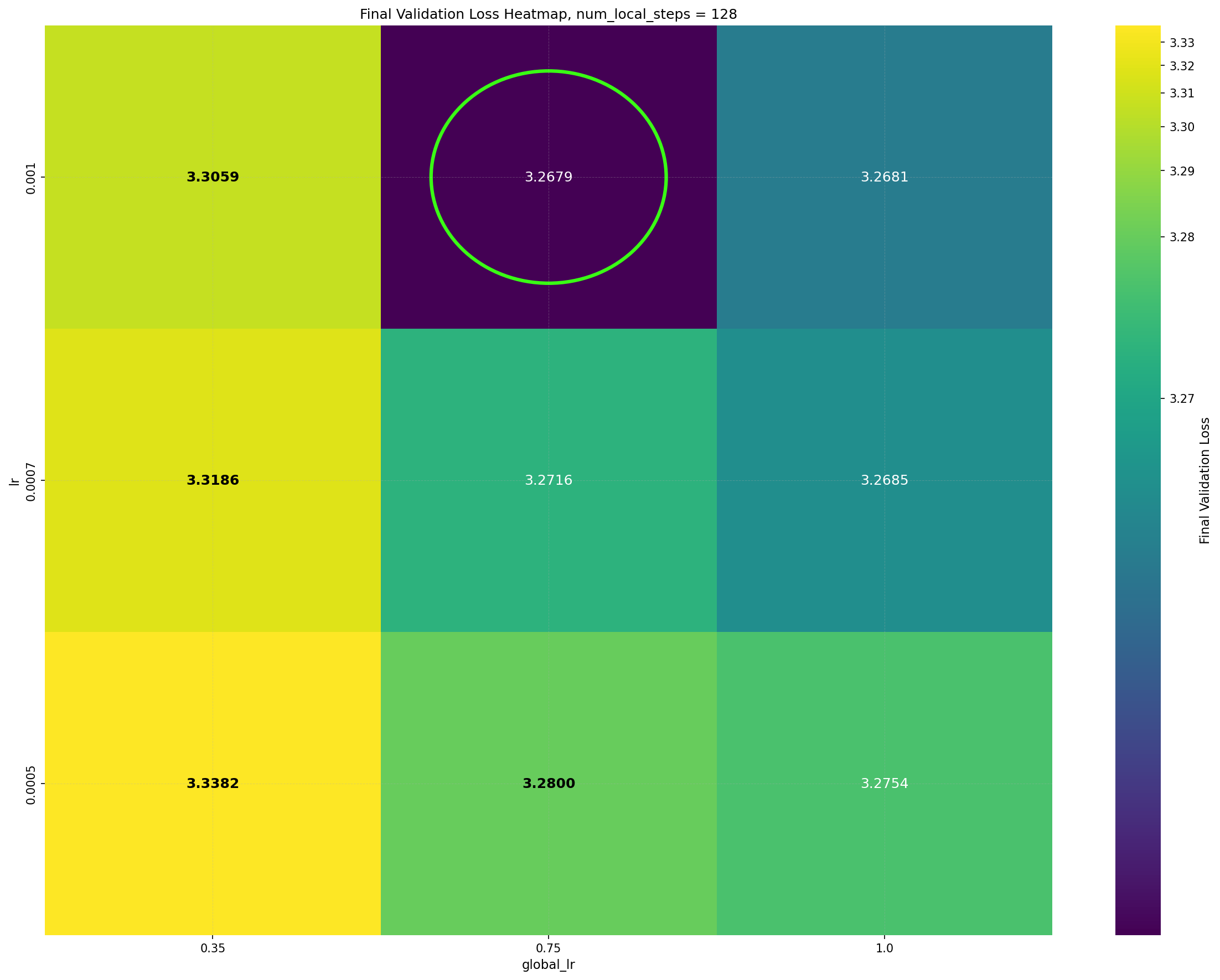
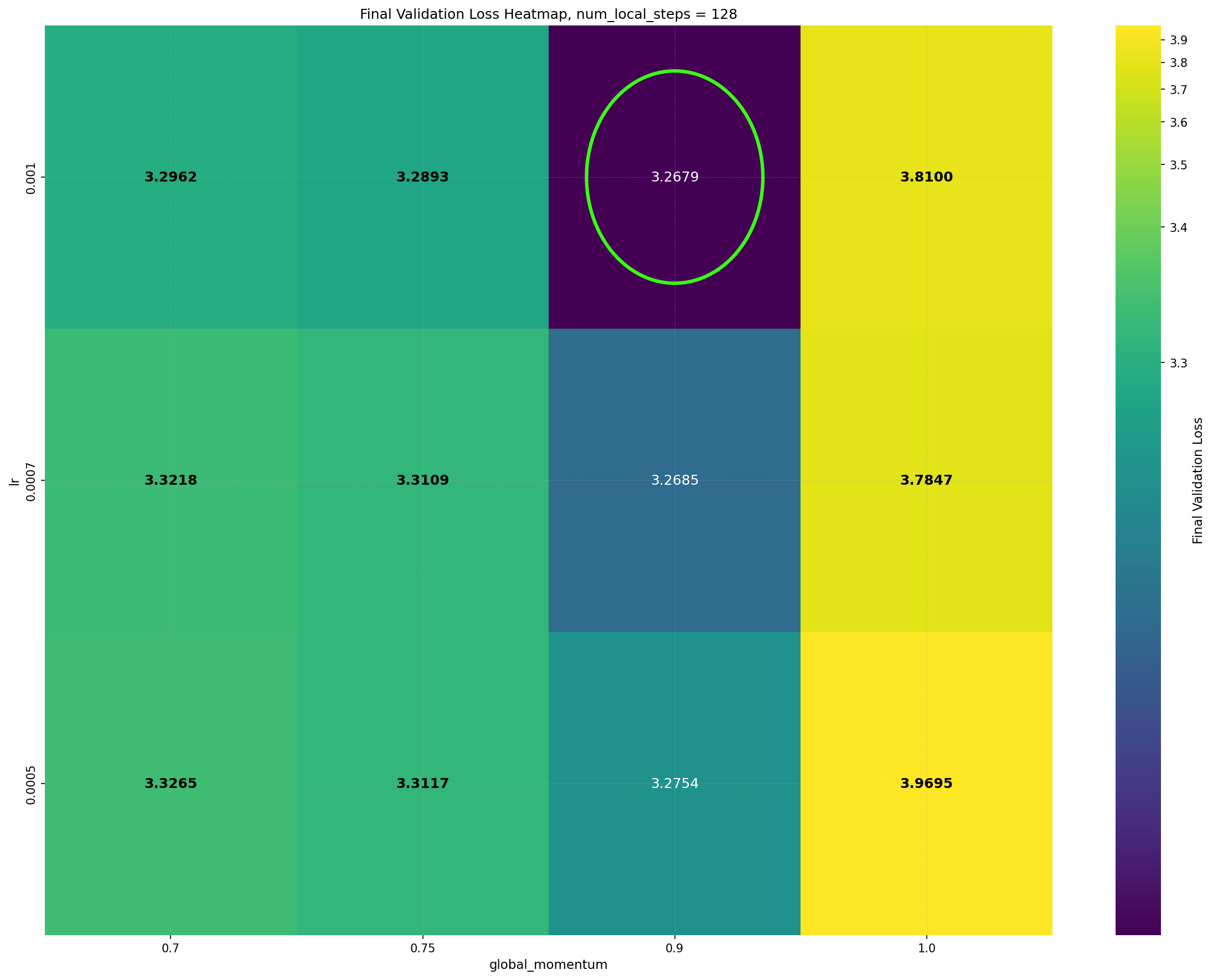
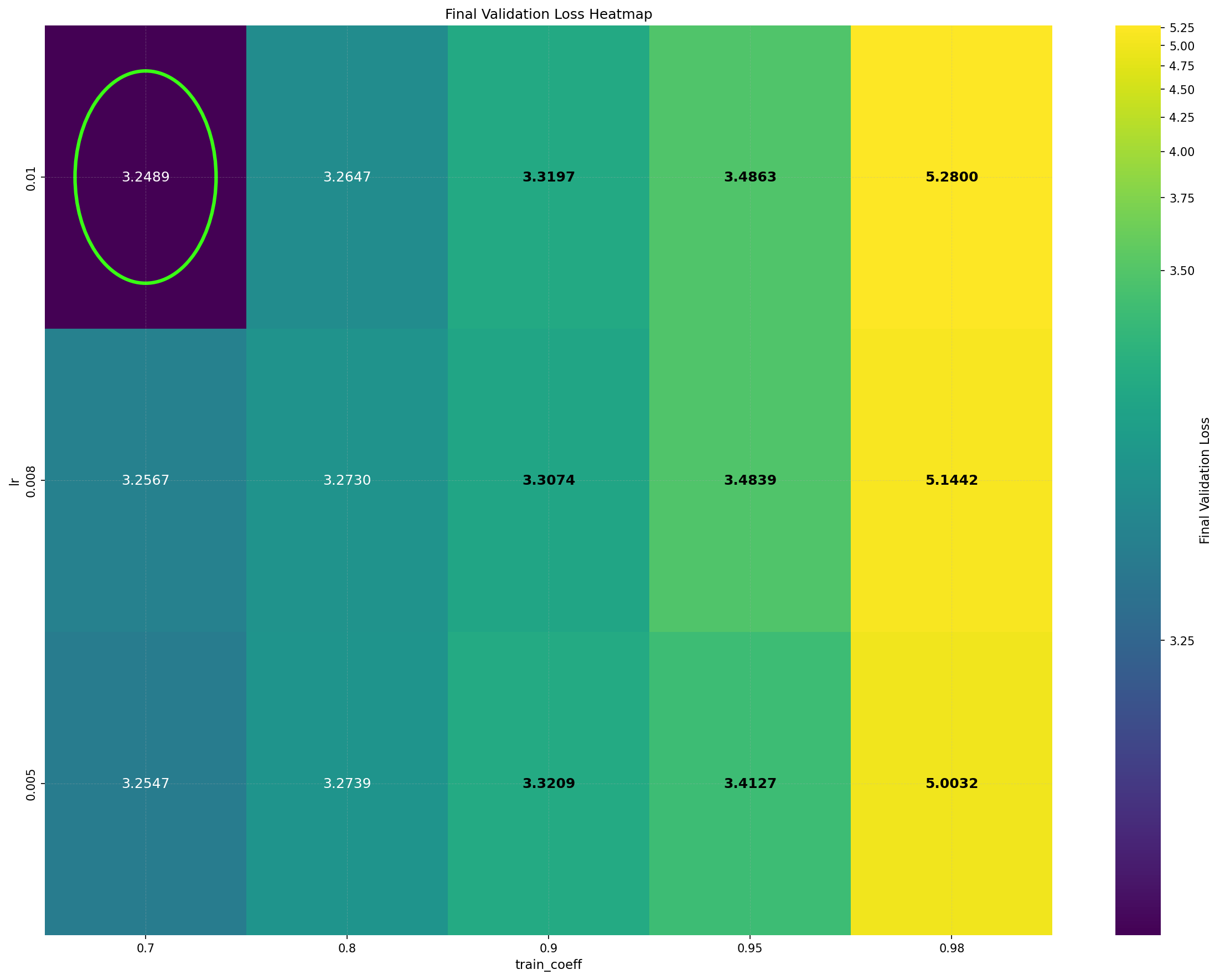
Intriguingly, DiLoCo’s performance initially improves as the number of inner steps increases. With each inner step, DiLoCo’s outer weights drift farther from its inner weights, similar to meta-learning optimizers such as Reptile (Nichol and Schulman, 2018) and First-Order MAML (Finn et al., 2017). As a result, updates to the outer weights occur only at periodic intervals, causing information from the data to be integrated in a discontinuous, choppy manner rather than smoothly at every iteration. This restriction on information flow to the outer weights appears unnecessary from an optimization perspective, yet counterintuitively improves its performance; see Figure 1a. (a) Both GPA and single-worker DiLoCo, when using AdamW as their base optimizer, outperform the tuned AdamW baseline for training a 160M parameter Llama model. Notably, increasing the number of inner steps (up to 64) improves the performance of single-worker DiLoCo. GPA instead updates the parameters at every step using a heuristic to choose interpolation constants that approximately match the number of inner steps for single-worker DiLoCo. Concurrently, the Schedule-Free optimizer recently won the AlgoPerf Algorithmic Efficiency challenge selftuning track (Dahl et al., 2023;Defazio et al., 2024). Its core novelty lies in computing gradients at a point that interpolates between the uniform average of past weights and the current weights. Empirically, Schedule-Free matches the performance obtained by using learning rate schedules without using any schedule explicitly, while providing stronger theoretical last-iterate convergence guarantees similar to Polyak-Ruppert averaging (Ruppert, 1988;Polyak, 1990;Polyak and Juditsky, 1992). However, its reliance on uniform averaging limits its flexibility and performance in some settings.
In this paper, we argue that these two lines of work -DiLoCo and Schedule-Free -are closely related and can be generalized and improved through a unified framework of primal averaging. Specifically, our contributions are as follows:
• We propose a novel generalization of Nesterov’s method in its primal averaging formulation called Generalized Primal Averaging (GPA). The method can be interpreted as a smoothed version of singleworker DiLoCo that incrementally averages iterates at every step. It can also be viewed as a subtle change of Schedule-Free that replaces uniform averaging with exponential moving averaging through a decoupled interpolation parameter to improve its practical performance.
• In contrast to single-worker DiLoCo, GPA eliminates the two-loop structure, thereby requiring only a single additional buffer with one less hyperparameter to tune. Because it incrementally averages iterates at every step, the method consistently exhibits more stable training behavior than single-worker DiLoCo.
• Our experiments demonstrate that GPA consistently outperforms single-worker DiLoCo and AdamW on dense 160 million and 1 billion parameter language models. We validate our results on different modalities through an 8 billion parameter Llama code generation model and through a vision workload using ImageNet ViT in both small-and large-batch settings. In particular, on the Llama-160M, 1B, and 8B models, we find that GPA provides speedups of 8.71%, 10.13%, and 9.58%, respectively, in terms of steps to reach the baseline validation loss. Likewise, GPA o
This content is AI-processed based on open access ArXiv data.