The structure of topology underpins much of the research on performance and robustness, yet available topology data are typically scarce, necessitating the generation of synthetic graphs with desired properties for testing or release. Prior diffusion-based approaches either embed conditions into the diffusion model, requiring retraining for each attribute and hindering real-time applicability, or use classifier-based guidance post-training, which does not account for topology scale and practical constraints. In this paper, we show from a discrete perspective that gradients from a pre-trained graph-level classifier can be incorporated into the discrete reverse diffusion posterior to steer generation toward specified structural properties. Based on this insight, we propose Classifier-guided Conditional Topology Generation with Persistent Homology (CoPHo), which builds a persistent homology filtration over intermediate graphs and interprets features as guidance signals that steer generation toward the desired properties at each denoising step. Experiments on four generic/network datasets demonstrate that CoPHo outperforms existing methods at matching target metrics, and we further validate its transferability on the QM9 molecular dataset.
Topology lies at the core of many applications (e.g., communication networks and protocol design) [35,36]. The arrangement of nodes and links fundamentally impacts routing efficiency, latency, throughput, fault tolerance, and other performance metrics. Prior studies have shown that protocol behavior (e.g. multicast scaling laws, routing state overhead) can vary dramatically across different topological configurations [2]. As a result, network designers must carefully consider topology in optimizing network performance network topologies is often difficult. Carrier and enterprise network graphs are typically proprietary, and even research testbeds reveal only limited or anonymized structural information due to security and privacy concerns [48]. This motivates the use of synthetic graph topology generators for network planning, simulation, benchmarking, and data sharing [1,7]. Indeed, realistic synthetic topologies serve as important tools to evaluate new protocols and algorithms in lieu of real networks. Such tools allow researchers to simulate network behavior on large-scale, representative topologies and to perform "what-if" analyses for new designs. Synthetic topology generation also facilitates anonymization: one can release a plausible network graph for public use without disclosing the true network, as long as the synthetic graph preserves key structural patterns of the original [65,69]. In general, the ability to algorithmically generate graphs with specified characteristics is critical for both networking research and practical network engineering. This motivates the problem of conditional topology generation: automatically creating graphs that satisfy user-defined constraints.
Early network topology generators were largely rule-based or random [19,54,59]. These approaches have limited ability to capture complex structural patterns observed in real-world networks. In the past decade, data-driven approaches [14,46,67] have emerged to learn generative models of graphs [67]. Deep graph generative models such as variational autoencoders [56] and generative adversarial networks [8] have been applied to produce graphs that emulate training examples. More recently, diffusion-based generative models have achieved remarkable success in image and audio synthesis [32,47,51], prompting their adoption for graph data. Diffusion models generate data by iteratively denoising random noise, effectively learning the reverse of a gradual noising process. Several researchers [6, 15-18, 26, 27, 37-39, 45, 55, 60, 68] have extended this paradigm to graph data, demonstrating its promise for graph generation.
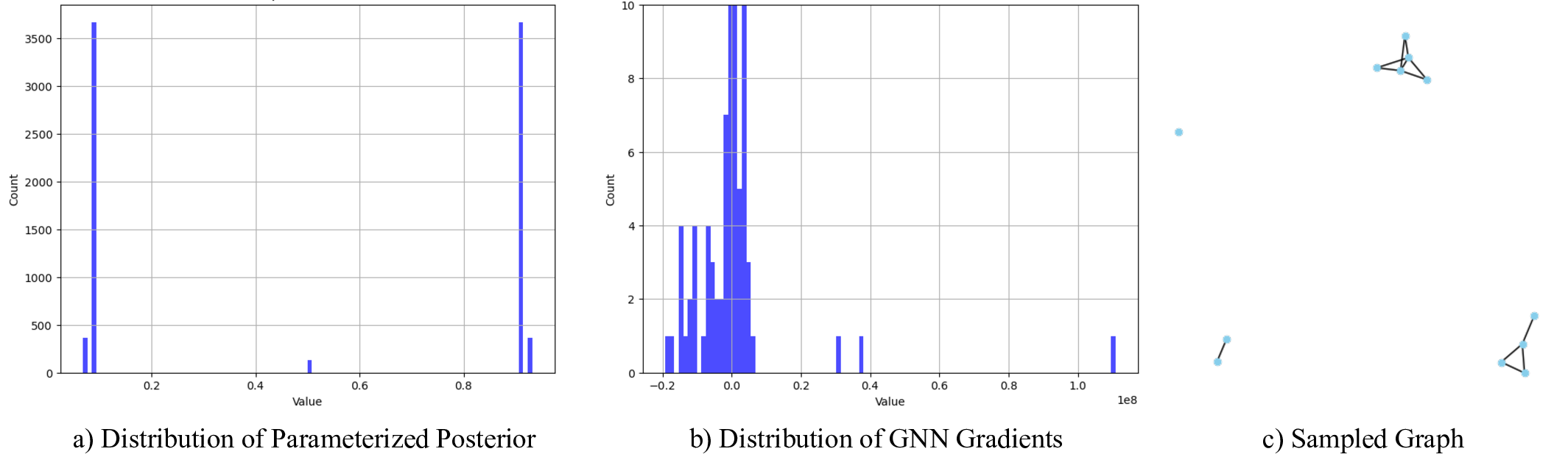
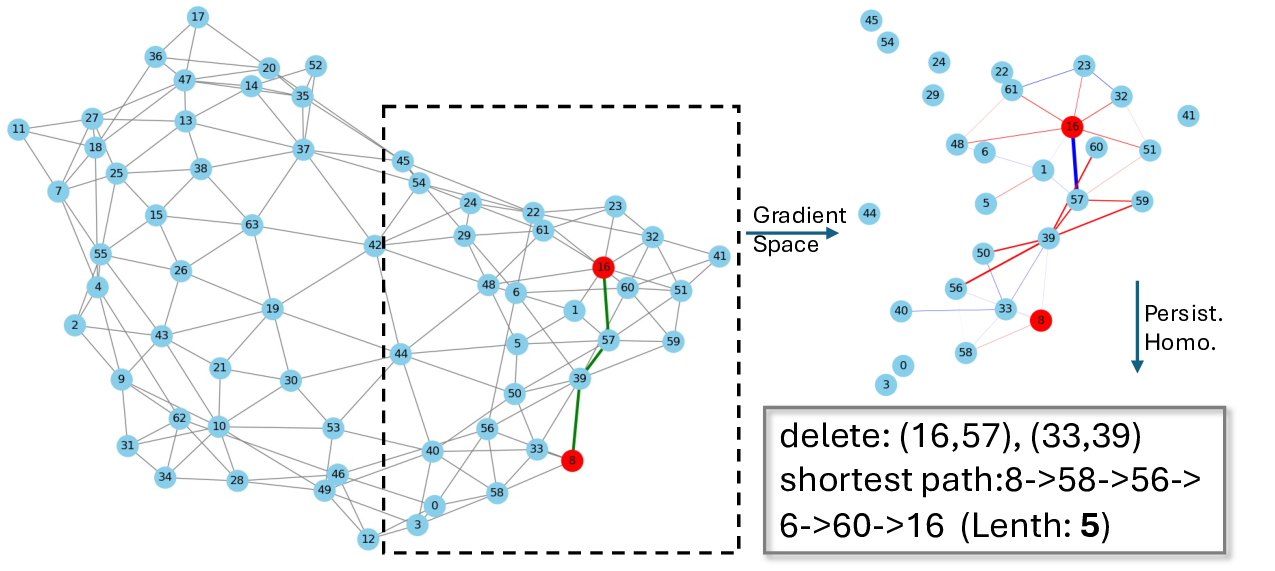
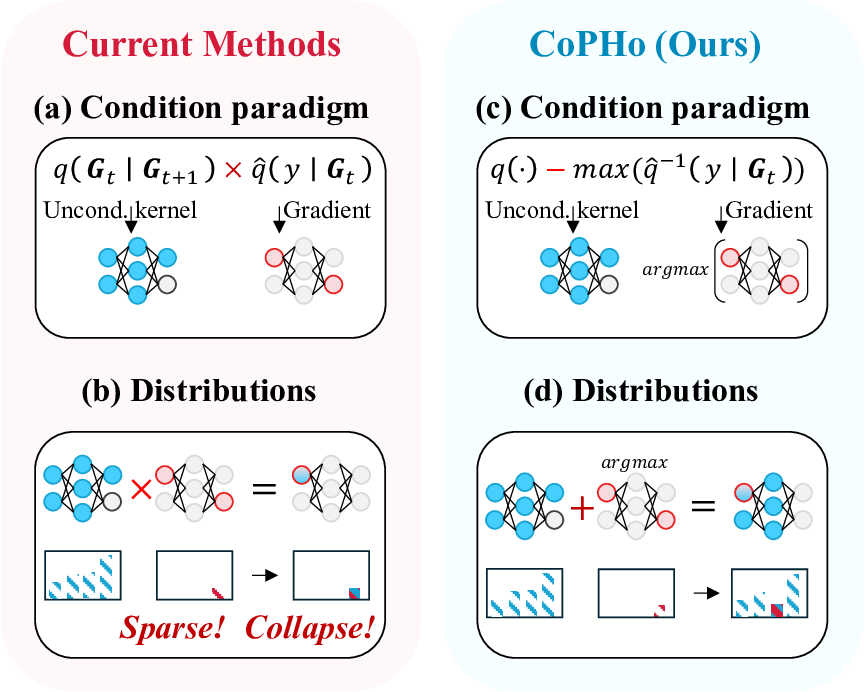
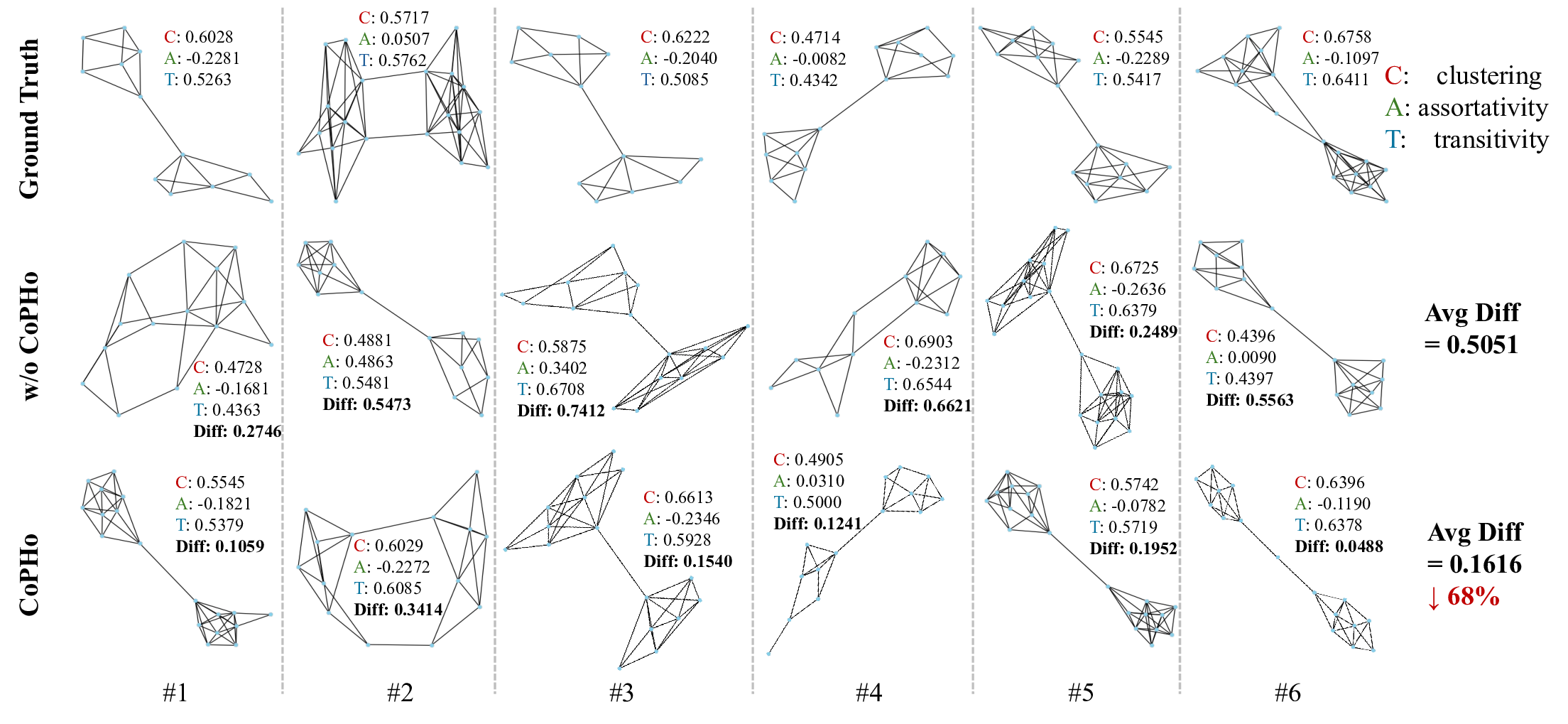
Despite these advances, significant challenges remain in controlling the topologies generated by diffusion models, which is an essential requirement for practical use in network topology design. Existing conditional diffusion-based approaches introduce constraints either during the forward noising process [42] or by applying classifier guidance in the reverse sampling phase [34]. Methods that integrate conditions into the forward stochastic differential equation train a distinct conditional score network for each target attribute, but this strategy imposes heavy computational burdens and requires extensive training data for every new specification, rendering it impractical when confronted with unseen conditions. Current classifier guidance methods [9], by contrast, apply classifier gradients at every denoising step . However, real-world network graphs are highly sensitive to even minor link changes, small edge perturbations can fracture connectivity or undermine resilience [5,43]. Moreover, practical topologies tend to be extremely sparse (edge density below 10%) [4,41], and training data are limited. Consequently, practitioners favor message-passing GNNs, such as GCN [29], GraphSAGE [21], and GIN [61], whose cost scales with the number of edges 𝑂 (𝐸), rather than fully-connected architectures [31,33,66,70] with 𝑂 (𝑛 2 ) complexity. In these message-passing GNNs, gradients only propagate along existing edges; as shown in Fig. 1, the sparsity of the gradient signals can cause the generated graph to collapse.
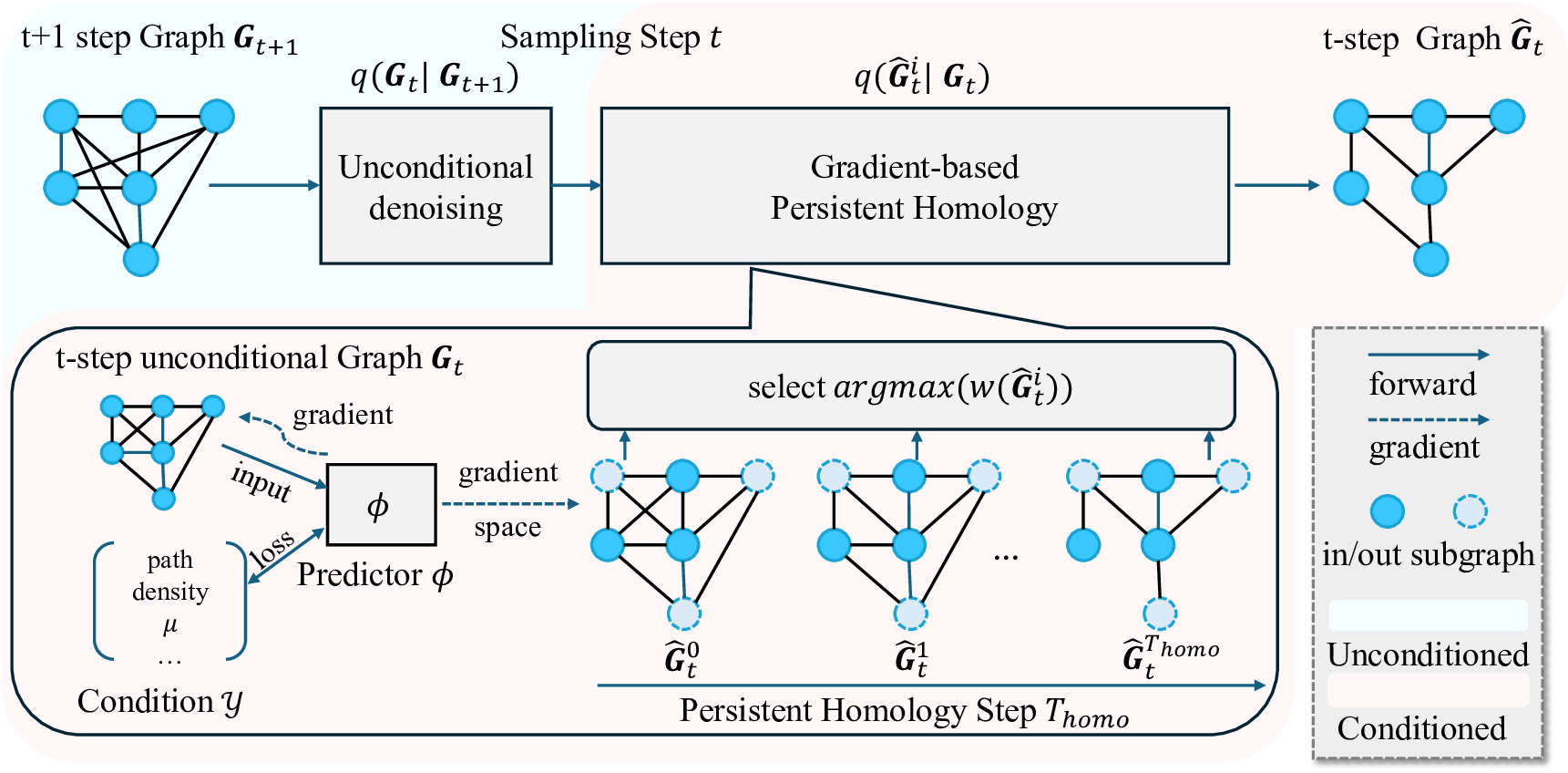
To address the limitations of existing methods by unifying classifier guidance and topological optimization under the diffusion paradigm, we propose Classifier-guided Conditional Topology Generation with Persistent Homology (CoPHo). In theory, we first establish that the gradient of a pretrained graph-property predictor can be rigorously integrated into the reverse-time denoising steps to enforce constraints without retraining the base diffusion model. Building on this foundation, CoPHo treats conditioning as an optimization problem in the space of persistent homology, leveraging the formal correspondence between classifier gradients and topological feature distances.
In practice, CoPHo proceeds by computing at each denoising step the gradient of the classifier with respect to the current unconditioned graph and
This content is AI-processed based on open access ArXiv data.