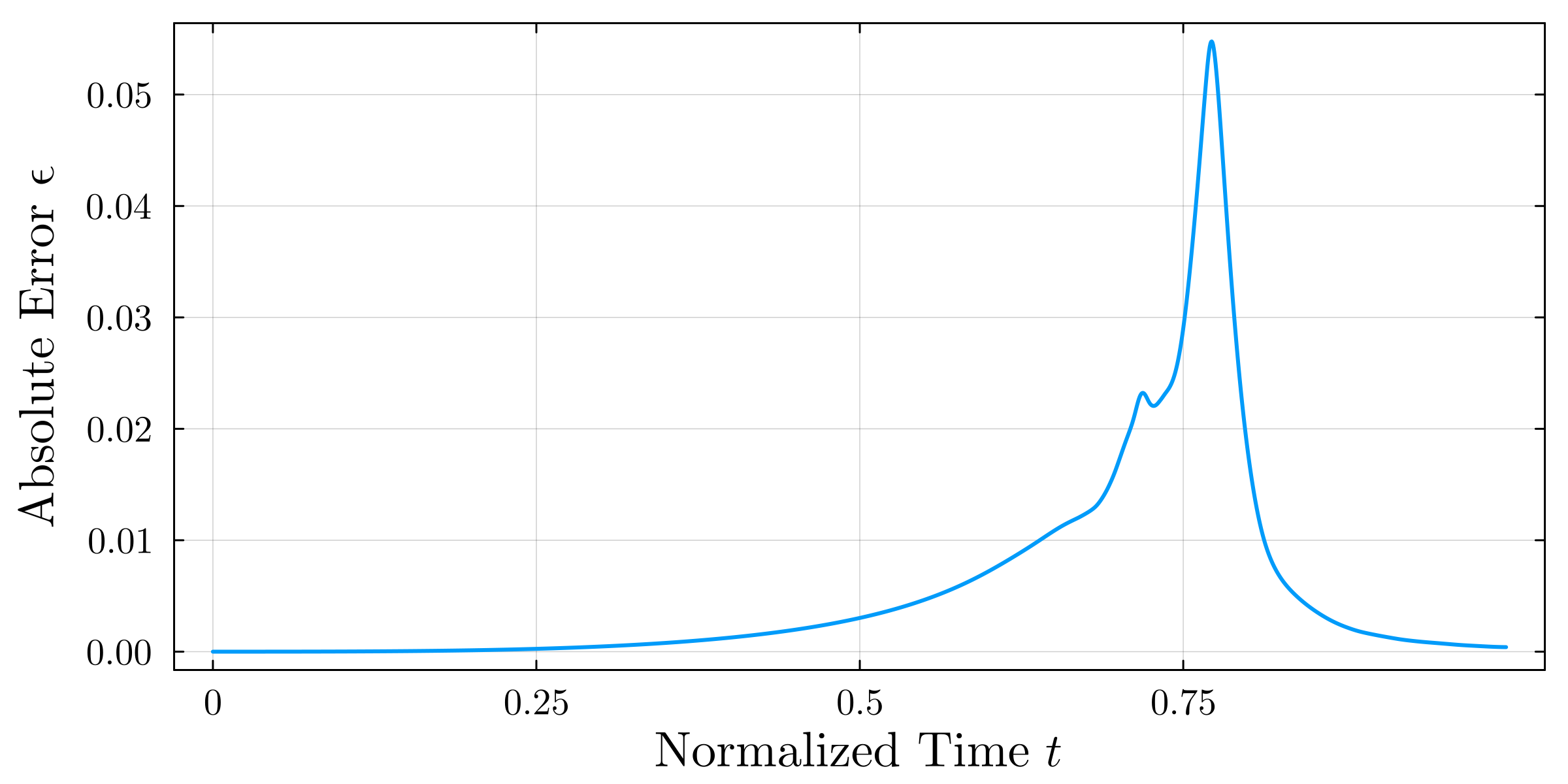
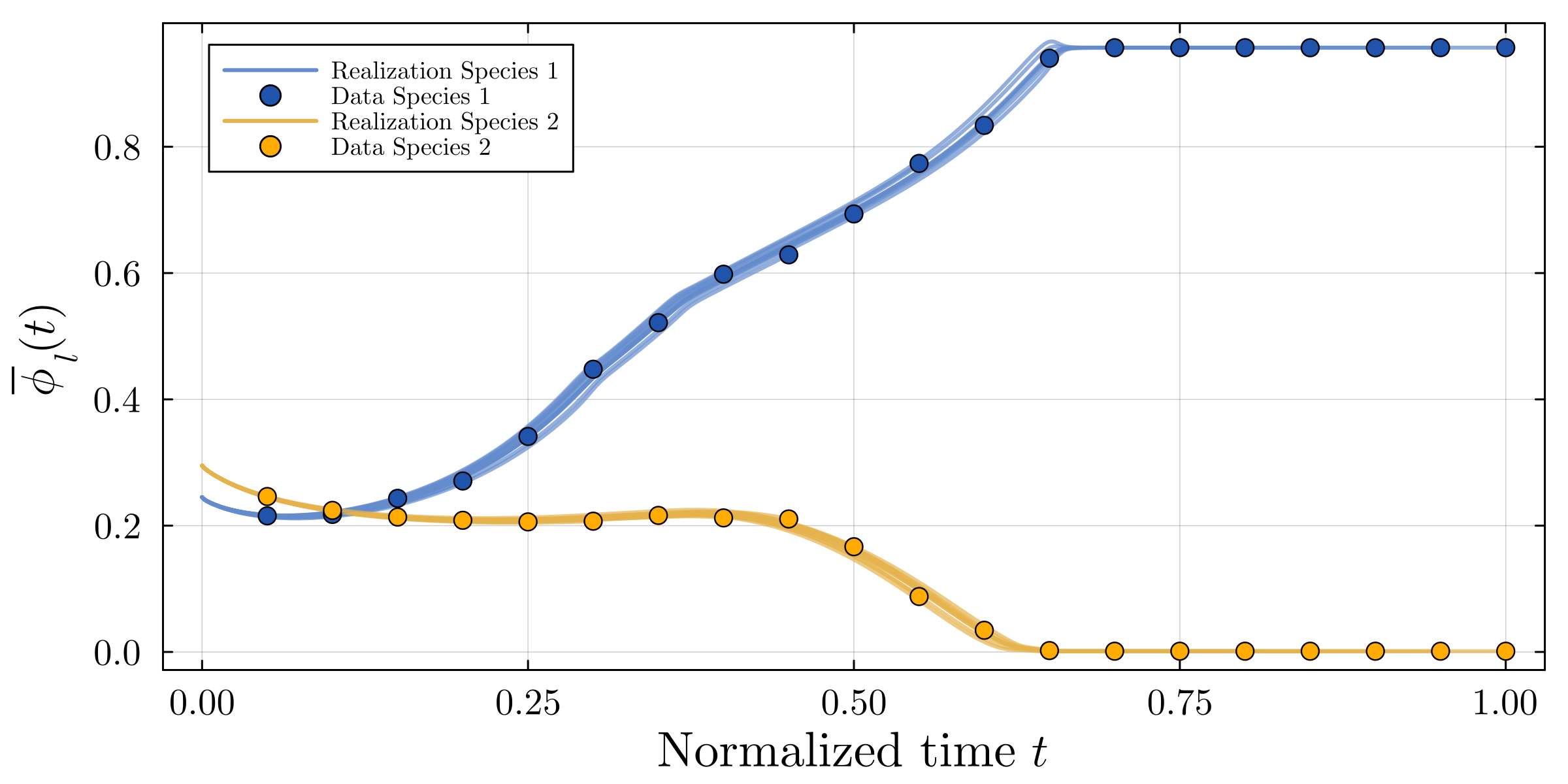
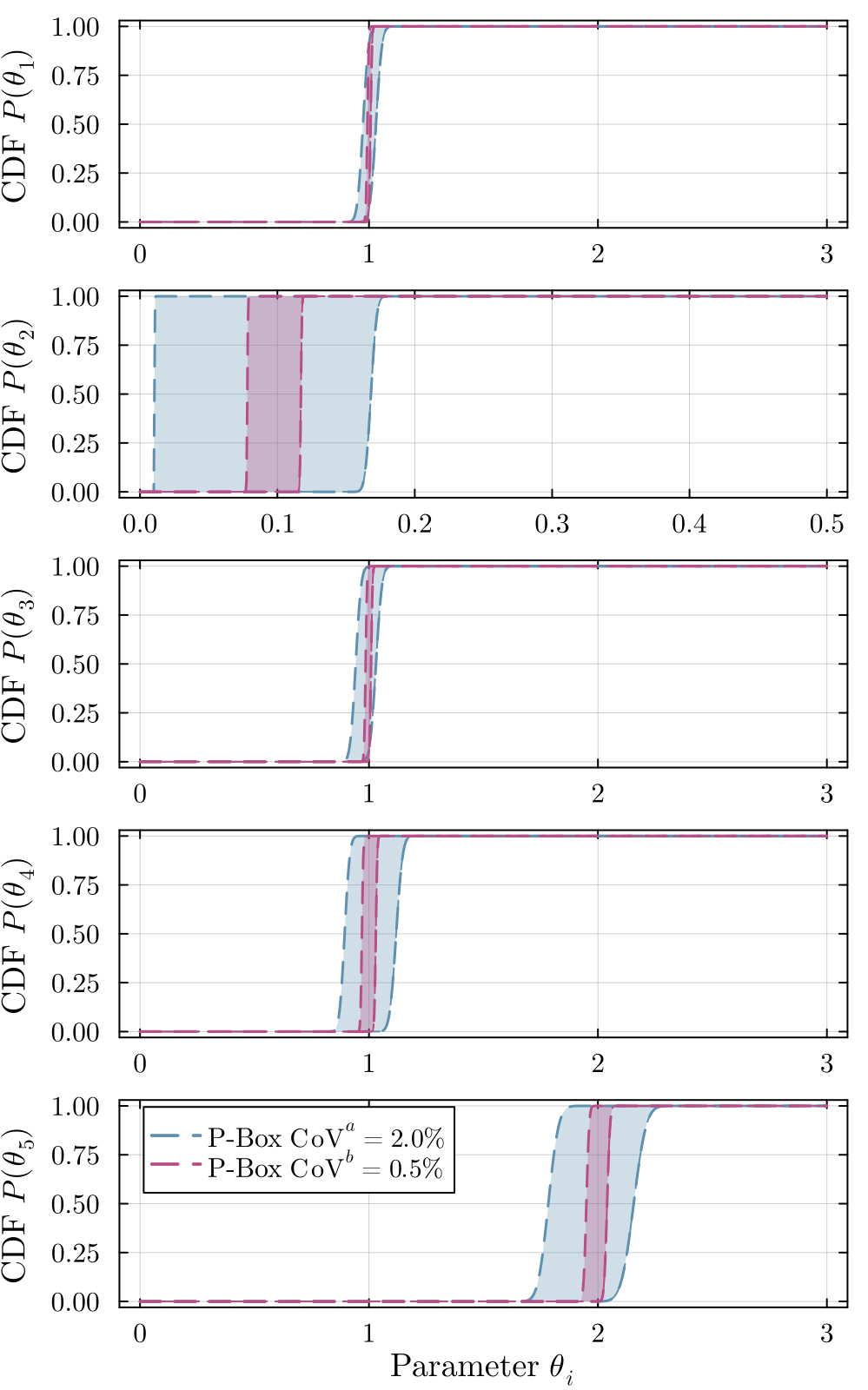
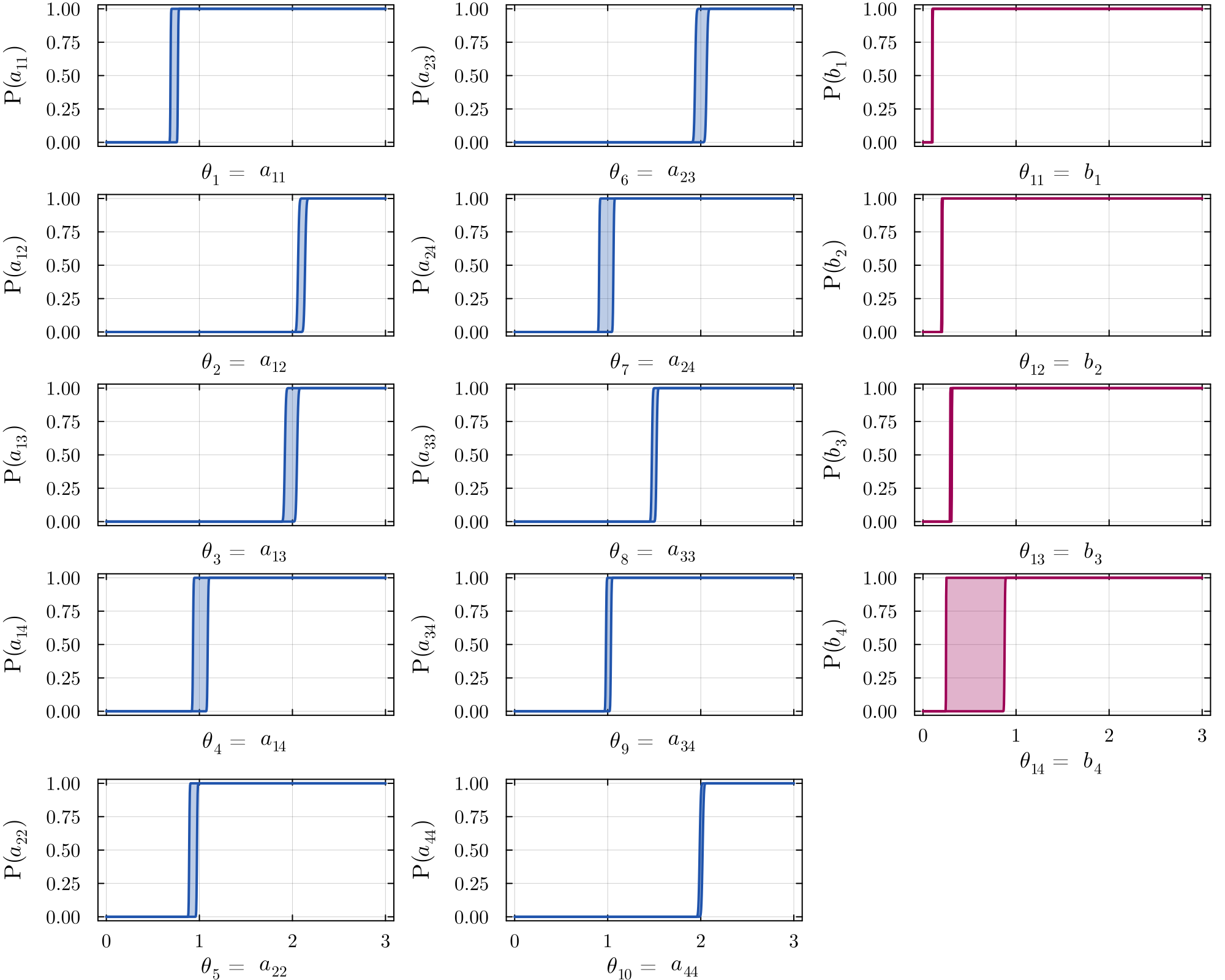
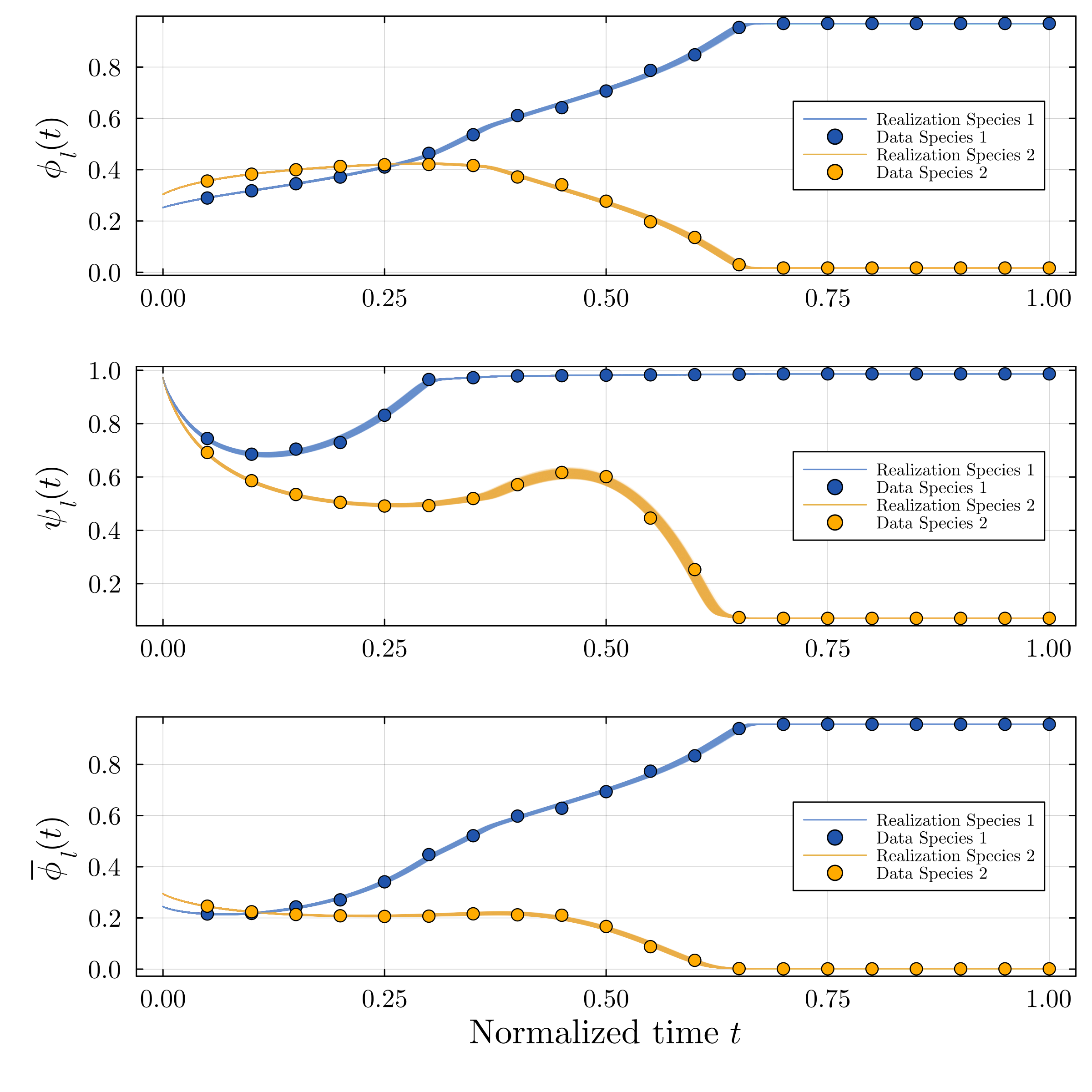
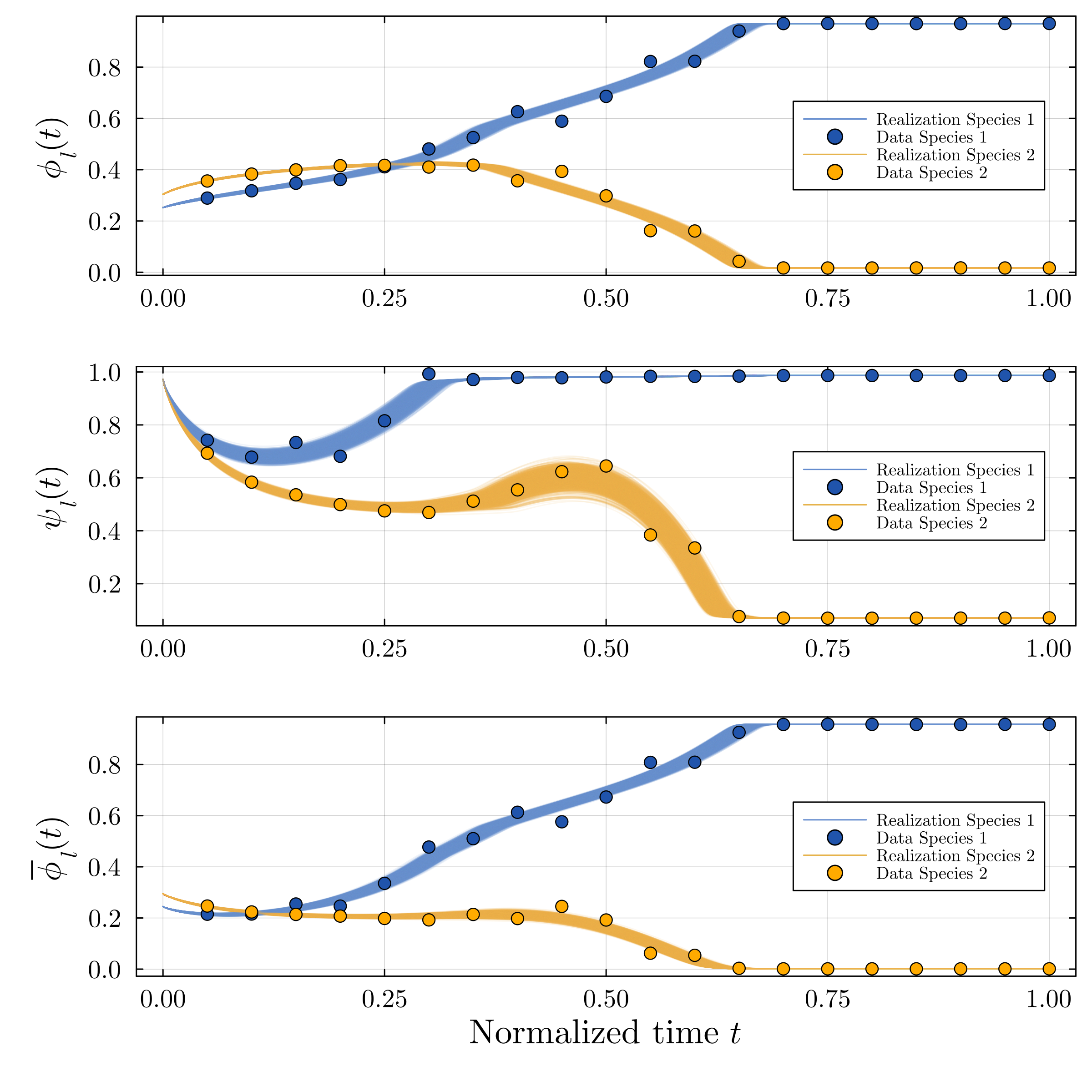
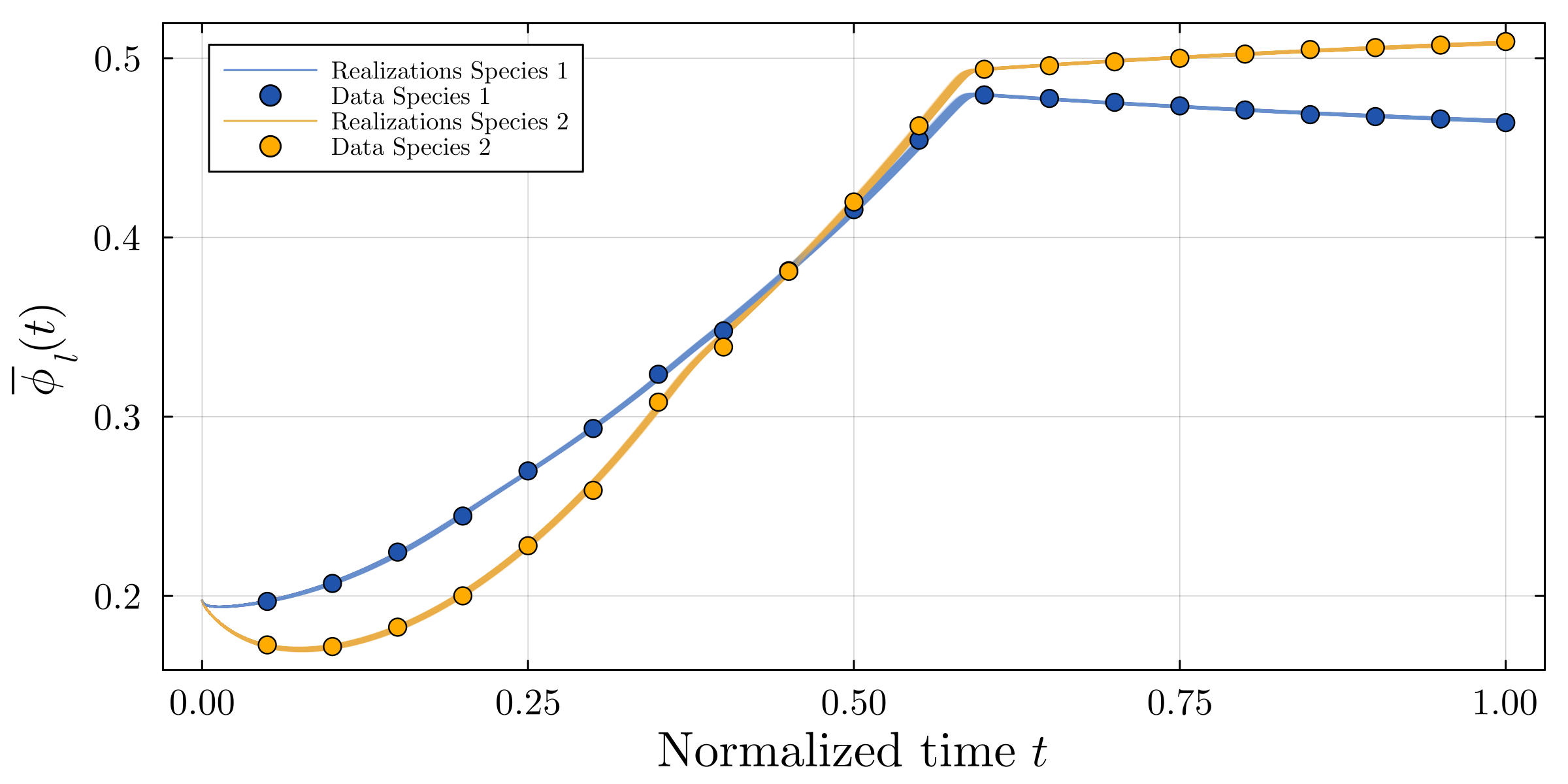
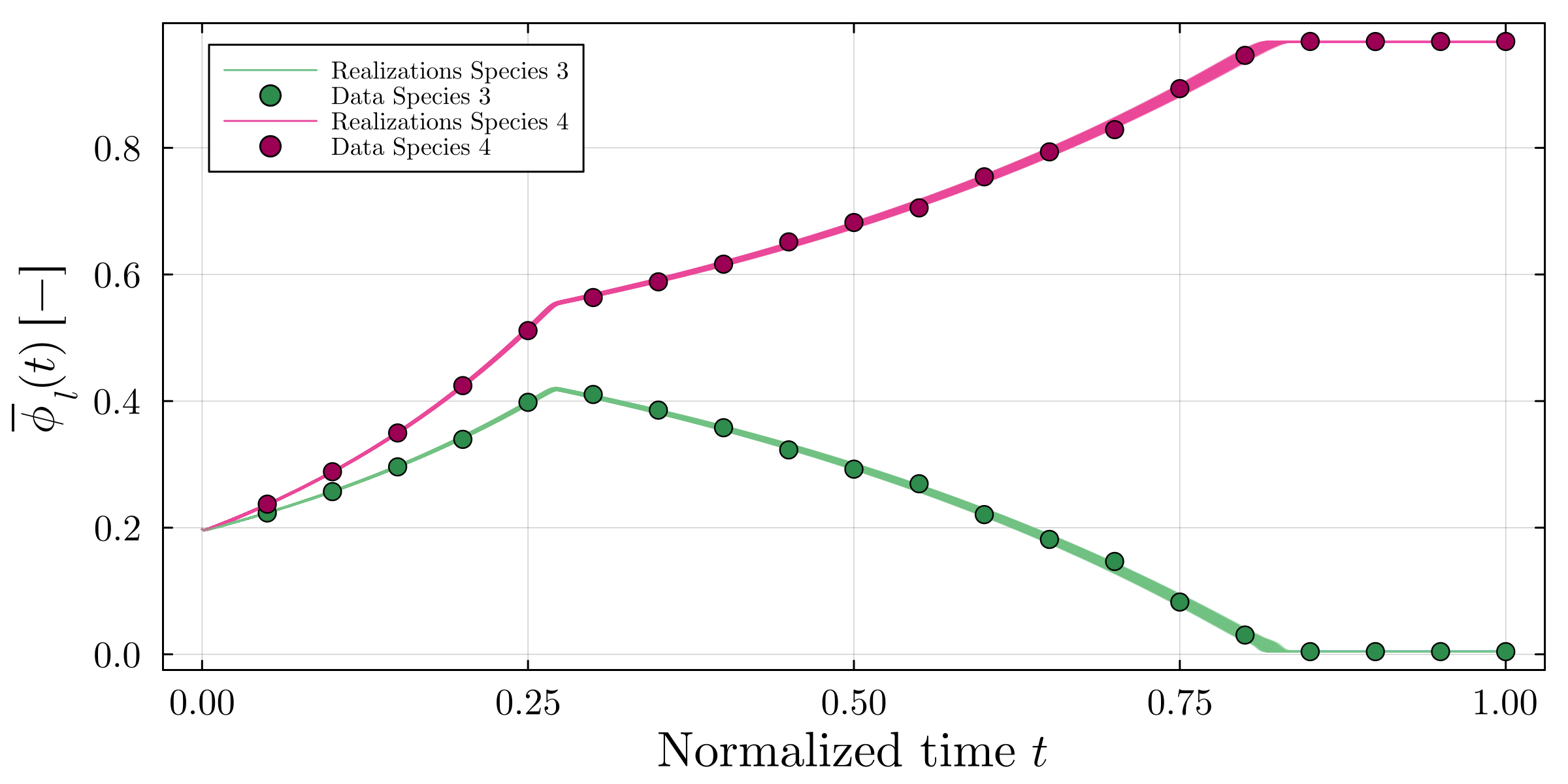
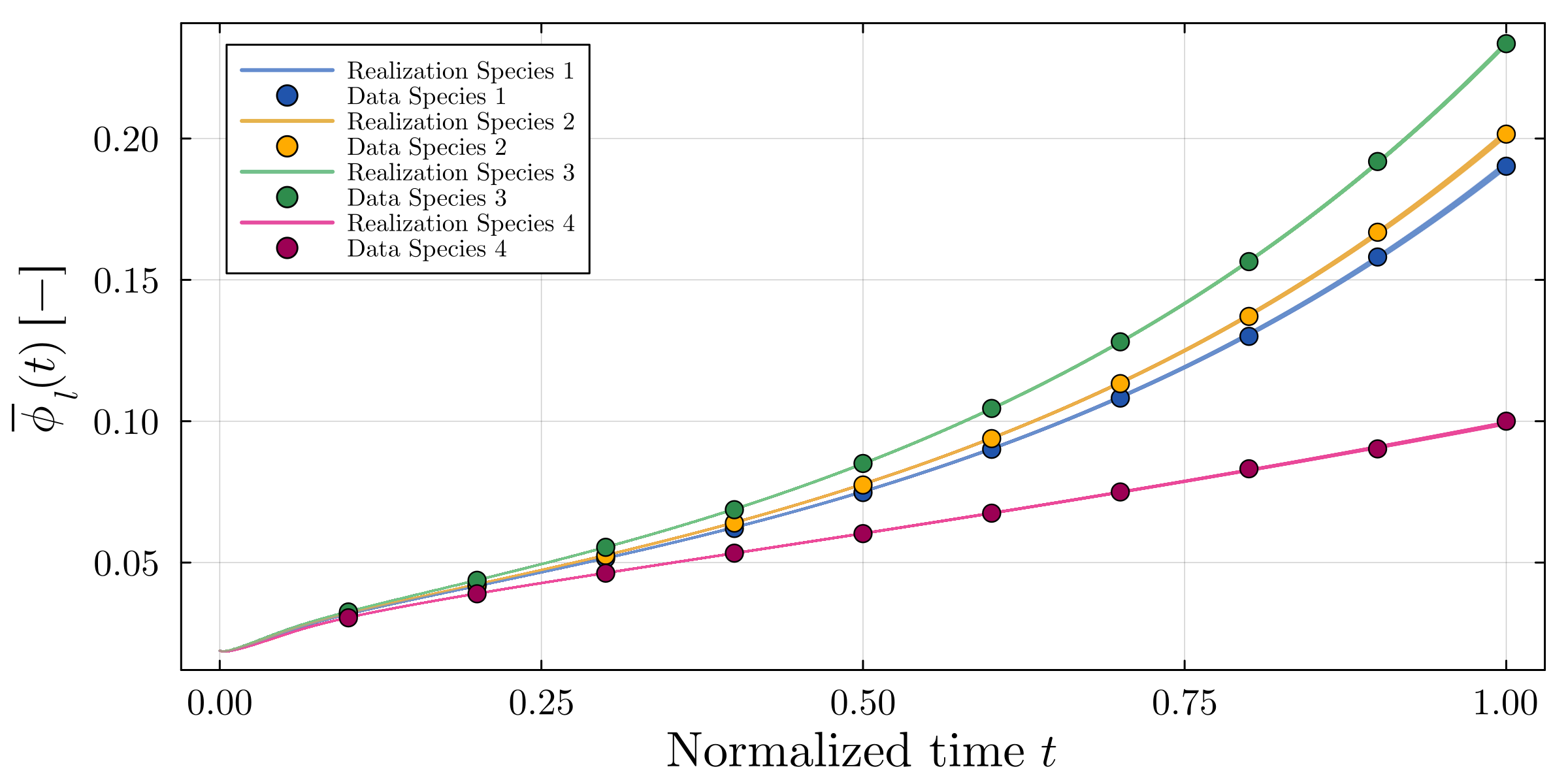
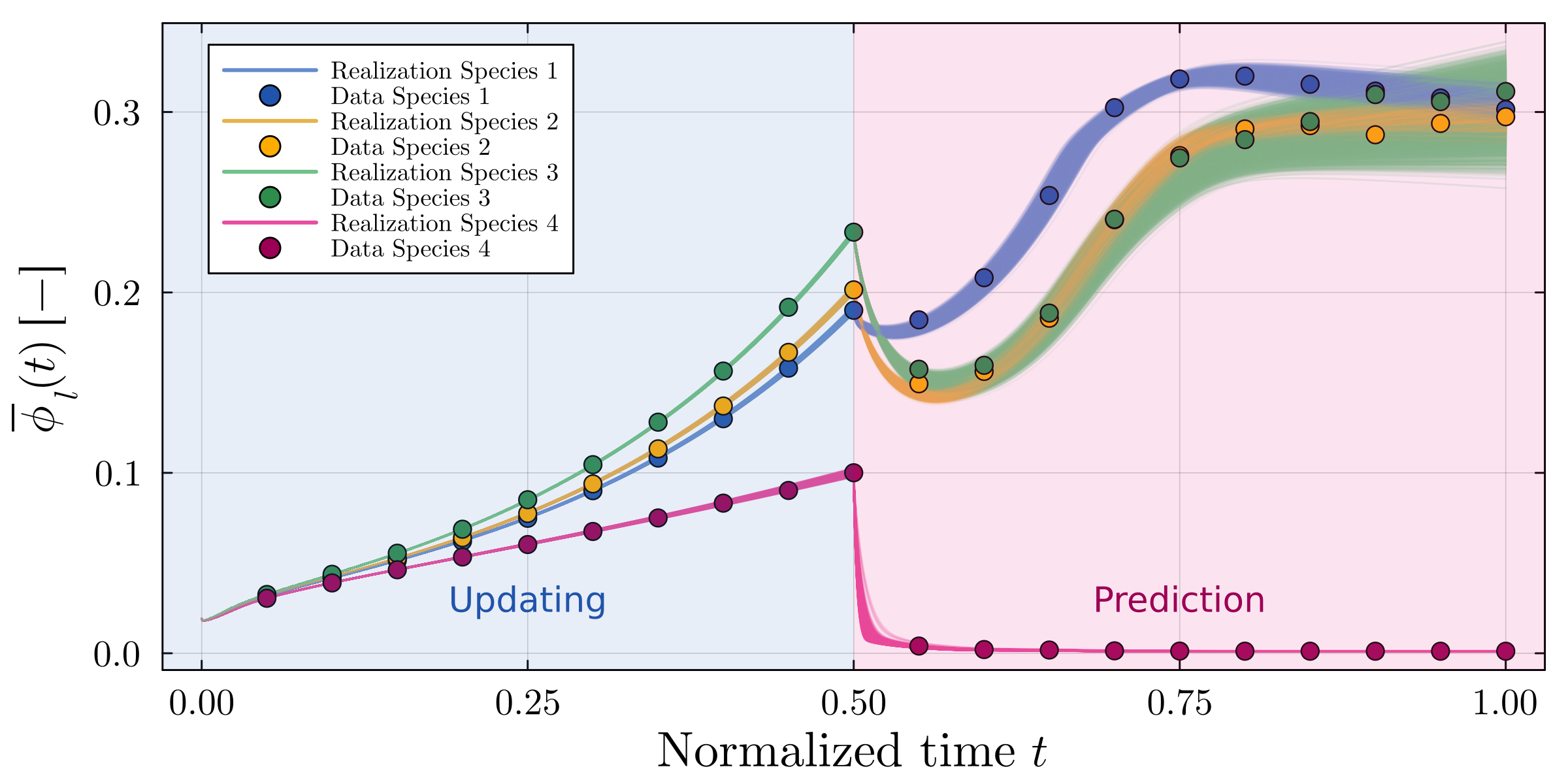
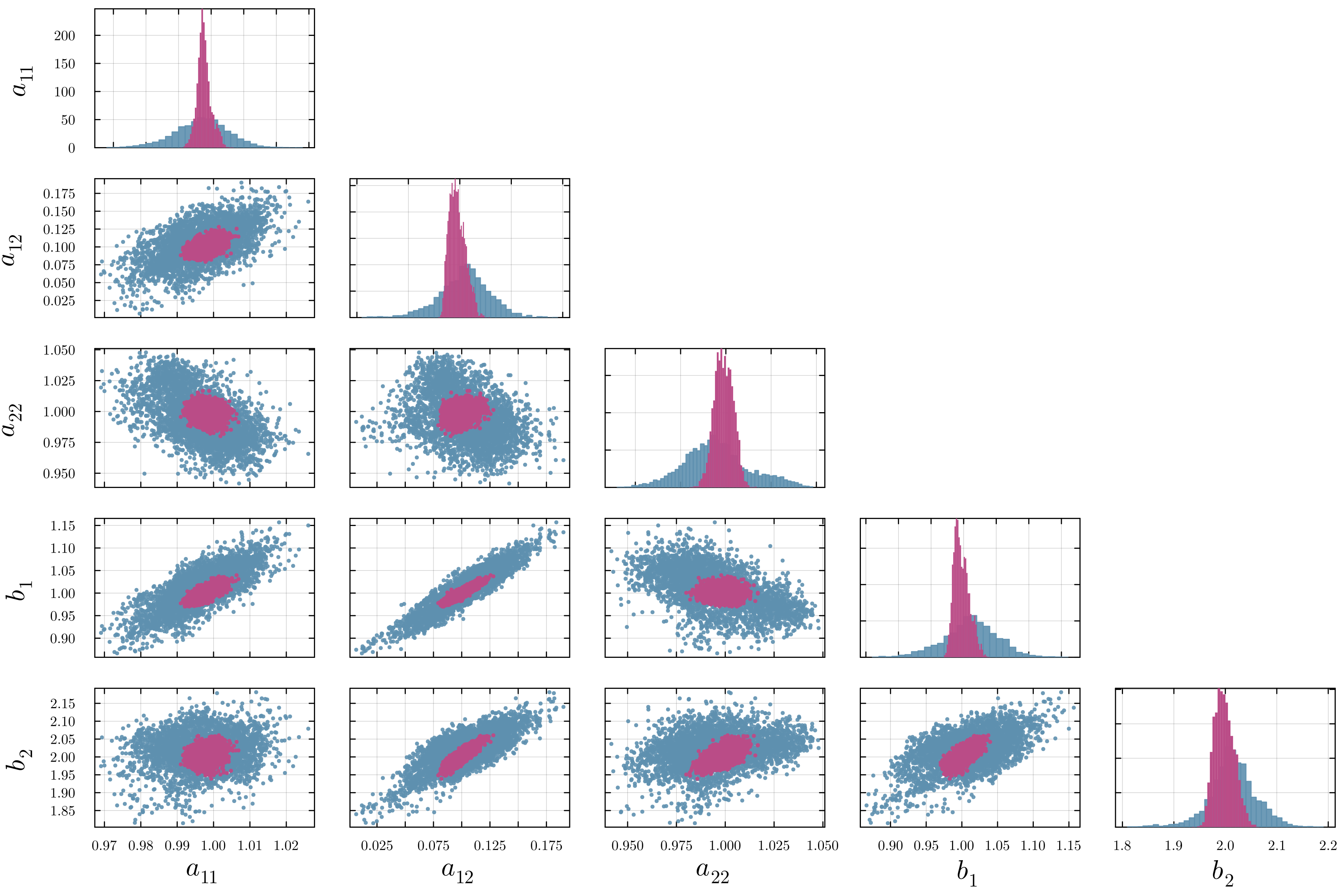
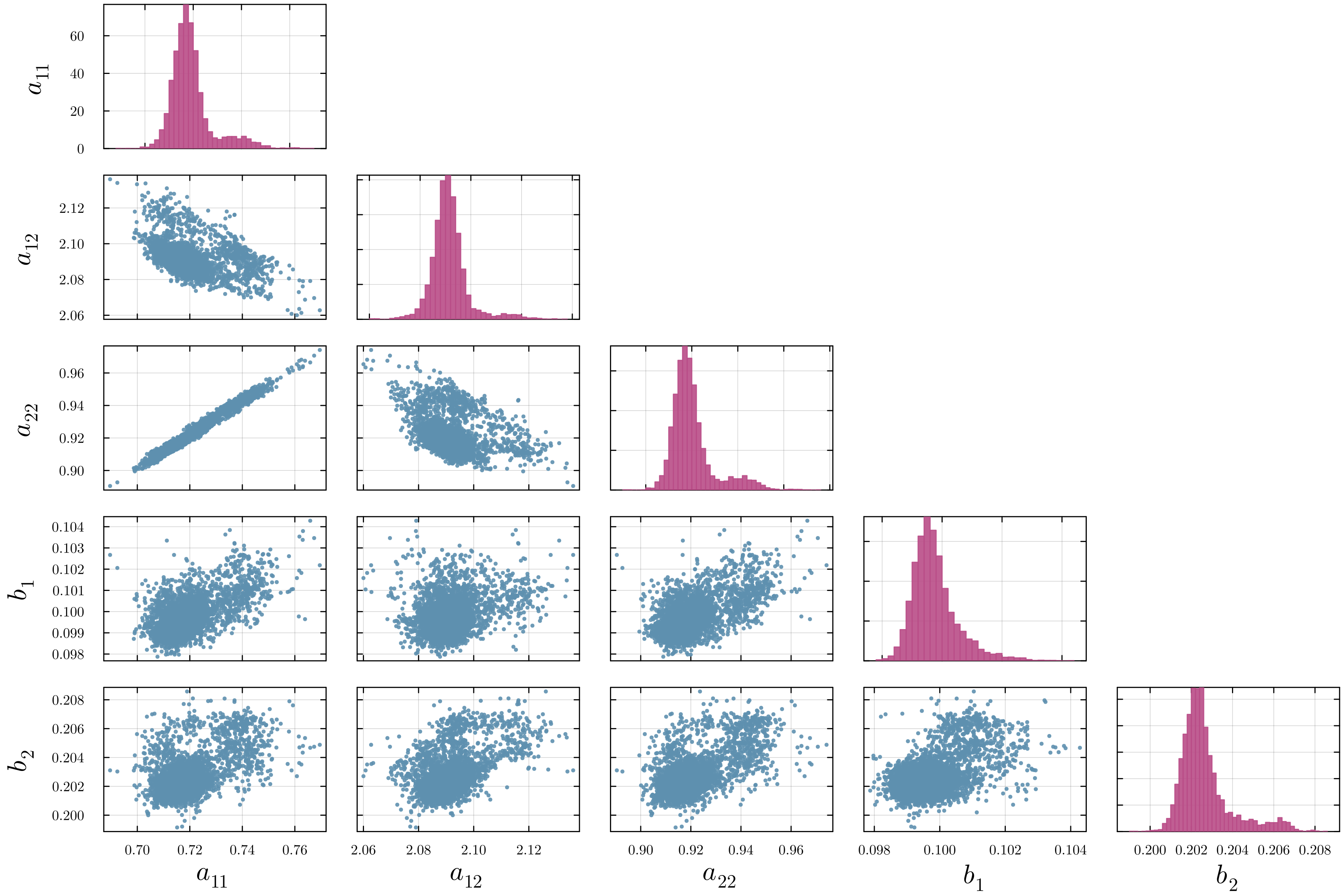
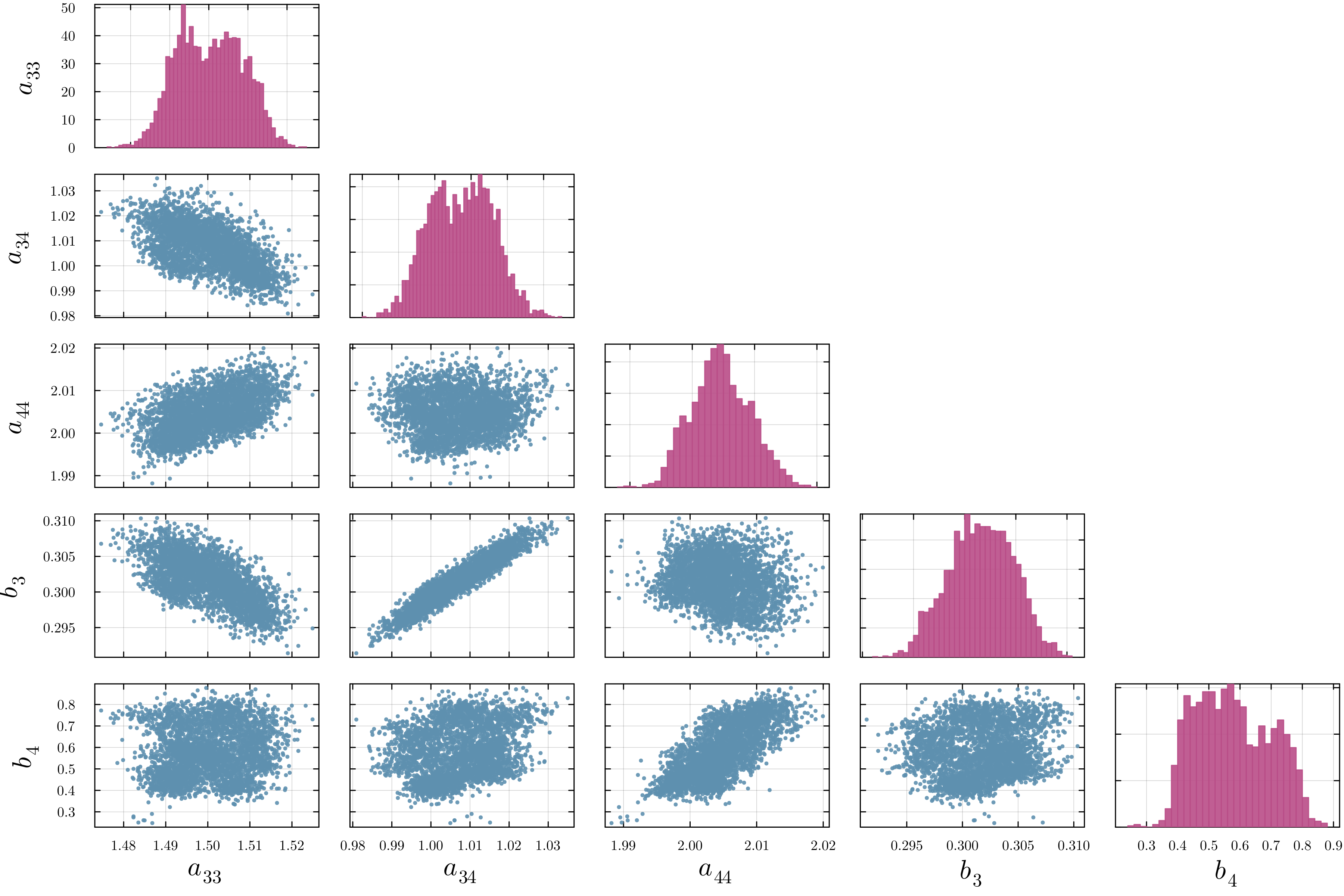
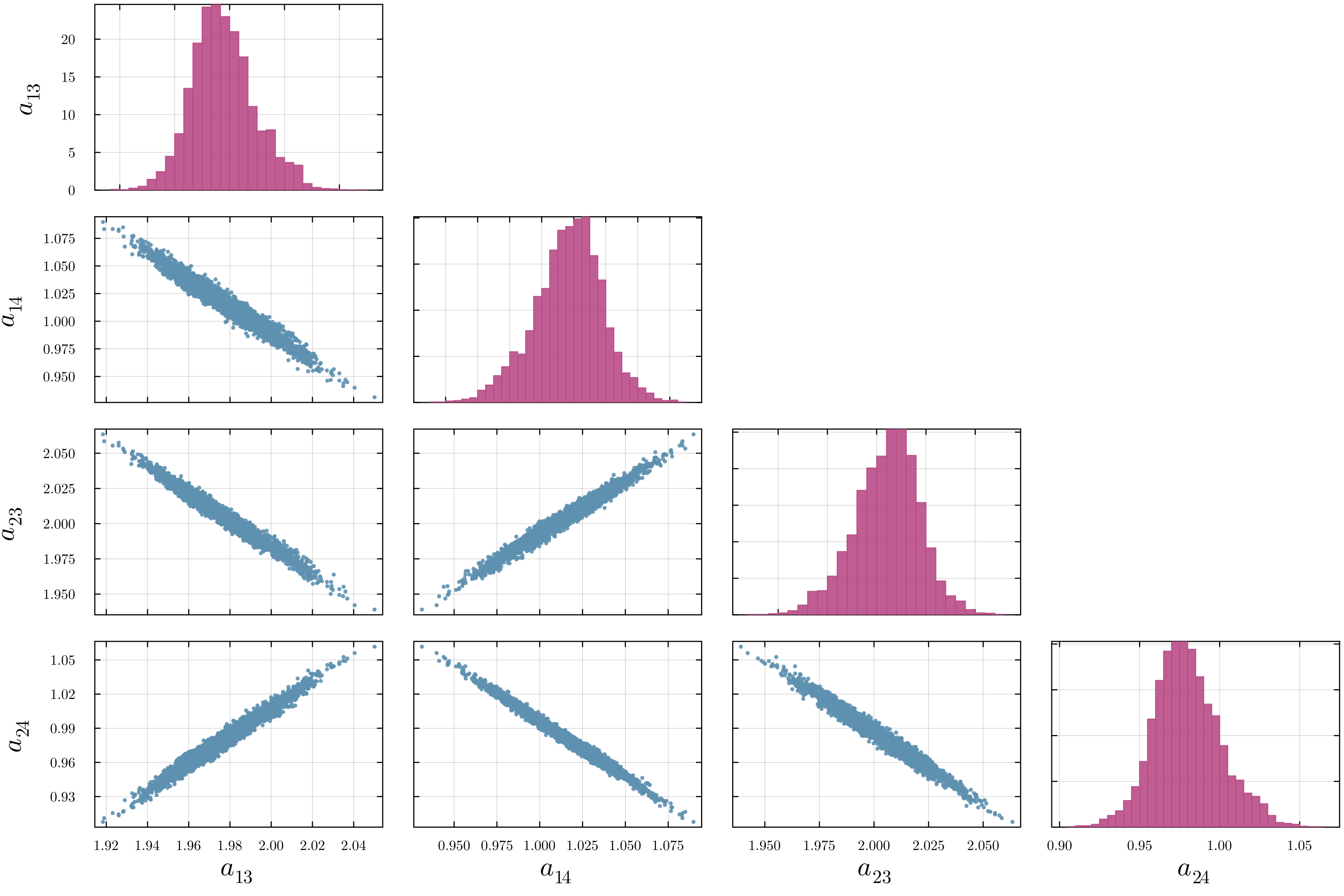
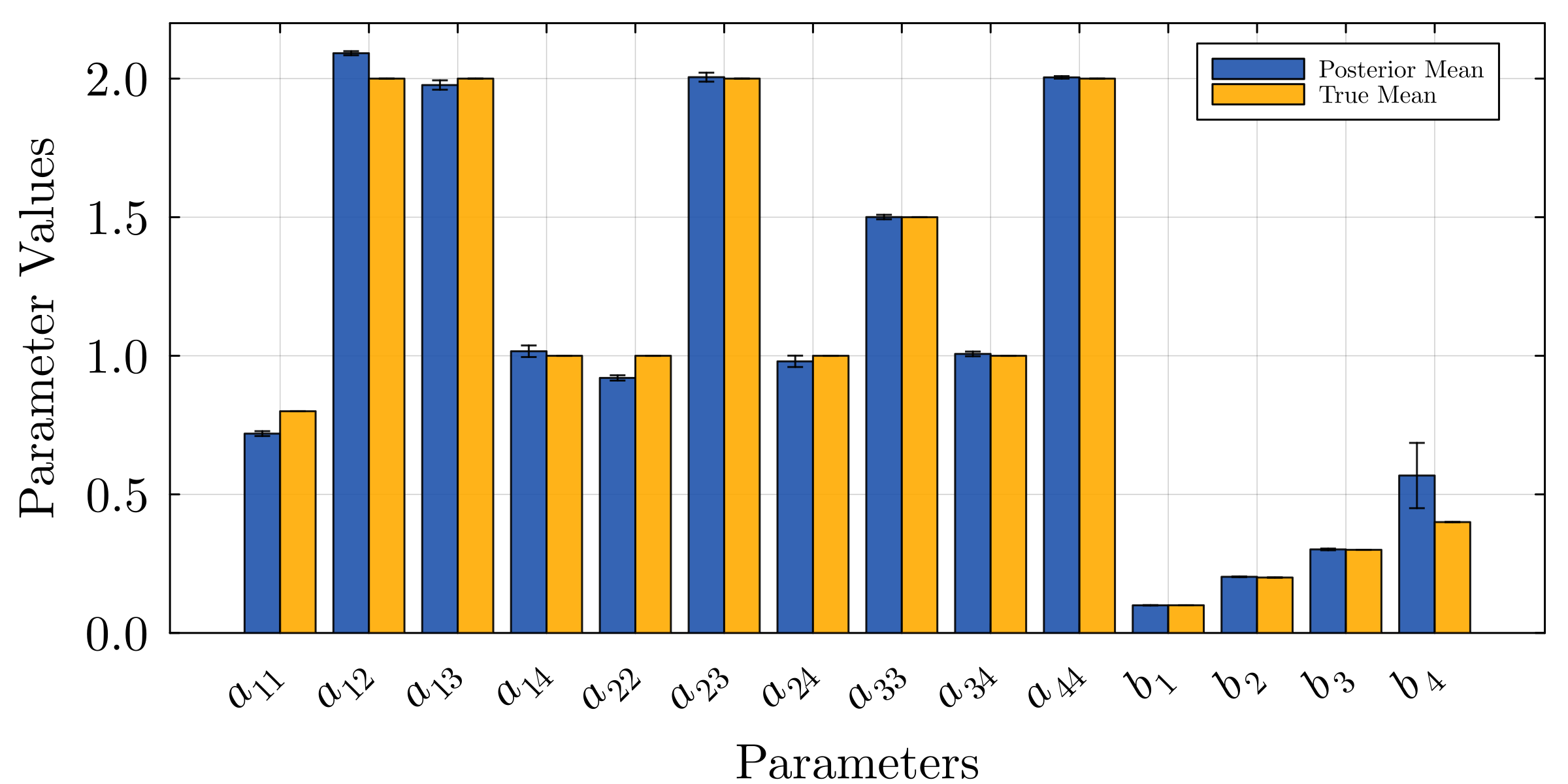
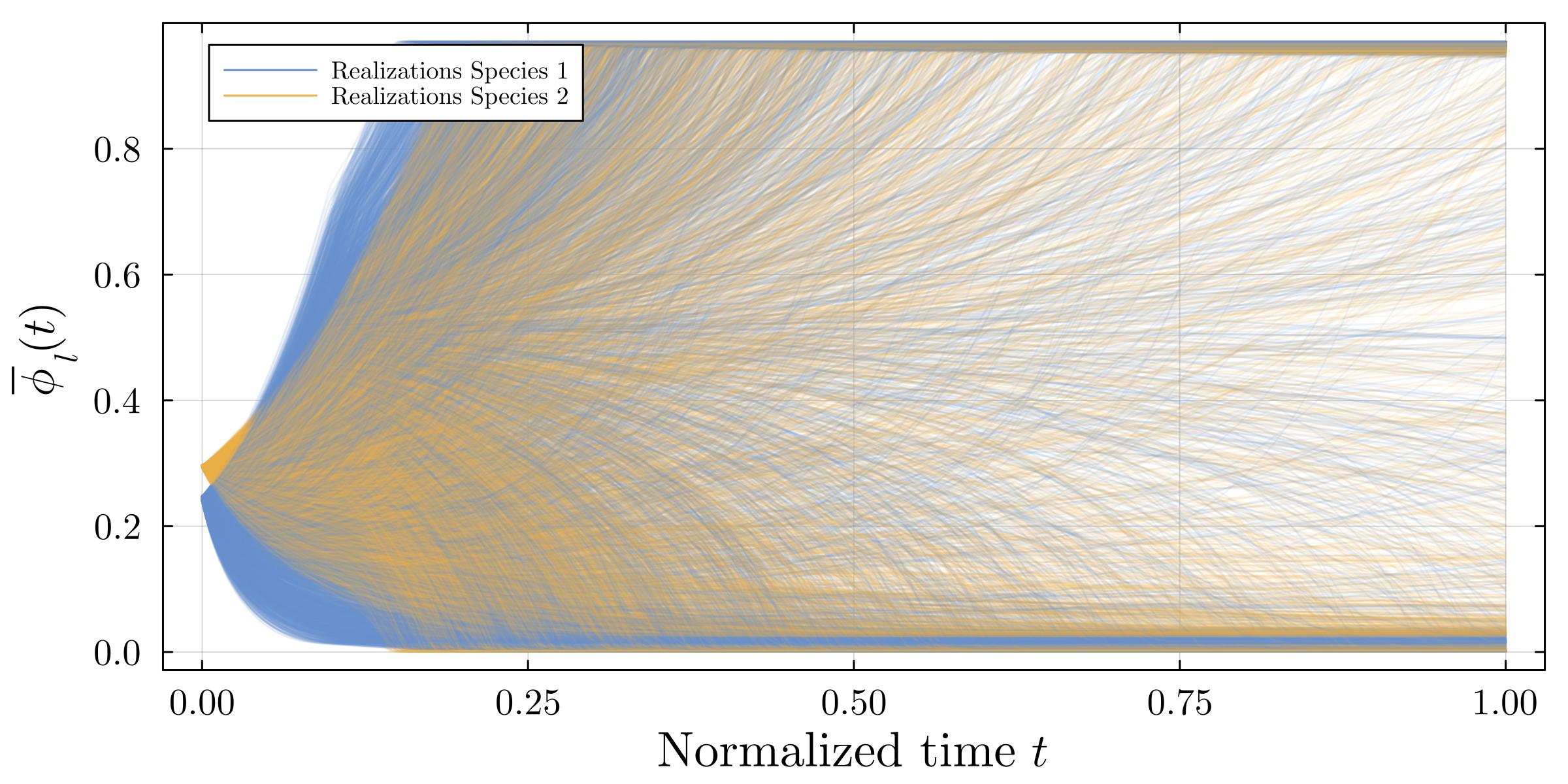
Accurate modeling of bacterial biofilm growth is essential for understanding their complex dynamics in biomedical, environmental, and industrial settings. These dynamics are shaped by a variety of environmental influences, including the presence of antibiotics, nutrient availability, and inter-species interactions, all of which affect species-specific growth rates. However, capturing this behavior in computational models is challenging due to the presence of hybrid uncertainties, a combination of epistemic uncertainty (stemming from incomplete knowledge about model parameters) and aleatory uncertainty (reflecting inherent biological variability and stochastic environmental conditions). In this work, we present a Bayesian model updating (BMU) framework to calibrate a recently introduced multi-species biofilm growth model. To enable efficient inference in the presence of hybrid uncertainties, we construct a reduced-order model (ROM) derived using the Time-Separated Stochastic Mechanics (TSM) approach. TSM allows for an efficient propagation of aleatory uncertainty, which enables single-loop Bayesian inference, thereby avoiding the computationally expensive nested (double-loop) schemes typically required in hybrid uncertainty quantification. The BMU framework employs a likelihood function constructed from the mean and variance of stochastic model outputs, enabling robust parameter calibration even under sparse and noisy data. We validate our approach through two case studies: a two-species and a four-species biofilm model. Both demonstrate that our method not only accurately recovers the underlying model parameters but also provides predictive responses consistent with the synthetic data.
Bacterial biofilms are structured microbial communities whose growth dynamics are influenced by environmental conditions, nutrient availability, antibiotics, and interspecies interactions [1]. A key feature of biofilms is their remarkable resilience: they can exhibit up to 1000-fold greater tolerance to antibiotics and environmental stressors compared to planktonic (free-floating) bacteria [2]. This inherent robustness contributes to the widespread presence of biofilms across diverse settings, such as natural ecosystems, industrial systems, and clinical environments. In industrial and environmental contexts, biofilms can play beneficial roles, such as in wastewater treatment processes [3]. However, they are also associated with numerous challenges, including persistent infections [4,5], medical device contamination [6], and infrastructure biofouling [7]. One particularly important area is oral biofilm formation, which can lead to infections around dental implants [8][9][10][11].
In many environments, biofilms are composed of multiple microbial species that compete for resources and respond collectively to external cues [12][13][14]. Understanding the dynamics of such multispecies biofilms and modeling these systems is critical for any application. Some fundamental interaction principles are outlined by James et al. [15] and they serve as a theoretical foundation of how the species interact, and also how they do not interact in some scenarios. Depending on the specific area of application, different aspects are modeled and different parameters are used to describe the physical and chemical processes of the biofilm growth. Ouidir et al. [16] review different approaches for the modeling of such systems and classify them by application to wastewaster treatment, soil, and biomedical applications. Specifically, they focus on biofilms in the oral cavity which is important for dental applications, also highlighted in [14,17].
A recently proposed continuum model by Klempt et al. [18], derived from the extended Hamilton principle, captures multi-species biofilm growth by introducing abstract material parameters. However, these parameters are typically unknown and subject to uncertainty. Combined with the inherent stochasticity of biological processes, this presents a significant challenge for constructing predictive and physically meaningful models. Accurate parameter inference is thus essential to identify underlying biofilm properties from data and enable robust modeling.
Various strategies for calibrating biological models have been proposed. Frequentist approaches, such as those reviewed by Read et al. [19], rely on statistical tests (e.g., Kolmogorov-Smirnov) to compare model output distributions with data. Other works follow similar strategies [20][21][22][23]. In contrast, Bayesian inference provides a probabilistic framework for parameter estimation that naturally incorporates uncertainty [24,25]. While Bayesian methods offer interpretability and flexibility, their computational cost remains a key limitation. Recent developments, including modern Markov Chain Monte Carlo (MCMC), sequential Monte Carlo, and Approximate Bayesian Computation (ABC), have helped mitigate this burden [24].
Despite their advantages, parameter calibration is often neglected in biofilm modeling. For example, Shewa et al. [23] and Rittmann et al. [26] note that default literature values are frequently used instead of performing parameter calibration. Recent studies have demonstrated the value of Bayesian inference for biofilm models, including parameter estimation with quorum sensing [27] and the inference of rheological properties from experimental data [28]. In the field of computational mechanics, Willmann et al. [29] propose a Bayesian framework for the calibration of a model of multi-physics bioflm model introduced in Ref. [30]. The authors present an approach that can also handle unavoidable uncertainty and reduces the computational cost through the use of a Gaussian process surrogate for the log-likelihood. Further, different discrepancy metrics are introduced and compared in their study.
The problem to estimate parameters under uncertainty with limited experimental data is also present in many other fields of applications. One such application is the estimation of parameters of constitutive models in computational mechanics. Wollner et al. [31] present a Bayesian inference framework which they apply to the parameter estimation of the hyperelastic Ogden model. A summary of approaches common in applications in mechanical and civil engineering are given in Ref. [32]. There, again, we come back to Bayesian inference which allows for the handling of the unknown parameters through a posterior probability distribution of said parameters conditioned on the observed data. In engineering applications this is commonly referred to as Bayesian model updating (BMU) and related to the contribution of Beck and Katafygiotis [33].
Building
This content is AI-processed based on open access ArXiv data.