Human cognition spans perception, memory, intuitive judgment, deliberative reasoning, action selection, and social inference, yet these capacities are often explained through distinct computational theories. Here we present a unified mathematical framework in which diverse cognitive processes emerge from a single geometric principle. We represent the cognitive state as a point on a differentiable manifold endowed with a learned Riemannian metric that encodes representational constraints, computational costs, and structural relations among cognitive variables. A scalar cognitive potential combines predictive accuracy, structural parsimony, task utility, and normative or logical requirements. Cognition unfolds as the Riemannian gradient flow of this potential, providing a universal dynamical law from which a broad range of psychological phenomena arise. Classical dual-process effects--rapid intuitive responses and slower deliberative reasoning--emerge naturally from metric-induced anisotropies that generate intrinsic time-scale separations and geometric phase transitions, without invoking modular or hybrid architectures. We derive analytical conditions for these regimes and demonstrate their behavioural signatures through simulations of canonical cognitive tasks. Together, these results establish a geometric foundation for cognition and suggest guiding principles for the development of more general and human-like artificial intelligence systems.
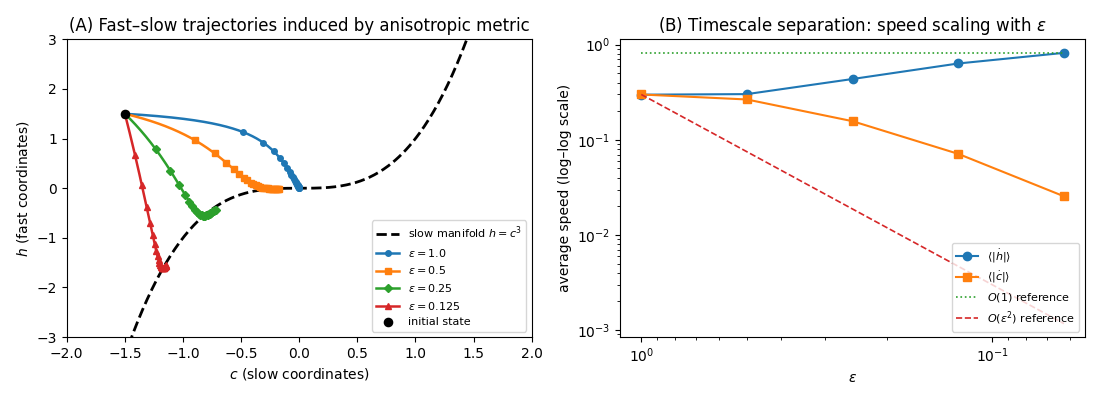
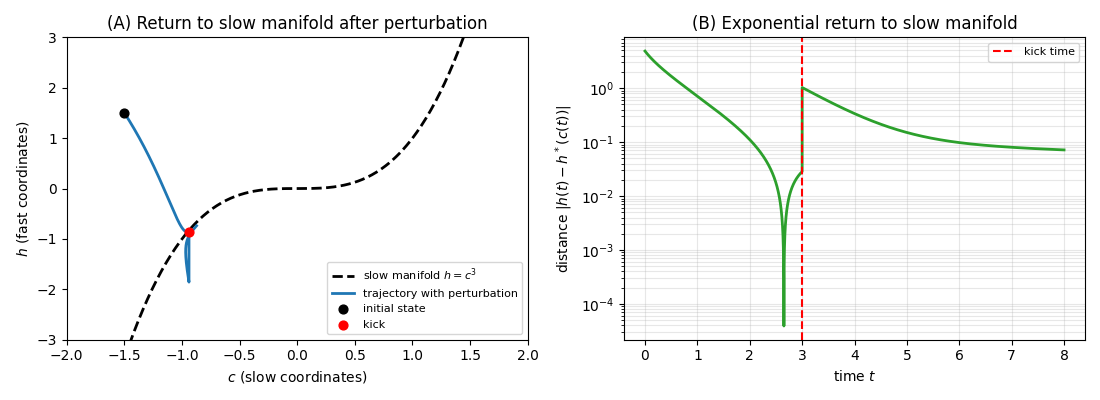
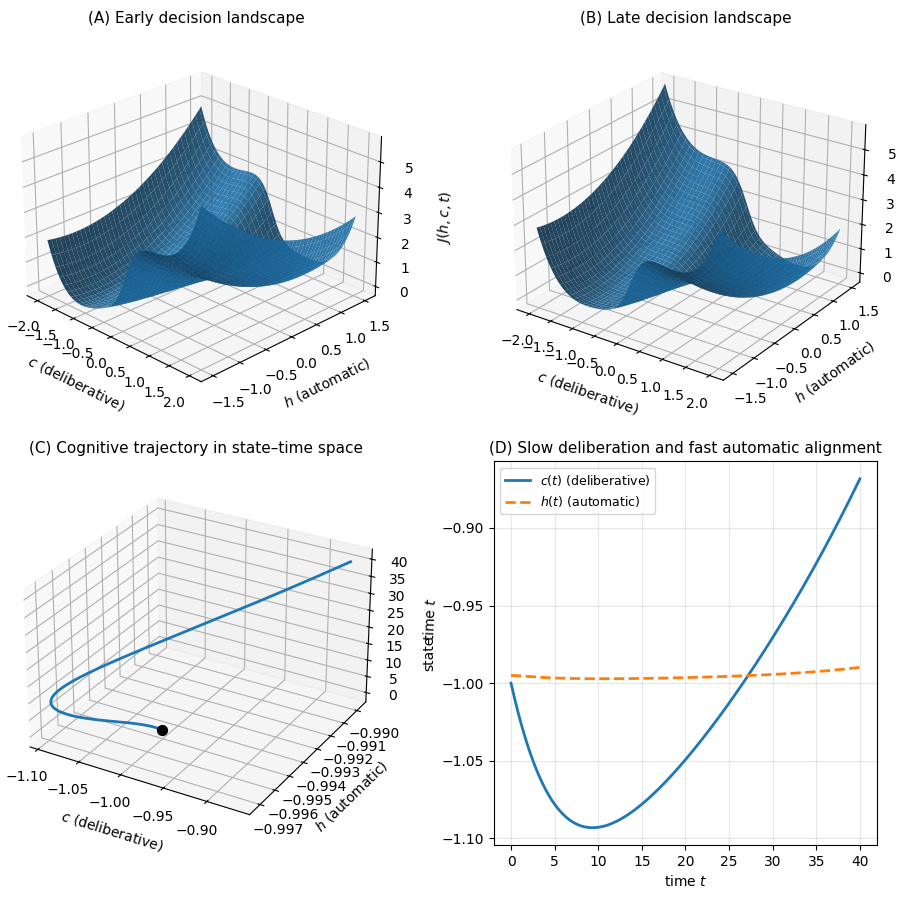
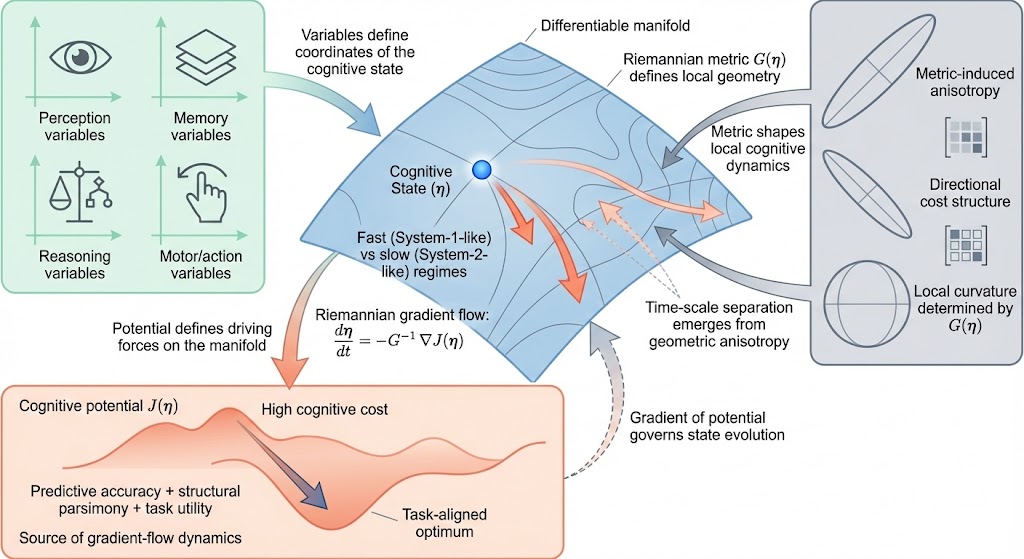
. Geometric representation of the cognitive state and its dynamics. The cognitive state is modelled as a point on a differentiable manifold whose geometry captures relationships among perceptual, memory, motor, and reasoning variables. The Riemannian metric encodes representational constraints and computational costs, shaping the local curvature of cognitive space. A cognitive potential integrates predictive, structural and task-related drives into a scalar landscape over the manifold. Cognition unfolds as gradient flow on this landscape, with steep directions producing rapid, intuitive dynamics and shallow directions supporting slower, deliberative exploration. Together, these geometric components provide a unified computational structure from which diverse cognitive regimes emerge.
Together, these results establish a geometric foundation for cognition, showing that a single mathematical principle can generate multiple cognitive regimes and unify previously disparate theories. This framework suggests new links between cognitive science, 22 neuroscience and artificial intelligence, and provides a route toward a general theory of adaptive intelligent behaviour.
In this section, we formalise cognition as a gradient flow on a geometric space. We begin by defining the cognitive state, cognitive potential, and Riemannian metric, then present basic properties of the resulting dynamical system.
In our formulation, cognition is expressed as the evolution of an internal state driven by the minimisation of a scalar objective. To make this precise, we introduce two basic mathematical objects: the cognitive state, which describes the agent’s internal configuration at time t, and the cognitive potential, a scalar quantity that evaluates the quality, efficiency, or coherence of that configuration.
Definition 1 (Cognitive state and cognitive potential). The cognitive state at time t is represented by a vector η(t) = η 1 (t), η 2 (t), . . . , η n (t) ∈ R n , and the cognitive potential is a function J : R n → R, η → J(η), which we assume to be twice continuously differentiable, J ∈ C 2 .
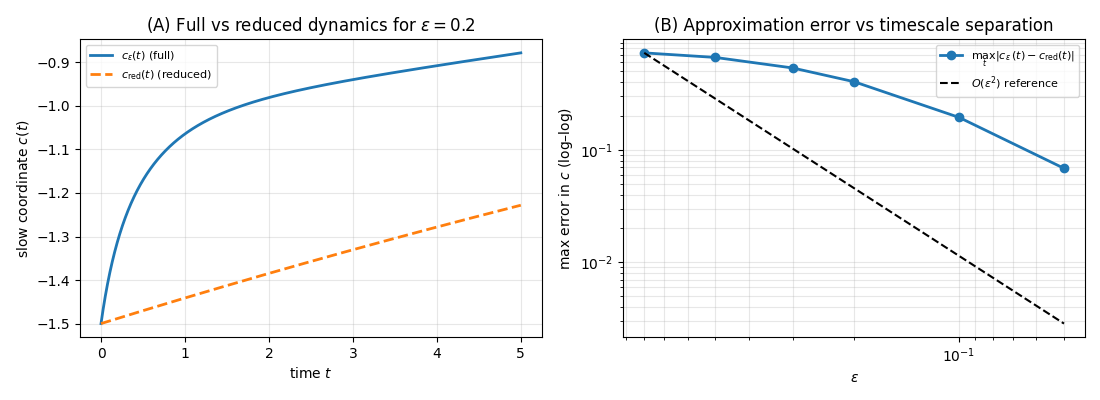
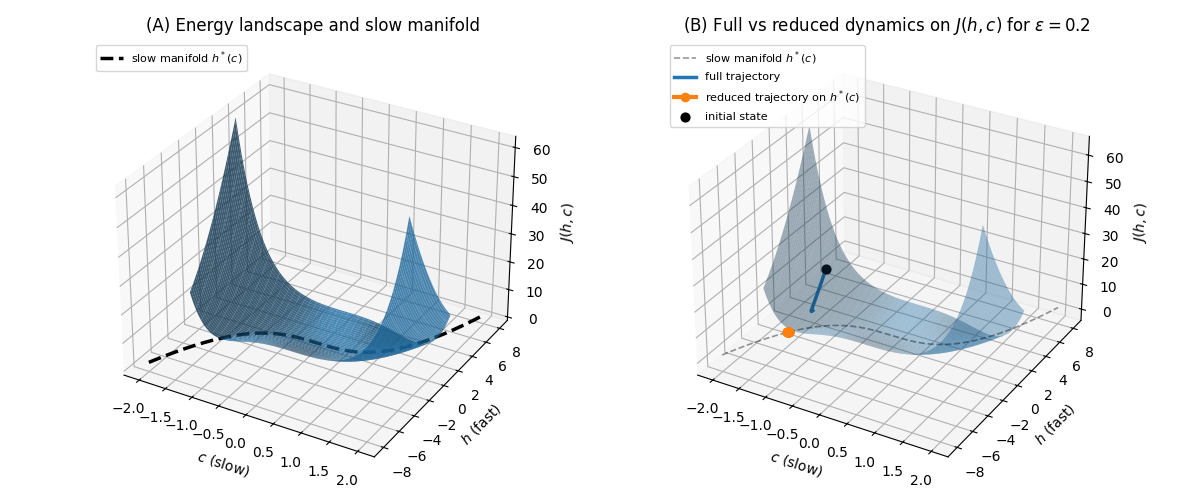
The assumption J ∈ C 2 ensures that both the gradient ∇J and the Hessian ∇ 2 J exist and vary smoothly. This regularity is essential for the framework developed below: gradient-flow dynamics require ∇J; stability and curvature-based analyses rely on ∇ 2 J; and the fast-slow decomposition used to model intuitive versus deliberative cognition depends on smoothness to apply classical geometric singular perturbation theory. Together, these conditions guarantee that the resulting cognitive dynamics are well-defined and amenable to rigorous geometric analysis.
The function J(η) assigns a real-valued score to each cognitive state and serves as a global cognitive objective. Its role is analogous to a loss function in machine learning or to a potential-energy landscape in physics, providing a unified quantity that governs the system’s internal dynamics. Crucially, J integrates the diverse pressures that shape cognition into a single scalar potential: prediction accuracy, representational simplicity, decision-theoretic utility, logical or normative consistency, and the resource or computational costs associated with maintaining and transforming internal representations. In the sections that follow, we show how these heterogeneous drives can be expressed within a common geometric framework and how their joint optimisation yields coherent cognitive behaviour.
Cognition involves balancing several competing pressures simultaneously-such as predicting the world accurately, selecting effective actions, maintaining internal consistency, generalising from limited information, and minimising cognitive effort. Rather than treating these as separate objectives, we combine them into a single scalar potential,
where J prediction penalises mismatch between internal predictions and observations, J complexity penalises unnecessary representational or structural complexity, J reward captures task utility or goal-directed value, J norms encodes logical, social, or consistency constraints, J effort reflects computational or attentional costs, and • • • indicates that additional task-or domain-specific components may be included. Together, these components form a unified cognitive potential that captures the trade-offs inherent to cognition. The smoothness of J ensures that its gradient and curvature are well defined, laying the foundation for the geometric gradient-flow framework developed below.
To describe how the cognitive state evolves over time, we endow the cognitive manifold with a geometry that specifies which directions in state space are easy or difficult to move through. This geometry is encoded by a Riemannian metric, 23,24 which in our formulation is represented in coordinates by a positive-definite matrix that may vary with the state.
a symmetric, positive-definite matrix whose entries encode the local geometric structure of the cognitive manif
This content is AI-processed based on open access ArXiv data.