Let $\mathcal{P}$ be the surface of a convex polyhedron with $n$ vertices. We consider the two-point shortest path query problem for $\mathcal{P}$: Constructing a data structure so that given any two query points $s$ and $t$ on $\mathcal{P}$, a shortest path from $s$ to $t$ on $\mathcal{P}$ can be computed efficiently. To achieve $O(\log n)$ query time (for computing the shortest path length), the previously best result uses $O(n^{8+ε})$ preprocessing time and space [Aggarwal, Aronov, O'Rourke, and Schevon, SICOMP 1997], where $ε$ is an arbitrarily small positive constant. In this paper, we present a new data structure of $O(n^{6+ε})$ preprocessing time and space, with $O(\log n)$ query time. For a special case where one query point is required to lie on one of the edges of $\mathcal{P}$, the previously best work uses $O(n^{6+ε})$ preprocessing time and space to achieve $O(\log n)$ query time. We improve the preprocessing time and space to $O(n^{5+ε})$, with $O(\log n)$ query time. Furthermore, we present a new algorithm to compute the exact set of shortest path edge sequences of $\mathcal{P}$, which are known to be $Θ(n^4)$ in number and have a total complexity of $Θ(n^5)$ in the worst case. The previously best algorithm for the problem takes roughly $O(n^6\log n\log^*n)$ time, while our new algorithm runs in $O(n^{5+ε})$ time.
Let P denote the surface of a convex polyhedron with n vertices. We can represent P by a planar graph with additional geometric information describing the location of vertices and edges. By Euler's formula, the number of edges and faces in P is O(n). Each face of P is a convex polygon. We can assume that each face is associated with a coordinate system on its supporting plane, i.e., the plane containing the face. For any two points s and t on P, let π(s, t) denote a shortest path from s to t on P, and its length, denoted by d(s, t), is called the geodesic distance between s and t. We use |π(s, t)| to denote the number of edges in the path. Two-point shortest path queries. We consider the two-point shortest path query problem for P: Construct a data structure so that a shortest s-t path π(s, t) can be computed efficiently for any two query points s, t ∈ P. The previously best result was given by Aggarwal, Aronov, O'Rourke, and Schevon [1]. To achieve O(log n) query time to compute the geodesic distance d(s, t), their data structure requires O(n 8+ϵ ) space and O(n 8+ϵ ) preprocessing time. Throughout the paper, ϵ represents an arbitrarily small positive constant. Their query algorithm does not output the path π(s, t). No further progress had been made on this problem in the 35 years since their result was first announced in 1990. In this paper, we improve preprocessing time and space to O(n 6+ϵ ) while still achieving the O(log n) query time for computing d(s, t). In addition, our query algorithm can output π(s, t) in additional O(|π(s, t)|) time.
The edge-face case. In the edge-face case, one query point is required to lie on one of the edges of P. For this case, the previously best result was also given in [1]. To achieve O(log n) query time for computing d(s, t), the data structure in [1] uses O(n 6+ϵ ) space and preprocessing time. We present a new data structure of O(n 5+ϵ ) space and preprocessing time, with O(log n) query time. In addition, π(s, t) can be output in additional O(|π(s, t)|) time. In particular, given an edge e of P, we can construct a data structure of O(n 4+ϵ ) space and preprocessing time, such that for any query (s, t) with s ∈ e and t ∈ P, d(s, t) can be computed in O(log n) time and π(s, t) can be output in additional O(|π(s, t)|) time.
Note that Cook IV and Wenk [24] considered a special case in which s is required to be on a given edge e of P and t is required to be on another edge P. They constructed a data structure of O(n 5 ) space in O(n 5 log n) time such that d(s, t) can be computed in O(log 2 n) time for any query (s, t). Hence, our above result, which works for a more general type of queries, even improves upon their work in this restricted setting.
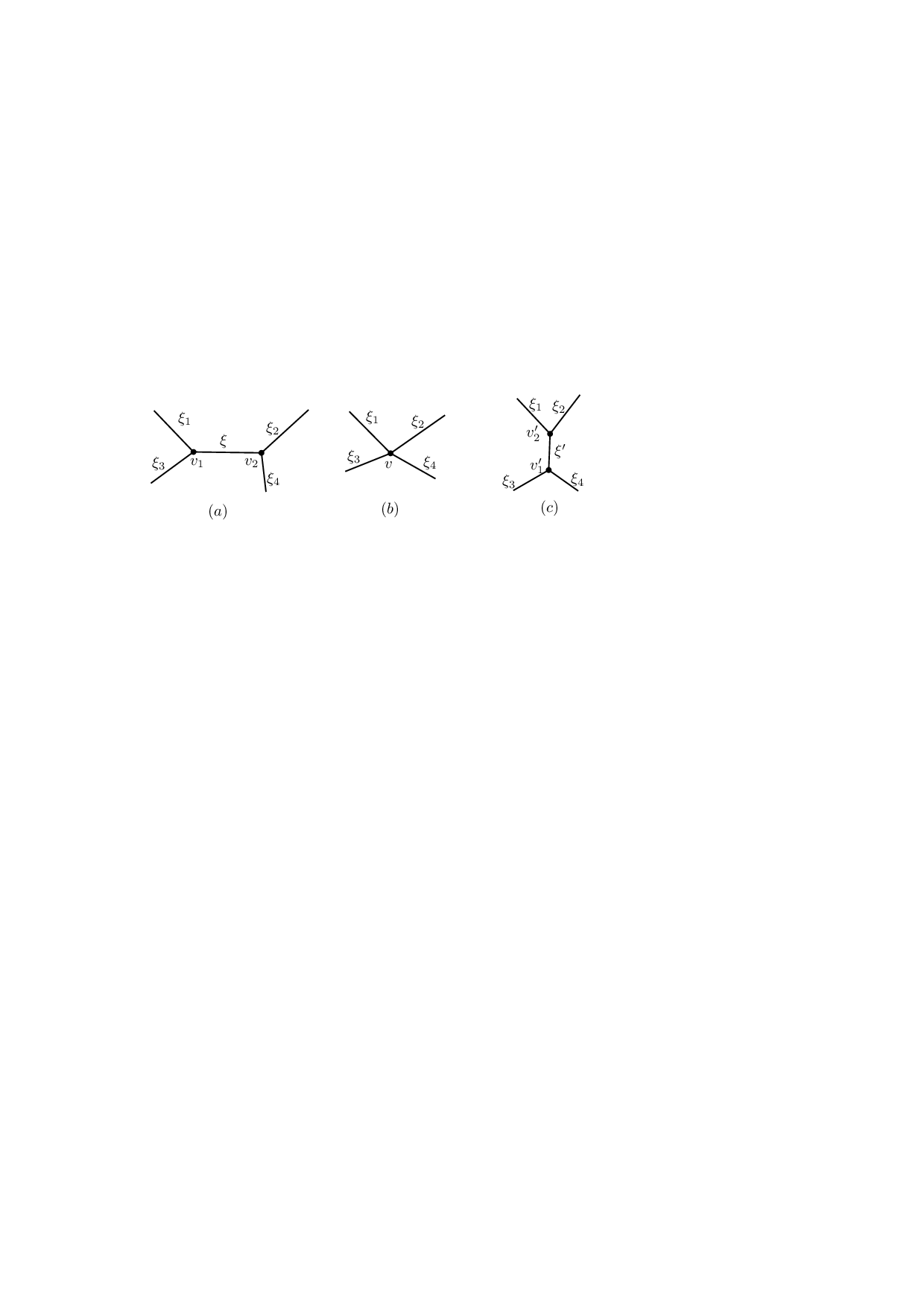
Shortest path edge sequences. For any shortest path π(s, t) on P, it has the following properties [43]: (1) π(s, t) can cross every edge of P at most once; (2) the intersection between π(s, t) and any face of P is a single line segment; (3) the interior of π(s, t) cannot contain any vertex of P. Furthermore, there is an unfolding property: If we unfold all faces of P intersected by π(s, t) into one plane, then π(s, t) becomes a line segment in the unfolded plane. The sequence of edges of P crossed by π(s, t) is called the edge sequence of π(s, t). Once the edge sequence of π(s, t) is known, π(s, t) can be easily obtained due to the unfolding property.
A sequence of edges of P is a shortest path edge sequence if it is the sequence of edges crossed by a shortest path on P. It is known that the number of shortest path edge sequences of P is O(n 4 ) and this bound is tight in the worst case [34]. Computing all shortest path edge sequences will be useful for understanding the structure of shortest paths on P and also useful for designing algorithms to compute obstacle-avoiding paths among polyhedral obstacles in the 3D space [38,39,41].
Schevon and O’Rourke [38] gave an algorithm that can compute all shortest path edge sequences in O(n 9 log n) time. Based on a so-called star unfolding, Agarwal, Aronov, O’Rourke, and Schevon [1] gave an improved algorithm of roughly O(n 6 log n log * n) time, and later Cook IV and Wenk [24] devised an alternative algorithm of the same runtime using kinetic Voronoi diagrams [19]. In this paper, we present a new algorithm of O(n 5+ϵ ) time. This is the first progress on the runtime for the problem since the algorithm of [1] was first announced in 1990.
Note that since the number of shortest path edge sequences can be Θ(n 4 ) and each sequence can have Ω(n) edges in the worst case [34], it requires Ω(n 5 ) time to explicitly list all edges in all edge sequences. Therefore, our algorithm, which runs in O(n 5+ϵ ) time, is almost optimal for that purpose.
Note that all above algorithms are for computing the exact set of shortest path edge sequences. Computing a superset of them is easier and algorithms were also known [1,24,41].
Shortest paths on polyhedral surfaces have been extensively studied
This content is AI-processed based on open access ArXiv data.