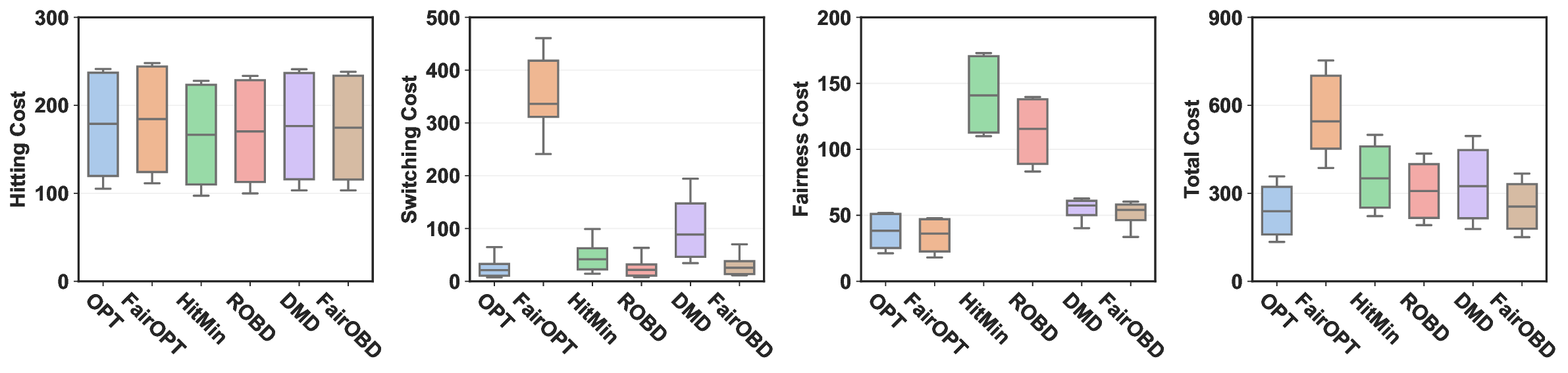
Fairness and action smoothness are two crucial considerations in many online optimization problems, but they have yet to be addressed simultaneously. In this paper, we study a new and challenging setting of fairness-regularized smoothed online convex optimization with switching costs. First, to highlight the fundamental challenges introduced by the long-term fairness regularizer evaluated based on the entire sequence of actions, we prove that even without switching costs, no online algorithms can possibly achieve a sublinear regret or finite competitive ratio compared to the offline optimal algorithm as the problem episode length $T$ increases. Then, we propose FairOBD (Fairness-regularized Online Balanced Descent), which reconciles the tension between minimizing the hitting cost, switching cost, and fairness cost. Concretely, FairOBD decomposes the long-term fairness cost into a sequence of online costs by introducing an auxiliary variable and then leverages the auxiliary variable to regularize the online actions for fair outcomes. Based on a new approach to account for switching costs, we prove that FairOBD offers a worst-case asymptotic competitive ratio against a novel benchmark -- the optimal offline algorithm with parameterized constraints -- by considering $T\to\infty$. Finally, we run trace-driven experiments of dynamic computing resource provisioning for socially responsible AI inference to empirically evaluate FairOBD, showing that FairOBD can effectively reduce the total fairness-regularized cost and better promote fair outcomes compared to existing baseline solutions.
Smoothed decision-making is critical to reducing abrupt and even potentially dangerous large action changes in many online optimization problems, e.g., energy production scheduling in power grids, object tracking, motion planning, and server capacity provisioning in data centers, among others [47,55,2]. Mathematically, action smoothness can be effectively achieved by including into the optimization objective a switching cost that penalizes temporal changes in actions. The added switching cost essentially equips the online optimization objective with a (finite) memory of the previous actions and also creates substantial algorithmic challenges. As such, it has received a huge amount of attention in the last decade, with a quickly growing list of algorithms developed under various settings (see [50,3,32,45,30,55,47,13,34,11] and the references therein).
Additionally, (long-term) fairness is a crucial consideration that must be carefully addressed in a variety of online optimization problems, especially those that can profoundly impact individuals’ well-being and social welfare. For example, sequential allocation of social goods to different individuals/groups must be fair without discrimination [6,49], the surging environmental costs of geographically distributed AI data centers must be fairly distributed across different regions as mirrored in recent repeated calls by various organizations and government agencies [22,10,28,23], and AI model performance and resource provisioning must promote social fairness without adversely impacting certain disadvantaged individuals/groups [43]. If not designed with fairness in mind, online algorithms can further perpetuate or even exacerbate societal biases, which can disproportionately affect certain groups/individuals and amplify the already widening socioeconomic disparities. Therefore, fairness in online optimization is not just a matter of ethical concern but also a necessity for ensuring broader social responsibility.
The incorporation of a long-term fairness regularizer into the objective function can effectively achieve fairness in online optimization by mitigating implicit or explicit biases that could otherwise be reinforced [6,40,39,28]. Despite its effectiveness in promoting fairness, the added fairness regularizer presents significant challenges for online optimization [6,40]. This arises from the lack of complete future information, which is required to evaluate the fairness regularizer. Intuitively, online decision-makers prioritize immediate cost reduction, reacting to sequentially revealed information, potentially neglecting the long-term consequences of the decision sequence.
Recent research has started to explore fairness in various online problems, such as online resource allocation, using primal-dual techniques [39,6,35]. However, a major limitation of current fair online algorithms lies in their reliance on the assumption that per-round objective functions are independent of historical actions. This assumption plays a pivotal role in both algorithm design and theoretical analysis (e.g., [6,7]). For instance, in a simple resource allocation scenario, while the maximum allowable action at time t and its corresponding reward may depend on past allocation decisions through the remaining budget, the revenue or reward function at time t is assumed to depend only on the current allocation decision and remain independent of these historical decisions. However, these methods fall short in addressing online problems where the per-round objective function is directly impacted by historical actions, such as those involving switching costs, as detailed in Section 2.
In this paper, we study fairness-regularized smoothed online optimization with switching costs, a new and challenging setting that has not been considered in the literature to our knowledge. More specifically, we incorporate a fairness regularizer that captures the long-term impacts of online actions, and aim to minimize the sum of a per-round hitting cost, switching cost, and a long-term fairness cost. To simultaneously address the tension between minimizing the hitting cost, switching cost, and fairness cost, we propose FairOBD (Fairness-regularized Online Balanced Descent).
Optimizing the long-term cost with a sequentially revealed context sequence is widely recognized as a challenging problem (e.g., [39,6,7,12,38,26]). A common strategy to address this challenge involves decomposing the long-term fairness cost into a sequence of online costs by introducing an auxiliary variable (e.g. [8,41,35], which effectively converts the fairness cost into an equivalent longterm constraint. However, the key limitation of existing methods is the requirement of independence between per-round objective functions, which is violated by the switching cost. Specifically, given the updated Lagrangian multiplier, the per-round online objective depends on the previous irrevocable action due to the switching cost. Thi
This content is AI-processed based on open access ArXiv data.