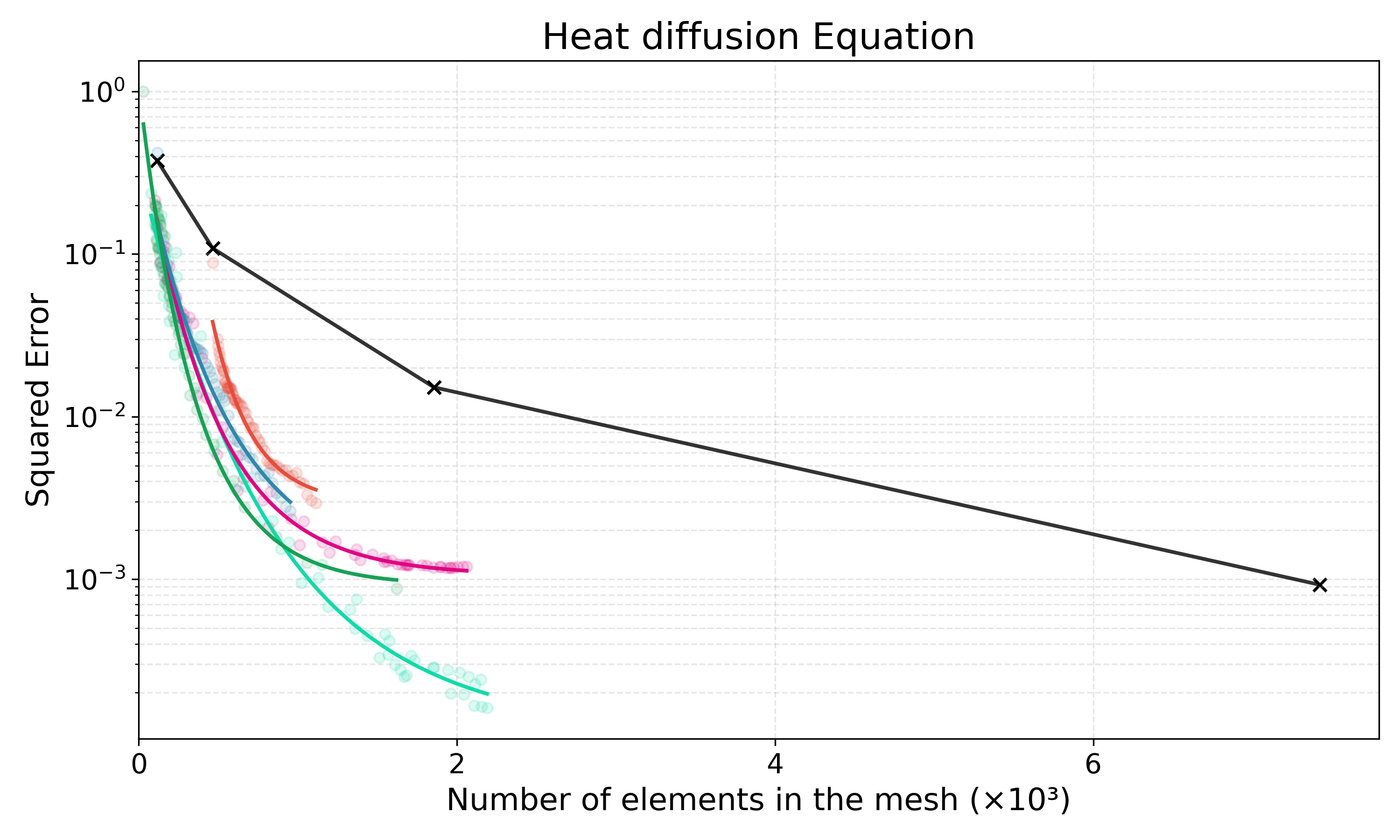
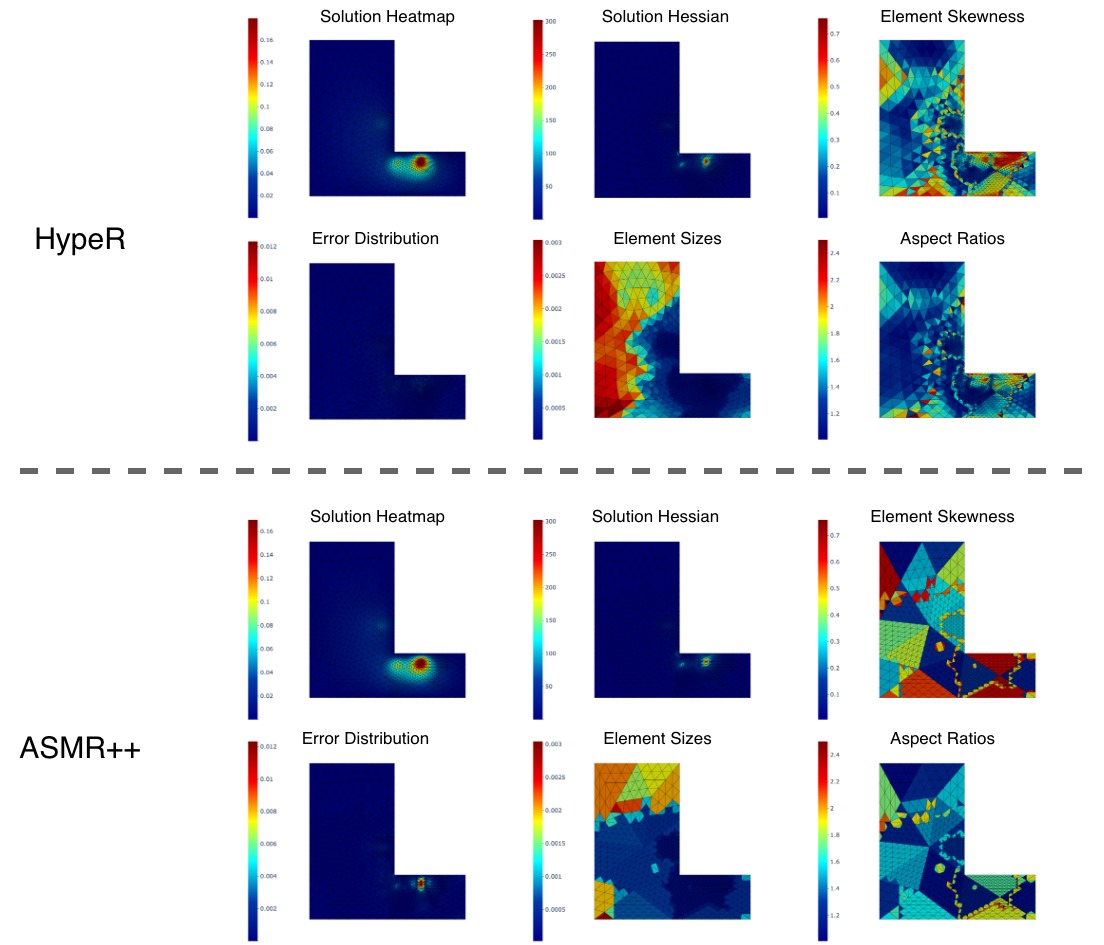
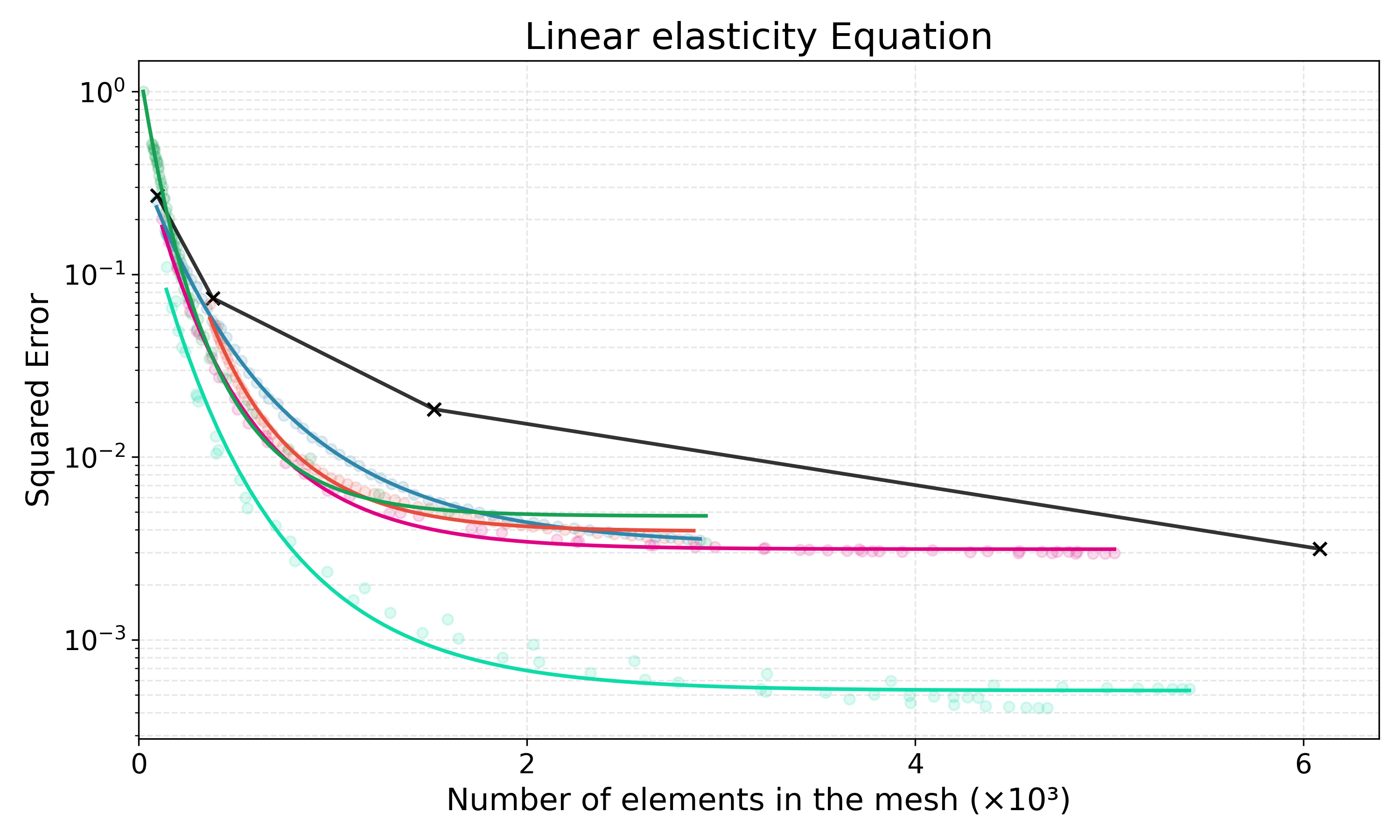
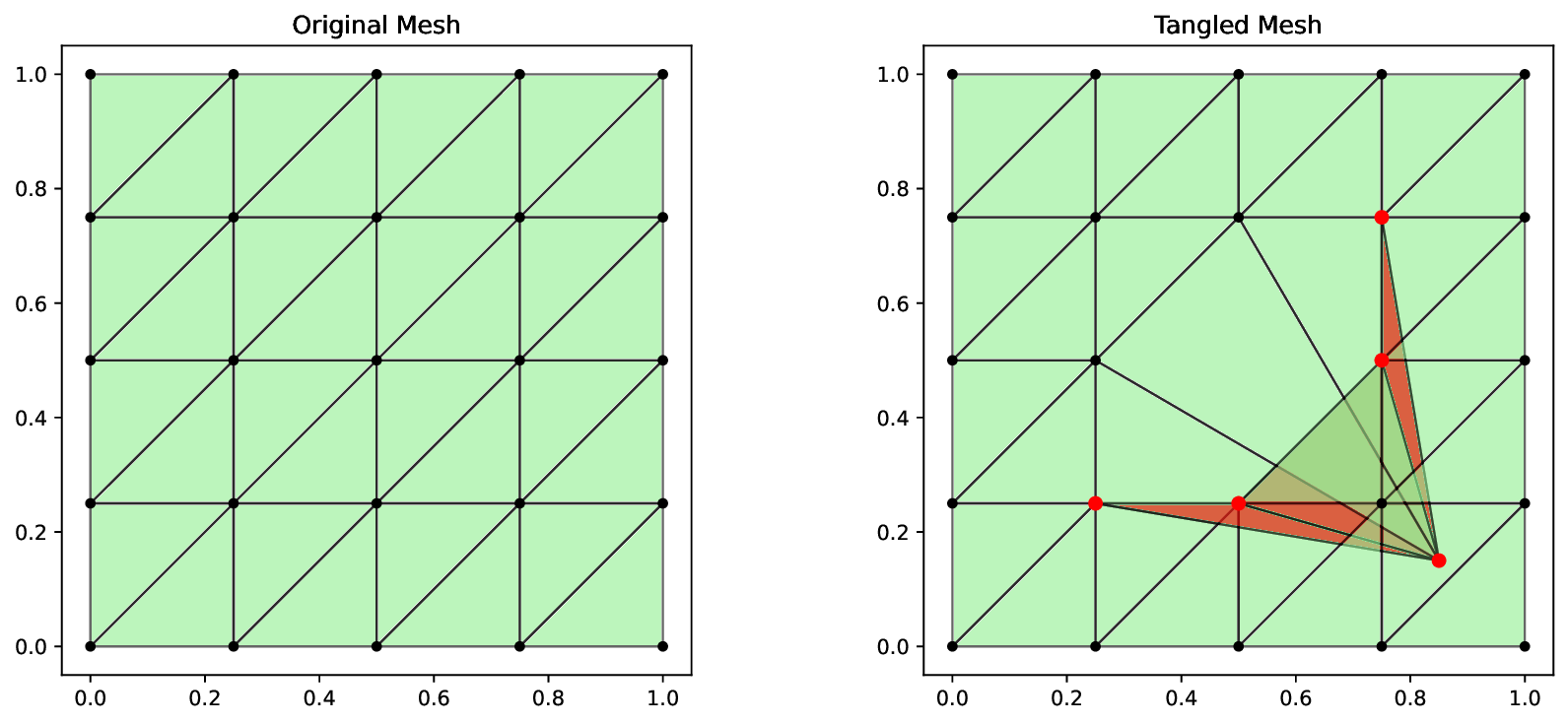
Adaptive mesh refinement is central to the efficient solution of partial differential equations (PDEs) via the finite element method (FEM). Classical $r$-adaptivity optimizes vertex positions but requires solving expensive auxiliary PDEs such as the Monge-Ampère equation, while classical $h$-adaptivity modifies topology through element subdivision but suffers from expensive error indicator computation and is constrained by isotropic refinement patterns that impose accuracy ceilings. Combined $hr$-adaptive techniques naturally outperform single-modality approaches, yet inherit both computational bottlenecks and the restricted cost-accuracy trade-off. Emerging machine learning methods for adaptive mesh refinement seek to overcome these limitations, but existing approaches address $h$-adaptivity or $r$-adaptivity in isolation. We present HypeR, a deep reinforcement learning framework that jointly optimizes mesh relocation and refinement. HypeR casts the joint adaptation problem using tools from hypergraph neural networks and multi-agent reinforcement learning. Refinement is formulated as a heterogeneous multi-agent Markov decision process (MDP) where element agents decide discrete refinement actions, while relocation follows an anisotropic diffusion-based policy on vertex agents with provable prevention of mesh tangling. The reward function combines local and global error reduction to promote general accuracy. Across benchmark PDEs, HypeR reduces approximation error by up to 6--10$\times$ versus state-of-art $h$-adaptive baselines at comparable element counts, breaking through the uniform refinement accuracy ceiling that constrains subdivision-only methods. The framework produces meshes with improved shape metrics and alignment to solution anisotropy, demonstrating that jointly learned $hr$-adaptivity strategies can substantially enhance the capabilities of automated mesh generation.
Partial differential equations (PDEs) model a vast array of physical phenomena, from fluid dynamics and heat transfer to structural mechanics and electromagnetic fields Evans (2010); LeVeque (2007). The finite element method (FEM) has emerged as the predominant numerical method for solving PDEs at scale, offering robustness, well-established error bounds, and mature software implementations Brenner and Scott (2008); Ern and Guermond (2004). However, even with highly optimized solvers, the computational cost of simulations grows rapidly with the number of degrees of freedom (DOFs). Denoting by N the total number of DOFs, memory requirements typically grow superlinearly, and the cost of direct sparse factorization scales as O(N 3/2 ) in two dimensions and as O(N 2 ) in three dimensions. By contrast, optimal multigrid or multilevel iterative methods can in many cases achieve O(N ) complexity Saad (2003). This makes large-scale problems computationally prohibitive Babuška and Suri (1994), motivating mesh adaptation: strategically redistributing mesh resolution HypeR (single fwd pass)
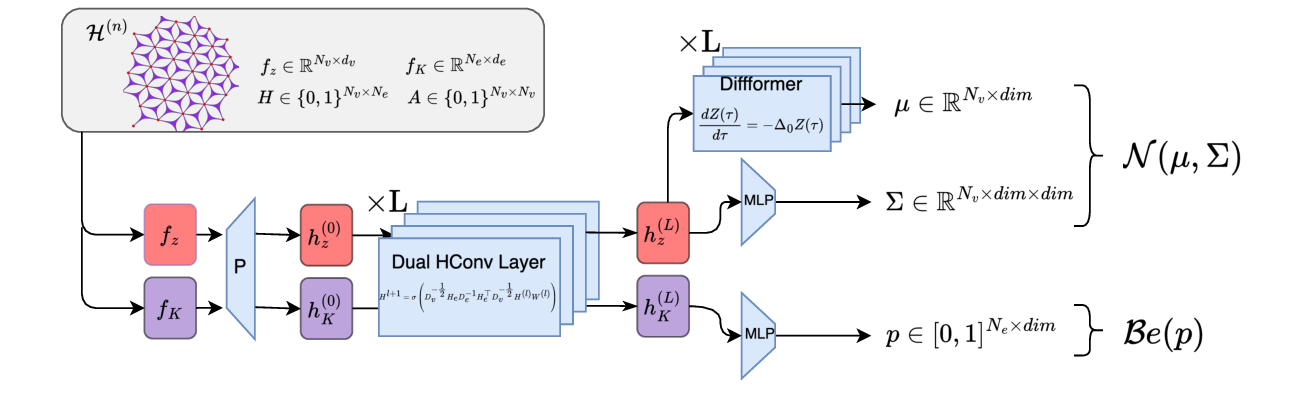
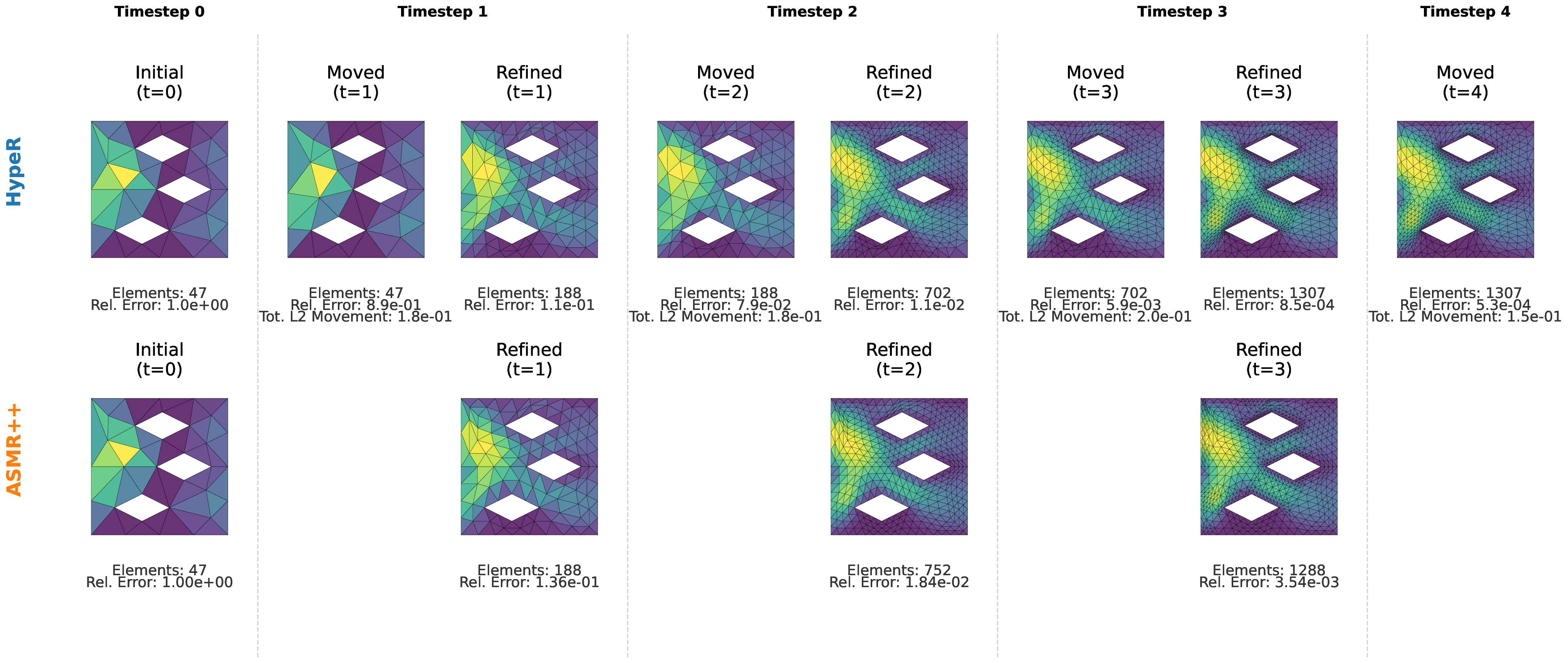
Figure 1: A high-level schematic of the HypeR framework at inference. Starting from an initial coarse mesh T (0) , the HypeR policy network is applied iteratively. At each step, the network takes the current mesh T (n) and, in a single forward pass, jointly outputs the refinement vector b (n) and the vertex relocation map Φ(Z (n) ) to produce the next adapted mesh T (n+1) .
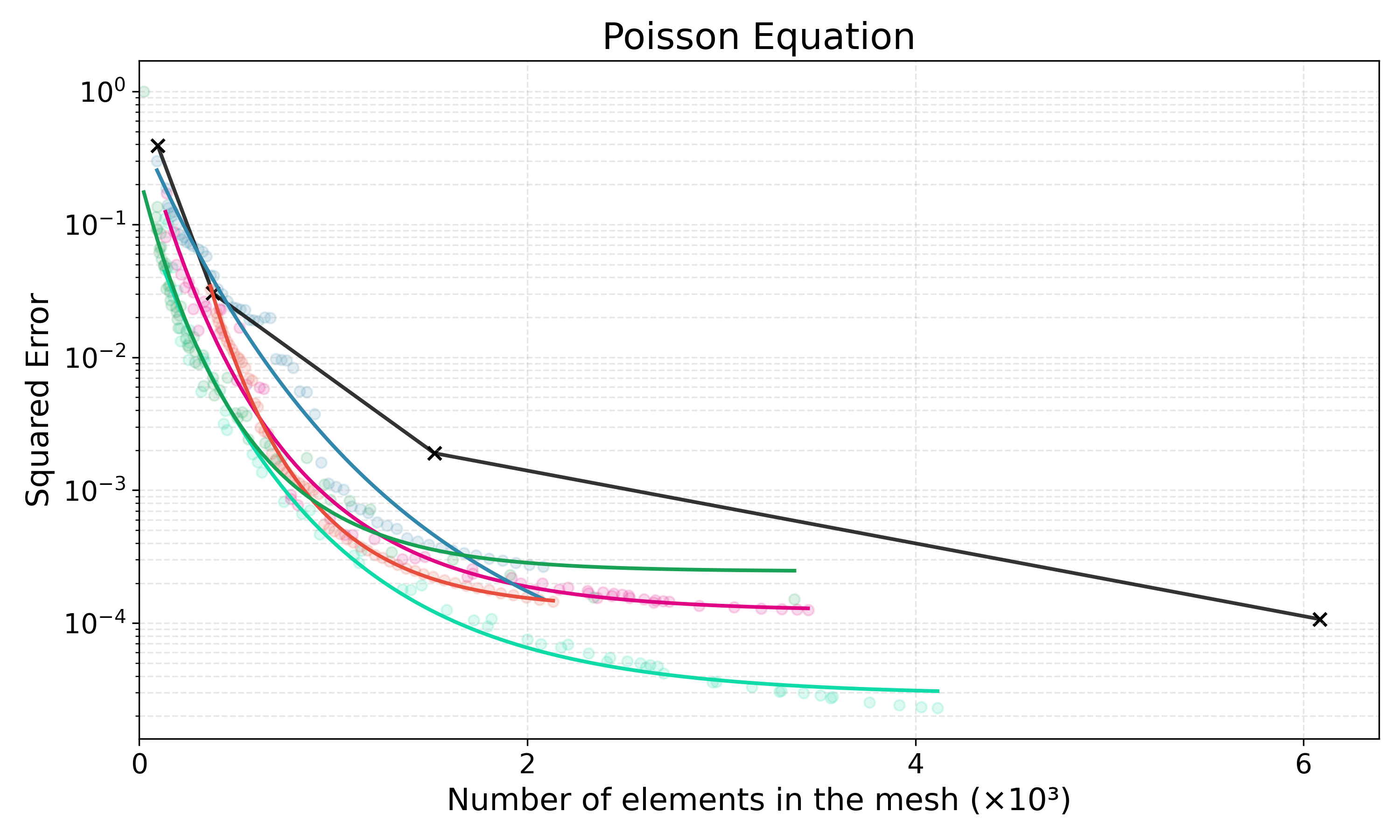
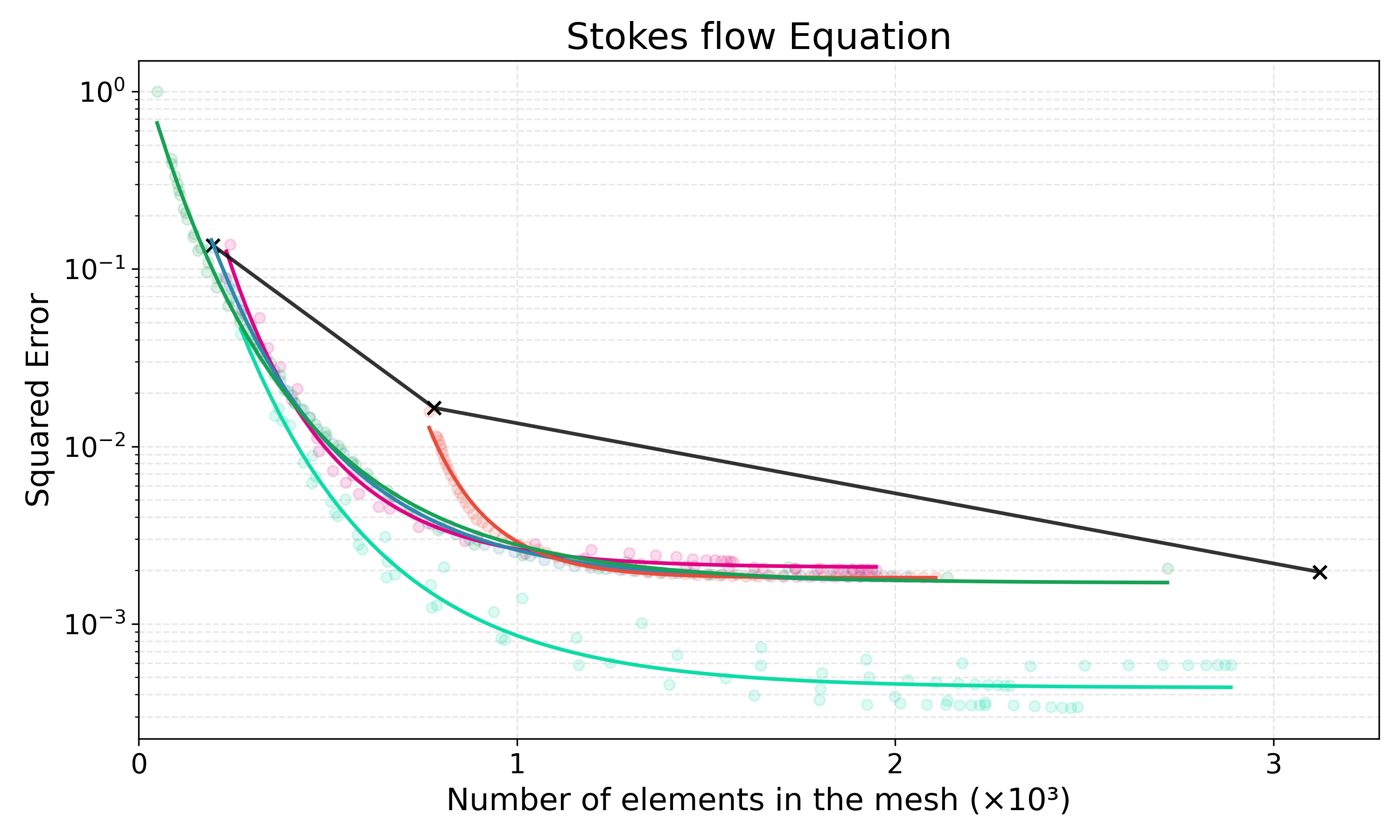
(i.e., the local density of DOFs or mesh vertices) that optimizes the cost-accuracy trade-off in order to capture solution features where they matter most. Classical mesh adaptation strategies include two complementary techniques, each addressing different aspects of the accuracy-efficiency trade-off. h-adaptation modifies mesh topology through element subdivision or coarsening, dynamically adjusting local resolution based on a posteriori error estimators. Popular approaches include the Zienkiewicz-Zhu (ZZ) superconvergent patch recovery technique Zienkiewicz and Zhu (1992), which estimates element-wise errors η K through gradient reconstruction, and Dörfler marking strategies Dörfler (1996), which refine elements contributing to a fixed fraction of the total error Verfürth (1996); Ainsworth and Oden (2000). In contrast, r-adaptation relocates a fixed number of mesh vertices while preserving connectivity, optimizing vertices positions through a continuous mapping Φ. This typically requires solving auxiliary PDE problems, such as the Monge-Ampère equation for optimal transport-based mesh movement Budd et al. (2009); Delzanno et al. (2008); Huang and Russell (2011). While h-methods can arbitrarily increase resolution, they suffer from exponential growth in DOFs. In contrast, r-methods maintain a fixed number of DOFs, but are limited by the initial mesh topology. The optimal strategy -hr-adaptation -combines both approaches, yet traditional numerical methods treat them sequentially, missing potential synergies and requiring complex bookkeeping of element hierarchies and projection operators Alauzet and Loseille (2016); Bank and Xu (2003). Crucially, these combined techniques inherit the computational bottlenecks of both modalities, from solving expensive auxiliary PDEs to costly error indicator computations, limiting their practical efficiency.
An emerging field of machine learning methods has sought to overcome these computational bottlenecks, but existing approaches have largely addressed h-adaptivity or r-adaptivity in isolation. For h-adaptation, deep reinforcement learning (RL) offers a fundamentally different paradigm. By formulating mesh adaptation as a Markov Decision Process (MDP) with state space S (mesh configurations), action space A (adaptation operations), and reward function R (error reduction), RL agents can learn policies π : S → A that optimize longterm error-efficiency trade-offs Sutton and Barto (2018) (see Appendix C for detailed RL foundations). This approach has shown promise, with methods like ASMR++ Freymuth et al. (2024a) employing swarm-based multi-agent RL to achieve order of magnitude speedups over uniform refinement. In parallel, graph neural network (GNN) approaches have targeted r-adaptation. Many of these, such as the M2N Song et al. (2022) and UM2N Zhang et al. (2024) families, are trained in a supervised manner to imitate the complex mappings generated by classical auxiliary PDE solvers. A distinct GNN-based strategy, employed by G-Adaptivity Rowbottom et al. (2025), bypasses these expensive targets and instead learns to directly minimize FEM error through differentiable simulation. However, each of these methods addresses only one aspect of mesh adaptation, inheriting fundamental limitations: h-only methods cannot exceed uniform refinement accuracy on the initial topology, while r-only methods cannot add DOFs for emerging features.
In this work, we present HypeR, a deep RL framework that computes relocation and refinement ac
This content is AI-processed based on open access ArXiv data.