The performance of algorithms, methods, and models tends to depend heavily on the distribution of cases on which they are applied, this distribution being specific to the applicative domain. After performing an evaluation in several domains, it is highly informative to compute a (weighted) mean performance and, as shown in this paper, to scrutinize what happens during this averaging. To achieve this goal, we adopt a probabilistic framework and consider a performance as a probability measure (e.g., a normalized confusion matrix for a classification task). It appears that the corresponding weighted mean is known to be the summarization, and that only some remarkable scores assign to the summarized performance a value equal to a weighted arithmetic mean of the values assigned to the domain-specific performances. These scores include the family of ranking scores, a continuum parameterized by user preferences, and that the weights to consider in the arithmetic mean depend on the user preferences. Based on this, we rigorously define four domains, named easiest, most difficult, preponderant, and bottleneck domains, as functions of user preferences. After establishing the theory in a general setting, regardless of the task, we develop new visual tools for two-class classification.
The development of algorithms, methods, and models is often complicated by two types of uncertainty. First, the applicative domain, and thus the distribution of inputs, is rarely unique and precisely known during development. Second, user preferences regarding tradeoffs affecting the achievable performance (e.g., to what degree do they prefer false negatives to false positives in classification?) are also generally not precisely known and can differ from one user to another.
Developers can, of course, implement various techniques (continual learning, test-time adaptation, domain adaptation [1], domain generalization [2], . . . ) to make their entity -the term used in this paper for algorithm, method, or model-usable in various domains, but the achievable performance still varies from one domain to another. After evaluating the developed entity in several domains, the developer is left with many questions, such as: Which domains are the strengths and weaknesses of the developed entities? Which domains have the greatest influence on average performance? Which domains constitute the bottlenecks for the average performance improvement? We need to address these questions from the end-user preferences perspective.
The objective of this paper is to rigorously demonstrate that, no matter what the task is, by taking an adequate way of averaging the domain-specific performances (i.e., the summarization introduced in [3]) as well as an adequate family of scores (i.e., the ranking scores introduced in [4]), the easiest domain, most difficult domain, preponderant domain, and bottleneck domain become all well-defined and relative to some easy to interpret user preferences.
Our contributions are threefold: 1. Theoretical contribution on scores. We highlight the fact that the expected value scores (including all unconditional probabilistic scores) and the expected value ratio scores (including all probabilistic conditional scores and all ranking scores) have the remarkable property that the value taken for the averaged performance obtained by the summarization technique [3] is equal to some weighted arithmetic mean of the values taken for the domain-specific performances, and provide closed-form formulas to compute these weights.
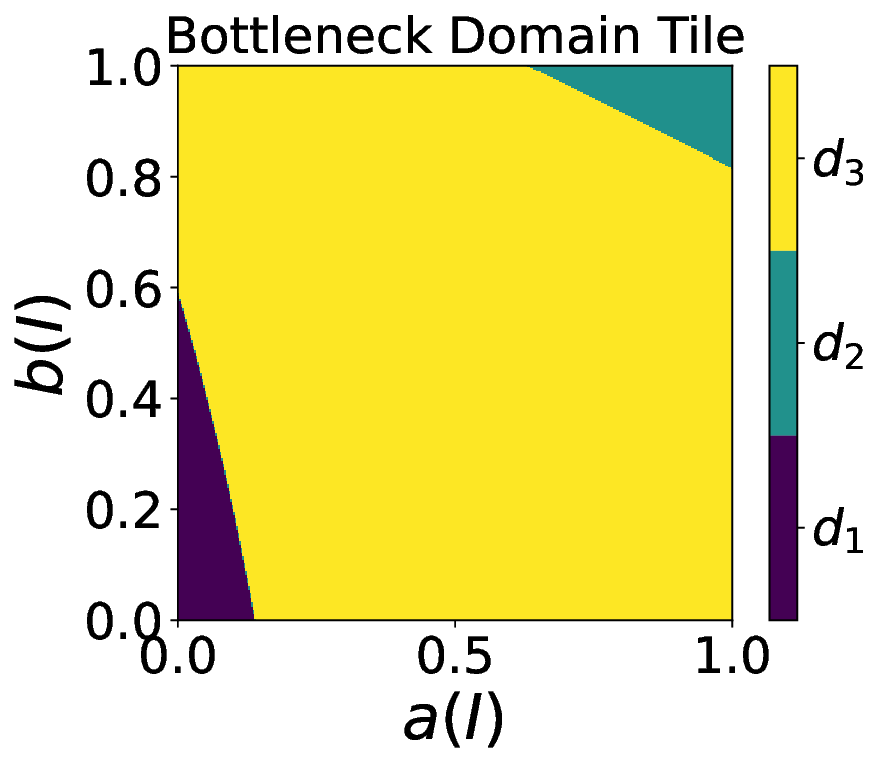
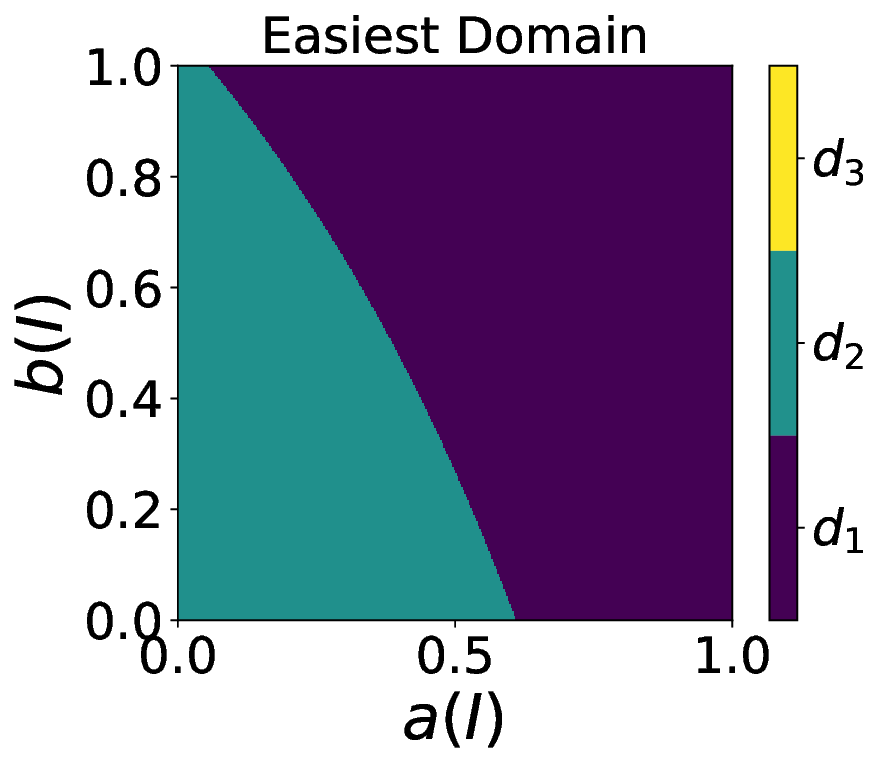
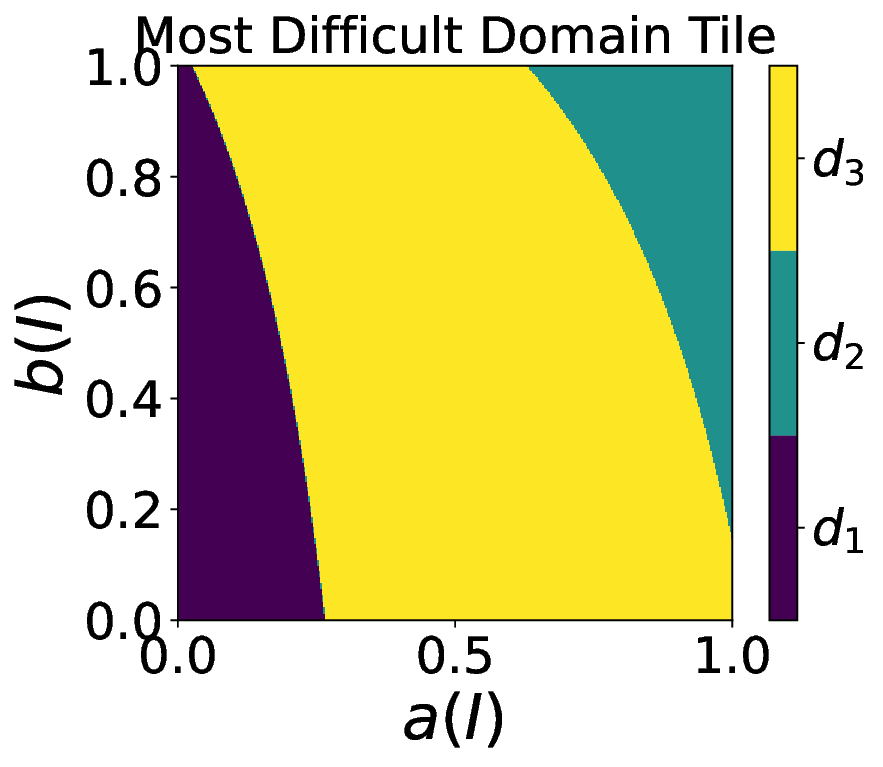
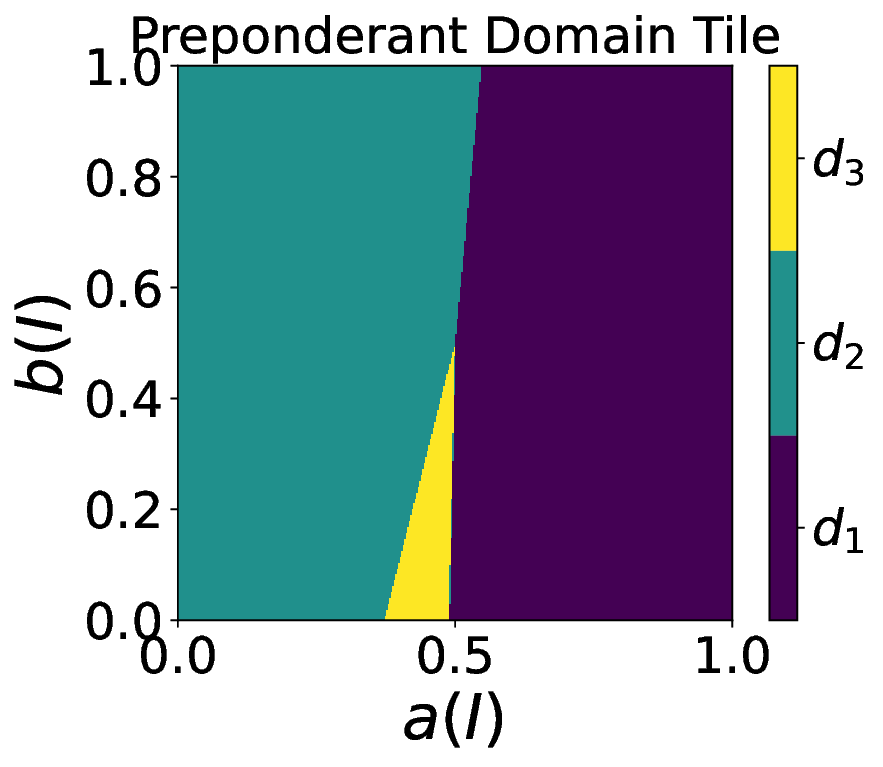
Capitalizing on the remarkable property and focusing on the family of ranking scores [4], we rigorously define the easiest, most difficult, preponderant, and bottleneck domains as functions of a random variable that can be used to encode some user preferences for any task. 3. Contribution on visualization tools. In the case of two-class crisp classification, we introduce new variants of the Tile, called flavors [5,6], that allow us to visualize in a square how the easiest, most difficult, preponderant, and bottleneck domains depend on the user preferences. Notations. Following [3,4,6], we consider a probabilistic framework. A performance is a probability measure (e.g., a normalized confusion matrix for a classification task) on a measurable space (Ω, Σ), where Ω is the sample space and Σ the event space. The set of all performances is denoted by P (Ω,Σ) . We denote the set of domains by D, the performance in the domain d by P d , and the weight arbitrarily given to the domain d by λ d .
In this paper, we build upon the summarization [3], which is a probabilistic performance averaging technique that preserves the relationships between scores and preserves the probabilistic meaning of both unconditional and conditional probabilistic scores. It is applicable regardless of the task. The summarized performance P is the following mixture of performances:
As noticed in [3], for some remarkable scores X, the summarization leads to
We call λ d the domain weight and ω X,d the summarization weight.
Formulas for the weights for expected value scores. We parameterize these scores by a random variable V and define them as
, where E is the mathematical expectation. With these scores, eq. ( 2) holds and the summarization weights do not depend on the performance:
Formulas for the weights for expected value ratio scores. We parameterize these scores by two random variables, V 1 and V 2 ̸ = 0, and define them as
. With these scores, eq. ( 2) also holds, but contrary to the expected value scores, the summarization weights depend on the performance:
Equations ( 3) and ( 4) generalize the ones given in [3], in the particular case of unconditional and conditional probabilistic scores, respectively.
In addition, we also build upon the ranking scores [4], which establish a connection between the performances P , the task (modeled through a random variable S called satisfaction), and some user preferences (modeled through a nonnegative random variable I called importance). These scores induce meaningful performance orderings [4], in the sense that these orderings satisfy the fundamental axioms of performance-based ranking. They are defined as:
where dom(R I ) = {P ∈ P (Ω,Σ) : E P [I] ̸ = 0}. As R I = X EV R I
This content is AI-processed based on open access ArXiv data.