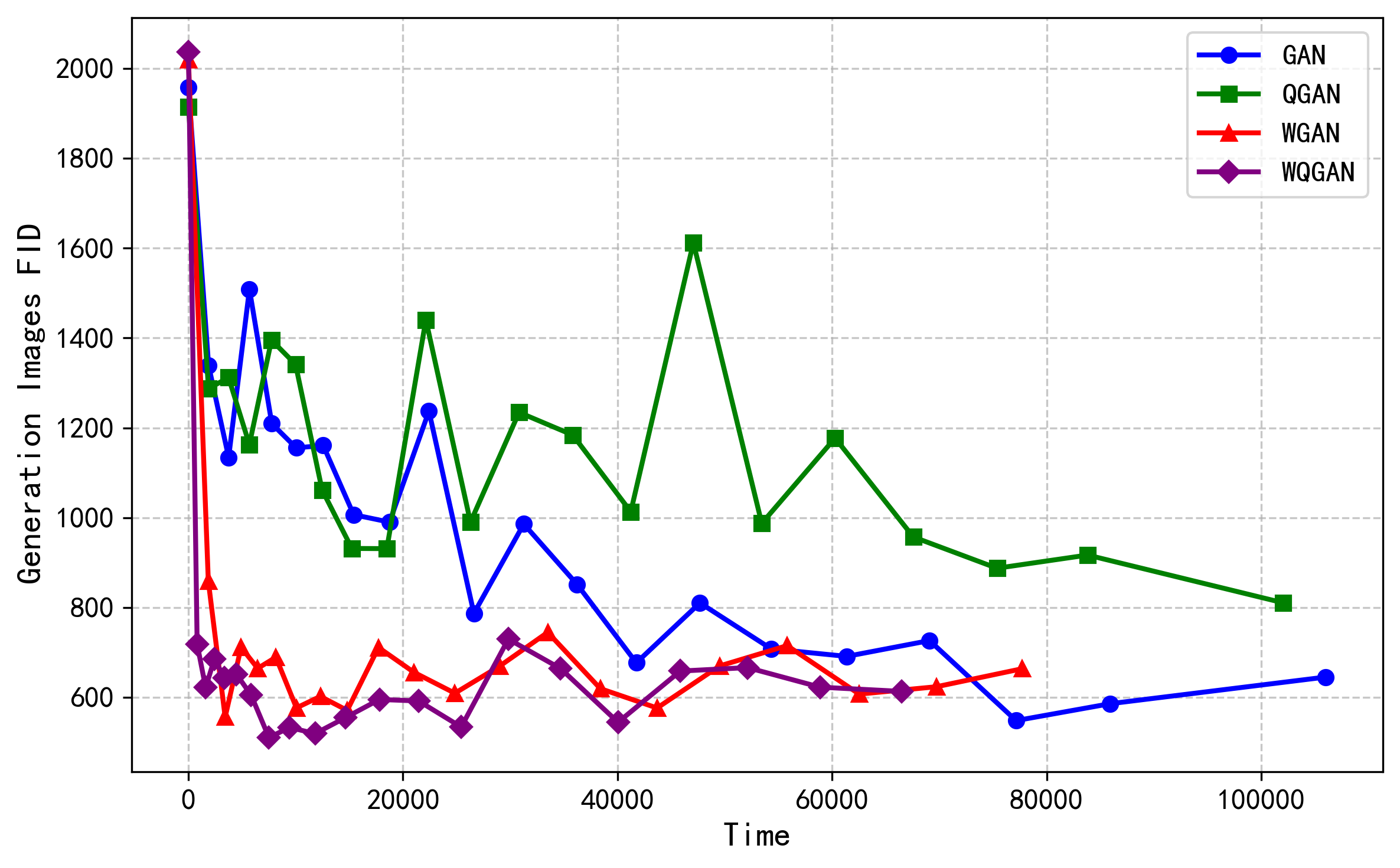
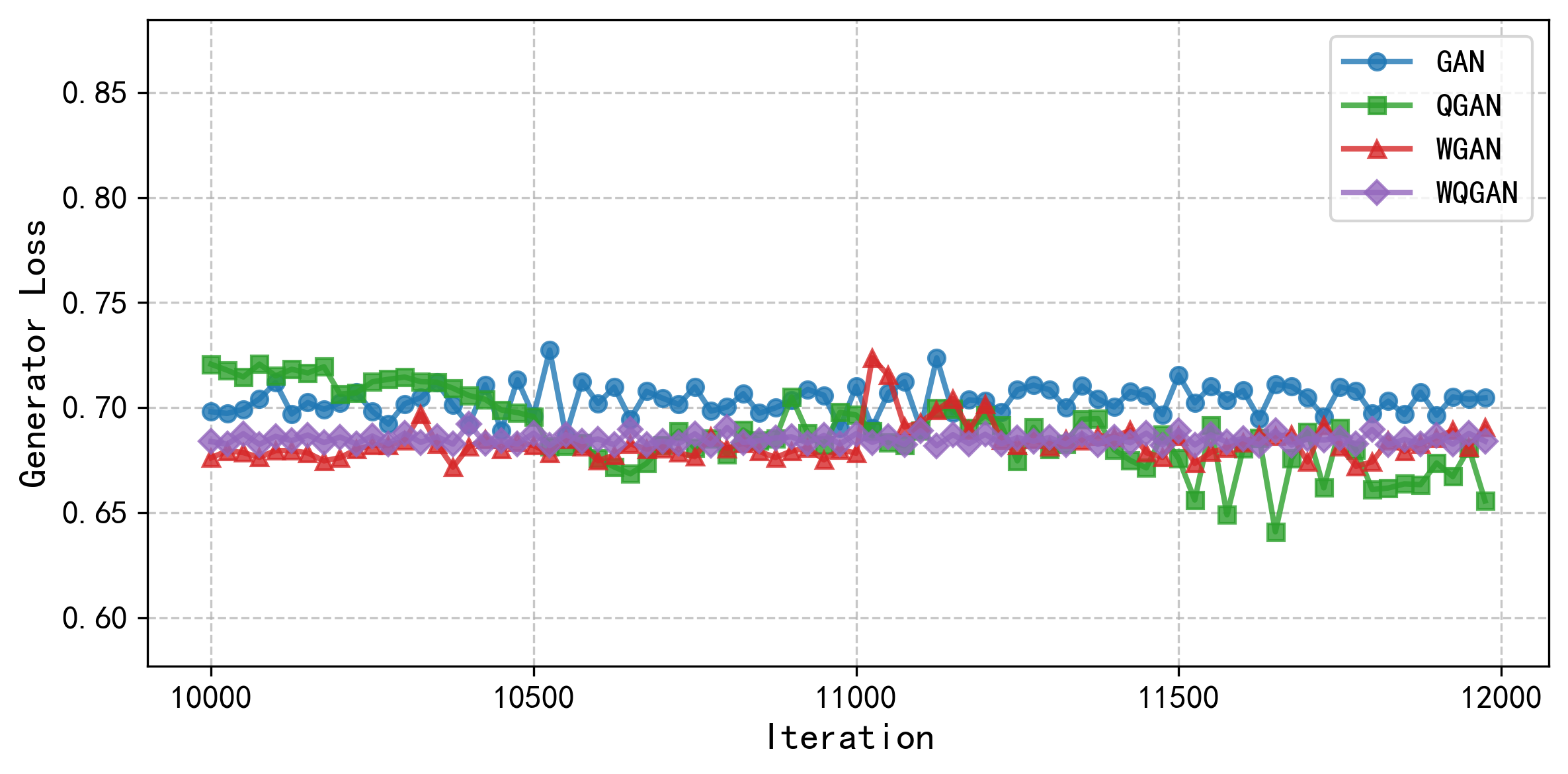
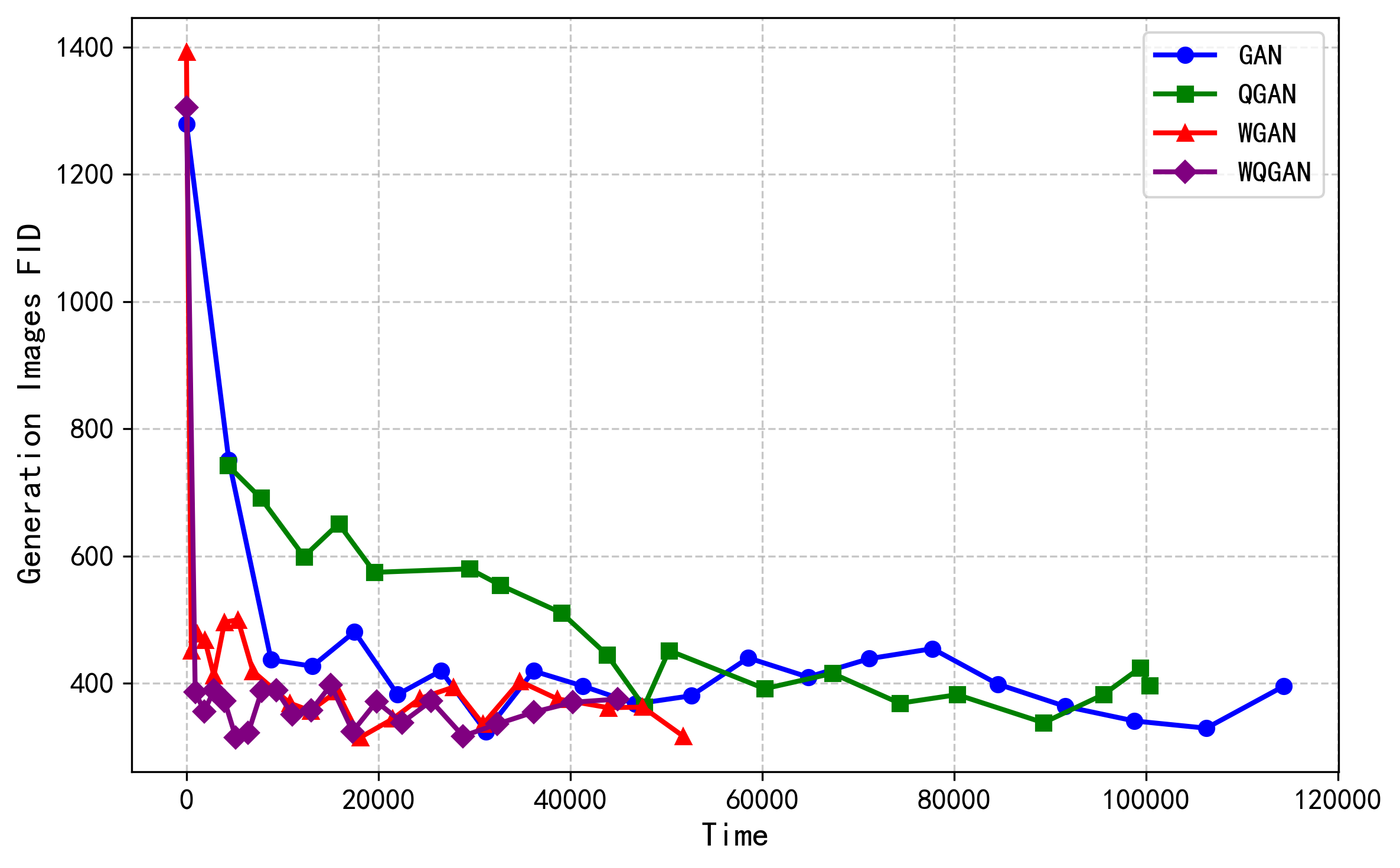
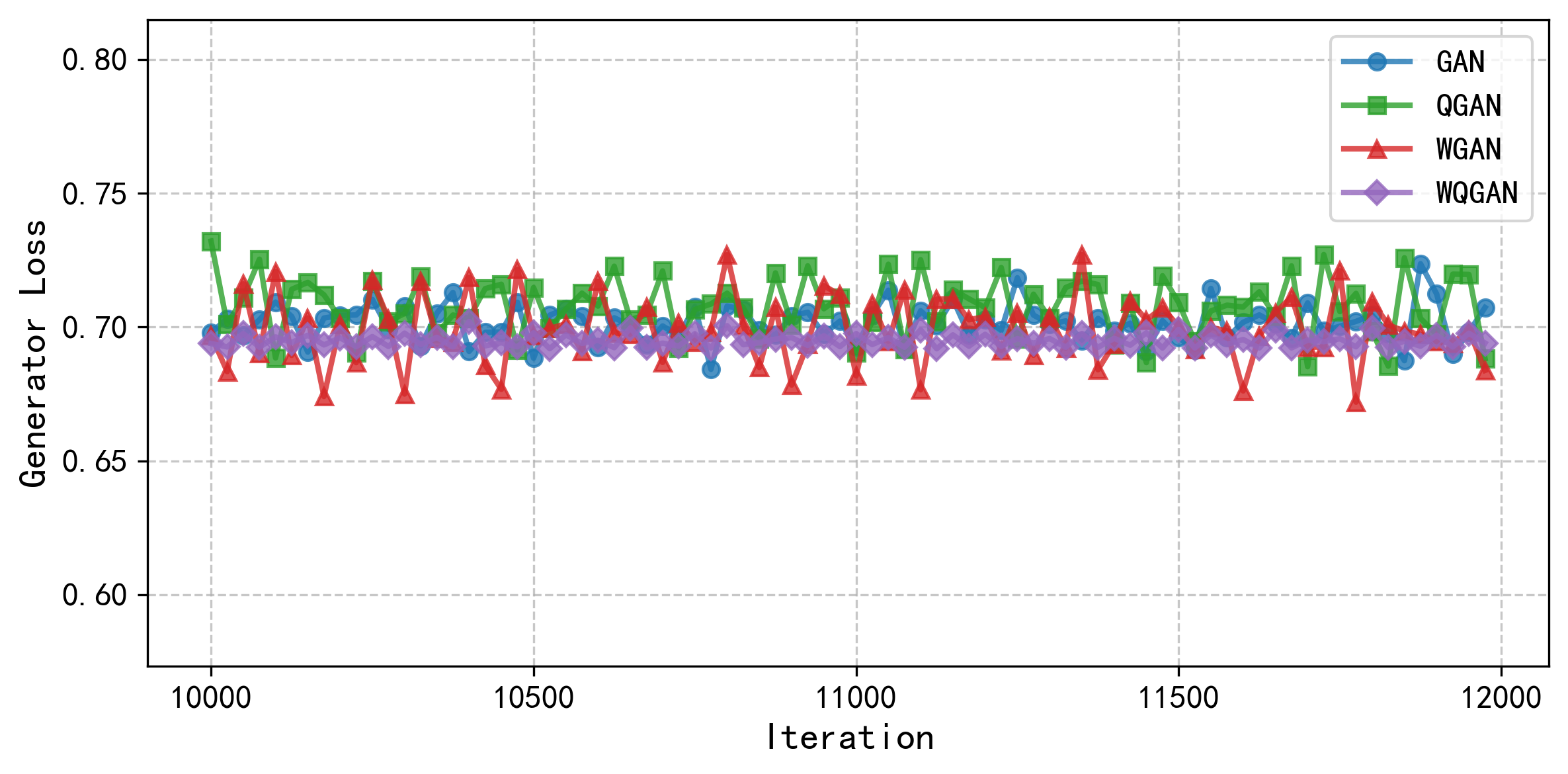
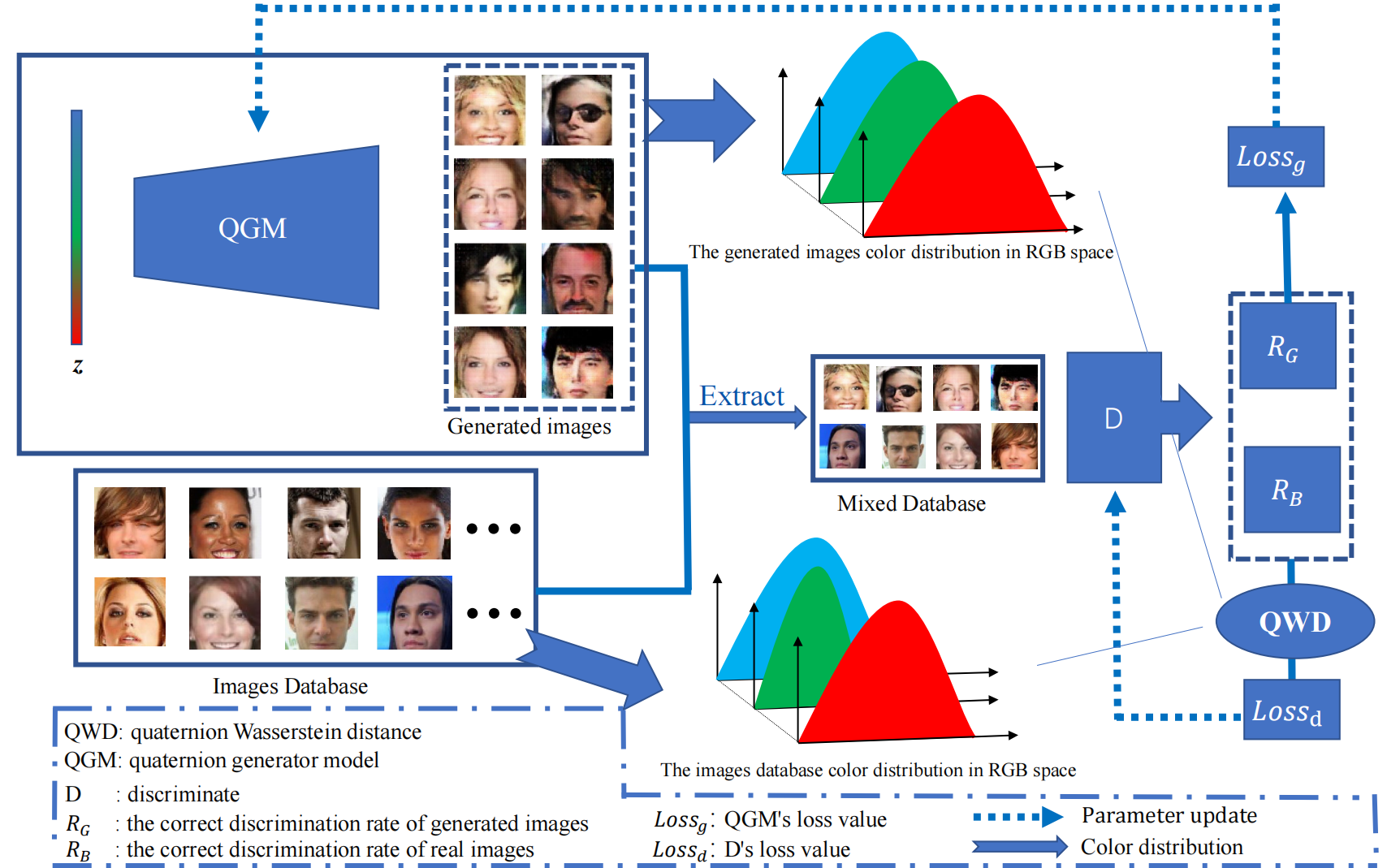
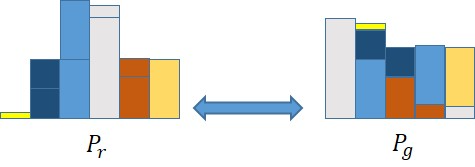
Color image generation has a wide range of applications, but the existing generation models ignore the correlation among color channels, which may lead to chromatic aberration problems. In addition, the data distribution problem of color images has not been systematically elaborated and explained, so that there is still the lack of the theory about measuring different color images datasets. In this paper, we define a new quaternion Wasserstein distance and develop its dual theory. To deal with the quaternion linear programming problem, we derive the strong duality form with helps of quaternion convex set separation theorem and quaternion Farkas lemma. With using quaternion Wasserstein distance, we propose a novel Wasserstein quaternion generative adversarial network. Experiments demonstrate that this novel model surpasses both the (quaternion) generative adversarial networks and the Wasserstein generative adversarial network in terms of generation efficiency and image quality.
1. Introduction. Color image generation models can be utilized for tasks such as image inpainting, denoising, and style transfer. Quaternion generative adversarial networks (QGANs) have attracted attention for their ability to preserve relationships among color image channels. However, using Jensen-Shannon divergence as an evaluation metric may not effectively quantify the relationship between real and generated images. Wasserstein distance serves as a robust measure of assessing distances between two distributions. Nevertheless, the theory of quaternion Wasserstein distance (QWD) is still in the early stages of development. This paper aims to introduce a novel Wasserstein quaternion generative adversarial network (WQGAN) model by deriving QWD and its dual form.
Generative adversarial networks (GAN) have been put into various practical applications as a generative model [3]. The training stability of GAN has been an difficult challenge to overcome since it was introduced in 2014 [11]. Many methods are proposed to improve the generative ability of GAN. Deep networks are first introduced into the GAN architecture with the proposition of deep convolutional generative adversarial networks (DCGAN) [29]. DCGAN improves the stability of the model and lays the foundation for the development of GANs. However, its model still suffers from mode collapse and needs further improvement. The authors systematically demonstrate what is the problem with the original GAN [1] and propose the Wasserstein generative adversarial networks (WGAN) [2]. The introduction of Wasserstein distance provides research direction for later GANs.
The Wasserstein theory is a core component of the latest Optimal Transport (OT) theory. Recently, OT, as an emerging mathematical tool, has brought new ideas and solutions to the field of machine learning, gradually becoming a research hotspot. The core idea of optimal transport originated from a classic mathematical problem, aiming to find an optimal way to transport the mass in one probability distribution to another while minimizing the transportation cost [23]. Its classic formulation is the Kantorovich problem [19], which precisely measures the transportation cost from one point to another through a carefully defined cost function.
To improve problem solvability and transportation plan characteristics, entropy regularization [28] is introduced to make transportation smoother and more uniform, avoiding over-concentration. As a core metric of optimal transport, the Wasserstein distance can accurately characterize distribution differences [7], laying a foundation for subsequent applications. In supervised learning, optimal transport can serve as an innovative loss function to capture subtle distribution differences or combine with cross-entropy loss to enhance model performance, and it also ensures model fairness through data adjustment and optimizes evaluation indicators [9; 4; 26]. In unsupervised learning, optimal transport supports the design of encoding and decoding in Variational Autoencoders [20; 34]. WGAN uses it to replace traditional divergence for optimizing GAN performance [10], then SNGAN [25] and BigGAN further improve training stability based on this. However, these generative models ignore inter-channel correlations when processing color images, easily leading to color deviations.
Quaternion is an excellent tool used in many methods of image processing. Two new nonlocal self-similarity (NSS)-based quaternion matrix completion (QMC) and quaternion tensor completion (QTC) algorithms are presented to deal with the color image problems in [18], where nonlocal self-similarity technique is introduced to reduce the low-rank prior requirement. To preserve the structure of color channels when restoring color images, a quaternion-based weighted nuclear norm minimization (WNNM) method is proposed [17]. Furthermore, a novel quaternion-based weighted schatten p-norm minimization (WSNM) model is proposed for tackling color image restoration problems with preliminary theoretical convergence analysis [36]. A novel method named QLNM-QQR based on quaternion Qatar Riyal decomposition and quaternion L 1,2 -norm is proposed to reduces computational complexity by avoiding the need for calculating the QSVD of large quaternion matrices [14]. Then a new method called quaternion nuclear norm minus Frobenius norm minimization is employed into color image reconstruction by capturing RGB channels relationships comprehensively in [12]. For color image inpainting, a quaternion matrix completion method through untrained QCNN is proposed [24]. Quaternion circulant matrix can be block-diagonalized into 1-by-1 block and 2-by-2 block matrices by permuted discrete quaternion Fourier transform matrix, this shows that the inverse of a quaternion cyclic matrix can be determined quickly and efficiently [27], laying the groundwork for the rest of the image study.
Quaternion was first introduced into GAN and applied to c
This content is AI-processed based on open access ArXiv data.