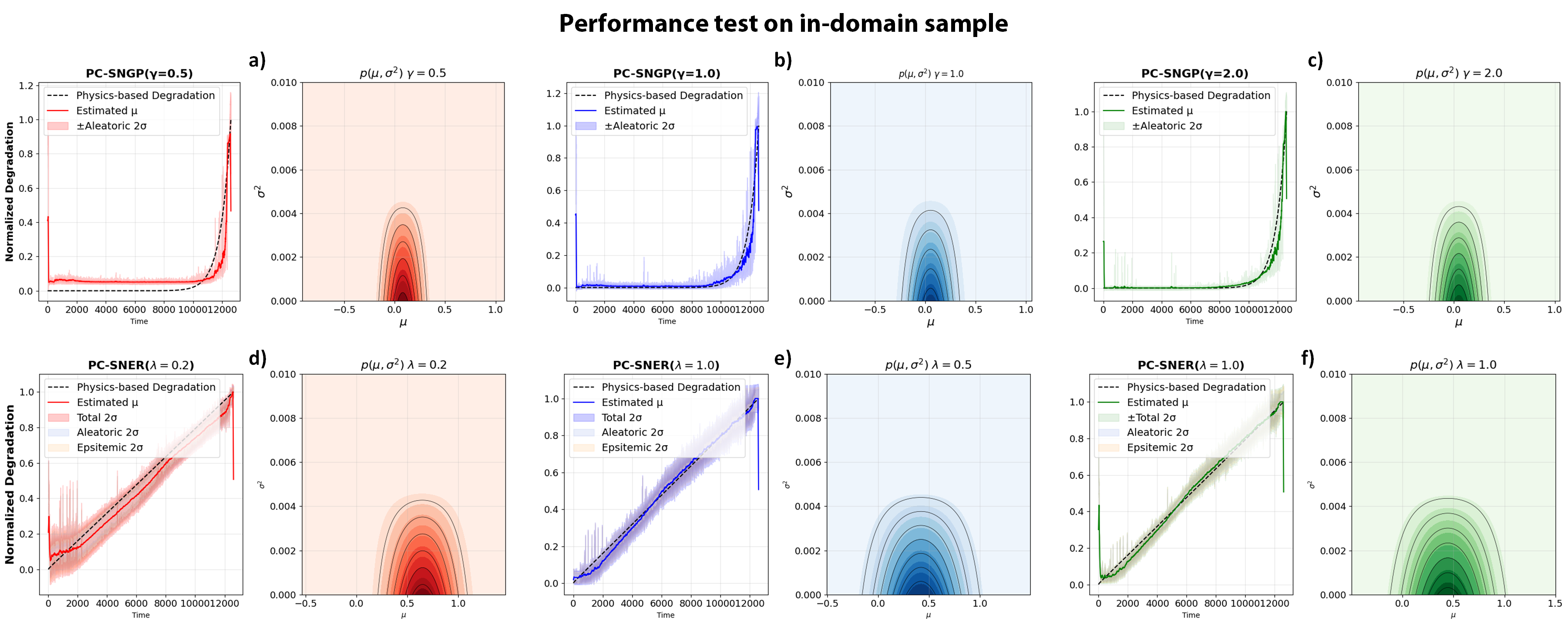
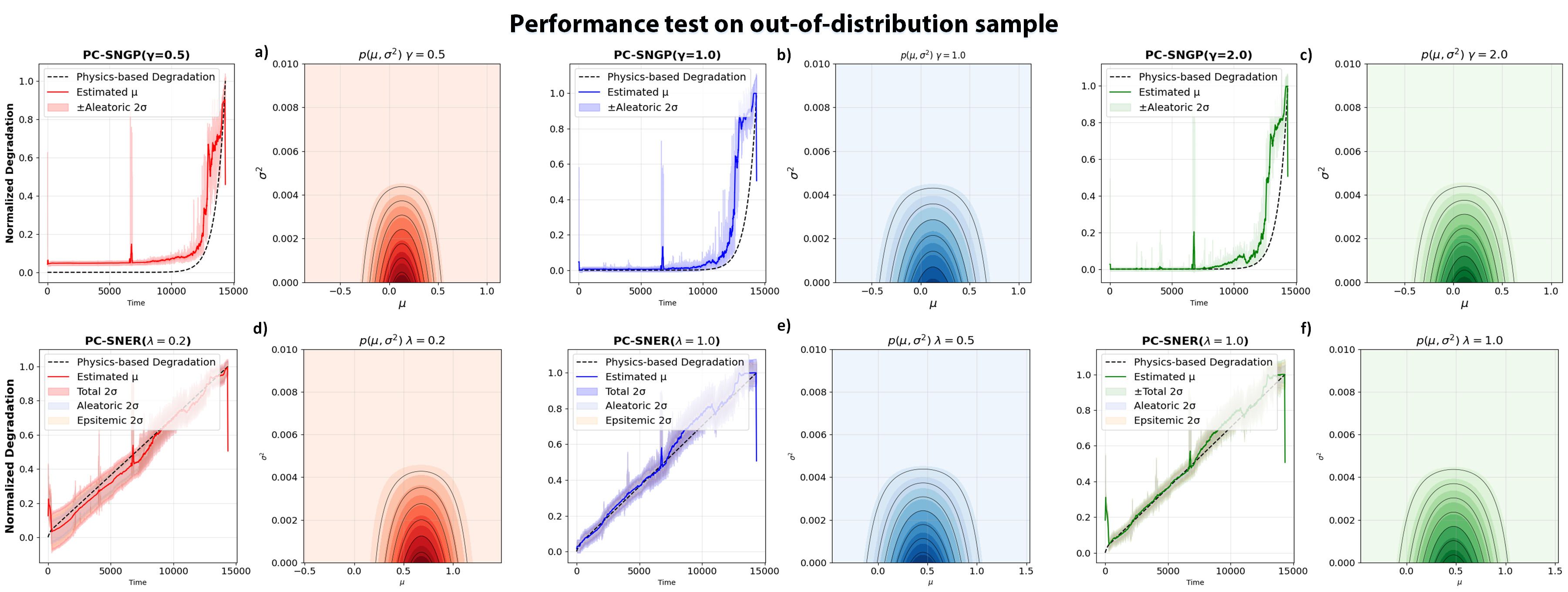
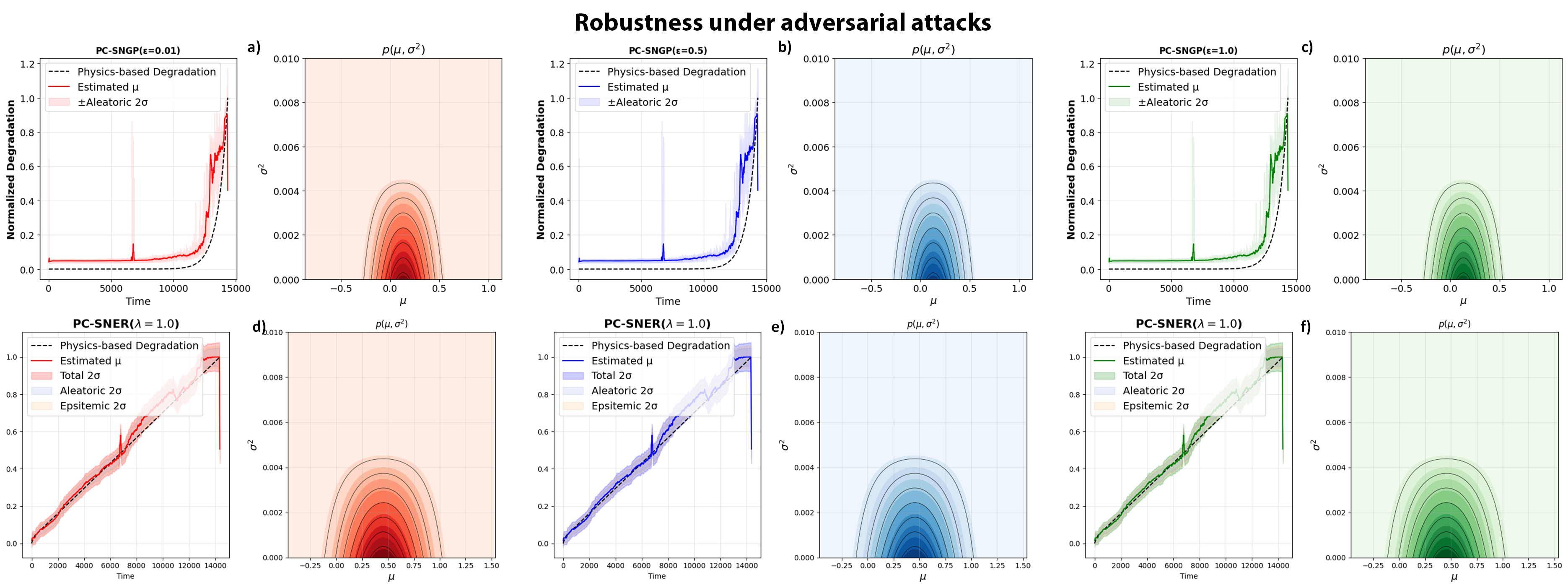
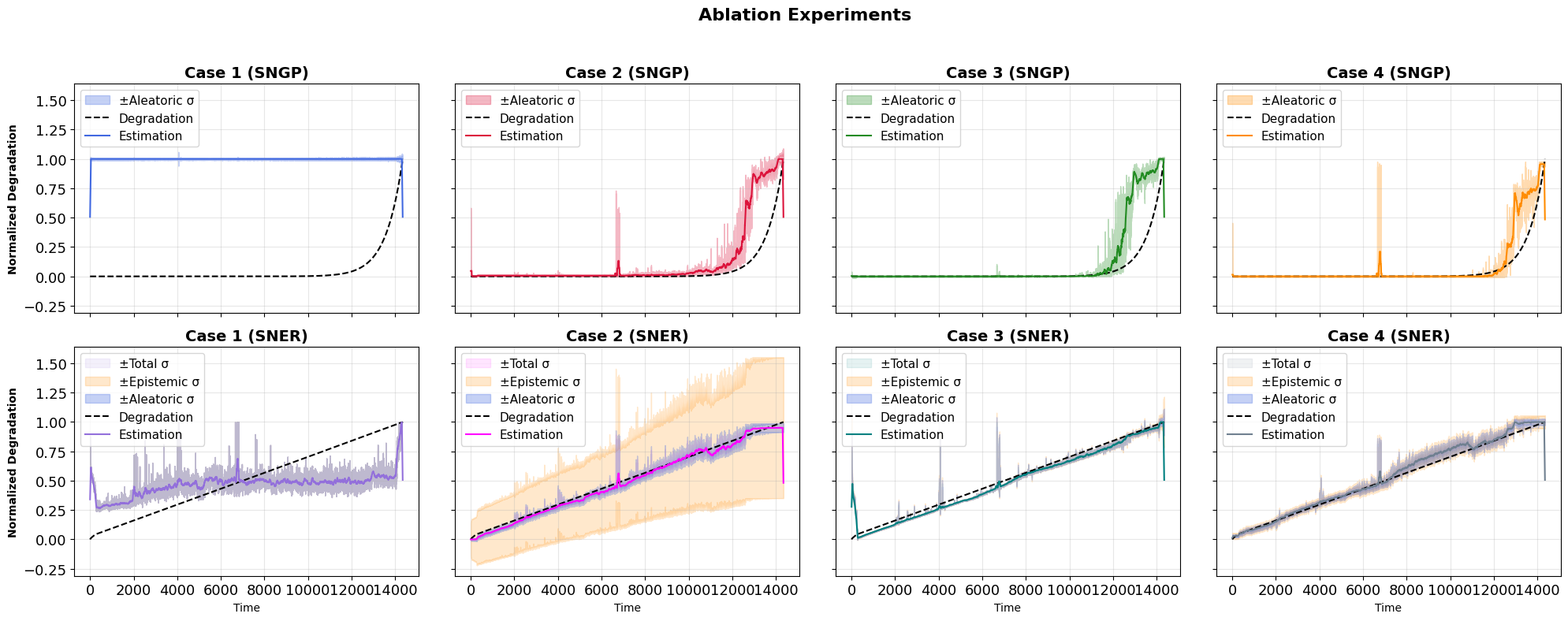
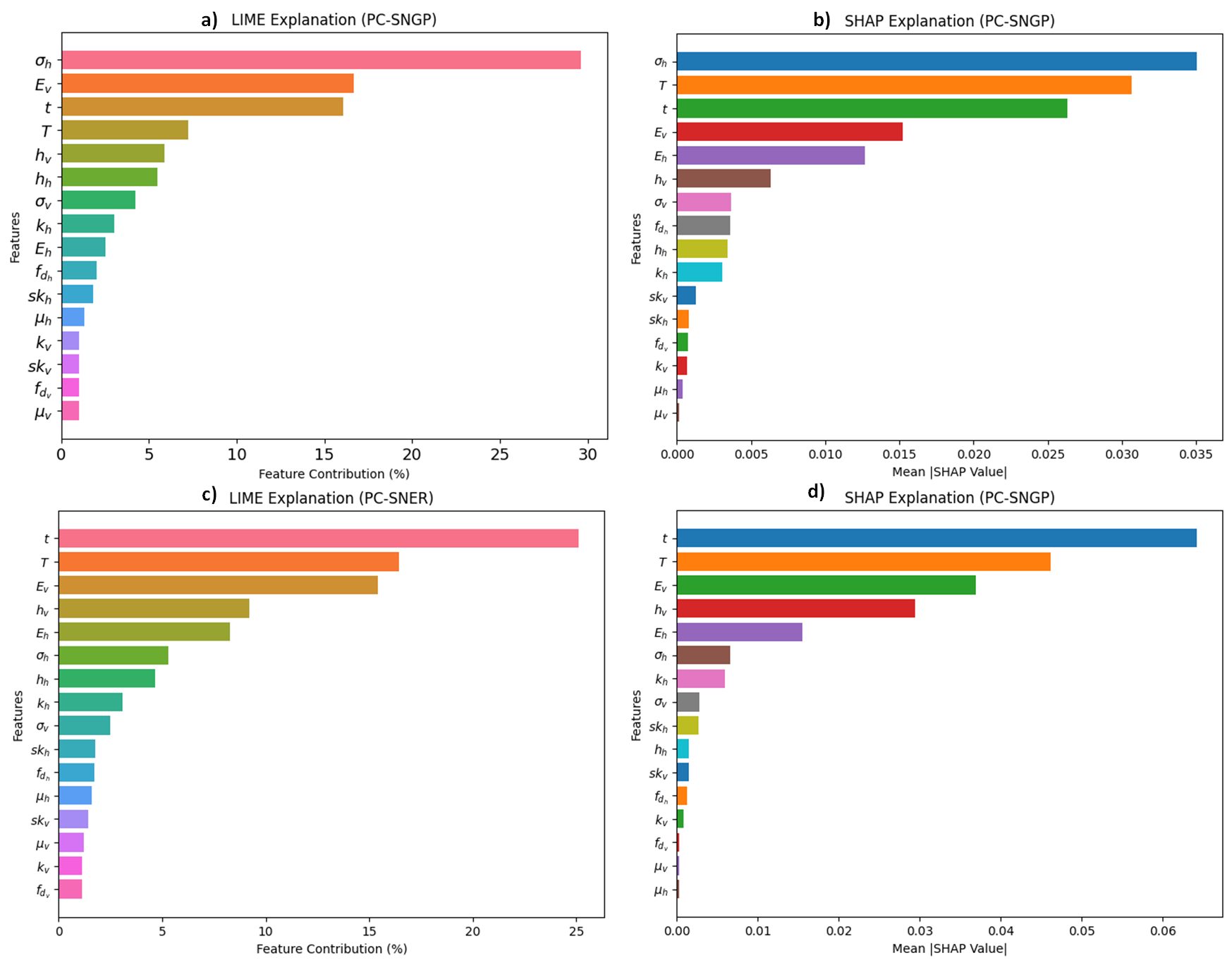
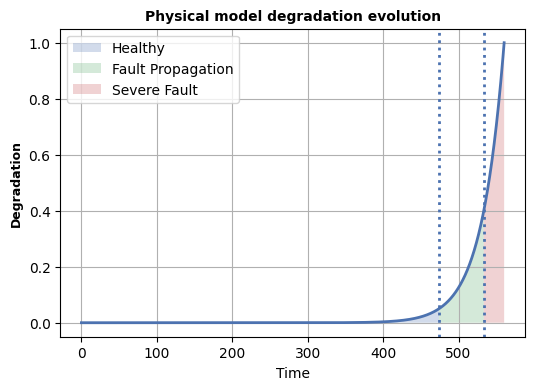
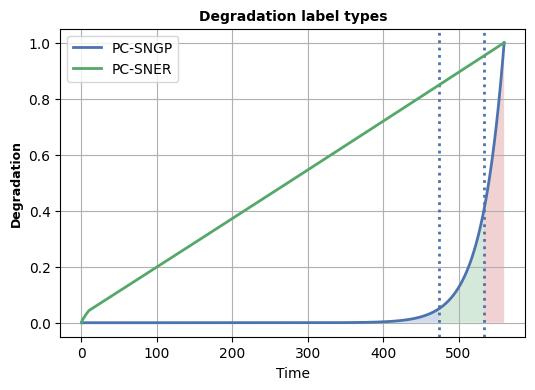
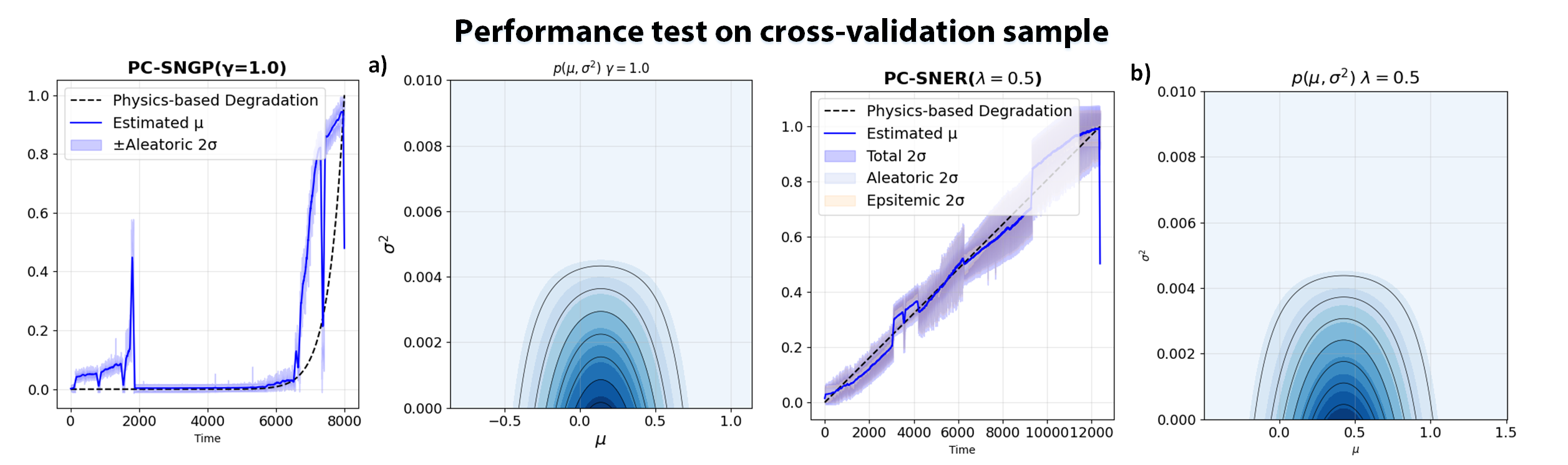
Accurate and uncertainty-aware degradation estimation is essential for predictive maintenance in safety-critical systems like rotating machinery with rolling-element bearings. Many existing uncertainty methods lack confidence calibration, are costly to run, are not distance-aware, and fail to generalize under out-of-distribution data. We introduce two distance-aware uncertainty methods for deterministic physics-guided neural networks: PG-SNGP, based on Spectral Normalization Gaussian Process, and PG-SNER, based on Deep Evidential Regression. We apply spectral normalization to the hidden layers so the network preserves distances from input to latent space. PG-SNGP replaces the final dense layer with a Gaussian Process layer for distance-sensitive uncertainty, while PG-SNER outputs Normal Inverse Gamma parameters to model uncertainty in a coherent probabilistic form. We assess performance using standard accuracy metrics and a new distance-aware metric based on the Pearson Correlation Coefficient, which measures how well predicted uncertainty tracks the distance between test and training samples. We also design a dynamic weighting scheme in the loss to balance data fidelity and physical consistency. We test our methods on rolling-element bearing degradation using the PRONOSTIA, XJTU-SY and HUST datasets and compare them with Monte Carlo and Deep Ensemble PGNNs. Results show that PG-SNGP and PG-SNER improve prediction accuracy, generalize reliably under OOD conditions, and remain robust to adversarial attacks and noise.
Uncertainty quantification (UQ) involves assessing the degree of confidence in a system's predictions and is commonly categorized into two types: aleatoric uncertainty, arising from inherent variability or noise in data; and epistemic uncertainty, stemming from incomplete knowledge or uncertainty in model parameters [1]. UQ is critical in high-stakes applications where decision-making errors can lead to significant economic consequences. One of the prominent challenges in the industrial landscape is accurately estimating the degradation of rolling-element bearings (REBs), which account for about 40% to 50% of failures in industrial rotating machinery [2]. These failures are often attributed to operating under harsh temperatures and variable load conditions. To solve this problem, substantial research has focused on predictive modeling strategies, which are typically divided into two broad categories: (1) physics-based models (PBMs) and (2) data-driven models (DDMs).
PBMs utilize differential equations derived from first principles to represent system degradation. These models are component-specific and adhere to physical laws, ensuring consistency and interpretability. Guo et al. [3] introduced a quasi-static degradation model for REBs that integrates centrifugal expansion, thermal deformation, load distribution, and Hertzian contact mechanisms to enhance stress distribution estimation. Gabrieli et al. [4] introduced a degradation assessment approach based on the Equivalent Damaged Volume (EDV) concept, which combines run-to-failure experimental data with a lumped parameter model. The EDV quantifies defect severity by comparing measured vibration signals to those generated through simulation based on defect geometry. Yang et al. [5] developed an electromechanically coupled digital twin incorporating a stepper motor and deep groove ball-bearing dynamics. Their model simulates rolling-element trajectories, contact forces, and vibration signatures under varying speeds and fault conditions. Ohana et al. [6] presented a spall-focused framework incorporating dynamic response modeling, strain field analysis, spall damage progression, and oil debris monitoring for enhanced fault characterization. Despite these advances, PBMs exhibit notable limitations: (1) they require extensive domain expertise and mathematical modeling knowledge; (2) their performance often degrades in complex systems due to unavoidable modeling simplifications; (3) they lack adaptability to real-time operational variations and generally do not support online parameter updating; (4) their robustness to perturbations is limited unless explicitly modeled within mathematical equations; and (5) they do not quantify the uncertainty in their predictions.
DDMs uncover the hidden relationships within condition monitoring data through machine learning (ML) techniques. With the advancement of ML techniques such as CNN [7], LSTM [8], GRU [9], and attention [10], we have seen significant improvement and accomplishment in degradation estimation for REBs. However, most existing approaches have traditionally focused on deterministic, point-based predictions, neglecting the inherent uncertainty in outputs. Liu et al. [8] utilized LSTM to forecast future bearing operation trends with an exponential degradation model used to estimate the RUL. A dynamic 3σ interval combined with a voting mechanism enables adaptive fault-start time prediction. Jiang et al. [11] proposed a hybrid TCN-MSA model that combines a causally inflated temporal CNN to capture long-term dependencies and frequency domain features. A multihead self-attention mechanism was applied to identify feature significance during bearing degradation. Qi et al. [12] extracted advanced entropy and sparsity-based health indicators from multiband filtered signals and selected the optimal indicator via a proposed evaluation criterion. A constrained Support Vector Data Description (SVDD) was used to detect anomalies and identify the Start Prediction Time (SPT).
Recently, increasing attention has turned to quantifying uncertainty in DDMs, recognizing their importance in safetycritical applications. Contemporary research can be categorized into two types based on methodological approach used: (1) deterministic models and (2) probabilistic models. Deterministic modeling uses the same deterministic feed-forward neural network (NN) and models the output layer to predict the mean µ and variance σ 2 [13]. Pan et al. [14] proposed a meta-weighted NN with three subnetworks-drift, diffusion, and weight nets-for predicting the RUL of turbopump bearings. Their approach integrates meta-learning-based sample reweighting to mitigate negative transfer and diffusion-based uncertainty estimation to distinguish between in-and out-of-distribution data. The method utilizes convolutional architectures and fine-tuned gradient-based optimization to adaptively improve the prediction accuracy and reliability across domains. Probabili
This content is AI-processed based on open access ArXiv data.