Knowledge graph embedding (KGE) relies on the geometry of the embedding space to encode semantic and structural relations. Existing methods place all entities on one homogeneous manifold, Euclidean, spherical, hyperbolic, or their product/multi-curvature variants, to model linear, symmetric, or hierarchical patterns. Yet a predefined, homogeneous manifold cannot accommodate the sharply varying curvature that real-world graphs exhibit across local regions. Since this geometry is imposed a priori, any mismatch with the knowledge graph's local curvatures will distort distances between entities and hurt the expressiveness of the resulting KGE. To rectify this, we propose RicciKGE to have the KGE loss gradient coupled with local curvatures in an extended Ricci flow such that entity embeddings co-evolve dynamically with the underlying manifold geometry towards mutual adaptation. Theoretically, when the coupling coefficient is bounded and properly selected, we rigorously prove that i) all the edge-wise curvatures decay exponentially, meaning that the manifold is driven toward the Euclidean flatness; and ii) the KGE distances strictly converge to a global optimum, which indicates that geometric flattening and embedding optimization are promoting each other. Experimental improvements on link prediction and node classification benchmarks demonstrate RicciKGE's effectiveness in adapting to heterogeneous knowledge graph structures.
The manifold hypothesis (Fefferman et al., 2016) suggests that real-world data, despite residing in high-dimensional spaces, tend to concentrate near low-dimensional manifolds. This insight forms the theoretical foundation for a wide range of representation learning approaches, especially knowledge graph embedding. In KGE, entities and relations are mapped into continuous geometric embedding spaces, where distances and transformations are designed to capture the underlying semantic and structural patterns (Cao et al., 2024). Such embeddings have become the backbone of various reasoning tasks, including link prediction (Chami et al., 2020;Sun et al., 2019;Zhang et al., 2019), entity classification (Ji et al., 2015;Xie et al., 2016;Yu et al., 2022), and knowledge completion (Abboud et al., 2020;Zhang et al., 2021;2020a).
Following the manifold hypothesis, the development of KGE methods increasingly focuses on identifying geometric spaces that better align with the underlying structure of knowledge graphs (Cao et al., 2024). Early KGE works primarily leveraged the Euclidean manifold due to its simplicity and translation invariance properties (Bordes et al., 2013). However, Euclidean embeddings cannot capture the non-linear structures prevalent in real-world knowledge graphs, such as hierarchical and cyclic patterns, due to their inherently curved geometry (Nickel & Kiela, 2017). To overcome this limitation, recent approaches have extended KGE to non-Euclidean manifolds, such as hyperbolic spaces for hierarchical relations (Balazevic et al., 2019;Chami et al., 2020;?;Wang et al., 2021) and spherical spaces for symmetric or periodic structures (Lv et al., 2018;Dong et al., 2021;Xiao et al., 2015). These advances better model specific structural motifs, but fall short of reflecting the rich local geometric heterogeneity in real knowledge graphs, which often comprise dense clusters, sparse chains, asymmetric relations, and layered hierarchies.
To model this complexity, more flexible embedding approaches have emerged, either employing dynamic curvature combinations (Yuan et al., 2023;Liu et al., 2024) or leveraging product manifolds composed of multiple simpler geometries (Xiong et al., 2022;Zheng et al., 2022;Cao et al., 2022;Li et al., 2024), yet they still rely on a predefined and static geometric prior. This leads to a critical yet under-addressed issue:
A homogeneous geometric prior, predefined before observing the data, forces embeddings to adapt to the “geometrically rigid” space, rather than shaping embedding space by real data manifold.
Specifically, the core limitation lies in the use of a predefined manifold, which enforces uniform geometric constraints that fail to capture the localized curvature heterogeneity of real-world knowledge graphs. This misaligns the embedding space with the intrinsic manifold of the data, the optimal representation under the manifold hypothesis, resulting in degrading the embedding quality and impairing downstream reasoning (a comprehensive review of related work is provided in Appendix B.).
To resolve this misalignment, we propose RicciKGE, a curvature-aware KGE framework that couples the KGE loss gradient with the local discrete curvature (Fu et al., 2025;Naama et al., 2024) via an extended Ricci flow (Choudhury, 2024). Unlike static manifold-based methods, RicciKGE allows manifold geometry and entity embeddings to co-evolve in a closed feedback loop: curvature drives the metric to smooth curved regions and guide embedding updates, while the updated embeddings reshape curvature in return. This self-consistent process continuously aligns geometry with structure, eliminating the distortion induced by global geometric priors.
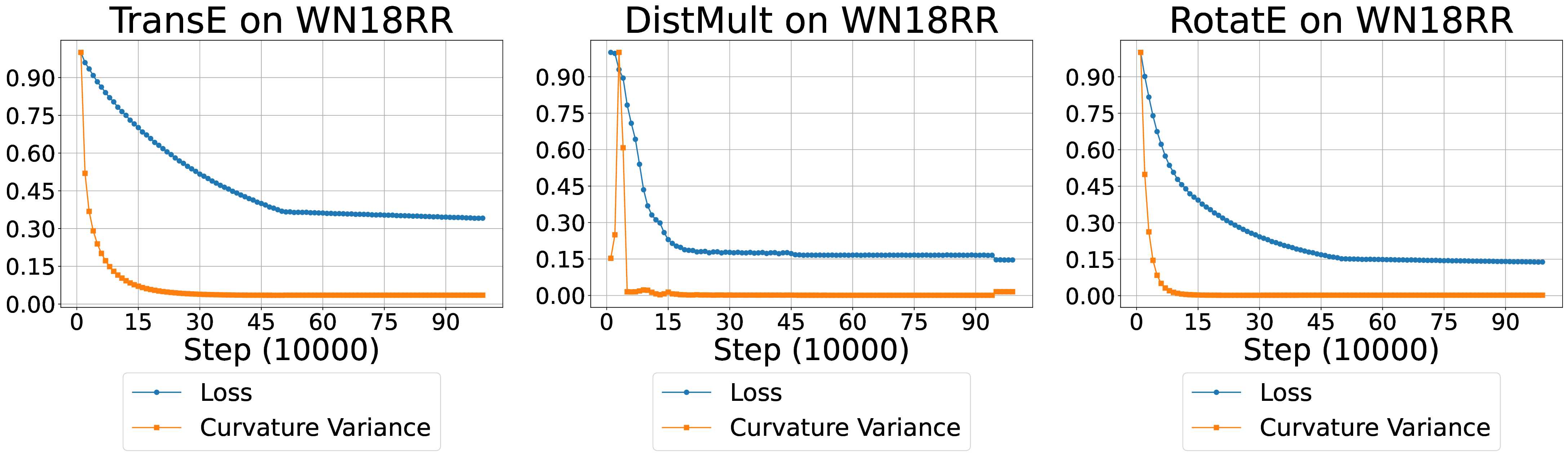
To theoretically ground this coupling, we establish convergence guarantees for the co-evolution process. Under mild geometric assumptions (Hebey, 2000;Saloff-Coste, 1994) and continuity/convexity conditions, we prove that all edge-wise Ricci curvatures decay exponentially to zero, thereby flattening the latent manifold toward a Euclidean geometry. Importantly, during this decay process, the local heterogeneity of curvature is not annihilated but gradually absorbed into the embedding updates through the extended Ricci flow, enabling entity embeddings to encode these geometric irregularities.
Building on this absorption mechanism, we theoretically prove that the KGE objective still converges linearly to a global optimum under the evolving geometry. Since only entity embeddings remain learnable while curvature vanishes asymptotically, the final embeddings both preserve the imprints of local curvature variations and achieve global convergence.
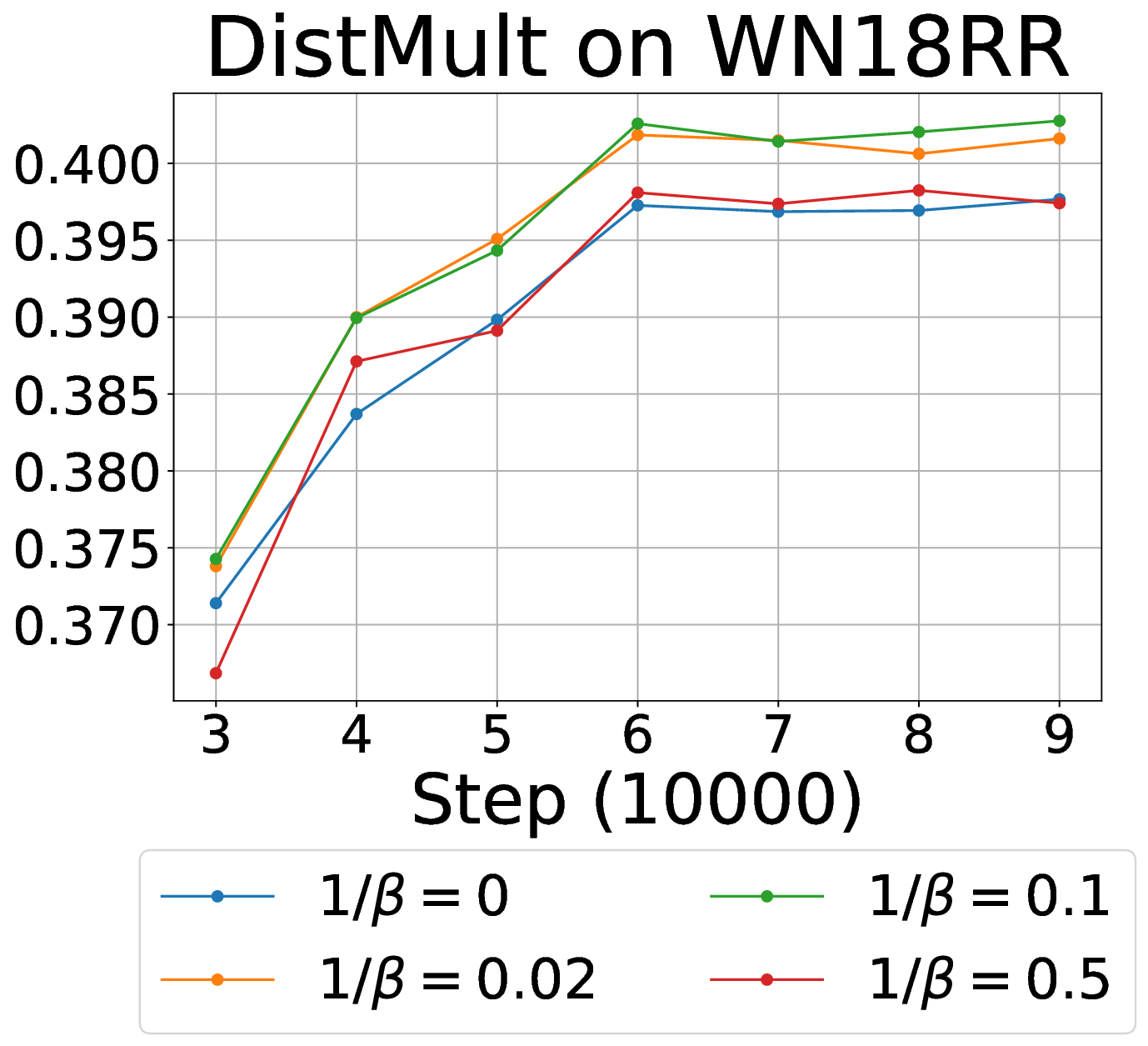
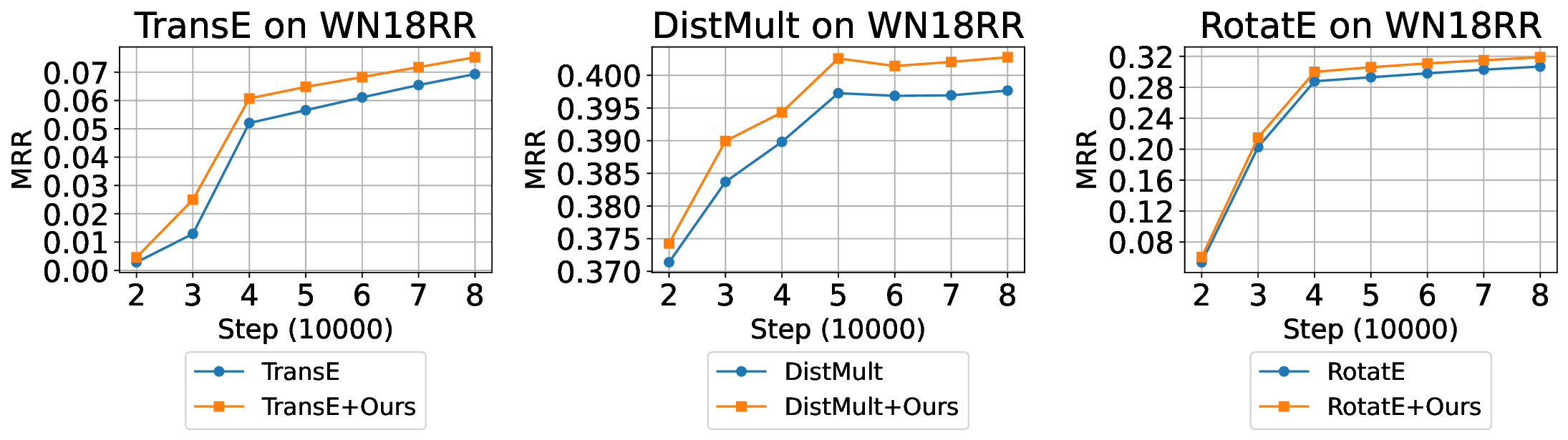
Empirical results demonstrate that RicciKGE delivers consistent performance gains in two fundamental tasks. In link prediction, injecting RicciKGE’s dynamic curvature flow into a variety of classical KGE models (Bordes et al., 2013;Yang et al., 2014;Sun et al., 2019;Chami et al., 2020;Li et al., 2024) with diffe
This content is AI-processed based on open access ArXiv data.