The homogenized harmonic balance finite element (FE) method enables efficient nonlinear eddy-current simulations of 3-D devices with lamination stacks by combining the harmonic balance method with a frequency-domain-based homogenization technique. This approach avoids expensive time stepping of the eddy-current field problem and allows the use of a relatively coarse FE mesh that does not resolve the individual laminates. In this paper, we extend the method to handle excitation signals with a dc bias. To achieve this, we adapt the original homogenization technique to better account for ferromagnetic saturation. The resulting formula for the homogenized reluctivity is evaluated using a look-up table computed from a 1-D FE simulation of a lamination and containing the average magnetic flux density in the lamination and the corresponding skin depth. We compare the results of the proposed method to those from a fine-mesh transient reference simulation. The tests cover different levels of ferromagnetic saturation and frequencies between 50 Hz and 10 kHz. For moderate ferromagnetic saturation, the method gives a good approximation of the eddy-current losses and the magnetic energy, with relative errors below 10%, while reducing the required number of degrees of freedom at 10 kHz by 1.5 orders of magnitude. This results in a reduction in simulation time from 2 days on a contemporary server to 90 minutes on a standard workstation.
W HEN simulating 3-D inductor models with laminated yokes or cores, the finite-element (FE) mesh does not only have to resolve the individual laminations, which usually have a thickness of 1 mm or less, but also the skin depth δ, which scales with the frequency f according to 1 / √ f . Hence, for simulations at frequencies in the kilohertz range, the number of degrees of freedom (DoFs) necessary in a bruteforce approach becomes prohibitive for most realistic models and one must apply a homogenization technique [1].
If a nonlinear B-H curve is considered, the only available option is to resort to multiscale methods. There are different variants of such methods, but the main idea is always to decompose the problem into a macroscale problem, discretized on a coarse FE mesh, and many microscale problems discretized on fine FE meshes [2], [3]. The macroscale problem and the microscale problems are coupled and are solved iteratively, which typically results in rather complex numerical schemes that are not well-suited for large 3-D models.
To address this issue, we have developed the homogenized harmonic balance finite element method (HomHBFEM) [4], which combines a frequency-domain-based homogenization [5] for the laminations with the harmonic balance finite element method (HBFEM) [6]. In this way, ferromagnetic saturation is included without costly time-stepping, and the eddy-current effects in the laminations are captured without the need for a very large FE mesh.
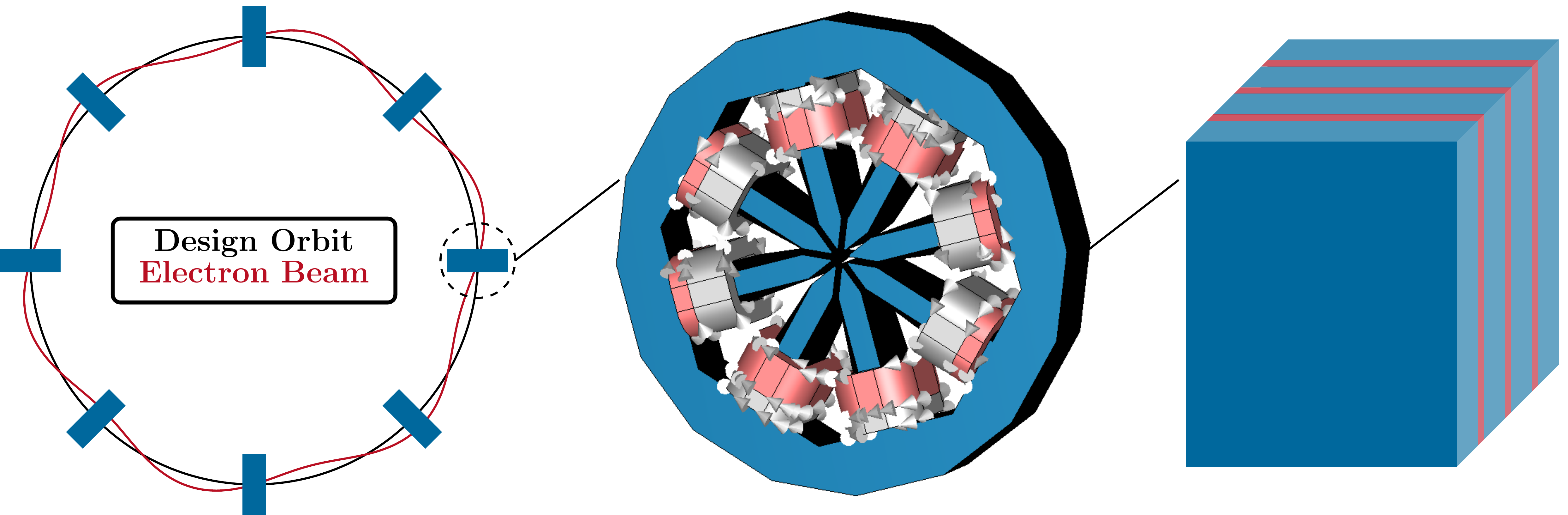
The HomHBFEM has enabled, for the first time, nonlinear eddy-current simulations of the fast corrector (FC) magnets (Fig. 1) for PETRA IV, the next-generation synchrotron radi-Corresponding author:
J.-M. Christmann (email: janmagnus.christmann@tu-darmstadt.de). This work was supported by Deutsches Elektronen-Synchrotron DESY, Hamburg, Germany. ation source at Deutsches Elektronen-Synchrotron DESY [7]. Hundreds of these FC magnets will be distributed around the 2.3 km circumference of the particle accelerator to correct deviations of the electron beam from the design orbit. They will be part of a feedback system and combine fast and slow correction in one magnet. Hence, the excitation current will have dc-and ac-components up to the kilohertz range, which are determined during operation by a control algorithm based on measurements of the deviations from the design orbit [8]. So far, the HomHBFEM was only applicable in case of a pure ac excitation. In this work, we extend the range of applicability to a harmonic excitation with a dc bias in order to enable an investigation of the FC magnets’ dynamic behavior with a more realistic excitation.
The remainder of this article is structured as follows. In Section II, we briefly introduce the nonlinear magnetoquasistatic (MQS) problem and the HBFEM, before explaining the standard HomHBFEM. Section III deals with the extension of the HomHBFEM to the dc-biased case. Although a naive extension is possible and theoretically straightforward, it performs poorly in practice. Therefore, we propose a more refined approach, which forms the main contribution arXiv:2512.06978v1 [cs.CE] 7 Dec 2025 of this paper. In Section IV, the refined approach is verified by comparing its results for a 3-D laminated inductor model to a transient reference simulation conducted in CST Studio Suite ® using an adequately fine FE mesh. In this context, we also show the superior performance of the refined approach compared to the naive one. Finally, Section V concludes this article.
The strong form of the ⃗ A * -formulation [9] of the nonlinear MQS problem reads
where t indicates the time, ⃗ r the position vector, σ the conductivity, ν the reluctivity, ⃗ J s the source current density, and the unknown ⃗ A is the magnetic vector potential. The magnetic flux density ⃗ B can be computed as ⃗ B = ∇ × ⃗ A and is related to the magnetic field strength ⃗ H via ⃗ H = ν ⃗ B. The reluctivity depends on time since it depends on the solution due to the nonlinearity of the B-H curve. Note that we only consider non-hysteretic B-H curves throughout this work.
To numerically approximate the solution of Eq. ( 1), the corresponding weak formulation is discretized in space with edge elements according to the FE method [10].
To avoid costly time-stepping of the discretized problem, the HBFEM transforms the problem into frequency domain and uses a multiharmonic approach to account for the nonlinearity. This approach approximates the solution with a Fourier series truncated at a certain maximum harmonic order m ∈ N, leading to the complex-valued system of equations min{m,n+m} k=max{-m,n-m} [11]. In this equation, ω f is the fundamental angular frequency, ⌢ a n is the vector gathering the DoFs of the n-th harmonic of the magnetic vector potential, ⌢ ⌢ j s,n is the discretized n-th harmonic of the source current density, M σ is the mass matrix, and K ν k denotes the stiffness matrix computed with the k-th harmonic of the reluctivity. We indicate that each
This content is AI-processed based on open access ArXiv data.