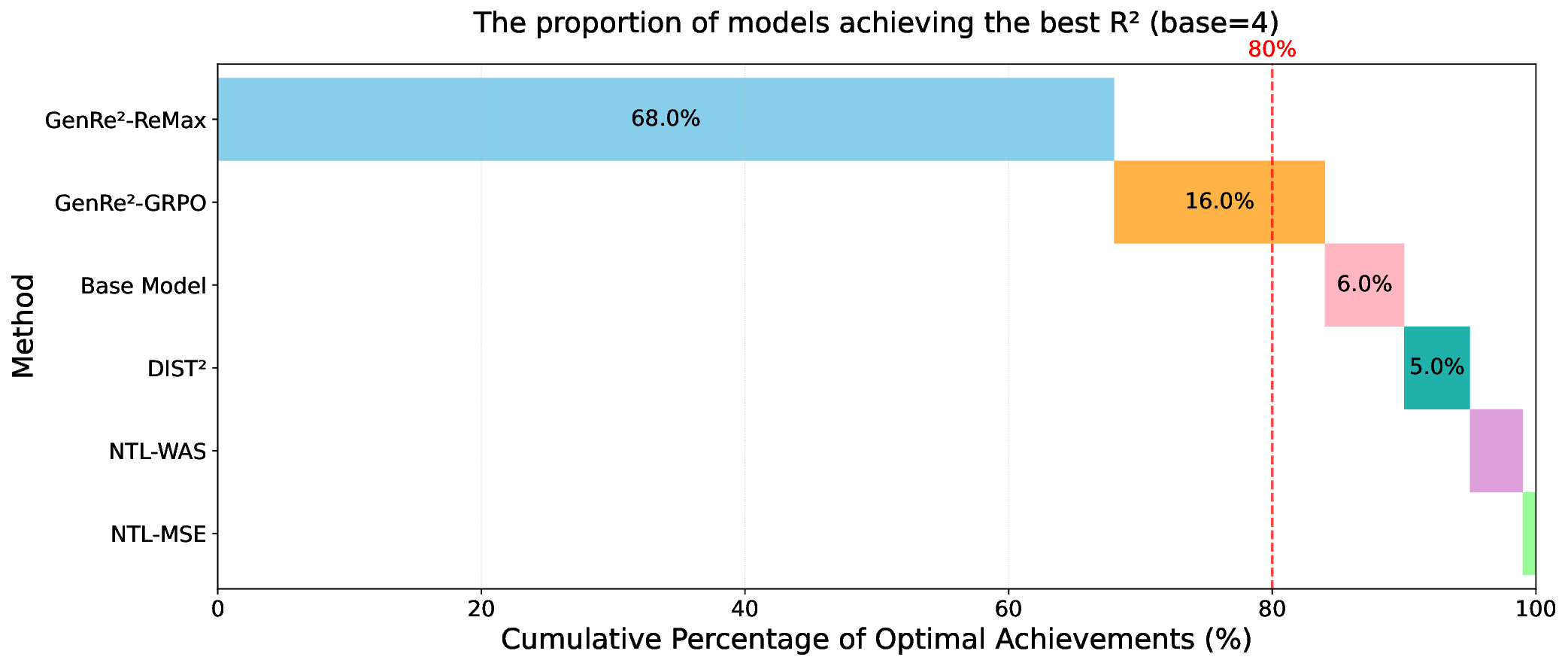
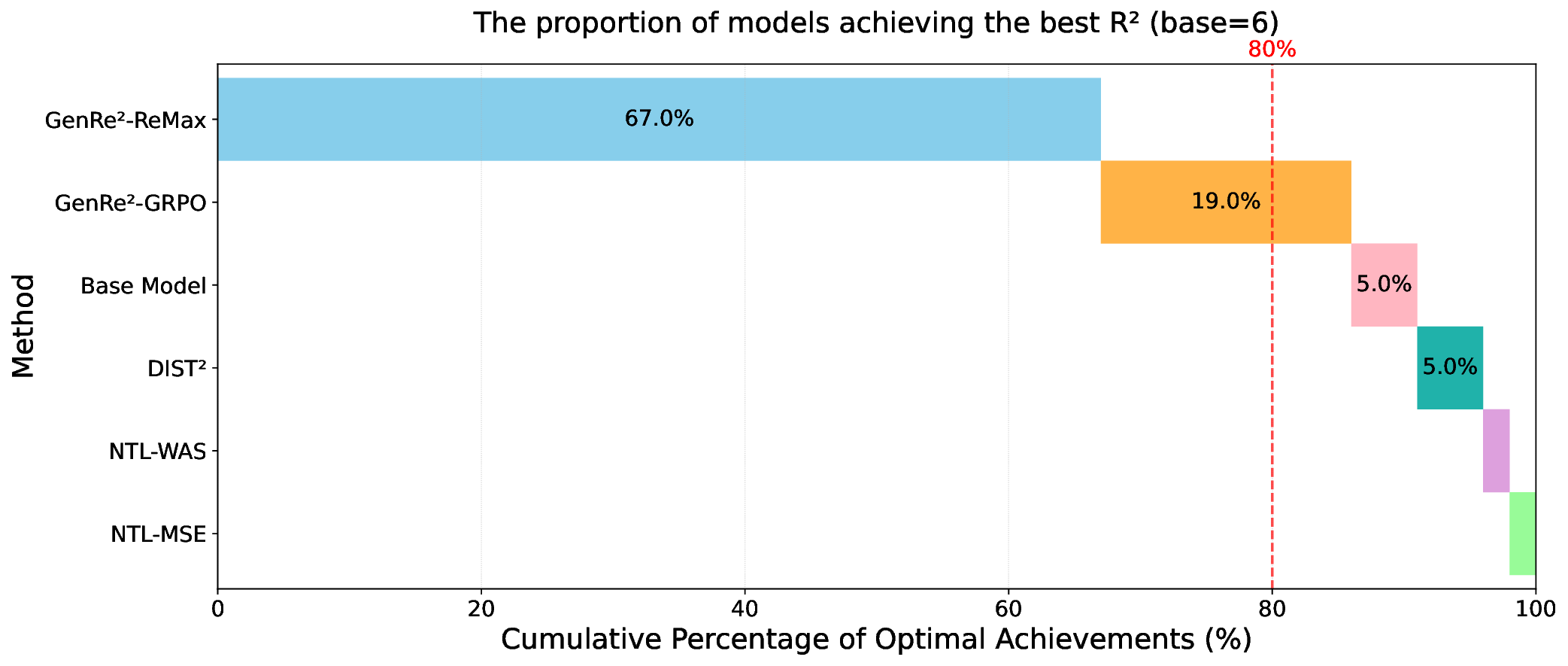
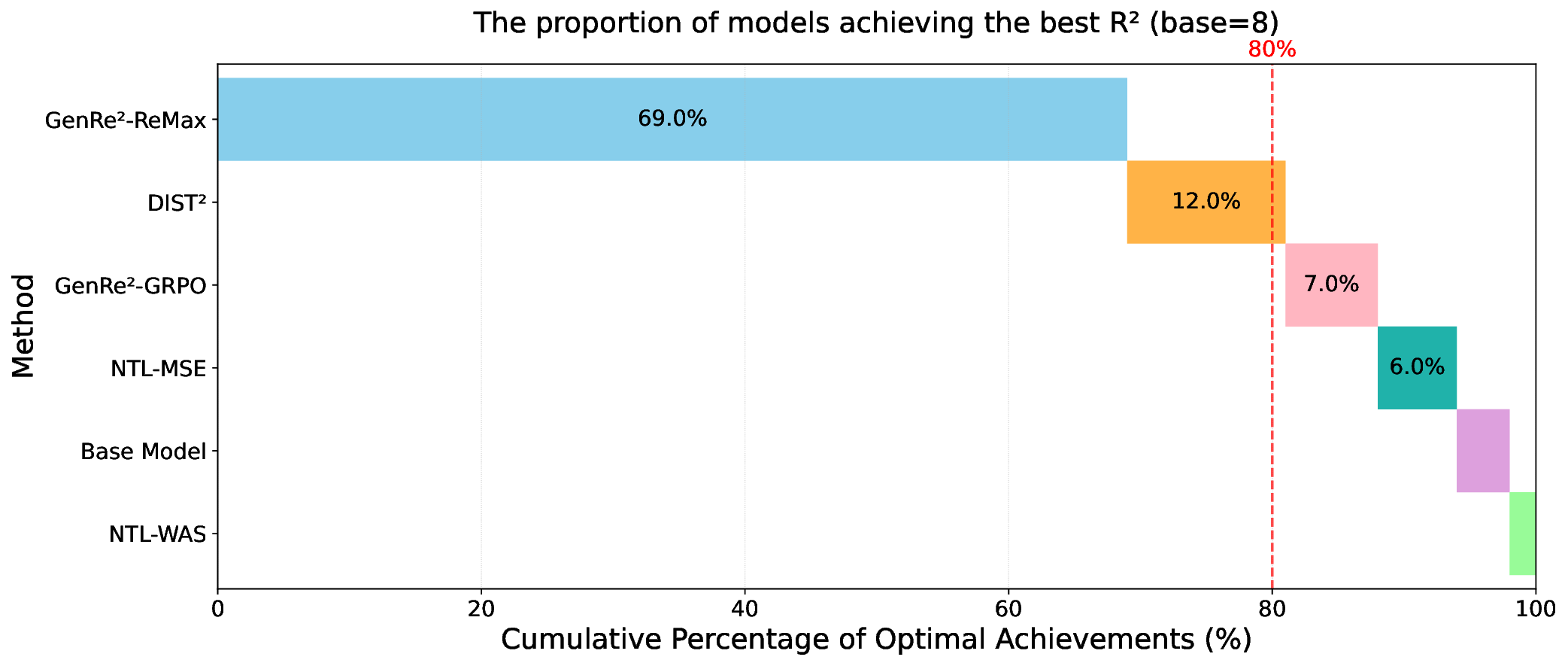
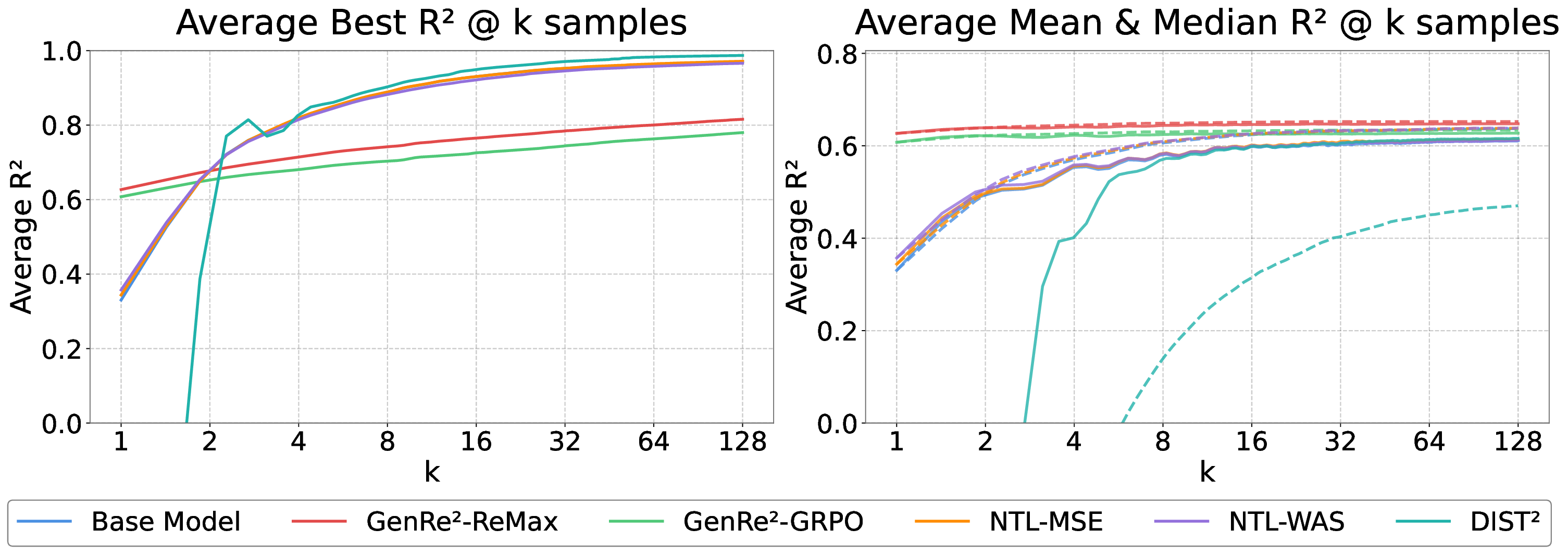
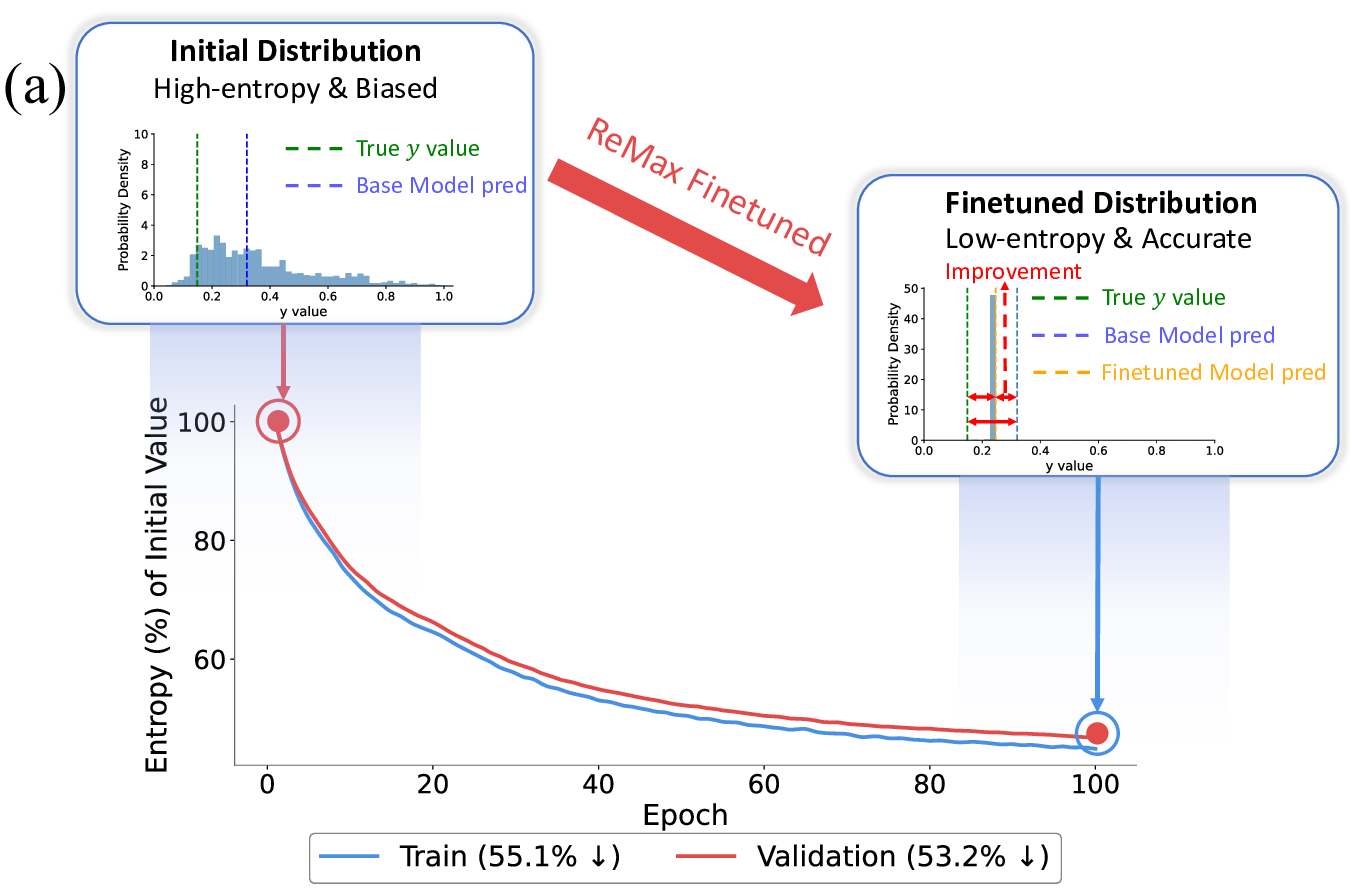
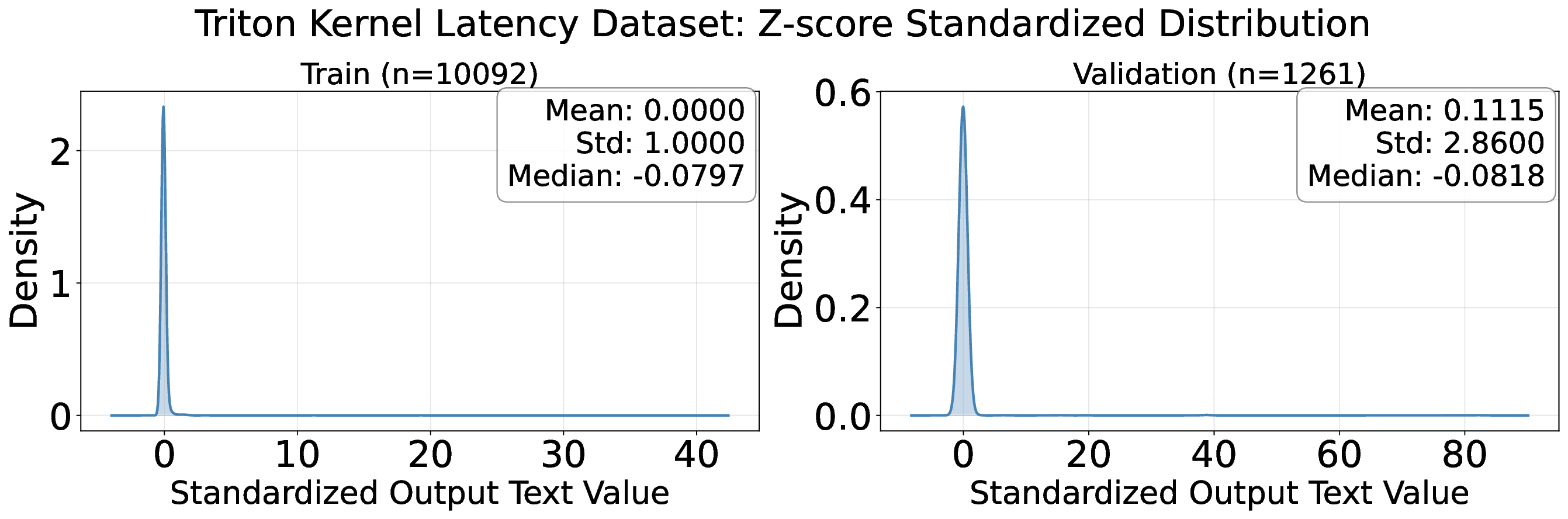
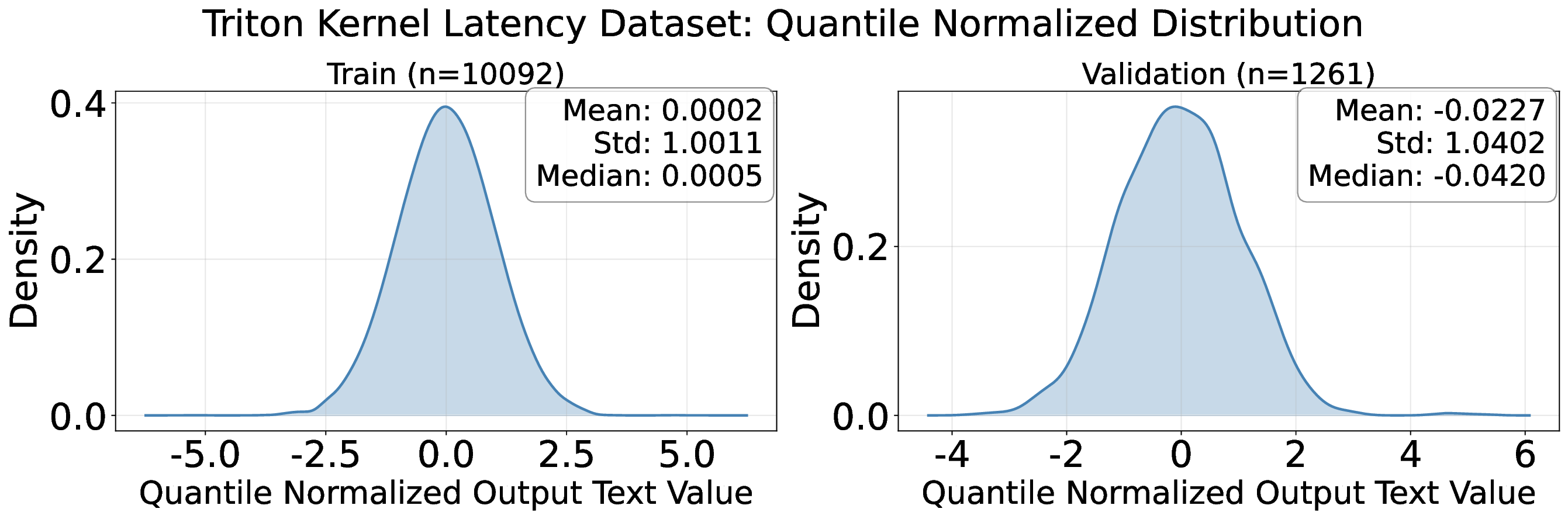
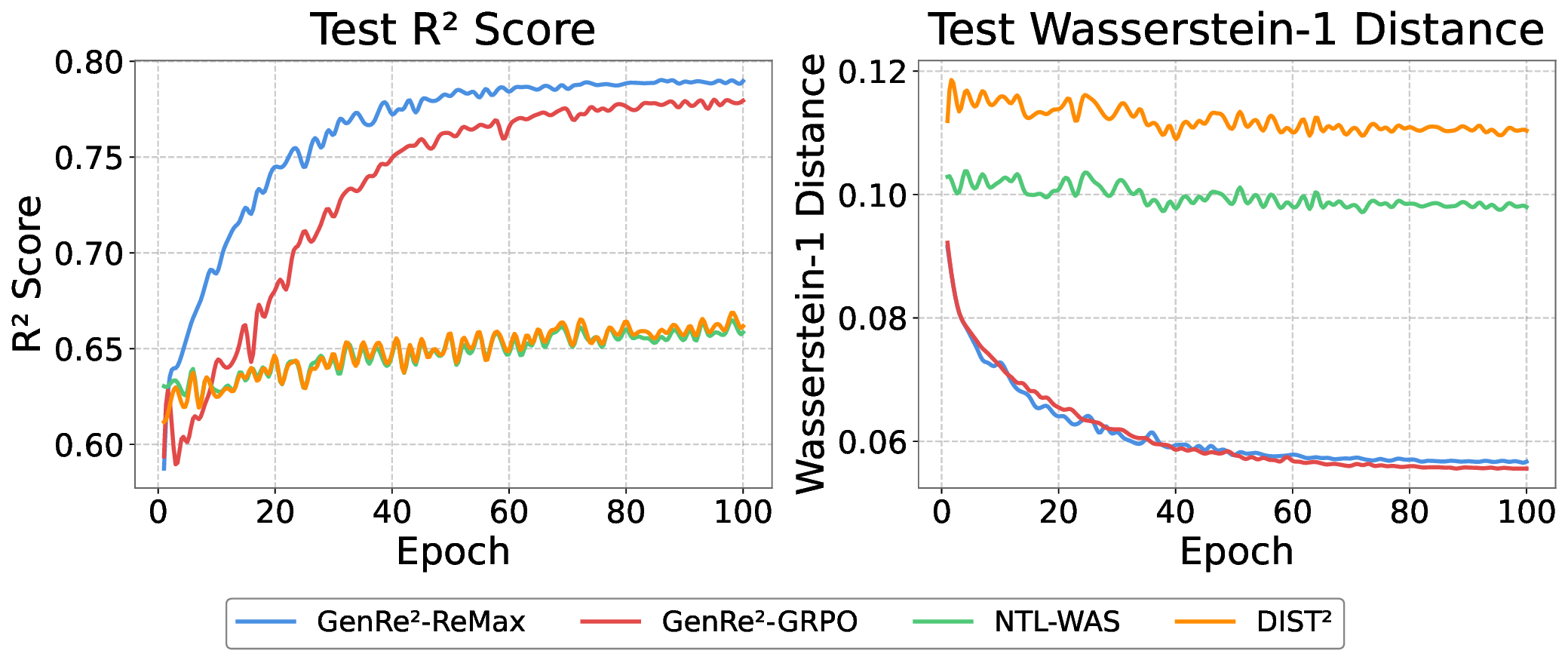
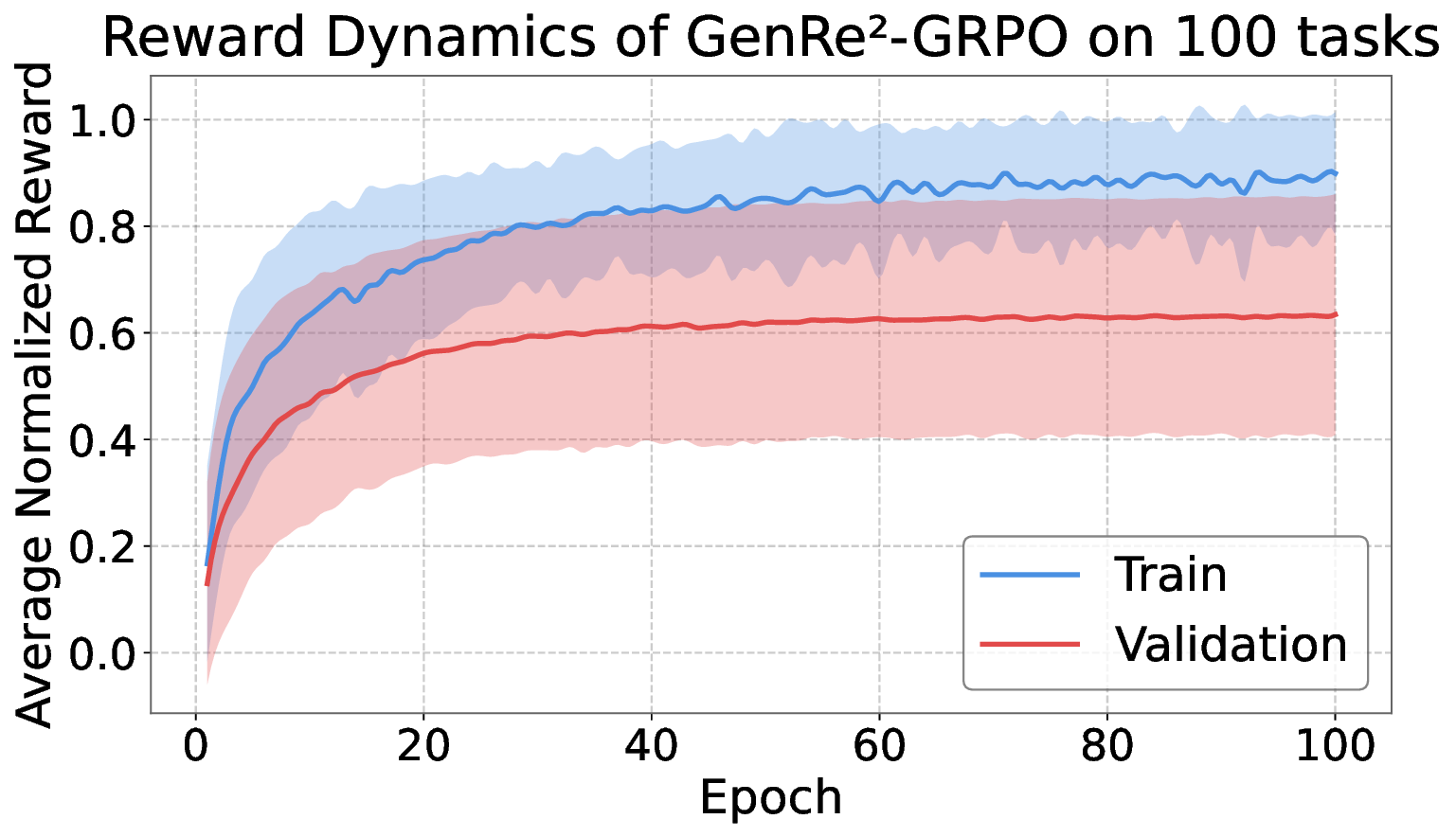
Decoding-based regression, which reformulates regression as a sequence generation task, has emerged as a promising paradigm of applying large language models for numerical prediction. However, its progress is hindered by the misalignment between discrete token-level objectives (e.g., cross-entropy) and continuous numerical values. Existing approaches relying on token-level constraints often fail to capture the global magnitude of the target value, limiting their precision and generalization. In this paper, we propose to unlock the potential of decoding-based regression via Reinforcement Learning (RL). We formulate the generation process as a Markov Decision Process, utilizing sequence-level rewards to enforce global numerical coherence. Extensive experiments on tabular regression and code metric regression demonstrate that our method (specifically with ReMax and GRPO) consistently outperforms both state-of-the-art token-level baselines and traditional regression heads, showing the superiority of introducing sequence-level signals. Our analysis further reveals that RL significantly enhances sampling efficiency and predictive precision, establishing decoding-based regression as a robust and accurate paradigm for general-purpose numerical prediction.
Regression, the task of predicting continuous targets from input representations, stands as a fundamental role of machine learning (Bishop, 2006;Van Breugel & Van Der Schaar, Preprint. Working in progress. 2024), with wide applications across critical domains ranging from scientific discovery (Hu et al., 2024) to industrial scenarios (He et al., 2025). Traditional regression methods, including Gaussian Processes (Rasmussen & Williams, 2006) and tree-based models (Chen & Guestrin, 2016;Prokhorenkova et al., 2018), excel due to their robustness and interpretability (Sahakyan et al., 2021). However, with the advent of the deep learning era and the increasing complexity of data, there has been a paradigm shift towards deep-learning (DL) based regressors (Jiang et al., 2025;Ye et al., 2024). These methods leverage the power of representation learning to map high-dimensional inputs into latent spaces, subsequently modeling the target value through specialized regression heads.
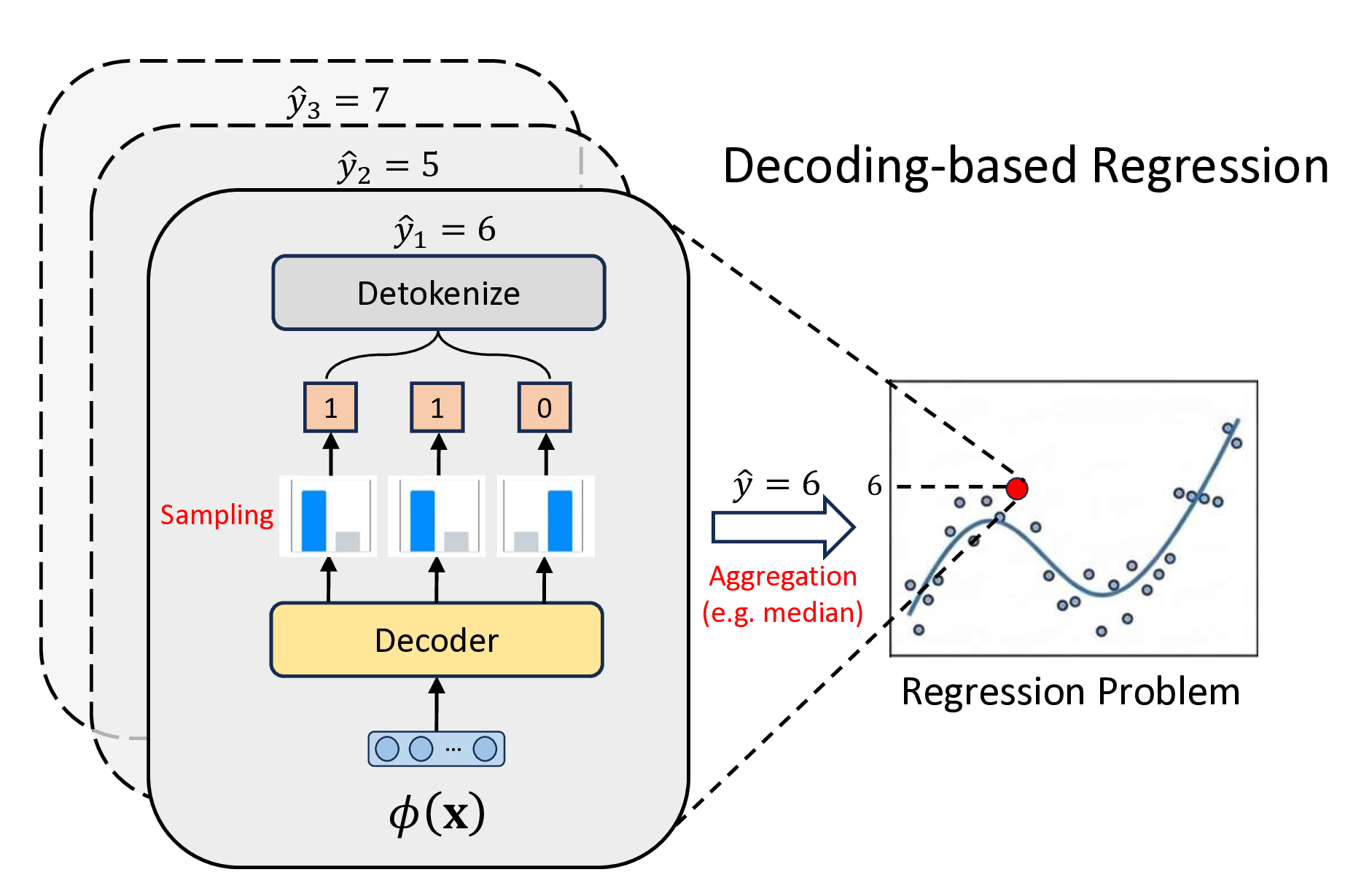
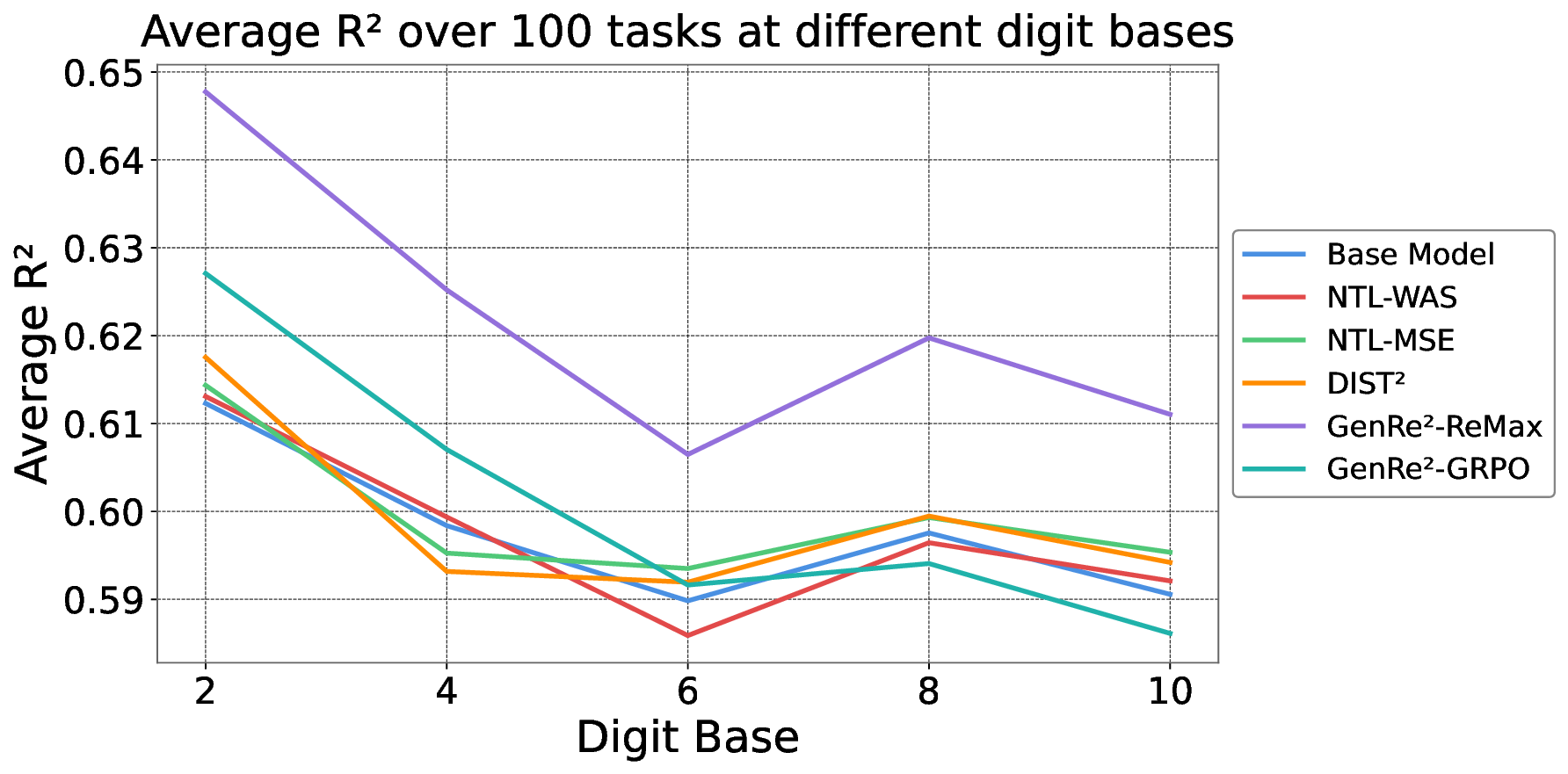
For DL-based regressors, there have been some design philosophies of regression heads to map latent representations to continuous targets. The most common approach, the pointwise head, projects representations directly to a scalar but often fails to capture the uncertainty or the complex multimodality of the target distribution (Lakshminarayanan et al., 2017). To address this, parametric distribution heads model outputs as predefined distributions (e.g., Gaussian), yet they rely on rigid assumptions that may not hold in real-world scenarios (Imani & White, 2018). Alternatively, the Riemann head (or histogram head) discretizes the continuous output into finite bins, converting regression into classification (Bellemare et al., 2017;Imani & White, 2018), showing great robustness (Imani et al., 2024) and performance (Müller et al., 2022). However, these methods primarily operate on structured data, limiting their ability to perform regression on the vast and diverse spectrum of unstructured data (e.g., text or code). This limitation has motivated recent studies to leverage Large Language Models (LLMs) for universal regression (Vacareanu et al., 2024;Song et al., 2024;Tchuindjo & Khattab, 2025). A key development in this line of work is decoding-based regression (Song & Bahri, 2025), which reformulates regression as a discrete sequence generation task and can be trained over large amounts of regression data (x, y) represented as text. As illustrated in Figure 1, this approach reformulates regression as a next-token prediction task by tokenizing continuous values (e.g., via base-B passes through an encoder to produce the representation ϕ(x), which is then processed by a decoder. The model performs multiple sampling trials to generate several discrete token sequences (e.g., the binary representation <1><1><0>). These sequences are individually detokenized into corresponding scalar values (shown in the stacked layers as ŷ1 = 6, ŷ2 = 5, ŷ3 = 7). Finally, these scalar values are combined via an aggregation strategy (e.g., median) to produce the final prediction ŷ = 6.
expansion). Unlike traditional scalar regressors, decodingbased regression not only can handle unstructured raw data, but also leverages the strong sequential modeling capabilities of Transformers to capture complex distributions (Song et al., 2024). Furthermore, the generative approach of decoding-based regression mitigates the susceptibility to reward hacking often seen in scalar or histogram baselines (Chen et al., 2024;Yu et al., 2025), producing more robust and calibrated predictions, which align with the recent observations from generative reward models (Mahan et al., 2024;Zhang et al., 2025c). The concept of decodingbased regression gives rise to Regression Language Model (RLM) (Song et al., 2024), which demonstrates great potential in diverse applications ranging from industrial prediction (Akhauri et al., 2025a;b) to black-box optimization (Nguyen et al., 2024;Tan et al., 2025).
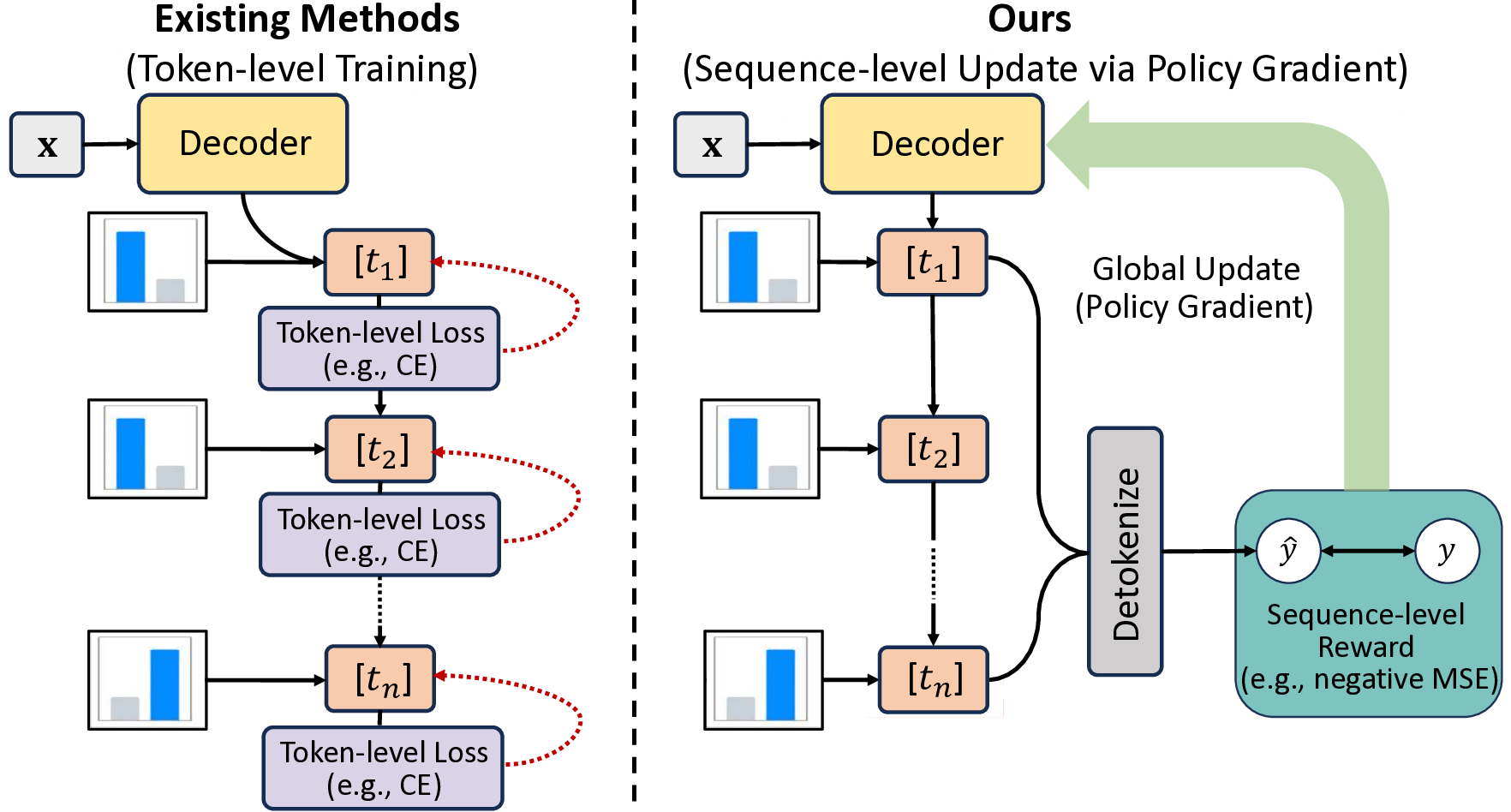
However, despite its promise, the potential of decodingbased regression remains unlocked. The critical barrier lies in the misalignment between the widely used Cross-Entropy (CE) loss and the numerical nature of the regression task (Lukasik et al., 2025). CE treats tokens as independent categories, ignoring their ordinal value and the entire magnitude of the detokenized number. While recent works have attempted to mitigate this via token-level distance penalties, e.g., NTL (Zausinger et al., 2025) and DIST 2 (Chung et al., 2025), a fundamental limitation remains: these methods operate locally on individual tokens and overlook the cumulative error over the entire sequence (Selvam, 2025), which can lead to catastrophic outcomes in the original numerical space (Song et al., 2024;Song & Bahri, 2025). Thus, there is an urgent need for a method that is inherently aware of sequence-level numerical magnitude.
In this paper, we propose Generative Reinforced Regressor (GenRe 2 ) to bridge this gap. We reformu
This content is AI-processed based on open access ArXiv data.